Partial Differential Equations Toolbox. Инструментарий решения дифференциальных уравнений в частных производных
Пособие содержит описание основных инструментальных средств и функций PDE Toolbox MATLAB. PDE Toolbox является средством решения задач математической физики в двумерной расчетной области. Пособие предназначено для студентов математических и технических специальностей, а также аспирантов, инженеров, научных работников.
Автор - В.Е.Шмелев.
Содержание
1. Конечноэлементная технология решения задач математической физики
1.1. Конечноэлементная аппроксимация. Понятие о функциях формы
1.2. Проекционная формулировка конечноэлементных методов
1.2.1. Математическая основа проекционных методов
1.2.2. Метод Галеркина с конечными элементами
1.2.3. Применение метода Галеркина с конечными элементами к эллиптическому PDE
2. Работа пользователя с GUI-приложением PDE Toolbox Matlab
2.1. Команды меню приложения PDETool
2.2. Инструментальная панель PDETool
2.3. Список стандартных краевых задач PDETool
2.3.3. Механические напряжения в упругой среде с изотропными линейными свойствами
2.3.4. Перемещения в упругой напряжённо-деформированной среде с изотропными линейными свойствами
2.3.5. Электростатическая задача
2.3.6. Магнитостатическая задача
2.3.7. Переменное гармоническое электромагнитное поле
2.3.8. Стационарное электрическое поле в проводящей среде
2.4. Режимы работы приложения PDETool
2.4.1. Режим ввода (прорисовки) геометрии
2.4.2. Режим ввода граничных условий
2.4.3. Режим ввода параметров (коэффициентов) PDE
2.4.4. Режим генерации и изменения конечноэлементной сетки
2.4.5. Режим решения PDE-задачи
2.5. Визуализация решения краевой задачи
2.5.1. Визуализация решения скалярных эллиптических PDE
2.5.2. Визуализация решения стационарных краевых задач других типов
2.5.3. Визуализация решения нестационарных краевых задач
2.6. Сохранение PDE–модели в виде m-файла
3. Состав графического интерфейса пользователя PDE Toolbox Matlab
3.2. Свойства объектов axes
3.2.1. Свойства объекта axes PDEAxes
3.2.2. Свойства объекта axes draw
3.2.3. Свойства объекта axes solve
3.2.4. Свойства объекта axes zoom
3.3. Свойства объектов uimenu
3.3.1. Свойства uimenu PDEFileMenu и подчинённых объектов
3.3.2. Свойства uimenu PDEEditMenu и подчинённых объектов
3.3.3. Свойства uimenu PDEOptMenu и подчинённых объектов
Введение
Большинство физических процессов, происходящих в природе и технике, описывается дифференциальными уравнениями. Различают обыкновенные дифференциальные уравнения (ОДУ, ODE) и дифференциальные уравнения в частных производных (PDE), которые иначе называются уравнениями математической физики. Первые, как правило, описывают процессы в устройствах и системах с сосредоточенными параметрами. Вторые описывают процессы в системах с пространственно–распределёнными параметрами. Важнейшим частным случаем таких систем являются физические поля.
С философской точки зрения поле – это невещественный вид материи, оказывающий силовое воздействие на вещественные тела и определяемый в каждой точке физического пространства некоторым множеством скалярных, векторных, тензорных, матричных и других величин. С математической точки зрения поле – это функция пространства и времени. Причём, как было сказано выше, распределение значений этой функции может носить скалярный, векторный, тензорный, матричный характер; значением функции может быть математический объект сложной структуры.
Пакет Partial Differential Equation (PDE) содержит средства для численного моделирования нестационарных физических полей, описываемых уравнениями в частных производных второго порядка. В пакете используется проекционный метод Галёркина с конечными элементами [1, 2, 3]. Команды и графический интерфейс пакета могут быть использованы для математического моделирования физических полей в двумерной расчётной области применительно к широкому классу инженерных и научных приложений, включая задачи сопротивления материалов, расчёты электромагнитных устройств, задачи тепломассопереноса и диффузии [4].
Основные свойства PDE Toolbox MATLAB:
-
Полноценный графический интерфейс для обработки PDE второго порядка
-
Автоматический и адаптивный выбор конечноэлементной сетки
-
Задание граничных условий: Дирихле, Неймана и смешанные
-
Гибкая постановка задачи с использованием синтаксиса языка MATLAB
-
Полностью автоматическое сеточное разбиение и выбор величины конечных элементов
-
Нелинейные и адаптивные расчётные схемы
-
Возможность визуализации полученного в ходе решения PDE распределения требуемых физических величин, демонстрация принятого разбиения и анимационные эффекты.
Примечание. Векторные величины и поля будут обозначаться жирным шрифтом. В математических выражениях обычная операция умножения (умножение матриц, скалярное произведение векторов, внутреннее произведение тензоров любой валентности с одинарным поглощением индексов, умножение нескалярных математических объектов на скаляр) будет обозначаться значком * (звёздочка) или отсутствием знака операции. Векторное произведение будет обозначаться ** (две звёздочки подряд). Эти обозначения введены для того, чтобы форматированные формулы корректно обрабатывались любым текстовым конвертором и отпадала необходимость вводить в текст объекты Equation Editor. Минимизация в тексте количества таких объектов существенно сэкономит память и позволит читать данный документ на маломощных компьютерах.
1. Конечноэлементная технология решения задач математической физики
Для решения PDE задачи всю расчётную область представляют в виде совокупности неперекрывающихся геометрических фигур достаточно простой формы. Размеры таких фигур как правило бывают малы по сравнению с размерами расчётной области. Эти элементарные фигуры называют конечными элементами. Трёхмерные расчётные области обычно разбивают на многогранники, а двумерные – на многоугольники. Простейшие многогранники (прямолинейные четырёхузловые тетраедры) и простейшие многоугольники (прямолинейные трёхузловые треугольники) называют симплекс-элементами. Вся совокупность конечных элементов в расчётной области называется конечноэлементной сеткой. Вершины этих многогранников или многоугольников называют узлами конечноэлементной сетки.
Пусть в результате расчёта известно узловое распределение некоторой физической величины. Для простоты будем полагать, что эта величина скалярная. Обозначим её латинской буквой u. Узловое распределение этой величины может быть описано столбцовой матрицей, которую обозначим [u(у)]. В этой матрице каждой строке соответствует узел конечноэлементной сетки. Распространение узлового распределения на все возможные точки расчётной области называют конечноэлементной аппроксимацией. В общем случае конечноэлементное аппроксимирующее выражение имеет вид [1, 2, 3]:
u(Q) = [N](Q)*[u(у)] , (1.1)
где Q – точка наблюдения, имеющая свои координаты;
[N](Q) – матрица-строка функций формы.
В пределах отдельно взятого конечного элемента:
u(Q) = [N(e)](Q)*[u(e)] , (1.2)
где [N(e)](Q) – матрица-строка функций формы конечного элемента;
[u(e)] – узловое распределение физической величины в пределах конечного элемента.
Функции формы – это функции “интерполяционной природы” [1, 2, 3], обладающие следующими свойствами:
-
Ni(Qi) = 1;
-
Ni(Qj) = 0;
-
Ni(Qk) = 0;Nj(Qk) = 0;
-
Ni(Q) = в общем случае любое значение,
но для симплекс-элементов Ni(Q) I [0;1] .
Здесь обозначено: i, j – номера узлов некоторого конечного элемента; Qi, Qj – узлы конечного элемента; Qk – точка, не принадлежащая конечному элементу; Q – точка, принадлежащая конечному элементу; Ni – скалярное поле, называемое функцией формы i-го узла; Nj – скалярное поле, называемое функцией формы j-го узла.
PDE Toolbox Matlab поддерживает только симплекс-элементы, для которых характерны линейные функции формы:
[N(e)](Q) = [a] + [ax]*x + [ay]*y ,
где x, y – координаты точки наблюдения Q;
[a], [ax], [ay] – матрицы-строки коэффициентов функций формы конечного элемента, которые в соответствии со свойствами 1 – 4 вычисляются по формуле:
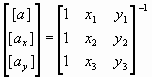 ,
,
где 1,2,3 – локальные номера узлов конечного элемента (далее для краткости – просто “элемента”).
Функции формы позволяют легко определять в пределах каждого элемента пространственные дифференциальные операторы первого порядка от скалярного или векторного поля по известному узловому распределению
grad u = grad [N(e)] * [u(e)]; div A = grad [N(e)] * [A(e)]; rot A = grad [N(e)] ** [A(e)],
где [A(e)] – узловое распределение векторного поля A в пределах элемента;
grad [N(e)] = [ax]*1x + [ay]*1y ;
1x , 1y – единичные базисные векторы (орты) декартовой системы координат.
1.2. Проекционная формулировка конечноэлементных методов
Существует вариационная и проекционная формулировка конечноэлементных методов. PDE Toolbox Matlab поддерживает только проекционную формулировку. Проекционные конечноэлементные методы являются частным случаем методов взвешенных невязок.
1.2.1. Математическая основа проекционных методов
Пусть в N-мерной области G евклидова пространства EN необходимо рассчитать распределение некоторой физической величины, которое описывается дифференциальным уравнением в частных производных (PDE):
L u – f = 0 , x ![]() G (1.3)
G (1.3)
с граничными условиями
LГ u = f Г , x ![]() Г ,
Г ,
где u=u(x) – анализируемая физическая величина; x – точка пространства EN ,
L и LГ – дифференциальные операторы; Г – граница области G; функции f, f Г описывают распределение внутренних и граничных источников исследуемого поля.
Рассмотрим пространство M функций, определённых на области G, такое, что если u1(x) ![]() M , u2(x)
M , u2(x) ![]() M , то
M , то
u3(x) = a1u1(x)+a2u2(x) ![]() M (любая линейная комбинация функций, принадлежащих пространству M, также принадлежит пространству M). Введём скалярное произведение функций:
M (любая линейная комбинация функций, принадлежащих пространству M, также принадлежит пространству M). Введём скалярное произведение функций:
(u,v) = ![]() dG ,
dG ,
тогда нормой функции u I M будем называть неотрицательное число
||u|| = (u,u)1/2 , расстоянием между функциями u и v будем называть величину, равную норме ||u–v||. Такое пространство M называется гильбертовым пространством [5].
Методы взвешенных невязок (проекционные методы) [1, 6] можно разделить на три большие группы:
1) граничные методы (если приближённое решение точно удовлетворяет дифференциальному уравнению);
2) внутренние методы (когда приближённое решение точно удовлетворяет граничным условиям);
3) смешанные методы (не удовлетворяются ни граничные условия, ни дифференциальное уравнение).
К граничным методам можно отнести метод Трефца, методы граничных элементов и др. [5, 7, 8, 9].
Рассмотрим некоторые внутренние методы. Введём невязку приближённого решения ua дифференциального уравнения (1.3): R = L ua – f . Приближённое решение ua представим в виде:
ua(x) = u0(x) + ![]() ,
,
где ![]() – известные аналитические функции, которые часто называют пробными; ai – коэффициенты, которые подлежат определению; u0(x) выбирается так, чтобы функция ua по возможности наиболее точно удовлетворяла граничным условиям. Уравнения для определения коэффициентов ai можно получить исходя из условия:
– известные аналитические функции, которые часто называют пробными; ai – коэффициенты, которые подлежат определению; u0(x) выбирается так, чтобы функция ua по возможности наиболее точно удовлетворяла граничным условиям. Уравнения для определения коэффициентов ai можно получить исходя из условия:
(R,wk(x))=0, где k = 1, …, N’ ;
wk(x) называется весовой, или поверочной функцией. В соответствии с выбором вида функций wk(x) различают метод подобластей, метод коллокаций, метод наименьших квадратов, метод Галёркина (когда в качестве весовых функций берутся пробные: wk(x)=![]() ) и другие [6].
) и другие [6].
1.2.2. Метод Галеркина с конечными элементами
Важное место среди вариационных и проекционных методов занимают конечноэлементные методы (методы конечных элементов (МКЭ)) [1, 2, 3, 6]. Рассмотрим краевую задачу (1.3) для трёхмерной односвязной области Vс границей S. Пусть область V+S пространственно дискретизована: будем считать, что она “натянута” на Mузлов с фиксированными координатами xi, yi, zi, i=1, … M. Тогда конечноэлементная аппроксимация приближённого решения ua краевой задачи (1.3) имеет вид (1.1).
Пусть поверхность S состоит из двух частей: S=S1+S2. Пусть на части граничной поверхности S1 задано распределение искомой величины u:
u = поверхностное распределение, (1.4)
а на части граничной поверхности S2 задано распределение нормальной или тангенциальной составляющей некоторого дифференциального оператора распределения искомой величины u:
n*LГ u или n**LГ u = поверхностное распределение. (1.5)
(1.4) называются граничными условиями первого рода (условиями Дирихле), (1.5) – граничными условиями второго рода (условиями Неймана). При решении PDE (1.3) граничные условия первого рода удовлетворяются путём задания соответствующих значений величины u в граничных узлах.
Если использовать метод Галёркина применительно к аппроксимации (1.1), то дифференциальное уравнение (1.3) преобразуется в интегральное матричное уравнение относительно узловых значений искомой величины:
![]() L ([N]*[u(у)]) dV =
L ([N]*[u(у)]) dV = ![]() f dV . (1.6)
f dV . (1.6)
Матрица [u(у)] может быть вынесена за знак объёмного интеграла справа. Если дифференциальный оператор Lсодержит порядка z , то необходимо гарантировать кусочную дифференцируемость производных порядка z –1 от используемых функций формы [N] [1], иначе в точках их разрыва производные порядка z будут неограничены, что приведёт к появлению неопределённостей в интегралах, содержащихся в (1.6).
В [1] показано, что интеграл в левой части (1.6) может быть заменён выражением вида
![]() *(D [N]) dV*[u(у)] +
*(D [N]) dV*[u(у)] + ![]() dS ,
dS ,
где операторы E и D имеют более низкий порядок дифференцирования, чем исходный оператор L. Такая замена даёт возможность понизить требования к гладкости функций формы [N].
Модифицированное таким образом уравнение (1.6) можно преобразовать в алгебраическое матричное уравнение вида [K]*[u(у)] = [F] . Для выполнения такого преобразования интегралы в модифицированном уравнении (1.6) можно вычислять путём суммирования по конечным элементам. Однако поверхностные интегралы по внутренним границам элементов в сумме должны обращаться в нуль (если в расчётной области отсутствуют поверхностные источники моделируемого поля), иначе данное интегральное преобразование не будет иметь смысла. Если функции формы имеют полиномиальный вид, то объёмные интегралы могут быть вычислены аналитически [10 и др.]. Однако для элементов высокого порядка, как правило, используется численное интегрирование. Аналитическое интегрирование приводит к существенной экономии вычислительных ресурсов, однако на практике мало применяется из-за трудности получения расчётных формул и усложнения программирования.
Как и в конечно-разностных методах, основным свойством получаемых систем алгебраических уравнений является ленточная или профильная структура матрицы коэффициентов (матрицы “жёсткости” [2]), а также слабая заполненность внутри ленты или профиля. Поэтому для хранения таких систем в памяти ЭВМ используют технологию разреженных матриц [11, 12, 13]. Прямым методам технологии разреженных матриц свойственно заполнение матриц в процессе факторизации. Поэтому наряду с прямыми применяются также итерационные методы. Прямые и итерационные методы реализованы в ядре MATLAB в виде операций и функций над разреженными матрицами.
1.2.3. Применение метода Галеркина с конечными элементами к эллиптическому PDE
Большинство стационарных скалярных задач математической физики второго порядка может быть сведено к решению эллиптического уравнения в частных производных:
–div(c*grad(u)) + a*u = f . (1.7)
Для простоты будем полагать, что (1.7) записано относительно скалярного поля u, коэффициенты c и a также скалярные. Пусть коэффициенты c и a распределены в расчётной области неравномерно. Применение метода Галёркина с конечными элементами к уравнению (1.7) даёт следующее интегральное уравнение:
![]() (–div(c*grad(u)) + a*u) dV =
(–div(c*grad(u)) + a*u) dV = ![]() f dV , (1.8)
f dV , (1.8)
Чтобы понизить порядок дифференциального оператора в левой части (1.8), нужно матрицу-столбец весовых функций, равных функциям формы, загнать под знак дивергенции:
![]() div([N]T*c*grad(u)) dV +
div([N]T*c*grad(u)) dV + ![]() grad[N]T*c*grad(u) + [N]T a*u) dV =
grad[N]T*c*grad(u) + [N]T a*u) dV = ![]() f dV .
f dV .
Применим теорему о дивергенции к первому интегралу последнего уравнения, перенесём его в правую часть и применим конечноэлементную аппроксимацию (1.1) к искомому полю u:
![]() grad[N]T*c*grad[N] + [N]T a [N]) dV*[u(у)] =
grad[N]T*c*grad[N] + [N]T a [N]) dV*[u(у)] = ![]() f dV +
f dV + ![]() *c*grad(u)*dS
*c*grad(u)*dS
или короче [K]*[u(у)] = [F] , (1.9)
где [K] = ![]() grad[N]T*c*grad[N] + [N]T a [N]) dV – глобальная матрица коэффициентов (матрица “жёсткости” [2]);
grad[N]T*c*grad[N] + [N]T a [N]) dV – глобальная матрица коэффициентов (матрица “жёсткости” [2]);
[F] = ![]() f dV +
f dV + ![]() *c*grad(u)*dS – глобальная матрица-столбец правой части (матрица “нагрузок”).
*c*grad(u)*dS – глобальная матрица-столбец правой части (матрица “нагрузок”).
При выполнении расчётов глобальное матричное уравнение (1.9) формируется путём накопления при рассмотрении всех конечных элементов:
[K] = ![]() ; [F] =
; [F] = ![]() ,
,
где [K(e)] =![]() grad[N(e)]T*c*grad[N(e)] + [N(e)]T a [N(e)]) dV – локальная (элементная) матрица коэффициентов;
grad[N(e)]T*c*grad[N(e)] + [N(e)]T a [N(e)]) dV – локальная (элементная) матрица коэффициентов;
[F(e)] =![]() f dV – элементная матрица правой части;
f dV – элементная матрица правой части;
[F(Гe)] =![]() *c*grad(u)*dS – граничноэлементная матрица правой части;
*c*grad(u)*dS – граничноэлементная матрица правой части;
V(e) – объём конечного элемента;
S(e) – поверхностный элемент границы расчётной области,
dS – векторный дифференциал площади граничной поверхности (понятие о векторе площади поверхности см. в [14]). Если распределение скалярных коэффициентов c, a и источника поля f можно аппроксимировать кусочно-однородным (постоянным в пределах каждого элемента) распределением, то c, a, f можно выносить за знаки соответствующих элементных интегралов.
Поверхностный интеграл в правой части (1.9) соответствует граничным условиям Неймана (1.5)
n*c*grad(u) = поверхностное распределение.
При реальных расчётах эти граничные условия могут быть учтены путём вычисления данного поверхностного интеграла при рассмотрении соответствующих граничных элементов (граничными элементами называются грани конечных элементов, принадлежащие границе расчётной области). Граничные условия Дирихле (1.4) учитываются путём задания соответствующих значений величины u в граничных узлах. Задание значений в некоторых узлах конечноэлементной сетки осуществляется путём модификации матриц [K] и [F] [2]. При расчётах такая модификация производится в последнюю очередь непосредственно перед решением матричного уравнения (1.9).
При моделировании плоскопараллельных полей объёмные интегралы в (1.9) можно заменить на двумерные, а поверхностные – на криволинейные, учитывая, что
dV = z dU, dS = z dl**1z ,
и z можно сократить в левой и правой части (1.9). Здесь dU – дифференциал двумерной расчётной области в плоскости z=const, dl – векторный дифференциал длины границы расчётной области. Как было сказано выше, PDE Toolbox MATLAB поддерживает только симплекс–элементы и только двумерные краевые задачи. В связи с этим формулы для вычисления элементных матриц, соответствующих эллиптическому PDE (1.7), имеют вид:
[K(e)] = 0,5 c(e) ![]() (e)*([ax]T [ax] + [ay]T [ay]) + a(e)
(e)*([ax]T [ax] + [ay]T [ay]) + a(e) 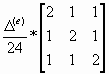 ;
;
[F(e)] = f(e) 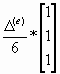 ;
;
[F(Гe)] = ![]() =
= ![]() *|
*|![]() l(Гe)|*
l(Гe)|* ![]() , (1.10)
, (1.10)
где c(e), a(e), f(e) – постоянные значения параметров уравнения (1.7) в пределах конечного элемента;
![]() (e) – определитель элемента, равный его удвоенной площади;
(e) – определитель элемента, равный его удвоенной площади;
![]() l(Гe) =
l(Гe) = ![]() x(Гe)*1x +
x(Гe)*1x + ![]() y(Гe)*1y – вектор длины граничного элемента;
y(Гe)*1y – вектор длины граничного элемента;
b(Гe) = ![]() *1x +
*1x + ![]() *1y = c*grad(u) – постоянное значение вектора в пределах граничного элемента (в соответствии с заданными граничными условиями Неймана).
*1y = c*grad(u) – постоянное значение вектора в пределах граничного элемента (в соответствии с заданными граничными условиями Неймана).
Формулы (1.10) следуют из соотношений, свойственных двумерным симплекс-элементам [2]:
![]() ;
; ![]() ,
,
где L – отрезок прямой, l – его длина; a, b, c – произвольные целые числа >=0;
![]() (e) = det
(e) = det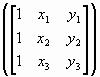 .
.
Грубо говоря, конечноэлементная технология решения задач математической физики сводится к вычислению элементных матриц, соответствующих заданному PDE, сборке из них глобального матричного уравнения, решению этого уравнения и анализу узлового распределения искомой величины.
2. Работа пользователя с GUI-приложением PDE Toolbox Matlab
Особое место среди всех функций PDE Toolbox Matlab занимают pdeinit и pdetool. Эти функции запускают GUI–приложение PDETool, которое позволяет пользователю пакета в интерактивном режиме выполнять операции по подготовке PDE модели (прорисовка геометрии, задание граничных условий и распределения коэффициентов PDE и др.), решать PDE и визуализировать решение (в том числе и производить анимацию нестационарных процессов). Функция pdetool с входными параметрами выполняет различные команды GUI–приложения PDETool. В пакете PDE Toolbox она реализована как рекурсивная функция.
Запуск приложения:
pdeinit или pdetool
После запуска приложения на экране появится окно, изображённое на рис. 2.1. Как видно, окно приложения состоит из главного меню (первая строка), панели инструментов (вторая строка), строки ввода “Set formula”, объекта axes для отображения геометрии расчётной области, информационной строки “Info” и кнопки закрытия приложения “Exit".
Рис.2.1. Общий вид окна приложения PDETool
Работа по решению краевой задачи начинается с прорисовки геометрии расчётной области. Для прорисовки геометрии и иных действий с расчётной моделью можно воспользоваться командами меню или панелью инструментов.
2.1. Команды меню приложения PDETool
Команды меню объединены в группы, которые представлены в виде пунктов в главном меню PDETool. Щелчок мышью по одному из пунктов приводит к развёртыванию подменю, пунктами которого являются команды соответствующей группы (см. рис. 2.2).
Группа команд File содержит файловые команды (открытие, сохранение и печать файлов) и команды общего назначения (создание новой модели и закрытие приложения PDETool).
Группа команд Edit содержит команды редактирования PDE модели (в т.ч. и с использованием системного буфера).
Группа команд Options содержит команды установки (изменения) режимов работы приложения PDETool.
Группа команд Draw содержит команды прорисовки и редактирования геометрических объектов в PDE модели.
Группа команд Boundary содержит команды ввода и редактирования граничных условий, показа номеров граничных сегментов и зон расчётной области, а также команды удаления границ между зонами.
Группа команд PDE содержит команды ввода и редактирования параметров (коэффициентов PDE), показа номеров зон расчётной области.
Группа команд Mesh содержит команды работы с конечноэлементной сеткой (генерация, сгущение (переопределение), регуляризация, показ номеров объектов сетки и их параметров качества, экспорт).
Группа команд Solve содержит команды решения PDE, ввода и редактирования параметров решателя PDE.
Группа команд Plot содержит команды визуализации решения PDE.
Window – переключение между окнами MATLAB.
Help – команды работы со справочной системой MATLAB.
Рис. 2.2. Появление подменю при выборе пункта главного меню
2.1.1. File
New (Ctrl+N) – Создать новую PDE модель.
Область координатных осей очищается, переменные, описывающие PDE модель, освобождаются. Если в это время была открыта несохранённая PDE модель, то раскроется диалоговое окно, предлагающее сохранить её.
Open… (Ctrl+O) – Открыть ранее сохранённую в m-файле PDE модель.
Перед открытием файла будет развёрнута стандартная диалоговая панель открытия файла. Вид этой панели показан в [15] (см. описание команды uigetfile графического интерфейса пользователя (GUI) MATLAB). Двойной щелчок по нужному m-файлу или выбор файла и нажатие кнопки “Открыть” приводит к передаче управления этому m-файлу, в результате выполнения которого в окне PDETool появится загружаемая PDE модель.
Save (Ctrl+S) – Сохранение в виде m-файла открытой PDE модели.
Открытая PDE модель сохраняется под текущим именем. Существующий m-файл заменяется.
Save As… (Сохранить как) – Сохранение в виде m-файла открытой PDE модели.
Перед сохранением раскроется стандартная диалоговая панель записи файла. Вид этой панели показан в [15] (см. описание команды uiputfile GUI MATLAB). Ввод имени файла в строку ввода “Имя файла” и нажатие кнопки “Сохранить” приведёт к сохранению файла. Если файл с таким именем существует, то раскроется диалоговое окно, предлагающее заменить существующий файл.
Print… – Печать фигуры PDETool.
Exit (Ctrl+W) – Закрытие приложения PDETool.
Если в это время была открыта несохранённая PDE модель, то раскроется диалоговое окно, предлагающее сохранить её.
2.1.2. Edit
Undo (Ctrl+Z) – Отмена последнего действия.
Cut (Ctrl+X) – Вырезать выделенный геометрический объект и поместить его в буфер.
Copy (Ctrl+C) – Копировать выделенный геометрический объект в буфер.
Paste (Ctrl+V) – Вставить геометрический объект из буфера.
По данной команде развёртывается диалоговое окно “Paste”, содержащее три строки ввода: “X-axis displacement", " Y-axis displacement", "Number of repeats”. Первая строка ввода – смещение по оси x, вторая – по оси y, третья – количество повторений операции вставки. Нажатие кнопки “OK” приведёт к выполнению операции.
Clear (Ctrl+R) – Удалить выделенный геометрический объект.
Перечисленные команды группы Edit действуют только в режиме ввода геометрии (Draw Mode). Выделение одного геометрического объекта производится щелчком мыши по имени объекта. Щелчки с одновременным удержанием клавиши Shift позволяют производить множественное выделение и выборочную отмену выделения.
Select All (Ctrl+A) – Выделить всё.
В режиме Draw Mode выделяются все геометрические объекты. В режиме ввода и редактирования граничных условий выделяются все внешние граничные сегменты (внутренние не выделяются). В режиме ввода и редактирования коэффициентов PDE (PDE Mode) выделяются все зоны расчётной области. В остальных режимах приложения PDETool пункт главного меню Edit заблокирован.
2.1.3. Options
Grid – Показать/ скрыть координатную сетку в объекте Axes.
Grid Spacing… – Установить лимиты и шаг координатной сетки.
По этой команде развёртывается диалоговое окно “Grid Spacing”, предлагающее ввести пределы осей x и y, а также перечень меток по осям x и y. Нажатие кнопки “Apply” приводит к установлению введённых значений параметров. Нажатие кнопки “Done” приводит к закрытию диалогового окна
Snap – Округлять координаты указателя мыши при показе их значений пользователю.
В правой части инструментальной панели имеется область отображения значений координат x и y точки, в которой находится указатель мыши (см. рис. 2.1, 2.2). Если режим Snap включён, то отображаемые координаты округляются до ближайших значений координат линий сетки. Иначе выдаётся по четыре значащие цифры каждой координаты.
Axes Limits – Установить значения пределов координатных осей.
По данной команде разворачивается диалоговое окно “Axes Limits”, предлагающее ввести нужные значения. Нажатие кнопки “Apply” приводит к установлению введённых значений параметров. Нажатие кнопки “Close” приводит к закрытию диалогового окна.
Axes Equal – Установить на экране одинаковый масштаб по осям x и y.
Turn Off Toolbar Help – Запретить/ Разрешить выдачу подсказок по кнопкам инструментальной панели PDETool.
В нижней правой части фигуры PDETool (рис.2.1, 2.2) имеется область подсказок “Info”. Если указатель мыши подвести к кнопке инструментальной панели, то в названной области будет выдана подсказка о назначении этой кнопки (при выключенном режиме Turn Off Toolbar Help).
Zoom – Включить режим показа в увеличенном масштабе выделяемой прямоугольной области в PDE-модели.
Если при включенном режиме Zoom выделить мышью некоторую прямоугольную область, то сразу при отпускании левой кнопки мыши эта область будет показана в увеличенном масштабе (Axes Limits будут соответствовать границам этой области).
Application – Переключение типа PDE задачи.
По данной команде список отображается в виде подменю (см. рис.2.3).
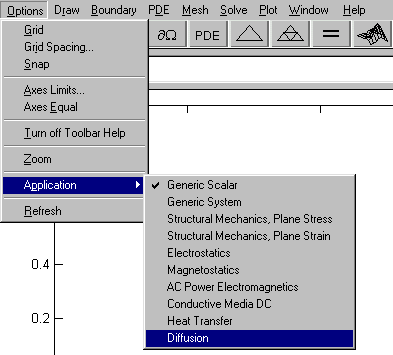
Рис. 2.3. Подменю, содержащее список краевых задач, поддерживаемых PDETool
Generic Scalar – скалярная краевая задача;
Generic System – система PDE;
Structural Mechanics, Plane Stress – задача теории упругости на недеформируемой сетке;
Structural Mechanics, Plane Strain – задача теории упругости на деформируемой сетке;
Electrostatics – PDE электростатики относительно скалярного электрического потенциала;
Magnetostatics – PDE магнитостатики относительно векторного магнитного потенциала;
AC Power Electromagnetics – переменное электромагнитное поле;
Conductive Media DC – электрическое поле постоянного тока в проводящей среде;
Heat Transfer – уравнение теплопередачи;
Diffusion – уравнение диффузии.
Refresh – Обновить изображение PDE-модели в поле axes.
Если изображение PDE-модели в поле axes по каким-либо причинам было запорчено, то по данной команде оно отображается снова.
2.1.4. Draw
Draw Mode – Переключение в режим ввода (прорисовки) геометрии.
В этом режиме возможно создание, уничтожение и изменение геометрических объектов в расчётной области.
Rectangle/square – Ввод прямоугольника или квадрата с помощью мыши.
Начальной точкой прямоугольника является его верхняя левая вершина. Если при вводе будет удерживаться клавиша Ctrl, то будет прорисовываться квадрат. Стороны прямоугольника всегда параллельны осям координат.
Rectangle/square (centered) – То же.
Начальной точкой прямоугольника является его центр.
Ellipse/circle – Ввод эллипса или круга с помощью мыши.
Начальной точкой эллипса является его верхняя левая точка. Если при вводе будет удерживаться клавиша Ctrl, то будет прорисовываться круг. Главные оси эллипса всегда параллельны осям координат.
Ellipse/circle (centered) – То же.
Начальной точкой эллипса является его центр.
Polygon – Прорисовка многоугольника с помощью мыши.с
Ввод производится отрезками ломаной линии, пока она не станет замкнутой.
Rotate – Поворот выделенных геометрических объектов на некоторый угол вокруг некоторой точки.
По данной команде раскрывается диалоговое окно “Rotate”, предлагающее ввести угол в градусах и координаты центра поворота (см. рис.2.4). Есть возможность осуществлять поворот относительно центра масс. Положительное направление поворота – против часовой стрелки.
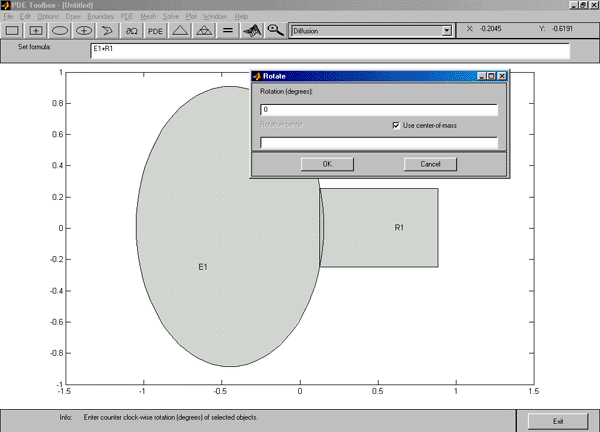
Рис. 2.4. Диалоговое окно “Rotate” на фоне фигуры PDETool
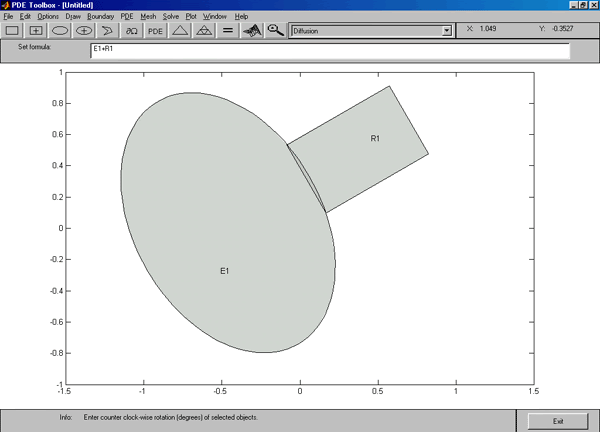
Рис. 2.5. Повёрнутые геометрические объекты
Как видно из рис. 2.4, это диалоговое окно содержит две строки ввода. По умолчанию угол поворота ротора 0 градусов, поворот осуществляется относительно центра масс выделенной совокупности геометрических объектов. На рис.2.4 оба геометрических объекта являются выделенными. Для примера повернём их относительно точки (x=–0.5; y=0) на 30 градусов против часовой стрелки. Результат показан на рис. 2.5.
Export Geometry Description, Set Formula, Labels… – Экспорт в базовую рабочую область переменных описания геометрии.
По данной команде развёртывается диалоговое окно “Export”, изображённое на рис. 2.6. В строке ввода этого окна содержатся имена переменных, описывающих геометрию расчётной области. Если нажать кнопку “OK”, то эти переменные будут записаны в рабочую область MATLAB.
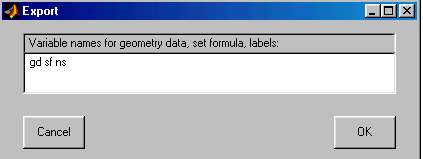
Рис. 2.6. Диалоговое окно экспорта геометрии
2.1.5. Boundary
Boundary Mode (Ctrl+B) – Переключение в режим ввода граничных условий (ГУ).
Specify Boundary Conditions… – Ввод параметров граничных условий.
По данной команде раскрывается диалоговое окно (рис.2.7), предлагающее ввести нужные значения параметров для всех или для выделенных граничных сегментов.
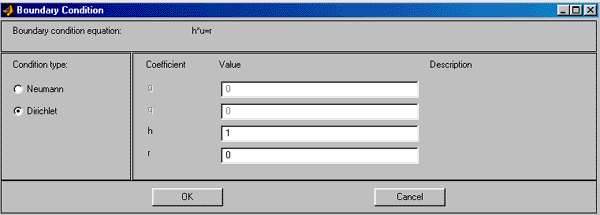
Рис. 2.7. Диалоговое окно ввода параметров граничных условий
Show Edge Labels – Показать номера граничных сегментов.
Если эту команду выполнить для геометрии, показанной на рис.2.5, то получим изображение, показанное на рис.2.8.
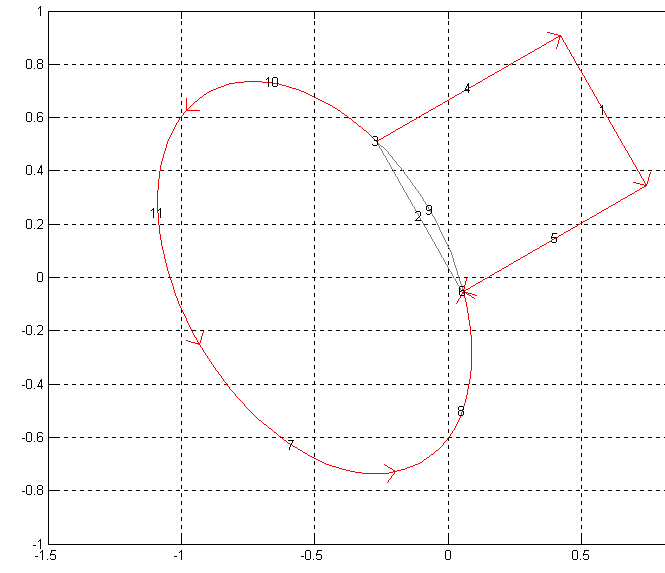
Рис. 2.8. Показ номеров граничных сегментов расчётной области.
Show Subdomain Labels – Показать номера зон.
Если для модели, изображённой на рис.2.8, отменить показ номеров граничных сегментов и выполнить эту команду, то получим изображение, показанное на рис. 2.9.
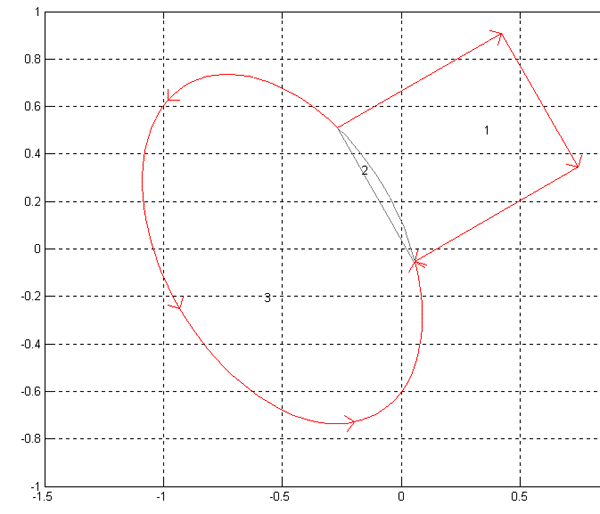
Рис. 2.9. Показ номеров зон в режиме ввода ГУ
Remove Subdomain Border – Удалить границу зон.
По данной команде удаляется граница раздела зон, которой принадлежат выделенные граничные сегменты, и производится автоматическая перенумерация зон.
Remove All Subdomain Borders – Удаление всех границ зон.
По данной команде удаляются все границы зон вне зависимости от выделения. Вся расчётная область станет зоной № 1.
Export Decomposed Geometry, Boundary Cond’s… – Экспорт в базовую рабочую область переменных описания граничных условий.
По данной команде развёртывается диалоговое окно “Export”, изображённое на рис. 2.10. В строке ввода этого окна содержатся имена переменных, описывающих граничные условия. Если нажать кнопку "OK”, то эти переменные будут записаны в рабочую область MATLAB.
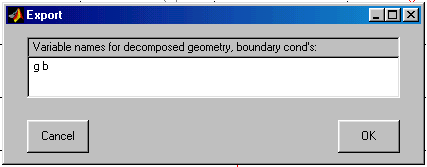
Рис. 2.10. Диалоговое окно экспорта геометрии, разбитой на зоны и ГУ
2.1.6. PDE
PDE Mode – Переключение в режим ввода параметров (коэффициентов) PDE.
Show Subdomain Labels – Показать номера зон.
Эта команда полностью аналогична соответствующей команде группы Boundary. Вид расчётной области в результате выполнения данной команды показан на рис.2.11.
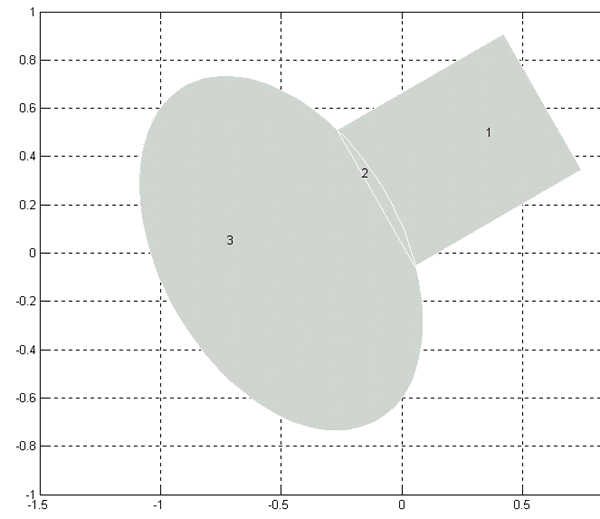
Рис. 2.11. Показ номеров зон в режиме PDE
PDE Specification… – Ввод параметров (коэффициентов) PDE.
По данной команде раскрывается диалоговое окно (рис.2.12), предлагающее ввести нужные значения параметров. Вводимые параметры относятся только к выделенным зонам; если выделенных нет, то ко всем зонам.
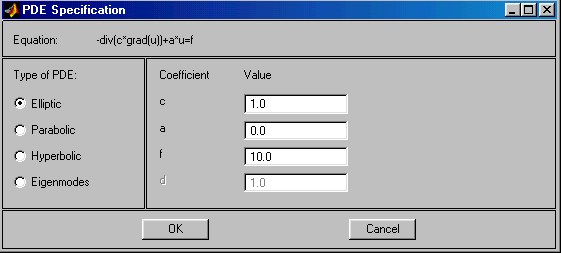
Рис.2.12. Диалоговое окно ввода коэффициентов PDE
Export PDE Coefficients… – Экспорт в базовую рабочую область переменных, описывающих распределение PDE коэффициентов в расчётной области.
По данной команде развёртывается диалоговое окно “Export”, изображённое на рис. 2.13. В строке ввода этого окна содержатся имена переменных, описывающих распределение коэффициентов PDE в расчётной области. Если нажать кнопку “OK”, то эти переменные будут записаны в рабочую область MATLAB.
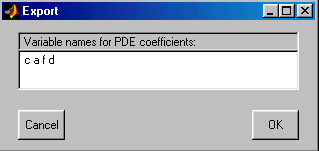
Рис.2.13. Диалоговое окно экспорта коэффициентов PDE
2.1.7. Mesh
Mesh Mode – Переключение в режим построения конечноэлементной сетки.
Если сетка не построена, то сетка генерируется и отображается в объекте axes фигуры PDETool. Иначе сетка не генерируется, а отображается.
Initialize Mesh (Ctrl+I) – Инициализация (генерация) конечноэлементной сетки.
Начальный вариант сетки генерируется независимо от существования и текущего состояния сетки.
Refine Mesh (Ctrl+M) – Переопределение (сгущение) конечноэлементной сетки во всей расчётной области.
На рис.2.14 показан начальный, а на рис.2.15 – один раз переопределённый вариант конечноэлементной сетки.
Рис.2.14. Сетка, генерируемая по команде Initialize Mesh
Рис.2.15. Сетка, получаемая по команде Refine Mesh
Jiggle Mesh – Регуляризация конечноэлементной сетки.
Конечноэлементная сетка перестраивается (узлы перемещаются) таким образом, чтобы показатель нерегулярности всех конечных элементов не превышал установленной в PDETool величины.
Undo Mesh Change – Отменить последнее изменение конечноэлементной сетки.
Например, если сетка, изображённая на рис.2.15, только что получена командой Refine Mesh, то по команде Undo Mesh Change мы получим сетку, изображённую на рис.2.14.
Display Triangle Quality – Отобразить в цвете значения показателя регулярности для всех конечных элементов (треугольников) сетки.
Если применить данную команду к сетке, изображённой на рис.2.15, то получим изображение, показанное на рис.2.16.
Show Node Labels – Показать номера узлов конечноэлементной сетки.
Show Triangle Labels – Показать номера конечных элементов (треугольников).
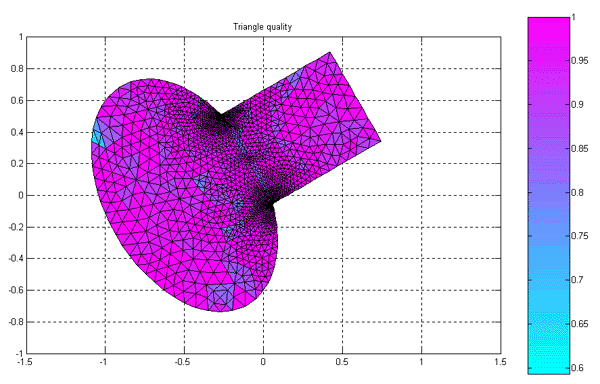
Рис.2.16. Показ регулярности конечных элементов по всей расчётной области
Parameters… – Установить параметры генератора сетки.
По данной команде раскрывается диалоговое окно (рис.2.17), предлагающее ввести нужные значения параметров.
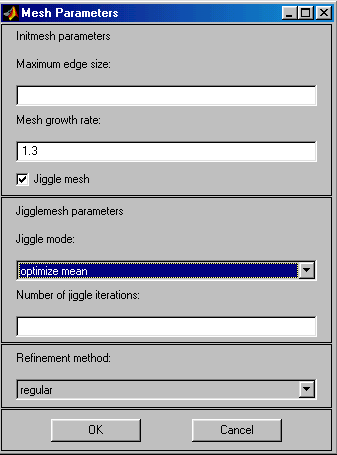
Рис.2.17. Диалоговое окно ввода параметров режима генерации, регуляризации и переопределения сетки
Export Mesh – Экспорт конечноэлементной сетки в базовую рабочую область.
По данной команде развёртывается диалоговое окно “Export”, изображённое на рис. 2.18. В строке ввода этого окна содержатся имена переменных, описывающих конечноэлементную сетку. Если нажать кнопку “OK”, то эти переменные будут записаны в рабочую область MATLAB.
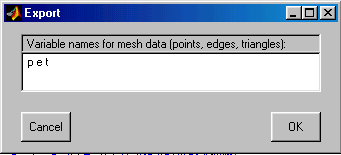
Рис.2.18. Диалоговое окно экспорта переменных конечноэлементной сетки
2.1.8. Solve
Solve PDE (Ctrl+E) – Решить краевую задачу (вычислить узловое распределение искомой величины).
Parameters… – Установить параметры решателя PDE.
По данной команде раскрывается диалоговое окно (рис.2.19), предлагающее ввести нужные значения параметров.
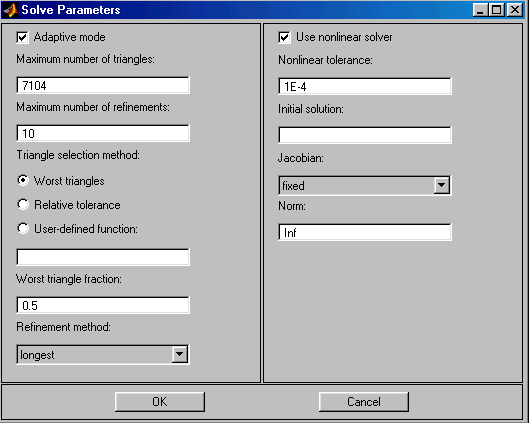
Рис.2.19. Диалоговое окно ввода параметров решателя PDE
Диалоговое окно, изображённое на рис.2.19, состоит из двух панелей. Левая панель предназначена для редактирования параметров адаптивного режима решения PDE. Смысл каждого из параметров панели показан в описании функции adaptmesh. Если кнопка “Adaptive mode” выключена, то соответствующие параметры недоступны для редактирования. Правая панель предназначена для редактирования параметров нелинейного решателя PDE. Смысл каждого из параметров панели показан в описании функции pdenonlin. Если кнопка “Use nonlinear solver” выключена, то соответствующие параметры недоступны для редактирования.
Export Solution… – Экспорт решения (узлового распределения) в базовую рабочую область.
По данной команде развёртывается диалоговое окно “Export”, изображённое на рис. 2.20. В строке ввода этого окна содержится имя переменной, содержащей узловое распределение решения PDE. Если нажать кнопку “OK”, то эта переменная будет записана в рабочую область MATLAB.
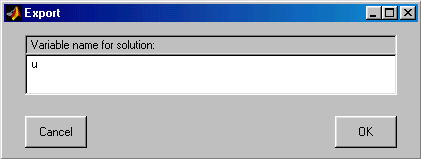
Рис.2.20. Диалоговое окно экспорта решения PDE
2.1.9. Plot
Plot Solution (Ctrl+P) – Отобразить решение PDE.
По этой команде в объекте axes окна PDETool будет графически показано распределение решения PDE в расчётной области в соответствии с установленными значениями параметров визуализации решения.
Parameters… – Установить параметры отображения решения.
По данной команде раскрывается диалоговое окно (рис.2.21), предлагающее ввести нужные значения параметров.
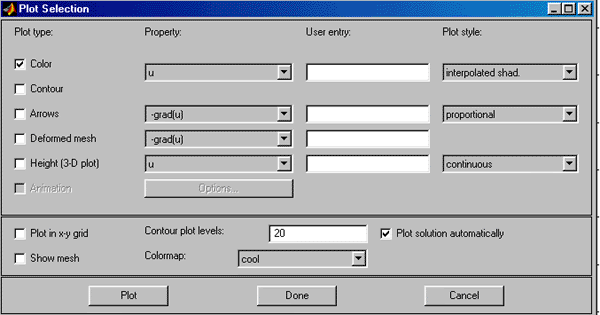
Рис.2.21. Диалоговое окно ввода параметров визуализации решения PDE
Диалоговое окно, изображённое на рис.2.21, состоит из двух панелей. Верхняя панель состоит из четырёх колонок: Plot type, Property, User entry, Plot style. Колонка “Plot type” состоит окон контроля (check box), позволяющих указать, что требуется графически отображать: Color – цветной план рассчитанного поля, Contour – изолинии поля; Arrows – показ векторного поля стрелочками; Deformed mesh – отображение поля на деформированной сетке; Height (3D plot) – отображение скалярного поля в виде поверхностного графика в отдельной фигуре MATLAB; Animation – анимация решения нестационарной задачи. Колонка “Property” состоит из ниспадающих меню, позволяющих выбрать визуализируемое поле. Если в соответствующем ниспадающем меню нет требуемого поля, то можно воспользоваться строками ввода в колонке “User entry” в соответствии с правилами, действующими при подготовке входных параметров функций assempde, parabolic, hyperbolic. Колонка “Plot style” содержит ниспадающие меню, позволяющие выбрать стили визуализации соответствующих полей: interpolated shad – использование кусочно-линейной интерполяции при отображении, flat shading – отображение в кусочно-постоянном виде; proportional – каждая стрелочка имеет длину, пропорциональную модулю вектора в соответствующей точке наблюдения, normalized – все стрелочки имеют одинаковую длину; continuous – непрерывная интерполяция при построении поверхностного графика, discontinuous – кусочно-постоянный поверхностный график. Нижняя панель состоит из трёх окон контроля (check box), строки ввода и ниспадающего меню. Plot in x-y grid – построение на x-y сетке; Show mesh – показать конечноэлементную сетку; Plot solution automatically – автоматическая визуализация решения, получаемого в результате выполнения команды меню “Solve PDE". Contour plot levels – число линий равного уровня отображаемого скалярного поля. Colormap – выбор палитры цветного плана скалярного поля. Внизу диалогового окна имеются три кнопки: Plot, Done, Cancel. Plot – отобразить решение PDE с учётом вновь указанных режимов; Done – принять введённые режимы; Cancel – отменить изменения режимов и закрыть диалоговое окно.
Export Movie… – Экспорт в базовую рабочую область переменной, содержащей информацию, необходимую для анимации решения нестационарной PDE задачи.
2.1.10. Window и Help
Window – Переключение между окнами, фигурами и приложениями MATLAB.
Подменю содержит список соответствующих окон.
Группа команд Help:
-
Help… (Ctrl+H) – Открыть стандартное окно справочной системы MATLAB.
-
About… – О приложении PDETool.
2.2. Инструментальная панель PDETool
Инструментальная панель содержит кнопки, дублирующие некоторые команды меню. Её общий вид показан на рис.2.22.
![]()
Рис.2.22. Вид инструментальной панели PDETool
![]() – Ввод прямоугольника или квадрата с помощью мыши.
– Ввод прямоугольника или квадрата с помощью мыши.
Начальной точкой прямоугольника является его верхняя левая вершина. Если при вводе будет удерживаться клавиша Ctrl, то будет прорисовываться квадрат. Стороны прямоугольника всегда параллельны осям координат. Эта кнопка является полным аналогом команды Draw/ Rectangle/square. При нажатии этой кнопки PDETool автоматически переходит в режим прорисовки геометрии.
![]() – Ввод прямоугольника или квадрата с помощью мыши.
– Ввод прямоугольника или квадрата с помощью мыши.
Начальной точкой прямоугольника является его центр. Эта кнопка является полным аналогом команды Draw/ Rectangle/square (centered). При нажатии этой кнопки PDETool автоматически переходит в режим прорисовки геометрии.
![]() – Ввод эллипса или круга с помощью мыши.
– Ввод эллипса или круга с помощью мыши.
Начальной точкой эллипса является его верхняя левая точка. Если при вводе будет удерживаться клавиша Ctrl, то будет прорисовываться круг. Главные оси эллипса всегда параллельны осям координат. Эта кнопка является полным аналогом команды Draw/ Ellipse/circle. При нажатии этой кнопки PDETool автоматически переходит в режим прорисовки геометрии.
![]() – Ввод эллипса или круга с помощью мыши.
– Ввод эллипса или круга с помощью мыши.
Начальной точкой эллипса является его центр. Эта кнопка является полным аналогом команды Draw/ Ellipse/circle (centered). При нажатии этой кнопки PDETool автоматически переходит в режим прорисовки геометрии.
![]() – Прорисовка многоугольника.
– Прорисовка многоугольника.
Ввод производится отрезками ломаной линии, пока она не станет замкнутой. Эта кнопка является полным аналогом команды Draw/ Polygon. При нажатии этой кнопки PDETool автоматически переходит в режим прорисовки геометрии.
![]() – Переключение в режим ввода граничных условий.
– Переключение в режим ввода граничных условий.
Эта кнопка является полным аналогом команды Boundary/ Boundary Mode.
![]() – Ввод параметров (коэффициентов) PDE для всей расчётной области или для выделенных зон. Эта кнопка является полным аналогом команды PDE/ PDE Specification. При нажатии этой кнопки нужно учитывать, что режим работы PDETool не переключается.
– Ввод параметров (коэффициентов) PDE для всей расчётной области или для выделенных зон. Эта кнопка является полным аналогом команды PDE/ PDE Specification. При нажатии этой кнопки нужно учитывать, что режим работы PDETool не переключается.
![]() – Инициализация (генерация) конечноэлементной сетки.
– Инициализация (генерация) конечноэлементной сетки.
Эта кнопка является полным аналогом команды Mesh/ Initialize Mesh. При нажатии этой кнопки PDETool автоматически переходит в режим построения конечноэлементной сетки.
![]() – Переопределение (сгущение) конечноэлементной сетки во всей
– Переопределение (сгущение) конечноэлементной сетки во всей
расчётной области. Эта кнопка является полным аналогом команды
Mesh/ Refine Mesh. При нажатии этой кнопки PDETool автоматически переходит в режим построения конечноэлементной сетки.
![]() – Решить краевую задачу (вычислить узловое распределение искомой
– Решить краевую задачу (вычислить узловое распределение искомой
величины). Эта кнопка является полным аналогом команды Solve/ Solve PDE. При нажатии этой кнопки PDE решается, если заданы все необходимые параметры PDE модели (граничные условия и коэффициенты PDE определены, сетка сгенерирована) независимо от текущего режима PDETool. Переключение режимов не происходит. Если эту кнопку нажать в режиме Draw Mode, то изображение геометрии расчётной области исчезает из объекта axes. Это изображение можно восстановить принудительным переключением в другой режим.
Команда Options/ Refresh не восстановит изображение.
![]() – Установить параметры отображения решения.
– Установить параметры отображения решения.
Эта кнопка является полным аналогом команды Plot/ Parameters.
![]() – Включить/ выключить режим Zoom.
– Включить/ выключить режим Zoom.
Выполняется такое же действие, как по команде Options/Zoom.
В панели инструментов имеется ниспадающее меню, которое содержит список краевых задач, поддерживаемых приложением PDETool. Если это меню кликнуть левой кнопкой мыши, то оно раскроется. Вид раскрытого ниспадающего меню показан на рис.2.23.
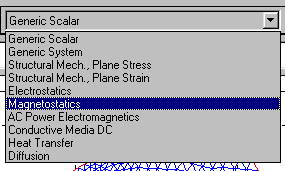
Рис.2.23. Ниспадающее меню панели инструментов PDETool
Ниспадающее меню панели инструментов выполняет те же действия, что и команда Options/ Application.
На правом конце панели инструментов имеется указатель значений координат точки наблюдения ![]() , в которой в данный момент находится указатель мыши. Этот указатель весьма полезен при интерактивной работе пользователя с PDE моделью во всех режимах работы PDETool.
, в которой в данный момент находится указатель мыши. Этот указатель весьма полезен при интерактивной работе пользователя с PDE моделью во всех режимах работы PDETool.
Непосредственно под панелью инструментов расположена строка ввода Set Formula. Она должна содержать формулу описания геометрии расчётной области. По синтаксису это должно быть выражение, операндами которого являются метки (идентификаторы) геометрических объектов. Операция объединения обозначается знаком +(плюс), операция исключения – знаком –(минус), операция пересечения – знаком умножения *(звёздочка). Эта строка ввода доступна для редактирования только в режиме Draw Mode.
В качестве примера рассмотрим геометрию, показанную на рис. 2.5, 2.8. Формулу “E1+R1” заменим на “(E1+R1)-(E1*R1)” и перейдём в режим Boundary Mode с показом номеров граничных сегментов. В результате получим изображение, показанное на рис.2.24. Как видно, граничные сегменты №№ 2 и 9 стали внешними по отношению к расчётной области (на рисунке они показаны красным цветом). Конечноэлементная сетка показана на рис.2.25.
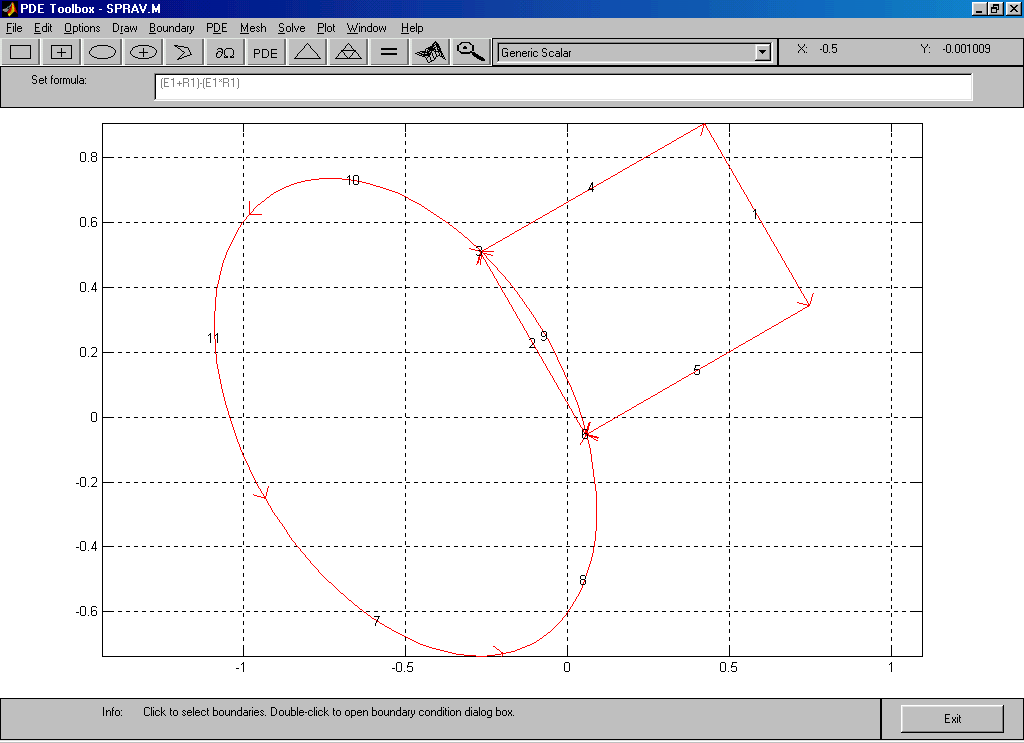
Рис.2.24. Изменение внешней границы расчётной области в результате изменения формулы описания геометрии
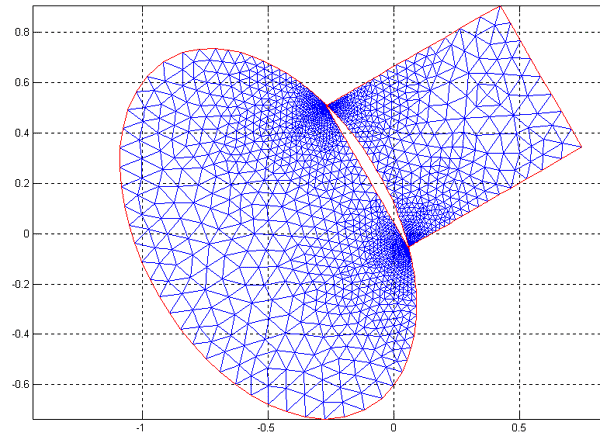
Рис.2.25. Конечноэлементная сетка, соответствующая геометрии на рис.2.24
2.3. Список стандартных краевых задач PDETool
2.3.1. Скалярные краевые задачи: эллиптические, параболические, гиперболические, задачи на собственные частоты
Скалярное PDE – это дифференциальное уравнение относительно одного скалярного поля, содержащее пространственные дифференциальные операторы второго и нулевого порядка. В PDETool скалярная краевая задача названа “Generic Scalar”. Если PDE не содержит дифференциальных операторов по времени, то такое уравнение называется стационарным. В PDE Toolbox это эллиптическое PDE. Скалярное эллиптическое PDE имеет следующий вид:
–div(c*grad u) + a*u = f , (2.1)
где c, a – коэффициенты PDE, f – правая часть PDE (источник скалярного поля u). В PDETool c, a, f – скалярные поля, которые можно задавать аналитически в виде выражений. В выражениях могут содержаться переменные x, y, sd. Здесь x, y – координаты точки наблюдения, sd – номер зоны, которой принадлежит точка наблюдения. Для каждой зоны можно задавать своё выражение для любого коэффициента PDE. Если в “Solve Parameters" PDETool установлен флажок “Use nonlinear solver” (включен нелинейный решатель PDE), то в выражения для коэффициентов PDE могут входить также переменные u, ux, uy. Здесь u – решение PDE (2.1) в точке наблюдения; ux – ![]() , uy –
, uy – ![]() в точке наблюдения.
в точке наблюдения.
PDETool поддерживает также решение нестационарных PDE: параболических и гиперболических. Нестационарным называется PDE, содержащее дифференциальные операторы по времени. Скалярное параболическое PDE имеет следующий вид:
d*![]() – div(c*grad u) + a*u = f , (2.2)
– div(c*grad u) + a*u = f , (2.2)
скалярное гиперболическое PDE имеет вид:
d*![]() – div(c*grad u) + a*u = f , (2.3)
– div(c*grad u) + a*u = f , (2.3)
где d, c, a – коэффициенты PDE, f – правая часть PDE. В PDETool d, c, a, f – скалярные переменные (в общем случае поля), которые можно задавать аналитически в виде выражений. В выражениях могут содержаться переменные x, y, sd, t, где t – момент времени. Для каждой зоны можно задавать своё выражение для любого коэффициента PDE, входящего в (2.2) или (2.3). PDETool может решать только линейные параболические или гиперболические PDE. Это означает, что в выражениях для коэффициентов PDE запрещается использовать переменные u, ux, uy. PDETool решает уравнение (2.2) или (2.3) для моментов времени time = 0:1:10 (перенастройка этого режимного параметра невозможна).
PDETool может решать также задачу на собственные значения эллиптического PDE. Этой задаче соответствует уравнение вида:
–div(c*grad u) + a*u = ![]() d*u . (2.4)
d*u . (2.4)
При некоторых значениях ![]() уравнение (2.4) не имеет единственного решения относительно скалярного поля u. Такие значения
уравнение (2.4) не имеет единственного решения относительно скалярного поля u. Такие значения ![]() называются собственными значениями эллиптического PDE (эллиптической краевой задачи). Решая задачу на собственные значения, можно исследовать численную устойчивость стационарных и нестационарных PDE (и соответствующих краевых задач). Можно также определять собственные частоты и параметры затухания колебаний пространственно–распределённых систем.
называются собственными значениями эллиптического PDE (эллиптической краевой задачи). Решая задачу на собственные значения, можно исследовать численную устойчивость стационарных и нестационарных PDE (и соответствующих краевых задач). Можно также определять собственные частоты и параметры затухания колебаний пространственно–распределённых систем.
PDETool поддерживает два варианта граничных условий: граничные условия первого рода (Дирихле) и граничные условия второго рода (Неймана). Условия Дирихле имеют вид:
h*u = r ,
где h, r – скалярные коэффициенты.
Условия Неймана имеют вид:
n*c*grad u + q*u = g ,
где n – вектор единичной внешней нормали к границе расчётной области; c – коэффициент PDE; q и g – скалярные коэффициенты.
Коэффициенты h, r, q, g можно задавать в виде скалярных полей аналитическими выражениями. В этих выражениях можно использовать переменные x и y. Если включен режим нелинейного решателя (в случае эллиптического PDE), то можно использовать переменные u, ux, uy. Их смысл показан выше.
Если r или g = 0, то граничные условия называются нулевыми. Если в задаче на собственные значения заданы ненулевые граничные условия, то они автоматически заменяются на нулевые.
2.3.2. Системы скалярных PDE
Приложение PDETool поддерживает решение двух скалярных PDE. В PDETool краевая задача, основанная на такой системе, имеет название “Generic System”. Система двух скалярных эллиптических PDE имеет следующий вид:
–div(c11*grad u1 + c12*grad u2) + a11*u1 + a12*u2 = f1
–div(c21*grad u1 + c22*grad u2) + a21*u1 + a22*u2 = f2 , (2.5)
где u1, u2 – искомые скалярные поля; cij, aij – скалярные коэффициенты системы PDE; f1 , f2 – правая часть (источники скалярных полей u1, u2).
Систему (2.5) можно записать в матричной форме:
–div([c]*grad [u]) + [a]*[u] = [f] , (2.6)
где [u] – искомое матричное поле (размерность матрицы (2,1)); [c], [a], [f] – матричные коэффициенты PDE.
Поскольку PDETool решает уравнения математической физики в двумерной расчётной области, систему (2.5) со скалярными коэффициентами cij можно представить как векторное PDE с тензорными коэффициентами второй валентности:
–div(c*grad u) + a*u = f ,
где c, a – тензорные коэффициенты PDE; f – векторная правая часть (источник искомого векторного поля u), причём индекс 1 в (2.5) соответствует x составляющей вектора, а индекс 2 – y составляющей.
Коэффициенты cij, aij, f1 , f2 можно задавать в виде скалярных полей аналитическими выражениями. В этих выражениях можно использовать переменные x, y, sd, которые интерпретируются как матрицы-строки размера (1,NE), где NE – число конечных элементов в расчётной области. Если включен режим нелинейного решателя, то можно использовать переменные u, ux, uy (при интерпретации выражения они имеют размер (2,NE)).
Система скалярных параболических PDE в матричной форме имеет следующий вид:
[d]*![]() – div([c]*grad [u]) + [a]*[u] = [f] , (2.7)
– div([c]*grad [u]) + [a]*[u] = [f] , (2.7)
система скалярных гиперболических PDE в матричной форме имеет вид:
[d]*![]() – div([c]*grad [u]) + [a]*[u] = [f] , (2.8)
– div([c]*grad [u]) + [a]*[u] = [f] , (2.8)
где [d], [c], [a] – матричные коэффициенты PDE (размерность матричных полей (2,2)), [f] – матричная правая часть PDE (размерность матричного поля (2,1)). В PDETool компоненты матричных полей [d], [c], [a], [f] можно задавать в виде выражений. В этих выражениях можно использовать переменные x, y, sd, t, где t – момент времени (скалярная переменная), размерность остальных переменных при интерпретации выражений описана выше. PDETool решает матричное PDE (2.7) или (2.8) также для моментов времени time = 0:1:10 (перенастройка этого режимного параметра невозможна).
PDETool может решать также задачу на собственные значения системы скалярных эллиптических PDE. Этой задаче соответствует матричное PDE вида:
–div([c]*grad [u]) + [a]*[u] = ![]() [d]*[u] . (2.9)
[d]*[u] . (2.9)
PDETool поддерживает три варианта граничных условий: граничные условия первого рода (Дирихле), граничные условия второго рода (Неймана) и смешанные (Mixed). Условия Дирихле имеют вид:
[h]*[u] = [r] ,
где [h] – матричный коэффициент размера (2,2), [r] – матричная правая часть размера (2,1).
Условия Неймана имеют вид:
n*[c]*grad [u] + [q]*[u] = [g] ,
где n – вектор единичной внешней нормали к границе расчётной области; [c] – матричный коэффициент PDE; [q] – матричный коэффициент размера (2,2), [g] – матричная правая часть размера (2,1).
Смешанные условия (Mixed) имеют вид:
{[h]*[u] = [r] ; n*[c]*grad [u] + [q]*[u] = [g] + [h]T*[m]} ,
где вторая строка матрицы [h] состоит из нулей; [m] – матрица-столбец множителей Лагранжа, вычисляемых автоматически таким образом, чтобы выполнялись условия Дирихле.
Компоненты матричных коэффициентов [h], [r], [q], [g] можно задавать в виде скалярных полей аналитическими выражениями. В этих выражениях можно использовать переменные x и y. Если включен режим нелинейного решателя (в случае системы эллиптических PDE), то можно использовать переменные u, ux, uy. При интерпретации выражений переменные x и y имеют размерность (1,ne), переменные u, ux, uy имеют размерность (2,ne), где ne – число граничных элементов. В выражениях можно использовать скалярную переменную t, которая означает момент времени.
В краевых задачах “Generic Scalar” и “Generic System” поддерживаются только нулевые начальные условия. В PDETool нет команд переопределения начальных условий.
2.3.3. Механические напряжения в упругой среде с изотропными линейными свойствами
Стационарное поле механических напряжений в твёрдом теле характеризуется пространственным распределением следующих физических величин [16]:
тензор (второй валентности) механического напряжения ![]() , тензор (второй валентности) деформации e, вектор перемещения u. Источником этого поля является пространственное распределение вектора объёмной плотности нагружающей силы (нагрузки) f. При записи уравнений внешнее произведение тензоров любой валентности будем обозначать
, тензор (второй валентности) деформации e, вектор перемещения u. Источником этого поля является пространственное распределение вектора объёмной плотности нагружающей силы (нагрузки) f. При записи уравнений внешнее произведение тензоров любой валентности будем обозначать ![]() .
.
Линеаризованные уравнения теории упругости имеют вид:
e = 0,5*(grad u + ![]() u) ;
u) ;
–div ![]() = f – уравнение равновесия в отсчётной конфигурации;
= f – уравнение равновесия в отсчётной конфигурации;
![]() =
= ![]() *tr(e)*1 + 2
*tr(e)*1 + 2![]() e – уравнение, описывающее изотропные упругие свойства вещества; здесь 1 – единичный шаровой тензор второй валентности.
e – уравнение, описывающее изотропные упругие свойства вещества; здесь 1 – единичный шаровой тензор второй валентности.
Из последнего уравнения видно, что линейные изотропные упругие свойства вещества характеризуются двумя параметрами ![]() и
и ![]() , которые называются коэффициентами Ламэ:
, которые называются коэффициентами Ламэ: ![]() – модуль упругости;
– модуль упругости; ![]() – модуль сдвига. В справочной литературе приводятся также и другие параметры упругих свойств вещества: модуль объёмного сжатия
– модуль сдвига. В справочной литературе приводятся также и другие параметры упругих свойств вещества: модуль объёмного сжатия ![]() ; модуль Юнга E =
; модуль Юнга E = ![]() ; коэффициент Пуассона
; коэффициент Пуассона ![]() . Коэффициенты Ламэ могут быть выражены через модуль Юнга и коэффициент Пуассона:
. Коэффициенты Ламэ могут быть выражены через модуль Юнга и коэффициент Пуассона:
![]() ;
; ![]() . (2.10)
. (2.10)
С учётом сказанного определяющее линеаризованное уравнение теории упругости имеет вид:
![]() =
= ![]() *div u *1 +
*div u *1 + ![]() *(grad u +
*(grad u + ![]() u) .
u) .
Это уравнение связывает поле тензора напряжений с полем вектора перемещений. Если его подставить в уравнение равновесия, то получится линеаризованное уравнение математической физики относительно поля вектора перемещений:
–grad(![]() div u) – div(
div u) – div(![]() (grad u +
(grad u + ![]() u)) = f . (2.11)
u)) = f . (2.11)
PDETool решает уравнение (2.11). По команде “PDE/PDE Specification” разворачивается диалоговое окно ввода коэффициентов PDE, изображённое на рис. 2.26. В этом окне коэффициенты PDE имеют следующие имена: E – модуль Юнга; nu – коэффициент Пуассона; Kx – x-составляющая объёмной плотности нагружающей силы; Ky – y-составляющая объёмной плотности нагружающей силы; rho – плотность вещества. Коэффициенты Ламэ, входящие в (2.11), вычисляются по формулам (2.10). По умолчанию E = 1E3; nu = 0,3; Kx = 0; Ky = 0; rho = 1. Коэффициент rho в режиме “Elliptic” игнорируется.
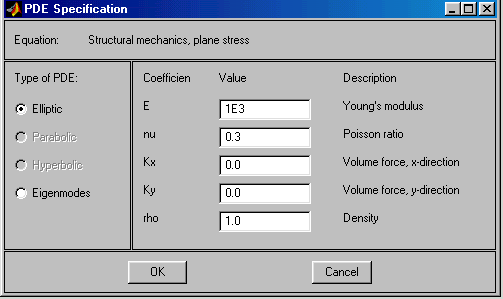
Рис.2.26. Диалоговое окно ввода коэффициентов PDE теории упругости
Граничные условия задаются так же, как и в случае “Generic System”. Нестационарные краевые задачи теории упругости в PDETool не поддерживаются.
Задаче на собственные значения соответствует векторное PDE вида:
–grad(![]() div u) – div(
div u) – div(![]() (grad u +
(grad u + ![]() u)) = L
u)) = L![]() u , (2.12)
u , (2.12)
где ![]() – плотность вещества; L – собственное значение краевой задачи.
– плотность вещества; L – собственное значение краевой задачи.
Коэффициенты PDE, показанные на рис.2.26, можно задавать в виде скалярных полей с помощью выражений. Синтаксис такой же, как и в случае “Generic System”. Краевая задача теории упругости на недеформируемой сетке названа в PDETool "Structural Mech, Plane Stress".
2.3.4. Перемещения в упругой напряжённо-деформированной среде с изотропными линейными свойствами
Здесь так же, как и в предыдущем случае, решается PDE вида (2.11) или (2.12), коэффициенты Ламэ рассчитываются по формуле (2.10). После решения PDE производится поправка координат точек наблюдения (узлов сетки) на величину соответствующих компонентов вектора перемещения u. Например, если расчётной областью является прямоугольник x![]() [–1;1], y
[–1;1], y![]() [–1;1], причём на прямой x=1 заданы нулевые граничные условия Дирихле, а на остальных границах – нулевые условия Неймана, коэффициенты PDE равны E=1E3, nu=0.3, Kx=10, Ky=0, то x–компонента вектора перемещения в среднем будет отличаться от “Structural Mech, Plane Stress” на 13%, а y–компонента – на 25%. Краевая задача теории упругости на деформируемой сетке названа в PDETool "Structural Mech, Plane Strain”. Диалоговое окно ввода коэффициентов PDE выглядит так же, как и на рис. 2.26.
[–1;1], причём на прямой x=1 заданы нулевые граничные условия Дирихле, а на остальных границах – нулевые условия Неймана, коэффициенты PDE равны E=1E3, nu=0.3, Kx=10, Ky=0, то x–компонента вектора перемещения в среднем будет отличаться от “Structural Mech, Plane Stress” на 13%, а y–компонента – на 25%. Краевая задача теории упругости на деформируемой сетке названа в PDETool "Structural Mech, Plane Strain”. Диалоговое окно ввода коэффициентов PDE выглядит так же, как и на рис. 2.26.
2.3.5. Электростатическая задача
Электростатическим называют постоянное поле неподвижных электрических зарядов. Это поле можно рассматривать как частный случай электромагнитного поля. Источниками электростатического поля являются свободные электрические заряды и электрические диполи. Электростатическое поле может длительно существовать в совершенном диэлектрике. Уравнения электростатики в дифференциальной форме имеют вид:
rot E = 0; div D = ![]() , (2.13)
, (2.13)
где E – пространственное распределение вектора напряжённости электрического поля; D – поле вектора электрического смещения; ![]() – скалярное поле объёмной плотности электрического заряда. В случае линейных изотропных диэлектрических свойств среды уравнение материальной связи между векторами E и D имеет вид:
– скалярное поле объёмной плотности электрического заряда. В случае линейных изотропных диэлектрических свойств среды уравнение материальной связи между векторами E и D имеет вид:
D = ![]() E + Pr , (2.14)
E + Pr , (2.14)
где ![]() – абсолютная диэлектрическая проницаемость среды;
– абсолютная диэлектрическая проницаемость среды; ![]() = 8,85*10-12 Ф/м – абсолютная диэлектрическая проницаемость вакуума (основная электрическая постоянная);
= 8,85*10-12 Ф/м – абсолютная диэлектрическая проницаемость вакуума (основная электрическая постоянная); ![]() – относительная диэлектрическая проницаемость среды; Pr – векторное поле остаточной электрической поляризованности среды. Скалярное поле
– относительная диэлектрическая проницаемость среды; Pr – векторное поле остаточной электрической поляризованности среды. Скалярное поле ![]() и векторное поле Pr являются пространственно- распределёнными источниками электростатического поля.
и векторное поле Pr являются пространственно- распределёнными источниками электростатического поля.
Поле вектора E является безвихревым, поэтому его можно представить в виде градиента некоторого скалярного поля
E = – grad![]() , (2.15)
, (2.15)
где ![]() – скалярный электрический потенциал. Подставив соотношение (2.15) в (2.14), а затем в (2.13), получим
– скалярный электрический потенциал. Подставив соотношение (2.15) в (2.14), а затем в (2.13), получим
div (![]() grad
grad ![]() ) = –
) = –![]() + div Pr (2.16)
+ div Pr (2.16)
(2.16) является уравнением электростатики относительно скалярного электрического потенциала. Если обе части (2.16) разделить на –![]() , то получим:
, то получим:
–div (![]() grad
grad ![]() ) =
) = ![]() /
/![]() –
– ![]() div Pr (2.17)
div Pr (2.17)
PDE Toolbox MATLAB не поддерживает наличие в расчётной области тел, обладающих остаточной поляризованностью. Значит, поддерживается только такая электростатическая задача, в которой Pr = 0. В PDETool краевая задача электростатики базируется на уравнении (2.17), у которого последнее слагаемое в правой части равно нулю.
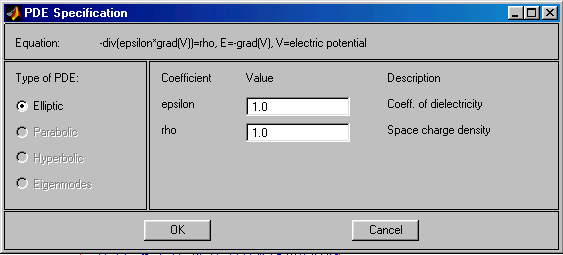
Рис.2.27. Диалоговое окно ввода коэффициентов PDE электростатики
На рис.2.27 показан вид диалогового окна ввода коэффициентов PDE электростатической задачи. Здесь приняты следующие обозначения переменных (полей): V – скалярный электрический потенциал; E – вектор напряжённости электрического поля; epsilon – относительная диэлектрическая проницаемость; rho – объёмная плотность электрического заряда, делённая на абсолютную диэлектрическую проницаемость вакуума. По умолчанию epsilon = 1; rho = 1. Коэффициенты PDE, показанные на рис.2.27, можно задавать в виде скалярных полей с помощью выражений. Синтаксис такой же, как и в случае “Generic Scalar".
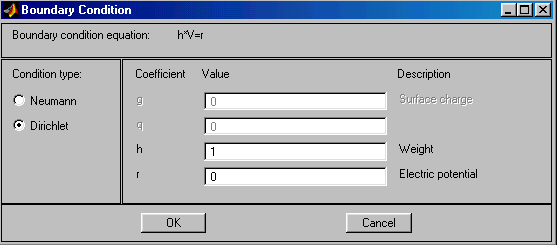
Рис.2.28. Диалоговое окно ввода граничных условий Дирихле
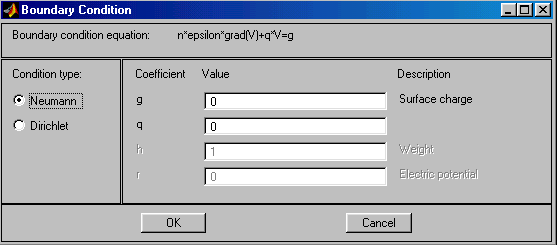
Рис.2.29. Диалоговое окно ввода граничных условий Неймана
На рис.2.28, 2.29 показан вид диалоговых окон ввода граничных условий для краевой задачи электростатики и значения соответствующих параметров по умолчанию. Как видно, ввод граничных условий осуществляется так же, как и в случае “Generic Scalar”. Отличие заключается только в обозначении искомой переменной (там u, а здесь V).
Краевая задача электростатики названа в PDETool "Electrostatics".
2.3.6. Магнитостатическая задача
Магнитостатическим называют магнитное поле, источниками которого являются постоянные электрические токи и остаточная намагниченность ферромагнитных тел. Рассмотрим уравнения магнитостатического поля в дифференциальной форме. Одно из этих уравнений получило название "закон полного тока":
rot H = ![]() , (2.18)
, (2.18)
где H - пространственное распределение вектора напряжённости магнитного поля; ![]() - векторное поле плотности тока (при анализе магнитостатического поля можно считать, что все токи обусловлены действием сторонних источников тока). Второе уравнение называется законом непрерывности линий магнитной индукции:
- векторное поле плотности тока (при анализе магнитостатического поля можно считать, что все токи обусловлены действием сторонних источников тока). Второе уравнение называется законом непрерывности линий магнитной индукции:
div B = 0, (2.19)
где B - пространственное распределение вектора магнитной индукции. Уравнения магнитостатики (2.18), (2.19) должны дополняться уравнением, описывающим магнитные свойства вещества и связывающим между собой векторы H и B. Такое уравнение называется уравнением материальной связи. В случае линейных изотропных диэлектрических свойств среды уравнение материальной связи между векторами H и B имеет вид:
B = ![]() H + Br или H =
H + Br или H =![]() (B - Br), (2.20)
(B - Br), (2.20)
где ![]() - абсолютная магнитная проницаемость среды;
- абсолютная магнитная проницаемость среды; ![]() = 4
= 4![]() *10-7 Гн/м - абсолютная магнитная проницаемость вакуума (основная магнитная постоян-ная);
*10-7 Гн/м - абсолютная магнитная проницаемость вакуума (основная магнитная постоян-ная); ![]() - относительная магнитная проницаемость среды; Br - векторное поле остаточной магнитной индукции среды;
- относительная магнитная проницаемость среды; Br - векторное поле остаточной магнитной индукции среды;![]() =
= ![]() - удельное магнитное сопротивление среды. Векторные поля и Br являются пространственно - распределёнными источниками магнитостатического поля.
- удельное магнитное сопротивление среды. Векторные поля и Br являются пространственно - распределёнными источниками магнитостатического поля.
Из уравнения (2.19) следует, что векторное поле B можно представить в виде ротора некоторого векторного поля:
B = rot A (2.21)
Здесь векторное поле A называется векторным магнитным потенциалом.
Подставив (2.21) в (2.20), а затем (2.20) в (2.18), получим
rot ![]() ( rot A) =
( rot A) = ![]() + rot
+ rot ![]() ( Br) (2.22)
( Br) (2.22)
(2.22) является уравнением магнитостатического поля относительно векторного магнитного потенциала. Если ввести обозначение A' = A/ ![]() - векторный магнитный потенциал, измеряемый в единицах тока, то (2.22) примет вид
- векторный магнитный потенциал, измеряемый в единицах тока, то (2.22) примет вид
rot (![]() rot A') =
rot A') = ![]() + rot (
+ rot ( ![]() Mr) , (2.23)
Mr) , (2.23)
где Mr = Br/ ![]() - векторное поле остаточной намагниченности вещества.
- векторное поле остаточной намагниченности вещества.
PDE Toolbox MATLAB не поддерживает наличие в расчётной области тел, обладающих остаточной намагниченностью. Значит, поддерживается только такая магнитостатическая задача, в которой Mr = 0.
В случае двумерного магнитостатического поля ![]() =
= ![]() *1z; A' = A'*1z . По-этому при Mr=0 в соответствии с правилами векторного анализа уравнение (2.23) примет следующий вид:
*1z; A' = A'*1z . По-этому при Mr=0 в соответствии с правилами векторного анализа уравнение (2.23) примет следующий вид:
-div ![]() ( grad A') =
( grad A') =![]() (2.24)
(2.24)
(такое преобразование корректно только в случае изотропных магнитных свойств вещества).
В PDETool краевая задача магнитостатики базируется на уравнении (2.24).
На рис.2.30 показан вид диалогового окна ввода коэффициентов PDE маг-нитостатической задачи. Здесь приняты следующие обозначения переменных (полей): A - векторный магнитный потенциал A'; B - вектор магнитной индук-ции; mu - относительная магнитная проницаемость; J - плотность тока. По умолчанию mu = 1; J = 1. Коэффициенты PDE, показанные на рис.2.30, можно задавать в виде скалярных полей с помощью выражений. Синтаксис такой же, как и в случае "Generic Scalar".
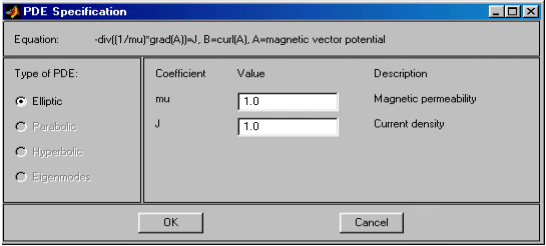
Рис.2.30. Диалоговое окно ввода коэффициентов PDE магнитостатики
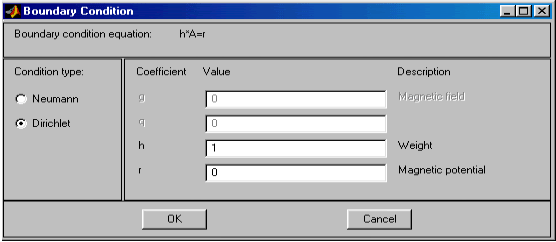
Рис.2.31. Диалоговое окно ввода граничных условий Дирихле
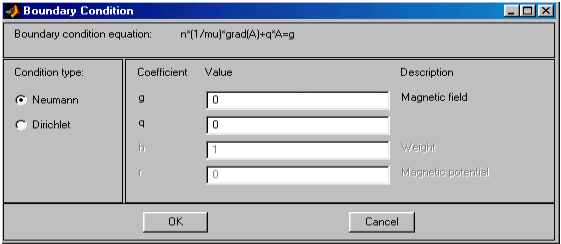
Рис.2.32. Диалоговое окно ввода граничных условий Неймана
На рис. 2.31, 2.32 показан вид диалоговых окон ввода граничных условий для краевой задачи магнитостатики и значения соответствующих параметров по умолчанию. Как видно, ввод граничных условий осуществляется так же, как и в случае "Generic Scalar". Отличие заключается только в обозначении искомой переменной (там u, а здесь A).
Краевая задача магнитостатики названа в PDETool "Magnetostatics".
2.3.7. Переменное гармоническое электромагнитное поле
Электромагнитное поле, в котором токи, заряды, потенциалы и составляющие векторов меняются по гармоническому закону с одной и той же заданной частотой, называется гармоническим электромагнитным полем. Для анализа таких полей в PDE Toolbox MATLAB используется метод комплексных ампли-туд, который применяется также в теории цепей синусоидального тока.
Пусть в некоторой точке наблюдения Q задан вектор N(Q,t), декартовы со-ставляющие которого изменяются во времени по гармоническому закону:
N(Q,t) = Nxm(Q)*sin( ![]() t+
t+ ![]() x)*1x+Nym(Q)*sin(
x)*1x+Nym(Q)*sin( ![]() t+
t+ ![]() y)*1y+Nzm(Q)*sin(
y)*1y+Nzm(Q)*sin( ![]() t+
t+ ![]() z)*1z = Nxsm(Q)*sin(
z)*1z = Nxsm(Q)*sin( ![]() t)*1x+Nxcm(Q)*cos(
t)*1x+Nxcm(Q)*cos(![]() t)*1x+Nysm(Q)*sin(
t)*1x+Nysm(Q)*sin( ![]() t)*1y+Nycm(Q)*cos(
t)*1y+Nycm(Q)*cos( ![]() t)*1y+Nzsm(Q)*sin(
t)*1y+Nzsm(Q)*sin( ![]() t)*1z+Nzcm(Q)*cos(
t)*1z+Nzcm(Q)*cos( ![]() t)*1z , (2.25)
t)*1z , (2.25)
где Nxm(Q), Nym(Q), Nzm(Q) - амплитуды x,y,z-составляющих вектора N(Q,t); ![]() x,
x, ![]() y,
y, ![]() z - начальные фазы x,y,z-составляющих вектора N(Q,t); Nxsm(Q), Nysm(Q), Nzsm(Q) - амплитуды x,y,z-синусных составляющих вектораN(Q,t); Nxcm(Q), Nycm(Q), Nzcm(Q) - амплитуды x,y,z-косинусных составляющих вектора N(Q,t);
z - начальные фазы x,y,z-составляющих вектора N(Q,t); Nxsm(Q), Nysm(Q), Nzsm(Q) - амплитуды x,y,z-синусных составляющих вектораN(Q,t); Nxcm(Q), Nycm(Q), Nzcm(Q) - амплитуды x,y,z-косинусных составляющих вектора N(Q,t); ![]() - круговая (циклическая) частота изменения вектора.
- круговая (циклическая) частота изменения вектора.
Комплексной амплитудой вектора N(Q,t), изменяющегося по гармоническому закону (2.25), называется вектор, определяемый выражением
Nm(Q) = Nxm(Q)*exp(j ![]() x)*1x+Nym(Q)*exp(j
x)*1x+Nym(Q)*exp(j ![]() y)*1y+Nzm(Q)*exp(j
y)*1y+Nzm(Q)*exp(j ![]() z)*1z = (Nxsm(Q)+j*Nxcm(Q))*1x+(Nysm(Q)+j*Nycm(Q))*1y+(Nzsm(Q)+j*Nzcm(Q))*1z . (2.26)
z)*1z = (Nxsm(Q)+j*Nxcm(Q))*1x+(Nysm(Q)+j*Nycm(Q))*1y+(Nzsm(Q)+j*Nzcm(Q))*1z . (2.26)
Комплексным действующим значением вектора N(Q,t) называется вектор, x,y,z-составляющими которого являются комплексные действующие значения этих же составляющих вектора N(Q,t):
N(Q) = Nx(Q)*exp(j ![]() x)*1x+Ny(Q)*exp(j
x)*1x+Ny(Q)*exp(j ![]() y)*1y+Nz(Q)*exp(j
y)*1y+Nz(Q)*exp(j ![]() z)*1z = (Nxs(Q)+j*Nxc(Q))*1x+(Nys(Q)+j*Nyc(Q))*1y+(Nzs(Q)+j*Nzc(Q))*1z , (2.27)
z)*1z = (Nxs(Q)+j*Nxc(Q))*1x+(Nys(Q)+j*Nyc(Q))*1y+(Nzs(Q)+j*Nzc(Q))*1z , (2.27)
где Nx(Q) = ![]() = Nxm(Q)/
= Nxm(Q)/![]() ; Ny(Q) = Nym(Q)/
; Ny(Q) = Nym(Q)/![]() ; Nz(Q) = Nzm(Q)/
; Nz(Q) = Nzm(Q)/![]() ; Nxs(Q) = Nxsm(Q)/
; Nxs(Q) = Nxsm(Q)/![]() ; Nxc(Q) = Nxcm(Q)/
; Nxc(Q) = Nxcm(Q)/![]() ; Nys(Q) = Nysm(Q)/
; Nys(Q) = Nysm(Q)/![]() ; Nyc(Q) = Nycm(Q)/
; Nyc(Q) = Nycm(Q)/![]() ; Nzs(Q) = Nzsm(Q)/
; Nzs(Q) = Nzsm(Q)/![]() ; Nzc(Q) = Nzcm(Q)/
; Nzc(Q) = Nzcm(Q)/![]() , т.е. N(Q) = Nm(Q)/
, т.е. N(Q) = Nm(Q)/![]() .
.
Соотношение (2.26) устанавливает взаимно-однозначное соответствие меж-ду гармонически изменяющимся вектором N(Q,t) и его комплексной амплиту-дой Nm(Q). Соотношение (2.27) устанавливает взаимно-однозначное соответст-вие между гармонически изменяющимся вектором N(Q,t) и его комплексным действующим значением N(Q). Соотношения (2.26), (2.27) позволяют исклю-чить время из уравнений математической физики.
В общем случае переменное электромагнитное поле в неподвижной среде описывается уравнениями Максвелла в пространственно-временной форме:
rot H = ![]() п - закон полного тока. Здесь
п - закон полного тока. Здесь ![]() п - векторное поле полной плот-ности электрического тока:
п - векторное поле полной плот-ности электрического тока: ![]() п =
п = ![]() +
+ ![]() пр+
пр+ ![]() см,
см, ![]() - плотность тока сторонних источников;
- плотность тока сторонних источников; ![]() пр - плотность тока проводимости;
пр - плотность тока проводимости; ![]() см - плотность тока смещения,
см - плотность тока смещения, ![]() см =
см = ![]() ;
;
rot (E-Eс) = -![]() - закон электромагнитной индукции. Здесь Eс - век-торное поле сторонней составляющей напряжённости электрического поля;
- закон электромагнитной индукции. Здесь Eс - век-торное поле сторонней составляющей напряжённости электрического поля;
div D =![]() - "теорема Гаусса" в дифференциальной форме;
- "теорема Гаусса" в дифференциальной форме;
div B = 0 - закон непрерывности линий магнитной индукции.
Уравнения Максвелла можно записать в терминах комплексных действую-щих значений векторов электромагнитного поля:
rot H = ![]() п - закон полного тока в комплексной форме;
п - закон полного тока в комплексной форме; ![]() п =
п =![]() +
+ ![]() пр+
пр+ ![]() см;
см; ![]() см = j
см = j![]() D;
D;
rot (E-Eс) = -j![]() B - закон электромагнитной индукции в комплексной форме;
B - закон электромагнитной индукции в комплексной форме;
div D = ![]() , div B = 0 - "теорема Гаусса" и закон непрерывности линий магнитной индукции в комплексной форме. Комплексную форму уравнений Максвелла иначе называют пространственно-частотной формой.
, div B = 0 - "теорема Гаусса" и закон непрерывности линий магнитной индукции в комплексной форме. Комплексную форму уравнений Максвелла иначе называют пространственно-частотной формой.
Последние уравнения Максвелла дополняются уравнениями материальной связи, связывающими между собой пары векторов (E, D), (H, B), (E, ![]() пр). Если среда обладает линейными электрофизическими свойствами (а только в этом случае может существовать гармоническое электромагнитное поле), то уравнения материальной связи имеют вид:
пр). Если среда обладает линейными электрофизическими свойствами (а только в этом случае может существовать гармоническое электромагнитное поле), то уравнения материальной связи имеют вид:
D = ![]() E - уравнение диэлектрических свойств вещества;
E - уравнение диэлектрических свойств вещества;
B = ![]() H или H =
H или H = ![]() B - уравнение магнитных свойств вещества;
B - уравнение магнитных свойств вещества;
![]() пр =
пр = ![]() E - уравнение электропроводящих свойств вещества (закон Ома в дифференциальной форме). В эти уравнения входят следующие параметры электрофизических свойств вещества на фиксированной частоте
E - уравнение электропроводящих свойств вещества (закон Ома в дифференциальной форме). В эти уравнения входят следующие параметры электрофизических свойств вещества на фиксированной частоте ![]() :
:
![]() - комплексная абсолютная диэлектрическая проницаемость вещества;
- комплексная абсолютная диэлектрическая проницаемость вещества;
![]() - комплексная абсолютная магнитная проницаемость вещества;
- комплексная абсолютная магнитная проницаемость вещества;
![]() - комплексное удельное магнитное сопротивление вещества;
- комплексное удельное магнитное сопротивление вещества;
![]() - удельная электрическая проводимость вещества.
- удельная электрическая проводимость вещества.
Введём понятие индуцированной плотности тока:
![]() и =
и = ![]() пр+
пр+ ![]() см = (
см = ( ![]() +
+![]() j
j![]() )E. Введём также понятие эффективного вектора элек-трического смещения: Dэфф=
)E. Введём также понятие эффективного вектора элек-трического смещения: Dэфф= ![]() и/(j
и/(j![]() ) = (
) = (![]() +
+![]() /(j
/(j![]() ))E =
))E = ![]() эфф*E. Последнее со-отношение можно назвать обобщённым уравнением электрических свойств вещества.
эфф*E. Последнее со-отношение можно назвать обобщённым уравнением электрических свойств вещества.
Часто при анализе гармонических электромагнитных полей корректное задание объёмно-распределённых источников ЭДС Eс вызывает значительные за-труднения. В таких случаях эти источники задают в виде поля -rot Eс, которое называют полем сторонней плотности магнитного тока ![]() м (
м ( ![]() м = -rot Eс).
м = -rot Eс).
С учётом введённых обозначений система уравнений Максвелла с уравне-ниями материальной связи имеет вид:
{ rot H = ![]() +j
+j![]()
![]() эфф*E; rot E = -
эфф*E; rot E = - ![]() м-j
м-j![]() B; H =
B; H = ![]() B } (2.28)
B } (2.28)
Для вывода уравнения математической физики, которое может служить ос-новой для постановки краевой задачи, нужно ввести понятие электродинамиче-ских потенциалов:
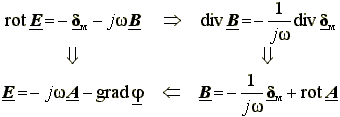 , (2.29)
, (2.29)
где A - комплексный векторный магнитный потенциал;![]() - комплексный скалярный электрический потенциал. Подставляя (2.29) в (2.28) и исключая из (2.28) векторы H, E, B, получим систему уравнений математической физики относительно электродинамических потенциалов:
- комплексный скалярный электрический потенциал. Подставляя (2.29) в (2.28) и исключая из (2.28) векторы H, E, B, получим систему уравнений математической физики относительно электродинамических потенциалов:
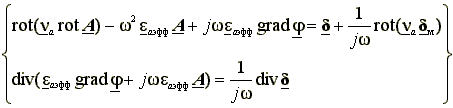 (2.30)
(2.30)
Система уравнений (2.30) справедлива для общего случая гармонических электромагнитных полей (трёхмерных и двумерных). В случае плоскопараллельного поля A = A*1z, ![]() =
= ![]() *1z, div A = 0,
*1z, div A = 0, ![]() = 0, следовательно при
= 0, следовательно при ![]() м = 0 система (2.30) сводится к одному PDE вида
м = 0 система (2.30) сводится к одному PDE вида
-div ( ![]() grad A) -
grad A) - ![]() A =
A = ![]()
или -div ( ![]() grad A) +
grad A) + ![]() A =
A =![]() (2.31)
(2.31)
Если ввести обозначение A' = A/![]() , то уравнение (2.31) примет следующий вид:
, то уравнение (2.31) примет следующий вид:
-div ( ![]() grad A') +
grad A') + 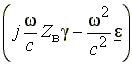 A' =
A' = ![]() , (2.32)
, (2.32)
где c = (![]()
![]() )-0.5 = 2.9979*108 м/с - скорость света в вакууме; Zв = (
)-0.5 = 2.9979*108 м/с - скорость света в вакууме; Zв = ( ![]() /
/![]() )0.5 = 376,7 Ом - волновое сопротивление вакуума [17]. Уравнение (2.32) можно записать также относительно z-составляющей комплексной напряжённости электрического поля:
)0.5 = 376,7 Ом - волновое сопротивление вакуума [17]. Уравнение (2.32) можно записать также относительно z-составляющей комплексной напряжённости электрического поля:
-div ( ![]() grad E) +
grad E) + .gif) E =
E = ![]() , (2.33)
, (2.33)
В PDETool краевая задача анализа гармонического электромагнитного поля базируется на уравнении (2.32) или (2.33) с нулевой правой частью (т.е. при ![]() =0). На рис.2.33 показан вид диалогового окна ввода коэффициентов PDE этой краевой задачи. Здесь приняты следующие обозначения переменных (полей): E - векторный магнитный потенциал A' (в случае (2.32)) или напряжённость электрического поля E (в случае (2.33)); mu - комплексная относительная магнитная проницаемость
=0). На рис.2.33 показан вид диалогового окна ввода коэффициентов PDE этой краевой задачи. Здесь приняты следующие обозначения переменных (полей): E - векторный магнитный потенциал A' (в случае (2.32)) или напряжённость электрического поля E (в случае (2.33)); mu - комплексная относительная магнитная проницаемость ![]() ; omega - отношение циклической частоты к скорости света в вакууме
; omega - отношение циклической частоты к скорости света в вакууме ![]() /c; sigma - произведение волнового сопротивления вакуума на удельную электрическую проводимость Zв
/c; sigma - произведение волнового сопротивления вакуума на удельную электрическую проводимость Zв![]() ; epsilon - комплексная относительная диэлектрическая проницаемость
; epsilon - комплексная относительная диэлектрическая проницаемость ![]() . По умолчанию mu = 1; omega = 1; sigma = 1; epsilon = 1. Коэффициенты PDE, показанные на рис.2.33, можно задавать в виде скалярных полей с помощью выражений. Синтаксис такой же, как и в случае "Generic Scalar".
. По умолчанию mu = 1; omega = 1; sigma = 1; epsilon = 1. Коэффициенты PDE, показанные на рис.2.33, можно задавать в виде скалярных полей с помощью выражений. Синтаксис такой же, как и в случае "Generic Scalar".
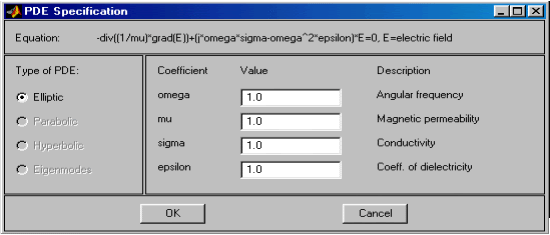
Рис.2.33. Диалоговое окно ввода коэффициентов PDE гармонического поля
Рис.2.34. Диалоговое окно ввода граничных условий Дирихле
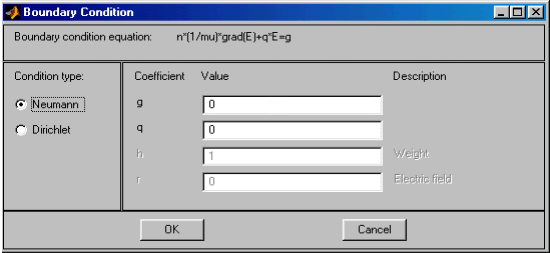
Рис.2.35. Диалоговое окно ввода граничных условий Неймана
На рис.2.34, 2.35 показан вид диалоговых окон ввода граничных условий для краевой задачи гармонического поля и значения соответствующих пара-метров по умолчанию. Как видно, ввод граничных условий осуществляется так же, как и в случае "Generic Scalar". Отличие заключается только в обозначении искомой переменной (там u, а здесь E).
Краевая задача анализа гармонического электромагнитного поля названа в PDETool "AC Power Electromagnetics".
2.3.8. Стационарное электрическое поле в проводящей среде
Электрическое поле в проводящей среде характеризуется пространственным распределением вектора напряженности электрического поля и вектора плотности тока.
Уравнения электрического поля в дифференциальной форме имеют вид:
rot (E - Eс) = 0 (2.34)
div ( ![]() +
+ ![]() пр) = 0 (2.35)
пр) = 0 (2.35)
![]() пр =
пр = ![]() E , (2.36)
E , (2.36)
где E - вектор полной напряжённости электрического поля; Eс - сторонняя составляющая вектора напряжённости электрического поля; ![]() - вектор сторонней плотности электрического тока;
- вектор сторонней плотности электрического тока; ![]() пр - вектор плотности тока проводимости;
пр - вектор плотности тока проводимости; ![]() - удельная электрическая проводимость вещества.
- удельная электрическая проводимость вещества.
(2.34) представляет собой второй закон Кирхгофа в дифференциальной форме, (2.35) - первый закон Кирхгофа в дифференциальной форме, (2.36) - закон Ома в дифференциальной форме.
При составлении математических моделей электрического поля в проводящей среде источником векторного поля E можно считать пространственное распределение вектора сторонней напряженности электрического поля Eс (объемно - распределенные источники ЭДС); источником векторного поля плотности тока проводимости ![]() пр можно считать пространственное распределение вектора сторонней плотности тока
пр можно считать пространственное распределение вектора сторонней плотности тока ![]() (объемно - распределенные источники тока).
(объемно - распределенные источники тока).
Из уравнения (2.34) следует, что E = Eс - grad![]() , где
, где ![]() - скалярный электрический потенциал. Если последнее соотношение подставить в (2.36) и полу-ченное выражение подставить в (2.35), то получим уравнение математической физики относительно скалярного электрического потенциала, описывающее стационарное электрическое поле в проводящей среде:
- скалярный электрический потенциал. Если последнее соотношение подставить в (2.36) и полу-ченное выражение подставить в (2.35), то получим уравнение математической физики относительно скалярного электрического потенциала, описывающее стационарное электрическое поле в проводящей среде:
-div (![]() grad
grad![]() ) = -div (
) = -div (![]() +
+ ![]() Eс) (2.37)
Eс) (2.37)
Сравнив уравнение (2.37) с уравнением электростатики (2.16), можно установить аналогию между электрическим полем постоянных токов в проводнике и электростатическим полем в диэлектрике.
Для сравнения запишем уравнения и физические величины, описывающие эти поля, и сведем их в таблицу.
| Электростатическое поле | Электрическое поле в проводящей среде |
| rot E = 0 | rot (E - Eс) = 0 |
| div D = |
div |
| D = |
|
| E = -grad |
E - Eс = -grad |
| D | |
| Pr | |
В PDETool краевая задача анализа стационарного электрического поля в проводящей среде базируется на уравнении (2.37).
На рис.2.36 показан вид диалогового окна ввода коэффициентов PDE этой краевой задачи. Здесь приняты следующие обозначения переменных (полей): V - скалярный электрический потенциал ![]() ; E - вектор индуцированной состав-ляющей напряжённости электрического поля; sigma - удельная электрическая проводимость вещества
; E - вектор индуцированной состав-ляющей напряжённости электрического поля; sigma - удельная электрическая проводимость вещества ![]() ; q - сток эквивалентной сторонней плотности тока
; q - сток эквивалентной сторонней плотности тока
-div (![]() +
+ ![]() Eс) или объёмная плотность тока источника, "закачиваемого" в ана-лизируемую систему из внешней цепи (измеряется а амперах на кубометр). По умолчанию sigma = 1; q = 1. Коэффициенты PDE, показанные на рис.2.36, мож-но задавать в виде скалярных полей с помощью выражений. Синтаксис такой же, как и в случае "Generic Scalar".
Eс) или объёмная плотность тока источника, "закачиваемого" в ана-лизируемую систему из внешней цепи (измеряется а амперах на кубометр). По умолчанию sigma = 1; q = 1. Коэффициенты PDE, показанные на рис.2.36, мож-но задавать в виде скалярных полей с помощью выражений. Синтаксис такой же, как и в случае "Generic Scalar".
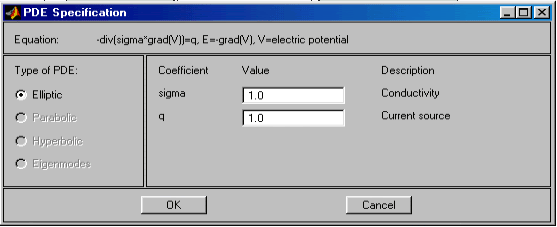
Рис.2.36. Диалоговое окно ввода коэффициентов PDE электрического поля
постоянного тока в проводящей среде
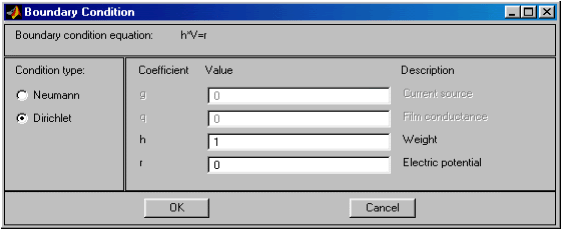
Рис.2.37. Диалоговое окно ввода граничных условий Дирихле
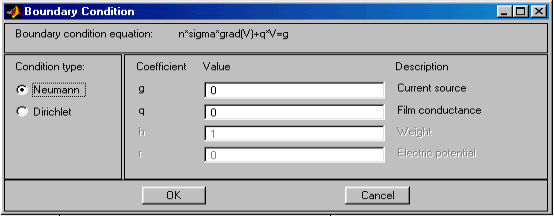
Рис.2.38. Диалоговое окно ввода граничных условий Неймана
На рис.2.37, 2.38 показан вид диалоговых окон ввода граничных условий для краевой задачи анализа стационарного электрического поля в проводящей среде и значения соответствующих параметров по умолчанию. Как видно, ввод граничных условий осуществляется так же, как и в случае "Generic Scalar". От-личие заключается только в обозначении искомой переменной (там u, а здесь V).
Краевая задача анализа электрического поля постоянного тока названа в PDETool "Conductive Media DC".
Краевая задача магнитостатики названа в PDETool "Magnetostatics".
2.3.9. Теплопередача
Тепловое поле характеризуется пространственным распределением температуры и плотности потока тепловой мощности.
Уравнения теплового поля в дифференциальной форме имеют вид:
div pт = Q - ![]() U/
U/ ![]() t (2.38)
t (2.38)
pт = -k*grad T (2.39)
![]() U/
U/ ![]() t =
t = ![]() (
( ![]() CT)/
CT)/ ![]() t =
t = ![]() C
C ![]() T/
T/ ![]() t , (2.40)
t , (2.40)
где pт - плотность потока тепловой мощности, Вт/м2; Q - объёмная плотность мощности сторонних источников тепла, Вт/м3; U - объёмная плотность внутренней тепловой энергии вещества, Дж/м3; k - теплопроводность вещества, ВтК-1м-1; T - температура, К; ![]() - плотность вещества, кг/м3; C - удельная теплоёмкость вещества, Дж кг-1 К-1. (2.38) - фундаментальное уравнение теплового поля; (2.39) - уравнение, описывающее теплопроводящие свойства вещества; (2.40) - уравнение, описывающее динамические тепловые свойства вещества.
- плотность вещества, кг/м3; C - удельная теплоёмкость вещества, Дж кг-1 К-1. (2.38) - фундаментальное уравнение теплового поля; (2.39) - уравнение, описывающее теплопроводящие свойства вещества; (2.40) - уравнение, описывающее динамические тепловые свойства вещества.
Подставив (2.39) и (2.40) в (2.38), получим:
![]() C
C ![]() T/
T/ ![]() t - div(k*grad T) = Q (2.41)
t - div(k*grad T) = Q (2.41)
(2.41) - уравнение теплопроводности относительно поля температур. Это уравнение описывает динамический режим теплового поля. В статическом режиме ![]() T/
T/ ![]() t = 0, поэтому уравнение теплопроводности приобретает следующий вид:
t = 0, поэтому уравнение теплопроводности приобретает следующий вид:
-div(k*grad T) = Q (2.42)
(2.41) называют параболическим уравнением, а (2.42) - эллиптическим.
В PDETool краевая задача теплопроводности базируется на уравнениях (2.41), (2.42).
На рис.2.39 показан вид диалогового окна ввода коэффициентов PDE этой краевой задачи. Здесь приняты следующие обозначения переменных (полей): rho - плотность вещества ![]() ; C - удельная теплоёмкость вещества C; k - теплопроводность вещества k; Q - объёмная плотность мощности сторонних источников тепла Q. В поле "Equation" этого окна показан вид уравнения теплопроводности. Второе слагаемое правой части уравнения в этом окне записано некорректно. "h*(Text-T)" - это не объёмно распределённый источник тепла, а составляющая плотности потока тепловой мощности через внешнюю границу расчётной области, пропорциональная разности температур окружающей среды и границы расчётной области. На самом деле это слагаемое относится к граничным условиям, которые в задачах электромагнетизма называются "импедансными". Здесь h - коэффициент конвективного или кондуктивного теплообмена расчётной области с окружающей средой, Вт м-2К-1; Text - температура окружающей среды при бесконечном удалении от расчётной области (здесь предполагается, что расчётная область окружена бесконечной однородной средой без источников тепла); T - температура границы расчётной области. По умолчанию rho=1, C=1, k=1, Q=1, h=1, Text=0. В режиме "Elliptic" ввод коэффициентов rho и C запрещён.
; C - удельная теплоёмкость вещества C; k - теплопроводность вещества k; Q - объёмная плотность мощности сторонних источников тепла Q. В поле "Equation" этого окна показан вид уравнения теплопроводности. Второе слагаемое правой части уравнения в этом окне записано некорректно. "h*(Text-T)" - это не объёмно распределённый источник тепла, а составляющая плотности потока тепловой мощности через внешнюю границу расчётной области, пропорциональная разности температур окружающей среды и границы расчётной области. На самом деле это слагаемое относится к граничным условиям, которые в задачах электромагнетизма называются "импедансными". Здесь h - коэффициент конвективного или кондуктивного теплообмена расчётной области с окружающей средой, Вт м-2К-1; Text - температура окружающей среды при бесконечном удалении от расчётной области (здесь предполагается, что расчётная область окружена бесконечной однородной средой без источников тепла); T - температура границы расчётной области. По умолчанию rho=1, C=1, k=1, Q=1, h=1, Text=0. В режиме "Elliptic" ввод коэффициентов rho и C запрещён.
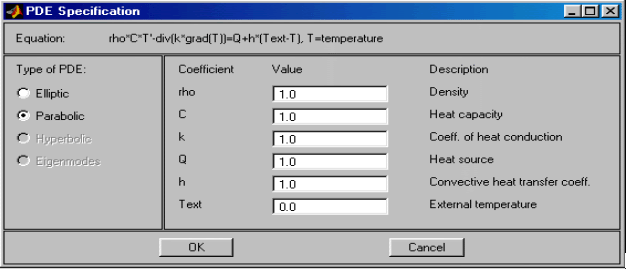
Рис.2.39. Диалоговое окно ввода коэффициентов PDE теплопроводности
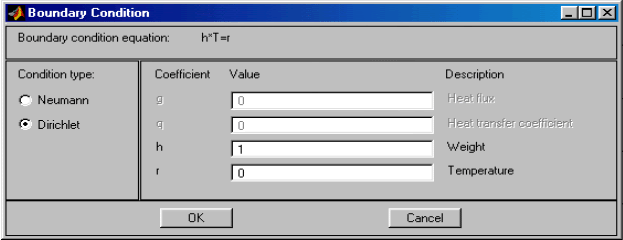
Рис.2.40. Диалоговое окно ввода граничных условий Дирихле
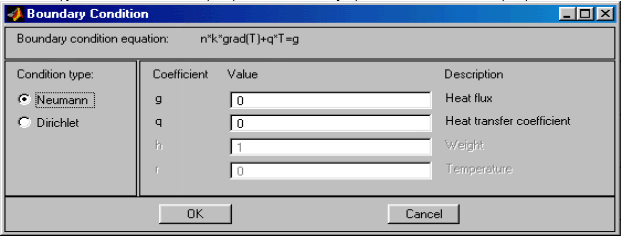
Рис.2.41. Диалоговое окно ввода граничных условий Неймана
На рис.2.40, 2.41 показан вид диалоговых окон ввода граничных условий для краевой задачи теплопроводности и значения соответствующих параметров по умолчанию. Как видно, ввод граничных условий осуществляется так же, как и в случае "Generic Scalar". Отличие заключается только в обозначении искомой переменной (там u, а здесь T).
Краевая задача анализа теплового поля названа в PDETool "Heat Transfer".
2.3.10. Уравнение диффузии
Пространственное распределение концентрации некоторого вещества-примеси в неподвижной среде - "растворителе" описывается уравнением диффузии:
![]() c/
c/ ![]() t - div(D*grad c) = Q , (2.43)
t - div(D*grad c) = Q , (2.43)
где c - объёмная концентрация, кг/м3; D - коэффициент диффузии, м2/с;
D*grad c - плотность потока переноса примеси в процессе диффузии, кг м-2 с-1;
Q - объёмная плотность источника примеси, кг м-3 с-1.
Уравнение (2.43) описывает динамический режим поля концентрации примеси в неподвижном "растворителе". В статическом режиме ![]() c/
c/ ![]() t = 0, поэтому уравнение диффузии приобретает следующий вид:
t = 0, поэтому уравнение диффузии приобретает следующий вид:
-div(D*grad c) = Q , (2.44)
(2.43) называют параболическим уравнением, а (2.44) - эллиптическим.
В PDETool краевая задача диффузии базируется на уравнениях (2.43), (2.44).
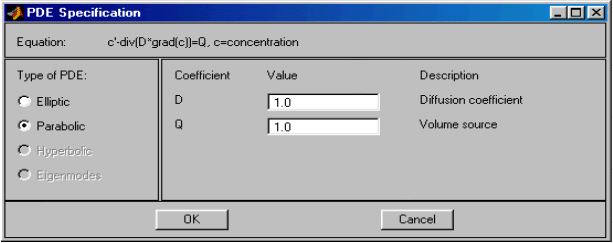
Рис.2.42. Диалоговое окно ввода коэффициентов PDE диффузии
На рис.2.42 показан вид диалогового окна ввода коэффициентов PDE этой краевой задачи. Здесь приняты следующие обозначения переменных (полей): D - коэффициент диффузии D; Q - объёмная плотность источника примеси Q. Эти коэффициенты в диалоговом окне вводятся одинаково независимо от режима "Elliptic" или "Parabolic". По умолчанию D=1, Q=1.
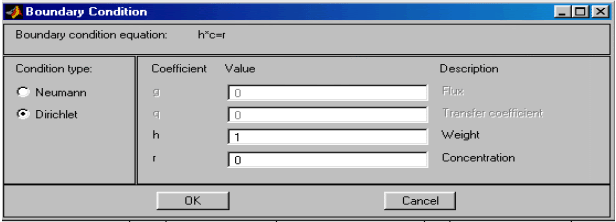
Рис.2.43. Диалоговое окно ввода граничных условий Дирихле
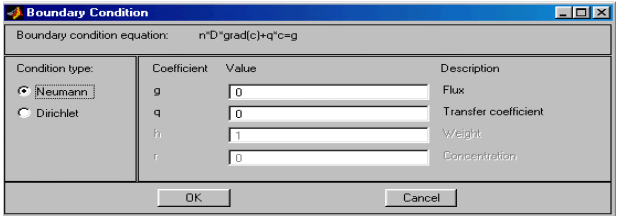
Рис.2.44. Диалоговое окно ввода граничных условий Неймана
На рис.2.43, 2.44 показан вид диалоговых окон ввода граничных условий для краевой задачи диффузии и значения соответствующих параметров по умолчанию. Как видно, ввод граничных условий осуществляется так же, как и в случае "Generic Scalar". Отличие заключается только в обозначении искомой переменной (там u, а здесь c).
Краевая задача анализа теплового поля названа в PDETool "Diffusion".
2.4. Режимы работы приложения PDETool
2.4.1. Режим ввода (прорисовки) геометрии
Приложение PDETool переходит в режим ввода (прорисовки) геометрии по команде Draw Mode. В этом режиме возможно создание, уничтожение и изменение геометрических объектов в расчётной области (см. 2.1.4). Геометрическим объектом называется стандартная геометрическая фигура, поддерживаемая PDETool, входящая в состав расчётной модели и отображаемая в поле axes PDETool. Стандартными геометрическими фигурами являются прямоугольник (в частном случае квадрат), эллипс (в частном случае круг), многоугольник.
Создание геометрических объектов осуществляется командами меню группы “Draw": "Rectangle/square", "Rectangle/square (centered)", "Ellipse/circle", "Ellipse/circle (centered)", "Polygon", – или при помощи соответствующих кнопок инструментальной панели. Созданные геометрические объекты отображаются в поле axes закрашенными серым цветом неокаймлёнными областями. Внутри каждой такой геометрической фигуры изображается метка (идентификатор) объекта (см. рис. 2.4, 2.5 – метки E1, R1). Геометрические объекты в PDETool можно создавать с помощью функций PDE Toolbox MATLAB из командного окна или из выполняемых m-файлов. Такими функциями являются pderect, pdecirc, pdeellip, pdepoly. Если геометрические объекты создаются командами меню или инструментальными кнопками, то уникальные имена (метки) им присваиваются автоматически. Если объект создаётся функцией PDE Toolbox MATLAB, то его идентификатор задаётся одним из входных параметров функции.
Один или несколько геометрических объектов можно выделить. Чтобы выделить один объект, нужно сделать по нему или по его идентификатору одинарный щелчок мышью. Чтобы выделить несколько геометрических объектов, нужно, удерживая клавишу Shift, сделать одинарные щелчки по выбранным объектам или их идентификаторам. Визуальным признаком выделенного объекта является окаймление его чёрным контуром. На рис. 2.4, 2.5 оба геометрических объекта (эллипс E1 и прямоугольник R1) являются выделенными. Все геометрические объекты расчётной области можно выделить командой меню Edit/Select All или нажатием клавиши Ctrl+A. Полностью отменить выделение можно, сделав щелчок мышью вне геометрических объектов, но в поле axes.
Удалить выделенные объекты можно с помощью команды меню Edit/Clear или нажатием клавиши Ctrl+R или Delete. Если выделенных объектов нет, то данная команда или нажатие указанных клавиш не приведёт ни к каким изменениям.
В PDETool поддерживается три вида изменений геометрических объектов: поворот вокруг некоторого центра, параллельный перенос и изменение размеров. Поворот совокупности выделенных объектов вокруг произвольного центра или вокруг “центра масс” достаточно подробно описан в 2.1.4 (команда Draw/Rotate) и проиллюстрирован рис. 2.4, 2.5. Чтобы провести параллельный перенос, нужно подвести указатель мыши к одному из выделенных объектов, нажать левую кнопку мыши и, удерживая её, переместить указатель мыши. Вслед за ним будут перемещаться все выделенные объекты.
Для редактирования свойств геометрического объекта (включая изменение размеров) нужно сделать по нему двойной щелчок мышью. В результате двойного щелчка развернётся диалоговое окно. Вид диалогового окна зависит от типа геометрического объекта.
Рис. 2.45. Вид диалогового окна редактирования свойств круга
На рис. 2.45 показан вид диалогового окна редактирования свойств круга. X–center, Y–center – координаты центра круга. Radius – радиус круга. Name – идентификатор (метка) объекта. Все эти параметры могут редактироваться. Нажатие кнопки OK приведёт к закрытию диалогового окна и изменению свойств объекта, что сразу же будет видно в поле axes. Нажатие кнопки Cancel приведёт к закрытию диалогового окна и игнорированию изменений в строках редактирования. На рис. 2.46 показан вид диалогового окна редактирования свойств эллипса. A-semiaxes – первая полуось эллипса. B-semiaxes – вторая полуось. Rotation – угол поворота осей эллипса (в градусах). Положительное направление поворота – против часовой стрелки. Если Rotation=0, то первая ось горизонтальная, а вторая – вертикальная.
Рис. 2.46. Вид диалогового окна редактирования свойств эллипса
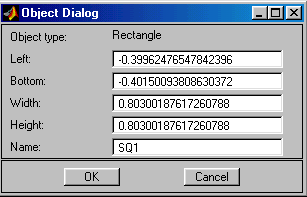
Рис. 2.47. Вид диалогового окна редактирования свойств прямоугольника
Объектом “Прямоугольник” (“Rectangle”) называется прямоугольник, стороны которого параллельны координатным осям. Вид диалогового окна редактирования свойств прямоугольника показан на рис. 2.47. Left – координата x самой левой точки прямоугольника. Bottom – координата y самой нижней точки прямоугольника. Width – ширина прямоугольника (в направлении оси x). Height – высота (в направлении оси y).
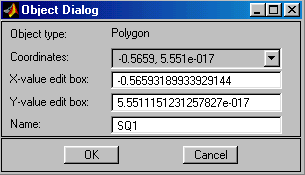
Рис. 2.48. Вид диалогового окна редактирования свойств многоугольника
Диалоговое окно редактирования свойств многоугольника, показанное на рис. 2.48, содержит ниспадающее меню координат вершин (“Coordinates”), строку редактирования координаты x выбранной вершины (“X-value edit box”), строку редактирования координаты y выбранной вершины (“Y-value edit box”), строку редактирования идентификатора (имени) графического объекта (“Name”). Редактирование свойств многоугольника с помощью диалогового окна, изображённого на рис. 2.48, производится следующим образом: 1) с помощью ниспадающего меню выбирается нужная вершина, 2) вводятся новые значения координат x и y этой вершины в строки редактирования “X-value edit box” и “Y-value edit box", 3) операции 1 и 2 повторяются для всех требуемых вершин, 4) при необходимости вводится новое имя в строку “Name”, 5) нажимается кнопка OK.
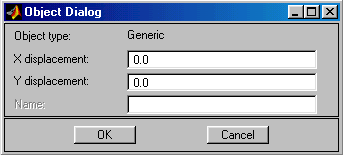
Рис. 2.49. Диалоговое окно параллельного переноса совокупности выделенных объектов
Если в расчётной области выделено несколько графических объектов, то двойной щелчок в одном из выделенных объектов приведёт к развёртыванию диалогового окна, изображённого на рис. 2.49. Строки ввода “X displacement” и “Y displacement” задают x- и y- составляющие вектора параллельного переноса. Нажатие кнопки OK приведёт к выполнению переноса, что сразу же станет заметно в поле axes.
Метод “двойного щелчка” может быть весьма полезен при редактировании свойств графических объектов, если требуется их точное позиционирование в расчётной области. Если во время двойного щелчка левой кнопкой мыши её указатель переместится, то текущие значения параметров свойств объекта могут измениться. Для предотвращения этого нежелательного явления двойной щелчок можно делать правой кнопкой мыши.
В режиме Draw Mode доступна для редактирования строка ввода PDETool "Set formula”, расположенная под панелью инструментов. Более подробно об этом написано в подразделе 2.2.
Переменные описания геометрии PDE модели могут быть экспортированы в базовую рабочую область MATLAB. Команда экспорта описана в 2.1.4. Там же показано диалоговое окно экспорта (рис. 2.6). По умолчанию имена этих переменных gd, sf, ns:
gd – матрица геометрических объектов (каждый столбец соответствует объекту). Первый элемент столбца – код типа объекта: 1 – круг, 2 – многоугольник, 3 – прямоугольник, 4 – эллипс. Описание элементов столбцов матрицы gd сведено в таблицу.
| Элементы столбца | Типы геометрических объектов | |||
| 1 – тип объекта |
1 – круг | 2 – многоугольник | 3 – прямоугольник | 4 – эллипс |
| 2 | x- координата центра | число вершин | 4 | x- координата центра |
| 3 | y- координата центра | x- координаты всех вершин | x- координаты четырёх вершин | y- координата центра |
| 4 | радиус | первая полуось | ||
| 5 | 0 | вторая полуось | ||
| 6 | 0 | угол поворота осей (градусы) | ||
| 7 | 0 | y- координаты всех вершин в той же последовательности | y- координаты этих же четырёх вершин | 0 |
| 8 | 0 | 0 | ||
| 9 | 0 | 0 | ||
| 10 | 0 | 0 | ||
| 11 | 0 | 0 | 0 | 0 |
sf – строка символов, содержащая формулу геометрии расчётной области. Её синтаксис описан в 2.2.
ns – числовая матрица, каждому столбцу которой соответствует геометрический объект. Элементами столбца являются ASCII-коды символов имени соответствующего объекта. Число строк матрицы ns равно числу символов самого длинного имени геометрического объекта. Более короткие имена дополняются нулевыми кодами.
2.4.2. Режим ввода граничных условий
Приложение PDETool переходит в режим ввода граничных условий по команде Boundary Mode. В этом режиме возможен ввод и редактирование граничных условий как для всей границы расчётной области, так и для отдельных её сегментов. Граничным сегментом называется геометрически и логически однородный участок границы расчётной области или границы раздела двух зон. В первом случае граничный сегмент называют внешним, а во втором случае – внутренним. В этом режиме возможно также выделение либо отмена выделения любой совокупности внешних или внутренних сегментов. Возможно удаление внутренних сегментов. В PDETool внешние сегменты отображаются красными или синими криволинейными отрезками (см. рис. 2.8, 2.9). Стрелки на этих отрезках указывают положительное направление обхода. Красный цвет указывает на заданные граничные условия Дирихле, а синий – Неймана. Каждый внешний сегмент может принадлежать только одной зоне. Внутренние сегменты отображаются криволинейными отрезками серого цвета без стрелок. Выделенные сегменты (внешние и внутренние) отображаются чёрным цветом.
Одинарный щелчок левой или правой кнопкой мыши по сегменту приводит к его выделению с отменой выделения всех остальных сегментов. Такое же действие производится, если при щелчке правой кнопкой удерживается клавиша Shift. Одинарный щелчок левой кнопкой мыши по сегменту с удержанием клавиши Shift приводит к инвертированию его выделения без отмены выделения всех остальных сегментов. Выделение и отмена выделения внешних и внутренних сегментов происходит совершенно независимо друг от друга.
Двойной щелчок левой или правой кнопкой мыши по невыделенному внешнему сегменту приводит к развёртыванию диалогового окна ввода граничных условий (см. рис. 2.7) для этого сегмента независимо от ранее сделанных выделений. Двойной щелчок левой или правой кнопкой мыши по выделенному внешнему сегменту приводит к развёртыванию диалогового окна ввода граничных условий (см. рис. 2.7) для всей совокупности выделенных внешних сегментов.
Двойной щелчок левой кнопкой мыши по внешнему сегменту с одновременным удержанием клавиши Shift приводит к инвертированию выделения данного сегмента и раскрытию диалогового окна ввода граничных условий для полученной совокупности внешних сегментов. Удержание клавиши Shift никак не влияет на действия, производимые в результате двойного щелчка правой кнопкой мыши по внешнему или внутреннему сегменту.
Для внутренних сегментов двойной щелчок левой кнопкой мыши полностью аналогичен одинарному щелчку; одинарные и двойные щелчки правой кнопкой мыши не вызывают никаких действий. Ввод граничных условий для внутренних сегментов запрещён. Разрешена только операция удаления с помощью команд меню (см. 2.1.5).
Для внешних сегментов разрешённой является только операция ввода граничных условий. Практически все возможные виды диалоговых окон показаны на рис. 2.7, 2.28, 2.29, 2.31, 2.32, 2.34, 2.35, 2.37, 2.38, 2.40, 2.41, 2.43, 2.44.
Переменные описания граничных условий PDE модели могут быть экспортированы в базовую рабочую область MATLAB. Команда экспорта описана в 2.1.5. Там же показано диалоговое окно экспорта (рис. 2.10). По умолчанию имена этих переменных g, b:
g – матрица описания граничных сегментов, каждому столбцу которой соответствует граничный сегмент. Первая строка матрицы g содержит коды типов граничных сегментов. Вторая и третья строки – начальные и конечные x координаты сегментов. Четвёртая и пятая строки – начальные и конечные y координаты сегментов. Шестая и седьмая строки содержат номера зон, примыкающих слева и справа к граничному сегменту.
Геометрические типы граничных сегментов:
-
Дуга окружности. Код типа = 1. Строки 8, 9 – координаты центра окружности.
-
Отрезок прямой. Код типа = 2.
-
Дуга эллипса. Код типа = 4. Строки 8, 9 – координаты центра эллипса. Строки 10, 11 – большая и малая полуоси эллипса. Строка 12 - угол поворота в радианах против часовой стрелки относительно начального положения эллипса.
Неописанные элементы строк матрицы g содержат нули.
b – матрица описания граничных условий, каждому столбцу которой соответствует граничный сегмент.
Строка 1: 1 – внешний сегмент; 0 – внутренний;
строка 2: 1 – Дирихле; 2 – Неймана;
строка 3: длина выражения для коэффициента q (см. диалоговые окна);
строка 4: длина выражения для коэффициента g;
строка 5: длина выражения для коэффициента h;
строка 6: длина выражения для коэффициента r;
далее подряд ASCII-коды выражений для q, g, h, r.
В случае необходимости столбцы матрицы b дополняются нулями.
Матрица b может использоваться в качестве входного аргумента функций adaptmesh, assemb, assempde,hyperbolic, parabolic, pdeeig, pdenonlin, poisolv.
2.4.3. Режим ввода параметров (коэффициентов) PDE
Приложение PDETool переходит в режим ввода коэффициентов PDE по команде PDE Mode. В этом режиме возможен ввод распределения коэффициентов PDE в зонах расчётной области. Возможно также выделение и отмена выделения зон.
Одинарный щелчок левой или правой кнопкой мыши по зоне приводит к её выделению с отменой выделения всех остальных зон. Такое же действие производится, если при щелчке правой кнопкой удерживается клавиша Shift. Одинарный щелчок левой кнопкой мыши по зоне с удержанием клавиши Shift приводит к инвертированию её выделения без отмены выделения всех остальных зон.
Двойной щелчок левой или правой кнопкой мыши по невыделенной зоне приводит к развёртыванию диалогового окна ввода коэффициентов PDE (см. список стандартных краевых задач 2.3). для этой зоны независимо от ранее сделанных выделений. Двойной щелчок левой или правой кнопкой мыши по выделенной зоне приводит к развёртыванию диалогового окна ввода коэффициентов PDE (см. 2.3) для всей совокупности выделенных зон.
Двойной щелчок левой кнопкой мыши по зоне с одновременным удержанием клавиши Shift приводит к инвертированию выделения данной зоны и раскрытию диалогового окна ввода коэффициентов PDE для полученной совокупности зон. Удержание клавиши Shift никак не влияет на действия, производимые в результате двойного щелчка правой кнопкой мыши по зоне.
Диалоговые окна ввода коэффициентов PDE, а также синтаксис выражений, вписываемых в строки ввода, показаны в подразделе 2.3 данного пособия.
Переменные описания распределения коэффициентов PDE в расчётной области могут быть экспортированы в базовую рабочую область MATLAB. Команда экспорта описана в 2.1.6. Там же показано диалоговое окно экспорта (рис. 2.10). По умолчанию имена этих переменных c, a, f, d:
c, a, f, d – конечноэлементное распределение коэффициентов c, a, f, d в уравнениях (2.1), (2.2), (2.3), (2.4). Если краевая задача связана с решением одного скалярного PDE, то эти переменные представляют собой строки символов с выражениями, которые были вписаны в строки ввода диалогового окна ввода коэффициентов PDE. Если при вводе какого-либо коэффициента заданы разные выражения для разных зон, то соответствующая переменная MATLABа представляет собой строку символов, состоящую из последовательности выражений для зон, разделённых восклицательным знаком, например,
a =
1+sqrt(x^2+y^2)!sin(x+y)!2*x
В данном примере в зоне №1 a=’1+sqrt(x^2+y^2)’, и зоне №2 a=’sin(x+y)’, в зоне №3 a=’2*x’.
Если краевая задача связана с решением системы двух скалярных PDE вида (2.6), (2.7), (2.8), (2.9), то эти переменные представляют собой матрицы символов:
f – матрица символов, первая строка которой представляет собой выражение для правой части первого PDE, вторая строка – выражение для правой части второго PDE. Ниже показан пример матрицы f для случая, когда в разных зонах заданы разные выражения:
f =
0.0!x+y!1.0
1.0!1.0!1.0
a – матрица символов, состоящая из четырёх строк: первая строка – выражение для a11, вторая – для a21, третья – для a12, четвёртая – для a22. Ниже показан пример матрицы a для случая, когда в разных зонах заданы разные выражения:
a =
1.0!1.0!1.0
2.0!2.0!2.0
3.0!sin(sqrt(x^2+y^2))!3.0
4.0!4.0!4.0
В этом примере в зоне №2 коэффициент a12 представлен выражением, описывающим зависимость этого коэффициента от координат x и y. Из этого примера видно, что в случае необходимости строки символов в конце дополняются пробелами.
Матрица d полностью аналогична матрице a.
Если матричный коэффициент [c] в уравнениях (2.6), (2.7), (2.8), (2.9) можно представить в виде произведения скалярной величины на единичную матрицу eye(2,2), то переменная c представляет собой строку символов с выражением, описывающим распределение этой скалярной величины в расчётной области. Если для разных зон заданы разные выражения, то переменная c представляет собой строку символов, состоящую из последовательности выражений для зон, разделённых восклицательным знаком, например,
c =
y+1.0!x+y!x+1.0
Если матрица [c] в уравнениях (2.6), (2.7), (2.8), (2.9) является диагональной, то переменная c представляет собой матрицу символов, состоящую из шести строк: 1-я строка – выражение для коэффициента с11, 2-я строка – нуль, 3-я строка – выражение для коэффициента с11, 4-я строка – выражение для коэффициента с22, 5-я строка – нуль, 6-я строка – выражение для коэффициента с22. Например,
c =
1.0
0
1.0
y+1.0
0
y+1.0
Если для разных зон заданы разные выражения, то каждая строка матрицы символов c представляет собой последовательность выражений для зон, разделённых восклицательным знаком, например,
c =
1.0!x+2.0!1.0
0!0!0
1.0!x+2.0!1.0
y+1.0!y+1.0!y+2.0
0!0!0
y+1.0!y+1.0!y+2.0
Если матрица [c] в уравнениях (2.6), (2.7), (2.8), (2.9) является полной, то независимо от её симметрии переменная c представляет собой матрицу символов, состоящую из 16 строк: 1-я строка – выражение для коэффициента с11, 2-я строка – нуль, 3-я строка – нуль, 4-я строка – выражение для коэффициента с11, 5-я строка – выражение для коэффициента с21, 6-я строка – нуль, 7-я строка – нуль, 8-я строка – выражение для коэффициента с21, 9-я строка – выражение для коэффициента с12, 10-я строка – нуль, 11-я строка – нуль, 12-я строка – выражение для коэффициента с12, 13-я строка – выражение для коэффициента с22, 14-я строка – нуль, 15-я строка – нуль, 16-я строка – выражение для коэффициента с22. Например,
c =
1.0
0
0
1.0
x+2
0
0
x+2
x+2
0
0
x+2
y+1.0
0
0
y+1.0
Если для разных зон заданы разные выражения, то каждая строка матрицы символов c представляет собой последовательность выражений для зон, разделённых восклицательным знаком. Это видно из предыдущих примеров.
Матрицы c, a, f, d могут использоваться в качестве входных аргументов функций adaptmesh, assemb, assempde,hyperbolic, parabolic, pdeeig, pdenonlin, poisolv.
2.4.4. Режим генерации и изменения конечноэлементной сетки
GUI-приложение PDETool переключается в режим генерации и изменения конечноэлементной сетки по одной из команд меню группы Mesh: Mesh Mode, Initialize Mesh, Refine Mesh, Jiggle Mesh, Undo Mesh Change, Display Triangle Quality (см. 2.1.7). В режиме Mesh Mode в поле axes фигуры PDETool видно изображение конечноэлементной сетки (рис. 2.14, 2.15, 2.16). Синие линии (рис. 2.14, 2.15) – рёбра конечных элементов, красные линии – границы расчётной области или линии раздела зон.
По команде Mesh/Parameters можно установить параметры режима генерации конечноэлементной сетки (см. рис. 2.17):
-
Maximum edge size – максимальная длина стороны генерируемых треугольников (по умолчанию – пустое значение, т.е. не лимитируется);
-
Mesh growth rate – максимальный показатель нерегулярности треугольников. В PDETool и вообще в PDE Toolbox MATLAB в качестве такого показателя используется отношение максимальной длины стороны треугольника к минимальной;
-
Кнопка Jiggle mesh – если эта кнопка включена, то в процессе генерации сетки производится также её регуляризация, в противном случае регуляризация не производится. Регуляризация сводится к смещению узлов сетки, чтобы показатель регулярности треугольников был максимален;
Параметр Jiggle mode может принимать одно из трёх возможных значений (они вводятся с помощью ниспадающего меню):
- on – независимо от результата по команде Jiggle mesh выполняется заданное число итераций регуляризации сетки;
- optimize minimum – критерием оптимизации сетки является минимальный по всей сетке показатель регулярности треугольника; итерационный процесс досрочно завершается, если этот показатель достигнет значения 0.6;
- optimize mean – критерием оптимизации сетки является средний по всей сетке показатель регулярности треугольника; итерационный процесс досрочно завершается, если этот показатель достигнет значения 0.9; -
Number of jiggle iterations – максимальное число итераций регуляризации сетки (пустое значение соответствует одной итерации, если Jiggle mode = on; 20 итерациям в противном случае);
-
Параметр Refinement method может принимать одно из двух возможных значений (они вводятся с помощью ниспадающего меню):
- regular – “регулярное переопределение”, когда каждый переопределяемый треугольник разделяется на четыре треугольника;
- longest – треугольники делятся на два так, что большая сторона делится пополам.
Показателем регулярности треугольника называется безразмерная величина, определяемая по формуле:
q = 4*sqrt(3)*a/(h12+h22+h32), (2.45)
где a – площадь треугольника; h1, h2, h3 – длины сторон треугольника.
Экспорт конечноэлементной сетки в базовую рабочую область осуществляется командой Export Mesh. Вид диалогового окна экспорта показан на рис. 2.18. Рассмотрим назначение и структуру матриц описания конечноэлементной сетки.
Первая переменная (по умолчанию её имя p) – матрица узлов конечноэлементной сетки, каждый столбец которой соответствует узлу. Первая строка – координаты x узлов, вторая строка – координаты y узлов.
Вторая переменная (по умолчанию её имя e) – матрица граничных элементов на границах раздела зон или всей расчётной области:
- столбцам соответствуют граничные элементы (стороны конечных элементов, принадлежащие границам раздела зон или границе расчётной области);
- первые две строки – номера начальных и конечных узлов граничных элементов;
- строки 3, 4 – длина “дуги” от начала граничного сегмента до начального и конечного узла граничного элемента, отнесённая к длине “дуги” граничного сегмента;
- строка 5 – номера граничных сегментов (см. 2.1.5, 2.4.2), которым принадлежат граничные элементы;
- строки 6, 7 – номера зон, примыкающих слева и справа к граничным элементам (“слева” и “справа” – имеется в виду при движении от начала к концу граничного сегмента, т.е. по направлению его обхода);
Третья переменная (по умолчанию её имя t) – матрица треугольных конечных элементов (столбцам соответствуют треугольники):
- t(1:3,ie) – глобальные номера узлов треугольника с номером ie,
t(4,ie) – номер зоны, которой принадлежит треугольник с номером ie.
Матрицы p, e, t имеют важнейшее значение для решения PDE вне PDETool, а также для анализа результатов расчёта моделируемых полей. Эти матрицы используются в качестве входных параметров для большинства функций PDE Toolbox MATLAB.
Пусть имеется расчётная область, изображённая на рис. 2.50. Тогда в результате выполнения команды Init Mesh конечноэлементная сетка при задании параметров генерации по умолчанию будет иметь вид, изображённый на рис.2.51. Если задать максимальную длину стороны треугольника равной 0.2, то инициализируемая сетка примет вид, изображённый на рис. 2.52. Варьирование параметром Jiggle mode не приводит к видимым изменениям сетки, однако приводит к изменению показателей регулярности сетки.
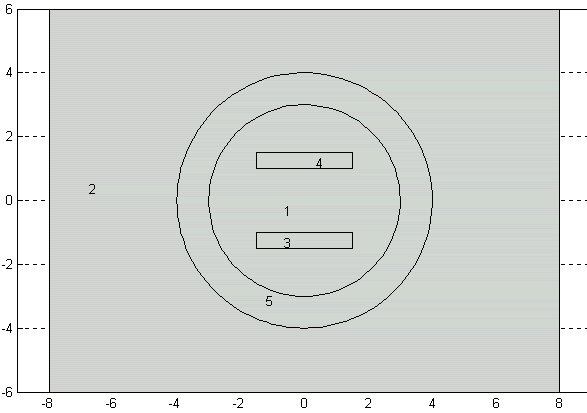
Рис. 2.50. Пример расчётной области для генерации сетки

Рис. 2.51. Конечноэлементная сетка при задании параметров генерации
по умолчанию
Сетка на рис.2.51 имеет следующие показатели регулярности: средний 0.93009, минимальный 0.48292. То же при Jiggle mode = on: средний 0.92621, минимальный 0.44772. При Jiggle mode = optimize minimum: средний 0.90042, минимальный 0.52005.
Рис. 2.52. Конечноэлементная сетка при Maximum edge size = 0.2
Сетка на рис.2.52 имеет следующие показатели регулярности: средний 0.9606, минимальный 0.66925. То же при Jiggle mode = on: ошибка. При Jiggle mode = optimize minimum: средний 0.91631, минимальный 0.59303.
На рис. 2.53 показана сетка (рис. 2.51), полученная по команде Refine mesh при задании параметров по умолчанию.
Рис. 2.53. Сетка, переопределённая методом ‘regular’
Рис. 2.54. Сетка, переопределённая методом ‘longest’
В заключение можно отметить, что для генерации мелкой сетки нежелательно задавать малые значения параметра Maximum edge size, т.к. это приводит к резкому увеличению времени построения сетки. Например, сетка, изображённая на рис. 2.52, генерировалась не менее 5 мин на компьютере с процессором Athlon 1000 и оперативной памятью 256 МБ. Задание малых значений параметра Maximum edge size оправдано в тех случаях, когда требуется получение максимально симметричной сетки. Во всех остальных случаях предпочтительнее генерировать сетку при задании параметров по умолчанию, а затем переопределять её столько раз, сколько нужно. Таким способом мелкая сетка генерируется гораздо быстрее.
2.4.5. Режим решения PDE-задачи
GUI-приложение PDETool переходит в режим решения PDE задачи по команде Solve/Solve PDE (см. 2.1.8). В этом режиме происходит формирование глобальной разреженной матрицы коэффициентов, глобальной правой части, а также решение большой разреженной системы уравнений относительно узлового распределения искомой величины, входящей в PDE или систему PDE. Когда заканчивается процесс решения, PDETool переходит либо в режим визуализации решения, либо в предыдущий режим, в котором была подана команда Solve/Solve PDE. Режим решения PDE-задачи сопровождается интенсивной работой процессора и математического сопроцессора ЭВМ (занятость процессора близка к 100%), поэтому работа других приложений MATLAB и WINDOWS в это время значительно замедляется, если PDETool работает под управлением MATLAB 6. Если PDETool работает под управлением MATLAB 5, то переключение между задачами и приложениями в это время невозможно.
Время решения и точность зависят от числа узлов, количества элементов, регулярности сетки, типа краевой задачи (см. 2.3), вида PDE (эллиптическое, параболическое, гиперболическое), значений коэффициентов PDE (действительные или комплексные: в последнем случае время решения больше примерно в восемь раз), а также от параметров решателя PDE. Параметры решателя PDE можно настраивать по команде Solve/Parameters (см. 2.1.8). Вид диалогового окна, которое разворачивается по данной команде, изображён на рис. 2.19. Параметры этого диалогового окна влияют только на процесс решения эллиптических PDE.
Решение эллиптических PDE
PDETool поддерживает четыре (2*2) режима решения эллиптических PDE:
– без переопределения сетки и адаптивный режим;
– режим линейного и режим нелинейного решателя.
Если флаг “Adaptive mode” (см. рис. 2.19) сброшен (это бывает по умолчанию), то это соответствует режиму без переопределения сетки, иначе – адаптивному режиму. Адаптивным называется режим многократного решения PDE с частичным переопределением (сгущением) конечноэлементной сетки на каждом итерационном шаге. В неадаптивном режиме решение PDE производится только один раз на заданной сетке. Этот режим не порождает никаких сообщений в командном окне MATLAB, если не возникает никаких ненормальных ситуаций. В адаптивном режиме на каждом итерационном шаге в командное окно выдаётся сообщение о количестве элементов текущей сетки. В конце итерационного процесса в командное окно выдаётся сообщение о причине завершения процесса.
Рассмотрим настраиваемые параметры адаптивного режима (см. рис. 2.19).
"Maximum number of triangles” – ограничение максимального числа элементов сетки после переопределения. Если на каком-либо итерационном шаге число конечных элементов превысит заданное значение, то этот шаг будет последним, и в командное окно MATLAB будет выдано сообщение “Maximum number of triangles obtained”. При развёртывании диалогового окна ввода параметров PDETool автоматически заносит в соответствующее поле рекомендуемое значение (оно зависит от размерности текущей сетки).
"Maximum number of refinements” – максимальное число итераций, связанных с переопределением конечноэлементной сетки. Если в соответствующее поле ввести значение n, то будет всего n+1 итераций (nпереопределений сетки). После последней итерации в командное окно MATLAB будет выдано сообщение “Maximum number of refinement passes obtained” (если раньше не наступит другое условие завершения итерационного процесса).
Параметр “Triangle selection method” может принимать одно из трёх значений:
- ”Worst triangles” – на каждом итерационном шаге для переопределения (деления) выбираются “худшие треугольники”, т.е. конечные элементы, показатель регулярности которых меньше некоторого порогового значения;
- ”Relative tolerance” – на каждом итерационном шаге для переопределения (деления) выбираются конечные элементы, в которых оценка относительной погрешности решения превышает заданное значение;
- ”User defined function” – на каждом итерационном шаге для переопределения (деления) выбираются конечные элементы в соответствии с условием, описанным в функции, заданной пользователем. Если выбирается это значение путём нажатия “радиокнопки”, то в соответствующее поле нужно ввести имя пользовательской функции.
"Worst triangle fraction” – пороговое значение показателя регулярности конечных элементов. Нужное числовое значение вводится в соответствующую строку ввода.
"Relative tolerance” – в эту строку ввода нужно вписать пороговое значение оценки относительной погрешности решения, которое используется для выбора треугольников, подлежащих переопределению.
"Function parameter” – в эту строку ввода нужно вписать пороговое значение, возвращаемое пользовательской функцией, которое используется для выбора треугольников, подлежащих переопределению.
"Refinement method” – параметр, который может принимать одно из следующих двух значений, выбираемых с помощью ниспадающего меню: “regular” или “longest” (по умолчанию) (см. подраздел 2.4.4 – режимы переопределения конечноэлементной сетки).
Пусть в адаптивном режиме нужно рассчитать распределение гармонического электромагнитного поля в системе с цилиндрическим электромагнитным экраном (геометрия расчётной области изображена на рис. 2.50). Для простоты зададим частоту равной нулю (это равносильно решению магнитостатической задачи). Решение начнём с сетки, изображённой на рис. 2.51. Зададим следующие значения параметров адаптивного режима: "Maximum number of triangles" = 10000; "Maximum number of refinements" = 8; "Triangle selection method" = "Worst triangles"; "Worst triangle fraction" = 0.5; "Refinement method" = "longest". В результате выполнения команды Solve PDE будет выполнено 9 итераций (8 переопределений сетки). В командное окно MATLAB будут выданы следующие сообщения:
Number of triangles: 512
Number of triangles: 642
Number of triangles: 917
Number of triangles: 1181
Number of triangles: 1845
Number of triangles: 2980
Number of triangles: 4154
Number of triangles: 6811
Number of triangles: 9472
Maximum number of refinement passes obtained
Итоговая конечноэлементная сетка, содержащая 9472 треугольника, изображена на рис. 2.55, а картина линий магнитной индукции (изолиний векторного магнитного потенциала) – на рис. 2.56. Из рис. 2.55 видно, что параметры адаптивного режима заданы неоптимально: в стальном экране (зона №5) сетка получилась более крупной, чем в воздухе вне экрана (зона №2).
Рис. 2.55. Конечноэлементная сетка, переопределённая в адаптивном режиме
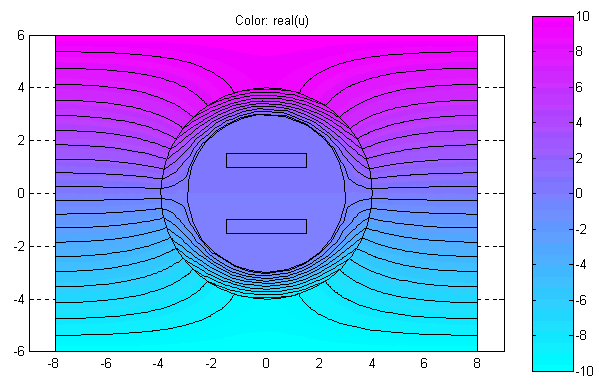
Рис. 2.56. Картина линий магнитной индукции в системе с экраном
Адаптивное переопределение сетки зависит от распределения коэффициентов PDE в расчётной области. Если для этой же электромагнитной системы задать частоту изменения внешнего электрического поля равной 2 кГц, то коэффициенты PDE станут комплексными. Итоговая конечноэлементная сетка при задании тех же значений параметров адаптивного режима будет иметь вид, изображённый на рис. 2.57. Всего элементов в этой сетке 8163. Линии равного уровня действующего значения напряжённости электрического поля показаны на рис. 2.58.
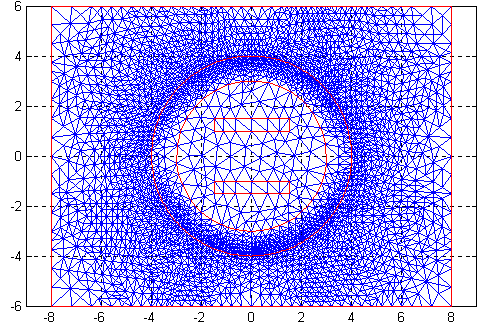
Рис. 2.57. Конечноэлементная сетка, переопределённая в адаптивном режиме
на частоте 2 кГц
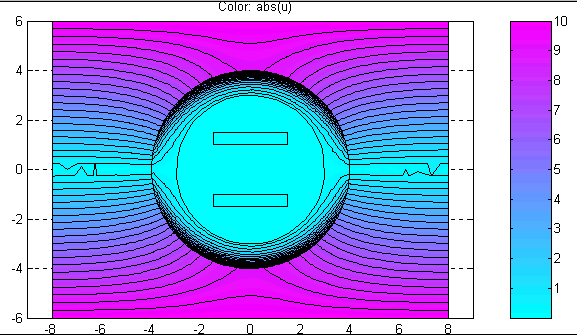
Рис. 2.58. Картина изолиний действующего значения напряжённости электрического поля на частоте 2 кГц
Если коэффициенты PDE зависят от искомой величины или от её пространственных дифференциальных операторов, то такая краевая задача называется нелинейной. Для решения таких задач нужно включать режим нелинейного решателя. Этот режим включается путём установки флага “Use nonlinear solver” в диалоговом окне, изображённом на рис. 2.19. В этом режиме происходит многократное формирование и решение глобального разреженного матричного уравнения относительно узлового распределения искомой величины и уточнение на каждом итерационном шаге элементного распределения коэффициентов PDE в соответствии с заданной на входе в задачу зависимостью. Пусть в режиме нелинейного решателя нужно рассчитать распределение магнитостатического поля в системе с цилиндрическим экраном (геометрия расчётной области изображена на рис. 2.50). Решение проведём на стандартной статической сетке, состоящей из 16529 узлов и 32768 элементов. В зоне №5 (в цилиндрическом экране) зададим нелинейные магнитные свойства: mu=120./(1+ux.^2+uy.^2), соответствующие насыщению кривой намагничивания. Параметры нелинейного решателя зададим по умолчанию. После подачи команды Solve PDE приложение PDETool перейдёт в режим решения на несколько минут. После окончания итерационного процесса в командном окне MATLAB появятся следующие сообщения:
Iteration Residual Step size Jacobian: fixed
0 10.0000000000
1 1.2095626662 1.0000000
2 0.2265940939 1.0000000
3 0.1512438266 0.2500000
4 0.0265846460 0.5000000
5 0.0227498179 0.5000000
6 0.0058274763 0.5000000
7 0.0038948862 0.5000000
8 0.0012155895 0.5000000
9 0.0007607710 0.5000000
10 0.0002378939 0.5000000
11 0.0001551291 0.5000000
12 0.0000453249 0.5000000
Картина линий магнитной индукции, соответствующая полученному решению, показана на рис. 2.59.
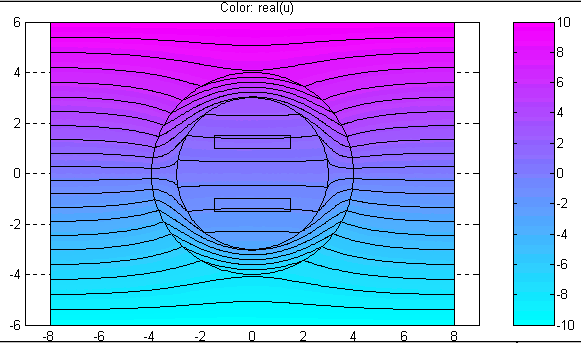
Рис. 2.59. Картина линий магнитной индукции в системе с экраном при нелинейных магнитных свойствах
Рассмотрим настраиваемые параметры режима нелинейного решателя (см. рис. 2.19).
"Nonlinear tolerance” – оценка нормы относительной погрешности решения PDE при которой итерационный процесс можно заканчивать (по умолчанию 1E-4).
"Initial solution” – начальное решение (с него начинается итерационный процесс, по умолчанию – нуль).
Параметр “Jacobian” может принимать одно из трёх возможных значений:
’fixed’ – аппроксимация якобиана по матрице “жёсткости” (по умолчанию);
’lumped’) – аппроксимация якобиана, основанная на численном дифференцировании коэффициентов;
’full’) - вычисление полного якобиана, основанное на разреженной версии функции numjac.
"Norm" – Относительная норма “энергетического функционала” (по умолчанию inf).
В режиме нелинейного решателя выполняется не более 25 итераций. Этот параметр не перенастраивается.
Решение параболических и гиперболических PDE
Параболические и гиперболические PDE – это нестационарные PDE. PDE Toolbox MATLAB поддерживает решение только линейных нестационарных уравнений и только на статической сетке. PDETool поддерживает решение нестационарных PDE только при нулевых начальных условиях и только для моментов времени time=0:1:10.
Пусть требуется решить параболическое PDE (2.2) с коэффициентами d=c=1, a=f=0, а в зоне №5 c=1/120. Распределение искомой величины u в моменты времени t=1:1:10 показано на рис. 2.60 – 2.69. По окончании решения в командном окне MATLAB появятся следующие сообщения:
Time: 1
Time: 2
Time: 3
Time: 4
Time: 5
Time: 6
Time: 7
Time: 8
Time: 9
Time: 10
88 successful steps
0 failed attempts
178 function evaluations
1 partial derivatives
20 LU decompositions
177 solutions of linear systems
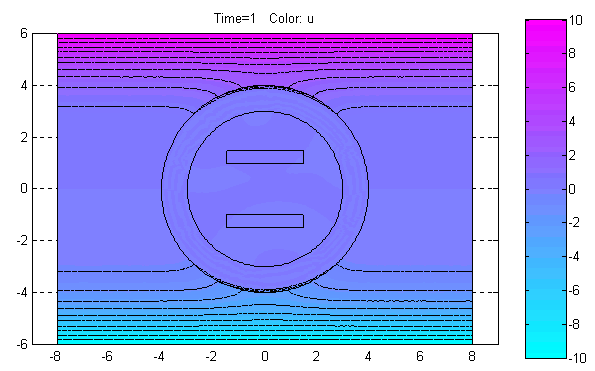
Рис. 2.60. Распределение искомой величины в момент времени t=1
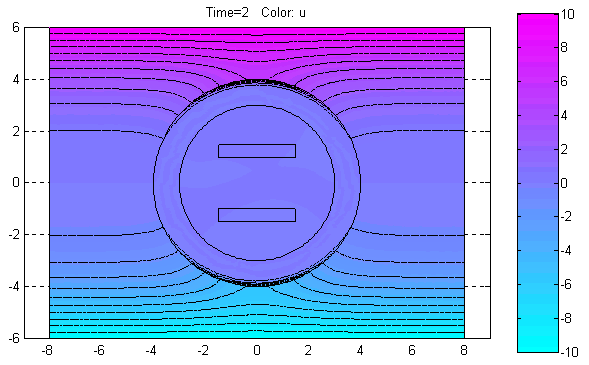
Рис. 2.61. Распределение искомой величины в момент времени t=2
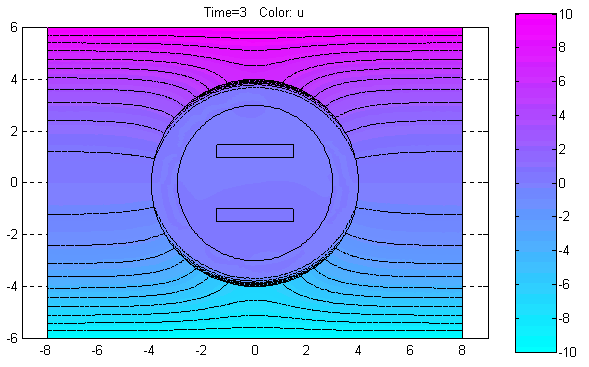
Рис. 2.62. Распределение искомой величины в момент времени t=3
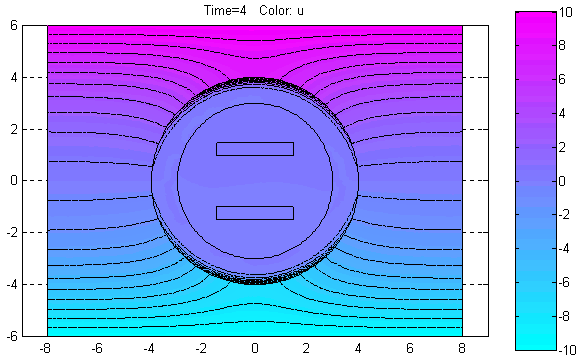
Рис. 2.63. Распределение искомой величины в момент времени t=4
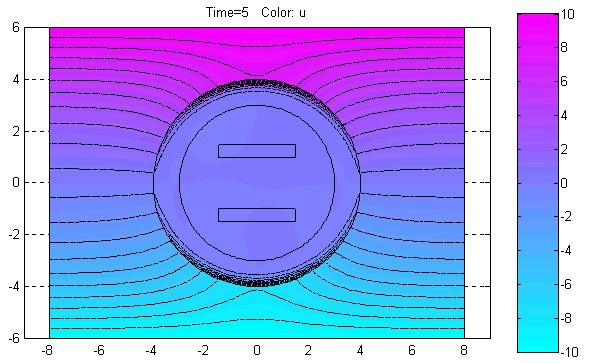
Рис. 2.64. Распределение искомой величины в момент времени t=5
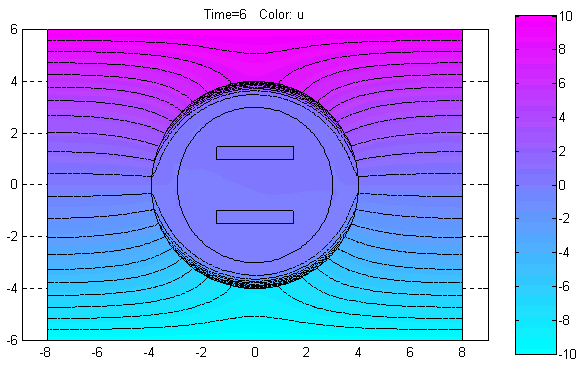
Рис. 2.65. Распределение искомой величины в момент времени t=6
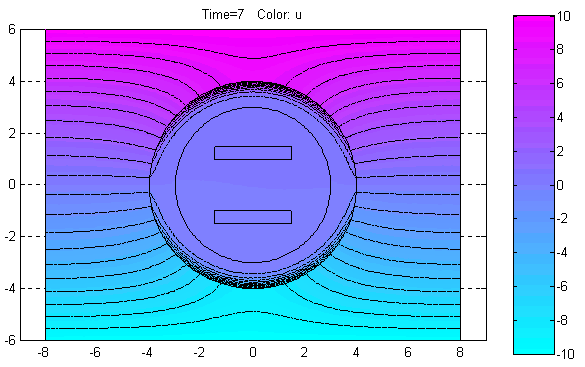
Рис. 2.66. Распределение искомой величины в момент времени t=7
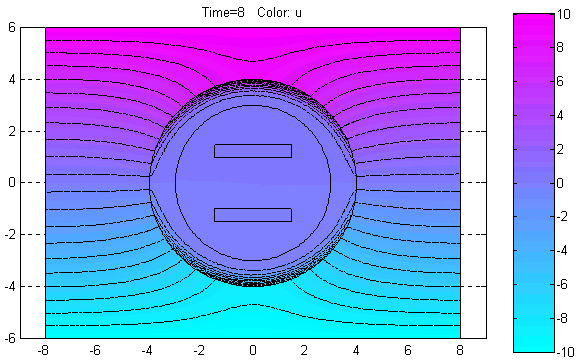
Рис. 2.67. Распределение искомой величины в момент времени t=8
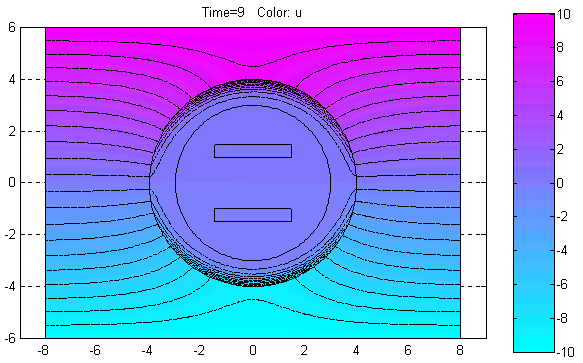
Рис. 2.68. Распределение искомой величины в момент времени t=9
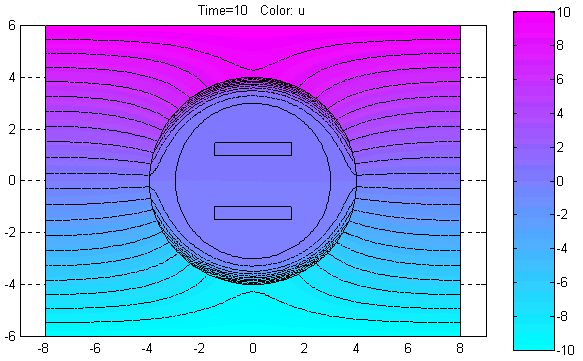
Рис. 2.69. Распределение искомой величины в момент времени t=10
По команде Export Solution происходит экспорт в базовую рабочую область MATLAB узлового распределения решения PDE. По умолчанию узловое распределение искомой величины записывается в переменную под именем u. В случае одного скалярного эллиптического PDE u представляет собой матрицу-столбец с числом элементов NP, где NP – число узлов конечноэлементной сетки. В случае системы двух скалярных эллиптических PDE u – матрица-столбец, состоящая и 2*NP элементов. Первые NP элементов относятся к первой переменной в системе PDE, следующие NP элементов – ко второй переменной. В случае одного нестационарного PDE u – прямоугольная матрица размера (NP,11), где каждому столбцу соответствует свой момент времени: столбцу №1 соответствует t=0, столбцу №2 – t=1, … столбцу №11 – t=10. В случае системы двух скалярных нестационарных PDE u – прямоугольная матрица размера (2*NP,11).
2.5. Визуализация решения краевой задачи
GUI-приложение PDETool переходит в режим визуализации решения по команде меню Plot/Plot Solution. Картина отображаемого в объекте axes поля зависит от параметров визуализации, которые можно настроить командой Plot/Parameters. Вид диалогового окна настройки параметров визуализации показан на рис. 2.21. Краткое описание каждого элемента этого диалогового окна дано в п. 2.1.9. Содержание пунктов ниспадающих меню в колонке “Property” первой панели этого окна зависит от типа решённой краевой задачи (см. список стандартных краевых задач PDETool, подраздел 2.3).
2.5.1. Визуализация решения скалярных эллиптических PDE
2.5.1. Визуализация решения скалярных эллиптических PDE
Если в колонке “Plot type” установить флаги “Color” и “Contour”, остальные параметры режима задать по умолчанию, то картина поля будет иметь вид, аналогичный показанному на рис. 2.56. Если при том же решении PDE установить также флаг “Show mesh”, то картина поля примет вид, показанный на рис. 2.70. Флаг “Show mesh” действует только при установленном флаге “Color”, во всех остальных случаях флаг “Show mesh” игнорируется.
Рис. 2.70. Визуализация рассчитанного поля при установленных флагах “Color", "Contour” и “Show mesh"
Если предполагать, что на рис. 2.56, 2.70 показана картина магнитостатического поля и что отображаемой величиной является векторный магнитный потенциал, то показать векторное поле магнитной индукции можно следующим образом. Сбросим флаги “Color” и “Contour”, установим флаг “Arrows”. Во втором ниспадающем меню "Property" выберем "user entry". Во второй строке ввода “User entry”введём “[uy;-ux]”. В результате выполнения команды визуализации получим картину, изображённую на рис. 2.71. А если ещё во втором ниспадающем меню “Plot style” выбрать “normalized”, то картина примет вид, показанный на рис. 2.72.
Рис. 2.71. Визуализация векторного поля в режиме “proportional"
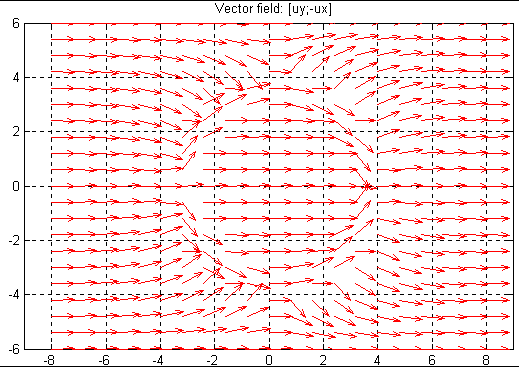
Рис. 2.72. Визуализация векторного поля в режиме “normalized"
Векторное поле, рассчитанное в PDETool, можно визуализировать в виде деформированной сетки. Для демонстрации этой возможности в столбце “Plot type” установим флаг “Deformed mesh"; "Property"="user entry"; "User entry”=[u;zeros(size(u))]. Картина поля (рис. 2.56, 2.70) в этом случае примет вид, показанный на рис. 2.73.
Рис. 2.73. Визуализация векторного поля в виде деформированной сетки
Вообще, при графическом изображении векторного поля в PDETool в строке ввода “User entry” указывается выражение, значением которого является либо матрица-столбец, либо прямоугольная матрица, состоящая из двух строк. В первом случае столбец должен состоять из 2*NP членов, где NP – число узлов конечноэлементной сетки. Первая половина столбца – узловое распределение x-составляющей векторного поля, вторая половина – узловое распределение y-составляющей. Во втором случае первая строка – элементное распределение x-составляющей векторного поля, вторая строка – элементное распределение y-составляющей.
Рис. 2.74. Трёхмерный график скалярного поля в виде конечноэлементной сетки
Отображение скалярного поля в виде трёхмерного графика происходит при установленном флаге “Height (3D plot)”. Если все остальные флаги сброшены, то скалярное поле, изображённое на рис. 2.56, 2.70, примет вид, показанный на рис. 2.74. Если ещё установить флаг “Plot in x-y grid”, который действует только при установленном флаге “Height (3D plot)”, то трёхмерный график примет вид, показанный на рис. 2.75. Трёхмерный график приобретает наиболее наглядный вид при установленных флагах “Color", "Plot in x-y grid", "Show mesh” (см. рис. 2.76).
Рис. 2.75. Трёхмерный график скалярного поля с трёхмерной координатной сеткой
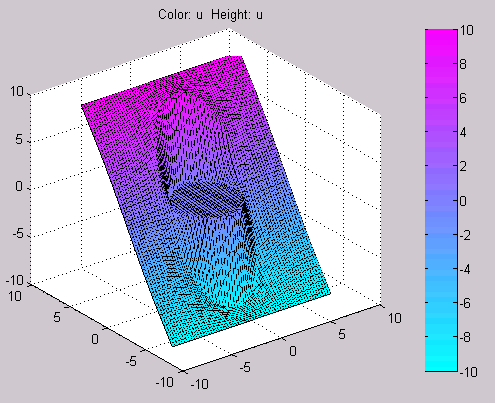
Рис. 2.76. Цветной трёхмерный график скалярного поля с показом сеток
2.5.2. Визуализация решения стационарных краевых задач других типов
Как было сказано выше, ниспадающие меню группы Property окна ввода параметров визуализации (см. рис. 2.21) зависят от типа решённой краевой задачи. Поэтому есть смысл перечислить состав пунктов этих меню для различных типов краевых задач в соответствии с подразделом 2.3. Перечень этих пунктов сведём в таблицу.
| Тип краевой задачи | Флаг группы Plot type, к которому относится ниспадающее меню | Пункты ниспадающего меню группы Property | Описание пунктов меню (что визуализируется при выборе данного пункта меню) |
| Generic scalar | "Color", "Contour", а также "Height (3D plot)" |
u | узловое распределение рассчитанного скалярного поля |
| abs(grad(u)) | элементное распределение модуля градиента рассчитанного скалярного поля | ||
| abs(c*grad(u)) | элементное распределение модуля “функции потока” (*) | ||
| user entry | узловое или элементное распределение скалярной величины, интересующей пользователя | ||
| "Arrows" | – grad(u) | элементное распределение величины, противоположной градиенту рассчитанного скалярного поля | |
| – c*grad(u) | элементное распределение векторной “функции потока” (*) | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| "Deformed mesh" | – grad(u) | элементное распределение величины, противоположной градиенту рассчитанного скалярного поля | |
| – c*grad(u) | элементное распределение векторной “функции потока” (*) | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| Generic system | "Color", "Contour", а также "Height (3D plot)" |
u | узловое распределение первого скалярного поля, относительно которого решалось PDE |
| v | узловое распределение второго скалярного поля, относительно которого решалось PDE | ||
| abs(u,v) | узловое распределение sqrt(u.^2+v.^2) | ||
| user entry | узловое или элементное распределение скалярной величины, интересующей пользователя | ||
| "Arrows" | (u,v) | узловое распределение векторной величины, равной u*1x+v*1y | |
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| "Deformed mesh" | (u,v) | узловое распределение векторной величины, равной u*1x+v*1y | |
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| Structural Mech, Plane Stress, Structural Mech, Plane Strain |
"Color", "Contour", а также "Height (3D plot)" |
x displacement (u) | узловое распределение x-составляющей вектора перемещения |
| y displacement (v) | узловое распределение y-составляющей вектора перемещения | ||
| abs(u,v) | узловое распределение модуля вектора перемещения | ||
| ux | частные производные x- и y-компонентов вектора перемещения по пространственным координатам | ||
| uy | |||
| vx | |||
| vy | |||
| x strain | xx-составляющая тензора деформации | ||
| y strain | yy-составляющая тензора деформации | ||
| shear strain | xy- и yx-составляющая тензора деформации (он симметричный) | ||
| x stress | xx-составляющая тензора механического напряжения | ||
| y stress | yy-составляющая тензора механического напряжения | ||
| shear stress | xy- и yx-составляющая тензора механического напряжения (он тоже симметричный) | ||
| 1 st principal strain | первое главное значение деформации | ||
| 2 nd principal strain | второе главное значение деформации | ||
| 1 st principal stress | первое главное значение напряжения | ||
| 2 nd principal stress | второе главное значение напряжения | ||
| von Mises stress | эффективное значение напряжения | ||
| user entry | узловое или элементное распределение скалярной величины, интересующей пользователя | ||
| "Arrows" | (u,v) | узловое распределение вектора перемещения | |
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| "Deformed mesh" | (u,v) | узловое распределение вектора перемещения | |
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| Electrostatics | "Color", "Contour", а также "Height (3D plot)" |
electric potential | узловое распределение скалярного электрического потенциала |
| electric field | элементное распределение модуля напряжённости электрического поля | ||
| electric displacement | элементное распределение модуля электрического смещения, делённого на абсолютную диэлектрическую проницаемость вакуума | ||
| user entry | узловое или элементное распределение скалярной величины, интересующей пользователя | ||
| "Arrows" | electric field | элементное распределение вектора напряжённости электрического поля | |
| electric displacement | элементное распределение вектора электрического смещения, делённого на абсолютную диэлектрическую проницаемость вакуума | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| "Deformed mesh" | electric field | элементное распределение вектора напряжённости электрического поля | |
| electric displacement | элементное распределение вектора электрического смещения, делённого на абсолютную диэлектрическую проницаемость вакуума | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| Magnetostatics | "Color", "Contour", а также "Height (3D plot)" |
magnetic potential | узловое распределение z-составляющей векторного магнитного потенциала, измеряемого в единицах тока |
| magnetic flux density | элементное распределение модуля магнитной индукции, делённой на абсолютную магнитную проницаемость вакуума | ||
| magnetic field | элементное распределение модуля напряжённости магнитного поля | ||
| user entry | узловое или элементное распределение скалярной величины, интересующей пользователя | ||
| "Arrows" | magnetic flux density | элементное распределение вектора магнитной индукции, делённой на абсолютную магнитную проницаемость вакуума | |
| magnetic field | элементное распределение вектора напряжённости магнитного поля | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| "Deformed mesh" | magnetic flux density | элементное распределение вектора магнитной индукции, делённой на абсолютную магнитную проницаемость вакуума | |
| magnetic field | элементное распределение вектора напряжённости магнитного поля | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| AC Power Electro-magnetics | "Color", "Contour", а также "Height (3D plot)" |
electric field | узловое распределение z-составляющей вектора комплексной напряжённости электрического поля |
| magnetic flux density | sqrt(ux.^2+uy.^2)/om*cc , где om – циклическая частота, cc – скорость света в вакууме |
||
| magnetic field | элементное распределение, описанное в предыдущем пункте, делённое почленно на элементное распределение относительной магнитной проницаемости | ||
| current density | узловое распределение z-составляющей вектора комплексной плотности тока, умноженной на волновое сопротивление вакуума | ||
| resistive heating rate | некорректно вычисляемое узловое распределение объёмной плотности мощности тепловых потерь при протекании тока проводимости | ||
| user entry | узловое или элементное распределение скалярной величины, интересующей пользователя | ||
| "Arrows" | magnetic flux density | [uy;-ux]/om*cc | |
| magnetic field | то же, почленно делённое на элементное распределение относительной магнитной проницаемости | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| "Deformed mesh" | magnetic flux density | [uy;-ux]/om*cc | |
| magnetic field | то же, почленно делённое на элементное распределение относительной магнитной проницаемости | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| Conductive Media DC | "Color", "Contour", а также "Height (3D plot)" |
electric potential | узловое распределение скалярного электрического потенциала |
| electric field | элементное распределение модуля напряжённости электрического поля | ||
| current density | элементное распределение модуля плотности тока проводимости | ||
| user entry | узловое или элементное распределение скалярной величины, интересующей пользователя | ||
| "Arrows" | electric field | элементное распределение вектора напряжённости электрического поля | |
| current density | элементное распределение вектора плотности тока проводимости | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| "Deformed mesh" | electric field | элементное распределение вектора напряжённости электрического поля | |
| current density | элементное распределение вектора плотности тока проводимости | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| Heat Transfer | "Color", "Contour", а также "Height (3D plot)" |
temperature | узловое распределение температуры |
| temperature gradient | элементное распределение модуля градиента температуры | ||
| heat flux | элементное распределение модуля плотности потока тепловой мощности | ||
| user entry | узловое или элементное распределение скалярной величины, интересующей пользователя | ||
| "Arrows" | temperature gradient | элементное распределение вектора градиента температуры | |
| heat flux | элементное распределение вектора плотности потока тепловой мощности | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| "Deformed mesh" | temperature gradient | элементное распределение вектора градиента температуры | |
| heat flux | элементное распределение вектора плотности потока тепловой мощности | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| Diffusion | "Color", "Contour", а также "Height (3D plot)" |
concentration | узловое распределение концентрации примеси |
| concentration gradient | элементное распределение модуля градиента концентрации | ||
| flux | элементное распределение модуля плотности потока переноса примеси | ||
| user entry | узловое или элементное распределение скалярной величины, интересующей пользователя | ||
| "Arrows" | concentration gradient | элементное распределение вектора градиента концентрации | |
| flux | элементное распределение вектора плотности потока переноса примеси | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| "Deformed mesh" | concentration gradient | элементное распределение вектора градиента концентрации | |
| flux | элементное распределение вектора плотности потока переноса примеси | ||
| user entry | узловое или элементное распределение векторной величины, интересующей пользователя | ||
| (*) Векторное поле c*grad(u) в PDE Toolbox MATLAB называют “функцией потока”. В электростатической задаче это электрическое смещение, делённое на абсолютную диэлектрическую проницаемость вакуума. В магнитостатической задаче это напряжённость магнитного поля. В задаче анализа постоянного электрического поля в проводящей среде это плотность тока проводимости. В задаче анализа теплового поля это плотность потока тепловой мощности. В задаче решения уравнения диффузии это плотность потока переноса примеси. | |||
Если для метода визуализации, отмечаемого флагом, выбран пункт ниспадающего меню “user entry”, то в соответствующую строку ввода “User entry” нужно вписать матричное выражение, описывающее скалярное или векторное поле, которое надо отобразить в поле axes фигуры PDETool. Значением этого выражения для векторного поля должна быть матрица, формат которой описан в п. 2.5.1. Для скалярного поля это либо матрица-столбец размера (NP,1), либо матрица-строка размера (1,NE), где NP – число узлов конечноэлементной сетки, NE – число конечных элементов. В случае скалярной краевой задачи любого типа в выражении можно применять следующие переменные: u – рассчитанное в ходе решения PDE скалярное поле в виде столбцовой матрицы узлового распределения; ux, uy – матрицы-строки элементного распределения частной производной по x и по y названного выше скалярного поля. В случае векторной краевой задачи (“Generic system", "Structural Mech, Plane Stress", "Structural Mech, Plane Strain”) можно также использовать переменные v, vx, vy. Их смысл расшифрован в таблице. В любом случае с помощью функции evalin можно ссылаться на переменные, находящиеся в рабочей области MATLAB.
В случае визуализации комплексного скалярного или векторного поля (см. “AC Power Electromagnetics” в таблице) после выполнения соответствующей команды разворачивается диалоговое окно предупреждения о том, что мнимая часть отображаемого поля игнорируется (см. рис. 2.77).
Рис. 2.77. Окно предупреждения, разворачиваемое при попытке визуализации комплексного поля
2.5.3. Визуализация решения нестационарных краевых задач
Если решено параболическое или гиперболическое PDE, то в колонке “Plot type” диалогового окна настройки параметров визуализации (рис. 2.21) доступен для установки флаг “Animation”, который позволяет производить анимацию имеющегося решения нестационарной краевой задачи. Если при установленном флаге “Animation” нажать кнопку “Plot”, то развернётся отдельная фигура, в которой будет производиться анимация. При нажатии кнопки “Options” (эта кнопка находится в колонке “Property”) разворачивается диалоговое окно настройки параметров анимации, вид которого показан на рис. 2.78.
Рис. 2.78. Вид диалогового окна настройки параметров анимации
Анимация производится следующим образом. В поле axes отдельной фигуры в реальном масштабе времени с шагом 1 секунда производится смена кадров распределения визуализируемого поля (это происходит, если не установлен флаг “Replay movie”). Кадры сменяются до момента времени t=10с. Далее процесс повторяется сначала в десятикратно ускоренном масштабе по времени. Последующие повторения процесса смены кадров происходят в соответствии с установленными параметрами настройки “Animation rate” и “Number of repeats". Animation rate – временной масштаб ускорения смены кадров; Number of repeats – число повторений анимации в заданном масштабе по времени.
Если решено нестационарное PDE, то в диалоговом окне “Plot Selection” (см. рис. 2.21) доступно для использования ниспадающее меню “Time for plot”, выбор пункта которого определяет момент времени, в который нужно отобразить рассчитанное распределение поля без режима анимации. В этом случае остальные параметры режима визуализации действуют так же, как это описано в пп. 2.5.1, 2.5.2. Пример неанимационной визуализации решения нестационарного PDE показан на рис. 2.60 – 2.69.
Рис. 2.79. Диалоговое окно экспорта анимации
Если в PDETool анимация хотя бы один раз была произведена, то становится доступной для выполнения команда Plot/Export Movie. По этой команде разворачивается диалоговое окно экспорта анимации, вид которого показан на рис. 2.79. Нажатие кнопки “OK” приведёт к экспорту в базовую рабочую область MATLAB переменной (по умолчанию её имя M), содержащей RGB-коды графических кадров анимации. Эта переменная представляет собой массив структур размера (1,11), состоящих из двух полей: 'cdata' и 'colormap'. Первое поле представляет собой трёхмерный массив типа uint8 размера (a,b,3), где a, b – размеры в пикселях кадра анимации по горизонтали и вертикали. Второе поле обычно бывает пустое (размер (0,0)). Переменная M может использоваться для анимации решения краевой задачи вне приложения PDETool. Для этого можно воспользоваться функцией movie ядра MATLAB.
2.5.4. Палитры визуализации
В диалоговом окне настройки параметров визуализации (рис. 2.21) есть ниспадающее меню “Colormap”, содержащее список доступных для использования цветовых палитр. На рис. 2.80 – 2.88 показаны примеры использования различных цветовых палитр для визуализации скалярного поля.
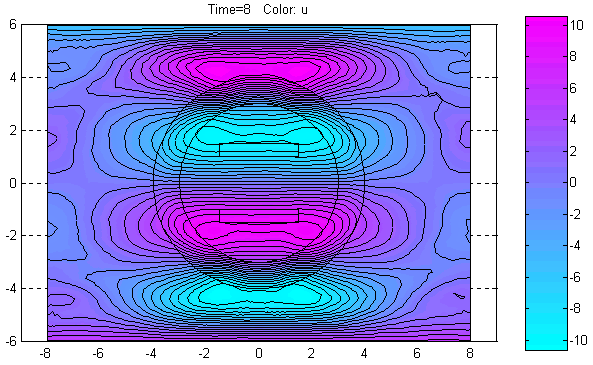
Рис. 2.80. Использование палитры cool для визуализации скалярного поля
Рис. 2.81. Использование палитры gray для визуализации скалярного поля
Рис. 2.82. Использование палитры bone для визуализации скалярного поля
Рис. 2.83. Использование палитры pink для визуализации скалярного поля
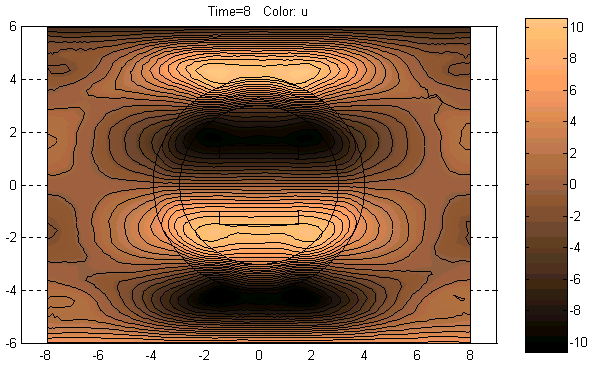
Рис. 2.84. Использование палитры copper для визуализации скалярного поля
Рис. 2.85. Использование палитры hot для визуализации скалярного поля
Рис. 2.86. Использование палитры jet для визуализации скалярного поля
Рис. 2.87. Использование палитры hsv для визуализации скалярного поля
Рис. 2.88. Использование палитры prism для визуализации скалярного поля
2.6. Сохранение PDE–модели в виде m-файла
По командам File/Save, File/Save As происходит сохранение PDE–модели в виде m-файла (см. описание команд PDETool, п.2.1.1). m-файл представляет собой m-функцию без входных и выходных параметров, имеющую имя pdemodel. Каждый оператор этого m-файла вызывает функцию графического интерфейса пользователя (GUI) или пакета PDE Toolbox MATLAB. Ниже приведён пример такого m-файла.
function pdemodel
[pde_fig,ax]=pdeinit;
pdetool('appl_cb',7);
set(ax,'DataAspectRatio',[1 1 1]);
set(ax,'PlotBoxAspectRatio',[9 6 1]);
set(ax,'XLim',[-9 9]);
set(ax,'YLim',[-6 6]);
set(ax,'XTickMode','auto');
set(ax,'YTickMode','auto');
pdetool('gridon','on');
% Geometry description:
pderect([-8 8 -6 6],'R1');
pdecirc(0,0,4,'C1');
pdecirc(0,0,3,'C2');
pderect([-1.5 1.5 1 1.5],'R2');
pderect([-1.5 1.5 -1 -1.5],'R3');
set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','R1+C1+C2+R2+R3')
% Boundary conditions:
pdetool('changemode',0)
pdesetbd(5,...
'dir',...
1,...
'1',...
'-10')
pdesetbd(4,...
'neu',...
1,...
'0',...
'0')
pdesetbd(2,...
'dir',...
1,...
'1',...
'10')
pdesetbd(1,...
'neu',...
1,...
'0',...
'0')
% Mesh generation:
setuprop(pde_fig,'Hgrad',1.3);
setuprop(pde_fig,'refinemethod','regular');
pdetool('initmesh')
pdetool('refine')
pdetool('refine')
% PDE coefficients:
pdeseteq(1,...
'1./(1.0)!1./(1.0)!1./(1.0)!1./(1.0)!1./(120)',...
'sqrt(-1)*(2*2*pi/3E8).*(0.0)-(2*2*pi/3E8).*(2*2*pi/3E8).*(1.0)!sqrt(-1)*(2*2*pi/3E8).*(0.0)-(2*2*pi/3E8).*(2*2*pi/3E8).*(1.0)!sqrt(-1)*(2*2*pi/3E8).*(0.0)-(2*2*pi/3E8).*(2*2*pi/3E8).*(1.0)!sqrt(-1)*(2*2*pi/3E8).*(0.0)-(2*2*pi/3E8).*(2*2*pi/3E8).*(1.0)!sqrt(-1)*(2*2*pi/3E8).*(5.6E4*376.7)-(2*2*pi/3E8).*(2*2*pi/3E8).*(1.0)',...
'0.0!0.0!0.0!0.0!0.0',...
'1.0!1.0!1.0!1.0!1.0',...
'0:10',...
'0.0',...
'0.0',...
'[0 100]')
setuprop(pde_fig,'currparam',...
['2*2*pi/3E8!2*2*pi/3E8!2*2*pi/3E8!2*2*pi/3E8!2*2*pi/3E8';...
'1.0!1.0!1.0!1.0!120 ';...
'0.0!0.0!0.0!0.0!5.6E4*376.7 ';...
'1.0!1.0!1.0!1.0!1.0 '])
% Solve parameters:
setuprop(pde_fig,'solveparam',...
str2mat('0','12288','10','pdeadworst',...
'0.5','longest','0','1E-4','','fixed','Inf'))
% Plotflags and user data strings:
setuprop(pde_fig,'plotflags',[6 1 1 1 1 1 1 0 0 0 0 1 1 1 0 0 0 1]);
setuprop(pde_fig,'colstring','abs(u)');
setuprop(pde_fig,'arrowstring','');
setuprop(pde_fig,'deformstring','');
setuprop(pde_fig,'heightstring','');
% Solve PDE:
pdetool('solve')
Как видно, в общем случае m-файл PDE–модели состоит из 8 разделов: Общая часть, Раздел описания геометрии, Раздел описания граничных условий, Раздел генерации конечноэлементной сетки, Раздел задания коэффициентов PDE, Раздел задания параметров решателя, Раздел задания параметров визуализации, Раздел решения PDE.
Общая часть
Общая часть состоит из заголовка m-функции, оператора запуска GUI-приложения PDETool, оператора установки типа решаемой стандартной краевой задачи, операторов настройки свойств графического объекта axes. PDETool запускается оператором
[pde_fig,ax]=pdeinit;
В переменную pde_fig записывается дескриптор фигуры PDETool, в переменную ax – дескриптор графического объекта axes этой фигуры. Если к моменту выполнения этого оператора фигура PDETool уже существовала, то запуск приложения PDETool не производится, а просто возвращаются и записываются дескрипторы.
Оператор
pdetool('appl_cb',kk);
настраивает приложение PDETool на решение стандартной PDE-задачи № kk в списке стандартных краевых задач (см. подраздел 2.3). В случае данного примера 7 – “AC Power Electromagnetics”, т.е. переменное гармоническое электромагнитное поле.
Оператор
set(ax,'DataAspectRatio',[1 1 1]);
устанавливает равный масштаб по всем координатным осям.
Оператор
set(ax,'PlotBoxAspectRatio',[9 6 1]);
устанавливает относительные размеры (на экране по координатным осям) отображаемой в axes области.
Операторы
set(ax,'XLim',[-9 9]);
set(ax,'YLim',[-6 6]);
устанавливают пределы координатных осей.
Операторы
set(ax,'XTickMode','auto');
set(ax,'YTickMode','auto');
устанавливают автоматическую разметку координатных осей.
Оператор
pdetool('gridon','on');
устанавливает режим показа линий координатной сетки.
В [15] дано достаточно подробное описание свойств объекта axes: 'DataAspectRatio', 'PlotBoxAspectRatio', 'XLim', 'YLim', 'XTickMode', 'YTickMode' и др.
Раздел описания геометрии
Этот раздел содержит операторы вызова функций прорисовки в PDETool геометрических объектов (см. состав пакета PDE Toolbox Matlab, раздел 4). В конце раздела описания геометрии записывается оператор, задающий средствами GUI формулу геометрии расчётной области (см. подраздел 2.2).
Операторы
pderect([-8 8 -6 6],'R1');
pdecirc(0,0,4,'C1');
pdecirc(0,0,3,'C2');
pderect([-1.5 1.5 1 1.5],'R2');
pderect([-1.5 1.5 -1 -1.5],'R3');
создают и прорисовывают геометрические объекты (в данном случае круги и прямоугольники).
Оператор
set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','R1+C1+C2+R2+R3')
задаёт формулу геометрии расчётной области (см. подраздел 2.2).
Раздел описания граничных условий
Этот раздел содержит оператор переключения PDETool в режим ввода граничных условий, а также операторы установки граничных условий для каждого граничного сегмента.
Оператор
pdetool('changemode',0)
переключает PDETool в режим ввода граничных условий.
Оператор
pdesetbd(Nsegm,Type,Mode,eh,er)
устанавливает граничное условие для сегмента № Nsegm. Type=’dir’ – граничное условие Дирихле; Type=’neu’ – граничное условие Неймана. Mode=1 – скалярное PDE; Mode=2 – система двух скалярных PDE. eh – строка символов, содержащая выражение для коэффициента h или q граничных условий. er – строка символов, содержащая выражение для коэффициента r или g граничных условий.
Раздел генерации конечноэлементной сетки
Этот раздел содержит операторы установки с помощью функции setuprop дополнительных свойств фигуры PDETool, влияющих на генерацию и переопределение сетки; раздел содержит также команды инициализации и переопределения сетки (см. п. 2.4.4). Команды подаются функцией pdetool.
Раздел задания коэффициентов PDE
Этот раздел состоит из двух операторов.
Оператор
pdeseteq(Type,c,a,f,d,tlist,u0,ut0,range)
устанавливает в PDETool распределение коэффициентов PDE в расчётной области. Type=1 – эллиптическое PDE; Type=2 – параболическое PDE; Type=3 – гиперболическое PDE; Type=4 – решение задачи на собственные значения. c,a,f,d – матрицы символов, описывающие в виде выражений распределение коэффициентов PDE в расчётной области (формат этих матриц описан в п. 2.4.3). tlist – строковое выражение, значением которого является матрица-строка – список моментов времени, для которых нужно получить решение PDE. u0,ut0 – строковые выражения, описывающие распределение в расчётной области начальных условий для искомой величины (u0) и для её производной по времени (ut0), синтаксис такой же, как и для c,a,f,d. range – строковое выражение, значением которого является массив-строка, состоящий из двух элементов; этот массив задаёт диапазон действительных частей искомых собственных значений PDE-задачи.
Оператор
setuprop(pde_fig,'currparam',...
['2*2*pi/3E8!2*2*pi/3E8!2*2*pi/3E8!2*2*pi/3E8!2*2*pi/3E8';...
'1.0!1.0!1.0!1.0!120 ';...
'0.0!0.0!0.0!0.0!5.6E4*376.7 ';...
'1.0!1.0!1.0!1.0!1.0 '])
определяет содержимое строк ввода диалогового окна ввода коэффициентов PDE для каждой зоны (см. рис. 2.12, п. 2.1.6).
Раздел задания параметров решателя
Этот раздел содержит оператор задания параметров решателя PDE. Дополнительному свойству 'solveparam' фигуры PDETool присваивается матрица символов, определяющая содержание строк ввода диалогового окна задания параметров решателя PDE (см. рис. 2.19, п. 2.1.8, п. 2.4.5).
Раздел задания параметров визуализации
Этот раздел содержит операторы установки дополнительных свойств фигуры PDETool, определяющих содержание строк ввода и состояние флагов диалогового окна ввода параметров визуализации решения PDE (см. рис. 2.21, п. 2.1.9, а также подраздел 2.5). Перечень и назначение этих свойств сведено в таблицу.
| Дополнительное свойство фигуры PDETool, устанавливаемое функциями setuprop, setappdata | Назначение свойства |
| 'colstring' | Содержание строки ввода “User entry”, относящейся к флагу “Color" |
| 'arrowstring' | Содержание строки ввода “User entry”, относящейся к флагу “Arrows" |
| 'deformstring' | Содержание строки ввода “User entry”, относящейся к флагу “Deformed mesh" |
| 'heightstring' | Содержание строки ввода “User entry”, относящейся к флагу “Height (3-D plot)" |
| 'plotflags' | Это свойство должно быть равно числовому массиву-строке, каждый элемент которого имеет следующее назначение: |
| 'plotflags'(1) | Номер пункта ниспадающего меню группы “Property”, относящегося к флагу “Color" |
| 'plotflags'(2) | Номер пункта ниспадающего меню группы “Plot style”, относящегося к флагу “Color" |
| 'plotflags'(3) | Номер пункта ниспадающего меню группы “Property”, относящегося к флагу “ Height (3-D plot)" |
| 'plotflags'(4) | Номер пункта ниспадающего меню группы “Plot style”, относящегося к флагу “ Height (3-D plot)" |
| 'plotflags'(5) | Номер пункта ниспадающего меню группы “Property”, относящегося к флагу “Arrows" |
| 'plotflags'(6) | Номер пункта ниспадающего меню группы “Plot style”, относящегося к флагу “Arrows" |
| 'plotflags'(7) | Номер пункта ниспадающего меню "Colormap" |
| 'plotflags'(8) | Флаг "Plot solution automatically": 1 – установлен; 0 – сброшен |
| 'plotflags'(9) | Флаг "Plot in x-y grid": 1 – установлен; 0 – сброшен |
| 'plotflags'(10) | Флаг "Show mesh": 1 – установлен; 0 – сброшен |
| 'plotflags'(11) | Флаг "Animation": 1 – установлен; 0 – сброшен |
| 'plotflags'(12) | Номер пункта ниспадающего меню "Time for plot" |
| 'plotflags'(13) | Флаг “Color”: 1 – установлен; 0 – сброшен |
| 'plotflags'(14) | Флаг “Contour”: 1 – установлен; 0 – сброшен |
| 'plotflags'(15) | Флаг “Height (3-D plot)”: 1 – установлен; 0 – сброшен |
| 'plotflags'(16) | Флаг “Arrows”: 1 – установлен; 0 – сброшен |
| 'plotflags'(17) | Флаг “Deformed mesh”: 1 – установлен; 0 – сброшен |
| 'plotflags'(18) | Номер пункта ниспадающего меню группы “Property”, относящегося к флагу “Deformed mesh" |
Раздел решения PDE
Этот раздел содержит команду решения PDE. Команда подаётся функцией pdetool.
3. Состав графического интерфейса пользователя PDE Toolbox Matlab
Этот раздел предназначен для разработчиков вычислительных сценариев, функций и GUI-приложений, взаимодействующих с приложением PDETool, в котором сосредоточен весь графический интерфейс пользователя PDE Toolbox MATLAB.
Рассмотрим структуру подчинённости графических объектов работающего приложения PDETool. Основным графическим объектом является фигура PDETool. В её непосредственном подчинении находится не менее 30 объектов трёх типов: axes, uimenu, uicontrol. Характеристика всех типов графических объектов дана в описании Графического Интерфейса Пользователя (GUI) MATLAB. На русском языке это описание представлено, например, в [15]. Здесь мы рассмотрим состав и свойства графических объектов, входящих конкретно в PDETool.
Состав графических объектов, подчинённых фигуре PDETool
| Состав графических объектов, находящихся в непосредственном подчинении фигуры PDETool в различных режимах работы приложения | |||
| Режим | Tag | Тип | Назначение |
| Draw mode, Boundary mode, PDE mode, Mesh mode, режим решения |
PDEAxes | axes | Поле показа геометрии расчётной области. Это основной объект axes фигуры PDETool (в предыдущих разделах, например, 2.6, он назывался просто “поле axes”). |
| zoom | axes | Кнопка инструментальной панели, дублирующая команду меню Options/Zoom (см. 2.1.3, 2.2) | |
| solve | axes | Кнопки инструментальной панели, дублирующие команды меню групп Boundary, PDE, Mesh, Solve (см. 2.2) | |
| draw | axes | Кнопки инструментальной панели, дублирующие команды меню группы Draw (см. 2.2) | |
| PDEFileMenu | uimenu | Группа команд File | |
| PDEEditMenu | uimenu | Группа команд Edit | |
| PDEOptMenu | uimenu | Группа команд Options | |
| PDEDrawMenu | uimenu | Группа команд Draw | |
| PDEBoundMenu | uimenu | Группа команд Boundary | |
| PDEPDEMenu | uimenu | Группа команд PDE | |
| PDEMeshMenu | uimenu | Группа команд Mesh | |
| PDESolveMenu | uimenu | Группа команд Solve | |
| PDEPlotMenu | uimenu | Группа команд Plot | |
| winmenu | uimenu | Пункт “Window” главного меню | |
| PDEHelpMenu | uimenu | Группа команд Help | |
| uicontrol | frame – группа управляющих элементов (фрейм) команды завершения GUI-приложения PDETool | ||
| uicontrol | pushbutton – кнопка вызова команды “Exit” завершения GUI-приложения PDETool | ||
| uicontrol | frame – окно подсказок и информационных сообщений | ||
| uicontrol | text – статический текст, содержащий заголовок этого окна “Info:” | ||
| PDEInfo | uicontrol | text – статический текст, содержащий подсказку или информационное сообщение, например, “Draw 2-D geometry.” | |
| uicontrol | frame – окно ввода формулы геометрии расчётной области | ||
| uicontrol | text – статический текст, содержащий заголовок этого окна “Set formula:” | ||
| PDEEval | uicontrol | edit – строка ввода формулы геометрии расчётной области (см. 2.2) | |
| uicontrol | frame – окно указателя значений координат точки наблюдения | ||
| uicontrol | text – статический текст “X:” | ||
| PDEXField | uicontrol | text – статический текст, показывающий значение координаты x точки наблюдения, например, “-6.653” | |
| uicontrol | text – статический текст “Y:” | ||
| PDEYField | uicontrol | text – статический текст, показывающий значение координаты y точки наблюдения, например, “-5.786” | |
| uicontrol | frame – окно выбора стандартной краевой задачи PDETool | ||
| PDEAppl | uicontrol | popupmenu – ниспадающее меню со списком стандартных краевых задач, поддерживаемых GUI-приложением PDETool (см. 2.2) | |
| Plot Solution |
Те же объекты, что и в предыдущих режимах. Кроме того: |
||
| PDESolBar | axes | Шкала значений отображаемой скалярной величины. Эта шкала никогда не имеет отношения к векторным величинам. | |
uimenu PDEHelpMenu имеет в своём подчинении два объекта uimenu, соответствующие командам меню группы Help (см. 2.1.10). uimenu winmenu имеет в своём подчинении столько объектов uimenu, сколько имеется активных окон в среде MATLAB. Каждому из этих uimenu соответствует команда меню группы Window (см. 2.1.10). Свойство ‘Tag’ этих объектов равно пустой строке.
Состав остальных подчинённых объектов uimenu сведём в таблицу.
| Структура подчинённости объектов uimenu | |||
| Свойство Tag объекта uimenu, соответствующего пункту главного меню | Свойство Tag подчинённого объекта uimenu | Соответствующая команда меню приложения PDETool (см. 2.1) | |
| PDEFileMenu | File/ New | см. 2.1.1 | |
| File/ Open | |||
| PDESave | File/Save | ||
| File/ Save As | |||
| File/ Print | |||
| File/ Exit | |||
| PDEEditMenu | PDEUndo | Edit/ Undo | см. 2.1.2 |
| PDECut | Edit/ Cut | ||
| PDECopy | Edit/ Copy | ||
| PDEPaste | Edit/ Paste | ||
| PDEClear | Edit/ Clear | ||
| PDESelall | Edit/ Select All | ||
| PDEOptMenu | PDEGrid | Options/ Grid | см. 2.1.3 |
| PDESpace | Options/ Grid Spacing | ||
| PDESnap | Options/ Snap | ||
| PDEAxMenu | Options/ Axes Limits | ||
| PDEAxeq | Options/ Axes Equal | ||
| PDEHelpoff | Options/ Turn off Toolbar Help | ||
| PDEZoom | Options/ Zoom | ||
| PDEAppMenu | Options/ Application | ||
| PDERefresh | Options/ Refresh | ||
| PDEDrawMenu | PDEDrawMode | Draw/ Draw Mode | см. 2.1.4 |
| PDERect | Draw/ Rectangle/ square | ||
| PDERectc | Draw/ Rectangle/ square (centered) | ||
| PDEEllip | Draw/ Ellipse/ circle | ||
| PDEEllipc | Draw/ Ellipse/ circle (centered) | ||
| PDEPoly | Draw/ Polygon | ||
| PDERotate | Draw/ Rotate | ||
| PDEExpGD | Draw/ Export Geometry Description, Set Formula, Labels | ||
| PDEBoundMenu | PDEBoundMode | Boundary/ Boundary Mode | см. 2.1.5 |
| PDEBoundSpec | Boundary/ Specify Boundary Conditions | ||
| PDEShowEdge | Boundary/ Show Edge Labels | ||
| PDEShowSub | Boundary/ Show Subdomains Labels | ||
| PDERemBord | Boundary/ Remove Subdomain Border | ||
| PDERemAllBord | Boundary/ Remove All Subdomain Borders | ||
| PDEExpBound | Boundary/ Export Decomposed Geometry, Boundary Cond’s | ||
| PDEPDEMenu | PDEMode | PDE/ PDE Mode | см. 2.1.6 |
| PDEShowPDESub | PDE/ Show Subdomains Labels | ||
| PDEParam | PDE/ PDE Specification | ||
| PDEExpParam | PDE/ Export PDE Coefficients | ||
| PDEMeshMenu Примечание: Одинаковые ‘Tag’ главного и подчинённого uimenu – недосмотр разработчиков пакета PDE Toolbox MATLAB. |
PDEMeshMenu | Mesh/ Mesh Mode | см. 2.1.7 |
| PDEInitMesh | Mesh/ Initialize Mesh | ||
| PDERefine | Mesh/ Refine Mesh | ||
| PDEJiggle | Mesh/ Jiggle Mesh | ||
| PDEUnrefine | Mesh/ Undo Mesh Change | ||
| PDETriQual | Mesh/ Display Triangle Quality | ||
| PDEShowNode | Mesh/ Show Node Labels | ||
| PDEShowTriangles | Mesh/ Show Triange Labels | ||
| PDEMeshParam | Mesh/ Parameters | ||
| PDEExpMesh | Mesh/ Export Mesh | ||
| PDESolveMenu | PDESolve | Solve/ Solve PDE | см. 2.1.8 |
| PDESolveParam | Solve/ Parameters | ||
| PDEExpSol | Solve/ Export Solution | ||
| PDEPlotMenu | PDEPlot | Plot/ Plot Solution | см. 2.1.9 |
| PDEPlotParam | Plot/ Parameters | ||
| PDEExpMovie | Plot/ Export Movie | ||
Состав объектов, подчинённых axes PDEAxes, зависит от состава геометрических объектов в расчётной области, режима работы PDETool, исходных данных PDE-задачи. Состав и свойства объектов, подчинённых axes draw, axes solve, axes zoom, зависят от состояния кнопок инструментальной панели. Состав объектов, подчинённых axes PDESolBar, меньше всего подвержен изменениям, поскольку этот объект появляется в фигуре PDETool только в режиме визуализации решения PDE-задачи. Все объекты axes фигуры PDETool имеют в своём подчинении объекты типов Line, Rectangle, Text, Patch, Image.
Теперь перейдём к описанию свойств объектов GUI PDETool.
3.1. Свойства фигуры PDETool
Если в приложение PDETool не загружена PDE-модель, то свойства фигуры PDETool имеют следующие значения.
Alphamap = linspace(0,1,64)
Это свойство задаёт 64 уровня коэффициента прозрачности графических объек-тов. Данное свойство поддерживается, начиная с версии MATLAB 6.0.
BackingStore = on
Это означает, включен режим экранной буферизации графических изображений при прорисовке изображений [15].
CloseRequestFcn = closereq
Это свойство определяет имя функции MATLAB, которая должна выполняться при закрытии фигуры и приложения PDETool.
Color = [1 1 1]
Это свойство определяет цвет фона фигуры. В данном случае - белый. В MATLAB 6 это свойство доступно для редактирования средством propedit.
Colormap = матрица размера (20,3), определяющая RGB-коды 20 предопреде-лённых цветов для формирования графических изображений [15].
CurrentAxes, CurrentCharacter, CurrentObject имеют пустые значения. Назначе-ния этих свойств, а также CurrentPoint, описаны в [15].
Dithermap = матрица размера (64,3)
DithermapMode = manual
Эти свойства определяют цветовую палитру и режим её использования, опи-санные в [15].
DoubleBuffer = off
Режим двойной буферизации при формировании изображений выключен [15].
FileName = пустая строка. Данное свойство поддерживается, начиная с версии MATLAB 6.0.
FixedColors = матрица размера (12,3), определяющая "применённые цвета", т.е. цвета, имеющиеся в изображении фигуры, но не представленные в свойстве Colormap [15].
IntegerHandle = off
Благодаря этому свойству дескриптор фигуры PDETool не является целым чис-лом. Это свойство нельзя изменить.
InvertHardcopy = on
Это относится к группе свойств управления печатью [15].
KeyPressFcn = pdetool keycall
Это свойство задаёт оператор MATLAB, который будет выполняться при нажа-тии любой клавиши, если фигура PDETool выбрана (активна). В данном случае вызывается одна из команд приложения PDETool.
MenuBar = none
Системное меню фигуры PDETool скрыто. Это свойство доступно для измене-ния функцией set. Такое действие бывает полезным, если иллюстрацию PDE-модели нужно вставить в документ прямо из PDETool.
MinColormap = [64]
Это свойство определяет минимальное количество цветов в палитре Colormap [15].
Name = PDE Toolbox - [Untitled]
Это свойство содержит имя файла загруженной PDE-модели. Загружаемая PDE-модель должна существовать в виде m-файла (см. 2.6).
NextPlot = add
Это свойство указывает, что при выводе графиков их надо добавлять в текущее окно.
NumberTitle = off
Это свойство запрещает системе MATLAB присваивать номер фигуре PDETool.
PaperUnits = inches
PaperOrientation = portrait
PaperPosition = [0.25 2.5 8 6]
PaperPositionMode = manual
PaperSize = [8.5 11]
PaperType = usletter
Эти свойства относятся к группе свойств управления печатью [15].
Pointer = arrow
Это свойство определяет символ указателя мыши в фигуре PDETool. В данном случае - стандартная стрелка.
PointerShapeCData = матрица размера (16,16)
Это свойство используется в том случае, когда форма символа указателя мыши задаётся пользователем [15].
PointerShapeHotSpot = [1 1]
Это свойство определяет пиксель указателя мыши, который фактически указы-вает точку экрана [15].
Position = [103 77 819 576]
Это свойство определяет положение фигуры PDETool на экране [15]. В данном случае - пикселях (см. свойство Units)
Renderer = painters
RendererMode = manual
Эти свойства доступны для редактирования средством propedit и задают метод визуализации фигуры и способ задания этого метода [15].
Resize = on
Это свойство разрешает перемещать и изменять размеры фигуры с помощью мыши.
ResizeFcn = пустая строка
Это свойство указывает, что при изменении размера фигуры PDETool процеду-ра ответного вызова не используется.
SelectionType = normal
Это свойство определяет способ последнего выбора мышью фигуры [15].
ShareColors = on
Это свойство описано в [15].
Units = pixels
Координаты вершин окна фигуры задаются в пикселях (см. свойство Position).
WindowButtonDownFcn = pdeselect select
WindowButtonMotionFcn = pdemtncb(0)
WindowButtonUpFcn =
Эти свойства определяют операторы MATLAB, выполняемые при отпускании кнопки мыши внутри окна фигуры, при перемещении указателя мыши по фигу-ре, а также при нажатии кнопки мыши внутри окна фигуры.
WindowStyle = normal
Окно фигуры - нормальное (а не модальное) окно [15].
BeingDeleted = off
Данное свойство поддерживается, начиная с версии MATLAB 6.0.
ButtonDownFcn =
Это свойство определяет оператор MATLAB, который будет выполняться в случае щелчка мышью по фигуре, но не по объектам-потомкам фигуры.
Children = матрица размера (26,1), содержащая дескрипторы объектов-потомков фигуры.
Clipping = on
Это свойство не используется.
CreateFcn =
DeleteFcn =
Эти свойства задают операторы MATLAB, выполняемые при создании и унич-тожении фигуры.
BusyAction = queue
Если выполняется процедура ответного вызова, и в это время происходит собы-тие, вызывающее запуск новой процедуры ответного вызова, то новая процеду-ра ставится в очередь и выполняется по завершении старой процедуры.
HandleVisibility = callback
Дескриптор фигуры доступен только для операторов, выполняющихся внутри процедуры ответного вызова [15].
HitTest = on
Фигура PDETool доступна для выбора с помощью мыши.
Interruptible = on
Разрешается прерывание выполнения процедур ответного вызова.
Parent = [0]
Родитель фигуры - всегда объект root.
Selected = off
Фигура выбрана - on, не выбрана - off.
SelectionHighlight = on
Это свойство не используется.
Tag = PDETool
В данном справочном руководстве и в PDE Toolbox все графические объекты идентифицируются по свойству 'Таg'.
Type = figure
Тип объекта PDETool - фигура.
UIContextMenu = []
Контекстное меню не создаётся и не используется.
UserData = матрица размера (1,7)
В этом свойстве многих графических объектов содержатся важнейшие выход-ные данные PDE-модели. Для PDETool это матрица-строка, содержащая список дескрипторов.
Visible = on
Фигура видимая.
Если в приложение PDETool не загружена PDE-модель, то свойство User-Data этой фигуры содержит список дескрипторов следующих графических объ-ёктов: uicontrol PDEXField, uicontrol PDEYField, далее пять нулей. Здесь надо учитывать, что PDETool без PDE-модели может работать только в режиме Draw Mode. Переключение PDETool в любой другой режим приведёт к загрузке стандартной демонстрационной PDE-модели.
Свойство UserData фигуры PDETool не зависит от режима работы этого приложения и от загруженной PDE-модели. Однако это свойство зависит от версии MATLAB и PDE Toolbox, а также от конфигурации компьютера, на ко-тором установлен MATLAB. Узнать назначение графических объектов, деск-рипторы которых хранятся в свойстве UserData фигуры PDETool, можно с по-мощью следующей последовательности операторов MATLAB:
h=findobj(allchild(0),'tag','PDETool');
u=get(h,'UserData');
ut=get(u,'Type');
ug=get(u,'Tag');
3.2. Свойства объектов axes
3.2.1. Свойства объекта axes PDEAxes
Как было сказано выше, объект axes PDEAxes - это основной объект axes фигуры PDETool (в предыдущих разделах, например, 2.6, он назывался просто "поле axes"). Этот графический объект выполняет роль поля показа геометрии расчётной области. Если в приложение PDETool не загружена PDE-модель, то свойства объекта axes PDEAxes имеют следующие значения.
ALim = [0 1]
ALimMode = auto
Эти свойства определяют диапазон изменения коэффициента прозрачности. Эти свойства поддерживаются в дескрипторной графике и GUI, начиная с версии MATLAB 6.0.
AmbientLightColor = [1 1 1]
Это свойство задаёт цвет фоновой подсветки объектов Light [15]. В данном случае - белый.
Box = on
Контур объекта axes PDEAxes отображается в виде прямоугольника [15].
CameraPosition = [0 0 19.2083]
CameraPositionMode = auto
CameraTarget = [0 0 0.5]
CameraTargetMode = auto
CameraUpVector = [0 1 0]
CameraUpVectorMode = auto
CameraViewAngle = [6.11935]
CameraViewAngleMode = auto
Эти свойства определяют параметры пространственного положения "камеры" [15] при показе изображения в поле axes.
CLim = [0 1]
CLimMode = auto
Эти свойства задают диапазон изменения цветов отображаемых подчинённых графических объектов [15].
Color = [1 1 1]
Цвет фона [15]. В данном случае - белый.
CurrentPoint = [ (2 by 3) double array]
Координаты точки, соответствующей последнему нажатию кнопки мыши в пределах данного объекта axes [15].
ColorOrder = [ (7 by 3) double array]
Порядок использования цветов при выводе множественных графиков [15]. Здесь в списке 7 цветов: синий, зелёный, красный, сине-зелёный, красно-синий, красно-зелёный, тёмно-серый.
DataAspectRatio = [1 1 1]
DataAspectRatioMode = manual
Эти свойства задают относительное масштабирование показываемого изображения вдоль осей x, y, z.
DrawMode = fast
Это свойство задаёт способ визуализации [15].
FontAngle = normal
Шрифт надписей без наклона.
FontName = Helvetica
Название шрифта надписей.
FontSize = [10]
Размер шрифта надписей.
FontUnits = points
Единицы измерения размера шрифта надписей. В данном случае - пункты (1 пункт = 1/72 дюйма).
FontWeight = normal
Толщина шрифта надписей. В данном случае - нормальная.
GridLineStyle = :
Стиль линий координатной сетки. В данном случае - пунктирные линии.
Layer = bottom
Размещение координатных осей и их маркеров. В данном случае - ниже "графика" [15].
LineStyleOrder = -
Это значение свойства означает, что все линии "графиков" - сплошные. См. также [15].
LineWidth = [0.5]
Толщина линий графиков равна 0.5 пункта.
NextPlot = replace
Не поддерживается режим отображения "множественных графиков". См. также [15].
PlotBoxAspectRatio = [3 2 1]
Относительное масштабирование поля объекта axes вдоль разных координатных осей [15].
PlotBoxAspectRatioMode = auto
Режим установки предыдущего свойства.
Projection = orthographic
В поле axes изображение показывается в ортографической (параллельной) проекции [15].
Position = [0.1 0.12 0.8 0.758519]
Положение axes PDEAxes в фигуре PDETool в нормализованных единицах.
TickLength = [0.01 0.025]
Длины меток на координатных осях [15].
TickDir = in
Направление меток - к полю графика [15].
TickDirMode = auto
Автоматический режим задания направления меток.
Title = [180]
Дескриптор объекта Text, который является заголовком объекта axes. В данном случае заголовок пустой.
Units = normalized
Единицы измерения для свойства Position [15].
View = [0 90]
Устаревшее свойство [15].
XColor = [0 0 0]
Цвет линии оси x. В данном случае - чёрный.
XDir = normal
Направление возрастания значений координат вдоль оси x. В данном случае - нормальное (слева направо).
XGrid = off
Линии координатной сетки вдоль координатной оси - не отображаются.
XLabel = [4.00037]
Дескриптор объекта Text - метки координатной оси x.
XAxisLocation = bottom
Ось x расположена ниже области графика.
XLim = [-1.5 1.5]
Пределы изменения координаты x в поле axes.
XLimMode = manual
Ручной способ задания пределов изменения координаты x в поле axes.
XScale = linear
Линейный масштаб вдоль оси x.
XTick = [ (1 by 7) double array]
Разметка координатной сетки вдоль оси x.
XTickLabel =
-1.5
-1
-0.5
0
0.5
1
1.5
Метки линий координатной сетки вдоль оси x. Значение свойства задаётся в виде матрицы символов.
XTickLabelMode = auto
Автоматический режим формирования меток линий координатной сетки вдоль оси x.
XTickMode = auto
Автоматический режим разметки координатной сетки вдоль оси x.
YColor = [0 0 0]
Цвет линии оси y. В данном случае - чёрный.
YDir = normal
Направление возрастания значений координат вдоль оси y. В данном случае - нормальное (снизу вверх).
YGrid = off
Линии координатной сетки вдоль координатной оси - не отображаются.
YLabel = [5.00037]
Дескриптор объекта Text - метки координатной оси y.
YAxisLocation = left
Ось y расположена левее области графика.
YLim = [-1 1]
Пределы изменения координаты y в поле axes.
YLimMode = manual
Ручной способ задания пределов изменения координаты y в поле axes.
YScale = linear
Линейный масштаб вдоль оси y.
YTick = [ (1 by 11) double array]
Разметка координатной сетки вдоль оси y.
YTickLabel = [ (11 by 4) char array]
Метки линий координатной сетки вдоль оси y. Значение свойства задаётся в виде матрицы символов.
YTickLabelMode = auto
Автоматический режим формирования меток линий координатной сетки вдоль оси y.
YTickMode = auto
Автоматический режим разметки координатной сетки вдоль оси y.
Далее следуют аналогичные свойства, относящиеся к оси z.
ZColor = [0 0 0]
ZDir = normal
ZGrid = off
ZLabel = [181]
ZLim = [0 1]
ZLimMode = auto
ZScale = linear
ZTick = [0 0.5 1]
ZTickLabel =
ZTickLabelMode = auto
ZTickMode = auto
BeingDeleted = off
Объект axes PDEAxes не может быть удалён вне процедуры ответного вызова.
ButtonDownFcn =
Процедура ответного вызова при отпускании (или нажатии) кнопки мыши [15].
Children = []
Подчинённых объектов (потомков) нет, т.к. PDE модель не загружена в PDETool. Следует учитывать, что на практике не все потомки бывают представлены в этом свойстве.
Clipping = on
Это свойство для объектов axes не задействовано [15].
Следующие свойства являются общими для графических объектов. Они кратко описаны выше (в подразделе 3.1).
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = callback
HitTest = on
Interruptible = on
Parent = [99.0002]
Selected = off
SelectionHighlight = on
Tag = PDEAxes
Type = axes
UIContextMenu = []
UserData = []
Visible = on
Независимо от режима работы приложения PDETool свойства XGrid, YGrid изменяются по команде Options/Grid. XLim, Ylim - по команде Options/Axes Limits. XTick, XTickLabel, Ytick, YTickLabel изменяются по команде Options/Grid Spacing. Названные здесь свойства изменяют также команды группы Options: Axes Equal, Zoom.
Свойство Children зависит от геометрии расчётной области PDE-задачи, а также от режима работы приложения PDETool. Пусть PDETool работает в режиме Draw Mode, и PDE-модель не загружена. В поле axes нарисуем прямоугольник. Тогда значением свойства Children станет массив размера (3,1), содержащий дескрипторы следующих объектов: line PDESelFrame, text PDELblSel, patch PDEMinReg. Последний из этих объектов - изображение созданного прямоугольника в виде закрашенной серым цветом области. Второй объект - надпись с именем (меткой) прямоугольника. Первый объект типа line - контур выделения геометрических объектов (в данном случае выделенным геометрическим объектом является созданный прямоугольник). Если отменить выделение прямоугольника, то значением свойства Children станет массив размера (2,1), потому что в результате отмены выделения будет уничтожен графический объект line PDESelFrame. Состав графических объектов, подчинённых axes, будет рассмотрен в одном из следующих подразделов.
3.2.2. Свойства объекта axes draw
Функционально графический объект axes draw представляет собой объединение пяти кнопок инструментальной панели, дублирующих команды меню группы Draw (см. 2.2). Свойства объекта axes draw зависят от состояния этих кнопок (одновременно может быть нажато не более одной кнопки; при нажатии любой кнопки этой группы PDETool автоматически переходит в режим Draw Mode). Пусть все кнопки отжаты. Тогда свойства объекта axes draw имеют следующие значения.
ALim = [0 1]
ALimMode = auto
AmbientLightColor = [1 1 1]
Box = on
CameraPosition = [0.5 0.5 9.16025]
CameraPositionMode = auto
CameraTarget = [0.5 0.5 0.5]
CameraTargetMode = auto
CameraUpVector = [0 1 0]
CameraUpVectorMode = auto
CameraViewAngle = [6.60861]
CameraViewAngleMode = auto
CLim = [0 1]
CLimMode = auto
Color = [0.752941 0.752941 0.752941]
CurrentPoint = [ (2 by 3) double array]
ColorOrder = [ (7 by 3) double array]
DataAspectRatio = [1 1 1]
DataAspectRatioMode = auto
DrawMode = normal
FontAngle = normal
FontName = Helvetica
FontSize = [10]
FontUnits = points
FontWeight = normal
GridLineStyle = :
Layer = top
LineStyleOrder = -
LineWidth = [0.5]
NextPlot = replace
PlotBoxAspectRatio = [1 1 1]
PlotBoxAspectRatioMode = auto
Projection = orthographic
Position = [0 0.96 0.2 0.04]
TickLength = [0.01 0.025]
TickDir = in
TickDirMode = auto
Title = [168]
Units = normalized
View = [0 90]
XColor = [0 0 0]
XDir = normal
XGrid = off
XLabel = [169]
XAxisLocation = bottom
XLim = [0 1]
XLimMode = manual
XScale = linear
XTick = []
XTickLabel =
XTickLabelMode = auto
XTickMode = manual
YColor = [0 0 0]
YDir = normal
YGrid = off
YLabel = [170]
YAxisLocation = left
YLim = [0 1]
YLimMode = manual
YScale = linear
YTick = []
YTickLabel =
YTickLabelMode = auto
YTickMode = manual
ZColor = [0 0 0]
ZDir = normal
ZGrid = off
ZLabel = [171]
ZLim = [0 1]
ZLimMode = auto
ZScale = linear
ZTick = [0 0.5 1]
ZTickLabel =
ZTickLabelMode = auto
ZTickMode = auto
BeingDeleted = off
ButtonDownFcn = btnpress
Children = [ (22 by 1) double array]
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = callback
HitTest = on
Interruptible = on
Parent = [99.0002]
Selected = off
SelectionHighlight = on
Tag = draw
Type = axes
UIContextMenu = []
UserData = [ (1 by 1) struct array]
Visible = off
Назначение свойств графического объекта axes описано в п. 3.2.1. Следует обратить внимание на свойства, выделенные жирным шрифтом. Свойства Type и Tag идентифицируют графический объект. Visible=off означает, что объект axes draw невидимый. Видимыми являются только его потомки, дескрипторы которых перечислены в свойстве Children. Подчинённые объекты, представленные в этом свойстве - это объекты типа line и patch, определяющие вид и состояние кнопок. Состояние кнопок влияет только на свойства подчинённых объектов и не влияет на их состав.
Для разработчиков связанных приложений и вычислительных сценариев важнейшим свойством является UserData. Для объекта axes draw это структура, состав и назначение полей которой представлены в следующей таблице.
| Название поля | Назначение |
| state | Обычный числовой массив размера (5,1), элементы которого хранят информацию о состоянии каждой кнопки: 0 - кнопка отжата; 1 - кнопка нажата. |
| buttonId | Матрица символов размера (5,6), в которой хранятся идентификаторы кнопок: 'rect ', 'rectc ', 'ellip ', 'ellipc', 'poly '. |
| pressType | Матрица символов размера (5,6), в которой хранятся типы нажатия кнопок. Все эти типы имеют значение 'toggle'. Это означает, что нажатие и отпускание кнопок фиксируется. |
| exFlag | Строка символов, имеющая значение 'no'. |
| callbacks | Матрица символов размера (5,24). Каждая строка - оператор MATLAB, выполняемый при нажатии соответствующей кнопки. Строки имеют следующие значения: 'pdetool('drawrect',1)', 'pdetool('drawrect',2)', 'pdetool('drawellipse',1)', 'pdetool('drawellipse',2)', 'pdetool('drawline')'. |
| buttonDownFcn | Матрица символов размера (5,1), состоящая из пробелов. Каждая строка этой матрицы - имя функции, вызываемой при нажатии соответствующей кнопки. Пробелы означают, что никакие функции не вызываются. |
| xOffset | Числовая матрица размера (5,1), содержащая относительные смещения координаты x для всех кнопок. Эти значения используются для того, чтобы определить, какая кнопка в пределах объекта axes draw нажата. |
| yOffset | Массив, равный zeros(5,1). Относительные смещения координаты y для всех кнопок равны нулю. |
| groupSize | Массив, равный [1 5]. Это означает, что объект axes draw состоит из одной группы кнопок: с первой по пятую. |
| uicontrolButtons | Пустой массив размера (0,0). Это означает, что ссылок на кнопки типа uicontrol нет. |
| Данная структура является значением свойства UserData для всех "кнопочных" объектов axes. | |
3.2.3. Свойства объекта axes solve
Функционально графический объект axes solve представляет собой объединение шести кнопок инструментальной панели, дублирующих команды меню групп Boundary, PDE, Mesh, Solve (см. 2.2). Свойства объекта axes solve имеют следующие значения.
ALim = [0 2]
ALimMode = auto
AmbientLightColor = [1 1 1]
Box = on
CameraPosition = [0.5 0.5 18.3205]
CameraPositionMode = auto
CameraTarget = [0.5 0.5 1]
CameraTargetMode = auto
CameraUpVector = [0 1 0]
CameraUpVectorMode = auto
CameraViewAngle = [6.60861]
CameraViewAngleMode = auto
CLim = [0.2047 1.1154]
CLimMode = auto
Color = [0.752941 0.752941 0.752941]
CurrentPoint = [ (2 by 3) double array]
ColorOrder = [ (7 by 3) double array]
DataAspectRatio = [1 1 2]
DataAspectRatioMode = auto
DrawMode = normal
FontAngle = normal
FontName = Helvetica
FontSize = [10]
FontUnits = points
FontWeight = normal
GridLineStyle = :
Layer = top
LineStyleOrder = -
LineWidth = [0.5]
NextPlot = replace
PlotBoxAspectRatio = [1 1 1]
PlotBoxAspectRatioMode = auto
Projection = orthographic
Position = [0.2 0.96 0.24 0.04]
TickLength = [0.01 0.025]
TickDir = in
TickDirMode = auto
Title = [219]
Units = normalized
View = [0 90]
XColor = [0 0 0]
XDir = normal
XGrid = off
XLabel = [220]
XAxisLocation = bottom
XLim = [0 1]
XLimMode = manual
XScale = linear
XTick = []
XTickLabel =
XTickLabelMode = auto
XTickMode = manual
YColor = [0 0 0]
YDir = normal
YGrid = off
YLabel = [221]
YAxisLocation = left
YLim = [0 1]
YLimMode = manual
YScale = linear
YTick = []
YTickLabel =
YTickLabelMode = auto
YTickMode = manual
ZColor = [0 0 0]
ZDir = normal
ZGrid = off
ZLabel = [198]
ZLim = [0 2]
ZLimMode = auto
ZScale = linear
ZTick = [0 1 2]
ZTickLabel =
ZTickLabelMode = auto
ZTickMode = auto
BeingDeleted = off
ButtonDownFcn = btnpress
Children = [ (26 by 1) double array]
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = callback
HitTest = on
Interruptible = on
Parent = [99.0002]
Selected = off
SelectionHighlight = on
Tag = solve
Type = axes
UIContextMenu = []
UserData = [ (1 by 1) struct array]
Visible = off
При необходимости указанные значения свойств можно сравнить со свойствами объекта axes draw (см 3.2.2). Назначение свойств графического объекта axes описано в п. 3.2.1. Следует обратить внимание на свойства, выделенные жирным шрифтом. Свойства Type и Tag идентифицируют графический объект. Visible=off означает, что объект axes solve невидимый. Видимыми являются только его потомки, дескрипторы которых перечислены в свойстве Children (у axes solve этих объектов больше, чем у axes draw). Подчинённые объекты, представленные в этом свойстве - это объекты типа line и patch, определяющие вид и состояние кнопок. Одновременно может быть нажата только одна кнопка. Кнопка может быть нажатой только в том случае, если на неё наведён указатель мыши и удерживается левая или правая кнопка мыши. Отпускание кнопки мыши приводит к немедленному выполнению соответствующей команды. Состояние кнопок axes solve влияет только на свойства подчинённых объектов и не влияет на их состав.
Состав и назначение полей структуры, которая является значением свойства UserData графического объекта axes solve, сведём в таблицу.
| Название поля | Назначение |
| state | Обычный числовой массив размера (6,1), элементы которого хранят информацию о состоянии каждой кнопки: 0 - кнопка отжата; 1 - кнопка нажата. |
| buttonId | Матрица символов размера (6,6), в которой хранятся идентификаторы кнопок: 'bounds', 'spec ', 'init ', 'refine', 'solve ', 'plot '. |
| pressType | Строка символов, имеющая значение 'flash'. Это означает, что при отпускании нажатой кнопки соответствующая команда выполняется немедленно. |
| exFlag | Строка символов, имеющая значение 'no'. |
| callbacks | Матрица символов размера (6,98). Каждая строка - оператор MATLAB, выполняемый при нажатии соответствующей кнопки. Строки имеют следующие значения: 'pdetool('boundmode')', 'pdetool('set_param')', 'pdetool('initmesh')', 'pdetool('refine')', 'pdetool('solve')', 'pdeptdlg('initialize', 0, getuprop(findobj(get(0, 'Children'), 'flat', 'Tag', 'PDETool'), 'plotstrings'))'. |
| buttonDownFcn | Матрица символов размера (6,1), состоящая из пробелов. Каждая строка этой матрицы - имя функции, вызываемой при нажатии соответствующей кнопки. Пробелы означают, что никакие функции не вызываются. |
| xOffset | Числовая матрица размера (6,1), содержащая относительные смещения координаты x для всех кнопок. Эти значения используются для того, чтобы определить, какая кнопка в пределах объекта axes solve нажата. |
| yOffset | Массив, равный zeros(6,1). Относительные смещения координаты y для всех кнопок равны нулю. |
| groupSize | Массив, равный [1 6]. Это означает, что объект axes solve состоит из одной группы кнопок: с первой по шестую. |
| uicontrolButtons | Пустой массив размера (0,0). Это означает, что ссылок на кнопки типа uicontrol нет. |
3.2.4. Свойства объекта axes zoom
Функционально графический объект axes zoom представляет собой кнопку инструментальной панели, дублирующей команду меню Options/ Zoom (см. 2.1.3, 2.2). Свойства объекта axes zoom имеют следующие значения.
ALim = [0 1]
ALimMode = auto
AmbientLightColor = [1 1 1]
Box = on
CameraPosition = [0.5 0.5 9.16025]
CameraPositionMode = auto
CameraTarget = [0.5 0.5 0.5]
CameraTargetMode = auto
CameraUpVector = [0 1 0]
CameraUpVectorMode = auto
CameraViewAngle = [6.60861]
CameraViewAngleMode = auto
CLim = [0 1]
CLimMode = auto
Color = [0.752941 0.752941 0.752941]
CurrentPoint = [ (2 by 3) double array]
ColorOrder = [ (7 by 3) double array]
DataAspectRatio = [1 1 1]
DataAspectRatioMode = auto
DrawMode = normal
FontAngle = normal
FontName = Helvetica
FontSize = [10]
FontUnits = points
FontWeight = normal
GridLineStyle = :
Layer = top
LineStyleOrder = -
LineWidth = [0.5]
NextPlot = replace
PlotBoxAspectRatio = [1 1 1]
PlotBoxAspectRatioMode = auto
Projection = orthographic
Position = [0.44 0.96 0.04 0.04]
TickLength = [0.01 0.025]
TickDir = in
TickDirMode = auto
Title = [222]
Units = normalized
View = [0 90]
XColor = [0 0 0]
XDir = normal
XGrid = off
XLabel = [223]
XAxisLocation = bottom
XLim = [0 1]
XLimMode = manual
XScale = linear
XTick = []
XTickLabel =
XTickLabelMode = auto
XTickMode = manual
YColor = [0 0 0]
YDir = normal
YGrid = off
YLabel = [224]
YAxisLocation = left
YLim = [0 1]
YLimMode = manual
YScale = linear
YTick = []
YTickLabel =
YTickLabelMode = auto
YTickMode = manual
ZColor = [0 0 0]
ZDir = normal
ZGrid = off
ZLabel = [225]
ZLim = [0 1]
ZLimMode = auto
ZScale = linear
ZTick = [0 0.5 1]
ZTickLabel =
ZTickLabelMode = auto
ZTickMode = auto
BeingDeleted = off
ButtonDownFcn = btnpress
Children = [ (5 by 1) double array]
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = callback
HitTest = on
Interruptible = on
Parent = [99.0002]
Selected = off
SelectionHighlight = on
Tag = zoom
Type = axes
UIContextMenu = []
UserData = [ (1 by 1) struct array]
Visible = off
Состав и назначение полей структуры, которая является значением свойства UserData графического объекта axes zoom, сведём в таблицу.
| Название поля | Назначение |
| state | Число, хранящее информацию о состоянии кнопки: 0 - кнопка отжата; 1 - кнопка нажата. |
| buttonId | Строка символов размера (1,4), равная 'zoom', в которой хранится идентификатор кнопки. |
| pressType | Строка символов, имеющая значение 'toggle'. Это означает, что нажатие и отпускание кнопки фиксируется. |
| exFlag | Строка символов, имеющая значение 'no'. |
| callbacks | Строка символов, равная 'pdetool('zoom')'. Это оператор MATLAB, выполняемый при нажатии кнопки. |
| buttonDownFcn | Строка символов, равная пробелу. Это означает, что никакие функции при нажатии кнопки не вызываются. |
| xOffset | Число нуль (см. предыдущие объекты axes). |
| yOffset | Число нуль (см. предыдущие объекты axes). |
| groupSize | Массив, равный [1 1]. Это означает, что объект axes zoom состоит из одной группы кнопок: с первой по первую. |
| uicontrolButtons | Пустой массив размера (0,0). Это означает, что ссылок на кнопки типа uicontrol нет. |
3.3. Свойства объектов uimenu
3.3.1. Свойства uimenu PDEFileMenu и подчинённых объектов
Пункт File главного меню обладает следующими свойствами.
Accelerator =
Клавиша быстрого доступа [15]. В данном случае не используется.
Callback =
Процедура ответного вызова [15], выполняемая при активизации данного пунк-та меню.
Checked = off
Индикатор выбора данного пункта меню сброшен [15].
Enable = on
Пункт меню доступен для активизации [15].
ForegroundColor = [0 0 0]
Цвет символов при отображении метки пункта меню. В данном случае - чёр-ный.
Label = &File
Текст метки пункта меню.
Position = [1]
Номер пункта меню. Для главного меню пункты отображаются слева направо.
Separator = off
Пункт меню отображается без разделительной линии перед ним.
Следующие свойства являются общими для всех графических объектов. Их на-значение описано в [15].
BeingDeleted = off
ButtonDownFcn =
Children = [ (6 by 1) double array]
Здесь перечислены дескрипторы подчинённых объектов (пунктов подменю).
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [99.0002]
Selected = off
SelectionHighlight = on
Tag = PDEFileMenu
Type = uimenu
UIContextMenu = []
UserData = [ (7 by 1) double array]
Visible = on
Свойство UserData представляет собой обычный числовой массив размера (7,1). В этом массиве хранятся флаги текущей PDE-задачи. Чтобы опытный пользователь GUI-приложения PDETool мог расшифровать назначение этих флагов, составим примерную таблицу соответствия между текущим состоянием PDE-задачи и значениями флагов.
| Текущее состояние PDE-задачи | Значения флагов Flags | ||||||
| №1 | №2 | №3 | №4 | №5 | №6 | №7 | |
| 1. PDE-модели нет ("новый" PDETool) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2. В режиме Draw Mode нарисован один или несколько геометрических объектов | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 3. С прорисованной геометрией переклю-чаемся в режим Boundary Mode | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 4. Переключаемся в режим PDE Mode | 1 | 4 | 0 | 1 | 0 | 0 | 0 |
| 5. Переключаемся в режим Mesh Mode | 1 | 2 | 0 | 0 | 1 | 0 | 0 |
| 6. Решили PDE без визуализации (т.е. по-сле решения остались в режиме Mesh Mode) | 1 | 2 | 0 | 0 | 0 | 1 | 0 |
| 7. Показали решение в поле axes (т.е. вы-полнили команду Plot Solution). В этом случае параметры режима визуализации на значения флагов не влияют. | 1 | 3 | 0 | 0 | 0 | 1 | 0 |
| 8. Переключаемся из состояния 4 в Draw Mode (даже если через Boundary Mode) | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 9. Переключаемся из состояния 5 в PDE Mode | 1 | 4 | 0 | 0 | 1 | 0 | 0 |
| 10. Переключаемся из состояния 5 в Boundary Mode (можно через PDE Mode) | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 11. Переключаемся из состояния 5 в Draw Mode (можно через PDE Mode, Boundary Mode) | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 12. Переключаемся из состояния 6 в PDE Mode | 1 | 4 | 0 | 0 | 0 | 1 | 0 |
| 13. Переключаемся из состояния 6 в Boundary Mode (можно через промежуточ-ные режимы) | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 14. Переключаемся из состояния 6 или 7 в Draw Mode (можно через промежуточные режимы) | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 15. В состоянии 6 сохраняем PDE-модель в виде m-файла | 0 | 2 | 0 | 0 | 0 | 1 | 0 |
| 16. Перезапускаем приложение PDETool и загружаем m-файл, созданный в состоянии 15 | 0 | 2 | 0 | 0 | 0 | 1 | 0 |
| 17. Загружаем m-файл PDE-модели, в ко-торой сетка сгенерирована, а PDE не решено | 0 | 2 | 0 | 0 | 1 | 0 | 1 |
| 18. Решаем без визуализации PDE для за-груженной модели | 0 | 2 | 0 | 0 | 0 | 1 | 0 |
| 19. В режиме Mesh Mode изменим сетку (по отношению к состоянию 18) | 1 | 2 | 0 | 0 | 1 | 0 | 0 |
| 20. Сохраним состояние 19 PDE-модели в виде m-файла | 0 | 2 | 0 | 0 | 1 | 0 | 0 |
| 21. Перезапускаем приложение PDETool и загружаем m-файл, созданный в состоянии 20 | 0 | 2 | 0 | 0 | 1 | 0 | 1 |
Проанализировав данные, содержащиеся в приведённой таблице, можно уз-нать назначение флагов Flags текущей PDE-задачи.
Flags(1) - флаг, указывающий, была ли изменена геометрия или конечно-элементная сетка с начала сеанса PDETool или с момента последнего сохране-ния PDE-модели или с момента загрузки текущей PDE-модели. Flags(1)=1 - да. Flags(1)=0 - нет.
Flags(2) - код текущего режима GUI-приложения PDETool. Flags(2)=0 - Draw Mode. Flags(2)=1 - Boundary Mode. Flags(2)=4 - PDE Mode. Flags(2)=2 - Mesh Mode. Flags(2)=3 - режим визуализации решения PDE-задачи.
Flags(3)=1 - "развитие" PDE-модели завершилось прорисовкой геометрии. В этом случае Flags([4 5 6])=[0;0;0]. В противном случае Flags(3)=0.
Flags(4)=1 - "развитие" PDE-модели завершилось заданием граничных ус-ловий или заданием коэффициентов PDE. В этом случае Flags([3 5 6])=[0;0;0]. В противном случае Flags(4)=0. Здесь надо учитывать, что при любом переклю-чении в режим Boundary Mode автоматически задаются граничные условия по умолчанию, если они ещё не были заданы; при любом переключении в режим PDE Mode автоматически задаются коэффициенты PDE по умолчанию, если они ещё не были заданы.
Flags(5)=1 - "развитие" PDE-модели завершилось генерацией конечноэле-ментной сетки. В этом случае Flags([3 4 6])=[0;0;0]. В противном случае Flags(5)=0.
Flags(6)=1 - "развитие" PDE-модели завершилось решением PDE-задачи. В этом случае Flags([3 4 5 7])=[0;0;0;0]. В противном случае Flags(6)=0.
Flags(7)=1 - текущая PDE-модель загружена из m-файла, но PDE не решено. В противном случае Flags(7)=0.
Свойства подчинённых объектов
Пункт подменю File/New обладает следующими свойствами.
Accelerator = n
Callback = pdetool('new')
Checked = off
Enable = on
ForegroundColor = [0 0 0]
Label = &New
Последний символ в этом свойстве - пробел!
Position = [1]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [6.00037]
Selected = off
SelectionHighlight = on
Tag =
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Пункт подменю File/Open обладает следующими свойствами.
Accelerator = o
Callback = pdetool('open')
Checked = off
Enable = on
ForegroundColor = [0 0 0]
Label = &Open...
Последний символ в этом свойстве - пробел!
Position = [2]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [6.00037]
Selected = off
SelectionHighlight = on
Tag =
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Пункт подменю File/Save обладает следующими свойствами.
Accelerator = s
Callback = pdetool('save')
Checked = off
Enable = off
Это свойство имеет значение 'off', если PDE-модели в поле axes нет или если в текущей ди-ректории нет m-файла с именем PDE-модели, находящейся в поле axes. В противном случае это свойство имеет значение 'on'.
ForegroundColor = [0 0 0]
Label = &Save
Последний символ в этом свойстве - пробел!
Position = [3]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [6.00037]
Selected = off
SelectionHighlight = on
Tag = PDESave
Основное назначение этого свойства - быстрый доступ к свойству Enable этого объекта.
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Пункт подменю File/ Save As обладает следующими свойствами.
Accelerator =
Callback = pdetool('save_as'),
Checked = off
Enable = on
ForegroundColor = [0 0 0]
Label = Save &As...
Position = [4]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [6.00037]
Selected = off
SelectionHighlight = on
Tag =
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Пункт подменю File/Print обладает следующими свойствами.
Accelerator =
Callback = pdetool('print')
Checked = off
Enable = on
ForegroundColor = [0 0 0]
Label = &Print...
Position = [5]
Separator = on
Этот пункт меню отделяется от предыдущих горизонтальной чертой.
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [6.00037]
Selected = off
SelectionHighlight = on
Tag =
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Пункт подменю File/Exit обладает следующими свойствами.
Accelerator = w
Callback = pdetool('exit')
Checked = off
Enable = on
ForegroundColor = [0 0 0]
Label = E&xit
Последний символ в этом свойстве - пробел!
Position = [6]
Separator = on
Этот пункт меню отделяется от предыдущих горизонтальной чертой.
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [6.00037]
Selected = off
SelectionHighlight = on
Tag =
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Дополнительных комментариев по свойствам объектов, подчинённых uimenu PDEFileMenu не требуется.
3.3.2. Свойства uimenu PDEEditMenu и подчинённых объектов
Пункт Edit главного меню обладает следующими свойствами.
Accelerator =
Callback =
Checked = off
Enable = on
Это свойство имеет значение 'on', если в поле axes есть PDE-модель, и PDETool работает в режиме Draw Mode (см. п. 2.4.1) или Boundary Mode (см. п. 2.4.2) или PDE Mode (см. п. 2.4.3). 'off' - в противном случае.
ForegroundColor = [0 0 0]
Label = &Edit
Position = [2]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = [ (6 by 1) double array]
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [99.0002]
Selected = off
SelectionHighlight = on
Tag = PDEEditMenu
Type = uimenu
UIContextMenu = []
UserData = []
Это свойство равно пустому массиву, если текущая PDE-модель ни разу не бы-ла сохранена (см. подраздел 2.6), т.е. если она не имеет имени. В противном случае это свойство равно строке символов, содержащей полное имя m-файла текущей PDE-модели, включая имя диска, путь доступа и имя файла с расши-рением.
Visible = on
Свойства подчинённых объектов
Пункт подменю Edit/Undo обладает следующими свойствами.
Accelerator = z
Callback = pdetool('undo')
Checked = off
Enable = off
Это свойство равно 'on' только в том случае, когда PDETool работает в режиме интерактив-ного построения многоугольника (когда многоугольник ещё не достроен). Соответствующая команда удаляет последнюю построенную сторону многоугольника.
ForegroundColor = [0 0 0]
Label = &Undo
Последний символ в этом свойстве - пробел!
Position = [1]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [13.0004]
Selected = off
SelectionHighlight = on
Tag = PDEUndo
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Пункт подменю Edit/Cut обладает следующими свойствами.
Accelerator = x
Callback = pdetool('cut',1)
Checked = off
Enable = on
Это свойство имеет значение 'on' только в режиме Draw Mode (см. п. 2.4.1). 'off' - во всех остальных режимах.
ForegroundColor = [0 0 0]
Label = Cu&t
Последний символ в этом свойстве - пробел!
Position = [2]
Separator = on
Этот пункт меню отделяется от предыдущих горизонтальной чертой.
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [13.0004]
Selected = off
SelectionHighlight = on
Tag = PDECut
Type = uimenu
UIContextMenu = []
UserData = [ (10 by 1) double array]
Это свойство представляет собой буфер "вырезки и вставки" геометрических объектов. Формат этого массива такой же, как и у матрицы геометрических объектов (см. матрицу gd, п. 2.4.1).
Visible = on
Пункт подменю Edit/Copy обладает следующими свойствами.
Accelerator = c
Callback = pdetool('cut',2)
Checked = off
Enable = on
Это свойство имеет значение 'on' только в режиме Draw Mode (см. п. 2.4.1). 'off' - во всех остальных режимах.
ForegroundColor = [0 0 0]
Label = &Copy
Последний символ в этом свойстве - пробел!
Position = [3]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [13.0004]
Selected = off
SelectionHighlight = on
Tag = PDECopy
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Пункт подменю Edit/Paste обладает следующими свойствами.
Accelerator = v
Callback = pdepsdlg
Checked = off
Enable = on
Это свойство имеет значение 'on' только в том случае, если PDETool работает в режиме Draw Mode (см. п. 2.4.1) и если буфер "вырезки и вставки" геометрических объектов не пус-той.
ForegroundColor = [0 0 0]
Label = &Paste...
Последний символ в этом свойстве - пробел!
Position = [4]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [13.0004]
Selected = off
SelectionHighlight = on
Tag = PDEPaste
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Пункт подменю Edit/Clear обладает следующими свойствами.
Accelerator = r
Callback = pdetool('clear')
Checked = off
Enable = on
Это свойство имеет значение 'on' только в режиме Draw Mode (см. п. 2.4.1). 'off' - во всех остальных режимах.
ForegroundColor = [0 0 0]
Label = Clea&r
Последний символ в этом свойстве - пробел!
Position = [5]
Separator = on
Этот пункт меню отделяется от предыдущих горизонтальной чертой.
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [13.0004]
Selected = off
SelectionHighlight = on
Tag = PDEClear
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Пункт подменю Edit/ Select All обладает следующими свойствами.
Accelerator = a
Callback = pdeselect('select',1)
Checked = off
Enable = on
Это свойство равно 'on' всегда, когда свойство Enable объекта uimenu PDEEditMenu равно 'on'.
ForegroundColor = [0 0 0]
Label = Select &All
Последний символ в этом свойстве - пробел!
Position = [6]
Separator = on
Этот пункт меню отделяется от предыдущих горизонтальной чертой.
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [13.0004]
Selected = off
SelectionHighlight = on
Tag = PDESelall
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
3.3.3. Свойства uimenu PDEOptMenu и подчинённых объектов
Пункт Options главного меню обладает следующими свойствами.
Accelerator =
Callback =
Checked = off
Enable = on
ForegroundColor = [0 0 0]
Label = &Options
Position = [3]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = [ (9 by 1) double array]
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [99.0002]
Selected = off
SelectionHighlight = on
Tag = PDEOptMenu
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Эти свойства в комментариях не нуждаются.
Свойства подчинённых объектов
Пункт подменю Options/Grid обладает следующими свойствами.
Accelerator =
Callback = pdetool gridon
Checked = on
Это свойство равно 'on' (а пункт меню отмечен галочкой), если включен режим показа коор-динатной сетки в поле axes (см. п. 2.1.3). Если этот режим отключен, то свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = &Grid
Position = [1]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [20.0004]
Selected = off
SelectionHighlight = on
Tag = PDEGrid
Type = uimenu
UIContextMenu = []
UserData = []
Visible = on
Пункт подменю Options/ Grid Spacing обладает следующими свойствами.
Accelerator =
Callback = pdetool spacing
Checked = off
Enable = on
ForegroundColor = [0 0 0]
Label = Gr&id Spacing...
Position = [2]
Separator = off
Общие свойства этого объекта за исключением свойства Tag такие же, как и у uimenu PDE-Grid.
Tag = PDESpace
Пункт подменю Options/Snap обладает следующими свойствами.
Accelerator =
Callback = pdetool('snapon')
Checked = off
Это свойство равно 'on' (а пункт меню отмечен галочкой), если включен режим округления координат указателя мыши при показе их значений пользователю (см. п. 2.1.3). Если этот режим отключен, то свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = &Snap
Position = [3]
Separator = off
Общие свойства этого объекта за исключением свойства Tag такие же, как и у uimenu PDE-Grid.
Tag = PDESnap
Пункт подменю Options/ Axes Limits обладает следующими свойствами.
Accelerator =
Callback = pdetool axlim
Checked = off
Enable = on
ForegroundColor = [0 0 0]
Label = &Axes Limits...
Position = [4]
Separator = on
Общие свойства этого объекта за исключением свойства Tag такие же, как и у uimenu PDE-Grid.
Tag = PDEAxMenu
Пункт подменю Options/ Axes Equal обладает следующими свойствами.
Accelerator =
Callback = pdetool axeq
Checked = off
Это свойство равно 'on' (а пункт меню отмечен галочкой), если включен режим одинакового масштаба по осям x и y в поле axes (см. п. 2.1.3). Если этот режим отключен, то свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = Axes &Equal
Position = [5]
Separator = off
Общие свойства этого объекта за исключением свойства Tag такие же, как и у uimenu PDE-Grid.
Tag = PDEAxeq
Пункт подменю Options/ Turn off Toolbar Help обладает следующими свой-ствами.
Accelerator =
Callback = pdetool helponoff
Checked = on
Это свойство равно 'on' (а пункт меню отмечен галочкой), если включен режим запрета вы-дачи подсказок по кнопкам инструментальной панели PDETool (см. п. 2.1.3). Если этот ре-жим отключен, то свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = &Turn off Toolbar Help
Position = [6]
Separator = on
Общие свойства этого объекта за исключением свойства Tag такие же, как и у uimenu PDE-Grid.
Tag = PDEHelpoff
Пункт подменю Options/Zoom обладает следующими свойствами.
Accelerator =
Callback = pdetool zoom
Checked = off
Это свойство равно 'on' (а пункт меню отмечен галочкой), если включен режим показа в увеличенном масштабе выделяемой прямоугольной области в PDE-модели (см. п. 2.1.3). Ес-ли этот режим отключен, то свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = &Zoom
Position = [7]
Separator = on
Общие свойства этого объекта за исключением свойства Tag такие же, как и у uimenu PDE-Grid.
Tag = PDEZoom
Пункт подменю Options/Application обладает следующими свойствами.
Accelerator =
Callback =
Checked = off
Enable = on
ForegroundColor = [0 0 0]
Label = A&pplication
Position = [8]
Separator = on
Общие свойства этого объекта за исключением Children и Tag такие же, как и у uimenu PDE-Grid.
Children = [ (10 by 1) double array]
В этом массиве хранятся дескрипторы объектов uimenu, каждый из которых соответствует своей краевой задаче (см. рис. 2.3, п. 2.1.3, подраздел 2.3).
Tag = PDEAppMenu
Пункт подменю Options/Refresh обладает следующими свойствами.
Accelerator =
Callback = pdetool refresh
Checked = off
Enable = on
ForegroundColor = [0 0 0]
Label = &Refresh
Position = [9]
Separator = on
Общие свойства этого объекта за исключением свойства Tag такие же, как и у uimenu PDE-Grid.
Tag = PDERefresh
Свойства объектов, подчинённых uimenu PDEAppMenu
Пункт подменю Generic Scalar (см. рис. 2.3, п. 2.1.3) обладает следующими свойствами.
Accelerator =
Callback = pdetool('appl_cb',1)
Checked = on
Это свойство равно 'on' (а соответствующий пункт подменю отмечен галочкой), если при-ложение PDETool работает в режиме краевой задачи "Generic Scalar" (см. также п. 2.3.1). В противном случае это свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = Generic Scalar
Position = [1]
Separator = off
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [28.0004]
Selected = off
SelectionHighlight = on
Tag =
Type = uimenu
UIContextMenu = []
UserData = [1]
Это свойство равно свойству Position
Visible = on
Пункт подменю Generic System (см. рис. 2.3, п. 2.1.3) обладает следующими свойствами.
Accelerator =
Callback = pdetool('appl_cb',2)
Checked = off
Это свойство равно 'on' (а соответствующий пункт подменю отмечен галочкой), если при-ложение PDETool работает в режиме краевой задачи "Generic System" (см. также п. 2.3.2). В противном случае это свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = Generic System
Position = [2]
Separator = off
Общие свойства этого объекта и всех следующих объектов, подчинённых uimenu PDEAppMenu, за исключением свойства UserData такие же, как и у uimenu Generic Scalar. У объектов, подчинённых uimenu PDEAppMenu, свойство UserData равно свойству Position.
Пункт подменю Structural Mechanics, Plane Stress (см. рис. 2.3, п. 2.1.3) об-ладает следующими свойствами.
Accelerator =
Callback = pdetool('appl_cb',3)
Checked = off
Это свойство равно 'on' (а соответствующий пункт подменю отмечен галочкой), если при-ложение PDETool работает в режиме краевой задачи "Structural Mechanics, Plane Stress" (см. также п. 2.3.3). В противном случае это свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = Structural Mechanics, Plane Stress
Position = [3]
Separator = off
Пункт подменю Structural Mechanics, Plane Strain (см. рис. 2.3, п. 2.1.3) об-ладает следующими свойствами.
Accelerator =
Callback = pdetool('appl_cb',4)
Checked = off
Это свойство равно 'on' (а соответствующий пункт подменю отмечен галочкой), если при-ложение PDETool работает в режиме краевой задачи "Structural Mechanics, Plane Strain" (см. также п. 2.3.4). В противном случае это свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = Structural Mechanics, Plane Strain
Position = [4]
Separator = off
Пункт подменю Electrostatics (см. рис. 2.3, п. 2.1.3) обладает следующими свойствами.
Accelerator =
Callback = pdetool('appl_cb',5)
Checked = off
Это свойство равно 'on' (а соответствующий пункт подменю отмечен галочкой), если при-ложение PDETool работает в режиме краевой задачи "Electrostatics" (см. также п. 2.3.5). В противном случае это свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = Electrostatics
Position = [5]
Separator = off
Пункт подменю Magnetostatics (см. рис. 2.3, п. 2.1.3) обладает следующими свойствами.
Accelerator =
Callback = pdetool('appl_cb',6)
Checked = off
Это свойство равно 'on' (а соответствующий пункт подменю отмечен галочкой), если при-ложение PDETool работает в режиме краевой задачи "Magnetostatics" (см. также п. 2.3.6). В противном случае это свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = Magnetostatics
Position = [6]
Separator = off
Пункт подменю AC Power Electromagnetics (см. рис. 2.3, п. 2.1.3) обладает следующими свойствами.
Accelerator =
Callback = pdetool('appl_cb',7)
Checked = off
Это свойство равно 'on' (а соответствующий пункт подменю отмечен галочкой), если при-ложение PDETool работает в режиме краевой задачи "AC Power Electromagnetics" (см. также п. 2.3.7). В противном случае это свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = AC Power Electromagnetics
Position = [7]
Separator = off
Пункт подменю Conductive Media DC (см. рис. 2.3, п. 2.1.3) обладает сле-дующими свойствами.
Accelerator =
Callback = pdetool('appl_cb',8)
Checked = off
Это свойство равно 'on' (а соответствующий пункт подменю отмечен галочкой), если при-ложение PDETool работает в режиме краевой задачи "Conductive Media DC" (см. также п. 2.3.8). В противном случае это свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = Conductive Media DC
Position = [8]
Separator = off
Пункт подменю Heat Transfer (см. рис. 2.3, п. 2.1.3) обладает следующими свойствами.
Accelerator =
Callback = pdetool('appl_cb',9)
Checked = off
Это свойство равно 'on' (а соответствующий пункт подменю отмечен галочкой), если при-ложение PDETool работает в режиме краевой задачи "Heat Transfer" (см. также п. 2.3.9). В противном случае это свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = Heat Transfer
Position = [9]
Separator = off
Пункт подменю Diffusion (см. рис. 2.3, п. 2.1.3) обладает следующими свой-ствами.
Accelerator =
Callback = pdetool('appl_cb',10)
Checked = off
Это свойство равно 'on' (а соответствующий пункт подменю отмечен галочкой), если при-ложение PDETool работает в режиме краевой задачи "Heat Transfer" (см. также п. 2.3.10). В противном случае это свойство равно 'off'.
Enable = on
ForegroundColor = [0 0 0]
Label = Diffusion
Position = [10]
Separator = off
Комментарии
В виде одного файла, книжки -- можно?
Мой опыт таких задач -- https://hub-back.exponenta.ru/storage/users/25814/files/sSMg4Mt2rM6Mwv2d3byZrbOF9eVSQi93CSnRPjE2.PDF
Е.Гаев
http://sula.nau.edu.ua/ukr/person/gaev/mystudents.html