Список функций Optimization Toolbox
Информация в данной статье относится к релизам программы MATLAB ранее 2016 года, и поэтому может содержать устаревшую информацию в связи с изменением функционала инструментов. С более актуальной информацией вы можете ознакомиться в разделе документация MATLAB на русском языке.
В статье приведено описание основных функций Optimization Toolbox.
Нелинейная оптимизация (функций)
- fminbnd – поиск функции одной переменной для фиксированного интервал
- fmincon - поиск минимума нелинейной задачи с ограничениями
- fminsearch – поиск минимума функции нескольких переменных без ограничений
- fminunc – поиск минимума функции нескольких переменных без ограничений
- fseminf – поиск минимума полубесконечной нелинейной функции нескольких переменных с ограничениями
Нелинейная минимизация многокритериальных функций
- fgoalattain – решение многокритериальной (векторной) задачи достижения цели
- fminimax – решение задачи минимакса
Линейный метод наименьших квадратов (для матричных задач)
- lsqlin – решение линейной задачи с ограничениями методом наименьших квадратов
- lsqnonneg - решение неотрицательной задачи методом наименьших квадратов
Нелинейный метод наименьших квадратов (для функций)
- lsqcurvefit – решение нелинейной задачи аппроксимации кривых (подбора данных) методом наименьших квадратов
- lsqnonlin - решение нелинейной задачи методом наименьших квадратов (нелинейный подбор данных)
Нелинейный метод определения нуля (решение уравнений)
Минимизация матричных задач
- linprog – решение задачи линейного программирования
- quadprog – решить квадратичную задачу математического программирования
Утилиты
- fzmult - умножение при сохранении основного базисом для нуль-пространства.
- gangster - обнуление <небольших> компонентов с учетом структурного ранга.
- optimget – получить значения параметров опций оптимизации
- optimset - создать или отредактировать структуру параметров опций оптимизации
Демонстрация крупно-масштабных методов
- circustent - квадратичное программирование для нахождения формы цирка шапито
- molecule - расчет молекулярной структуры с помощью нелинейной минимизации без ограничений
- optdeblur - устранение размытости изображений с помощью ограниченного линейного метода наименьших квадратов
Демонстрация средне-масштабных методов
- optdemo - меню демонстраций
- tutdemo - учебный прогон
- bandemo - минимизация банановой функции
- goaldemo - достижение цели
- dfildemo - проектирование фильтра с конечной точностью (требует Toolbox Обработки Сигналов)
- datdemo - подбор данных для кривой
Целочисленное программирование
- bintprog - Решение задачи целочисленного программирования вида
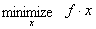 при условии
при условии 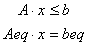
fminbnd – поиск функции одной переменной для фиксированного интервал
Синтаксис:
x = fminbnd(fun,x1,x2)
x = fminbnd(fun,x1,x2,options)
x = fminbnd(fun,x1,x2,options,P1,P2,...)
[x,fval] = fminbnd(...)
[x,fval,exitflag] = fminbnd(...)
[x,fval,exitflag,output] = fminbnd(...)
Описание:
fminbnd находит минимум функции одной переменной для фиксированного интервала.
- x = fminbnd(fun,x1,x2) возвращает значение x, которое является локальным минимумом скалярной функции, представленной как fun в интервале x1 < x < x2.
that is a local minimizer of the scalar valued function that is described - x = fminbnd(fun,x1,x2,options) производит оптимизацию с параметрами, заданными в структуре опций
- x = fminbnd(fun,x1,x2,options,P1,P2,...) предусматривает дополнительные аргументы P1, P2, и т.д., которые передаются в целевую функцию fun. Используйте опции =[], как заполнитель, если опции не устанавливаются как таковые.
- [x,fval] = fminbnd(...) возвращает значение целевой функции, вычисленной fun от как x
- [x,fval,exitflag] = fminbnd(...) возвращает значение exitflag, которое описывает выходные условия fminbnd.
- [x,fval,exitflag,output] = fminbnd(...) возвращает выходную структуру с информацией об оптимизации.
Аргументы:
Входные аргументы.
Таблица, Входные аргументы, содержит общее описание аргументов передаваемых в fminbnd.
Данный раздел содержит детальное описание fun и других опций.
| fun Функция, подлежащая минимизации. |
fun есть такая функция, которая принимает некий скаляр х и возвращает скаляр f, целевую функцию в точке х. Функция fun может быть задана виде некого описателя функции. x = fminbnd(@myfun,x0) где myfun есть функция MATLAB, определенная как function f = myfun(x) f = ... % Вычисляет значение функции в точке x.fun так же может быть внутренним объектом x = fminbnd(inline('sin(x*x)'),x0); |
| options | Опции обеспечивают учет специфических деталей функции виде параметров options. |
Выходные аргументы.
Таблица 4-2, Выходные аргументы, содержит общее описание аргументов, возвращаемых fminbnd. Данный раздел включает специфические детали для exitflag и output:
| exitflag | Описывает выходные условия:
|
| output | Структура, которая содержит информацию об оптимизации. Поле данной структуры включает:
|
Options
Параметры опций оптимизации для fminbnd. Вы можете использовать optimset, для того, что бы установить или изменить поля в структуре параметров options. Для детальной информации смотри Таблицу 4-3. Параметры опций оптимизации.
| Display | Уровень отображения. 'off' - отображение не выводится; 'iter' отображение выводится на каждой итерации; 'final' (по умолчанию) отображение только выходной информации. 'notify' (по умолчанию) отображение выходной информации в случае только, если функция не сходится. |
| MaxFunEvals | Максимальное число допустимых оценок функции. Maximum number of function evaluations allowed. |
| MaxIter | Максимальное число допустимых итераций. |
| TolX | Конечное допустимое отклонение по х. |
Пример:
Минимум имеет место для
x = fminbnd(@sin,0,2*pi)
x = 4.7124
Значение функции в точке минимума будет
y = sin(x)
y =
-1.0000
Для того, что бы найти минимум функции на интервале (0, 5), сперва запишем М-файл
function f = myfun(x)
f = (x-3).^2 - 1;
Далее вызовем программу оптимизации.
x = fminbnd(@myfun,0,5)
что дает решение
x =
3
Значение в точке минимума будет
y = f(x)
y =
-1
Алгоритм:
fminbnd из М-файл. В основу алгоритма положены Метод золотого сечения и параболической интерполяции. Фортран-программа, реализующая точно такой же алгоритм проведена в [1].
Ограничения:
Подлежащая минимизации функция должна быть непрерывной. Fminbnd может давать только локальные значения.
Fminbnd часто дает медленную сходимость, когда решения находится на границе интервала.
Fmincon часто дает более быстрое и более точное решение.
Fminbnd оперирует только с реальными переменными.
Литература:
- Forsythe, G.E., M.A. Malcolm, and C.B. Moler, Computer Methods for Mathematical Computations, Prentice Hall, 1976.
fmincon - поиск минимума нелинейной задачи с ограничениям
Синтаксис:
x = fmincon(fun,x0,A,b)
x = fmincon(fun,x0,A,b,Aeq,beq)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2, ...)
[x,fval] = fmincon(...)
[x,fval,exitflag] = fmincon(...)
[x,fval,exitflag,output] = fmincon(...)
[x,fval,exitflag,output,lambda] = fmincon(...)
[x,fval,exitflag,output,lambda,grad] = fmincon(...)
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(...)
Описание:
fmincon находит минимум для скалярной функции нескольких переменных с ограничениями начиная с начального приближения. В общем случае, эта задача относится к нелинейной оптимизации с ограничениями или к нелинейному программированию.
- x = fmincon(fun,x0,A,b) начинает с точки x0 и находит минимум от х для функции представленной как fun при условии выполнения линейных неравенств A*x <= b. x0 может быть скаляром, вектором или матрицей.
- x = fmincon(fun,x0,A,b,Aeq,beq) минимизирует fun при условии выполнения линейных равенств Aeq*x = beq, а так же A*x <= b. Устанавливается A=[] и b=[] в случае отсутствия неравенств.
- x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub) определяет набор нижних и верхних ограничений на конструируемые переменные х так, что решение всегда находится в диапазоне lb <= x <= ub. Устанавливается Aeq=[] and beq=[] в случае отсутствия равенств.
- x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) подчиняет минимизацию определенных в nonlcon fmincon нелинейных неравенств c(x) или равенств ceq(x) такому оптимуму, что c(x) <= 0 и ceq(x) = 0. Устанавливается lb=[] и/илиr ub=[] в случае отсутствия ограничений.
- x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) проводит минимизацию с оптимизационными параметрами, определенными в структурной опции.
- x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2,...) передает зависящие от типа задачи параметры непосредственно в функции fun и nonlcon. Передает пустые матрицы заменители для A, b, Aeq, beq, lb, ub, nonlcon и options в случае, если эти аргументы не являются необходимыми.
- [x,fval] = fmincon(...) возвращает значение целевой функции fun как решение от х.
- [x,fval,exitflag] = fmincon(...) возвращает значение exitflag, которое содержит описание выходных условий fmincon.
- [x,fval,exitflag,output] = fmincon(...) возвращает структурный выход с информацией об оптимизации.
- [x,fval,exitflag,output,lambda] = fmincon(...) возвращает структурную lambda с полями, содержащими множители Лагранжа в виде решения от х.
- [x,fval,exitflag,output,lambda,grad] = fmincon(...) возвращает значение градиента от fun в виде решения от х.
- [x,fval,exitflag,output,lambda,grad,hessian] = fmincon(...) возвращает значения матрицы Гессе от fun в виде решения от х.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в fmincon. Данные подраздел "Аргументы" приводит функционально-специфические детали для fun, nonlcon и options:
| fun Подлежащая минимизации функция. |
fun есть такая функция, которая принимает скаляр х и возвращает скаляр f, т.е. целевая функция от х. Функция fun может задаваться с помощью описателя функций x = fmincon(@myfun,x0,A,b) где myfun есть такая функция MATLAB, что function f = myfun(x) f = ... % Вычисление функции в точке х fun так же может быть и внутренним объектом x = fmincon(inline('norm(x)^2'),x0,A,b); Если градиент от fun может быть вычислен и опция options.GradObj равна 'on' посредством установки options = optimset('GradObj','on') то функция fun должна во втором выходном аргументе возвращать значение аргумента g, как вектора от х. Отметим, что посредством проверки значения nargout данная функция может обойти расчет g в случае когда fun вызывается только с одним выходным аргументом (случай, когда для оптимизационного алгоритма необходимо только значение f, а не g). function [f,g] = myfun(x) f = ... % Вычисление функции в точке х if nargout > 1 % fun вызывается с двумя выходными аргументами g = ... % Расчет градиента как функции от х end Градиент состоит из частных производных от f в точке x. Т.е. i-ая компонента g есть частная производная от f по i-ой компоненте от х. Если матрица Гессе к тому же может быть рассчитана и опция options.Hessian есть 'on', т.е. options = optimset('Hessian','on'), то функция fun должна возвращать значения матрицы Гессе Н в виде симметричной матрицы от х на месте третьего аргумента. Отметим, что посредством контроля значения nargout можно обойти расчет Н, тогда fun вызывается только с одним или двумя выходными аргументами (случай, когда для оптимизационного алгоритма необходимо только значение f и g, а не Н). function [f,g,H] = myfun(x) f = ... % Расчет значения целевой функции от х if nargout > 1 % fun вызывается с двумя выходными аргументами g = ... % Расчет градиента как функции от х if nargout > 2 H = ... % расчет матрицы Гессе от х end Матрица Гессе являются матрицей вторых частных производных от f в точке x. Т.е. (i,j)-ая компонента Н есть вторая частная производная от f по |
| nonlcon Функция, которая вычисляет нелинейные ограничения виде неравенств c(x) <= 0 и нелинейные ограничения виде равенств ceq(x) = 0. |
Функция nonlcon принимает вектор х и возвращает два вектора c и ceq. Вектор с содержит нелинейные неравенства при расчете от х и ceq содержит нелинейные равенства при расчете от х. Функция nonlcon может быть определена как описатель функции. x = fmincon(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon) где mycon есть функция MATLAB, определенная как function [c,ceq] = mycon(x) c = ... % вычисляет нелинейные ограничения в виде неравенств от х. ceq = ... % вычисляет нелинейные ограничения в виде равенств от х. Если к тому же градиенты ограничений могут быть рассчитаны и опция options.GradConstr равна 'on' посредством options = optimset('GradConstr','on') то функция nonlcon так же должна возвращаться как третий и четвертый выходные аргументы, GC - как градиент от c(x) и GCeq как как градиент от ceq(x). Отметим, что посредством контроля значения nargout данная функция может обойти расчет GC и GCeq при этом nonlcon вызывается только с двумя выходными аргументами (в данном случае алгоритм оптимизации нуждается только в значениях c и ceq а не GC и GCeq). function [c,ceq,GC,GCeq] = mycon(x) c = ... % Нелинейные неравенства от х ceq = ... % Нелинейные равенства от х if nargout > 2 % Nonlcon вызываентся с 4 выходнымизначениями GC = ... % Градиенты неравенств GCeq = ... % Градиенты равенств end Если nonlcon возвращает вектор с с m компонентами и х имеет длину n, где n есть длина x0, то градиент GC c(x) есть матрица n х m, где GC(i,j) будут частные производные от c(j) по x(i) (т.е. j-ая колонка GC есть градиент j-го ограничения виде неравенств c(j)). Аналогично, если ceq имеет p компонент, то градиент GCeq ceq(x) есть матрица n х p, где GCeq(i,j) будут частные производные от ceq(j) по x(i) (т.е. j-ая колонка GCeq есть градиент j-го ограничения виде равенств ceq(j)). |
| options | Опции обеспечивают учет специфических деталей функции виде параметров options. |
Выходные аргументы.
Таблица 4-2. "Выходные аргументы", содержат общее описание возвращаемых fmincon аргументов. В этом разделе приводятся общие специфические детали для величин exitflag, lambda и output:
| exitflag | Описывает выходные условия.
|
| lambda | Структура, которая содержит множители Лагранжа при решении по х (разделенном по типам условий). Поле структуры:
|
| output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Для крупно-масштабных (большой размерности) задач с краевыми ограничениями оптимальностью первого порядка будет бесконечная норма v.*g, где v определяется как Ограничения Бокса и g -градиент. Для крупно масштабных задач с только линейными ограничениями оптимальностью первого порядка будет бесконечная норма проекции градиента (т.е. градиент проецируется на нуль-пространство Aeq).
Options
Параметры оптимизационных опций, используемых в fmincon. Часть параметров используется ко всем алгоритмам, некоторые используются только для крупномасштабного алгоритма, а другие применимы только среднемасштабных алгоритмов. Можно использовать optimset для того, чтобы установить или изменить значения данных полей в структуре параметров опций.
Для детальной информации смотри Таблицу 4-3, Параметры Опций Оптимизации
Мы начнем с описания опции LargeScale, поскольку она устанавливает преимущественное право какой алгоритм использовать. Это только преимущественное право, поскольку должны быть выполнены определенные условия для того, что бы можно было использовать крупно-масштабный алгоритм. Для fmincon необходимо задавать градиент (смотри выше описание fun) или иначе будет использоваться средне-масштабный алгоритм.
| LargeScale | В случае установки 'on' используется, если это возможно, крупно-масштабный (большой размерности) алгоритм. Для использования средне-масштабного алгоритма устанавливается 'off'. |
Medium-Scale и Large-Scale Algorithms. Эти параметры используются как для средне-масштабного, так и крупно-масштабного алгоритмов:
| Diagnostics | Проводится печать диагностической информации о минимизируемой функции. |
| Display | Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации. |
| GradObj | Градиент определенный пользователем целевой функции. Смотри выше описание функции fun как в ней определить градиент. Для того, что бы использовать крупно-масштабный метод необходимо задавать указанный градиент. Это необязательно для средне-масштабного метода. |
| MaxFunEvals | Максимально число допустимых расчетов функции. |
| MaxIter | Максимально число допустимых итераций. |
| TolFun | Конечное допустимое отклонение по значению функции. |
| TolCon | Конечное допустимое отклонение по нарушению условий ограничения. |
| TolX | Конечное допустимое отклонение по значению х. |
Large-Scale Algorithm Only. Эти параметры используются только для крупно-масштабного алгоритма.
| Hessian | В случае установки 'on' в fmincon используется заданная пользователем матрица Гессе (задается в fun) или информация о матрице Гессе (при использовании HessMult) для целевой функции. В случае установки 'off' в fmincon используется матрице Гессе с расчетом с помощью конечных разностей. |
| HessMult | Указатель функции для умножения на матрицу Гессе. Для типа крупно-масштабных задач, эта функция рассчитывает произведение матрицы Гессе H*Y без реального формирования Н. Эта функция имеет форму W = hmfun(Hinfo,Y,p1,p2,...) где Hinfo и дополнительные параметры p1,p2,...включают в себя матрицы для расчета H*Y. Первый аргумент должен быть тот же самый, как и третий аргумент, возвращаемый целевой функцией fun. [f,g,Hinfo] = fun(x,p1,p2,...) параметры p1,p2,... являются теми же самыми параметрами, что передаются в fmincon (и в fun). fmincon(fun,...,options,p1,p2,...) Y есть матрица с тем же самым числом строк как и размерности данной задачи. W = H*Y, хотя H явно не формируется. fmincon использует Hinfo для расчета предварительных условий.  В качестве примера смотри Нелинейную Оптимизацию с Компактной, но Структурированной Матрицей Гессе и Ограничениями Типа Равенств. |
| HessPattern | Разреженный образ матрицы Гессе для конечных разностей. Если не является разумным в fun рассчитывать разреженную матрицу Гессе Н, то в fmincon крупно-масштабный метод может аппроксимировать Н через разреженные конечные разности (для градиентов) при условии, что структура разреженности для Н, т.е. местоположения nonzeros, задаются как определенные значения для HessPattern. В наихудшем случае, когда такая структура неизвестна, можно задать HessPattern, что является плотной матрицей, а полная конечноразностная аппроксимация будет рассчитываться на каждой итерации (что принимается по умолчанию). Это может быть очень дорогостоящим для больших задач, поэтому стоит затратить усилия на определение структуры разреженности. |
| MaxPCGIter | Максимальное число PCG (предварительно сопряженный градиент) итераций (Смотри ниже раздел Алгоритм). |
| PrecondBandWidth | Верхняя полоса предварительной обработки для PCG. По умолчанию используется диагональная начальная подготовка (верхняя полоса из 0). Для некоторых задач увеличение полосы снижает число итераций PCG. |
| TolPCG | Конечное допустимое число итераций PCG. |
| TypicalX | Типичные значения х. |
Только для средне-масштабного алгоритма. Эти параметры используются только для средне-масштабного алгоритма.
| DerivativeCheck | Сравнение вводимых пользователем производных (градиенты цели или ограничивающих условий) с конечноразностными производными. |
| DiffMaxChange | Максимальное изменение в переменных для конечно-разностных градиентов. |
| DiffMinChange | Минимальное изменение в переменных для конечно-разностных градиентов. |
Примеры:
Найти значение х, которые минимизируют ![]() , начиная с точки x = [10; 10; 10] и с учетом ограничений
, начиная с точки x = [10; 10; 10] и с учетом ограничений
![]()
Прежде всего, запишем М-файл, который возвращает скалярное значение f как функции от х.
function f = myfun(x)
f = -x(1) * x(2) * x(3);
Далее перепишем ограничения в виде меньше или равно константе.
![]()
Поскольку оба ограничения являются линейными, то представим их как матричные неравенства ![]() , где
, где
![]() ......
...... ![]()
Далее зададим начальную точку и запустим программу оптимизации.
x0 = [10; 10; 10]; % начальное предположение о решении
[x,fval] = fmincon(@myfun,x0,A,b)
После 66 расчетов функции решение будет
x =
24.0000
12.0000
12.0000
где значение функции будет
fval =
-3.4560e+03
и оценка ограничений в виде линейных неравенств <= 0 дает
A*x-b=
-72
0
Примечания:
Крупно-масштабная оптимизация. Для того, что бы использовать крупно-масштабный метод в fun необходимо задать градиент (а в опции options.GradObj установить 'on'). Производится предупреждение (warning) при условии, что градиент не задан, а опция options.LargeScale не равна 'off'. Допускается, что в функции fmincon значение g(x) будет приближенным градиентом, но, однако, эта опция не рекомендуется, поскольку большинство оптимизационных кодов значительно более грубое, чем истинные значения используемых градиентов.
Крупно-масштабный метод для fmincon наиболее эффективен в том случае, когда также рассчитывается и матрица вторых производных, т.е. матрице Гессе H(x). Однако оценка истинных значений матрицы Гессе не требуется. Например, если можно ввести структуру разреженности матрицы Гессе (используя определенный параметр опции HessPattern), то тогда fmincon рассчитывает разреженную конечноразностную аппроксимацию для H(x).
Если х0 не является строго вычисляемым, то fmincon выбирает новую (центрированную) строго вычисляемую начальную точку.
Если компоненты х не имеют верхнего (или нижнего) предела, то fmincon принимает, что соответствующие компоненты ub (или lb) устанавливаются как Inf (бесконечность) (или -Inf для lb) в противоположность произвольному, но очень большому положительному (или отрицательному в случае нижней границы) числу.
Следует отметить несколько аспектов относительно линейной условной оптимизации.
- Плотная (или достаточно плотная) колонка матрицы Aeq может привести к значительному переполнению и компьютерным затратам.
- fmincon удаляет (численно) линейно зависимые строки в Aeq; однако такая операция влечет за собой многократно повторяемую матричную факторизацию и, следовательно, может быть затратной в случае большого количества зависимостей.
- Каждая итерация влечет за собой задачу разрежения методом наименьших квадратов для матрицы
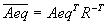 .
.
Средне-масштабная оптимизация. По-видимому, если явно определить равенства с помощью Aeq и beq, то будут более лучшие численные результаты, по сравнению с случаем неявного определения с помощью lb и ub.
Если имеются ограничения в виде равенств, а также определяются и удаляются зависимые равенства в квадратичной подзадаче, то печатается 'dependent' в заголовке Процедуры (когда запрашивается вывод опции options.Display = 'iter'). Зависимые равенства удаляются только тогда, когда эти равенства являются непротиворечивыми, при этом задача является недопустимой и в заголовке Процедуры печатается 'infeasible'.
Алгоритм:
Крупно-масштабная оптимизация. По умолчанию fmincon выберет крупно-масштабный алгоритм, если пользователь введет градиент в fun (и установит опцию GradObj как 'on') и если только существуют верхний и нижний ограничения, а также ограничения в виде линейных равенств. Данный алгоритм является реализацией метода доверительных подпространств и основан на методе внутренних отражений Ньютона, описанного в [1], [2]. Каждая итерация включает в себя приближенное решение крупной линейной системы с помощью метода предварительно сопряженных градиентов(PCG). Смотри описания доверительной области и метода предварительно сопряженных градиентов в разделе "Крупно-Масштабные Алгоритмы".
Средне-масштабная оптимизация. fmincon использует метод Последовательного Квадратичного Программирования (SQP). В данном методе на каждой итерации решается подзадача Квадратичного Программирования (QP). Вид матрицы Гессе для функции Лагранжа обновляется на каждой итерации с помощью формулы BFGS (смотри fminunc, литература [7], [8]).
Линейный поиск проводится с помощью функции полезности аналогично тому, как было предложено [4], [5], и [6].
Подзадача QP решается с помощью постоянной активной стратегии, аналогично тому, как было предложено в [3]. Полное описание алгоритма можно найти в разделе Условная Оптимизация в "Введении в Алгоритмы".
Более подробно об используемом алгоритме смотри Реализация SQP в "Введении в Алгоритмы".
Диагностика:
Крупно-масштабная оптимизация. Программа для крупно-масштабной задачи не допускает равенства верхней и нижней границ. Например, если
lb(2) = = ub(2), то fmincon выдает ошибку
Равенство верхней и нижней границ не допустимо для крупно-масштабного метода
Вместо этого следует использовать ограничения в виде равенств и средне-масштабный метод.
Если есть только ограничения в виде равенств, то можно все же использовать крупно-масштабный метод. Но если есть оба случая равенств и границ, то необходимо использовать средне-масштабный метод.
Ограничения:
Минимизируемые функции и ограничения должны быть непрерывными. fmincon может давать только локальные решения.
Если задача является недопустимой, то fmincon пытается минимизировать значение максимального ограничения.
Целевая функция и функция для ограничений должны быть реальными, то есть они не могут возвращать комплексные значения.
Крупно-масштабная оптимизация. Для того, что бы использовать крупно-масштабный алгоритм, пользователь должен в fun задать градиент (а также установить опцию GradObj как 'on'), а так же можно задавать только верхнюю и нижнюю границы, или только должны быть ограничения в виде линейных равенств, а в Aeq число строк не может быть больше числа колонок. Aeq является типичным примером разреженности. Относительно большей информации о постановке задачи, области применения и задания исходных данных смотри таблицу 1-4, Область Определения и Требования к Крупно-Масштабным Задачам.
В настоящее время, если в fun аналитически задан градиент, то для сравнения аналитического градиента с его конечно-разностным значением в крупно-масштабном методе нельзя использовать параметр опции DerivativeCheck. Вместо этого, для контроля производной следует использовать средне-масштабный метод с установкой опционного параметра MaxIter как 0 итераций. Затем запустить задачу с крупно-масштабным методом.
Сопутствующие функции: @ (function_handle), fminbnd, fminsearch, fminunc, optimset
Литература:
- Coleman, T.F. and Y. Li, "An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds" SIAM Journal on Optimization, Vol. 6, pp. 418-445, 1996.
- Coleman, T.F. and Y. Li, "On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds" Mathematical Programming, Vol. 67, Number 2, pp. 189-224, 1994.
- Gill, P.E., W. Murray, and M.H. Wright, Practical Optimization, Academic Press, London, 1981.
- Han, S.P., "A Globally Convergent Method for Nonlinear Programming" Journal of Optimization Theory and Applications, Vol. 22, p. 297, 1977.
- Powell, M.J.D., "A Fast Algorithm for Nonlineary Constrained Optimization Calculations" Numerical Analysis, ed. G.A. Watson, Lecture Notes in Mathematics, Springer Verlag, Vol. 630, 1978.
- Powell, M.J.D., "The Convergence of Variable Metric Methods For Nonlinearly Constrained Optimization Calculations" Nonlinear Programming 3, (O.L. Mangasarian, R.R. Meyer, and S.M. Robinson, eds.) Academic Press, 1978.
fminsearch – поиск минимума функции нескольких переменных без ограничений 
Синтаксис:
x = fminsearch(fun,x0)
x = fminsearch(fun,x0,options)
x = fminsearch(fun,x0,options,P1,P2,...)
[x,fval] = fminsearch(...)
[x,fval,exitflag] = fminsearch(...)
[x,fval,exitflag,output] = fminsearch(...)
Описание:
fminsearch находит минимум скалярной функции нескольких переменных, стартуя с некоторой начальной точки. В общем, задача относится к нелинейной оптимизации без ограничений
- x = fminsearch(fun,x0) начинает с точки x0 и находит локальный минимум от х для описанной в fun функции. x0 может быть скаляром, вектором или матрицей.
- x = fminsearch(fun,x0,options) минимизирует с параметрами оптимизации, определенными в структурной опции.
- x = fminsearch(fun,x0,options,P1,P2,...) передает зависимые от задачи параметры P1, P2 и т.д. непосредственно в функцию fun. Используется опция = [] как структурный ноль, если опции не определены.
- [x,fval] = fminsearch(...) возвращает в fval значение целевой функции fun как решение от x.
- [x,fval,exitflag] = fminsearch(...) возвращает значение exitflag, котрое содержит выходные условия fminsearch.
- [x,fval,exitflag,output] = fminsearch(...) возвращаетструктурный выход с информацией об оптимизации.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание передаваемых в fminsearch аргументов. Данный раздел включает детали функционирования для fun и опций:
| fun Подлежащая минимизации функция. |
fun есть некая функция, которая принимает вектор х и возвращает скаляр f, как целевую функцию от х. Функция fun моет быть определена, как описатель функции. x = fminsearch(@myfun,x0,A,b) где myfun есть некая функция MATLAB, такая что function f = myfun(x) f = ... % Расчет значения функции от х fun также может быть внутренним объектом x = fminsearch(inline('norm(x)^2'),x0,A,b); |
| options | Опции обеспечивают детали функционирования параметров опций. |
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых fminsearch. В этом разделе приводятся общие специфические детали для величин exitflag и output:
| exitflag | Описывает выходные условия.
|
| output | Структура с информацией об оптимизации. Поля структуры:
|
Options
Параметры оптимизационных опций, используемых в fminsearch. Можно использовать optimset для того, чтобы установить или изменить значения данных полей в структуре параметров опций. Смотри таблиц 4-3. Параметра опций оптимизации. Для детальной информации
| Display | Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' отображение только конечной информации, 'notify' (принимается по умолчанию) отображение только в случае, если функция не сходится |
| MaxFunEvals | Максимально число допустимых расчетов функции. |
| MaxIter | Максимально число допустимых итераций. |
| TolFun | Конечное допустимое отклонение по значению функции |
| TolX | Конечное допустимое отклонение по значению х. |
Примеры:
Минимизировать одномерную функцию f(x) = sin(x) + 3.
Для того, что использовать М-файл, т.е. fun = 'myfun', создается файл myfun.m.
function f = myfun(x)
f = sin(x) + 3;
Далее для поиска минимума от fun вблизи 2 вызывается fminsearch
x = fminsearch(@myfun,2)
Для минимизации функции f(x) = sin(x) + 3 используется внутренний объект
f = inline('sin(x)+3');
x = fminsearch(f,2);
Алгоритмы:
fminsearch использует метод симплексного поиска [1]. Это метод прямого поиска, который в отличие от fminunc не использует численные или аналитические значения градиентов.
Если n есть длина х, то в n-мерном пространстве симплекс характеризуется n+1 различными векторами, являющимися его вершинами. В двумерном пространстве симплекс является треугольником, в трех-мерном пространстве – пирамидой. На каждом шаге поиска генерируется новая точка или текущий симплекс. Значение функции в новой точке сравнивается с значениями функций в вершинах симплекса и, как правило, одна из вершин становится новой точкой. Образующей новый симплекс. Данный шаг повторяется до тех пор, пока диаметр симплекса не будет меньше заданной точности.
В общем, fminsearch является менее эффективным для задач с порядком больше, чем два. Однако, если задача является существенно разрывной, то fminsearch может быть более устойчивым.
Ограничения:
fminsearch часто может производить разрывные решения, в особенности если это не рассматривается точка вблизи данного решения. fminsearch может давать только локальные решения.
fminsearch минимизирует только реальные числа, т.е. х должен состоять только из реальных чисел и f(x) должна возвращать только реальные числа.. Когда х содержит комплексные переменные, то они должны быть разделены на реальную и мнимую части.
Смотри также:
@ (function_handle), fminbnd, fminunc, inline, optimset
Литература:
- Lagarias, J.C., J. A. Reeds, M. H. Wright, and P. E. Wright, "Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions," SIAM Journal of Optimization, Vol. 9 Number 1, pp.112-147, 1998.
fminunc – поиск минимума функции нескольких переменных без ограничений 
Синтаксис:
x = fminunc(fun,x0)
x = fminunc(fun,x0,options)
x = fminunc(fun,x0,options,P1,P2,...)
[x,fval] = fminunc(...)
[x,fval,exitflag] = fminunc(...)
[x,fval,exitflag,output] = fminunc(...)
[x,fval,exitflag,output,grad] = fminunc(...)
[x,fval,exitflag,output,grad,hessian] = fminunc(...)
Описание:
- fminunc находит минимум скалярной функции нескольких переменных, стартуя с некоторой начальной точки. В общем, задача относится к нелинейной оптимизации без ограничений
- x = fminunc(fun,x0) начинает с точки x0 и находит локальный минимум от х для описанной в fun функции. x0 может быть скаляром, вектором или матрицей.
- x = fminunc(fun,x0,options) минимизирует с параметрами оптимизации, определенными в структурной опции.
- x = fminunc(fun,x0,options,P1,P2,...) передает зависимые от задачи параметры P1, P2 и т.д. непосредственно в функцию fun. Передается пустая матрица в случае опции по использованию значений по умолчанию
- [x,fval] = fminunc(...) возвращает в fval значение целевой функции fun как решение от x.
- [x,fval,exitflag] = fminunc возвращает значение exitflag, которое содержит выходные условия.
- [x,fval,exitflag,output] = fminunc(...) возвращает структурный выход с информацией об оптимизации.
- [x,fval,exitflag,output,grad] = fminunc(...) возвращает в grad значение градиента fun как решение от х.
- [x,fval,exitflag,output,grad,hessian] = fminunc(...) возвращает в hessian значение матрицы Гессе целевой функции fun как решение от х.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание передаваемых в to fminunc аргументов. Данный раздел включает детали функционирования для fun и опций:
| fun Подлежащая минимизацифункция. |
fun есть некая функция, которая принимает вектор х и возвращает скаляр f, как целевую функцию от х. Функция fun может быть определена, как описатель функции. x = fminunc (@myfun,x0) где myfun есть некая функция MATLAB, такая что function f = myfun(x) f = ... % Расчет значения функции от х fun также может быть внутренним объектом x = fminunc (inline('norm(x)^2'),x0); Если градиент от fun может быть вычислен и опция options.GradObj равна 'on' посредством установки options = optimset('GradObj','on'), то функция fun должна во втором выходном аргументе возвращать значение аргумента g, как вектора от х. Отметим, что посредством проверки значения nargout данная функция может обойти расчет g в случае, когда fun вызывается только с одним выходным аргументом (случай, когда для оптимизационного алгоритма необходимо только значение f, а не g). function [f,g] = myfun(x) Если матрица Гессе к тому же может быть рассчитана и опция options.Hessian есть 'on', т.е. options = optimset('Hessian','on'), то функция fun должна возвращать значения матрицы Гессе Н в виде симметричной матрицы от х на месте третьего аргумента. Отметим, что посредством контроля значения nargout можно обойти расчет Н, тогда fun вызывается только с одним или двумя выходными аргументами (случай, когда для оптимизационного алгоритма необходимо только значение f и g, а не Н). function [f,g,H] = myfun(x) По определению матрица Гессе является симметричной. |
| options | Опции обеспечивают учет специфических деталей функции виде параметров options. |
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых fminunc. аргументов. В этом разделе приводятся общие специфические детали для величин exitflag и output:
|
exitflag |
Описывает выходные условия.
|
| output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Options
fminunc использует указанные параметры оптимизации. Часть параметров используется ко всем алгоритмам, некоторые используются только для крупномасштабного алгоритма, а другие применимы только среднемасштабных алгоритмов. Можно использовать optimset для того, чтобы установить или изменить значения данных полей в структуре параметров опций. Для детальной информации смотри Таблицу 4-3, Параметры Опций Оптимизации
Мы начнем с описания опции LargeScale, поскольку она устанавливает преимущественное право какой алгоритм использовать. Это только преимущественное право, поскольку должны быть выполнены определенные условия для того, что бы можно было использовать крупно-масштабный алгоритм. Для fminunc необходимо задавать градиент (смотри выше описание fun) или иначе будет использоваться средне-масштабный алгоритм.
| LargeScale | В случае установки 'on' используется крупно-масштабный, если это возможно, алгоритм. Для использования средне-масштабного алгоритма устанавливается 'off'. |
Large-Scale and Medium-Scale Algorithms Эти параметры используются как для средне-масштабного, так и крупно-масштабного алгоритмов:
| Diagnostics | Проводится печать диагностической о минимизируемой функции. |
| Display | Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации. |
| GradObj | Градиент определенный пользователем целевой функции. Смотри выше описание функции fun как в ней определить градиент. Для того, что бы использовать крупно-масштабный метод необходимо задавать указанный градиент. Это необязательно для средне-масштабного метода. |
| MaxFunEvals | Максимально число допустимых расчетов функции. |
| MaxIter | Максимально число допустимых итераций. |
| TolFun | Конечное допустимое отклонение по значению функции |
| TolX | Конечное допустимое отклонение по значению х. |
Large-Scale Algorithm Only. Эти параметры используются только для крупно-масштабного алгоритма
| Hessian | В случае установки 'on' в fmincon используется заданная пользователем матрица Гессе (задается в fun) или информация о матрице Гессе (при использовании HessMult) для целевой функции. В случае установки 'off' в fmincon используется матрице Гессе из расчета конечных разностей. | |
| HessMult | Указатель функции для умножения на матрицу Гессе. Для типа крупно-масштабных задач, эта функция рассчитывает произведение матрицы Гессе H*Y без реального формирования Н. Эта функция имеет форму W = hmfun(Hinfo,Y,p1,p2,...) Где Hinfo и дополнительные параметры p1,p2,...включают в себя матрицы для расчета H*Y. Первый аргумент должен быть тот же самый, как и третий аргумент, возвращаемый целевой функцией fun. [f,g,Hinfo] = fun(x,p1,p2,...) Параметры p1,p2,... являются теми же самыми параметрами, что передаются в fminunc (и в fun). fminunc(fun,...,options,p1,p2,...) Y есть матрица с тем же самым числом строк как и размерности данной задачи. W = H*Y, хотя H явно не формируется. fminunc использует Hinfo для расчета предварительных условий.
|
|
| HessPattern | Разреженный шаблон матрице Гессе для конечных разностей. Если не является разумным в fun рассчитывать разреженную матрицу Гессе Н, то в fminunc крупно-масштабный метод может аппроксимировать Н через разреженные конечные разности (для градиентов) при условии, что структура разреженности для Н, т.е. местоположения nonzeros, задаются как определенные значения для HessPattern. В наихудшем случае, когда такая структура неизвестна, можно задать HessPattern, что является плотной матрицей, а полная конечноразностная аппроксимация будет рассчитываться на каждой итерации (что принимается по умолчанию). Это может быть очень дорогостоящим для больших задач, поэтому стоит затратить усилия на определение структуры разреженности. | |
| MaxPCGIter | Максимальное число PCG (предварительно сопряженный градиент) итераций (Смотри ниже раздел Алгоритм). | |
| PrecondBandWidth | Верхняя полоса предварительной обработки для PCG. По умолчанию используется диагональная начальная подготовка (верхняя полоса из 0). Для некоторых задач увеличение полосы снижает число итераций PCG. | |
| TolPCG | Конечное допустимое число итераций PCG. | |
| TypicalX | Типичные значения х. |
Только для средне-масштабного алгоритма. Эти параметры используются только для средне-масштабного алгоритма.
| DerivativeCheck | Сравнение вводимых пользователем производных (градиентов) с конечноразностными производными. |
| DiffMaxChange | Максимальное изменение в переменных для конечно-разностных градиентов |
| DiffMinChange | Минимальное изменение в переменных для конечно-разностных градиентов |
| LineSearchType | Выбор алгоритма линейного поиска |
Примеры:
Найти минимальное значение функции
Для использования М-файла, построим файл myfun.m.
function f = myfun(x)
f = 3*x(1)^2 + 2*x(1)*x(2) + x(2)^2; % Стоимостная функция
Далее для нахождения минимума myfun вблизи [1,1] вызовем fminunc.
x0 = [1,1];
[x,fval] = fminunc(@myfun,x0)
После нескольких итераций будут возвращены решение от х и fval, значение функции в точке х.
x =
1.0e-008 *
-0.7914 0.2260
fval =
1.5722e-016
Для минимизации данной функции с заданным градиентом модифицируем М-файл myfun.m так, что бы градиент был вторым выходным аргументом.
function [f,g] = myfun(x)
f = 3*x(1)^2 + 2*x(1)*x(2) + x(2)^2; % функция стоимости
if nargout > 1
g(1) = 6*x(1)+2*x(2);
g(2) = 2*x(1)+2*x(2);
end
также отметим, что значение градиента будут доступным только, если построить структуру опций оптимизации посредством использования optimset для установки опции options.GradObj как 'on'.
options = optimset('GradObj','on');
x0 = [1,1];
[x,fval] = fminunc(@myfun,x0,options)
После нескольких итераций будут возвращены решение от х и fval, значение функции в точке х.
x =
1.0e-015 *
-0.6661 0
fval2 =
1.3312e-030
Для минимизации функции f(x) = sin(x) + 3 используем внутренний объект
f = inline('sin(x)+3');
x = fminunc(f,4)
который возвращает решение
x =
4.7124
Примечания:
Отметим, fminsearch не является предпочтительным выбором для решения задач с суммами квадратов.
В этом случае лучше использовать программуlsqnonlin, которая оптимизирована для данного типа задач.
Для использования крупно-масштабного метода градиент необходимо задавать в fun (а опция options.GradObj устанавливается как 'on'). Если градиент не задан и опция options.LargeScale не равна 'off', то выдается предупреждение.
Алгоритмы:
Крупно-масштабная оптимизация. По умолчанию fminunc выберет крупно-масштабный алгоритм, если пользователь введет градиент в fun (и установит опцию GradObj как 'on'). Данный алгоритм является реализацией метода доверительных подпространств и основан на методе внутренних отражений Ньютона, описанного в 2],[3]. Каждая итерация включает в себя приближенное решение крупной линейной системы с помощью метода предварительно сопряженных градиентов(PCG). Смотри описания доверительной области и метода предварительно сопряженных градиентов в разделе “Крупно-Масштабные Алгоритмы”.
Средне-масштабная оптимизация. fminunc при установке опции options.LargeScale как 'off' использует квази-Ньютоновский метод с смешанной процедурой квадратичного и кубического поиски. Данный квази-Ньютоновский метод использует формулу BFGS ([1],[5],[8],[9]) для модернизации приближенного значения матрицы Гессе. Формула DFP ([4],[6],[7]), которая аппроксимирует обратную матрицу Гессе, задается с помощью установки опции options.HessUpdate как 'dfp' (и опции options.LargeScale как 'off'). Метод наискорейшего спуска выбирается при установке опции options.HessUpdate как 'steepdesc' и (опции options.LargeScale как 'off'), хотя это и не рекомендуется.
Принимаемый по умолчанию метод линейного поиска, т.е. когда опция options.LineSearchType устанавливается как 'quadcubic', обеспечивается методом смешанной квадратичной и кубической интерполяции и экстраполяции. Гарантированный метод кубического полинома выбирается путем установки опции options.LineSearchType как 'cubicpoly'. В общем, второй метод требует меньшего расчета функции, но большего расчета градиентов. Таким образом, если не требуется больших затрат для расчета градиента, то метод линейного поиска с помощью кубического полинома является предпочтительным. Полное описание алгоритмов имеется в разделе Стандартные Алгоритмы.
Ограничения:
Минимизируемые функции и ограничения должны быть непрерывными. fmincon может давать только локальные решения.
fminunc минимизирует только реальные числа, то есть х должно состоять только из реальной части f(x) должна возвращать только реальные числа. В случае, если х содержит комплексные переменные, то они должны быть разделены на реальную и мнимую части.
Крупно-масштабная оптимизация. Для того, что использовать крупно-масштабный алгоритм, пользователь должен в fun задать градиент (а также установить опцию GradObj как 'on'). Относительно большей информации о используемых формулировках задачи и задаваемых исходных данных смотри таблицу 1-4, Область Определения и Требования к Крупо-Масштабным Задачам.
В настоящее время, если в fun аналитически задан градиент, то для сравнения аналитического градиента с его конечно-разностным значением в крупно-масштабном методе нельзя использовать параметр опции DerivativeCheck. Вместо этого, для контроля производной следует использовать средне-масштабный метод с установкой опционного параметра MaxIter как 0 итераций. Затем запустить задачу с крупно-масштабным методом.
Сопутствующие функции: @ (function_handle), fminsearch, inline, optimset
Литература:
- Broyden, C.G., "The Convergence of a Class of Double-Rank Minimization Algorithms," Journal Inst. Math. Applic., Vol. 6, pp. 76-90, 1970.
- Coleman, T.F. and Y. Li, "An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds," SIAM. Journal on Optimization, Vol. 6, pp. 418-445, 1996.
- Coleman, T.F. and Y. Li, "On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds," Mathematical Programming, Vol. 67, Number 2, pp. 189-224, 1994.
- Davidon, W.C., "Variable Metric Method for Minimization," A.E.C. Research and Development Report, ANL-5990, 1959.
- Fletcher, R.,"A New Approach to Variable Metric Algorithms," Computer Journal, Vol. 13, pp. 317-322, 1970.
- Fletcher, R., "Practical Methods of Optimization," Vol. 1, Unconstrained Optimization, John Wiley and Sons, 1980.
- Fletcher, R. and M.J.D. Powell, "A Rapidly Convergent Descent Method for Minimization," Computer Journal, Vol. 6, pp. 163-168, 1963.
- Goldfarb, D., "A Family of Variable Metric Updates Derived by Variational Means," Mathematics of Computing, Vol. 24, pp. 23-26, 1970.
- Shanno, D.F., "Conditioning of Quasi-Newton Methods for Function Minimization," Mathematics of Computing, Vol. 24, pp. 647-656, 1970.
fseminf – поиск минимума полубесконечной нелинейной функции нескольких переменных с ограничениями 
Поиск минимума полубесконечной нелинейной функции нескольких переменных с ограничениями при условии 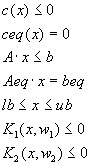
где x, b, beq, lb и ub - векторы, A и Aeq - матрицы, и c(x) и ceq(x) и Ki(x,wi) есть возвращающие векторы функции, f(x) – функция, которая возвращает скаляр. f(x), c(x) и ceq(x) могут быть нелинейными функциями. Эти векторы (или матрицы) есть непрерывные функции как от х, так и от дополнительного набора переменных ![]() . Переменные
. Переменные ![]() являются векторами, как правило, длины два.
являются векторами, как правило, длины два.
Синтаксис:
x = fseminf(fun,x0,ntheta,seminfcon)
x = fseminf(fun,x0,ntheta,seminfcon,A,b)
x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq)
x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,lb,ub)
x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,lb,ub,options)
x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,...
lb,ub,options,P1,P2,...)
[x,fval] = fseminf(...)
[x,fval,exitflag] = fseminf(...)
[x,fval,exitflag,output] = fseminf(...)
[x,fval,exitflag,output,lambda] = fseminf(...)
Описание:
fseminf находит минимум полубесконечной скалярной функции с ограничениями от нескольких переменных, начиная с начальной точки отчета.
Задача состоит в том, что бы найти такой минимум от (x), что бы ограничения включали все возможные значения ![]() (или
(или ![]() ). Поскольку невозможно вычислить все возможные значения
). Поскольку невозможно вычислить все возможные значения ![]() , то область должна быть взята повсеместно, что бы можно было рассчитывать подходящие дискретные наборы значений.
, то область должна быть взята повсеместно, что бы можно было рассчитывать подходящие дискретные наборы значений.
- x = fseminf(fun,x0,ntheta,seminfcon) начинает с точки х0 и находит минимум функции fun с полубесконечными ограничениями ntheta, определенными в seminfcon.
- x = fseminf(fun,x0,ntheta,seminfcon,A,b) аналогично пытается удовлетворить линейным неравенствам A*x <= b.
- x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq) минимизирует объект с учетом линейных равенств. При отсутствии неравенств устанавливается A=[] и b=[].
- x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,lb,ub) определяет набор нижних и верхних ограничений на конструируемые переменные х так, что решение всегда находится в диапазоне lb <= x <= ub.
- x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,lb,ub,options) проводит минимизацию с учетом определенных в структурных опциях оптимизационных параметров.
- x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,lb,ub,options, P1,P2,...) передает зависящие от типа задачи параметры непосредственно в функции fun и seminfcon. Передает пустые матрицы заменители для A, b, Aeq, beq, lb, ub, nonlcon и options в случае, если эти аргументы не являются необходимыми.
- [x,fval] = fseminf(...) возвращает значение целевой функции fun как решение от х.
- [x,fval,exitflag] = fseminf(...) возвращает значение exitflag, которое содержит описание выходных условий.
- [x,fval,exitflag,output] = fseminf(...) возвращает структурный выход с информацией об оптимизации.
- [x,fval,exitflag,output,lambda] = fseminf(...)возвращает структурную lambda с полями, содержащими множители Лагранжа в виде решения от х.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в fseminf. Данный подраздел приводит функционально-специфические детали для fun, ntheta, options и seminfcon::
|
fun Подлежащая минимизации функция. |
fun есть такая функция, которая принимает скаляр х и возвращает скаляр f, т.е. целевую функцию от х. Функция fun может задаваться с помощью описателя функций x = fseminf(@myfun,x0,ntheta,seminfcon) где myfun есть такая функция MATLAB, что function f = myfun(x) f = ... % Вычисление функции в точке х fun так же может быть и внутренним объектом. fun = inline('sin(x''*x)'); Если градиент от fun может быть вычислен и опция options.GradObj равна 'on' посредством установки options = optimset('GradObj','on') то функция fun должна в втором выходном аргументе возвращать значение аргумента g, как вектора от х. Отметим, что посредством проверки значения nargout данная функция может обойти расчет g в случае когда fun вызывается только с одним выходным аргументом (случай, когда для оптимизационного алгоритма необходимо только значение f, а не g). function [f,g] = myfun(x) |
| ntheta | Число полубесконечных ограничений |
| options | Опции обеспечивают учет специфических деталей функции виде параметров options. |
| seminfcon | Функция, которая вычисляет вектор ограничений в виде нелинейных неравенств, с, ограничений в виде нелинейных равенств, ceq, и полубесконечные ограничения ntheta (векторы или матрицы) K1, K2,..., Kntheta, рассчитанные по всему интервалу S в точке х. seminfcon может быть определена как функциональный указатель. x = fseminf(@myfun,x0,ntheta,@myinfcon) где myinfcon есть функция MATLAB, что function [c,ceq,K1,K2,...,Kntheta,S] = myinfcon(x,S) % Исходный выборочный интервал if isnan(S(1,1)), S = ...% S имеет ntheta строк и 2 колонки end w1 = ...% Расчет выборочного набора w2 = ...% Расчет выборочного набора ... wntheta = ... % Расчет выборочного набора K1 = ... % 1-ое полубесконечное ограничение от x и w K2 = ... % 2-ое полубесконечное ограничение от x и w ... Kntheta = ...% Последнее полубесконечное ограничение от x и w c = ... % Расчет нелинейных неравенств от x ceq = ... % Расчет нелинейных равенств от x S есть рекомендованный выборочный интервал, который может быть использован или seminfcon.не использован. Возвращает [] для с или ceq, если такие ограничения не определены. Векторы или матрицы K1, K2, ..., Kntheta включают в себя полубесконечные ограничения, определенные для выборочного набора значений независимых переменных w1, w2, ... wntheta, соответственно. Двухколонковая матрица S включает в себя рекомендованный интервал значений w1, w2, ...wntheta, которые используются для расчета K1, K2, ... Kntheta. i-ая S содержит рекомендованный интервал для оценки Ki. Если Ki есть вектор то используется только S(i,1) (во второй колонке могут быть все нули). Если Ki есть матрица, то S(i,2) используется для выборки строк в Ki, а S(i,1) используется для выборочного интервала колонок для Ki (смотри Двумерный пример). На первой итерации S есть NaN, поэтому с помощью seminfcon должны быть определены некоторые исходные выборочные интервалы. |
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых fseminf аргументов. В этом разделе приводятся общие специфические детали для величин exitflag, lambda и output:
| exitflag | Описывает выходные условия.
|
| lambda | Структура, которая содержит множители Лагранжа при решении по х (разделенном по типам условий). Поле структуры:
|
| output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Options
Параметры оптимизационных опций, используемых в fmincon. Можно использовать optimset для того, чтобы установить или изменить значения данных полей в структуре параметров опций. Для детальной информации смотри Таблицу 4-3, Параметры Опций Оптимизации
| DerivativeCheck | Сравнение приведенных пользователем производных (градиентов) с конечноразностными производными. |
| Diagnostics | Проводится печать диагностической информации о минимизируемой функции. |
| DiffMaxChange | Максимальное изменение в переменных для конечно-разностных градиентов. |
| DiffMinChange | Минимальное изменение в переменных для конечно-разностных градиентов. |
| Display | Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации. |
| GradObj | Градиент определенный пользователем целевой функции. Смотри выше описание функции fun как в ней определить градиент. Для того, что бы использовать крупно-масштабный метод необходимо задавать указанный градиент. Это необязательно для средне-масштабного метода. |
| MaxFunEvals | Максимально число допустимых расчетов функции. |
| MaxIter | Максимально число допустимых итераций. |
| TolCon | Конечное допустимое отклонение по нарушению условий ограничения. |
| TolFun | Конечное допустимое отклонение по значению функции. |
| TolX | Конечное допустимое отклонение по значению х. |
Замечания:
Установленный в seminfcon рекомендованный выборочный интервал S на протяжении расчета может быть изменен с помощью оптимизационной подпрограммы fseminf, поскольку отличные от рекомендованного интервала значения могут оказаться более подходящими для эффективности или точности. Кроме того, для конечной области, во всем диапазоне допускается изменять заданный тип оптимизации, что не приводит к существенным изменениям в числе локальных минимумов для ![]() .
.
Примеры:
Одномерный пример
Найти значения х при которых будет минимальным выражение
![]()
where
![]()
![]()
для всех значений ![]() и
и ![]() и по всему диапазону
и по всему диапазону
![]()
![]()
Отметим, полубесконечные ограничения являются одномерными, то есть векторами. Поскольку ограничения должны быть в форме ![]() , то их надо рассчитать как
, то их надо рассчитать как
![]()
![]()
В первую очередь запишем М-файл для расчетов целевой функции
function f = myfun(x,s)
% Целевая функция
f = sum((x-0.5).^2);
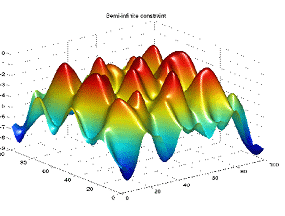
Во-вторых, составим М-файл для ограничений под названием mycon.m. Введем в программу рисование поверхностного графика полубесконечных ограничений всякий раз, как вызывается mycon. Это дает возможность увидеть изменения ограничений по мере минимизации Х.
function [c,ceq,K1,s] = mycon(X,s)
% Начальный выборочный интервал
if isnan(s(1,1)),
s = [2 2];
end
% Набор выборок
w1x = 1:s(1,1):100;
w1y = 1:s(1,2):100;
[wx,wy] = meshgrid(w1x,w1y);
% Полубесконечное ограничение
K1 = sin(wx*X(1)).*cos(wx*X(2))-1/1000*(wx-50).^2 -...
sin(wx*X(3))-X(3)+sin(wy*X(2)).*cos(wx*X(1))-...
1/1000*(wy-50).^2-sin(wy*X(3))-X(3)-1.5;
% не имеющие предела нелинейные ограничения
c = []; ceq=[];
% Mesh plot
m = surf(wx,wy,K1,'edgecolor','none','facecolor','interp');
camlight headlight
title('Semi-infinite constraint')
drawnow
Далее запустим подпрограмму оптимизации
x0 = [0.25, 0.25, 0.25]; % Начальное предположение
[x,fval] = fseminf(@myfun,x0,1,@mycon)
После девяти итераций решение будет
x =
0.2926 0.1874 0.2202
и значение функции для данного решения
fval =
0.0091
Цель заключалась в том, что бы минимизировать целевую функцию с выполнением полубесконечных ограничений. Оценка mycon как решение от х анализ максимального элемента матрицы К1 показывает, что ограничение легко выполняется.
[c,ceq,K1] = mycon(x,[0.5,0.5]); % Выборочный интервал 0.5
max(max(K1))
ans =
-0.0027
Данный вызов mycon производит surf plot, что демонстрирует полубесконечное ограничение от х.
Двухмерный пример
Найти значения х при которых будет минимальным выражение
![]()
где
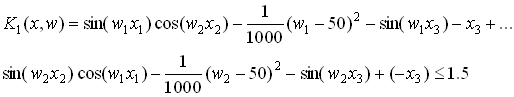
для всех значений ![]() и
и ![]() и по всему диапазону
и по всему диапазону
![]()
![]()
Стартовая точка x=[0.25, 0.25, 0.25].
Отметим, что полубесконечное ограничение является двухмерным, то есть матрицей.
В первую очередь запишем М-файл для расчетов целевой функции
function f = myfun(x,s)
% Целевая функция
f = sum((x-0.2).^2);
Алгоритм:
fseminf использует методы кубической и квадратичной интерполяции для расчета пиковых значений для полубесконечных ограничений. Данные значения пиков используются для формирования набора ограничений, что передается в метод SQP так же как для функции fmincon. Когда число ограничений изменяется, то множители Лагранжа перераспределяются в новый набор ограничений.
Расчет для рекомендованного выборочного интервала использует разницу между интерполированным значением пика и значением пика, фигурирующем в наборе данных, что необходимо для того, что бы оценить больше или меньше точек необходимо брать в расчет. Эффективность интерполяции так же принимается во внимание путем экстраполяции кривой и ее сравнения с другими точками на кривой.
Рекомендованный выборочный интервал снижается в случае, если значения пиков берутся вблизи границ ограничений, т.е. около нуля.
Для большей детализации используемого алгоритма и типов процедур, распечатываемых под заголовком Процедуры при установке опции options.Display = 'iter' смотри реализация SQP в разделе "Ведении в Алгоритмы".
Ограничения:
Минимизируемые функции, ограничения и полубесконечные ограничения должны быть непрерывными функциями от х и w. fseminf может давать только локальные решения.
Если задача является недопустимой, то fseminf пытается минимизировать значение максимального ограничения.
Смотри так же:
@ (function_handle), fmincon, optimset
fgoalattain – решение многокритериальной (векторной) задачи достижения цел
Найти ![]() y при условии, что
y при условии, что 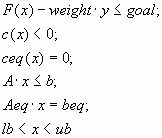
где x, weight (вес), goal (цель), b, beq, lb и ub – векторы; A и Aeq – матрицы; с(x), сeq(x), и F(x) есть функции, которые возвращают вектора. F(x),с(x) и сeq(x) могут быть нелинейными функциями.
Синтаксис:
x = fgoalattain(fun,x0,goal,weight)
x = fgoalattain(fun,x0,goal,weight,A,b)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2,...)
[x,fval] = fgoalattain(...)
[x,fval,attainfactor] = fgoalattain(...)
[x,fval,attainfactor,exitflag] = fgoalattain(...)
[x,fval,attainfactor,exitflag,output] = fgoalattain(...)
[x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(...)
Описание:
fgoalattain решает задачу достижения цели, которая является одной из формулировок задач для векторной оптимизации.
- x = fgoalattain(fun,x0,goal,weight) пытается создать целевую функцию задаваемую как fun и принимающую определенные целевые значения goal путем изменения x, начиная с х0, с весом weight.
- x = fgoalattain(fun,x0,goal,weight,A,b) решает задачу достижения цели, соответствующую системе линейных неравенств A*x <= b.
- x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq) решает задачу достижения цели, соответствующую так же системе линейных равенств Aeq*x = beq. Устанавливает определенные A=[] и b=[], если неравенства отсутствуют.
- x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub) определяет набор нижних и верхних ограничений на конструируемые переменные х, так что бы искомое решение находилось в диапазоне lb <= x <= ub.
- x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon) подгоняет задачу достижения цели под условия нелинейных неравенств c(x) или нелинейных равенств ceq(x) задаваемых в nonlcon. fgoalattain проводит такую оптимизацию, что c(x) <= 0 и ceq(x) = 0. Устанавливает lb=[] и/или ub=[], если нет ограничений.
- x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,... options) проводит минимизацию при параметрах оптимизации, задаваемых в структуре options.
- x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2,...) переводит связанные с задачей параметры P1, P2 и т.д. непосредственно в функции fun и nonlcon. Переводит пустые матрицы в структурные нули для A, b, Aeq, beq, lb, ub, nonlcon и options, если эти переменные не являются необходимыми.
- [x,fval] = fgoalattain(...) возвращает значения целевых функций, вычисляемых для fun при расчете х.
- [x,fval,attainfactor] = fgoalattain(...) возвращает коэффициент достижения при расчете х.
- [x,fval,attainfactor,exitflag] = fgoalattain(...) возвращает значение exitflag, которое характеризует условия задачи fgoalattain.
- [x,fval,attainfactor,exitflag,output] = fgoalattain(...) возвращает структурный выход, который содержит информацию о процессе оптимизации.
- [x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(...) возвращает структурную lambda, поля которой содержат множители Лагранжа при расчете х.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов передаваемых в fgoalattain. Этот раздел определяет детали описания функций fun, goal, nonlcon, options, и weight:
| fun Функция, которую необходимо минимизировать. |
fun есть функция, которая принимает вектор х и возвращает вектор F, т.е. целевые функции от х. Функция fun может быть специфицирована как указатель функции x = fgoalattain(@myfun,x0,goal,weight) где myfun есть такая функция MATLAB, что function F = myfun(x) F = ... % Вычисляет значения функций от x.fun - так же может быть внутренним объектом. x = fgoalattain(inline('sin(x.*x)'),x0,goal,weight); Для того, что бы целевая функция была как можно ближе к значению цели (т.е. не больше чем и не меньше чем), то устанавливают options.GoalsExactAchieve на ряд целей, который должны находиться в окрестности значений goal. Такие цели должны ,быть секционированы в первых элементах вектора F, возвращаемого в fun. Если градиент целевой функции может быть дополнительно рассчитан и options.GradObj задана как 'on' посредством options = optimset('GradObj','on') то тогда функция fun должна возвращать, как второй выходной аргумент, градиентное значение G в виде матрицы от х. Отметим, что путем проверки значения аргумента nargout данная функция может обойти расчет G, т.е. когда fun вызывается только с одним выходным аргументом (это случай когда для оптимизационного алгоритма нужно значения F а не G). function [F,G] = myfun(x) F = ... % Вычисляет значения функций от x. if nargout > 1 % два выходных аргумента G = ... % Вычисляет значения градиента от x end Градиент состоит из частных производных dF/dx для всякой F в в точке х. Если F есть вектор длины m и х имеет длину n, где n есть длина вектора x0, то тогда градиент G для F(x) есть матрица nхm, где G(i,j) есть частные производные от F(j) по x(i), (т.е. j-ая колонка G есть градиент по j целевой функции F(j)). |
| goal Вектор текущих значений цели. |
Этот вектор имеет ту же самую длину, что и ряд целей F, возвращаемых функцией fun. Fgoalattain пытается оптимизировать значения вектора F для того, что бы достигнуть целевых значений, задаваемых в goal. |
| nonlcon Функция, которая вычисляет нелинейные ограничения виде неравенств c(x) <= 0 и нелинейные ограничения виде равенств ceq(x) = 0. |
Функция nonlcon принимает вектор х и возвращает два вектора c и ceq. Вектор с содержит нелинейные неравенства при расчете от х и ceq содержит нелинейные равенства при расчете от х. Функция nonlcon может быть определена как описатель функции. x = fgoalattain(@myfun,x0,goal,weight,A,b,Aeq,beq,... lb,ub,@mycon) где mycon есть функция MATLAB, определенная как function [c,ceq] = mycon(x) c = ... % вычисляет нелинейные ограничения в виде неравенств от х. ceq = ... % вычисляет нелинейные ограничения в виде равенств от х. Если к тому же градиенты ограничений могут быть рассчитаны и опция options.GradConstr равна 'on' посредством options = optimset('GradConstr','on') то функция nonlcon так же должна возвращаться как третий и четвертый выходные аргументы, GC – как градиент от c(x) и GCeq как как градиент от ceq(x). Отметим, что посредством контроля значения nargout данная функция может обойти расчет GC и GCeq при этом nonlcon вызывается только с двумя выходными аргументами (в данном случае алгоритм оптимизации нуждается только в значениях c и ceq а не GC и GCeq). function [c,ceq,GC,GCeq] = mycon(x) c = ... % Нелинейные неравенства от х ceq = ... % Нелинейные равенства от х if nargout > 2 % Nonlcon вызываентся с 4 выходнымизначениями GC = ... % Градиенты неравенств GCeq = ... % Градиенты равенств end Если nonlcon возвращает вектор с m компонентами и х имеет длину n, где n есть длина x0, в этом случае градиент GC c(x) будет матрица n х m, где GC(i,j) есть частные производные от c(j) по x(i) (т.е. j-ая колонка GC есть градиент j-го ограничения виде неравенств c(j)). Аналогично, если ceq имеет p компонент, то градиент GCeq ceq(x) есть матрица n х p, где GCeq(i,j) будут частные производные от ceq(j) по x(i) (т.е. j-ая колонка GCeq есть градиент j-го ограничения в виде равенств ceq(j)). |
| options | Опции обеспечивают учет специфических деталей функции виде параметров options. |
| weight Вектор веса weight используется для контроля относительного недостижения или передостижения цели для fgoalattain. |
В том случае когда все значения goal отличны от нуля, то для того что бы обеспечить ту же самую долю не- или передостижения активных целей, следует установить весовую функцию виде abs(goal). (Активные цели есть такой набор целей, которые служит препятствием для дальнейшего улучшения цели в данном решении).В случае, когда весовая функция weight положительна, то fgoalattain стремится обеспечить цели меньшие, чем значения goal. Для того, что бы обеспечить целевые функции больше, чем значения goal, правильнее будет установить вес отрицательным, чем положительным. Для того, что бы обеспечить целевые функции как можно ближе к значениям goal, следует использовать параметр GoalsExactAchieve и включить цель в качестве первого элемента для возвращаемого посредством fun вектора (см. описание fun и options выше). |
Выходные аргументы.
Таблица 4-2. "Выходные аргументы" содержат общее описание возвращаемых fgoalattain аргументов. В этом разделе приводятся общие специфические детали для величин attainfactor, exitflag, lambda и output:
| attainfactor | Количество пере- или недостигнутых целей (goals). Если attainfactor – отрицательный то цели передостигнуты, если attainfactor – положительный, то цели недостигнуты. |
| exitflag | Описывает выходные условия.
|
| lambda | Структура, которая содержит множители Лагранжа при решении по х (разделенном по типам условий). Поле структуры:
|
| output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Options
Параметры опций оптимизации, используемые в fgoalattain. Можно использовать optimset, для что бы установить или изменить значения поля параметров опций оптимизации. Для детальной информации смотри Таблицу 4-3. "Параметры опций оптимизации".
| DerivativeCheck | Сравнение введенных пользователем значением производных (градиенты функции цели или ограничений) с конечно-разностными аналогами производных. |
| Diagnostics | Печать диагностической информации о минимизируемой или решаемой или функции. |
| DiffMaxChange | Максимальное изменение переменных конечноразностных градиентов. |
| DiffMinChange | Минимальное изменение переменных конечноразностных градиентов. |
| Display | Уровень отображения. 'off' – отображение не выводится; 'iter' отображение выводится на каждой итерации; 'final' (по умолчанию) отображение только выходной информации. |
| GoalsExactAchieve | Определяет число целей goals, которые "точно" достигнуты, то есть не включает то, что переопределено или недостигнуто. |
| GradConstr | Градиент для определенных пользователем ограничений. Смотри выше описание nonlcon как определить градиент в nonlcon. |
| GradObj | Градиент для определенных пользователем целевой функции. Смотри выше описание fun как определит градиент в fun. Градиент должен быть включен, для того что бы можно было использовать крупно-масштабный метод. Это не обязательно для средне масштабного метода. |
| MaxFunEvals | Максимальное число допустимых оценок функции. |
| MaxIter | Максимальное число допустимых итераций. |
| MeritFunction | Используется целевая функция полезности достижения/минимакса, если установлено 'multiobj'. Используется функции полезности fmincon, если установлено 'singleobj'. |
| TolCon | Конечное допустимое отклонение по нарушению условий ограничения. |
| TolFun | Конечное допустимое отклонение по значению функции. |
| TolX | Конечное допустимое отклонение по х. |
Примеры
Рассмотрим линейную систему дифференциальных уравнений.
Автоматический регулятор по выходу обратной связи, К, сконструирован так, что бы была система с замкнутым контуром
![]()
Характеристические значения системы с замкнутым контуром определяются из матриц A, B, C и K по использованию команды eig(A+B*K*C). Характеристические значения замкнутого контура должны быть на реальных осях в комплексной области слева от точек [-5,-3,-1]. Для того, что бы не переполнялись входные значения, ни один из элементов К не может быть больше чем 4 или меньше чем -4.
Система является двух входной, двух выходной, с разомкнутым контуром, неустойчивой системой, матрицы анализа состояний будут
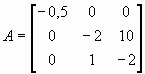
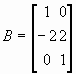
![]()
Установка значений цели (goal) для характеристических значений замкнутого контура инициализируется как
goal = [-5,-3,-1];
Для обеспечения одинаковой доли для пере- или недостижения в активных целях в данном решении весовая матрица weight устанавливается как abs(goal).
Начиная с регулятора K = [-1,-1; -1,-1] сперва напишем М-файл eigfun.m.
function F = eigfun(K,A,B,C)
F = sort(eig(A+B*K*C)); % Оценка целей
Далее введем матрицу системы и запустим подпрограмму оптимизации.
A = [-0.5 0 0; 0 -2 10; 0 1 -2];
B = [1 0; -2 2; 0 1];
C = [1 0 0; 0 0 1];
K0 = [-1 -1; -1 -1]; % Инициализирует матрицу регулятора
goal = [-5 -3 -1]; % устанавливает значения goal для характеристических значений
weight = abs(goal) % устанавливает вес по одинаковой доле
lb = -4*ones(size(K0)); % устанавливает нижнюю границу для регулятора
ub = 4*ones(size(K0)); % устанавливает верхнюю границу для регулятора
options = optimset('Display','iter'); % установка параметров отображения
[K,fval,attainfactor] = fgoalattain(@eigfun,K0,...
goal,weight,[],[],[],[],lb,ub,[],options,A,B,C)
Данные пример может быть выполнен при помощи демонстрационной программы goaldemo. После 12 итераций решение будет
Активные условия ограничений:
1
2
4
9
10
K =
-4.0000 -0.2564
-4.0000 -4.0000
fval =
-6.9313
-4.1588
-1.4099
attainfactor = -0.3863
Обсуждение
Коэффициент достижения указывает, что каждая цель достигнута, по крайней мере, с вероятностью свыше 38.63% от исходных расчетных целей (goals). Активные ограничения, в случае 1 и 2, являются такими ограничениями, которые устанавливают барьер дальнейшему улучшению и для которых доля передостижения точно удовлетворена. Три ограничения по нижней границе также являются активными.
В приведенном выше расчете оптимизатор пытается получить цель меньше, чем goal. В наихудшем случае, для задачи, когда цели должны быть как можно ближе goal, задаются опции options.GoalsExactAchieve с учетом числа требуемых целей.
Рассмотрим приведенную задачу так, как если бы нужно было, что бы все характеристические значения были равны значениям целей (goal). Решение данной задачи осуществляется запуском fgoalattain с опцией options.GoalsExactAchieve, равной 3.
options = optimset('GoalsExactAchieve',3);
[K,fval,attainfactor] = fgoalattain(...
@eigfun,K0,goal,weight,[],[],[],[],lb,ub,[],options,A,B,C)
После порядка семи итераций решение будет:
K =
-1.5954 1.2040
-0.4201 -2.9046
fval =
-5.0000
-3.0000
-1.0000
attainfactor = 1.0859e-20
В данном случае оптимизатор пытался подогнать цели к goal. Коэффициент достижения (1.0859e-20) указывает, что цели точно были достигнуты.
Примечания:
В данной задаче существуют неоднородности в случае, когда характеристические значения становятся комплексными, это и объясняет почему сходимость является медленной. Хотя в основу метода положено, что функции непрерывны, однако данный метод способен предпринимать шаги по достижению решения, поскольку неоднородность не присутствует в конечной точке решения. В случае, когда цели и goal являются комплексными, fgoalattain старается достигнуть goal в смысле наименьших квадратов.
Алгоритм:
Многокритериальная оптимизация относится к одновременной минимизации некого набора целей.
Одна из формулировок данной задачи, что и реализовано в fgoalattain, есть задача достижения цели по Gembicki [3]. Это положено в основу структуры набора значений цели для целевой функции. Полное обсуждение многокритериальной оптимизации находится в разделе Стандартный Алгоритм.
В данной версии, дополнительная переменная используется как некая фиктивный параметр, для того, что бы одновременно минимизировать вектор цели F(x), а цель (goal) есть такой набор значений, что цели являются достижимыми. В общем случае, до начала оптимизации, не известно достигнуты ли цели goal (недостижение) или будут минимизированы меньше, чем goal (передостижение). Вектор веса (weight) контролирует относительное недостижение или передостижение целей.
Fgoalattain использует метод Последовательного Квадратичного Программирования (SQP), который достаточно подробно описан в разделе Стандартные Алгоритмы. Модификации реализованы для линейного поиска и определителя матрицы Гессе. В случае линейного поиска функция полезности (см. [1] и [4]) используется в сочетании с предложенной в [5], [6] функцией полезности. Линейный поиск заканчивается, если какая либо из функций полезности демонстрирует улучшение. Так же используется модифицированный определитель матрицы Гессе (см. [1] и [4]), что дает преимущества для специальных типов задач. Полное описание используемых модификаций в разделе Метод Достижения Цели "Введения в Алгоритмы". Установка опции options.MeritFunction = 'singleobj' задает использование функции полезности и определителя матрицы Гессе в программе fmincon.
Коэффициент достижения g определяется в данном решении. Отрицательные значения g указывают на передостижение цели (goal). Более детально используемый алгоритм можно посмотреть в разделе Реализация SQP в "Введении в Алгоритмы", а типы процедур распечатываются под заголовком Процедуры при установке опции options.Display = 'iter'.
Ограничения:
Цели должны быть непрерывными. fgoalattain может получать только локальные значения.
Сопутствующие функции: @ (function_handle), fmincon, fminimax, optimset
Ссылки
- Brayton, R.K., S.W. Director, G.D. Hachtel, and L.Vidigal, "A New Algorithm for Statistical Circuit Design Based on Quasi-Newton Methods and Function Splitting," IEEE Transactions on Circuits and Systems, Vol. CAS-26, pp. 784-794, Sept. 1979.
- Fleming, P.J. and A.P. Pashkevich, Computer Aided Control System Design Using a Multi-Objective Optimisation Approach, Control 1985 Conference, Cambridge, UK, pp. 174-179.
- Gembicki, F.W., "Vector Optimization for Control with Performance and Parameter Sensitivity Indices," Ph.D. Dissertation, Case Western Reserve Univ., Cleveland, OH, 1974.
- Grace, A.C.W., "Computer-Aided Control System Design Using Optimization Techniques," Ph.D. Thesis, University of Wales, Bangor, Gwynedd, UK, 1989.
- Han, S.P., "A Globally Convergent Method For Nonlinear Programming," Journal of Optimization Theory and Applications, Vol. 22, p. 297, 1977.
- Powell, M.J.D., "A Fast Algorithm for Nonlineary Constrained Optimization Calculations," Numerical Analysis, ed. G.A. Watson, Lecture Notes in Mathematics, Springer Verlag, Vol. 630, 1978.
fminimax – решение задачи минимакс
Синтаксис:
x = fminimax(fun,x0)
x = fminimax(fun,x0,A,b)
x = fminimax(fun,x0,A,b,Aeq,beq)
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub)
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2,...)
[x,fval] = fminimax(...)
[x,fval,maxfval] = fminimax(...)
[x,fval,maxfval,exitflag] = fminimax(...)
[x,fval,maxfval,exitflag,output] = fminimax(...)
[x,fval,maxfval,exitflag,output,lambda] = fminimax(...)
Описание:
fminimax минимизирует наихудшие значения системы функций нескольких переменных, начиная с стартовой оценки. Эти значения могут быть с ограничениями. В общем смысле, эта задача относится к проблеме минимакса.
- x = fminimax(fun,x0) начинает с точки x0 и находит решение минимакса от х для функции, описанной в fun.
- x = fminimax(fun,x0,A,b) решает задачу минимакса с условием линейных неравенств A*x <= b.
- x = fminimax(fun,x,A,b,Aeq,beq) ) решает задачу минимакса с условием линейных равенств Aeq*x = beqas well. Устанавливается A=[] и b=[] в случае отсутствия неравенств.
- x = fminimax(fun,x,A,b,Aeq,beq,lb,ub) определяет набор нижней и верхней границ для расчетных параметров так, что решение всегда находится в диапазоне lb <= x <= ub.
- x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) накладывает на задачу минимакса ограничения типа неравенств c(x) или равенств ceq(x), задаваемых в nonlcon. fminimax минимизирует таким образом, что c(x) <= 0 и ceq(x) = 0. Устанавливается lb=[] и/илиr ub=[] в случае отсутствия границ.
- x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) проводит оптимизацию с учетом параметров оптимизации, определенных в опциях структур
- x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2,...) передает зависимые от задачи параметры P1, P2 и т.д., непосредственно в функции fun и nonlcon. Передает пустые матрицы в виде структурных нулей для A, b, Aeq, beq, lb, ub, nonlcon и опцийв случае, если эти аргументы не являются необходимыми.
- x,fval] = fminimax(...) возвращает значение целевой функции как решение от x.
- [x,fval,maxfval] = fminimax(...) возвращает максимальное значение функции как решение от x.
- [x,fval,maxfval,exitflag] = fminimax(...) возвращает значение exitflag, которое содержит выходные условия для fminimax.
- [x,fval,maxfval,exitflag,output] = fminimax(...) возвращает структурный выход с информацией об оптимизации.
- [x,fval,maxfval,exitflag,output,lambda] = fminimax(...) возвращает структурную lambda поля которой содержат множители Лагранжа, как решение от х.
Аргументы:
Входные аргументы.
Таблица 4-1. Входные аргументы. Содержит общее описание передаваемых в fminimax аргументов
Данный раздел включает детали функционирования для fun, nonlcon и options:
| fun Подлежащая минимизации функция. |
fun есть некая функция, которая принимает вектор х и возвращает вектор F, как целевую функцию от х. Функция fun моет быть определена, описатель функции.x = fminimax(@myfun,x0) где myfun есть такая функция МАТЛАБ, что function F = myfun(x) F = ... % Вычисляет значение функции от х fun также может быть внутренним объектом. x = fminimax(inline('sin(x.*x)'),x0); Для того, что бы минимизировать абсолютные значения, как в наиболее неблагоприятном случае, для любых элементов вектора F(x) (т.е. min{max abs{F(x)}}), распределим эти цели по первым элементам F и установим опцию options.MinAbsMax как число таких целей. Если можно рассчитать градиент целевой функции и опция options.GradObj равна 'on' посредством установки options = optimset('GradObj','on') то тогда функция fun должна возвращать, в своем втором выходном аргументе, значение градиента G как матрицы от х. Отметим, посредством контроля значения nargout функция может избежать расчета G при условии, что myfun вызывается только с одним выходным аргументом (это тот случай, когда для оптимизационного алгоритма необходимо только значение F а не G). function [F,G] = myfun(x) F = ... % Вычисляет значения функций от х if nargout > 1 % два выходных аргумента G = ... % Расчет градиентов от х end Данный градиент состоит из частных производных dF/dx для каждого F в точке х. Если F есть вектор длины m и х имеет размерность n, где n есть размерность для x0, то тогда градиент G от F(x) есть матрица n-х-m, а G(i,j) будут частные производные от F(j) по x(i) (т.е. в G j-ая колонка есть градиент от j-ой целевой функции (j)). |
| nonlcon Функция, которая вычисляет нелинейные ограничения виде неравенств c(x) <= 0 и нелинейные ограничения виде равенств ceq(x) = 0. |
Функция nonlcon принимает вектор х и возвращает два вектора c и ceq. Вектор с содержит нелинейные неравенства при расчете от х и ceq содержит нелинейные равенства при расчете от х. Функция nonlcon может быть определена как описатель функции. x = fminimax(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon) где mycon есть функция MATLAB, определенная как function [c,ceq] = mycon(x) c = ... % вычисляет нелинейные ограничения в виде неравенств от х. ceq = ... % вычисляет нелинейные ограничения в виде равенств от х. Если к тому же градиенты ограничений могут быть рассчитаны и опция options.GradConstr равна 'on' посредством options = optimset('GradConstr','on') то функция nonlcon так же должна возвращаться как третий и четвертый выходные аргументы, GC – как градиент от c(x) и GCeq как как градиент от ceq(x). Отметим, что посредством контроля значения nargout данная функция может обойти расчет GC и GCeq при этом nonlcon вызывается только с двумя выходными аргументами (в данном случае алгоритм оптимизации нуждается только в значениях c и ceq а не GC и GCeq). c = ... % Nonlinear inequalities at x ceq = ... % Nonlinear equalities at x if nargout > 2 % nonlcon called with 4 outputs GC = ... % Gradients of the inequalities GCeq = ... % Gradients of the equalities endЕсли nonlcon возвращает вектор с с m компонентами и х имеет длину n, где n есть длина x0, то градиент GC c(x) есть матрица n х m, где GC(i,j) будут частные производные от c(j) по x(i) (т.е. j-ая колонка GC есть градиент j-го ограничения виде неравенств c(j)). Аналогично, если ceq имеет p компонент, то градиент GCeq ceq(x) есть матрица n х p, где GCeq(i,j) будут частные производные от ceq(j) по x(i) (т.е. j-ая колонка GCeq есть градиент j-го ограничения виде равенств ceq(j)). |
| options. | Опции обеспечивают учет специфических деталей функции виде параметров options. |
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых fminimax. В этом разделе приводятся общие специфические детали для величин exitflag, lambda, maxfval, и output:
| exitflag | Описывает выходные условия.
|
| lambda | Структура, которая содержит множители Лагранжа при решении по х (разделенном по типам условий). Поле структуры:
|
| output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Options
Параметры оптимизационных опций, используемых в fminimax. Можно использовать optimset для того, чтобы установить или изменить значения данных полей в структуре параметров опций. Смотри таблиц 4-3. Параметра опций оптимизации. Для детальной информации
| DerivativeCheck | Сравнение вводимых пользователем производных (градиенты цели или ограничивающих условий) с конечноразностными производными. |
| Diagnostics | Печать диагностической информации о функции, подлежащей минимизации или решению. |
| DiffMaxChange | Максимальное изменение в переменных для конечно-разностных градиентов. |
| DiffMinChange | Минимальное изменение в переменных для конечно-разностных градиентов. |
| Display | Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации. |
| GradConstr | Градиент для определенных пользователем ограничений. Для того, что бы определить градиент в nonlcon смотри его описание выше. |
| GradObj | Градиент определенный пользователем целевой функции. Смотри выше описание функции fun как в ней определить градиент. Для того, что бы использовать крупно-масштабный метод необходимо задавать указанный градиент. Это необязательно для средне-масштабного метода. |
| MaxFunEvals | Максимально число допустимых расчетов функции. |
| MaxIter | Максимально число допустимых итераций. |
| MeritFunction | При установке 'multiobj' используется целевая (goal) функция полезности достижение/минимакс. При установке 'singleobj' используется функция полезности fmincon. |
| MinAbsMax | Число функций F(x), подлежащих минимизации в наихудшем случае для абсолютных значений. |
| TolCon | Конечное допустимое отклонение по нарушению условий ограничения. |
| TolFun | Конечное допустимое отклонение по значению функции. |
| TolX | Конечное допустимое отклонение по значению х. |
Примеры
Найти значения х, которые минимизирую максимальное значение
![]()
где 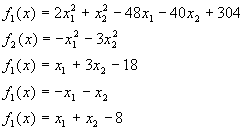
Сперва запишем М-файл, в котором рассчитываются пять функций от х.
function f = myfun(x)
f(1)= 2*x(1)^2+x(2)^2-48*x(1)-40*x(2)+304; % Цели
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1)- x(2);
f(5)= x(1) + x(2) - 8;
Долее запустим подпрограмму оптимизации
x0 = [0.1; 0.1]; % задается начальное предположение о решении
[x,fval] = fminimax(@myfun,x0)
После семи итераций решение будет
x =
4.0000
4.0000
fval =
-64.0000 -2.0000 -8.0000 -0.0000
Примечания
Число целей в наихудшем случае для абсолютного значения от минимизируемого F задается в опции options.MinAbsMax. такие цели следует разделять в первых элементах F.
Например, рассмотрим, приведенную выше задачу, в которой требуется найти значения х, так что бы минимизировать абсолютное значение
![]()
Такая задача решается запуском fminimax с следующими командами
x0 = [0.1; 0.1]; % задается начальное предположение о решении
options = optimset('MinAbsMax',5); % Минимизируются абсолютные значения
[x,fval] = fminimax(@myfun,x0,[],[],[],[],[],[],[],options);
После семи итераций решение будет
x =
4.9256
2.0796
fval =
37.2356 -37.2356 -6.8357 -7.0052 -0.9948
Если ограничения в виде равенств присутствуют, а зависимые равенства могут быть определены и удалены с помощью квадратичной подзадачи, то под заголовком Процедуры печатается 'dependent' (в случае если используется выходная опция options.Display='iter').
Зависимые равенства удаляются только тогда, когда эти равенства являются непротиворечивыми. Если система равенств является противоречивой, то подзадача будет неразрешимой и под заголовком Процедуры печатается 'infeasible'
Алгоритм:
fminimax использует метод последовательного квадратичного программирования (SQP) [1]. Модификации касаются линейного поиска и матрицы Гессе. В случае линейного поиска используется точное значение функции полезности (смотри [2] и [4]) совместно с функцией полезности, предложенной в [3] и [5]. Линейный поиск заканчивается, когда функция полезности показывает улучшение. Так же используется модифицированная матрица Гессе, что дает выигрыш для специализированной структуры данной задачи. При установке опции options.MeritFunction = 'singleobj' используется функция полезности и матрица Гессе в fmincon.
Для большей детализации используемого алгоритма и типов процедур, распечатываемых под заголовком Процедуры при установке опции options.Display='iter', смотри Реализация SQP в “Введении в Алгоритмы”.
Ограничения:
Минимизируемые функции и ограничения должны быть непрерывными. fminvf[ может давать только локальные решения.
Смотри также:
@ (function_handle), fgoalattain, lsqnonlin, optimset
Литература:
- Brayton, R.K., S.W. Director, G.D. Hachtel, and L.Vidigal, "A New Algorithm for Statistical Circuit Design Based on Quasi-Newton Methods and Function Splitting," IEEE Trans. Circuits and Systems, Vol. CAS-26, pp. 784-794, Sept. 1979.
- Grace, A.C.W., "Computer-Aided Control System Design Using Optimization Techniques," Ph.D. Thesis, University of Wales, Bangor, Gwynedd, UK, 1989.
- Han, S.P., "A Globally Convergent Method For Nonlinear Programming," Journal of Optimization Theory and Applications, Vol. 22, p. 297, 1977.
- Madsen, K. and H. Schjaer-Jacobsen, "Algorithms for Worst Case Tolerance Optimization," IEEE Transactions of Circuits and Systems, Vol. CAS-26, Sept. 1979.
- Powell, M.J.D., "A Fast Algorithm for Nonlineary Constrained Optimization Calculations," Numerical Analysis, ed. G.A. Watson, Lecture Notes in Mathematics, Springer Verlag, Vol. 630, 1978.
lsqlin – решение линейной задачи с ограничениями методом наименьших квадрато
![]() такие, что
такие, что 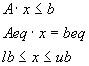
где С, A и Aeq есть матрицы d, b, beq, lb, ub и x есть векторы.
Синтаксис:
x = lsqlin(C,d,A,b)
x = lsqlin(C,d,A,b,Aeq,beq)
x = lsqlin(C,d,A,b,Aeq,beq,lb,ub)
x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0)
x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,options)
x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,options,p1,p2,...)
[x,resnorm] = lsqlin(...)
[x,resnorm,residual] = lsqlin(...)
[x,resnorm,residual,exitflag] = lsqlin(...)
[x,resnorm,residual,exitflag,output] = lsqlin(...)
[x,resnorm,residual,exitflag,output,lambda] = lsqlin(...)
Описание:
- x = lsqlin(C,d,A,b) решает систему C*x=d с точки зрения метода наименьших квадратов при условии A*x<=b, где C имеет размерность m-х-n.
- x = lsqlin(C,d,A,b,Aeq,beq) решает указанные выше задачу при условии дополнительного выполнения ограничений в виде равенств Aeq*x = beq. Если нет неравенств, то устанавливается A=[] и b=[].
- x = lsqlin(C,d,A,b,Aeq,beq,lb,ub) определяет набор нижних и верхних границ для проектируемых переменных х, так что решение всегда находится в диапазоне lb <= x <= ub. Если нет неравенств, то устанавливается Aeq=[] и beq=[].
- x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0) устанавливает начальную точку как х0. В случае отсутствия границ устанавливается lb=[] и b=[].
- x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,options) проводит оптимизацию с определенными в структурной опции параметрами оптимизации.
- x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,options,p1,p2,...) передает зависящие от типа задачи параметры р1, р2 и т.д. непосредственно в множители функции Якобина, если она существует. Необходимо определить множители функции Якобина с помощью параметра JacobMult в options.
- [x,resnorm] = lsqlin(...) возвращает значение квадрата нормы невязки от х. norm(C*x-d)^2.
- [x,resnorm,residual] = lsqlin(...) возвращает значение невязки, C*x-d.
- [x,resnorm,residual,exitflag] = lsqlin(...) возвращает значение exitflag, которое содержит описание выходных условий.
- [x,resnorm,residual,exitflag,output] = lsqlin(...) возвращает структурный выход с информацией об оптимизации
- [x,resnorm,residual,exitflag,output,lambda] = lsqlin(...) возвращает структурную lambda с полями, содержащими множители Лагранжа в виде решения от х.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в lsqcurvefit. Данные подраздел “Аргументы” приводит функционально-специфические детали параметров options:
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых lsqlin аргументов. В этом разделе приводятся общие специфические детали для величин exitflag, lambda и output:
| Exitflag | Описывает выходные условия.
|
| Lambda | Структура, которая содержит множители Лагранжа при решении по х (разделенном по типам условий). Поле структуры:
|
| Output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Для крупно-масштабных задач с краевыми ограничениями оптимальностью первого порядка будет бесконечная норма v.*g, где v определяется как Ограничения Бокса и g – градиент g = CTCx + CTd (смотри Линейный Метод Наименьших Квадратов)
Options
Параметры оптимизационных опций, используемых в lsqlin. Можно использовать optimset для того, чтобы установить или изменить значения данных параметров опций. Часть параметров используется ко всем алгоритмам, некоторые используются только для крупномасштабного алгоритма, а другие применимы только среднемасштабных алгоритмов.
Мы начнем с описания опции LargeScale, поскольку она устанавливает преимущественное право какой алгоритм использовать. Это только преимущественное право, поскольку должны быть выполнены определенные условия для того, что бы можно было использовать крупно-масштабный алгоритм. Для lsqlin, поскольку данная задача имеет только верхнюю и нижнюю границу, не задаются ограничения типа равенств или неравенств, причем по умолчанию используется крупно-масштабный метод, в противном - средне-масштабный метод.
| LargeScale | В случае установки 'on' используется, если это возможно, крупно-масштабный алгоритм. Для использования средне-масштабного алгоритма устанавливается 'off'. |
Medium-Scale and Large-Scale Algorithms. Эти параметры используются как для средне-масштабного, так и крупно-масштабного алгоритмов:
| Diagnostics | Проводится печать диагностической информации о минимизируемой функции. |
| Display | Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации. |
| MaxIter | Максимально число допустимых итераций. |
Large-Scale Algorithm Only. Эти параметры используются только для крупно-масштабного алгоритма
| JacobMult | Указатель функции для функции множителей Якобиана. В случае крупно-масштабной задачи данная функция вычисляет произведение матриц Якобиана J*Y, J'*Y или J'*(J*Y) без действительного формирования J. Такая функция имеет форму W = jmfun(Jinfo,Y,flag,p1,p2,...), где Jinfo и дополнительные параметры p1,p2,... включают в себя используемые для расчета J*Y (или J'*Y или J'*(J*Y)) матрицы. Первый аргумент Jinfo должен быть таким же, что и lsqlin, а p1,p2, … те же самые дополнительные параметры, какие передаются в lsqlin.lsqlin(Jinfo,...,options,p1,p2,...) Y есть матрица с тем же самым числом строк, что и размерность данной задачи.flag определяет какое произведение нужно вычислять. If flag == 0 then W = J'*(J*Y). If flag > 0 then W = J*Y. If flag < 0 then W = J'*Y. В каждом случае J явно не формируется. lsqlin использует Jinfo для расчета предварительных данных. В качестве примера смотри Квадратичную Оптимизацию с Компактной, но Структурированной Матрицей Гессе. |
| MaxPCGIter | Максимальное число PCG (предварительно сопряженный градиент) итераций (Смотри ниже раздел Алгоритм). |
| PrecondBandWidth | Верхняя полоса предварительной обработки для PCG. По умолчанию используется диагональная начальная подготовка (верхняя полоса из 0). Для некоторых задач увеличение полосы снижает число итераций PCG. |
| TolFun | Конечная допустимая точность значения функции. |
| TolPCG | Конечное допустимое число итераций PCG. |
| TypicalX | Типичные значения х. |
Примеры:
Найти решение метод наименьших квадратов для переопределенной системы ![]() при условии, что
при условии, что ![]() и
и ![]() .
.
Сперва введем коэффициенты матриц и верхние и нижние границы.
C = [
0.9501 0.7620 0.6153 0.4057
0.2311 0.4564 0.7919 0.9354
0.6068 0.0185 0.9218 0.9169
0.4859 0.8214 0.7382 0.4102
0.8912 0.4447 0.1762 0.8936];
d = [
0.0578
0.3528
0.8131
0.0098
0.1388];
A =[
0.2027 0.2721 0.7467 0.4659
0.1987 0.1988 0.4450 0.4186
0.6037 0.0152 0.9318 0.8462];
b =[
0.5251
0.2026
0.6721];
lb = -0.1*ones(4,1);
ub = 2*ones(4,1);
Далее обратимся к программе метода наименьших квадратов с линейными ограничениями
[x,resnorm,residual,exitflag,output,lambda] = ...
lsqlin(C,d,A,b,[ ],[ ],lb,ub);
Введя x, lambda.ineqlin, lambda.lower, lambda.upper получим
x =
-0.1000
-0.1000
0.2152
0.3502
lambda.ineqlin =
0
0.2392
0
lambda.lower =
0.0409
0.2784
0
0
lambda.upper =
0
0
0
0
Ненулевые элементы векторов в полях lambda указывают на активные ограничения при решении. В нашем случае, второе ограничения в виде неравенств (в lambda.ineqlin) и первое нижнее и второе нижнее граничные ограничения (в lambda.lower) являются активными ограничениями (т.е. решение находится на ограничительных условиях).
Примечания:
В случае отсутствия ограничений следует использовать оператор \. Смотри, например, x= A\b.
В общем, lsqlin определяет локальное решение.
По-видимому, более точные численные результаты будут, если с помощью Aeq и beq явно определить равенства вместо неявного использования lb и ub.
Крупно-масштабная оптимизация. Если х0 не является строго допустимым, то lsqlin выберет новую строго допустимую (центрированную) стартовую точку.
Если компоненты х не имеют верхних (или нижних границ), то lsqlin выберет, соответствующие компоненты ub (или lb) будут установлены как Inf (бесконечность) (или -Inf для lb) в отличие от произвольного, но очень большого положительного (или отрицательного в случае нижних границ) числа.
Алгоритм:
Крупно-масштабная оптимизация. В случае если приведенная в lsqlin имеет только верхние и нижние границы, т.е. не определены линейные неравенства или равенства, и матрица С имеет строк по крайней мере больше, чем колонок, то по умолчанию принимается крупно-масштабный алгоритм. Данный алгоритм является реализацией метода доверительных подпространств и основан на методе внутренних отражений Ньютона, описанного в [1]. Каждая итерация включает в себя приближенное решение крупной линейной системы с помощью метода предварительно сопряженных градиентов(PCG). Смотри описания Доверительной Области для Нелинейной Оптимизации и Метода Предварительно Сопряженных Градиентов в разделе “Крупно-Масштабные Алгоритмы”.
Средне-масштабная оптимизация. lsqlin при установке options.LargeScale как 'off', или когда приводятся линейные неравенства или равенства, базируется на методе quadprog, который использует метод активной системы, аналогично тому, что описано в [2]. Этот метод находит начальные решения путем решения задачи линейного программирования. Смотри Квадратичное Программирование в разделе “Введении в Алгоритмы”
Диагностика:
Крупно-масштабная оптимизация. Коды крупно-масштабного метода не допускают равенства верхней и нижней границ. Например, если lb(2) == ub(2), то lsqlin дает ошибку
Равные верхние и нижние границы не допустимы в данном крупно-масштабном методе.
Взамен этого используйте ограничения типа равенств и средне-масштабный метод.
К данному времени используемый средне-масштабный алгоритм должен решать задачу с ограничениями типа равенств.
Средне-масштабная оптимизация. Если матрицы С, А или Aeq являются разреженными и постановка задачи является неразрешимой в крупно-масштабном методе, то lsqlin дает предупреждение, что эти матрицы преобразуются до полных.
Предупреждение. Данная постановка задачи является пока недопустимой для разреженных матриц. Для разрешимости производится преобразование до полных.
Lsqlin дает предупреждение, если задача является недопустимой
Предупреждение. Ограничения являются слишком жесткими.
Нет допустимого решения
В этом случае lsqlin проводит минимизацию для ограничения с наибольшим нарушением.
Когда ограничения типа равенств являются недопустимыми, то lsqlin дает предупреждение
Предупреждение. Ограничения типа равенств являются слишком жесткими.
Нет допустимого решения
Ограничения:
К настоящему времени имеются только уровни отображения, при использовании опции параметров Отображения, 'off' и 'final'; итерационный вывод с опцией 'iter' отсутствует.
Смотри также: lsqnonneg, quadprog
Литература:
- Coleman, T.F. and Y. Li, "A Reflective Newton Method for Minimizing a Quadratic Function Subject to Bounds on Some of the Variables", SIAM Journal on Optimization, Vol. 6, Number 4, pp. 1040-1058, 1996.
- Gill, P.E., W. Murray, and M.H. Wright, Practical Optimization, Academic Press, London, UK, 1981.
lsqnonneg - решение неотрицательной задачи методом наименьших квадрато
![]() , такие, что
, такие, что![]() ,
,
где матрица С и вектор d являются коэффициентами целевой функции. Вектор х имеет ограничения как независимая переменная, т.е. он не может быть отрицательным.
Синтаксис:
x = lsqnonneg(C,d)
x = lsqnonneg(C,d,x0)
x = lsqnonneg(C,d,x0,options)
[x,resnorm] = lsqnonneg(...)
[x,resnorm,residual] = lsqnonneg(...)
[x,resnorm,residual,exitflag] = lsqnonneg(...)
[x,resnorm,residual,exitflag,output] = lsqnonneg(...)
[x,resnorm,residual,exitflag,output,lambda] = lsqnonneg(...)
Описание:
- x = lsqnonneg(C,d) возвращает вектор х, который является минимумом нормы (C*x-d) при условии x >= 0. С и d должны быть реальными.
- x = lsqnonneg(C,d,x0) использует точку х0 как стартовую при условии, что все x0 >= 0, в противном, используется вариант по умолчанию. Принимаемая по умолчанию точка есть начало координат (вариант по умолчанию принимается когда x0==[] или заданы только два входных аргумента).
- x = lsqnonneg(C,d,x0,options) проводит оптимизацию с определенными в структурной опции параметрами оптимизации.
- [x,resnorm] = lsqnonneg(...) возвращает значение квадрата удвоенной нормы невязки, norm(C*x-d)^2.
- [x,resnorm,residual] = lsqnonneg(...) возвращает значение невязки, C*x-d.
- [x,resnorm,residual,exitflag] = lsqnonneg(...) возвращает значение exitflag, которое содержит описание выходных условий для lsqnonneg.
- [x,resnorm,residual,exitflag,output] = lsqnonneg(...) возвращает структурный выход с информацией об оптимизации.
- [x,resnorm,residual,exitflag,output,lambda] = lsqnonneg(...) возвращает множители Лагранжа как вектор lambda.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в lsqnonneg. Данный подраздел приводит функционально-специфические детали для параметров
| Options | Можно использовать optimset для того, чтобы установить или изменить значения данных полей в структуре параметров опций. Для детальной информации смотри Таблицу 4-3, Параметры Опций Оптимизации |
| Display |
|
| TolX | Конечное допустимое отклонение по значению функции |
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых lsqnonneg аргументов. В этом разделе приводятся общие специфические детали для величин exitflag, lambda и output:
| exitflag | Описывает выходные условия.
|
| lambda | Вектор, который содержит множители Лагранжа. lambda(i)<=0 при условии, что x(i) (приблизительно) равны 0, и lambda(i) равно (приблизительно) 0 при условии, что x(i)>0. |
| output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Примеры:
Сравнение решения безусловной задачи методом наименьших квадратов с решением с помощью lsqnonneg для случая 4 на 2.
C = [
0.0372 0.2869
0.6861 0.7071
0.6233 0.6245
0.6344 0.6170];
d = [
0.8587
0.1781
0.0747
0.8405];
[C\d, lsqnonneg(C,d)] =
-2.5627 0
3.1108 0.6929
[norm(C*(C\d)-d), norm(C*lsqnonneg(C,d)-d)] =
0.6674 0.9118
Решение с помощью lsqnonneg не подходит достаточно хорошо как с помощью метода наименьших квадратов. Однако неотрицательное решение методом наименьших квадратов имеет неотрицательные компоненты.
Алгоритм:
lsqnonneg использует описанный в [1] алгоритм. Данный алгоритм стартует с некого набора возможных базовых векторов и вычисляет соотнесенный двойной вектор lambda. Далее выбирается базовый вектор, соответствующий максимальному значению lambda для того, что бы обменять это базис взамен другого возможного кандидата. Так продолжается до тех пор, пока не станет ![]() .
.
Примечания:
Задача с методом наименьших квадратов для неотрицательных значений есть подмножество задач с методом наименьших квадратов и линейными ограничениями.
Таким образом, когда С имеет больше строк, чем колонок (т.е. система является переопределенной)
![]()
эквивалентно тому, что
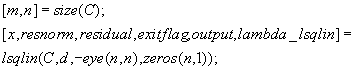
за исключением того, что ![]() .
.
Для задач с порядком больше 20 lsqlin может быть быстрее, чем lsqnonneg, с другой стороны lsqnonneg обычно является боле эффективной программой.
Смотри так же lsqlin, optimset
Литература:
1. Lawson, C.L. and R.J. Hanson, Solving Least Squares Problems, Prentice-Hall, Chapter 23, p. 161, 1974.
lsqcurvefit – решение нелинейной задачи аппроксимации кривых (подбора данных) методом наименьших квадрато
т.е при заданном массиве аргументов xdata и массиве функций ydata найти коэффициенты х, которые “лучше всего” удовлетворяют уравнению F(x, xdata);
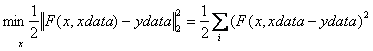
где xdata и ydata есть векторы и F(x, xdata) есть векторозначная функция.
Функция lsqcurvefit использует тот же самый алгоритм, что и lsqnonlin. Ее назначение состоит в том, что бы получить интерфейс, спроектированной специально для задач подбора данных.
Синтаксис
x = lsqcurvefit(fun,x0,xdata,ydata)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options,P1,P2,...)
[x,resnorm] = lsqcurvefit(...)
[x,resnorm,residual] = lsqcurvefit(...)
[x,resnorm,residual,exitflag] = lsqcurvefit(...)
[x,resnorm,residual,exitflag,output] = lsqcurvefit(...)
[x,resnorm,residual,exitflag,output,lambda] = lsqcurvefit(...)
[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqcurvefit(...)
Описание.
lsqcurvefit решает задачи нелинейного подбора данных. Для lsqcurvefit вводится задаваемая пользователем функция F(x, xdata), которая производит значение вектора. Размер вектора в задаваемой пользователем функции должен иметь тот же самый размер, что и ydata.
x = lsqcurvefit(fun,x0,xdata,ydata) начинает с точки х0 и находит коэффициенты х, которые наилучшим образом подбирают нелинейную функцию fun(x,xdata) по данным ydata (в смысле метода наименьших квадратов). ydata должно иметь тот же самый размер, что и возвращаемый в fun.вектор F (или матрица).
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub) ) определяет набор нижних и верхних границ для проектируемых переменных х, так что решение всегда находится в диапазоне lb <= x <= ub.
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options) проводит оптимизацию с определенными в структурной опции параметрами оптимизации. Если ограничений нет, то эта команда передает пустую матрицу в lb и ub
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options,P1,P2,...) передает зависящие от типа задачи параметры P1, P2 и т.д. непосредственно в функцию fun. Передает пустые матрицы заменители в опции, которые в качестве используемых по умолчанию парамктров.
[x,resnorm] = lsqcurvefit(...) возвращает значение квадрата нормы невязки от х.
sum{(fun(x,xdata)-ydata).^2}.
[x,resnorm,residual] = lsqcurvefit(...) возвращает значение невязки fun(x,xdata)-ydata, как решение от х.
[x,resnorm,residual,exitflag] = lsqcurvefit(...) возвращает значение exitflag, которое содержит описание выходных условий.
[x,resnorm,residual,exitflag,output] = lsqcurvefit(...) возвращает структурный выход с информацией об оптимизации.
[x,resnorm,residual,exitflag,output,lambda] = lsqcurvefit(...) возвращает структурную lambda с полями, содержащими множители Лагранжа в виде решения от х.
[x,resnorm,residual,exitflag,output,lambda,jacobian] = 99 99lsqcurvefit(...) Возвращает Якобиан от fun как решение от х.
Аргументы
Входные аргументы. Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в lsqcurvefit. Данные подраздел <Аргументы> приводит функционально-специфические детали для fun и options:
| Fun | Подлежащая подбору функция. fun есть такая функция, которая принимает вектор х и возвращает скаляр F, т.е. целевую функция от х. Функция fun может задаваться с помощью описателя функций x = lsqcurvefit(@myfun,x0,xdata,ydata) где myfun есть такая функция MATLAB, что function F = myfun(x,xdata) F = ... % Вычисление функции в точке х fun так же может быть и внутренним объектом. f = inline('x(1)*xdata.^2+x(2)*sin(xdata)',... 'x','xdata'); x = lsqcurvefit(f,x0,xdata,ydata); Если к тому же может быть рассчитан Якобиан и установленная с помощью опция options = optimset('Jacobian','on') если опция options.Jacobian равна 'on', то функция fun во втором выходном аргументе должна возвращать значение Якобиана J, как матрицы от х. Отметим, что посредством проверки значения nargout данная функция может обойти расчет J в случае, когда fun вызывается только с одним выходным аргументом (случай, когда для оптимизационного алгоритма необходимо только значение F, а не J). function [F,J] = myfun(x,xdata) F = ... % значения целевой функции от x if nargout > 1 % два выходных аргумента J = ... % Якобиан как функция от x End Если fun возвращает вектор (матрицу) из m компонентов и х имеет длину n, где n есть длина х0, то Якобиан J есть матрица m х n и J(i,j) будут частные производные от F(i) по x(j). (Отметим, что Якобиан J есть транспонирование градиента от F.) |
| options | Опции обеспечивают учет специфических деталей функции виде параметров options. |
Выходные аргументы. Таблица 4-2. "Выходные аргументы" содержат общее описание возвращаемых lsqcurvefit аргументов. В этом разделе приводятся общие специфические детали для величин exitflag, lambda, и output:
| exitflag | Описывает выходные условия > 0 Данная функция сходится к решению по х. 0 Максимальное число оценки функции или итерации было превышено < 0 Функция не сходится к некому решению. |
| lambda | Структура, которая содержит множители Лагранжа при решении по х (разделенном по типам условий). Поле структуры: lower Нижние границы lb upper Верхние границы ub |
| output | Структура, которая содержит информацию об оптимизации. Поле структуры: iterations Число выполненных итераций funcCount Число оценок функции algorithm Используемый алгоритм cgiterations Число PCG итераций (только для крупно-масштабного алгоритма) stepsize Окончательно принятый размер шага (только для средне-масштабного алгоритма) firstorderopt Измерение оптимальности первого порядка (только для алгоритма большой размерности). Для крупно-масштабной задачи большой размерности оптимальность первого порядка есть бесконечная норма градиента g = JTF (смотри нелинейный среднеквадратичный метод) |

Options
Параметры оптимизационных опций, используемых в lsqcurvefit. Часть параметров используется во всех алгоритмах, некоторые используются только для алгоритма большой размерности, а другие применимы только среднемасштабных алгоритмов средней размерности. Для того, чтобы установить или изменить значения данных полей в структуре параметров опций, можно использовать команду optimset Для детальной информации смотри Таблицу 4-3, Параметры Опций Оптимизации
Мы начнем с описания опции LargeScale, поскольку она устанавливает преимущественное право какой алгоритм использовать. Это только преимущественное право, поскольку должны быть выполнены определенные условия для того, что бы можно было использовать крупно-масштабный алгоритм большой размерности. Для крупно-масштабного алгоритма большой размерности, поскольку система нелинейных уравнений не может быть недоопределенной, число уравнений (число возвращаемых fun элементов F) должно быть, по крайней мере, длины х. Кроме того, только крупно-масштабный алгоритм большой размерности управляет ограничениями в виде границ.
LargeScale В случае установки 'on' используется крупно-масштабный, если это возможно, алгоритм большой размерности. Для использования средне-масштабного алгоритма средней размерности устанавливается значение 'off'.
Medium-Scale and Large-Scale Algorithms. Эти параметры используются как для алгоритмов средней размерности так и для алгоритмов большой размерности:
Diagnostics Проводится печать диагностической о минимизируемой функции.
Display Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации.
Jacobian При установке 'on', lsqcurvefit использует заданный пользователем Якобиан (определенный в fun), или информацию об Якобиане (при использовании JacobMult) для целевой функции. При установке 'off', lsqcurvefit аппроксимирует Якобиан с помощью конечных разностей.
MaxFunEvals Максимально число допустимых расчетов функции.
MaxIter Максимально число допустимых итераций.
TolFun Конечное допустимое отклонение по значению функции
TolX Конечное допустимое отклонение по значению х.
Large-Scale Algorithm Only. Конечное допустимое отклонение по значению х.
JacobMult Указатель функции для функции множителей Якобиана. В случае задачи большой размерности данная функция вычисляет произведение матриц Якобиана J*Y, J'*Y или J'*(J*Y) без действительного формирования J. Такая функция имеет форму
W = jmfun(Jinfo,Y,flag,p1,p2,...),
где Jinfo и дополнительные параметры p1,p2,... включают в себя используемые для расчета J*Y (или J'*Y или J'*(J*Y)) матрицы. Первый аргумент Jinfo должен быть таким же, что возвращаемый целевой функцией fun второй аргумент.
[F,Jinfo] = fun(x,p1,p2,...)
Переменные p1,p2,... есть дополнительные параметры, передаваемые в lsqcurvefit (и в fun).
lsqcurvefit (fun,...,options,p1,p2,...)
Y есть матрица с тем же самым числом строк, что и размерность данной задачи.
flag определяет какое произведение нужно вычислять.
If flag == 0 then W = J'*(J*Y).
If flag > 0 then W = J*Y.
If flag < 0 then W = J'*Y. В каждом случае J явно не формируется.
lsqcurvefit использует переменную Jinfo для расчета предварительных данных.

В качестве примера смотри Нелинейную Оптимизацию с Компактной, но Структурированной Матрицей Гессе и Ограничениями Типа Равенств.
JacobPattern Разреженные шаблоны Якобиана для конечного дифференцирования. В случае, если в fun неразумно вычислять матрицу Якобиана J, то lsqcurvefit может аппроксимировать J через заданные значения для JacobPattern. В наихудшем случае, когда эта структура неизвестна, можно установить JacobPattern, так что бы плотная матрица и полные конечно-разностные аппроксимации вычислялись на каждой итерации (что принимается по умолчанию в случае неустановки JacobPattern). Это может быть чрезвычайно затратным для больших задач, поэтому обычно заслуживает внимания усилия по определению степени разреженности структуры решаемой задачи.
MaxPCGIter Максимальное число PCG (предварительно сопряженный градиент) итераций (Смотри ниже раздел Алгоритм).
PrecondBandWidth Верхняя полоса предварительной обработки для PCG. По умолчанию используется диагональная начальная подготовка (верхняя полоса из 0). Для некоторых задач увеличение полосы снижает число итераций PCG.
TolPCG Конечное допустимое число итераций PCG.
TypicalX Типичные значения х.
Medium-Scale Algorithm Only. Эти параметры используются только для алгоритма средней размерности.
DerivativeCheck Сравнение вводимых пользователем производных (Якобиана) с конечноразностными производными.
DiffMaxChange Максимальное изменение в переменных для конечных-разностей
DiffMinChange Минимальное изменение в переменных для конечных-разностей
LevenbergMarquardt Выбор алгоритма Левенберга-Макуарда вместо Гаусса-Ньютона
LineSearchType Выбор алгоритма линейного поиска
Примеры
Векторы xdata и ydata имеют длину n. Требуется найти такие коэффициенты х, что бы они лучше всего подходили к уравнению
![]()
то есть нужно минимизировать
![]()
где F(x,xdata) = x(1)*xdata.^2 + x(2)*sin(xdata) + x(3)*xdata.^3, начнем с точки x0 = [0.3, 0.4, 0.1].
Сперва запишем М-файл, который возвращает F (F имеет n компонентов)
function F = myfun(x,xdata)
F = x(1)*xdata.^2 + x(2)*sin(xdata) + x(3)*xdata.^3;
Далее вызовем подпрограмму оптимизации
% Предположим, что xdata и ydata определены экспериментально
xdata = [3.6 7.7 9.3 4.1 8.6 2.8 1.3 7.9 10.0 5.4];
ydata = [16.5 150.6 263.1 24.7 208.5 9.9 2.7 163.9 325.0 54.3];
x0 = [10, 10, 10] % Начальное предположение
[x,resnorm] = lsqcurvefit(@myfun,x0,xdata,ydata)
Отметим, во время вызова lsqcurvefit предполагается, что xdata и ydata и являются векторами одного и того же размера. Они должны иметь один и тот же размер, поскольку возвращаемое в fun значение F должно иметь тот же самый размер, что и ydata.
После 33 оценок функции данный пример дает решение
x =
0.2269 0.3385 0.3021
% невязка или сумма квадратов
resnorm =
6.2950
Невязка не равна нулю, потому что в данном случае имеет место некоторый шум (экспериментальные ошибки) в представленных данных
Алгоритм
Оптимизация алгоритмов большой размерности.
По умолчанию lsqcurvefit выберет алгоритм большой размерности. Данный алгоритм является реализацией метода доверительных подпространств и основан на методе внутренних отражений Ньютона, описанного в [1], [2]. Каждая итерация включает в себя приближенное решение крупной линейной системы с помощью метода предварительно сопряженных градиентов(PCG). Смотри описания Доверительной Области и Метода Предварительно Сопряженных Градиентов в разделе <Крупно-Масштабные Алгоритмы>.
Оптимизация алгоритмов средней размерности.
lsqcurvefit при установке options.LargeScale как 'off' использует метод Левенберга-Макуарда [4], [5], [6] с линейным поиском. В качестве альтернативы может быть выбран метод Гаусса-Ньютона [3] с линейным поиском. Выбор алгоритма проводится при помощи установки опции options.LevenbergMarquardt. Установка options.LevenbergMarquardt как 'off' (и опции options.LargeScale как 'off') выбирается метод Гаусса-Ньютона, который обычно работает быстрее в случае небольшой невязки
![]() .
.
Принимаемый по умолчанию алгоритм линейного поиска, т.е. опция options.LineSearchType установлена как ''quadcubic', обеспечивается методом смешанной квадратичной и кубической полиноминальной интерполяции и экстраполяции. Защищенный кубической полиномиальный метод может быть задан при помощи установки опции LineSearchType как 'cubicpoly'. В общем случае, данный метод требует меньшего расчета функций, но большего обращения к расчету градиента. Таким образом, если градиенты приведены и могут быть вычислены без больших затрат, то метод с кубическим полиномиальным линейным поиском является предпочтительным. Используемые алгоритмы полностью описаны в разделе Стандартные Алгоритмы.
Диагностика
Оптимизация алгоритмов большой размерности.
Коды для оптимизации алгоритмов большой размерности не допускают равенства верхней и нижней границ. Например, если lb(2)==ub(2), то lsqlin выдает ошибку
Равенство верхней и нижней границ недопустимо.
lsqcurvefit не управляет ограничениями типа равенств, а имеется иная возможность формулировки границ в виднее равенств. В случае наличия ограничений типа равенств в качестве альтернативной формулировки используются функции fmincon, fminimax или fgoalattain, (где ограничения типа равенств уже могут быть включены.)
Ограничения
Минимизируемая функция должна быть непрерывной. Lsqcurvefit может давать только локальные решения.
lsqcurvefit оперирует только с реальными переменными (задаваемая пользователем функция должна возвращать только реальные значения). Если х имеет комплексные значения, то эти переменные должны быть разделены на мнимую и реальные части.
Оптимизация алгоритмов большой размерности.
Данный метод для алгоритмов большой размерности не допускает обращения к недоопределенным системам, он требует, что бы число уравнений, т.е. число строк в F было, по крайней мере, больше, чем число переменных. В случае недоопределенности системы в данном случае используется алгоритм средней размерности. Относительно дополнительной информации о постановке задачи, области применения и задания исходных данных смотри таблицу 1-4, Область Определения и Требования к Крупно-Масштабным Задачам.
В части предварительно сопряженных градиентов для формирования JTJ метода для алгоритма большой размерности (где J есть матрица Якоби) перед подготовкой данных используется предварительный расчет. Поэтому, строки матрицы J с большим числом ненулевых значений могут привести к особенно плотным произведениям JTJ, что, в свою очередь, может привести к усложнению расчетов для больших задач.
В настоящее время, если в fun аналитически задан градиент, то для сравнения аналитического градиента с его конечно-разностным значением в методе для алгоритмов большой размерности нельзя использовать параметр опции DerivativeCheck. Вместо этого, для контроля производной следует использовать метод для алгоритмов средней размерности с установкой опционного параметра MaxIter как 0 итераций. Затем следует запустить задачу с методом для алгоритмов большой размерности.
Смотри также
@ (function_handle), \, lsqlin, lsqnonlin, lsqnonneg, optimset
Литература
[1] Coleman, T.F. and Y. Li, "An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds," SIAM Journal on
Optimization, Vol. 6, pp. 418-445, 1996.
[2] Coleman, T.F. and Y. Li, "On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to
Bounds," Mathematical Programming, Vol. 67, Number 2, pp. 189-224, 1994.
[3] Dennis, J. E. Jr., "Nonlinear Least Squares," State of the Art in Numerical Analysis, ed. D. Jacobs, Academic Press, pp. 269-312,
1977.
[4] Levenberg, K., "A Method for the Solution of Certain Problems in Least Squares," Quarterly Applied Math. 2, pp. 164-168, 1944.
[5] Marquardt, D., "An Algorithm for Least Squares Estimation of Nonlinear Parameters," SIAM Journal Applied Math. Vol. 11, pp.
431-441, 1963.
[6] More, J. J., "The Levenberg-Marquardt Algorithm: Implementation and Theory," Numerical Analysis, ed. G. A. Watson, Lecture
Notes in Mathematics 630, Springer Verlag, pp. 105-116, 1977.
lsqnonlin - решение нелинейной задачи методом наименьших квадратов (нелинейный подбор данных
![]()
где L константа.
Синтаксис:
x = lsqnonlin(fun,x0)
x = lsqnonlin(fun,x0,lb,ub)
x = lsqnonlin(fun,x0,lb,ub,options)
x = lsqnonlin(fun,x0,eb,ub,options,P1,P2, ... )
[x,resnorm] = lsqnonlin(...)
[x,resnorm,residual] = lsqnonlin(...)
[x,resnorm,residual,exitflag] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output,lambda] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqnonlin(...)
Описание:
lsqnonlin решает нелинейную задачу методом наименьших квадратов, включая задачу нелинейного подбора данных.
До расчета значений f(x) (“суммы квадратов”), lsqnonlin требует задаваемой пользователем функции для расчета векторозначной функции.
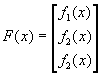
![]()
Далее, используя векторную терминологию, задача оптимизации может быть заново сформулирована как
![]()
где х есть вектор и F(x) есть функция, которая возвращает значение вектора
- x = lsqnonlin(fun,x0) начинает с точки х0 и находит минимум суммы квадратов описанной в fun функции. fun должна возвращать вектор значений, а не сумму квадратов значений. (В данном алгоритме fun(x) неявно суммируется и возводится в квадрат.)
- x = lsqnonlin(fun,x0,lb,ub) определяет набор нижних и верхних границ для проектируемых переменных х, так что решение всегда находится в диапазоне lb <= x <= ub.
- x = lsqnonlin(fun,x0,lb,ub,options) проводит оптимизацию с определенными в структурной опции параметрами оптимизации. Если ограничений нет, то передает пустую матрицу в lb и ub.
- x = lsqnonlin(fun,x0,lb,ub,options,P1,P2,...) передает зависящие от типа задачи параметры P1, P2 и т.д. непосредственно в функцию fun. Передает пустые матрицы заменители в опции, которые в качестве используемых по умолчанию.
- [x,resnorm] = lsqnonlin(...) возвращает значение квадрата нормы невязки от х. sum(fun(x).^2).
- [x,resnorm,residual] = lsqnonlin(...) возвращает значение невязки fun(x), как решение от х.
- [x,resnorm,residual,exitflag] = lsqnonlin(...) возвращает значение exitflag, которое содержит описание выходных условий.
- [x,resnorm,residual,exitflag,output] = lsqnonlin(...) возвращает структурный выход с информацией об оптимизации.
- [x,resnorm,residual,exitflag,output,lambda] = lsqnonlin(...) возвращает структурную lambda с полями, содержащими множители Лагранжа в виде решения от х.
- [x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqnonlin(...) Возвращает Якобиан от fun как решение от х.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в lsqnonlin. Данные подраздел “Аргументы” приводит функционально-специфические детали для fun и options:
|
fun Подлежащая минимизации сумма квадратов. |
fun есть такая функция, которая принимает вектор х и возвращает вектор F, т.е. целевую функция от х. Функция fun может задаваться с помощью описателя функций x = lsqnonlin(@myfun,x0) где myfun есть такая функция MATLAB, чтоfunction F = myfun(x) F = ... % Вычисление функции в точке х fun так же может быть и внутренним объектом. x = lsqnonlin(inline('sin(x.*x)'),x0); Если к тому же может быть рассчитан Якобиан и установленная с помощью options = optimset('Jacobian','on') опция options.Jacobian равна 'on', то функция fun во втором выходном аргументе должна возвращать значение Якобиана J, как матрицы от х. Отметим, что посредством проверки значения nargout данная функция может обойти расчет J в случае когда fun вызывается только с одним выходным аргументом (случай, когда для оптимизационного алгоритма необходимо только значение F, а не J). function [F,J] = myfun(x) |
| options | Опции обеспечивают учет специфических деталей функции виде параметров options. |
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых lsqnonlin аргументов. В этом разделе приводятся общие специфические детали для величин exitflag, lambda, и output:
| exitflag | Описывает выходные условия
|
| lambda | Структура, которая содержит множители Лагранжа при решении по х (разделенном по типам условий). Поле структуры:
|
| output | Структура, которая содержит информацию об оптимизации. Поле структуры:
Примечание. Сумма квадратов должна быть выражена явным образом. Взамен этого, Ваша функция должна возвращать вектор значений функции. Смотри примеры ниже |
Options
Параметры оптимизационных опций. Можно использовать optimset для того, чтобы установить или изменить значения данных полей в структуре параметров опций. Часть параметров используется во всех алгоритмах, некоторые используются только для крупномасштабного алгоритма, а другие применимы только среднемасштабных алгоритмов.
Мы начнем с описания опции LargeScale, поскольку она устанавливает преимущественное право какой алгоритм использовать. Это только преимущественное право, поскольку должны быть выполнены определенные условия для того, что бы можно было использовать крупно-масштабный алгоритм или средне-масштабный алгоритм. Для крупно-масштабного алгортма, поскольку система нелинейных уравнений не может быть недоопределенной, число уравнений (число возвращаемых fun элементов F) должно быть, по крайней мере, длины х. Более того, только крупно-масштабный алгоритм оперирует с граничными ограничениями
| LargeScale | В случае установки 'on' используется, если это возможно, крупно-масштабный алгоритм. Для использования средне-масштабного алгоритма устанавливается 'off'. |
Medium-Scale and Large-Scale Algorithms. Эти параметры используются как для средне-масштабного, так и крупно-масштабного алгоритмов:
| Diagnostics | Проводится печать диагностической информации о минимизируемой функции. |
| Display | Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации. |
| Jacobian | При установке 'on', fsolve использует заданный пользователем Якобиан (определенный в fun), или информацию об Якобиане (при использовании JacobMult) для целевой функции. При установке 'off', fsolve аппроксимирует Якобиан с помощью конечных разностей. |
| MaxFunEvals | Максимально число допустимых расчетов функции. |
| MaxIter | Максимально число допустимых итераций. |
| TolFun | Конечное допустимое отклонение по значению функции |
| TolX | Конечное допустимое отклонение по значению х. |
Large-Scale Algorithm Only. Эти параметры используются только для крупно-масштабного алгоритма:
| JacobMult | Указатель функции для функции множителей Якобиана. В случае крупно-масштабной задачи данная функция вычисляет произведение матриц Якобиана J*Y, J'*Y или J'*(J*Y) без действительного формирования J. Такая функция имеет форму W = jmfun(Jinfo,Y,flag,p1,p2,...), где Jinfo и дополнительные параметры p1,p2,... включают в себя используемые для расчета J*Y (или J'*Y или J'*(J*Y)) матрицы. Первый аргумент Jinfo должен быть таким же, что возвращаемый целевой функцией fun второй аргумент. [F,Jinfo] = fun(x,p1,p2,...) Параметры p1,p2,... есть дополнительные параметры, передаваемые в lsqnonlin (и в fun). lsqnonlin (fun,...,options,p1,p2,...) Y есть матрица с тем же самым числом строк, что и размерность данной задачи. flag определяет какое произведение нужно вычислять. If flag == 0 then W = J'*(J*Y). If flag > 0 then W = J*Y. If flag < 0 then W = J'*Y. В каждом случае J явно не формируется. lsqnonlin использует Jinfo для расчета предварительных данных. Примечание 'Jacobian' должен быть установлен как 'on' для того, чтобы передать Jinfo из fun в jmfun. В качестве примера смотри Нелинейную Оптимизацию с Компактной, но Структурированной Матрицей Гессе и Ограничениями Типа Равенств. |
| JacobPattern | Разреженные шаблоны Якобиана для конечного дифференцирования. В случае, если в fun неразумно вычислять матрицу Якобиана J, то lsqnonlin может аппроксимировать J через заданные разреженные конечные разности и структура J, т.е. расположения не нулей, обеспечиваемую как значения для JacobPattern. В наихудшем случае, когда эта структура неизвестна, можно установить JacobPattern, что бы плотная матрица и полные конечно-разностные аппроксимации вычислялись на каждой итерации (что принимается по умолчанию в случае неустановки JacobPattern). Это может быть чрезвычайно затратным для больших задач, поэтому обычно заслуживает внимания усилие по определению разреженной структуры. |
| MaxPCGIter | Максимальное число PCG (предварительно сопряженный градиент) итераций (Смотри ниже раздел Алгоритм). |
| PrecondBandWidth | Верхняя полоса предварительной обработки для PCG. По умолчанию используется диагональная начальная подготовка (верхняя полоса из 0). Для некоторых задач увеличение полосы снижает число итераций PCG. |
| TolPCG | Конечное допустимое число итераций PCG. |
| TypicalX | Типичные значения х. |
Medium-Scale Algorithm Only. Эти параметры используются только для средне-масштабного алгоритма.
| DerivativeCheck | Сравнение вводимых пользователем производных (Якобиана) с конечноразностными производными. |
| DiffMaxChange | Максимальное изменение в переменных для конечных-разностей. |
| DiffMinChange | Минимальное изменение в переменных для конечных-разностей. |
| LevenbergMarquardt | Выбор алгоритма Левенберга-Макуарда вместо Гаусса-Ньютона. |
| LineSearchType | Выбор алгоритма линейного поиска. |
Примеры:
Найти х, которые минимизируют
![]()
начнем с точки x = [0.3, 0.4].
Поскольку lsqnonlin предполагает, что сумма квадратов явно не формируется в пользовательской функции, то передаваемая в lsqnonlin функция должна взамен этого вычислять векторозначную функцию.
![]()
от ![]() до 10 (то есть, F должен иметь k компонентов).
до 10 (то есть, F должен иметь k компонентов).
Сперва запишем М-файл, который вычисляет к компонентов F
function F = myfun(x)
k = 1:10;
F = 2 + 2*k-exp(k*x(1))-exp(k*x(2));
Далее вызовем подпрограмму оптимизации
x0 = [0.3 0.4] % Начальнон приближение
[x,resnorm] = lsqnonlin(@myfun,x0) % Запускается оптимизатор
После 24 расчетов функции в данном примере решение будет.
x =
0.2578 0.2578
resnorm % невязка или сумма квадратов
resnorm =
124.3622
Алгоритм:
Крупно-масштабная оптимизация. По умолчанию lsqnonlin выберет крупно-масштабный алгоритм. Данный алгоритм является реализацией метода доверительных подпространств и основан на методе внутренних отражений Ньютона, описанного в [1], [2]. Каждая итерация включает в себя приближенное решение крупной линейной системы с помощью метода предварительно сопряженных градиентов(PCG). Смотри Метод Доверительной Области для Нелинейной оптимизации и Предварительно Сопряженных Градиентов в разделе “Крупно-Масштабные Алгоритмы”.
Средне-масштабная оптимизация. lsqnonlin при установке options.LargeScale как 'off' использует метод Левенберга-Макуарда [4], [5], [6] с линейным поиском. В качестве альтернативы может быть выбран метод Гаусса-Ньютона [3] с линейным поиском. Выбор алгоритма проводится при помощи установки опции options.LevenbergMarquardt. Установка options.LevenbergMarquardt как 'off' (и опции options.LargeScale как 'off') выбирается метод Гаусса-Ньютона, который обычно работает быстрее в случае небольшой невязки
![]() .
.
Принимаемый по умолчанию алгоритм линейного поиска, т.е. опция options.LineSearchType установлена как 'quadcubic', обеспечивается методом смешанной квадратичной и кубической полиноминальной интерполяции и экстраполяции. Защищенный кубической полиномиальный метод может быть выбран установкой опции LineSearchType как 'cubicpoly'. В общем, данный метод требует меньшего расчета функций, но большего обращения к расчету градиента. Таким образом, если градиенты приведены и могут быть вычислены без больших затрат, то метод с кубическим полиномиальным линейным поиском является предпочтительным. Используемые алгоритмы полностью описаны в разделе Стандартные Алгоритмы.
Диагностика:
Крупно-масштабная оптимизация. Коды крупно-масштабного метода не допускают равенства верхней и нижней границ. Например, если lb(2) == ub(2), то lsqlin дает ошибку
Равные верхние и нижние границы не допустимы в данном крупно-масштабном методе.
(lsqcurvefit не управляет ограничениями типа равенств, имеется иная возможность формулировки границ в виднее равенств. В случае наличия ограничений типа равенств в качестве альтернативной формулировки используются fmincon, fminimax или fgoalattain, где ограничения типа равенств могут быть включены.)
Ограничения:
Минимизируемая функция должна быть непрерывной. lsqnonlin может давать только локальные решения.
lsqnonlin оперирует только с реальными переменными. Если х имеет комплексные значения, то эти переменные должны быть разделены на мнимую и реальные части.
Крупно-масштабная оптимизация. Крупно-масштабный метод не разрешает недоопределенные системы, он требует, что бы число уравнений, т.е. число строк в F было, по крайней мере, больше, чем число переменных. Взамен этого в недоопределенном случае используется средне-масштабный алгоритм. (Если граничные ограничения все же имеются, то выдается предупреждение и задача решается с игнорированием границ). Относительно большей информации о постановке задачи, области применения и задания исходных данных смотри таблицу 1-4, Область Определения и Требования к Крупно-Масштабным Задачам.
В части предварительно сопряженных градиентов для формирования JTJ крупно-масштабного метода (где J есть матрица Якоби) используется предварительный расчет перед подготовкой данных, поэтому, строки матрицы J с большим числом ненулевых значений могут привести к особенно плотным произведениям JTJ, что, в свою очередь, может привести к усложнению расчетов для больших задач.
Если компоненты х не имеют верхних (или нижних) границ, то lsqnonlin выберет, что соответствующие компоненты ub (или lb) были установлены в бесконечность (или –бесконечность для нижних границ) в противоположность произвольному, но очень большому положительному (или отрицательному для нижних границ) числу.
В настоящее время, если в fun аналитически задан градиент, то для сравнения аналитического градиента с его конечно-разностным значением в крупно-масштабном методе нельзя использовать параметр опции DerivativeCheck. Вместо этого, для контроля производной следует использовать средне-масштабный метод с установкой опционного параметра MaxIter как 0 итераций. Затем запустить задачу с крупно-масштабным методом.
Средне-масштабная оптимизация. Средне-масштабный алгоритм не оперирует с ограничениями в виде границ.
Поскольку крупно-масштабный алгоритм не оперирует с недоопределенными системами, а средне-масштабный алгоритм не оперирует с ограничениями в виде границ, то задачи с такими характеристиками не могут быть разрешены в lsqnonlin.
Смотри также:
@ (function_handle), lsqcurvefit, lsqlin, optimset
Литература:
- Coleman, T.F. and Y. Li, "An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds," SIAM Journal on Optimization, Vol. 6, pp. 418-445, 1996.
- Coleman, T.F. and Y. Li, "On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds," Mathematical Programming, Vol. 67, Number 2, pp. 189-224, 1994.
- Dennis, J.E., Jr., "Nonlinear Least Squares," State of the Art in Numerical Analysis, ed. D. Jacobs, Academic Press, pp. 269-312, 1977.
- Levenberg, K.,"A Method for the Solution of Certain Problems in Least Squares," Quarterly Applied Math. 2, pp. 164-168, 1944.
- Marquardt, D.,"An Algorithm for Least Squares Estimation of Nonlinear Parameters," SIAM Journal Applied Math. Vol. 11, pp. 431-441, 1963.
- More, J.J., "The Levenberg-Marquardt Algorithm: Implementation and Theory," Numerical Analysis, ed. G. A. Watson, Lecture Notes in Mathematics 630, Springer Verlag, pp. 105-116, 1977.
fzero - нахождение нулей функции одной переменно
Синтаксис:
x = fzero(fun,x0)
x = fzero(fun,x0,options)
x = fzero(fun,x0,options,P1,P2,...)
[x,fval] = fzero(...)
[x,fval,exitflag] = fzero(...)
[x,fval,exitflag,output] = fzero(...)
Описание:
x = fzero(fun,x0) Пытается найти ноль для fun вблизи x0, если x0 есть скаляр. Возвращаемое в fzero значение х находится около точки, где fun меняет знак, или NaN в случае неудачи поиска. В этом случае поиск заканчивается, если интервал поиска расширяется до значений бесконечность, NaN или будут найдены комплексные значения.
Если вектор х0 имеет длину два, то fzero полагает, что х0 есть некий интервал, где знак fun(x0(1)) отличается от знака fun(x0(2)). Если это не верно, то будет иметь место ошибка. Вызов fzero с таким интервалом гарантирует, что fzero возвратит значение, где функция fun меняет знак.
Примечание. Вызов fzero с неким интервалом (х0 имеет два элемента) часто решается быстрее, чем его вызов со скаляром х0.
- x = fzero(fun,x0,options) проводит оптимизацию с определенными в структурной опции параметрами оптимизации.
- x = fzero(fun,x0,options,P1,P2,...) задает дополнительные аргументы P1, P2 и т.д., которые передаются в целевую функцию fun. Если опции не установлены, то в качестве заменителя используется options = [].
- [x,fval] = fzero(...) возвращает значение целевой функции fun как решение от х.
- [x,fval,exitflag] = fzero(...)возвращает значение exitflag, которое содержит описание выходных условий.
- [x,fval,exitflag,output] = fzero(...) возвращает структурный выход с информацией об оптимизации.
Примечание Для данных целей в приведенной программе нули рассматриваются как точки, где функция действительно пересекает, а не касается, оси х.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в fzero. Данный подраздел приводит функционально-специфические детали для fun и options:
|
fun Функция, для которой находится ноль. |
fun есть такая функция, которая принимает вектор х и возвращает скаляр f, целевая функция от х. Функция fun может задаваться с помощью описателя функций x = fzero(@myfun,x0) где myfun есть такая функция MATLAB, что function f = myfun(x) f = ... % Расчет значений функции от x fun так же может быть внутренним объектом. x = fzero(inline('sin(x*x)'),x0); |
| options | Опции оптимизации. Можно установить или изменить значения этих параметров при помощи optimset. fzero использует следующее поле структур для опций:
|
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых fzero аргументов. В этом разделе приводятся общие специфические детали для величин exitflag и output:
| exitflag | Описывает выходные условия.
|
| output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Примеры:
Найти значение нуля функции sin в точке вблизи 3
x = fzero(@sin,3)
x =
3.1416
Найти значение нуля функции cos между 1 и 2
x = fzero(@cos,[1 2])
x =
1.5708
Отметим, что cos(1) и cos(2) отличаются по знаку.
Найти ноль для функции
![]() ;
;
запишем М-файл под именем f.m.
function y = f(x)
y = x.^3-2*x-5;
Найти ноль вблизи точки 2
z = fzero(@f,2)
z =
2.0946
Поскольку данная функция является полиноминальной, то основные корни ([1 0 -2 -5]) определяют один и тот же реальный ноль, а так же будет еще комплексно сопряженная паря нулей:
2.0946
-1.0473 + 1.1359i
-1.0473 - 1.1359i
Алгоритм:
Команда fzero использует М-файл. Первоначально предложенный Деккером алгоритм основан на комбинации методов двоичного поиска, метода секущих и обратной квадратичной интерполяции. Версия на Алголе-60 (с некоторыми улучшениями) приведена в [1]. Версия на Фортране, что оставляет основу М-файла для fzero, приведена в [2].
Ограничения:
Коканда fzero определяет точку, где функция меняет знак. Если функция непрерывная, то это так же точка, где данная функция имеет близкое к нулю значение. Если функция не является непрерывной, то fzero может вместо нулей возвращать значения, которые являются разрывными точками. Например, fzero(@tan,1) возвращает 1.5708, что является точкой разрыва для тангенса.
Более того, команда fzero определяет ноль как точку, функция пересекает ось х. Точки, где функция касается, но не пересекает, оси х, не являются достоверными нулями. Например, y = x.^2 есть парабола, которая касается оси х в точке 0. Однако, поскольку функция нигде не пересекает ось х, то нулей не будет найдено. В случае функций без достоверных нулей, fzero работает до тех пор, пока не встретятся Inf, NaN или комплексное значение.
Смотри так же:
@ (function_handle), \, fminbnd, fsolve, inline, optimset, roots
Литература:
- [1] Brent, R., Algorithms for Minimization Without Derivatives, Prentice-Hall, 1973.
- [2] Forsythe, G. E., M. A. Malcolm, and C. B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1976.
fsolve – решение системы нелинейных уравнений
![]()
для x, где x есть вектор и F(x) есть такая функция, которая возвращает значение вектора.
Синтаксис:
x = fsolve(fun,x0)
x = fsolve(fun,x0,options)
x = fsolve(fun,x0,options,P1,P2, ... )
[x,fval] = fsolve(...)
[x,fval,exitflag] = fsolve(...)
[x,fval,exitflag,output] = fsolve(...)
[x,fval,exitflag,output,jacobian] = fsolve(...)
Описание:
fsolve находит корни (нули) системы нелинейных уравнений.
- x = fsolve(fun,x0) начинает с точки x0 и пытается решить описанные в fun уравнения.
- x = fsolve(fun,x0,options) проводит оптимизацию с определенными в структурной опции параметрами оптимизации.
- x = fsolve(fun,x0,options,P1,P2,...) передает зависящие от типа задачи параметры P1, P2 и т.д. непосредственно в функции fun. Передает пустые матрицы для опций для того, что бы использовать принимаемые по умолчанию значения опций.
- [x,fval] = fsolve(fun,x0) возвращает значение целевой функции fun как решение от х.
- [x,fval,exitflag] = fsolve(...) возвращает значение exitflag, которое содержит описание выходных условий.
- [x,fval,exitflag,output] = fsolve(...) возвращает структурный выход с информацией об оптимизации
- [x,fval,exitflag,output,jacobian] = fsolve(...) возвращает Якобиан от fun как решение от x.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в fsolve. Данный подраздел приводит функционально-специфические детали для fun и options:
|
fun Подлежащая решению система уравнений. |
fun есть такая функция, которая принимает вектор х и возвращает вектор F, нелинейные уравнения х. Функция fun может задаваться с помощью описателя функций x = fsolve(@myfun,x0) где myfun есть такая функция MATLAB, что function F = myfun(x) F = ... % Расчет значений функции от x fun так же может быть внутренним объектом. x = fsolve(inline('sin(x.*x)'),x0); Если к тому же может быть рассчитан Якобиан и установленная с помощью options = optimset('Jacobian','on') опция options.Jacobian равна 'on', то функция fun во втором выходном аргументе должна возвращать значение Якобиана J, как матрицы от х.Отметим, что посредством проверки значения nargout данная функция может обойти расчет J в случае, когда fun вызывается только с одним выходным аргументом (это случай, когда для оптимизационного алгоритма необходимо только значение F, а не J). function [F,J] = myfun(x) |
| options | Опции обеспечивают учет специфических деталей функции виде параметров options. |
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых fsolve. аргументов. В этом разделе приводятся общие специфические детали для величин exitflag и output:
| exitflag | Описывает выходные условия.
|
| output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Для крупно-масштабной или большой размерности задачи оптимальность первого порядка есть бесконечная норма градиента g = JTF (смотри нелинейный среднеквадратичный метод)
Options
Параметры оптимизационных опций, используемых в fsolve. Часть параметров используется ко всем алгоритмам, некоторые используются только для крупномасштабного алгоритма, а другие применимы только среднемасштабных алгоритмов. Можно использовать optimset для того, чтобы установить или изменить значения данных полей в структуре параметров опций.
Для детальной информации смотри Таблицу 4-3, Параметры Опций Оптимизации.
Мы начнем с описания опции LargeScale, поскольку она устанавливает преимущественное право какой алгоритм использовать. Это только преимущественное право, поскольку должны быть выполнены определенные условия для того, что бы можно было использовать крупно-масштабный алгоритм. Для fsolve, поскольку система нелинейных уравнений не может быть недоопределенной, число уравнений (или иначе число возвращаемых fun элементов F) должно быть, по крайней мере, длины х или в противном следует использоваться средне-масштабный алгоритм.
LargeScale В случае установки 'on' используется, если это возможно, крупно-масштабный алгоритм. Для использования средне-масштабного алгоритма устанавливается значение 'off'.
Medium-Scale и Large-Scale Algorithms. Эти параметры используются как для средне-масштабного, так и крупно-масштабного алгоритмов:
| Diagnostics | Проводится печать диагностической информации о минимизируемой функции. |
| Display | Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации. |
| Jacobian | При установке 'on', fsolve использует заданный пользователем Якобиан (определенный в fun), или информацию об Якобиане (при использовании JacobMult) для целевой функции. При установке 'off', fsolve аппроксимирует Якобиан с помощью конечных разностей. |
| MaxFunEvals | Максимально число допустимых расчетов функции. |
| MaxIter | Максимальное число допустимых итераций. |
| TolFun | Конечное допустимое отклонение по значению функции. |
| TolX | Конечное допустимое отклонение по значению х. |
Large-Scale Algorithm Only. Эти параметры используются только для крупно-масштабного алгоритма
| JacobMult | Указатель функции для функции множителей Якобиана. В случае крупно-масштабной задачи данная функция вычисляет произведение матриц Якобиана J*Y, J'*Y или J'*(J*Y) без действительного формирования J. Такая функция имеет форму W = jmfun(Jinfo,Y,flag,p1,p2,...), где Jinfo и дополнительные параметры p1,p2,... включают в себя используемые для расчета J*Y (или J'*Y или J'*(J*Y)) матрицы. Первый аргумент Jinfo должен быть таким же, как и возвращаемый целевой функцией fun второй аргумент.[F,Jinfo] = fun(x,p1,p2,...) Переменные p1,p2,... есть дополнительные параметры, передаваемые в fsolve (и в fun).fsolve (fun,...,options,p1,p2,...) Y есть матрица с тем же самым числом строк, что и размерность данной задачи.flag определяет какое произведение нужно вычислять. If flag == 0 then W = J'*(J*Y). If flag > 0 then W = J*Y. If flag < 0 then W = J'*Y.
В качестве примера смотри Нелинейную Оптимизацию с Компактной, но Структурированной Матрицей Гессе и Ограничениями Типа Равенств. |
|
| JacobPattern | Разреженные шаблоны Якобиана для конечного дифференцирования. В случае, если в fun неразумно вычислять матрицу Якобиана J, то lsqnonlin может аппроксимировать J через заданные разреженные конечные разности и структура J -- т.е. расположение не нулей – обеспечиваются как значения для JacobPattern. В наихудшем случае, когда эта структура неизвестна, можно установить JacobPattern, что бы плотная матрица и полные конечно-разностные аппроксимации вычислялись на каждой итерации (что принимается по умолчанию в случае неустановки JacobPattern). Это может быть чрезвычайно затратным для больших задач, поэтому обычно заслуживает внимания усилие по определению разреженной структуры. | |
| MaxPCGIter | Максимальное число PCG (предварительно сопряженный градиент) итераций (Смотри ниже раздел Алгоритм). | |
| PrecondBandWidth | Верхняя полоса предварительной обработки для PCG. По умолчанию используется диагональная начальная подготовка (верхняя полоса из 0). Для некоторых задач увеличение полосы снижает число итераций PCG. | |
| TolPCG | Конечное допустимое число итераций PCG. | |
| TypicalX | Типичные значения х. |
Medium-Scale Algorithm Only. Эти параметры используются только для средне-масштабного алгоритма.
| DerivativeCheck | Сравнение вводимых пользователем производных (Якобиана) с конечноразностными производными. |
| DiffMaxChange | Максимальное изменение в переменных для конечных-разностей. |
| DiffMinChange | Минимальное изменение в переменных для конечных-разностей. |
| LevenbergMarquardt | Выбор алгоритма Левенберга-Макуарда вместо Гаусса-Ньютона. |
| LineSearchType | Выбор алгоритма линейного поиска. |
Примеры:
Пример 1. В данном примере находятся нули для системы из двух уравнений и двух неизвестных
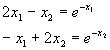
Таким образом, необходимо решить следующую систему уравнений от х
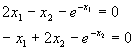
Начнем с точки x0 = [-5 -5].
Сперва запишем М-файл для расчета F или значений уравнений от х
function F = myfun(x)
F = [2*x(1) - x(2) - exp(-x(1));
-x(1) + 2*x(2) - exp(-x(2))];
Далее вызовем подпрограмму оптимизации
x0 = [-5; -5]; % примем начальное приближение за решение
options=optimset('Display','iter'); %Опция выходного отображения
[x,fval] = fsolve(@myfun,x0,options) % вызов оптимизатора
после 28 обращений к функциям нули будут найдены.
| Итерация | Func-расчет | f(x) | Норма шага | Оптимальность первого порядка | CG- итерации |
| 1 | 4 | 47071.2 | 1 | 2.29e+004 | 0 |
| 2 | 7 | 6527.47 | 1.45207 | 3.09e+003 | 1 |
| 3 | 10 | 918.372 | 1.49186 | 418 | 1 |
| 4 | 13 | 127.74 | 1.55326 | 57.3 | 1 |
| 5 | 16 | 14.9153 | 1.57591 | 8.26 | 1 |
| 6 | 19 | 0.779051 | 1.27662 | 1.14 | 1 |
| 7 | 22 | 0.00372453 | 0.484658 | 0.0683 | 1 |
| 8 | 25 | 9.21617e-008 | 0.0385552 | 0.000336 | 1 |
| 9 | 28 | 5.66133e-017 | 0.000193707 | 8.34e-009 | 1 |
Оптимизация завершена успешно:
Относительное изменение значений функции меньше, чем в OPTIONS.TolFun
x =
0.5671
0.5671
fval =
1.0e-008 *
-0.5320
-0.5320
Оптимизация завершена успешно:
Относительное изменение значений функции меньше, чем в OPTIONS.TolFun
x =
0.5671
0.5671
fval =
1.0e-08 *
-0.5320
-0.5320
Пример 2. Найти матрицу x, которая удовлетворяет уравнению
![]()
начнем с точки x= [1,1; 1,1].
Сперва запишем М-файл, необходимый для расчета решаемых уравнений.
function F = myfun(x)
F = x*x*x-[1,2;3,4];
Далее запустим подпрограмму оптимизации
x0 = ones(2,2); % примем начальное приближение за решение
options = optimset('Display','off'); % Выключим отображение
[x,Fval,exitflag] = fsolve(@myfun,x0,options)
Решение будет
x =
-0.1291 0.8602
1.2903 1.1612
Fval =
1.0e-03 *
0.1541 -0.1163
0.0109 -0.0243
exitflag =
1
и остаток будет близок к нулю.
sum(sum(Fval.*Fval))
ans =
3.7974e-008
Примечания:
Если система уравнений является линейной, то для ускорения и повышения точности следует использовать \ (оператор обратный слэш – смотри help slash). Например. Необходимо решить следующую систему линейных уравнений
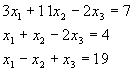
Данная задача формулируется и решается как
A = [ 3 11 -2; 1 1 -2; 1 -1 1];
b = [ 7; 4; 19];
x = A\b
x =
13.2188
-2.3438
3.4375
Алгоритм:
Данный метод основан на алгоритме метода нелинейных среднеквадратичных отклонений, используемого в lsqnonlin. Достоинство используемого метода среднеквадратичных отклонений состоит в том, что данная система уравнений не равна нулю вследствие малых погрешностей и потому, что она как раз не имеет нулей, кстати алгоритм приходит в точку с малым остатком. Однако, если Якобиан системы является вырожденным, то алгоритм может сходиться в точку, неявляющуюся решением системы уравнений (Смотри ниже Ограничения и Диагностика).
Крупно-масштабная оптимизация. По умолчанию fsolve выберет крупно-масштабный алгоритм. Данный алгоритм является реализацией метода доверительных подпространств и основан на методе внутренних отражений Ньютона, описанного в [1], [2]. Каждая итерация включает в себя приближенное решение крупной линейной системы с помощью метода предварительно сопряженных градиентов(PCG). Смотри описания доверительной области и метода предварительно сопряженных градиентов в разделе “Крупно-Масштабные Алгоритмы”.
Средне-масштабная оптимизация. fsolve при установке options.LargeScale как 'off' использует метод Гаусса-Ньютона [3] с линейным поиском. В качестве альтернативы может быть выбран метод Левенберга-Макуарда [4], [5], [6] с линейным поиском. Выбор алгоритма проводится при помощи установки опции options.LevenbergMarquardt. Установка options.LevenbergMarquardt как 'on' (и опции options.LargeScale как 'off') выбирается метод Левенберга-Макуарда.
Принимаемый по умолчанию алгоритм линейного поиска, т.е. опция options.LineSearchType установлена как 'quadcubic', обеспечивается методом смешанной квадратичной и кубической полиноминальной интерполяции и экстраполяции. Защищенный кубической полиномиальный метод может быть выбран установкой опции LineSearchType как 'cubicpoly'. В общем, данный метод требует меньшего расчета функций, но большего обращения к расчету градиента. Таким образом, если градиенты приведены и могут быть вычислены без больших затрат, то метод с кубическим полиномиальным линейным поиском является предпочтительным. Используемые алгоритмы полностью описаны в разделе Стандартные Алгоритмы.
Диагностика:
fsolve может сходиться к ненулевой точке и давать следующие сообщения:
Оптимизатор затормозился в точке, которая не является минимумом.
Повторите расчет с новой начальной точки.
В этом случае снова выполните fsolve но с другой начальной точки.
Ограничения:
Разрешаемая функция должна быть непрерывной. В случае успеха fsolve дает только один корень. fsolve может сходиться к ненулевой точке, то в этом случае необходимо пытаться стартовать с другой точки.
fsolve оперирует только с реальными переменными. Если х имеет комплексные значения, то эти переменные должны быть разделены на мнимую и реальные части.
Крупно-масштабная оптимизация. В настоящее время, если Якобиан задан аналитически в fun, то параметр опции DerivativeCheck нельзя использовать в крупно-масштабном методе для проведения сравнения аналитического Якобиана с конечно-разностным Якобианом. Вместо этого, для контроля производных используется средне-масштабный метод при установке опции MaxIter как 0 итераций. Далее, задача запускается снова уже с крупно-масштабным методом. Смотри Таблицу 1-4, Область Определения и Требования к Крупо-Масштабным Задачам относительно формулировки задачи и требуемой информации.
В части предварительно сопряженных градиентов для формирования JTJ крупно-масштабного метода (где J есть матрица Якоби) используется предварительный расчет перед подготовкой данных, поэтому, строки матрицы J с большим числом ненулевых значений могут привести к особенно плотным произведениям JTJ, что, в свою очередь, может привести к усложнению расчетов для больших задач.
Смотри также:
inline, lsqcurvefit, lsqnonlin, optimset
Литература:
- [1] Coleman, T.F. and Y. Li, "An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds," SIAM Journal on Optimization, Vol. 6, pp. 418-445, 1996.
- [2] Coleman, T.F. and Y. Li, "On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds," Mathematical Programming, Vol. 67, Number 2, pp. 189-224, 1994.
- [3] Dennis, J. E. Jr., "Nonlinear Least Squares," State of the Art in Numerical Analysis, ed. D. Jacobs, Academic Press, pp. 269-312.
- [4] Levenberg, K., "A Method for the Solution of Certain Problems in Least Squares," Quarterly Applied Mathematics 2, pp. 164-168, 1944.
- [5] Marquardt, D., "An Algorithm for Least-squares Estimation of Nonlinear Parameters," SIAM Journal Applied Mathematics, Vol. 11, pp. 431-441, 1963.
- [6] More, J. J., "The Levenberg-Marquardt Algorithm: Implementation and Theory," Numerical Analysis, ed. G. A.
- Watson, Lecture Notes in Mathematics 630, Springer Verlag, pp. 105-116, 1977.
linprog – решение задачи линейного программировани
![]() такие, что
такие, что 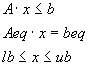
где f, x, b, beq, lb и ub есть векторы и A и Aeq есть матрицы.
Синтаксис:
x = linprog(f,A,b,Aeq,beq)
x = linprog(f,A,b,Aeq,beq,lb,ub)
x = linprog(f,A,b,Aeq,beq,lb,ub,x0)
x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options)
[x,fval] = linprog(...)
[x,fval,exitflag] = linprog(...)
[x,fval,exitflag,output] = linprog(...)
[x,fval,exitflag,output,lambda] = linprog(...)
Описание:
Linprog решает задачу линейного программирования.
- x = linprog(f,A,b) находит min f'*x при условии, что A*x <= b.
- x = linprog(f,A,b,Aeq,beq) решает указанные выше задачу при условии дополнительного выполнения ограничений в виде равенств Aeq*x = beq. Если нет неравенств, то устанавливается A=[] и b=[].
- x = linprog(f,A,b,Aeq,beq,lb,ub) определяет набор нижних и верхних границ для проектируемых переменных х, так что решение всегда находится в диапазоне lb <= x <= ub. Если нет неравенств, то устанавливается Aeq=[] и beq=[].
- x = linprog(f,A,b,Aeq,beq,lb,ub,x0) устанавливает начальную точку как х0. Эта опция имеет место только для средне-масштабного алгоритма (options.LargeScale равна 'off'). Принимаемый по умолчанию крупно-масштабный алгоритм игнорирует любую стартовую точку.
- x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options) проводит оптимизацию с определенными в структурной опции параметрами оптимизации.
- [x,fval] = linprog(...) возвращает значение целевой функции fun как решение от х: fval = f'*x.
- [x,lambda,exitflag] = linprog(...) возвращает значение exitflag, которое содержит описание выходных условий.
- [x,lambda,exitflag,output] = linprog(...) возвращает структурный выход с информацией об оптимизации
- [x,fval,exitflag,output,lambda] = linprog(...) Возвращает структурную lambda, чьи поля включают в себя множители Лагранжа как решение от х.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в linprog. Данный подраздел приводит функционально-специфические детали для параметров options
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых linprog аргументов. В этом разделе приводятся общие специфические детали для величин exitflag, lambda и output:
| exitflag | Описывает выходные условия.
|
| lambda | Структура, которая содержит множители Лагранжа при решении по х (разделенном по типам условий). Поле структуры:
|
| output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Options:
Параметры оптимизационных опций, используемых в linprog. Часть параметров используется ко всем алгоритмам, некоторые используются только для крупномасштабного алгоритма, а другие применимы только среднемасштабных алгоритмов. Можно использовать optimset для того, чтобы установить или изменить значения данных полей в структуре параметров опций. Для детальной информации смотри Таблицу 4-3, Параметры Опций Оптимизации
LargeScale В случае установки 'on' используется крупно-масштабный, если это возможно, алгоритм. Для использования средне-масштабного алгоритма устанавливается 'off'.
Medium-Scale и Large-Scale Algorithms. Эти параметры используются как для средне-масштабного, так и крупно-масштабного алгоритмов.
| Diagnostics | Проводится печать диагностической информации о минимизируемой функции. |
| Display | Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации. В настоящее время уровень 'iter' используется только для крупно-масштабного алгоритма. |
| MaxIter | Максимальное число допустимых итераций |
Large-Scale Algorithm Only. Эти параметры используются только для крупно-масштабного алгоритма:
| TolFun | Конечное допустимое отклонение по значению функции |
Примеры:
Найти такое х, что является минимумом от
![]()
при условии, что
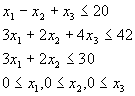
Сперва введем коэффициенты
f = [-5; -4; -6]
A = [1 -1 1
3 2 4
3 2 0];
b = [20; 42; 30];
lb = zeros(3,1);
Далее обратимся к программе линейного программирования
[x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb);
Вводя x, lambda.ineqlin и lambda.lower получим
x =
0.0000
15.0000
3.0000
lambda.ineqlin =
0
1.5000
0.5000
lambda.lower =
1.0000
0
0
Ненулевые элементы векторов в полях lambda указывают на активные ограничения при решении. В нашем случае, второе и третье ограничения в виде неравенств (в lambda.ineqlin) и первое нижнее граничное ограничение (в lambda.lower) являются активными ограничениями (т.е. решение находится на ограничительных условиях).
Алгоритм:
Крупно-масштабная оптимизация. Крупно-масштабный метод основан на LIPSOL (Линейное Решение для Внутренней Точки, [3]), которое является вариантом алгоритма предиктор-корректор Меротра ([2]), метод одновременного решения прямой и двойственной задач с внутренней точкой. Перед тем, как алгоритм начнет итерации, выполняется ряд подготовительных шагов. Смотри Крупно-Масштабное Линейное Программирование.
Средне-масштабная оптимизация. Linprog использует основанный на алгоритме квадратичного программирования метод проекций. linprog имеет активный набор методов и, таким образом, является вариантом хорошо известного симплексного метода для линейного программирования [1]. Он находит начальное допустимое решение путем первоначального решения задачи линейного программирования.
Диагностика:
Крупно-масштабная оптимизация. На первой стадии алгоритм может включать некоторую предподготовку ограничений (смотри Крупно-Масштабное Линейное Программирование в разделе “Крупно-Масштабный Алгоритм”). При этом может иметь место несколько ситуаций, когда linprog выдает сообщения о недопустимости. В каждом случае возвращаемый в linprog аргумент exitflag устанавливается в отрицательное значение, что указывает на ошибку.
Если в строке Aeq определены все нули, а соответствующий элемент beq не равен нулю, то выходное сообщение будет
Если для одного из элементов х обнаружено, что он не ограничен снизу, то выходное сообщение будет
Если одна из строк Aeq имеет только один ненулевой элемент, то присваиваемое значение для х вызывается как одноэлементное значение. В этом случае значение данной компоненты х может быть вычислено из Aeq и beq. Если вычисленное значение противоречит другому ограничивающему условию, то выходное сообщение будет
Если одноэлементная переменная может быть найдена, но решение противоречит верхней и нижней границам, то выходное сообщение будет
| Примечание. Предпроцессорные шаги являются интегральными. Например, хотя если матрица ограничивающих условий не содержит строки полностью из нулей, то прежде всего, другие предпроцессорные шаги могут получить данную ситуацию. |
Сразу после окончания предпроцессорной подготовки начинает работать итеративный раздел алгоритма до тех пор, пока не встретится какой-нибудь критерий останова. (Относительно большей информации о невязках, двойственной проблеме и связанных критериях останова смотри Крупно-Масштабное Линейное Программирование в разделе “Крупно-Масштабный Алгоритм”). Если невязки растут, вместо того, что бы становиться меньше, или невязки ни растут, ни сжимаются, то, соответственно, проявляется одно из следующих завершающих сообщений.
или
После отображения одного из этих посланий, следует одно из шести сообщений, указывающих, что это является результатом недопустимости двойственной, прямой или обеих задач сразу. Это сообщения различается в зависимости от того, как были обнаружены недопустимость или отсутствие границ.
Отметим что, например, прямая (целевая функция) может быть неограниченной, а невязка прямой, что определяется по выполнению ограничений прямой задачи, может быть небольшой.
Средне-масштабная оптимизация. Если задача является недопустимой, то linprog дает предупреждение
В данном случае linprog дает результат, который является минимумом наиболее худшего нарушения ограничений.
Когда ограничения типа равенств являются противоречивыми, linprog дает
Решения без ограничений привели к предупреждению.
В этом случае linprog возвращает значение х, которое удовлетворяет условиям ограничения
Ограничения:
Средне-масштабная оптимизация. К настоящему времени имеются только уровни отображения 'off' и 'final', по применению параметров отображения, итерационный выход по 'iter' не установлен.
Смотри также:
Литература:
- [1] Dantzig, G.B., A. Orden, and P. Wolfe, "Generalized Simplex Method for Minimizing a Linear from Under Linear Inequality Constraints," Pacific Journal Math. Vol. 5, pp. 183-195.
- [2] Mehrotra, S., "On the Implementation of a Primal-Dual Interior Point Method," SIAM Journal on Optimization, Vol. 2, pp. 575-601, 1992.
- [3] Zhang, Y., "Solving Large-Scale Linear Programs by Interior-Point Methods Under the MATLAB Environment,"
- Technical Report TR96-01, Department of Mathematics and Statistics, University of Maryland, Baltimore County, Baltimore, MD, July 1995.
quadprog – решить квадратичную задачу математического программировани
![]() , такую что
, такую что 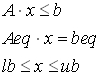
где H, A и Aeq есть матрицы, а f, b, beq, lb, ub и x есть векторы.
Синтаксис
x = quadprog(H,f,A,b)
x = quadprog(H,f,A,b,Aeq,beq)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options,p1,p2,...)
[x,fval] = quadprog(...)
[x,fval,exitflag] = quadprog(...)
[x,fval,exitflag,output] = quadprog(...)
[x,fval,exitflag,output,lambda] = quadprog(...)
Описание
- x = quadprog(H,f,A,b) возвращает вектор х, который минимизирует 1/2*x'*H*x + f'*x при условии A*x <= b.
- x = quadprog(H,f,A,b,Aeq,beq) решает указанную выше задачу с дополнительным выполнением ограничений типа равенства Aeq*x = beq.
- x = quadprog(H,f,A,b,Aeq,beq,lb,ub) определяет набор нижних и верхних границ для проектируемой переменной х, так что бы решение находилось в диапазоне lb <= x <= ub.
- x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0) устанавливает стартовую точку как x0.
- x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options) ) проводит оптимизацию с определенными в структурной опции параметрами оптимизации.
- x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options,p1,p2,...) передает параметры p1,p2,... в функцию множителей матрицы Гессе, определенную с помощью, если он имеется, параметра HessMult в данной структуре опций.
- [x,fval] = quadprog(...) возвращает значение целевой функции от х. fval = 0.5*x'*H*x + f'*x.
- [x,fval,exitflag] = quadprog(...) возвращает значение exitflag, который описывает выходные условия в quadprog.
- [x,fval,exitflag,output] = quadprog(...) возвращает структурный выход с информацией об оптимизации.
- [x,fval,exitflag,output,lambda] = quadprog(...) возвращает структурную lambda с полями, содержащими множители Лагранжа в виде решения от х.
Аргументы:
Входные аргументы.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в quadprog. Options задает функционально-специфические детали для параметров опций.
Выходные аргументы.
Таблица 4-2. “Выходные аргументы” содержат общее описание возвращаемых quadprog аргументов. В этом разделе приводятся общие специфические детали для величин exitflag, lambda и output:
| Eitflag | Описывает выходные условия.
|
| Lamda | Структура, которая содержит множители Лагранжа при решении по х (разделенном по типам aсловий). Поле структуры:
|
| Output | Структура, которая содержит информацию об оптимизации. Поле структуры:
|
Options
Параметры оптимизационных опций. Можно использовать optimset для того, чтобы установить или изменить значения данных полей в структуре параметров опций. Часть параметров используется ко всем алгоритмам, некоторые используются только для крупномасштабного алгоритма, а другие применимы только среднемасштабных алгоритмов.
Параметры для установки алгоритмического предпочтения
| LargeScale | В случае установки 'on' используется, если это возможно, крупно-масштабный алгоритм. Для использования средне-масштабного алгоритма устанавливается 'off'. '’on' более предпочтителен. Если в задаче имеются только верхние и нижние границы, т.е. отсутствуют линейные равенства и неравенства, то по умолчанию принимается крупно-масштабный алгоритм. Или, если в задаче для quadprog заданы только линейные равенства, т.е. верхней и нижней границ и не специфицированы линейные неравенства, а число равенств не больше, чем длина х, то по умолчанию данный алгоритм использует крупно-масштабный алгоритм. В противном, используется средне-масштабный алгоритм. |
Medium-Scale and Large-Scale Algorithms. Эти параметры используются как для средне-масштабного, так и крупно-масштабного алгоритмов:
| Diagnostics | Проводится печать диагностической информации о минимизируемой функции. |
| Display | Уровень отображения. 'off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации. |
| MaxIter | Максимально число допустимых итераций. |
Large-Scale Algorithm Only. Эти параметры используются только для крупно-масштабного алгоритма:
| HessMult | Указатель функции для функции множителей матрицы Гессе. В случае крупно-масштабной задачи данная функция вычисляет произведение матриц Гессе H*Y без действительного формирования H. Такая функция имеет форму W = hmfun(Hinfo,Y,p1,p2,...) где Hinfo и дополнительные параметры p1,p2,... включают в себя используемые для расчета H*Y матрицы. Hinfo должно быть таким же, что и первый аргумент в quadprog, а p1,p2,... есть те же дополнительные параметры, что передаются в quadprog.quadprog(Hinfo,...,options,... quadprog использует Hinfo для расчета предварительных данных. В качестве примера смотри Квадратичную Оптимизацию с Компактной, но Структурированной Матрицей Гессе. |
| MaxPCGIter | Максимальное число PCG (предварительно сопряженный градиент) итераций (Смотри ниже раздел Алгоритм). |
| PrecondBandWidth | Верхняя полоса предварительной обработки для PCG. По умолчанию используется диагональная начальная подготовка (верхняя полоса из 0). Для некоторых задач увеличение полосы снижает число итераций PCG. |
| TolFun | Конечная допустимая точность значения функции. TolFun используется в качестве выходного критерия для задач с простыми верхними и нижними границами (lb, ub). |
| TolPCG | Конечное допустимое число итераций PCG. TolPCG используется в качестве выходного критерия для задач, когда имеются только ограничения виде равенств (Aeq, beq). |
| TolX | Конечное допустимое отклонение по значению х. |
| TypicalX | Типичные значения х. |
Примеры:
Найти значения х, которые минимизируют
![]()
при условии, что
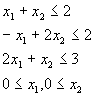
Сперва отметим, что данная в матичной записи будет как
![]()
где
![]() ,
, ![]() ,
, 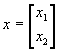
Введем эти коэффициенты матриц
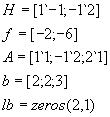
Далее запустим программу квадратичного программирования.
![]()
Что генерирует решение
x =
0.6667
1.3333
fval =
-8.2222
exitflag =
1
output =
iterations: 3
algorithm: 'medium-scale: active-set'
firstorderopt: []
cgiterations: []
lambda.ineqlin
ans =
3.1111
0.4444
0
lambda.lower
ans =
0
0
Ненулевые элементы вектора в полях lambda указывают на активные ограничения в данной задаче. В данном случае, первый и второй ограничения в виде неравенств (lambda.ineqlin) являются активными ограничениями (т.е. решение находится в пределах таких границ). Для данной задачи, все нижние границы являются неактивными.
Примечания:
В общем quadprog определяет локальное решение, хотя задача является строго выпуклой.
Вероятно, более лучшие численные результаты будут, если с помощью Aeq и beq явно специфицировать данные равенства вместо неявного использования lb и ub.
Если компоненты х не имеют верхних (или нижних границ), то quadprog выберет, соответствующие компоненты ub (или lb) будут установлены как Inf (бесконечность) (или -Inf для lb) в отличие от произвольного, но очень большого положительного (или отрицательного в случае нижних границ) числа.
Крупно-масштабная оптимизация. Если х0 не задано или х0 не является строго допустимым, то quadprog выберет новую строго допустимую (центрированную) стартовую точку
Если поставлена задача с ограничениями типа равенств и quadprog выявит отрицательную кривизну, то оптимизация заканчивается потому, что ограничения не достаточно выделяют область. В данном случае, exitflag возвратит значение -1, отобразится сообщение (даже не смотря на то, параметр отображения установлен как 'off'), а возвращаемый х не будет решением, а направлением отрицательной кривизны по отношению к H.
Для задач с просто нижними и верхними границами (lb, ub), quadprog выходит на основе значения TolFun. Для задач только с ограничениями типа равенств (Aeq, beq), то выход на основе TolPCG. Корректировка TolFun и TolPCG влияет на выходные результаты. TolX используется в обоих типах задач.
Алгоритм:
Крупно-масштабная оптимизация. В случае если приведенная в lsqlin имеет только верхние и нижние границы, т.е. не определены линейные неравенства или равенства, то по умолчанию принимается крупно-масштабный алгоритм. Или, если приведенная в quadprog задача имеет только линейные равенства, т.е. не специфицированы ни верхние и нижние границы, ни линейные неравенства, то по умолчанию принимается крупно-масштабный алгоритм.
Данный алгоритм является реализацией метода доверительных подпространств и основан на методе внутренних отражений Ньютона, описанного в [1]. Каждая итерация включает в себя приближенное решение крупной линейной системы с помощью метода предварительно сопряженных градиентов(PCG). Смотри Метод Доверительной Области для Нелинейной Оптимизации и Метода Предварительно Сопряженных Градиентов в разделе “Крупно-Масштабные Алгоритмы”.
Средне-масштабная оптимизация. lsqlin при установке options. quadprog использует метод активной системы, который также является проекционным методом, аналогично тому, что описано в [2]. Этот метод находит начальные решения путем решения задачи линейного программирования. Данный метод так же обсуждается в разделе Стандартные Алгоритмы.
Диагностика:
Крупно-масштабная оптимизация. Коды крупно-масштабного метода не допускают равенства верхней и нижней границ. Например, если lb(2) == ub(2), то lsqlin дает ошибку
Равные верхние и нижние границы не допустимы в данном крупно-масштабном методе.
Взамен этого используются ограничения типа равенств и средне-масштабный метод.
Если имеются только ограничения типа равенств, то еще можно использовать крупно-масштабный метод. Но если совместно есть, как равенства, так и границы, то необходимо использовать средне-масштабный метод.
Средне-масштабная оптимизация. Если решение является недопустимым, то quadprog дает предупреждение
Предупреждение. Ограничения являются слишком жесткими.
Нет допустимого решения
В этом случае quadprog проводит минимизацию для ограничения с наибольшим нарушением
Когда ограничения типа равенств являются противоречащими, то quadprog дает предупреждение
Предупреждение. Ограничения являются слишком жесткими.
Нет допустимого решения
Решения без ограничений, что может быть когда матрица Гессе является отрицательной полуопределенностью, могут привести к
Предупреждение. Решение не ограничено и бесконечно
Ограничения не являются достаточно жесткими.
В данном случае quadprog возвращает значение х, которое удовлетворяет данным ограничениям.
Ограничения:
К настоящему времени имеются только уровни отображения, при использовании опции параметров Отображения, 'off' и 'final'; итерационный вывод с опцией 'iter' отсутствует.
Решение для задач с бесконечностью или отрицательной бесконечностью часто является задачей без ограничений (в данном случае exitflag возвращается с отрицательным значением, что отмечает, что минимум не найден), а когда конечное решение все же существует, то quadprog может давать только локальный минимум, поскольку такая задача может быть невыпуклой.
Крупно-масштабная оптимизация. Линейный равенства могут быть зависимыми (т.е. Aeq должен иметь полный строчный ранг. Отметим, это означает что, Aeq не может иметь строк больше, чем столбцов. Если это все же имеет место, то взамен вызывается средне-мастабный алгоритм. Для большей информации о постановке задач и требуемой информации смотри Таблицу 1-4. Требования и Область Применения Крупно-Масштабных Задач
Литература:
- Coleman, T.F. and Y. Li, "A Reflective Newton Method for Minimizing a Quadratic Function Subject to Bounds on some of the Variables," SIAM Journal on Optimization, Vol. 6, Number 4, pp. 1040-1058, 1996.
- Gill, P. E. and W. Murray, and M.H. Wright, Practical Optimization, Academic Press, London, UK, 1981.
fzmult - умножение при сохранении основного базисом для нуль-пространства
Синтаксис:
W = fzmult(A,V)
W = fzmult(A,V,'transpose')
[W,L,U,pcol,P] = fzmult(A,V)
W = fzmult(A,V,TRANSPOSE,L,U,pcol,P)
Описание:
W = fzmult(A,V) - проводит расчет произведения W от матрицы Z на V, W = Z*V, где Z есть основной базис для нуль-пространства матрицы A. A должна быть разреженной матрицей m-х-n, где m < n, rank (A) = m и rank(A(1:m,1:m)) = m. V должна быть матрицей p-х-q, где p = n-m. Если V является разреженной, то W так же будет разреженной матрицей, в противном случае естественно, что матрица W будет полностью заполненной.
W = fzmult(A,V,'transpose') - проводит расчет произведения для транспонированного основного базиса V, то есть W = Z'*V. V должна быть матрицей p-х-q, где q = n-m. fzmult(A,V) есть то же самое, что и fzmult(A,V,[]).
[W,L,U,pcol,P] = fzmult(A,V) возвращает разреженный результат LU-факторизации матрицы A(1:m,1:m), то есть, A1 = A(1:m,1:m) и P*A1(:,pcol) = L*U.
W = fzmult(A,V,transpose,L,U,pcol,P) использует предварительно рассчитанную разреженную LU факторизацию матрицы x A(1:m,1:m), то есть, A1 = A(1:m,1:m) и P*A1(:,pcol) = L*U. операция транспонирования или производится в случае 'transpose' или нет в случае использования в командной строке символа [].
Базис нуль-пространства матрицы Z явным образом не формируется. Его неявное представление используется на основе разреженной факторизации матрицы A(1:m,1:m).
gangster - обнуление <небольших> компонентов с учетом структурного ранга
Синтаксис:
A = gangstr(M,tol)
Описание:
A = gangstr(M,tol) создает матрицу А с полным структурным рангом, таким, что А есть тоже, что и только за исключением относительно <небольших> элементов с заданной точностью tol, которые в А будут равны нулю. В случае необходимости в данном алгоритме проводится уменьшение точности tol, до тех пор пока не будет справедливо sprank(A) = sprank(M). В матрице М должна быть, по крайней мере, столько же колонок, что и число строк. По умолчанию принимается, что точность tol равна 1e-2.
gangstr идентифицирует элементы матрицы М, которые являются небольшими относительно точности tol, начиная в первую очередь с нормализации всех строк матрицы М, имеющих равную 1. Далее проводится проверка ненулевых значений в матрице М путем последовательного перебора все столбцов с последующей заменой нулями тех элементов, чью значения меньше по абсолютной величине величины tol* (максимальное абсолютное значение в данной колонке).
optimget – получить значения параметров опций оптимизаци
Синтаксис:
val = optimget(options,'param')
val = optimget(options,'param',default)
Описание:
val = optimget(options,'param') возвращает значения специализированного параметра в структуре опции оптимизации. Для того, что бы однозначно определить имя параметра, необходимо только напечатать достаточное количество определяющих символов. Это случай игнорируется для параметрических имен.
val = optimget(options,'param',default) по умолчанию возвращает, если в оптимизационных опциях не определены специализированные параметры, структуру опции. Отметим, что эта функциональная форма в первую очередь используется для оптимизационных функций.
Примеры:
Данный оператор возвращает значение параметра опции для отображения оптимизации в структуре, называемой как my_options.
val = optimget(my_options,'Display')
Данный оператор возвращает значение опционного параметра для отображения оптимизации в структуре называемой, как my_options (как и в предыдущем примере), за исключением того, что если параметр отображения не определен, то он возвращает значение 'final'.
optnew = optimget(my_options,'Display','final');
optimset - создать или отредактировать структуру параметров опций оптимизаци
Синтаксис:
options = optimset('param1',value1,'param2',value2,...)
optimset
options = optimset
options = optimset(optimfun)
options = optimset(oldopts,'param1',value1,...)
options = optimset(oldopts,newopts)
Описание:
- options = optimset('param1',value1,'param2',value2,...) Создает структуру параметров опций оптимизации, называемую как options и в которой специфицированные параметры (param) имеют специфицированные значения. Любой неспецифицированный параметр устанавливается как [] (параметры со значением [] указывают что, когда опция передаются в оптимизационную функцию, то для данных параметров используются принимаемые по умолчанию значения). Для того, что бы однозначно определить имя параметра, достаточно только набрать определяющие начальные символы. Такая операция не допускается для имен параметров.
- optimset без входных и выходных параметров отображает полный список параметров с их разрешенными значениями.
- options = optimset (без входных аргументов) создает опции из опционных структур, где все поля устанавливаются как [].
- options = optimset(optimfun) создает опции из опционных структур со всеми именами параметров и принимаемыми по умолчанию значениями, относящимися к оптимизационной функции optimfun.
- options = optimset(oldopts,'param1',value1,...) создает копию для oldopts, модифицируя специфицированные параметры с помощью специфицированных значений.
- options = optimset(oldopts,newopts) сочетает существующую опционную структуру oldopts с новой опционной структурой newopts. Всякий параметр в newopts с непустыми значениями перезаписывается на соответствующие старые параметры в oldopts.
Параметры:
Относительно более подробной информации об отдельных параметрах смотри страницы ссылок для функций оптимизации, использующих эти параметры, или Таблицу 4-3, Параметры Опций Оптимизации.
В списке ниже, значения в { } указывают на принимаемые по умолчанию значения, при этом часть параметров имеет различные принимаемые по умолчанию значения для различных функций оптимизации и поэтому в { } никаких значений не представлено.
Также можно просмотреть параметры оптимизации и принимаемые по умолчанию значения, если набрать optimset на командной линии.
Параметры оптимизации, используемые в обоих крупно-масштабном и средне-масштабном алгоритмах
| Diagnostics | 'on' | {'off'} |
| Display | 'off' | 'iter' | 'final' | 'notify' |
| GradObj | 'on' | {'off'} |
| Jacobian | 'on' | {'off'} |
| LargeScale | 'on' | {'off'} |
| MaxFunEvals | Положительное целое |
| MaxIter | Положительное целое |
| TolCon | Положительный скаляр |
| TolFun | Положительный скаляр |
| TolX | Положительный скаляр |
Параметры оптимизации, используемые только в крупно-масштабном алгоритме
| Hessian | 'on' | {'off'} |
| HessMult | function | {[]} |
| HessPattern | Разреженная матрица | {разреженная матрица из любых} |
| JacobMult | function | {[]} |
| JacobPattern | Разреженная матрица | {разреженная матрица из любых} |
| MaxPCGIter | Положительное целое | {больше 1 и не превосходящее (n/2)}, где n есть число элементов x0, т.е. для стартовой точки |
| PrecondBandWidth | Положительное целое | {0} | Inf |
| TolPCG | Положительный скаляр | {0.1} |
| TypicalX | Вектор от любых значений |
Параметры оптимизации, используемые только в средне-масштабном алгоритме
| DerivativeCheck | 'on' | {'off'} |
| DiffMaxChange | Положительный скаляр | {1e-1} |
| DiffMinChange | Положительный скаляр | {1e-8} |
| GoalsExactAchieve | Положительное скалярное целое | {0} |
| GradConstr | 'on' | {'off'} |
| HessUpdate | {'bfgs'} | 'dfp' | 'gillmurray' | 'steepdesc' |
| LevenbergMarquardt | 'on' | {'off'} |
| LineSearchType | 'cubicpoly' | {'quadcubic'} |
| MeritFunction | 'singleobj' | {'multiobj'} |
| MinAbsMax | Положительное скалярное целое | {0} |
Примеры:
Данная команда вызывается как options и создает структуру опций оптимизации, где параметр отображения Display устанавливается как 'iter' и параметр TolFun принимает значение 1e-8.
Данная команда вызывается как options и создает копию структуры опций, изменяя при этом значение параметра TolX и сохраняя новое значение в optnew.
Данная команда возвращает опции структуры опций лптимизации, которые вкючают в себя имена параметров и принимаемые по умолчанию соответствующие функции fminbnd значения
Если нужно только просмотреть принимаемые по умолчанию значения fminbnd, то можно просто набрать
или тоже самое
Смотри также: optimget
bintprog - Решение задачи целочисленного программирования вида 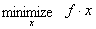 при условии
при условии 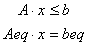
Синтаксис:
x = bintprog(f)
x = bintprog(f, A, b)
x = bintprog(f, A, b, Aeq, beq)
x = bintprog(f, A, b, Aeq, beq, x0)
x = bintprog(f, A, b, Aeq, beq, x0, options)
[x, fval] = bintprog(...)
[x,fval, exitflag] = bintprog(...)
[x, fval, exitflag, output] = bintprog(...)
Описание:
· x = bintprog(f)
· x = bintprog(f, A, b)
· x = bintprog(f, A, b, Aeq, beq)
· x = bintprog(f, A, b, Aeq, beq, x0)
· x = bintprog(f, A, b, Aeq, beq, x0, options)
· [x, fval] = bintprog(...)
· [x,fval, exitflag] = bintprog(...)
· [x, fval, exitflag, output] = bintprog(...)
Описание
x = bintprog(f) решает задачу целочисленного программирования
![]()
x = bintprog(f, A, b) задачу целочисленного программирования
![]() при условии
при условии ![]()
x = bintprog(f, A, b, Aeq, beq) решает предыдущую задачу при дополнительных условиях типа равенств
![]()
x = bintprog(f, A, b, Aeq, beq, x0) устанавливает начальную точку поиска в x0. Если точка x0 находится в недопустимой области, то команда bintprog принимает произвольную начальную точку.
x = bintprog(f, A, b, Aeq, Beq, x0, options) при оптимизации используется принимаемая по умолчанию опция из структуры options, которую можно задать с помощью функции optimset.
[x, fval] = bintprog(...) возвращает fval как значение целевой функции в точке x.
[x,fval, exitflag] = bintprog(...) возвращает параметр exitflag с описанием выходных условий команды bintprog. Более подробно описание даннлй функции и значения отдельных аргументов можно найти в разделе Выходные агументы.
[x, fval, exitflag, output] = bintprog(...) возвращает структуру output, которая содержит информацию о данных результатах оптимизации. См. радел Выходные агументы.
Входные аргументы
Далее в таблице приводится перечень входных аргументов команды bintprog.
| f | Вектор с коэффициентами линейной целевой функции. |
| A | Матрица с коэффициентами линейных ограничений типа неравенств |
| b | Вектор правой части линейных ограничений типа неравенств. |
| Aeq | Матрица с коэффициентами линейных ограничений типа равенств |
| beq | Вектор правой части линейных ограничений типа равенств. |
| x0 | Начальная точка поиска по данному алгоритму. |
| options | Структура опций для данного алгоритма. |
Выходные аргументы
Выходные параметры exitflag и output имеет ряд особенностей.
| exitflag | Некое целое число, идентифицируещее причину остановки алгоритма. Далее приводится перечень принимаемых значений и соответствующих причин останова алгоритма. | |
| 1 | Функция сошлась к некому решению x. | |
| 0 | Число итераций превысило значение options.MaxIter. | |
| -2 | Данная задача не имеет решения. | |
| -4 | Число перебранных узлов превышает значение options.MaxNodes. | |
| -5 | Время перебора превышает значение options.MaxTime. | |
| -6 | Число итераций решателя LP для некого узла при решении задачи LP-релаксации превысило значение options.MaxRLP. | |
| output | Структура с информацией о результатах оптимизации. Поле данной структуры имеет вид. | |
| iterations | Число выполненных итераций. | |
| nodes |
Число узлов перебора. | |
| time |
Превышение времени работы алгоритма. | |
| algorithm |
Используемый алгоритм. | |
| message |
Причина остановки работы алгоритма . | |
Опции
Далее приводится описание опций команды bintprog. Для установки или изменения значений поля данной структуры используется команда optimset.
| BranchStrategy | Тип алгоритма, используемого при выборе переменной ветвления в дереве поиска:
|
| Diagnostics | Отображение диагностической информации о данной функции. |
| Display | Уровень отображения. 'off' нет вывода отображения; 'iter' отображения выводится на каждой итерации.; 'final' (принимается по умолчанию) Отображение только при окончательном выводе. |
| DispNodeInterval | Интервал отображений узлов. |
| MaxIter | Максимальное число допустимых итераций. |
| MaxNodes | Максимальное число решений (или узлов) функции перебора. |
| MaxRLPIter | Максимальное число итераций решателя LP для некого узла при решении задачи LP-релаксации. |
| MaxTime | Максимальное количество времени в секундах для выполнения заданной функции. |
| NodeSearchStrategy | Стратегия алгоритма, используемого для отбора следующего узла при переборе в дереве поиска:
|
| TolCon | Конечный допустимый предел на нарушение заданного ограничения |
| TolFun | Конечный для значения функции. |
| TolXInteger | Допустимый предел, в котором рассматриваются значения переменных |
| TolRLPFun | Конечный допустимый предел на значение функции задачи редаксации линейного программирования. |
Алгоритм
В функции bintprog для решения задачи целочисленного программирования используется алгоритм линейного программирования (LP) на основе метода ветвей и границ. В данном алгоритме проводится перебор оптимальных решений задачи целочисленного программирования путем решения некого набора задач LP релаксации, в котором требование целочисленности переменных заменяется на более слабое ограничение ![]() . Данный алгоритм включает в себя:
. Данный алгоритм включает в себя:
- Перебор целочисленных допустимых решений.
- Корректировка наилучшей целочисленной допустимой точки по мере продвижения по дереву поиска.
- Проверка невозможности достижения более лучших целочисленных решений посредством рядя задач линейного программирования.
Далее приводится более детальное описание метода ветвей и границ.
Ветвление
Предложенный алгоритм образует дерево поиска путем многократного добавления ограничений на данную задачу, т.е. "ветвления". На этапе ветвления в алгоритме проводится выбор некой переменной х, чье текущее значение не является целым и, далее, накладываются ограничение xj = 0 для формирования одной ветви и ограничение xj = 1 для формирования другой ветви. Весь этот процесс может быть представлен в виде некоего двоичного дерева, узлы которого представляют собой дополнительно налагаемые ограничения. Далее на графике приводится иллюстрация законченного бинарного дерева для задачи с тремя переменными x1, x2 и x3. Отметим, что в общем случае порядок переменных при снижении уровней дерева может не соответствовать обычному порядку индексов переменных.
Решение о ветвлении
На каждом узле в данном алгоритме проводится решение задачи LP релаксации с учетом ограничений для данного узла и принимается решение о необходимости или ветвления или движения к другому узлу в зависимости от полученного результата. Имеются три возможности:
Если задача LP-релаксации для данной текущей точки является недопустимой или ее оптимальное значение больше, чем это значение в наилучшей точке целых значений, то алгоритм удаляет эту точку из данного дерева, после чего не проводится никаких переборов в ветвях ниже данного узла. Далее алгоритм переходит к анализу нового узла согласно методу, задаваемому опцией NodeSearchStrategy.
Если алгоритм определяет новую допустимую целочисленную точку с меньшим значением целевой функции, чем это было найдено ранее для наилучшей целой точки, то он корректирует наилучшую целевую точку и переходит к анализу следующего узла.
Если задача LP-релаксации является оптимальной, но не целочисленной, то значение оптимальной целевой функции задачи LP-релаксации является меньшим, чем в наилучшей целой точке, а алгоритм переходит на новую ветвь согласно методу, заданному опцией BranchStrategy.
Границы
Искомое решение задачи LP-релаксации определяет нижнюю границу для задачи бинарного целочисленного программирования. Если решение задачи LP-релаксации уже является бинарным целым вектором, то это решение определяет верхнюю границу задачи бинарного целочисленного программирования.
По мере прохождения большего числа узлов в дереве поиска в данном алгоритме проводится корректировка нижней и верхней границ целевой функции с учетом данных полученных на этапе границ. Подобная граница для целевой функции служит в качестве пороговой величины для отсечения излишних ненужных ветвей.
Ограничения по алгоритму
Алгоритм функции bintprog потенциально может перебрать все 2n бинарных целых векторов, где n есть число переменных. Поскольку для реализации полного алгоритма может потребоваться чрезмерно много времени, то, возможно, наложить некое ограничение на процедуры перебора с помощью следующих опций:
MaxRLPIter - Максимальное число итераций решателя LP для некого узла при решении задачи LP-релаксации.
MaxTime - Максимальное количество времени в секундах для выполнения заданной функции.
Более подробно информацию по данному разделу можно найти в разделе Опции.
Пример
Необходимо минимизировать функцию
![]()
при наличии ограничений
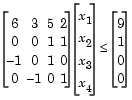 ,
,
где x1, x2, x3 и x4 являются бинарными целыми. Выполним следующие команды:
f = [-9; -5; -6; -4]; A = [6 3 5 2; 0 0 1 1; -1 0 1 0; 0 -1 0 1]; b = [9; 1; 0; 0]; x = bintprog(f,A,b) Optimization terminated successfully. x = 1 1 0 0
Литература
[1] Wolsey, Laurence A., Integer Programming, John Wiley & Sons, 1998.
[2] Nemhauser, George L. and Laurence A. Wolsey, Integer and Combinatorial Optimization, John Wiley & Sons, 1988.
[3] Hillier, Frederick S. and Lieberman Gerald J., Introduction to Operations Research, McGraw-Hill, 2001.
Комментарии