Справочник по MATLAB - Работа с разреженными матрицами (В.Г.Потемкин)
Информация в данной статье относится к релизам программы MATLAB ранее 2016 года, и поэтому может содержать устаревшую информацию в связи с изменением функционала инструментов. С более актуальной информацией вы можете ознакомиться в разделе документация MATLAB на русском языке.
При решении многих прикладных задач приходится иметь дело с разреженными матрицами, то есть с матрицами, имеющими много нулевых элементов. К числу таких задач в первую очередь следует отнести граничные задачи для систем дифференциальных уравнений в частных производных. Возникающие при этом модели - это, как правило, квадратные матрицы высокого порядка с конечным числом ненулевых диагоналей.
Известно, что матрица порядка n требует для своего хранения n2 байт оперативной памяти, а время вычислений пропорционально n3. Поэтому, когда количество неизвестных переменных достигает нескольких сотен, вычисления с полными матрицами становятся неэффективными и необходимо принимать во внимание степень разреженности матрицы, то есть отношение количества ненулевых элементов к общему количеству элементов матрицы.
Для разреженной матрицы S порядка m х n с количеством ненулевых элементов nnz(S) требования к объему оперативной памяти пропорциональны nnz. Вычислительная сложность операций над элементами массива также пропорциональна nnz, линейно зависит от m и n и не зависит от произведения m х n. Сложность такой операции как решение системы линейных уравнений с разреженной матрицей зависит от упорядочения элементов и заполненности матрицы, что обсуждается позднее в этой главе.
При работе с разреженными матрицами соблюдается фундаментальный принцип вычислительной сложности: время, необходимое для выполнения матричных операций над разреженной матрицей, пропорционально количеству арифметических операций над ненулевыми элементами. Это подтверждает широко распространенное правило: время вычислений пропорционально количеству операций с плавающей точкой.
В этой главе описан новый класс операций, реализованных в системе MATLAB, для работы с разреженными матрицами. Это операции хранения, преобразования, упорядочения, графического представления и решения систем линейных уравнений.
Элементарные разреженные матрицы
- SPARSE - формирование разреженной матрицы
- SPDIAGS - формирование диагоналей разреженной матрицы
- SPEYE - единичная разреженная матрица
- SPRANDN - случайная разреженная матрица
- SPRANDSYM - случайная разреженная симметрическая матрица
Преобразование разреженных матриц
- FIND - определение индексов ненулевых элементов
- FULL - преобразование разреженной матрицы в полную
- SPCONVERT - преобразование данных в ASCII-формате в массив разреженной структуры
Работа с ненулевыми элементами
- ISSPARSE - проверка на принадлежность к классу разреженных матриц
- NNZ - количество ненулевых элементов
- NONZEROS - формирование вектора ненулевых элементов
- NZMAX - количество ячеек памяти для размещения ненулевых элементов
- SPALLOC - выделить пространство памяти для разреженной матрицы
- SPFUN - вычисление функции только для ненулевых элементов
- SPONES - формирование матрицы связности
Характеристики разреженной системы
- NORMEST - оценка 2-нормы разреженной матрицы
- CONDEST - оценка числа обусловленности матрицы по 1-норме
- SPRANK - структурный ранг разреженной матрицы
Визуализация разреженных матриц
Алгоритмы упорядочения
- RANDPERM - формирование случайных перестановок
- COLPERM - упорядочение столбцов с учетом их разреженности
- DMPERM - DM-декомпозиция разреженной матрицы
- SYMRCM - RCM-упорядоченность
- COLMMD - упорядочение по разреженности столбцов
- SYMMMD - симметрическая упорядоченность
Операции над деревьями
- ETREE - дерево матрицы
- ETREEPLOT - построение дерева матрицы
- TREELAYOUT - разметить дерево
- TREEPLOT - пострение дерева матрицы
Вспомогательные операции
- SPPARMS - установка параметров для алгоритмов упорядочения и прямого решения линейных уравнений для разреженных матриц
- SYMBFACT - характеристики разложения Холецкого
- SPAUGMENT - формирование расширенной матрицы для метода наименьших квадратов
Элементарные разреженные матрицы
SPARSE - формирование разреженной матрицы
Синтаксис:
S = sparse(i, j, s, m, n, nzmax)
S = sparse(i, j, s, m, n)
S = sparse(i, j, s)
S = sparse(m, n)
S = sparse(A)
Описание:
Функция sparse - это встроенная функция, которая формирует матрицы в соответствии с правилами записи разреженных матриц, принятыми в системе MATLAB; количество входных аргументов этой функции - от 1 до 6.
Функция S = sparse(A) преобразовывает полную матрицу в разреженную, удаляя из описания нулевые элементы; если исходная матрица разреженная, то sparse(S) возвращает S.
Общая форма функции S = sparse(i, j, s, m, n, nzmax) использует строки массива [i j s] для формирования разреженной матрицы размера m х n с ненулевыми элементами, количество которых не превышает nzmax. Векторы i и j задают позиции элементов и являются целочисленными, а вектор c определяет числовое значение элемента матрицы, которое может быть действительным или комплексным. При формировании разреженной матрицы все строки вида [i j 0] из описания удаляются. Длина результирующего вектора s точно совпадает с количеством ненулевых элементов разреженной матрицы.
При формировании разреженной матрицы допускается использовать меньшее число входных аргументов, чем это требуется, а также ряд других упрощений. Так, один из аргументов i, j или s может быть скаляром, но при этом система MATLAB сама дополнит такой вектор до требуемой длины, которая определяется другими элементами.
Обращение вида S = sparse(i, j, s, m, n) предполагает по умолчанию, что nzmax = lenght(s).
Обращение вида S = sparse(i, j, s) предполагает, что m = max(i) и n = max(j); эти функции вычисляются раньше, чем будут удалены строки с нулевыми значениями s.
Обращение вида S = sparse(m, n) резервирует пространство для разреженной матрицы и равносильно обращению sparse([ ], [ ], [ ], m, n, 0), где все m х n элементов являются нулевыми.
Над разреженными матрицами могут совершаться любые арифметические, логические и индексные операции, то же справедливо и для смешанных операндов - полных и разреженных массивов. Операции с однородными операндами возвращают тот же тип операнда; в случае смешанных операндов, как правило, возвращается полный тип, за исключением случаев, когда в явном виде сохраняется разреженный тип. Например, при поэлементном умножении массивов A .* S, где S - разреженный массив.
Некоторые операции, например S >= 0, приводят к генерации так называемых BS(Big Space)-матриц, которые имеют разреженную структуру, но очень большое количество нулевых элементов.
Примеры:
Функция S = sparse(1:n, 1:n, 1) формирует единичную матрицу n х n с разреженной структурой и коэффициентом заполнения 1/n. Тот же результат может быть получен с помощью оператора S = sparse(eye(n, n)), но при этом промежуточная матрица будет иметь полную структуру.
Массив вида B = sparse(10000, 10000, pi), состоящий из одного элемента, вероятно, не очень полезен, но такое обращение допустимо. Не пытайтесь применить функцию full(B), вам потребуется 800 М памяти.
Следующая последовательность операторов сначала определяет структуру, а затем формирует разреженную матрицу.
[i, j, s] = find(S);
[m, n] = size(S);
S = sparse(i, j, s, m, n);
Сопутствующие функции: FULL, FIND, SPY, NONZEROS, NNZ, NZMAX, DIAG, SPONES, SPRANDSYM.
SPDIAGS - формирование диагоналей разреженной матрицы
Синтаксис:
[B, d] = spdiags(A)
B = spdiags(A, d)
A = spdiags(B, d, A)
A = spdiags(B, d, m, n)
Описание:
Функция spdiags расширяет возможности встроенной функции diag и позволяет работать с различными комбинациями следующих трех матриц, которые могут быть как входами, так и выходами функции spdiags:
A - матрица размера m х n, как правило (но не обязательно), разреженная с ненулевыми элементами на p диагоналях;
В - матрица размера min(m, n) х p, как правило (но не обязательно), полная, столбцы которой являются диагоналями A;
d - вектор длины p, целочисленные элементы которого определяют номера ненулевых диагоналей A (верхние диагонали нумеруются положительными числами, нижние - отрицательными).
Грубо говоря, матрицы A, B и вектор d связаны друг с другом следующим образом:
for k = 1:p
B(:, k) = diag(A, d(k))
end
Функция spdiags определяет следующие 4 операции в зависимости от количества входных аргументов:
- выделить все ненулевые диагонали:
[B, d] = spdiags(A); - выделить указанные диагонали:
B = spdiags(A); - заменить указанные диагонали матрицы A:
A = spdiags(B, d, A); - сформировать разреженную матрицу размера m х n по известным диагоналям:
A = spdiags(B, d, m, n);
Пример:
Сформировать трехдиагональную разреженную матрицу для разностного оператора 2-го порядка, заданного на сетке из n узлов.
n =5 ;
e = ones(n, 1);
A = spdiags([e -2*e e], -1:1, n, n)
Теперь из нее можно сформировать тестовую матрицу Уилкинсона wilkinson(n), изменяя элементы главной диагонали:
col = (abs(-(n-1)/2:(n-1)/2))';
A = spdiags(col, 0, A)
В заключение выделим ненулевые диагонали:
B = spdiags(A)
Сопутствующие функции: DIAG.
SPEYE - единичная разреженная матрица
Синтаксис:
S = speye(m, n)
S = speye(n)
Описание:
Функция speye(m, n) формирует разреженную матрицу размера m х n с единицами на главной диагонали и нулевыми внедиагональными элементами.
Функция speye(n) равносильна функции speye(n, n).
Пример:
Оператор A = speye(1000) формирует разреженный массив, соответствующий единичной матрице размера 1000 х 1000 и требует для этого всего 16 К памяти. Аналогичный конечный результат может быть получен с помощью оператора A = sparse(eye(1000,1000)), но в этом случае промежуточная матрица будет полной.
Сопутствующие функции: SPONES, SPALLOC.
SPRANDN - случайная разреженная матрица
Синтаксис:
R = sprandn(S)
R = sprandn(m, n, alpha)
R = sprandn(m, n, alpha, rcond)
Описание:
Матрица вида R = sprandn(S) имеет ту же структуру, которую имеет и разреженная матрица S, но при этом значения ее ненулевых элементов распределены по нормальному закону со средним, равным нулю и дисперсией 1.
Матрица вида R = sprandn(m, n, alpha) - это случайная разреженная матрица, которая имеет приблизительно alpha * m * n ненулевых элементов, распределенных по нормальному закону, где alpha - коэффициент заполнения со значением в пределах 0<= alpha<= 1.
Матрица вида R = sprandn(m, n, alpha, rcond) в дополнение к вышеперечисленным условиям имеет также число обусловленности по отношению к операции обращения, близкое к значению rcond. Если rcond - вектор длины lr<= min(m, n), то матрица R имеет в качестве первых lr сингулярных чисел значения вектора rcond, а остальные сингулярные числа равны нулю. В этом случае матрица R генерируется с помощью матриц случайных плоских вращений, которые применяются к диагональной матрице с заданным спектром сингулярных чисел. Такие матрицы играют важную роль при анализе алгебраических и топологических структур.
Сопутствующие функции: SPRANDSYM.
SPRANDSYM - случайная разреженная симметрическая матрица
Синтаксис:
R = sprandsym(S)
R = sprandsym(n, alpha)
R = sprandsym(n, alpha, rcond)
R = sprandsym(n, alpha, rcond, kind)
Описание:
Матрица R = sprandsym(S) - случайная симметрическая матрица, главная диагональ и нижние поддиагонали которой имеют ту же структуру, которую имеет и матрица S; значения ее ненулевых элементов распределены по нормальному закону со средним, равным нулю, и дисперсией 1.
Матрица вида R = sprandsym(n, alpha) - это случайная симметрическая разреженная матрица, которая имеет приблизительно alpha х m х n ненулевых элементов, распределенных по нормальному закону, где alpha - коэффициент заполнения со значением в пределах 0<= alpha<= 1 и каждый элемент сформирован в виде суммы нескольких нормально распределенных чисел.
Матрица R = sprandsym(n, alpha, rcond) имеет число обусловленности по отношению к операции обращения, равное rcond. Значения случайных элементов находятся в пределах [-1 1] и симметричны относительно нуля, однако закон распределения не является равномерным. Если rcond - вектор длины n, то матрица R имеет собственные значения, равные элементам вектора rcond; таким образом, если вектор rcond имеет положительные элементы, то матрица R является положительно определенной. В любом случае матрица R генерируется с помощью матриц случайных плоских вращений (матриц Якоби), которые применяются к диагональной матрице с заданным спектром собственных значений или числом обусловленности. Такие матрицы играют важную роль при анализе алгебраических и топологических структур.
Матрица R = sprandsym(n, alpha, rcond, kind) всегда является положительно определенной:
- если kind = 1, то матрица R формируется из положительно определенной диагональной матрицы с помощью матриц случайных плоских вращений с точно заданным числом обусловленности;
- если kind = 2, то матрица R формируется как смещенная сумма матриц внешних произведений; число обусловленности не соответствует заданному, но структура по сравнению с предыдущим случаем более компактна (участвует меньшее число поддиагоналей);
- если kind = 3, то предполагается форма R = sprandsym(S, alpha, rcond, 3) и матрица R имеет ту же структуру, которую имеет и матрица S, и число обусловленности приближенно равно 1/rcond, значение коэффициента заполнения alpha игнорируется.
Сопутствующие функции: SPRANDN.
Преобразование разреженных матриц
FIND - определение индексов ненулевых элементов
Синтаксис:
| k = find(x) | k = find(<условие>) | |
| [i, j] = find(X) | [i, j] = find(<условие>) | |
| [i, j, s] = find(X) | [i, j, s] = find(<условие>) |
Описание:
Функция k = find(x) определяет индексы ненулевых элементов вектора x; если таких элементов нет, то результатом является пустой вектор. Если входом является матрица X, то при данном способе вызова функции find она рассматривается как вектор-столбец x(i), образованный объединением столбцов исходной матрицы.
Функция [i, j] = find(X) возвращает индексы строк и столбцов ненулевых элементов матрицы X; часто используется при работе с разреженными матрицами.
Функция [i, j, s] = find(X) возвращает индексы, а также вектор-столбец s ненулевых элементов матрицы X.
Если в качестве аргумента функции find используется условие, то первые две функции обладают теми же свойствами, а функция [i, j, s] = = find(<условие>) будет формировать в качестве вектора s вектор единиц вместо значений ненулевых элементов.
Пример:
Пусть
M = magic(3)
| M = | 8 | 1 | 9 | |
| 3 | 5 | 7 | ||
| 4 | 9 | 2 |
Тогда применение функции find в форме
[i, j, m] = find(M); [i j m]
дает результат
| ans = | 1 | 1 | 8 | |
| 2 | 1 | 3 | ||
| 3 | 1 | 4 | ||
| 1 | 2 | 1 | ||
| 2 | 2 | 5 | ||
| 3 | 2 | 9 | ||
| 1 | 3 | 6 | ||
| 2 | 3 | 7 | ||
| 3 | 3 | 2 |
а в случае
[i, j, m] = find(M > 6); [i j m]
получим
| ans = | 1 | 1 | 1 | |
| 3 | 2 | 1 | ||
| 2 | 3 | 1 |
Сопутствующие функции: SPARSE, NONZEROS, RELOP (операции отношения).
FULL - преобразование разреженной матрицы в полную
Синтаксис:
A = full(S)
Описание:
Функция A = full(S) изменяет способ хранения матрицы в памяти компьютера; если исходная матрица A была полной, то функция full(A) возвращает A.
Пусть X - матрица размера m х n c nz = nnz(X) ненулевыми элементами. Тогда для размещения выхода функции full(X) требуется пространство для m * n действительных чисел, в то время как входная разреженная матрица sparse(X) требует пространства для размещения только nz действительных и nz + n целых чисел. Большинству компьютеров для хранения действительного числа нужно вдвое больше памяти, чем для целого. Для таких компьютеров хранение в форме sparse(X) будет экономичнее, чем в форме full(X), если коэффициент заполнения nnz/(m х n) < 2/3. Однако обработка разреженных матриц требует существенно большего числа операций, чем полных, так что коэффициент заполнения должен быть существенно меньше, чем 2/3, чтобы работа с разреженной матрицей оказалась более эффективной.
Пример:
Рассмотрим разреженную матрицу с коэффициентом заполнения около 2/3.
S = sparse(rand(200,200) < 2/3);
A = full(S); whos
| Name (переменная) | Size (размер массива) | Elements (количество элементов) | Bytes (размер памяти) | Density (коэффициент заполнения) | Complex (комплексная) |
| A | 200 by 200 | 40000 | 320000 | Full | No |
| S | 200 by 200 | 26797 | 322364 | 0.6699 | No |
В этом случае функции sparse(S) и full(S) требуют приблизительно одинакового объема памяти для хранения элементов.
Сопутствующие функции: SPARSE.
SPCONVERT - преобразование данных в ASCII-формате в массив разреженной структуры
Синтаксис:
S = spconvert(D)
Описание:
Обычные функции load и save поддерживают работу с массивами разреженной структуры, поэтому нет необходимости вводить специальные команды для загрузки и выгрузки разреженных массивов. Однако если внешний файл содержит данные о массиве разреженной структуры в ASCII-формате, то требуется преобразование этих данных во внутреннюю форму хранения. Предполагается, что внешний файл может быть организован в виде массива со структурой [i j s] или [i j r s], а число строк должно быть равно nnz или nnz + 1. Массив с тремя столбцами соответствует действительным элементам, а с четырьмя столбцами - комплексным. Последняя строка массива типа [m n 0] или [m n 0 0] может служить для задания размеров разреженной матрицы.
Функция spconvert применяется только для .mat- и ASCII-файлов. Если матрица D имеет разреженную структуру, то никаких преобразований не требуется.
Пример:
Допустим, что ASCII-файл uphill.dat содержит следующий массив данных:
| 1 | 1 | 1.000000000000000 |
| 1 | 2 | 0.500000000000000 |
| 2 | 2 | 0.333333333333333 |
| 1 | 3 | 0.333333333333333 |
| 2 | 3 | 0.250000000000000 |
| 3 | 3 | 0.200000000000000 |
| 1 | 4 | 0.250000000000000 |
| 2 | 4 | 0.200000000000000 |
| 3 | 4 | 0.166666666666667 |
| 4 | 4 | 0.142857142857143 |
| 4 | 4 | 0.000000000000000 |
Массив состоит из 11 строк.
Последовательность операторов
load uphill.dat
H = spconvert(uphill)
загружает данные и восстанавливает разреженную матрицу sparse(triu(hilb(4))) с учетом ошибок округления.
В данном случае последняя строка не является необходимой, поскольку размер матрицы был определен указанием ненулевого элемента (4, 4).
Работа с ненулевыми элементами
ISSPARSE - проверка на принадлежность к классу разреженных матриц
Синтаксис:
k = issparse(X)
Описание:
Функция issparse(X) принимает значение 1, если матрица X является разреженной, и 0, если полной.
Поскольку большинство функций системы MATLAB работает корректно с обоими типами матриц, то на практике применение функции issparse для распознавания типа матрицы достаточно редко.
Пример:
if issparse(X)
nrm = normest(X)
else
nrm = norm(X)
end
Сопутствующие функции: FULL, SPARSE.
NNZ - количество ненулевых элементов
Синтаксис:
nz = nnz(S)
Описание:
Функция nnz(S) определяет количество ненулевых элементов в разреженной матрице S.
Коэффициент заполнения разреженной матрицы, который выводится на экран по команде whos, определяется по формуле nnz(S)/prod(size(S)).
Поскольку большинство функций системы MATLAB работает корректно с обоими типами матриц, то на практике применение функции issparse для распознавания типа матрицы достаточно редко.
Сопутствующие функции: NONZEROS, NZMAX, FIND, ISSPARSE.
NONZEROS - формирование вектора ненулевых элементов
Синтаксис:
v = nonzeros(S)
Описание:
Функция nonzeros(S) формирует вектор ненулевых элементов матрицы, выбирая их по столбцам. Эта функция аналогична функции [i, j, v] = find(X), но в отличие от последней формирует только третий выход v. При этом, как правило, выполняется условие
length(v) = nnz(S) <= nzmax(S) <= prod(size(S)).
Сопутствующие функции: NNZ, NZMAX, FIND, ISSPARSE.
NZMAX - количество ячеек памяти для размещения ненулевых элементов
Синтаксис:
n = nzmax(S)
Описание:
Для полной матрицы F - это общее количество элементов, определяемое соотношением nzmax(F) = prod(size(F)); для разреженной - это количество ячеек для размещения ненулевых элементов. Как правило, функции nnz(S) и nzmax(S) дают одинаковые значения. Однако в случае операций над разреженными матрицами, в результате которых возникают новые ненулевые элементы, например операций умножения и LU-разложения, может быть выделено больше элементов памяти, чем это требуется при данном конкретном вычислении, то есть всегда выполняется условие nnz(S) <= nzmax(S).
Таким образом, величина nzmax(S) позволяет определить то максимальное количество элементов, которое может потребоваться при выполнении операций с разреженными матрицами в общем случае.
Сопутствующие функции: NNZ, NONZEROS, FIND, ISSPARSE.
SPALLOC - выделить пространство памяти для разреженной матрицы
Синтаксис:
S = spalloc(m, n, nzmax)
Описание:
Функция S= spalloc(m, n, nzmax) создает массив для разреженной матрицы размера m х n c учетом того, что количество ненулевых элементов не превышает nzmax. Затем матрица может быть заполнена по столбцам. Функция spalloc(m, n, nzmax) равносильна форме функции sparse([ ], [ ], [ ], m, n, nzmax).
Пример:
Если известно, что матрица имеет максимум 3 ненулевых элемента на столбец, то наиболее эффективный способ ее формирования следующий:
S = spalloc(n, n, 3*n);
for j =1:n
S(:, j) = { j-столбец }
end
Сопутствующие функции: SPARSE.
SPFUN - вычисление функции только для ненулевых элементов
Синтаксис:
f = spfun(‘fun’, S)
Описание:
Функция spfun применяет заданную функцию только к ненулевым элементам разреженной матрицы. Имя fun - это имя М-файла, в котором задана вычисляемая функция и который в качестве входного аргумента использует матрицу S.
Пример:
Функция вида f = spfun(‘exp’, S) вычисляет разреженную матрицу с тем же коэффициентом заполнения, который имеет и матрица S, если не учитывать появления элементов exp(-inf) ® 0. В то же время функция exp(S) применяет функцию exp к каждому элементу матрицы S и нулевые элементы становятся единичными.
SPONES - формирование матрицы связности
Синтаксис:
R = spones(S)
Описание:
Функция spones генерирует для заданной разреженной матрицы матрицу связности, которая имеет структуру матрицы S, в которой ненулевые элементы заменены на 1.
Примеры:
Функция c = sum(spones(S)) вычисляет количество ненулевых элементов каждого столбца.
Функция r = sum(spones(S’))’ вычисляет количество ненулевых элементов каждой строки. При этом соблюдается условие sum(c) = sum(r) = nnz(S).
Сопутствующие функции: ETREE, TREELAYOUT.
Характеристики разреженной системы
NORMEST - оценка 2-нормы разреженной матрицы
Синтаксис:
nrm = normest(S)
nrm = normest(S, tol)
[nrm, cnt] = normest(S)
Описание:
Эта функция изначально предназначалась для работы с разреженными матрицами, хотя она работает корректно и может быть полезна для оценки нормы и больших полных матриц.
Функция nrm = normest(S) вычисляет оценку 2-нормы матрицы S с относительной погрешностью 1e - 6 (по умолчанию).
Функция nrm = normest(S, tol) вычисляет оценку 2-нормы матрицы S с заданной относительной погрешностью tol.
Функция [nrm, cnt] = normest(S) позволяет определить количество использованных операций.
Алгоритм:
Каждая итерация включает операцию умножения матрицы S на ее транспонированную S’. Такие операции выполняются до тех пор, пока две последовательные оценки нормы не будут различаться в пределах заданной погрешности tol.
Файл normest размещен в каталоге toolbox\matlab\sparfun\normest.m.
Пример:
Матрица W = wilkinson(101) является трехдиагональной матрицей размера 101х101; ее порядок вполне достаточен, чтобы процедура вычисления нормы norm(full(W)), которая включает операцию svd(full(W)), проявила некоторые негативные свойства. Время вычисления на компьютере SPARC 1 cоставляет 4.13 с и определяет точное значение нормы 50,7462. В то же время процедура normest(sparse(W)) требует только 1.56 с и дает оценку нормы 50,7458.
Сопутствующие функции: СONDEST, NORM, SVD, RCOND.
CONDEST - оценка числа обусловленности матрицы по 1-норме
Синтаксис:
c = condest(A)
[c, v] = condest(A)
Описание:
Функция c = condest(A) вычисляет оценку числа обусловленности матрицы A по отношению к операции обращения. Для этого используется метод Хейджера (Hager) в модификации Хаема (Higham) [1]. Вычисленное значение с является нижней оценкой числа обусловленности матрицы A по 1-норме.
Функция [c, v] = condest(A), кроме того, вычисляет такой вектор v, который удовлетворяет соотношению ||Av|| = ||A||||v||/c. Таким образом, для больших c вектор v является аппроксимацией нуль-вектора матрицы A.
Эта функция применима как к действительным, так и к комплексным полным и разреженным матрицам.
Пример:
Сравнительная оценка нижней границы числа обусловленности матрицы W=wilkinson(101) при применении функций cond, rcond, condest:
| cond(W) | rcond(W) | condest(sparse(W)) |
| ans = 199.9410 | ans = 0.0065 | ans = 276.2827 |
Наилучшая оценка нижней границы вычисляется функцией condest.
Сопутствующие функции: СOND, RCOND, NORMEST.
Ссылки:
1. N.J. Higham. Fortran codes for estimating the one-norm of a real or complex matrix, with applications to condition estimation//ACM Trans. Math. Soft., 1988, Vol.14.P. 381-396.
SPRANK - структурный ранг разреженной матрицы
Синтаксис:
r = sprank(S)
Описание:
Функция r = sprank(S) вычисляет структурный ранг разреженной матрицы S. Он известен также под названиями максимальное сечение (maximum transversal), максимальное соответствие (maximum assignment) и максимальное совпадение (maximum matching), в терминах теории графов.
Для величины структурного ранга всегда выполняется условие
sprank(A) х rank(A);
более того, в точной арифметике с вероятностью 1 выполняется условие
sprank(A) == rank(sprandn(A)).
Пример:
Матрица размера 3 х 3 следующего вида
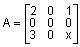
имеет структурный ранг sprank(A) = 2 при любом значении x; что касается ранга этой матрицы, то rank(A) = 2 всюду, кроме точки x = 3/2, где он равен единице.
Сопутствующие функции: DMPERM, RANK.
Визуализация разреженных матриц
GPLOT - построение графа
Синтаксис:
gplot(A, xy)
gplot(A, xy, lc)
[X, Y] = gplot(A, xy)
Описание:
Функция gplot(A, xy) осуществляет построение графа, заданного массивами A и xy. Граф G - это множество узлов, пронумерованных от 1 до n, и множество соединений (ребер) между ними. Для построения графа требуется две матрицы: матрица взаимосвязей A и матрица координат размещения узлов xy. Матрица взаимосвязей A такова, что ее элемент A(i, j) = 1, если узел i связан с узлом j; матрица координат узлов размера n х 2 определяет координаты узлов xy(i, :) = [x(i) y(i)].
Обращение в форме gplot(A, xy, lc) позволяет изменить цвет и тип линий, соединяющих узлы; по умолчанию принято lc = ‘r-’.
Функция вида [X, Y] = gplot(A, xy) формирует массив координат вершин графа, причем каждая пара вершин определена значениями типа NaN. Эти векторы могут быть использованы в дальнейшем для построения графа.
Пример:
Граф соединений, описываемый разреженной матрицей связности размера 60 х 60, напоминающий футбольный мяч или структуру молекулы углерода C60.
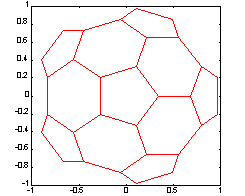
Сопутствующие функции: SPY, PLOT, TREEPLOT, TREELAYOUT.
SPY - визуализировать структуру разреженной матрицы
Синтаксис:
spy(S)
spy(S, ‘<цвет>‘)
Описание:
Функция spy(S) отображает на графике структуру произвольной матрицы S. Эта функция заменяет функцию format+, которая требует для вывода той же информации слишком много места на экране терминала.
Функция вида spy(S, ‘<цвет>‘) позволяет изменить цвет выводимых точек по правилам указания цвета для функции plot.
Сопутствующие функции: GPLOT, PLOT, SYMRCM, SYMMMD.
Алгоритмы упорядочения
RANDPERM - формирование случайных перестановок
Синтаксис:
p = randperm(n)
Описание:
Функция p = randperm(n) выполняет случайную перестановку целых чисел от 1 до n.
Сопутствующие функции: RAND, SPRANDN.
COLPERM - упорядочение столбцов с учетом их разреженности
Синтаксис:
j = colperm(S)
Описание:
Функция j = colperm(S) возвращает такой вектор перестановок j, что столбцы матрицы S(:, j) будут упорядочены по возрастанию числа ненулевых элементов. Эту процедуру целесообразно применять перед тем, как выполнить LU-разложение.
Если S - симметрическая матрица, то оказываются упорядоченными и строки и столбцы. Если к тому же матрица S является еще и положительно определенной, то такую процедуру перестановок целесообразно применять перед тем, как выполнить LLT-разложение.
Алгоритм:
Алгоритм очень прост, он реализует сортировку столбцов по числу ненулевых элементов и выглядит следующим образом:
[I, j] = find(S);
[ignore, p] = sort(diff(find(diff([0 j' inf]))));
Примеры:
Рассмотрим матрицу вида
A = [ones(1, n); ones(n-1, 1) speye(n-1, n-1)]
при n = 4
A = 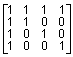 .
.
Ее LU-разложение представляет почти полную матрицу
lu(A)= 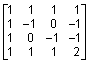 .
.
Функция упорядочения столбцов j = colperm(A) возвращает вектор перестановок j = [2:n 1], так что матрица A(j, j) имеет следующий вид:
A(j, j) = 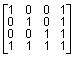 ,
,
а ее LU-разложение имеет такую же структуру ненулевых элементов, как исходная матрица A и массив A(j, j):
lu(A(j, j ) = 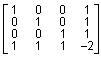 .
.
Сопутствующие функции: COLMMD, SYMMMD, LU, CHOL.
DMPERM - DM-декомпозиция разреженной матрицы
Синтаксис:
p = dmperm(S)
[p, q, r] = dmperm(S)
[p, q, r, s] = dmperm(S)
Описание:
Функция p = dmperm(S) возвращает вектор максимального соответствия; если исходная матрица S имеет полный столбцовый ранг, то матрица S(p, :) - является квадратной с ненулевой диагональю. Матрица S(p, :) называется декомпозицией Далмейджа - Мендельсона (Dulmage - Mendelsohn) или DM-декомпозицией.
Если S - приводимая матрица, то есть линейная система Sx = b может быть решена приведением S к верхней блочной треугольной форме, то такое решение может быть найдено методом обратной подстановки.
Функция [p, q, r] = dmperm(S) определяет такую перестановку строк p и такую перестановку столбцов q для квадратной матрицы S, что S(p, q) - матрица в верхней треугольной форме. Третий выходной аргумент r - это целочисленный вектор, который описывает границы блоков, так что блок k матрицы S(p, q) имеет следующие границы r(k) : r(k + 1) - 1.
Функция [p, q, r, s] = dmperm(S) определяет такую перестановку строк p и такую перестановку столбцов q для прямоугольной матрицы S, что S(p, q) - есть матрица в верхней треугольной форме. Границы k-го блока определяются параметрами r и s согласно соотношению (r(k) : r(k + 1) -1, s(k) : s(k + 1) -1).
В терминах теории графов диагональные блоки соответствуют компонентам Холла смежного графа матрицы A.
Сопутствующие функции: SPRANK.
SYMRCM - RCM-упорядоченность
Синтаксис:
r = symrcm(S)
Описание:
Функция r = symrcm(S) возвращает такой вектор упорядоченности для симметрической матрицы S, что S(r, r) будет концентрировать ненулевые элементы вблизи диагонали. Это хорошее упорядочение как для LU-, так и для LLT-разложения матрицы, что позволяет отказаться от работы с элементами, удаленными от диагонали. Такое упорядочение называется упорядочением Катхилла - Макки (Cuthill - McKee).
Для действительных симметрических разреженных матриц собственные значения S(r, r) совпадают с собственными значениями S, но времени на вычисление eig(S(r, r)) будет затрачиваться существенно меньше, чем для eig(S).
Пример:
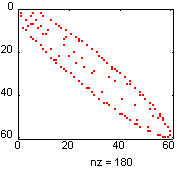
Рассмотрим матрицу bucky размера 60 х 60, которую связывают с футбольным мячом, куполом (Buckminster Fuller dome, отсюда название bucky), а в последнее время - с моделью атома углерода C60. Ее граф имеет 60 вершин, которые пронумерованы так, что половина из них находится в одной, а половина в другой полусфере (рис. а), и эти половины соединены вместе. Такая нумерация приводит к структуре матрицы, изображенной на рис. б.
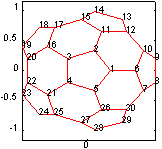 |
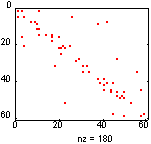 |
| а) | б) |
Применяя RCM-упорядочение
p = symrcm(B);
R = B(p, p);
spy(R)
получим матрицу с узкой полосой вблизи диагонали (рис. в), ширина которой может быть вычислена следующим образом:
[i, j] = find(B);
bw = max(i - j) + 1
Ширина полосы матрицы A равна 35, а матрицы R - 12.
 |
|
в) |
Сопутствующие функции: COLMMD, COLPERM, LU, CHOL, EIG, \.
Ссылки:
- George A., Liu J. Сomputer Solution of Large Sparse Positive Definite Systems. Prentice-Hall, 1981.
- Gilbert J. R., Moler C., Schreiber R. Sparse Matrices in MATLAB: Design and Implementation//SIAM Journal on Matrix Analysis and Applications. 1992. Vol. 13. P. 333-356.
COLMMD - упорядочение по разреженности столбцов
Синтаксис:
p = colmmd(S)
Описание:
Функция p = colmmd(S) возвращает такой вектор упорядоченности столбцов для несимметрической матрицы S, что S(:, p) будет иметь более разреженное LU-разложение, чем S.
Такое упорядочение автоматически применяется системой MATLAB при выполнении операций обращения \ и / при решении систем линейных уравнений с разреженными матрицами.
Алгоритм:
Алгоритм упорядочения по разреженности столбцов для симметрических матриц описан в обзоре Джорджа (George) и Лиу (Liu) [1]. Для несимметрических матриц аналогичный алгоритм разработан заново и описан в работе Гилберта (Gilbert), Моулера (Moler) и Шрайбера (Schriber) [2]. Он напоминает прежний алгоритм для матрицы A’ * A, но в действительности такая матрица не формируется.
На каждом шагу алгоритма из оставшихся выбирается вершина низшего порядка, то есть столбец, имеющий минимальное количество ненулевых элементов, удаляет эту вершину и строит новый граф, объединяя строки. После n шагов все столбцы оказываются удаленными и перестановка завершается. Для ускорения этого процесса используются специальные приемы для одновременного выполнения нескольких шагов.
Пример:
Коллекция разреженных матриц фирмы Harwell-Boeing включает тестовую матрицу abb313. Это прямоугольная матрица размера 313 х 176, связанная с задачей оценки по методу наименьших квадратов геодезических данных. При решении задачи возникает вспомогательная матрица S, генерируемая функцией spaugment. Она является квадратной и имеет порядок 489.
load abb313.mat
S = spaugment(abb313);
p = colmmd(S);
spy(S)
spy(S(:, p))
spy(lu(S))
spy(lu(S(:, p))
| lu(S) | lu(S(:, p)) |
| в) | г) |
Сопутствующие функции: SYMMMD, SYMRCM, COLPERM, LU, SPPARMS.
Ссылки:
- George A., Liu J. The evolution of the minimum degree ordering algorithm//SIAM Review. 1989. Vol. 31. P. 1-19.
- Gilbert J. R., Moler C., Schreiber R. Sparse Matrices in MATLAB: Design and Implementation//SIAM Journal on Matrix Analysis and Applications. 1992. Vol. 13. P. 333-356
SYMMMD - симметрическая упорядоченность
Синтаксис:
p = symmmd(S)
Описание:
Функция p = symmmd(S) возвращает такой вектор упорядоченности столбцов для симметрической положительно определенной матрицы S, что S(:, p) будет иметь более разреженное LLT-разложение, чем S.
Такое упорядочение автоматически применяется системой MATLAB при выполнении операций обращения \ и / при решении линейных систем с разреженными матрицами.
Алгоритм:
Алгоритм упорядочения для симметрических матриц основан на алгоритме упорядочения по разреженности столбцов. Фактически функция symmmd формирует матрицу K с такой структурой ненулевых элементов, что симметрическая матрица K’ * K имеет такую же структуру ненулевых элементов, как и исходная матрица S, а затем вызывается функция colmmd для K.
Пример:
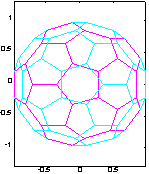
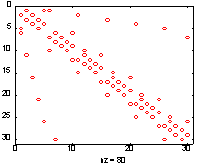
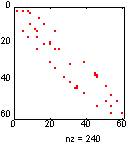
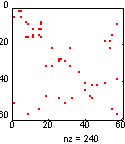
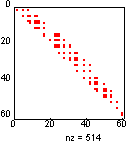
Сравним два алгоритма упорядочения, реализованные в виде функций symrcm и symmmd, которые предшествуют LLT-разложению (разложение Холецкого) матрицы bucky размера 60 х 60, которая описывает граф связности bucky (рис. а) и имеет структуру (рис. б).
Хотя эта задача и не является очень сложной, тем не менее поведение алгоритмов упорядочения является типичным. Применение функции symrcm порождает ленточную матрицу (рис. в), которая после LLT-разложения оказывается целиком заполненной внутри ленты (рис. д). Применение функции symmmd порождает ленточную матрицу с крупными блоками нулевых элементов (рис. г), которые не заполняются и в процессе LLT-разложения (рис. е). Следовательно, алгоритм симметрической разреженности требует меньшего времени и объема памяти в процессе LLT-разложения.
Сопутствующие функции: COLMMD, SYMRCM, COLPERM, CHOL, SPPARMS.
Ссылки:
1. Gilbert J. R., Moler C., Schreiber R. Sparse Matrices in MATLAB: Design and Implementation//SIAM Journal on Matrix Analysis and Applications. 1992. Vol. 13. P. 333-356.
 |
 |
| а) | б) |
 |
 |
| в) | г) |
 |
|
Операции над деревьями
ETREE - дерево матрицы
Синтаксис:
| p = etree(A) | [p, q] = etree(A) | |
| p = etree(A, ‘col’) | [p, q] = etree(A, ‘col’) | |
| p = etree(A, ‘sym’) | [p, q] = etree(A, ‘sym’) |
Описание:
Функция p = etree(A) возвращает структуру дерева для квадратной симметрической матрицы A; значение p(j) - это родитель столбца с номером j в дереве; если p(j) = 0, то столбец j - корень дерева.
Функция p = etree(A, ‘col’) возвращает структуру дерева для матрицы A’ * A.
Функция p = etree(A, ‘sym’) равносильна функции p = etree(A).
Функция [p, q] = etree(A, ...) в дополнение к структуре дерева возвращает также вектор перестановок столбцов q.
Пример:
Рассмотрим матрицу A следующего вида:
A = 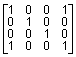 .
.
Эта матрица симметрическая и применение функции etree дает следующий результат:
[p, q] = etree(A)
p = 4 0 0 0
q = 2 3 1 4
Сопутствующие функции: ETREEPLOT, TREELAYOUT, TREEPLOT.
ETREEPLOT - построение дерева матрицы
Синтаксис:
etreeplot(A)
etreeplot(A, c, d)
Описание:
Функция etreeplot(A) строит дерево для квадратной матрицы A; если матрица несимметрическая - то для A + A’.
Функция etreeplot(A, c, d) в дополнение к построению дерева для квадратной матрицы A позволяет управлять путем задания параметров c и d соответственно цветом и символами обозначения узлов и ребер. Если один из параметров заменен на ‘’, то на график не будут выводиться либо ребра, либо узлы. Если эти параметры не указаны, то принимаются их значения по умолчанию.
Пример:
Рассмотрим матрицу A следующего вида:
A = 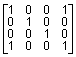 .
.
Эта матрица симметрическая, и применение функций etree и etreeplot дает следующие результаты:
[p, q] = etree(A)
etreeplot(A)
p = 4 0 0 0
q = 2 3 1 4
На рисунке показан график соответствующего дерева.
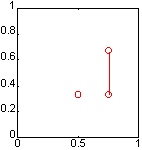
Сопутствующие функции: ETREE, TREELAYOUT, TREEPLOT.
TREELAYOUT - разметить дерево
Синтаксис:
[x, y, h, s] = treelayout(p, q)
Описание:
Функция [x, y, h, s] = treelayout(p, q) использует в качестве входных параметров вектор p(j), отождествляемый либо с родителем столбца с номером j в дереве, либо с корнем дерева, если p(j) = 0, а также вектор q перестановки столбцов. Если вектор q не указан, то он вычисляется в процессе выполнения функции.
Выходные параметры x и y - это векторы координат узлов дерева, которое размещается в пределах единичного квадрата, чтобы сделать график удобным для восприятия.
Дополнительные выходные параметры h и s определяют соответственно высоту и количество узлов.
Эту функцию целесообразно использовать в сочетании с функцией построения графа gplot.
Пример:
Рассмотрим матрицу A следующего вида:
A = 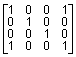 .
.
Эта матрица симметрическая, и применение функций etree, treelayout и gplot дает следующие результаты:
[p, q] = etree(A)
[x, y, h, s] = treelayout(p, q)
gplot(A, [x' y'],'r-'), hold on
gplot(A, [x' y'], 'go')
p = 4 0 0 0
q = 2 3 1 4
На рисунке показан график соответствующего дерева.
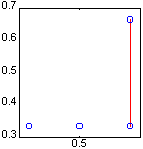
Сопутствующие функции: ETREE, ETREEPLOT, TREEPLOT.
TREEPLOT - пострение дерева матрицы
Синтаксис:
treeplot(p)
treeplot(p, c, d)
Описание:
Функция treeplot(p) строит дерево, если задан вектор p(j), отождествляемый либо с родителем столбца с номером j в дереве, либо с корнем дерева, если p(j) = 0.
Функция treeplot(p, c, d) в дополнение к построению дерева позволяет управлять цветом и символами обозначения узлов и ребер путем задания соответственно параметров c и d. Если один из параметров заменен на “, то на график не будут выводиться либо ребра, либо узлы. Если эти параметры не указаны, то принимаются их значения по умолчанию.
Пример:
Рассмотрим матрицу А следующего вида:
A = 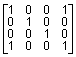 .
.
Эта матрица симметрическая, и применение функций etree и treeplot дает следующие результаты:
[p, q] = etree(A)
treeplot(p, ‘bo’, ‘r’)
p = 4 0 0 0
q = 2 3 1 4
На рисунке показан график соответствующего дерева.

Сопутствующие функции: ETREE, TREELAYOUT, ETREEPLOT.
Вспомогательные операции
SPPARMS - установка параметров для алгоритмов упорядочения и прямого решения линейных уравнений для разреженных матриц
Синтаксис:
spparms
values = spparms
[keys, values] = spparms
value = spparms(‘<ключ>‘)
spparms(‘<ключ>‘, <значение>)
spparms(<значения>)
Описание:
Работа с разреженными матрицами в системе MATLAB организована с помощью специального монитора SParse MONItor. Большинству пользователей знание служебных команд работы с монитором совершенно не обязательно. Эти команды предназначены только для тех пользователей, которые хотели бы увидеть и, возможно, изменить работу алгоритмов упорядочения и решения систем линейных уравнений.
Функция spparms сама по себе выводит на экран описания текущих установок.
Функция values = spparms выводит на экран значения этих установок.
Функция [keys, values] = spparms выводит вектор значений и символьную матрицу, строки которой являются ключами параметров монитора SParse MONItor.
Функция value = spparms(‘<ключ>‘) выводит значение параметра для данного ключа.
Функция spparms(‘<ключ>‘, <значение>) устанавливает один или более настраиваемый параметр, который используется в функциях упорядочения colmmd и symmmd, а также в операциях решения систем линейных уравнений / и \.
Функция spparms(values) применяется без выходных параметров и устанавливает значения, указанные во входном векторе.
Функция spparms(‘default’) устанавливает значения по умолчанию.
Функция spparms(‘tight’) устанавливает параметры алгоритмов упорядочения по разреженности к наиболее “строгим” значениям, что приводит к процедурам упорядочения без удаления строк, которые требуют большего времени выполнения.
В нижеследующей таблице приведены расшифровки ключей для параметров и их значений по умолчанию и в “строгом смысле”.
| Параметр | Ключ | Значения | |
| по умолчанию | в “строгом смысле” | ||
| values(1) | `spumoni` | 0.0 | |
| values(2) | `thr_rel` | 1.1 | 1.0 |
| values(3) | `thr_abs` | 1.0 | 0.0 |
| values(4) | `exact_d` | 0.0 | 1.0 |
| values(5)v | `supernd` | 3.0 | 1.0 |
| values(6) | `rreduce` | 3.0 | 1.0 |
| values(7) | `wh_frac` | 0.5 | 0.5 |
| values(8) | `autommd` | 1.0 | |
| values(9) | `aug_rel` | 0.001 | |
| values(10) | `aug_abs` | 0.0 | |
При этом ключи имеют следующие значения:
| Ключи | Значение |
| `spumoni` | Флаг монитора SParse MONItor: 0 - не выводит диагностических сообщений, по умолчанию; 1 - выводит информацию о выбранном алгоритме; 2 - выводит детальную информацию о работе алгоритмов упорядочения |
| `thr_rel`, `thr_abs` |
Порог минимальной разреженности thr_rel * mindegree + thr_abs |
| `exact_d` | 0 - использование приближенных значений разреженности; 0 - использование точных значений разреженности 0 - использование точных значений разреженности |
| `supernd` | Целое >= 1 - объединение узлов каждые supernd шагов |
| `rreduce` | Целое >= 1 - удаление строк каждые rreduce шагов |
| `wh_frac` | В процедуре colmmd строки с коэффициентом заполнения, превышающим wh_frac, пропускаются |
| `autommd` |  0 - в процедурах \ и / использовать упорядочение по разреженности 0 - в процедурах \ и / использовать упорядочение по разреженности |
| `aug_rel`, `aug_abs` |
Параметр масштабирования невязки в проблеме наименьших квадратов, равный aug_rel * max(max(abs(A))) + aug_abs. Например, при значениях aug_rel = 0 и aug_abs = 1 единичная матрица главного верхнего блока будет немасштабированной |
Примеры:
Ниже приведены примеры выполнения вспомогательных операций и указан русский перевод сообщений системы.
spparms (для значений по умолчанию)
| No SParse MONItor output. | Выходных данных SParse MONItor не формирует |
| mmd: threshold = 1.1 * mindegree + 1, using approximate degrees in A'*A, | mmd: <порог> = 1.1 * mindegree + 1; приближенные значения разреженности при работе с A'*A; |
| supernode amalgamation every 3 stages, | объединение узлов - каждые 3 шага; |
| row reduction every 3 stages, | редукция строк - каждые 3 шага; |
| withhold rows at least 50% dense in colmmd. | удерживать строки с разреженностью не менее 50 %. |
| Minimum degree orderings used by \ and /. | Для операций \ и / применять упорядочение по разреженности. |
| Residual scale parameter = 0.001 * max(abs(A)). | Параметр невязки: 0.001 * max(abs(A)). |
[keys, values] = spparms
| keys = | values = | |
| spumoni | 0 | |
| thr_rel | 1.1000 | |
| thr_abs | 1.0000 | |
| exact_d | 0 | |
| supernd | 3.0000 | |
| rreduce | 3.0000 | |
| wh_frac | 0.5000 | |
| autommd | 1.0000 | |
| aug_rel | 0.0010 | |
| aug_abs | 0 |
value = spparms('spumoni')
value = 0.
Сопутствующие функции: COLMMD, SYMMMD, \.
Ссылки:
1. Gilbert J. R., Moler C., Schreiber R. Sparse Matrices in MATLAB: Design and Implementation//SIAM Journal on Matrix Analysis and Applications. 1992. Vol. P. 333-356.
SYMBFACT - характеристики разложения Холецкого
Синтаксис:
count = symbfact(A)
count = symbfact(A, f)
[count, h, parent, post, R] = symbfact(A, f)
Описание:
Функция count = symbfact(A) вычисляет количество элементов в строках верхнего треугольного множителя разложения Холецкого исходной симметрической матрицы A. Эта функция выполняется значительно быстрее, чем chol(A).
Функция count = symbfact(A, `col`) анализирует матрицу A’*A, не формируя ее в явном виде.
Функция count = symbfact(A, `sym`) аналогична процедуре count = symbfact(A).
Функция [count, h, p, q, R] = symbfact(A, f) возвращает несколько дополнительных выходных параметров:
- h - высоту графа;
- p - параметры графа;
- q - вектор перестановки столбцов;
- R - матрицу связности для процедуры chol(A).
Пример:
Рассмотрим матрицу A следующего вида:
A = 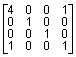 .
.
Эта симметрическая положительно определенная матрица, и применение функции chol(A) дает следующий результат:
L = chol(A)
L =
| 2.0000 | 0 | 0 | 0.5000 | |
| 0 | 1.0000 | 0 | 0 | |
| 0 | 0 | 1.0000 | 0 | |
| 0 | 0 | 0 | 0.8660 |
Применение функции symbfact(A) вычисляет количество элементов в строках матрицы L:
с = symbfact(A)
c = 2 1 1 1
Если к матрице A применить алгоритм симметрической упорядоченности, то ненулевые элементы в разложении Холецкого будут концентрироваться вблизи диагонали. Рассмотрим последовательность процедур
r = symmmd(A);
L = chol(A(r, r))
L =
| 1.0000 | 0 | 0 | 0 | |
| 0 | 1.0000 | 0 | 0 | |
| 0 | 0 | 2.0000 | 0.5000 | |
| 0 | 0 | 0 | 0.8660 |
c = symbfact(A(r, r))
c = 1 1 2 1
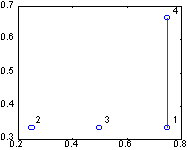
Обращение вида [count, h, p, q, R] = symbfact(A) вычисляет параметры для построения графа матрицы. Следующая последовательность операторов позволяет построить граф с пронумерованными вершинами.
[c, h, p, q] = symbfact(A)
[x, y] = treelayout(p, q);
gplot(A, [x' y'], 'bo'), hold on
gplot(A, [x' y'], 'r')
for j=1:size(A, 1)
text(x(j) + 0.02,y(j) + 0.02,int2str(j))
end
c = 2 1 1 1
h = 2
p = 4 0 0 0
q = 2 3 1 4
Сопутствующие функции: CHOL, ETREE.
SPAUGMENT - формирование расширенной матрицы для метода наименьших квадратов
Синтаксис:
S = spaugment(A)
S = spaugment(A, c)
Описание:
Функции S = spaugment(A) и S = spaugment(A, c) формируют разреженную квадратную симметрическую матрицу следующей блочной структуры:
S = [c*I A; A’ 0].
Такая расширенная матрица используется для минимизации квадратичной формы
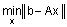 .
.
Если r = b - Ax выполняет роль невязки, а c - масштабирующий множитель, то решение методом наименьших квадратов сводится к решению следующей системы линейных уравнений:
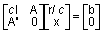 .
.
Если исходная матрица A имеет размер m х n, то расширенная матрица S имеет размер (m + n) х (m + n). В обозначениях системы MATLAB эту систему можно описать так:
S * [r/c; x] = [b; z],
где z = zeros(n, 1).
Определение оптимального значения для масштабного множителя с основано на вычислении значений min(svd(A)) и norm(r), что требует больших объемов расчетов. Если значение c не указано явно в виде второго параметра, то по умолчанию применяется значение max(abs(A)))/1000. Можно изменить это значение, если воспользоваться функцией spparms и задать другие значения для ключей aug_rel и aug_abs.
Операция решения систем линейных уравнений x = A\b автоматически формирует расширенную матрицу, определяя значение c по умолчанию.
Пример:
Рассмотрим простую систему из трех уравнений с двумя неизвестными.
x1 + 2x2 = 5;
3x1 = 6;
4x2 = 7.
Поскольку эта система небольших размеров, она может быть решена с использованием обычных конструкций системы MATLAB, в данном случае - полных матриц:
A = [ 1 2; 3 0; 0 4];
b = [5 6 7]’;
x = A \ b.
В результате получаем следующее решение по методу наименьших квадратов:
x =
1.9592
1.7041
Подход на основе расширенной матрицы использует функцию spaugment:
S = spaugment(A, 1),
которая формирует вспомогательную матрицу следующего вида:
full(S) = 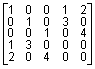 .
.
В этом примере использовано значение масштабного множителя c = 1 и для удобства чтения распечатана полная матрица S. Даже в этом простом примере более половины элементов матрицы S равны нулю.
Вспомогательная система использует также расширенный вектор для правой части, который формируется в виде
y = [b; 0; 0];
в результате решение вычисляется с помощью оператора решения системы линейных уравнений
z = S \ y,
где все матрицы являются квадратными, и для решения применяется метод исключения Гаусса вместо ортогонализации. В случае разреженных матриц при таком подходе используются меньшие объемы оперативной памяти.
Вычисленное решение имеет вид:
z =
| -0.3673 | |
| 0.1224 | |
| 0.1837 | |
| 1.9592 | |
| 1.7041 |
Здесь первые 3 компонента характеризуют вектор невязки r, а последние 2 компонента определяют решение x, которое совпадает с приведенным выше.
Комментарии