Справочник по MATLAB - Анализ и обработка данных (В.Г.Потемкин)
Информация в данной статье относится к релизам программы MATLAB ранее 2016 года, и поэтому может содержать устаревшую информацию в связи с изменением функционала инструментов. С более актуальной информацией вы можете ознакомиться в разделе документация MATLAB на русском языке.
В этой главе описаны функции системы MATLAB, которые предназначены для анализа и обработки данных, заданных в виде числовых массивов. Наряду с простейшими функциями вычисления среднего, медианы, коэффициентов корреляции элементов массива рассмотрены функции вычисления конечных разностей, градиента и аппроксимации Лапласиана. В отдельный раздел выделены функции аппроксимации и интерполяции. Представлены функции численного интегрирования, решения задачи Коши для систем ОДУ, а также минимизации функций одной и нескольких переменных. В состав функций обработки сигналов включены дискретное преобразование Фурье, функции свертки и фильтрации. В полном объеме функции обработки сигналов оформлены в виде специализированного пакета программ Signal Processing Toolbox.
Основные операции
- SUM, CUMSUM - суммирование элементов массива
- PROD, CUMPROD - произведение элементов массива
- SORT - сортировка элементов массива по возрастанию
- MAX - определение максимальных элементов массива
- MIN - определение минимальных элементов массива
- MEDIAN - определение срединных значений (медиан) элементов массива
- MEAN - определение средних значений элементов массива
- STD - определение стандартных отклонений элементов массива
- COV - определение ковариационной матрицы элементов массива
- CORRCOEF - определение коэффициентов корреляции элементов массива
- DIFF - вычисление конечных разностей и приближенное дифференцирование
- GRADIENT - конечные разности и приближенное вычислениеградиента функции от двух переменных
- DEL2 - пятиточечная аппроксимация Лапласиана
Аппроксимация и интерполяция данных
- POLYFIT - аппроксимация данных полиномом
- INTERPFT - аппроксимация периодической функции на основе быстрого преобразования Фурье
- ICUBIC - кубическая интерполяция функции одной переменной
- SPLINE, PPVAL, MKPP, UNMKPP - интерполяция функции одной переменной кубическим сплайном
- INTERP1 - одномерная табличная интерполяция
- INTERP2 - двумерная табличная интерполяция
- GRIDDATA - двумерная табличная интерполяция на неравномерной сетке
Численное интегрирование
Интегрирование обыкновенных дифференциальных уравнений (ОДУ)
Вычисление минимумов и нулей функции
- FMIN, FORTIONS - минимизация функции одной переменной
- FMINS - минимизация функции нескольких переменных
- FZERO - нахождение нулей функции одной переменной
- FPLOT - построение графиков функции одной переменной
Преобразование Фурье
- FFT, IFFT - одномерное дискретное прямое и обратное преобразования Фурье
- FFT2, IFFT2 - двумерное дискретное прямое и обратное преобразования Фурье
- FFTSHIFT - перегруппировка выходных массивов преобразований Фурье
Свертка и фильтрация
- CONV, DECONV - свертка одномерных массивов
- CONV2 - свертка двумерных массивов
- FILTER - дискретная одномерная фильтрация
- FILTER2 - дискретная двумерная фильтрация
- UNWRAP - корректировка фазовых углов
Основные операции
SUM, CUMSUM - суммирование элементов массива
Синтаксис:
sx = sum(X)
csx = cumsum(X)
Описание:
Функция sx = sum(X) в случае одномерного массива возвращает сумму элементов массива; в случае двумерного массива - это вектор-строка, содержащая суммы элементов каждого столбца.
Функция csx = cumsum(X), кроме того, возвращает все промежуточные результаты суммирования.
Пример:
Рассмотрим массив M = magic(3): M = magic(3)
| M = | 8 | 1 | 6 | |
| 3 | 5 | 7 | ||
| 4 | 9 | 2 |
| cumsum(M) | sum(M) | ||||||||||||||||||
|
|
Сопутствующие функции: CUMPROD, PROD.
PROD, CUMPROD - произведение элементов массива
Синтаксис:
px = prod(X)
cpx = cumprod(X)
Описание:
Функция px = prod(X) в случае одномерного массива возвращает произведение элементов массива; в случае двумерного массива - это вектор-строка, содержащая произведения элементов каждого столбца.
Функция cpx = cumprod(X), кроме того, возвращает все промежуточные результаты.
Пример:
Рассмотрим массив M = magic(3).
| M = | 8 | 1 | 6 | |
| 3 | 5 | 7 | ||
| 4 | 9 | 2 |
| cumprod(M) | prod(M) | ||||||||||||||||||
|
|
Сопутствующие функции: CUMSUM, SUM.
SORT - сортировка элементов массива по возрастанию
Синтаксис:
Y = sort(X)
[Y, I] = sort(X)
Описание:
Функция Y = sort(X) в случае одномерного массива упорядочивает элементы массива по возрастанию; в случае двумерного массива происходит упорядочение элементов каждого столбца.
Функция [Y, I] = sort(X) кроме массива упорядоченных элементов по столбцам возвращает массив индексов, позволяющих восстановить структуру исходного массива. Такое восстановление можно реализовать с помощью следующего цикла:
for j = 1:3
X(I(:, j), j) = Y(:, j);
end
Если анализируемый массив содержит комплексные элементы, то сортировка выполняется для массива abs(X).
Пример:
Рассмотрим массив M = magic(3).
| M = | 8 | 1 | 6 | |
| 3 | 5 | 7 | ||
| 4 | 9 | 2 |
[Y, I] = sort(M)
| Y = | 3 | 1 | 2 | I = | 2 | 1 | 3 | |
| 4 | 5 | 6 | 3 | 2 | 1 | |||
| 8 | 9 | 7 | 1 | 3 | 2 |
Сопутствующие функции: MIN, MAX, MEAN, MEDIAN, FIND.
MAX - определение максимальных элементов массива
Синтаксис:
Y = max(X)
[Y, I] = max(X)
C = max(A, B)
Описание:
Функция Y= max(X) в случае одномерного массива возвращает наибольший элемент; в случае двумерного массива - это вектор-строка, содержащая максимальные элементы каждого столбца. Таким образом, max(max(X)) - это наибольший элемент массива.
Функция [Y, I] = max(X) кроме самих максимальных элементов возвращает вектор-строку индексов этих элементов в данном столбце.
Функция C = max(A, B) возвращает массив C тех же размеров, какие имеют массивы A и B, каждый элемент которого есть максимальный из соответствующих элементов этих массивов.
Если анализируемый массив содержит комплексные элементы, то максимальные элементы определяются из условия max(abs(X)). Если массив содержит один или несколько элементов типа NaN, то результатом операции будет NaN.
Пример:
Рассмотрим массив M = magic(3).
| M = | 8 | 1 | 6 | |
| 3 | 5 | 7 | ||
| 4 | 9 | 2 |
| y = max(M) | [y, I] = max(M) | max(max(M)) |
| y = 8 9 7 | y = 8 9 7 I = 1 3 2 |
9 |
Сопутствующие функции: MIN, SORT.
MIN - определение минимальных элементов массива
Синтаксис:
Y = min(X)
[Y, I] = min(X)
C = min(A, B)
Описание:
Функция Y = min(X) в случае одномерного массива возвращает наименьший элемент; в случае двумерного массива - это вектор-строка, содержащая минимальные элементы каждого столбца. Таким образом, min(min(X)) - это наименьший элемент массива.
Функция [Y, I] = min(X) кроме самих минимальных элементов возвращает вектор-строку индексов этих элементов в данном столбце.
Функция C = min(A, B) возвращает массив C тех же размеров, какие имеют массивы A и B, каждый элемент которого есть минимальный из соответствующих элементов этих массивов.
Если анализируемый массив содержит комплексные элементы, то минимальные элементы определяются из условия min(abs(X)). Если массив содержит один или несколько элементов типа NaN, то результатом операции min будет NaN.
Пример:
Рассмотрим массив M = magic(3).
| M = | 8 | 1 | 6 | |
| 3 | 5 | 7 | ||
| 4 | 9 | 2 |
| y = min(M) | [y, I] = min(M) | min(min(M)) |
| y = 3 1 2 | y = 3 1 2 I = 2 1 3 |
1 |
Сопутствующие функции: MAX, SORT.
MEDIAN - определение срединных значений (медиан) элементов массива
Синтаксис:
mdx = median(X)
Описание:
Функция mdx = median(X) в случае одномерного массива возвращает значение срединного элемента; в случае двумерного массива - это вектор-строка, содержащая значение срединных элементов каждого столбца. Таким образом, median(median(X)) - это срединный элемент (медиана) массива, что совпадает со значением median(X(:)).
Пример:
Рассмотрим массив M = magic(4).
| M = | 16 | 2 | 3 | 13 | |
| 5 | 11 | 10 | 8 | ||
| 9 | 7 | 6 | 12 | ||
| 4 | 14 | 15 | 1 |
| mdx = median(M) | median(median(M)) | |
| mdx = 7 9 8 10 | ans = 8.5000 |
Сопутствующие функции: MEAN, STD, COV, CORRCOEF.
MEAN - определение средних значений элементов массива
Синтаксис:
mx = mean(X)
Описание:
Функция mx = mean(X) в случае одномерного массива возвращает арифметическое среднее элементов массива; в случае двумерного массива - это вектор-строка, содержащая арифметическое среднее элементов каждого столбца. Таким образом, mean(mean(X)) - это арифметическое среднее (математическое ожидание) элементов массива, что совпадает со значением mean(X(:)).
Пример:
Рассмотрим массив M = magic(4).
| M = | 16 | 2 | 3 | 13 | |
| 5 | 11 | 10 | 8 | ||
| 9 | 7 | 6 | 12 | ||
| 4 | 14 | 15 | 1 |
| mx = mean(M) | mean(mean(M)) | |
| mx = 8.5000 8.5000 8.5000 8.5000 | ans = 8.5000 |
Сопутствующие функции: MEDIAN, STD, COV, CORRCOEF.
STD - определение стандартных отклонений элементов массива
Синтаксис:
sx = std(X)
Описание:
Функция sx = std(X) в случае одномерного массива возвращает стандартное отклонение элементов массива; в случае двумерного массива - это вектор-строка, содержащая стандартное отклонение элементов каждого столбца.
Пример:
Рассмотрим массив M = magic(4).
| M = | 16 | 2 | 3 | 13 | |
| 5 | 11 | 10 | 8 | ||
| 9 | 7 | 6 | 12 | ||
| 4 | 14 | 15 | 1 |
sx = std(M)
sx = 5.4467 5.1962 5.1962 5.4467
Сопутствующие функции: MEDIAN, MEAN, COV, CORRCOEF.
COV - определение ковариационной матрицы элементов массива
Синтаксис:
C = cov(X)
C = cov(X, y)
Описание:
Функция C = cov(X) в случае одномерного массива возвращает дисперсию элементов массива; в случае двумерного массива, когда каждый столбец рассматривается как переменная, а каждая строка - как наблюдение, cov(X) - это матрица ковариаций, diag(cov(X)) - вектор дисперсий, sqrt(diag(cov(X))) - вектор стандартных отклонений для каждого столбца.
Функция C = cov(X, y), где массивы X и Y имеют одинаковое количество строк, равносильна функции cov([X Y]).
Пример: Рассмотрим массив M = magic(4)/norm(magic(4)).
| M = | 0.4706 | 0.0588 | 0.0882 | 0.3824 | |
| 0.1471 | 0.3235 | 0.2941 | 0.2353 | ||
| 0.2647 | 0.2059 | 0.1765 | 0.3529 | ||
| 0.1176 | 0.4118 | 0.4412 | 0.0294 |
| C = cov(X) | diag(cov(X)) | sqrt(diag(cov(X))) | ||||||||||||||||||||||||
|
|
|
Алгоритм: Вычисление матрицы ковариаций реализуется следующим алгоритмом:
[n, p] = size(X);
X = X - ones(n, 1) * mean(X);
C = X’ * X/(n - 1);
Сопутствующие функции: CORRCOEF, MEAN, STD.
CORRCOEF - определение коэффициентов корреляции элементов массива
Синтаксис:
S = corrcoef(X)
S = corrcoef(X, Y)
Описание:
Функция S = corrcoef(X) возвращает матрицу коэффициентов корреляции для двумерного массива, когда каждый столбец рассматривается как переменная, а каждая строка - как наблюдение.
Элементы матрицы S = corrcoef(X) связаны с элементами матрицы ковариаций C = cov(X) следующим соотношением:
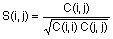 .
.
Функция S = corrcoef(X, Y), где массивы X и Y имеют одинаковое количество строк, равносильна функции corrcoef([X Y]).
Пример:
Рассмотрим массив M = magic(4)/norm(magic(4)).
| M = | 0.4706 | 0.0588 | 0.0882 | 0.3824 | |
| 0.1471 | 0.3235 | 0.2941 | 0.2353 | ||
| 0.2647 | 0.2059 | 0.1765 | 0.3529 | ||
| 0.1176 | 0.4118 | 0.4412 | 0.0294 |
| S = corrcoef(M) | C = cov(X) | ||||||||||||||||||||||||||||||||
|
|
Сопутствующие функции: COV, MEAN, STD.
DIFF - вычисление конечных разностей и приближенное дифференцирование
Синтаксис:
y = diff(x)
y = diff(x, n)
Описание:
Функция y = diff(x) вычисляет конечные разности. Если x - одномерный массив вида x = [x(1) x(2) ... x(n)], то diff(x) - это вектор разностей соседних элементов diff(x) = [x(2) - x(1) x(3) - x(2) ... x(n) - x(n-1)]. Количество элементов вектора x на единицу меньше количества элементов вектора diff(x). Если X - двумерный массив, то берутся разности столбцов diff(X) = X(2:m, :) - X(1:m-1, :).
Функция y = diff(x, n) вычисляет конечные разности порядка n, удовлетворяющие рекуррентному соотношению diff(x, n) = diff(x, n-1).
Аппроксимацией производной n порядка является отношение diff(y, n)./diff(x, n).
При наличии специализированного пакета Symbolic Math Toolbox [1] возможно реализовать точное дифференцирование в символьном виде, используя следующие функции пакета:
- diff(S) дифференцирует символьное выражение S по свободной переменной;
- diff(S, ‘v’) дифференцирует символьное выражение S по v;
- diff(S, n) и diff(S, ‘v’, n) дифференцирует n раз символьное выражение S;
- diff без аргументов дифференцирует предшествующее выражение.
Сопутствующие функции: GRADIENT, DEL2.
Ссылки:
1. Symbolic Mathematics Toolbox. User’s Guide. Natick: The MathWorks, Inc., 1994.
GRADIENT - конечные разности и приближенное вычислениеградиента функции от двух переменных
Синтаксис:
[px, py] = gradient(F)
[px, py] = gradient(F, dx, dy)
Описание:
Функция [px, py] = gradient(F) вычисляет конечные разности функции F(x, y), заданной на двумерной сетке и представляющей собой массив чисел.
Функция [px, py] = gradient(F, dx, dy) возвращает численные значения производных функции F в виде массивов px = dF/dx и py = dF/dy, где dx и dy могут быть скалярами, равными шагам разбиения сетки по осям x и y, либо векторами координат узлов сетки при разбиении с переменным шагом.
Пример:
Рассмотрим расчет и построение поля направлений для функции
F = 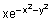
с использованием функции gradient.
[x, y] = meshgrid(-2:.2:2, -2:.2:2);
z = x .* exp(-x.^2 - y.^2);
[px, py] = gradient(z, .2, .2);
contour(z), hold on, quiver(px, py), hold off
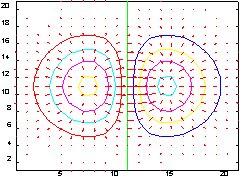
Сопутствующие функции: DIFF, DEL2, QUIVER, CONTOUR.
DEL2 - пятиточечная аппроксимация Лапласиана
Синтаксис:
V = del2(U)
Описание:
Функция V = del2(U) возвращает массив того же размера, каждый элемент которого равен разности среднего значения соседних элементов и элемента рассматриваемого узла. Узлы сетки во внутренней области имеют четырех соседей, а на границе и в углах - только трех или двух соседей.
Если массив U рассматривать как функцию U(x, y), вычисленную в точках квадратной сетки, то 4del2(U) является конечно-разностной аппроксимацией дифферренциального оператора Лапласа, примененного к функции U.
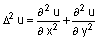 .
.
Пример:
Функция u(x, y) = x2 + y2 имеет лапласиан, равный D2u = 4, в чем можно убедиться, взглянув на графики этих функций.
[x, y] = meshgrid(-4:4, -3:3);
U = x.* x + y.* y,
U =
| 25 | 18 | 13 | 10 | 9 | 10 | 13 | 18 | 25 | |
| 20 | 13 | 8 | 5 | 4 | 5 | 8 | 13 | 20 | |
| 17 | 10 | 5 | 2 | 1 | 2 | 5 | 10 | 17 | |
| 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | |
| 17 | 10 | 5 | 2 | 1 | 2 | 5 | 10 | 17 | |
| 20 | 13 | 8 | 5 | 4 | 5 | 8 | 13 | 20 | |
| 25 | `8 | 13 | 10 | 9 | 10 | 13 | 18 | 25 |
V = 4 * del2(U),
V =
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
surfl(U), surfl(V)
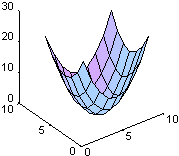 |
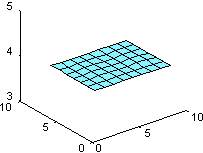 |
Сопутствующие функции: GRADIENT, DIFF.
Аппроксимация и интерполяция данных
POLYFIT - аппроксимация данных полиномом
Синтаксис:
p = polyfit(x, y, n)
Описание:
Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n +1, содержащая коэффициенты аппроксимирующего полинома.
Пример:
Рассмотрим аппроксимацию функции ошибки erf(x), которая является ограниченной сверху функцией, в то время как аппроксимирующие полиномы неограниченны, что приводит к ошибкам аппроксимации.
x = (0:0.1:2.5)';
y = erf(x);
вычислим коэффициенты аппроксимирующего полинома степени 6:
p = polyfit(x, y, 6)
p = 0.0084 -0.0983 0.4217 -0.7435 0.1471 1.1064 0.0004
вычислим значения полинома в точках сетки:
f = polyval(p, x);
сформируем следующую таблицу данных:
table = [x y f y-f]
table =
|
|
Из таблицы видно, что на отрезке [0 2.5] точность аппроксимации находится в пределах 3-4 знаков; построим графики функции и аппроксимирующего полинома на отрезке [0 5].
x = (0:0.1:5)';
y = erf(x);
f = polyval(p, x);
plot(x, y, 'ob', x, f, '-g'), » axis([0 5 0 2])
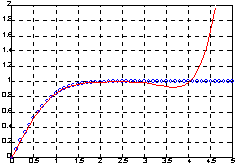
Как следует из анализа графика, аппроксимация вне отрезка [0 2.5] расходится.
Алгоритм:
Аппроксимация полиномом связана с вычислением матрицы Вандермонда V, элементами которой являются базисные функции
![]() ,
,
и последующим решением переопределенной системы линейных уравнений
Vp = y.
Пользователь может самостоятельно внести изменения в М-файл polyfit, чтобы применить другие базисные функции.
Сопутствующие функции: POLY, POLYVAL, VANDER.
INTERPFT - аппроксимация периодической функции на основе быстрого преобразования Фурье
Синтаксис:
yp = interpft(y, n)
Описание:
Функция yp = interpft(y, n) возвращает одномерный массив чисел, который является периодической функцией, определенной в n точках и аппроксимирующей одномерный массив y. Если length(x) = m, а интервал дискретности dx, то интервал дискретности для y определяется по формуле dy = dx * m/n, причем n всегда превышает m.
Пример:
Рассмотрим аппроксимацию функции y = sin(x), которая задана 11 точками на интервале [0 10].
x = 0:10; y = sin(x);
xp = 0:0.25:10;
yp = interpft(y, 41);
xt = 0:0.01:10; yt = sin(xt);
plot(xt, yt, 'r'), hold on, plot(x, y, 'ob', xp, yp)
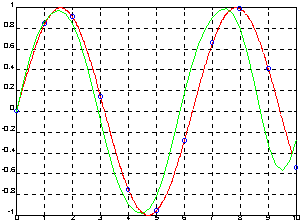
На графике построена точная функция y = sin(x) с указанием точек съема данных и ее аппроксимация в 41 точке. Как видно из графика, аппроксимация вне интервала [0 1.5] имеет нарастающую погрешность.
Сопутствующие функции: ICUBIC, SPLINE, INTERP1.
ICUBIC - кубическая интерполяция функции одной переменной
Синтаксис:
yi = icubic(y, xi)
yi = icubic(x, y, xi)
Описание:
Функция yi = icubic(y, xi) интерполирует значения функции y в точках xi внутри области определения функции, используя кубические полиномы. Если Y - двумерный массив, то интерполирующая кривая строится для каждого столбца. Если указано значение xi вне области определения функции, то результатом будет NaN.
Функция yi = icubic(x, y, xi) позволяет использовать более мелкую сетку xi при условии, что аргумент x изменяется монотонно и сетка равномерна.
Пример:
Зададим синусоиду всего 10 точками и проведем интерполяцию, используя мелкую сетку.
x = 0:10; y = sin(x);
xi = 0:.25:10;
yi = icubic(x, y, xi);
plot(x, y, 'o', xi, yi, ‘g’), grid.
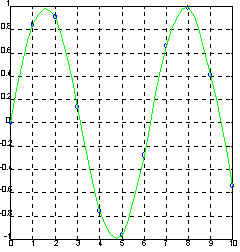
Сопутствующие функции: POLYFIT, SPLINE.
SPLINE, PPVAL, MKPP, UNMKPP - интерполяция функции одной переменной кубическим сплайном
Синтаксис:
| yi = spline(x, y, xi) | v = ppval(pp, xx) | |
| pp = spline(x, y) | [breaks, coefs, l, k] = unmkpp(pp) | |
| pp = mkpp(breaks, coefs) |
Описание:
Функция yi = spline(x, y, xi) интерполирует значения функции y в точках xi внутри области определения функции, используя кубические сплайны [1].
Функция pp = spline(x, y) возвращает pp-форму сплайна, используемую в М-файлах ppval, mkpp, unmkpp.
Функция v = ppval(pp, xx) вычисляет значение кусочно-гладкого полинома pp для значений аргумента xx.
Функция [breaks, coefs, l, k] = unmkpp(pp) возвращает характеристики кусочно гладкого полинома pp:
breaks - вектор разбиения аргумента;
coefs - коэффициенты кубических сплайнов;
l = length(breaks) - 1;
k = length(coefs)/l.
Функция pp = mkpp(breaks, coefs) формирует кусочно-гладкий полином pp по его характеристикам.
Пример:
Зададим синусоиду всего 10 точками и проведем интерполяцию кубическими сплайнами, используя мелкую сетку.
x = 0:10; y = sin(x);
xi = 0:.25:10;
yi = spline(x, y, xi);
plot(x, y, 'o', xi, yi, ‘g’), grid
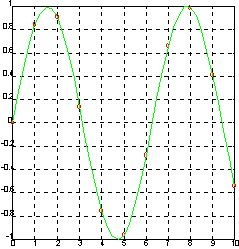
Определим pp-форму сплайна.
pp = spline(x, y);
[breaks, coeffs, l, k] = unmkpp(pp)
breaks = 0 1 2 3 4 5 6 7 8 9 10
coeffs =
| -0.0419 | -0.2612 | 1.1446 | 0 | |
| -0.0419 | -0.3868 | 0.4965 | 0.8415 | |
| 0.1469 | -0.5124 | -0.4027 | 0.9093 | |
| 0.1603 | -0.0716 | -0.9867 | 0.1411 | |
| 0.0372 | 0.4095 | -0.6488 | -0.7568 | |
| -0.1234 | 0.5211 | 0.2818 | -0.9589 | |
| -0.1684 | 0.1509 | 0.9538 | -0.2794 | |
| -0.0640 | -0.3542 | 0.7506 | 0.6570 | |
| 0.1190 | -0.5463 | -0.1499 | 0.9894 | |
| 0.1190 | -0.1894 | -0.8856 | 0.4121 |
l = 10
k = 4
Вычислим pp-форму в узловых точках сетки.
v = ppval(pp,x)
v =
| 0 | 0.8415 | 0.9093 | 0.1411 | -0.7568 | -0.9589 | -0.2794 | 0.6570 | 0.9894 | 0.4121 | -0.5440 |
Алгоритм:
Интерполяция сплайнами использует вспомогательные функции ppval, mkpp, unmkpp, которые образуют небольшой пакет для работы с кусочно-гладкими полиномами.
Существенно большие возможности для работы со сплайнами предо-ставляет пользователю специализированный пакет Spline Toolbox [2].
Сопутствующие функции: ICUBIC, INTERP1, POLYFIT, Spline Toolbox.
Ссылки:
- Carl de Boor. A Practical Guide to Splines. Berlin, 1978.
- Spline Toolbox. User’s Guide. Natick: The MathWorks, Inc., 1992.
INTERP1 - одномерная табличная интерполяция
Синтаксис:
yi = interp1(x, y, xi)
yi = interp1(x, y, xi, ‘<метод>‘)
Описание:
Функция yi = interp1(x, y, xi) строит интерполирующую кривую для одномерного массива y, заданного на сетке x; выходной массив yi может быть определен на более мелкой сетке xi. Если Y - двумерный массив, то интерполирующая кривая строится для каждого столбца. По умолчанию реализована линейная интерполяция.
Функция yi = interp1(x, y, xi, ‘<метод>‘) позволяет задать метод интерполяции:
| ‘linear’ | линейная | |
| ‘cubic’ | кубическая | |
| ‘spline’ | кубические сплайны |
Принято, что аргумент x изменяется монотонно; кроме того, для кубической интерполяции предполагается, что сетка по x равномерна.
Пример:
Зададим синусоиду всего 10 точками и проведем интерполяцию, используя мелкую сетку.
x = 0:10; y = sin(x);
xi = 0:.25:10;
yi = interp1(x, y, xi);
plot(x, y, 'o', xi, yi, ‘g’), hold on
yi = interp1(x, y, xi, ‘spline’ );
plot(x, y, 'ob', xi, yi, ‘m’), grid, hold off
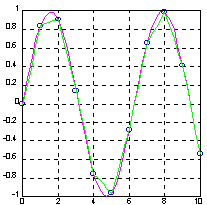
Алгоритм:
Методы линейной и кубической интерполяции реализуются довольно просто; что же касается интерполяции сплайнами, то в этом случае используются вспомогательные функции ppval, mkpp, unmkpp, которые образуют небольшой пакет для работы с кусочно-гладкими полиномами.
Существенно большие возможности пользователям для решения проблем интерполяции и аппроксимации предоставляет специализированный пакет Spline Toolbox [1].
Сопутствующие функции: INTERPFT, INTERP2, GRIDDATA.
Ссылки:
1. Spline Toolbox. User’s Guide. Natick: The MathWorks, Inc., 1992.
INTERP2 - двумерная табличная интерполяция
Синтаксис:
ZI = interp2(X, Y, XI, YI)
ZI = interp2(X, Y, XI, YI, ‘<метод>‘)
Описание:
Функция ZI = interp2(X, Y, XI, YI) интерполирует данные, определяющие некоторую поверхность на двумерной сетке {X, Y}; выходной массив ZI может быть определен на более мелкой сетке {XI, YI}. По умолчанию реализована линейная интерполяция.
Функция ZI = interp2(X, Y, XI, YI, ‘<метод>‘) позволяет задать метод интерполяции:
| ‘linear’ | линейная | |
| ‘cubic’ | кубическая |
Принято, что аргументы X и Y изменяются монотонно; кроме того, для кубической интерполяции предполагается, что сетка {X, Y} равномерна.
Пример:
Проведем интерполяцию функции peaks, используя мелкую сетку.
[X, Y] = meshgrid(-3:0.25:3);
Z = peaks(X, Y);
[XI, YI] = meshgrid(-3:0.125:3);
ZI = interp2(X, Y, Z, XI, YI);
mesh(X, Y, Z), hold on, mesh(XI, YI, ZI+15), hold off
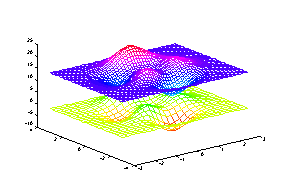
Сопутствующие функции: INTERPFT, INTERP1, GRIDDATA.
GRIDDATA - двумерная табличная интерполяция на неравномерной сетке
Синтаксис:
ZI = griddata(x, y, z, XI, YI)
[XI, YI, ZI] = griddata(x, y, z, XI, YI)
Описание:
Функция ZI = griddata(x, y, z, XI, YI) возвращает массив ZI, который определен на новой сетке {XI, YI} в результате интерполяции исходной функции z, заданной на неравномерной сетке {x, y}.
Функция [XI, YI, ZI] = griddata(x, y, z, XI, YI) кроме массива ZI возвращает массивы XI, YI, упорядоченные по аналогии с функцией meshgrid.
Пример:
Определим функцию на сетке, заданной 100 точками, выбранными случайно на отрезке [-2 2].
x = rand(100, 1) * 4 - 2;
y = rand(100, 1) * 4 - 2;
z = x.*exp(-x.^2 - y.^2);
Векторы x, y, z определяют 100 случайных точек на поверхности функции ZI, которую зададим на следующей равномерной сетке:
ti = -2:0.25:2;
[XI, YI] = meshgrid(ti, ti);
ZI = griddata(x, y, z, XI, YI);
Построим поверхность функции, полученной в результате интерполяции на неравномерной случайной сетке.
mesh(XI, YI, ZI), hold on, plot3(x, y, z, 'or')
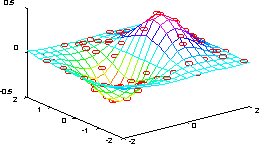
Сопутствующие функции: INTERP1, INTERP2.
Численное интегрирование
TRAPZ - интегрирование методом трапеций
Синтаксис:
I = trapz(x, y)
I = trapz(y)
Описание:
Функция I = trapz(x, y) вычисляет интеграл от функции y по переменной x, используя метод трапеций. Аргументы x и y могут быть одномерными массивами одинакового размера, либо массив Y может быть двумерным, но тогда должно выполняться условие size(Y, 1) = length(x). В последнем случае вычисляется интеграл для каждого столбца.
Функция I = trapz(y) вычисляет интеграл, предполагая, что шаг интегрирования постоянен и равен единице; в случае, когда шаг h отличен от единице, но постоянен, достаточно вычисленный интеграл умножить на h.
Примеры:
Вычислим интеграл
I = 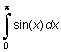 .
.
Его точное значение равно двум.
Выберем равномерную сетку
x = 0:pi/100:pi; y = sin(x);
тогда оба интеграла
I = trapz(x, y) и I = pi/100*trapz(y)
дают одинаковый результат:
I = 1.9998.
Образуем неравномерную сетку, используя генератор случайных чисел.
x = sort(rand(1,101)*pi); y = sin(x);
I = trapz(x, y)
I = 1.9987.
Результат еще менее точен, поскольку максимальный из шагов max(diff(x)) равен 0.1810
Сопутствующие функции: SUM, CUMSUM, QUAD, QUAD8.
QUAD, QUAD8 - вычисление интегралов методом квадратур
Синтаксис:
[I, cnt] = quad(‘<имя функции>‘, a, b)
[I, cnt] = quad(‘<имя функции>‘, a, b, tol)
[I, cnt] = quad(‘<имя функции>‘, a, b, tol, trace)
[I, cnt] = quad8(‘<имя функции>‘, a, b)
[I, cnt] = quad8(‘<имя функции>‘, a, b, tol)
[I, cnt] = quad8(‘<имя функции>‘, a, b, tol, trace)
Описание:
Квадратура - это численный метод вычисления площади под графиком функции, то есть вычисление определенного интеграла вида
I = 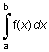 .
.
Функции quad и quad8 используют разные квадратурные формулы.
Функции [I, cnt] = quad(‘<имя функции>‘, a, b) и [I, cnt] = quad8(‘<имя функции>‘, a, b) вычисляют интеграл от заданной функции; последняя может быть как встроенной функцией, так и М-файлом. Переменная cnt содержит информацию о том, сколько раз в процессе интегрирования вычислялась подынтегральная функция.
Функции [I, cnt] = quad(‘<имя функции>‘, a, b, tol) и [I, cnt] = quad8(‘<имя функции>‘, a, b, tol) вычисляют интеграл с заданной относительной погрешностью tol. По умолчанию tol = 1e-3.
Функции [I, cnt] = quad(‘<имя функции>‘, a, b, tol, trace) и [I, cnt] = quad8(‘<имя функции>‘, a, b, tol, trace), когда аргумент trace не равен нулю, строят график, показывающий ход вычисления интеграла.
Примеры:
Вычислим интеграл
I = 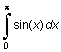 .
.
Его точное значение равно двум.
| [I, cnt] = quad('sin', 0, pi) | [I, cnt] = quad('sin', 0, pi, 1e-4, 1) | |
| I = 2.0000 | I = 2.0000 | |
| cnt = 17 | cnt = 33 |
Как следует из анализа полученных данных, при увеличении точности вычисления на порядок почти вдвое увеличивается трудоемкость расчетов. График с результатами промежуточных расчетов показан на рисунке.
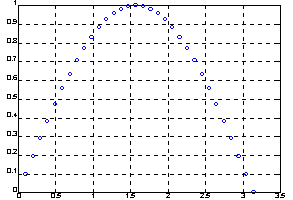
Алгоритм:
Функция quad использует квадратурные формулы Ньютона - Котеса 2-го порядка (правило Симпсона), а функция quad8 - формулы 8-го порядка [1-2]. При наличии в подынтегральной функции особенностей типа
I = 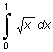
предпочтительнее использовать процедуру quad8.
Диагностические сообщения:
Функции quad и quad8 используют рекурсивный вызов. Для того чтобы предотвратить бесконечную рекурсию при вычислении сингулярных интегралов, глубина рекурсии ограничена уровнем 10. При достижении этого ограничения выдается сообщение
Recursion level limit reached in quad. Singularity likely.
В процедуре quad достигнута предельная глубина рекурсии. Функция, возможно, сингулярна.
Ограничения:
Функции quad и quad8 не позволяют интегрировать функции с особенностями типа
I = 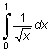 .
.
В этом случае рекомендуется выделить такие члены и проинтегрировать их аналитически, а к остатку применить процедуры quad и quad8.
Сопутствующие функции: SUM, CUMSUM, TRAPZ.
Ссылки:
- Forsythe G. E., Malcolm M. A., Moler C. B. Computer Methods for Mathematical Computations. Prentice-Hall, 1977.
- Справочник по специальным функциям: Пер. с англ./Под ред. М. Абрамовица и И. Стиган. М.: Наука, 1979.
Интегрирование обыкновенных дифференциальных уравнений (ОДУ)
ODE23, ODE45 - решение задачи Коши для систем ОДУ
Синтаксис:
[t, X] = ode23(‘<имя функции>‘, t0, tf, x0)
[t, X] = ode23(‘<имя функции>‘, t0, tf, x0, tol, trace)
[t, X] = ode45(‘<имя функции>‘, t0, tf, x0)
[t, X] = ode45(‘<имя функции>‘, t0, tf, x0, tol, trace)
Описание:
Функции ode23 и ode45 предназначены для численного интегрирования систем ОДУ. Они применимы как для решения простых дифференциальных уравнений, так и для моделирования сложных динамических систем.
Любая система нелинейных ОДУ может быть представлена как система дифференциальных уравнений 1-го порядка в явной форме Коши:
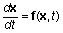 ,
,
где x - вектор состояния;
t - время;
f - нелинейная вектор-функция от переменных x, t.
Функции [t, X] = ode23(‘<имя функции>‘, t0, tf, x0, tol, trace) и [t, X] = = ode45(‘<имя функции>‘, t0, tf, x0, tol, trace) интегрируют системы ОДУ, используя формулы Рунге - Кутты соответственно 2-го и 3-го или 4-го и 5-го порядка.
Эти функции имеют следующие параметры:
Входные параметры:
‘<имя функции>‘ - строковая переменная, являющаяся именем М-файла, в котором вычисляются правые части системы ОДУ;
t0 - начальное значение времени; tfinal - конечное значение времени;
x0 - вектор начальных условий;
tol - задаваемая точность; по умолчанию для ode23 tol = 1.e-3, для ode45 tol = 1.e-6);
trace - флаг, регулирующий вывод промежуточных результатов; по умолчанию равен нулю, что подавляет вывод промежуточных результатов;
Выходные параметры:
t - текущее время;
X - двумерный массив, где каждый столбец соответствует одной переменной.
Примеры:
Рассмотрим дифференциальное уравнение 2-го порядка, известное как уравнение Ван дер Поля,

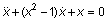
 .
.
Это уравнение может быть представлено в виде системы ОДУ в явной форме Коши:
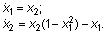
Первый шаг процедуры интегрирования - это создание М-файла для вычисления правых частей ОДУ; присвоим этому файлу имя vdpol.
function xdot = vdpol(t, x)
xdot = [x(2); x(2) .* (1 - x(1).^2) - x(1)];
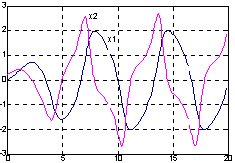
Чтобы проинтегрировать систему ОДУ, определяемых функцией vdpol в интервале времени 0 <= t <= 20, вызовем функцию ode23:
t0 = 0; tf = 20;
x0 = [0 0.25]'; %Начальные условия
[t, X] = ode23('vdpol', t0, tf, x0);
plot(t, X), grid, hold on
gtext('x1'), gtext('x2')
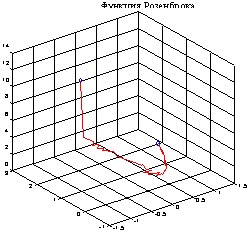
Рассмотрим простейший из известных примеров странного аттрактора - аттрактор Ресслера [1]:
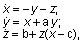
где параметры {a, b, c} имеют значения {0.2 0.2 5.7}, а начальное условие задается следующим образом: x0 = [-0.7 -0.7 1].
Для того чтобы проинтегрировать эту систему в интервале времени 0<= t<= 20, вызовем функцию ode45:
t0 = 0; tf = 20;
x0 = [-0.7 -0.7 1]’.%Начальные условия
[t, X] = ode45('ressler', t0, tf, x0);
comet3(X(:, 1), X(:, 2), X(:, 3)).
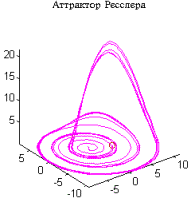
Алгоритм:
Функции ode23 и ode45 реализуют методы Рунге - Кутты с автоматическим выбором шага, описанные в работе [2]. Такие алгоритмы используют тем большее количество шагов, чем медленнее изменяется функция. Поскольку функция ode45 использует формулы более высокого порядка, обычно требуется меньше шагов интегрирования и результат достигается быстрее. Для сглаживания полученных процессов можно использовать функцию interp1.
Диагностические сообщения:
Если функции ode23 и ode45 не могут выполнить интегрирование во всем заданном диапазоне времени выдается сообщение
Singularity likely.
Система сингулярна.
В состав версии 4.0 помимо функций ode23 и ode45 включена также функция ode23p, которая позволяет в процессе интегрирования строить в трехмерном пространстве орбиты движения для трех первых переменных состояния. Перед обращением к этой функции пользователь должен задать диапазоны изменения этих переменных, чтобы определить размер графика, используя следующие операторы:
axis([x1min x1max x2min x2max x3min x3max]);
hold .
Для получения тех же результатов вместо этой не столь очевидной процедуры целесообразно использовать такую последовательность:
[t, X] = ode23(‘<имя функции>‘, t0, tf, x0, tol, trace);
comet3(X(:, 1), X(:, 2), X(:, 3));.
В этом случае построение орбиты реализуется автоматически, но после выполнения процедуры интегрирования. Кроме того, в данном случае пользователь может выбирать любые переменные состояния.
Для эффективного моделирования сложных динамических систем с непрерывным и дискретным временем рекомендуется использовать специализированную систему SIMULINK [3], входящую в состав программных продуктов, выпускаемых фирмой The MathWorks, Inc.
Ссылки:
- Хакен Г. Синергетика: иерархии неустойчивостей в самоорганизующихся системах и устройствах. М.: Мир, 1985. 423 с.
- Forsythe G. E., Malcolm M. A., Moler C. B. Computer Methods for Mathematical Computations. Prentice-Hall, 1977.
- SIMULINK. User’s Guide. Natick: The MathWorks, Inc., 1990.
Вычисление минимумов и нулей функции
FMIN, FORTIONS - минимизация функции одной переменной
Синтаксис:
xmin = fmin(‘<имя функции>‘, x1, x2)
xmin = fmin(‘<имя функции>‘, x1, x2, options)
[xmin, options] = fmin(‘<имя функции>‘, x1, x2, options, p1,..., p10)
options = foptions
Описание:
Функция xmin = fmin(‘<имя функции>‘, x1, x2) возвращает значение локального минимума функции в интервале x1<= x<= x2.
Функция xmin = fmin(‘<имя функции>‘, x1, x2, options) использует вектор управляющих параметров options, который включает 18 компонентов, описанных ниже. Он предназначен для настройки алгоритмов оптимизации, применяемых как в системе MATLAB, так и в пакете программ Optimization Toolbox [1]. Функция fmin использует только 3 из этих параметров: options(1), options(2), options(14).
Функция [xmin, options] = fmin(‘<имя функции>‘, x1, x2, options, p1,..., p10) позволяет передать до 10 параметров, а кроме того, возвращает вектор управляющих параметров options, которые использовались алгоритмом, и в частности, параметр options(10), фиксирующий количество выполненных итераций, и параметр options(8), содержащий минимальное значение функции.
Функция options = foptions возвращает вектор-строку исходных значений параметров, используемых функциями fmin и fmins системы MATLAB и функциями fminu, constr, attgoal, minimax, leastsq, fsolve пакета Optimization Toolbox. Значения по умолчанию присваиваются внутри функций оптимизации и могут отличаться от исходных значений.
| Опция | Назначение опции | Исходное значение | Значение по умолчанию |
| options(1) | Вывод промежуточных результатов: 0 - не выводятся; 1 - выводятся | 0 | 0 |
| options(2) | Итерационная погрешность для аргумента | 1e-4 | 1e-4 |
| options(3) | Итерационная погрешность для функции | 1e-4 | 1e-4 |
| options(4) | Терминальный критерий соблюдения ограничений | 1e-6 | 1e-6 |
| options(5) | Стратегия | 0 | 0 |
| options(6) | Оптимизация | 0 | 0 |
| options(7) | Алгоритм линейного поиска | 0 | 0 |
| options(8) | Значение целевой функции | 0 | 0 |
| options(9) | Для контроля градиента установить в 1 | 0 | 0 |
| options(10) | Количество выполненых итераций | 0 | 0 |
| options(11) | Количество вычисленных градиентов | 0 | 0 |
| options(12) | Количество вычисленных ограничений | 0 | 0 |
| options(13) | Количество ограничений в виде равенств | 0 | 0 |
| options(14) | Максимальное количество итераций, n - количество переменных | 0 | fmin: 500 fmins: 200хn |
| options(15) | Параметр, используемый прри наличии целевой функции | 0 | 0 |
| options(16) | Минимальное прриращение переменных при вычислении градиента | 1e-8 | 1e-8 |
| options(17) | Максимальное прриращение переменных при вычислении градиента | 0.1 | 0.1 |
| options(18) | Размер шага минимизации h | 0 | h <=1 |
Пример:
Вычислим приближенное значение p путем минимизации функции y = cos(x) на отрезке [3 4] с итерационной погрешностью по x - 1e-12.
[xmin, opt] = fmin('cos', 3, 4, [0, 1e-12]);
xmin = 3.141592654027715e+000
pi = 3.141592653589793e+000
norm(y-pi) = 4.3792e-010
Функция у = cos(x)
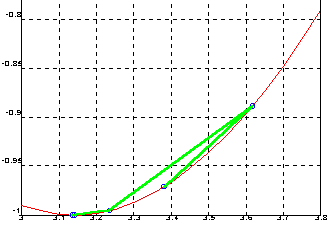
Обратите внимание, что итерационная погрешность (разница между двумя соседними итерациями) отличается от погрешности вычисления (разница между вычисленным и машинным значением p .
| Номер опции opt | Исходное значение | Значение при выходе из функции fmin | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Анализ таблицы подтверждает, что заданная итерационная погрешность opt(2) равна 1.0000e-012; минимальное значение функции opt(8) равно -1.0000e+000; число выполненных итераций opt(10) равно 9.0000e+000 при максимально допустимом числе итераций opt(14) = 5.0000e+002.
Алгоритм:
Функция fmin реализует методы “золотого сечения” и параболической интерполяции [2].
Сопутствующие функции: FMINS, FZERO, Optimization Toolbox.
Ссылки:
- Optimization Toolbox. User’s Guide. Natick: The MathWorks, Inc., 1991.
- Forsythe G. E., Malcolm M. A., Moler C. B. Computer Methods for Mathematical Computations. Prentice-Hall, 1976.
FMINS - минимизация функции нескольких переменных
Синтаксис:
xmin = fmins(‘<имя функции>‘, x0)
xmin = fmins(‘<имя функции>‘, x0, options)
[xmin, options] = fmins(‘<имя функции>‘, x0, options, [ ], arg1,..., arg10)
Описание:
Функция xmin = fmins(‘<имя функции>‘, x0) возвращает вектор xmin, соответствующий значению локального минимума функции в окрестности точки x0.
Функция xmin = fmins(‘<имя функции>‘, x0, options) использует вектор управляющих параметров options, который включает 18 компонентов, соответствующих функции foptions. Функция fmins использует только 4 из этих параметров: options(1), options(2), options(3), options(14).
Функция [xmin, options] = fmins(‘<имя функции>‘, x0, options, [ ], arg1,..., arg10) позволяет передать до 10 параметров; четвертый входной аргумент необходим, чтобы обеспечить совместимость с функцией fminu из пакета Optimization Toolbox [1]. Кроме того, возвращается вектор управляющих параметров options, которые использовались алгоритмом, и в частности, параметр options(10), фиксирующий количество выполненных итераций, и параметр options(8), содержащий минимальное значение функции.
Пример:
Рассмотрим классический пример минимизации функции Розенброка от двух переменных.
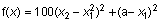 .
.
Минимум этой функции достигается в точке (a, a2) и равен нулю. В качестве начальной точки обычно выбирается точка (-1.2 1).
Определим М-файл rosenbr(x, a), обеспечивающий вычисление этой функции для заданного параметра a.
function y = rosenbr(x, a)
if nargin < 2, a = 1; end
y = 100 * (x(2) - x(1)^2)^2 + (a - x(1))^2;
Рассмотрим случай a = 1.
[xmin, opt] = fmins('rosenbr', [-1.2 1], [0, 1e-6]);
xmin = 9.999997969915502e-001 9.999995750683192e-001
| Номер опции opt | Исходное значение | Значение при выходе из функции fmin | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Анализ таблицы подтверждает, что заданная итерационная погрешность opt(2) равна 1.0000e-06; минимальное значение функции opt(8) равно 7.6989e-014; число выполненных итераций opt(10) равно 1.9900e+002 при максимально допустимом числе итераций opt(14) = 4.0000e+002.
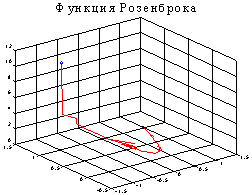
Рассмотрим случай, когда минимум сдвинут в точку (sqrt(2), 2).
[xmin, opt] = fmins('rosenbr', [-1.2 1], [0, 1e-6], [ ], sqrt(2));
xmin, opt(8), opt(10)
xmin = 1.414213634743838e+0002.000000234240279e+000
opt(8) = 9.2528e-014
opt(10) = 206
Алгоритм:
Функция fmins реализует метод Нелдера - Мида [2, 3], который является прямым методом, не требующим вычисления градиента или иной информации о производной, и связан с построением симплекса в n-мерном пространстве, который задается n+1-й вершиной. В двумерном пространстве симплекс - это треугольник, а в трехмерном - пирамида.
На каждом шагу алгоритма новая точка выбирается внутри или вблизи симплекса. Значение функции в этой точке сравнивается со значениями в вершинах симплекса, и, как правило, одна из вершин заменяется этой точкой, задавая тем самым новый симплекс. Эти итерации повторяются до тех пор, пока диаметр симплекса не станет меньше заданной величины итерационной погрешности по переменным x.
Сопутствующие функции: FMIN, FZERO, Optimization Toolbox.
Ссылки:
- Optimization Toolbox. User’s Guide. Natick: The MathWorks, Inc., 1991.
- Nelder J. A., Mead R. A Simplex Method for Function Minimization//Computer Journal. Vol. 7, P. 308-313.
- Dennis J. E., Woods D. J. New Computing Environments: Microcomputers in Large-Scale Computing, Ed. by A. Wouk. SIAM, 1987. P. 116-122.
FZERO - нахождение нулей функции одной переменной
Синтаксис:
z = fzero(‘<имя функции>‘, x0)
z = fzero(‘<имя функции>‘, x0, tol)
z = fzero(‘<имя функции>‘, x0, tol, trace)
Описание:
Функция z = fzero(‘<имя функции>‘, x0) находит нуль функции в окрестности точки x0.
Функция z = fzero(‘<имя функции>‘, x0, tol) возвращает результат с относительной погрешностью tol, задаваемой пользователем. По умолчанию tol = eps.
Функция z = fzero(‘<имя функции>‘, x0, tol, trace) позволяет выдавать на экран терминала промежуточные результаты поиска нуля функции.
Пример:
Вычислим действительные нули полинома f(x) = x4 - 4 * x3 + 12.
Сначала сформируем М-файл polynom4 для вычисления этой функции:
function y = polynom4(x)
y = x.^4 - 4*x.^3 + 12;
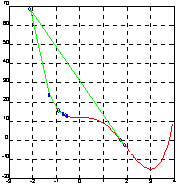
затем найдем корень полинома, стартуя из точки x0 = -0.5:
z = fzero(' polynom4', -0.5, eps, 1)
z = 1.746170944975038e+000;
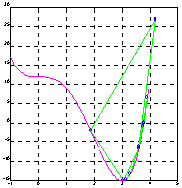
теперь найдем корень полинома, стартуя из точки x0 = 3.0:
z = fzero(' polynom4', 3, eps, 1)
z = 3.777351952771215e+000;
точные значения корней полинома могут быть вычислены с помощью функции
roots([1 -4 0 0 12])
ans =
| 3.777351952771212e+000 | |
| 1.746170944975038e+000 | |
| -7.617614488731261e-001 +1.113117638472703e+000i | |
| -7.617614488731261e-001 -1.113117638472703e+000i |
Нетрудно видеть, что оба подхода обеспечивают согласованные результаты.
На рис. а показана траектория движения из точки x0 = -0.5, а на рис. б - из точки x0 = 3.0.
 |
 |
| а) | б) |
Алгоритм:
Функция fzero использует методы деления отрезка пополам, секущей и обратной квадратической интерполяции [1, 2].
Сопутствующие функции: FMIN, ROOTS.
Ссылки:
- Brent R. Algorithms for Minimization Without Derivatives. Prentice-Hall, 1973.
- Forsythe G. E., Malcolm M. A., Moler C. B. Computer Methods for Mathematical Computations. Prentice-Hall, 1976.
FPLOT - построение графиков функции одной переменной
Синтаксис:
fplot(‘<имя функции>‘, [<интервал>])
fplot(‘<имя функции>‘, [<интервал>], n)
fplot(‘<имя функции>‘, [<интервал>], n, <приращение угла>)
fplot(‘<имя функции>‘, [<интервал>], n, <приращение угла>, <дробление шага>)
[x, Y] = fplot(‘<имя функции>‘, [<интервал>], n, <приращение угла>, <дробление шага>)
Описание:
Функция fplot(‘<имя функции>‘, [<интервал>]) строит график функции в заданном интервале [xmin xmax].
Функция fplot(‘<имя функции>‘, [<интервал>], n) строит график функции, разбивая интервал минимум на n частей. По умолчанию n = 25.
Функция fplot(‘<имя функции>‘, [<интервал>], n, <приращение угла>) строит график так, чтобы изменение угла наклона на соседнем участке отличалось не более чем на величину <приращение угла>. По умолчанию приращение угла = 10°.
Функция fplot(‘<имя функции>‘, [<интервал>], n, <приращение угла>, <дробление шага>) выполняет построение графика так, чтобы изменение угла наклона на соседнем участке отличалось не более чем на величину <приращение угла>, но требовало при этом не более чем k дроблений шага. По умолчанию <дробление шага> = 20.
Функция [x, Y] = fplot(‘<имя функции>‘, [<интервал>], n, <приращение угла>, <дробление шага>) возвращает абсциссы и ординаты функции в виде одномерного массива x и, возможно, двумерного массива Y. График при этом не строится. Построение графика можно выполнить в дальнейшем с помощью функции plot(x, y).
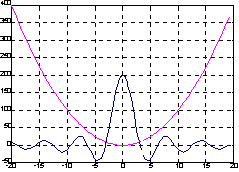
Пример:
Построим график функции, используя функцию fplot.
Сначала сформируем М-файл myfun 4 для вычисления двух функций:
function y = myfun(x)
y(:, 1) = 200 * sin(x) ./ x;
y(:, 2) = x .^ 2;
теперь построим график в интервале [-20 20] с разбиением интервала минимум на 50 частей и так, чтобы <приращение угла> не превышало 2°.
Преобразование Фурье
FFT, IFFT - одномерное дискретное прямое и обратное преобразования Фурье
Синтаксис:
| Y = fft(X) | X = ifft(Y) | |
| Y = fft(X, n) | X = ifft(Y, n) |
Описание:
Дискретные прямое и обратное преобразования Фурье для одномерного массива x длины N определяются следующим образом:
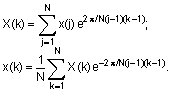
Функция Y = fft(X) вычисляет для массива данных X дискретное преобразование Фурье, используя FFT-алгоритм быстрого Фурье-преобразования. Если массив X двумерный, вычисляется дискретное преобразование каждого столбца.
Функция Y = fft(X, n) вычисляет n-точечное дискретное преобразование Фурье. Если length(X) < n, то недостающие строки массива X заполняются нулями; если length(X) > n, то лишние строки удаляются.
Функция X = ifft(Y) вычисляет обратное преобразование Фурье для массива Y.
Функция X = ifft(Y, n) вычисляет n-точечное обратное преобразование Фурье для массива Y.
Примеры:
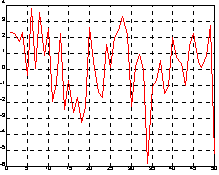
Основное назначение преобразования Фурье - выделить частоты регулярных составляющих сигнала, зашумленного помехами. Рассмотрим данные, поступающие с частотой 1000 Гц. Сформируем сигнал, содержащий регулярные составляющие с частотами 50 Гц и 120 Гц и случайную аддитивную компоненту с нулевым средним.
t = 0:0.001:0.6;
x = sin(2 * pi * 50 * t) + sin(2 * pi * 120 * t);
y = x + 2 * randn(size(t));
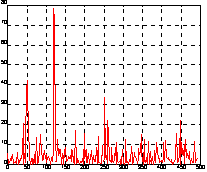
plot(y(1:50)), grid
На рис. а показан этот сигнал. Глядя на него, трудно сказать, каковы частоты его регулярных составляющих. Реализуя одномерное преобразование Фурье этого сигнала на основе 512 точек и построив график спектральной плотности (рис. б), можно выделить две частоты, на которых амплитуда спектра максимальна. Это частоты 120 и 50 Гц.
Y = fft(y, 512);
Pyy = Y.*conj(Y)/512;
f = 1000 * (0:255)/512;
figure(2), plot(f, Pyy(1:256)), grid
 |
 |
| а) | б) |
Алгоритм:
Если длина последовательности входных данных является степенью числа 2, то применяется алгоритм быстрого преобразования Фурье с основанием 2, имеющий максимальную производительность. Этот алгоритм оптимизирован для работы с действительными данными; если данные комплексные, то реализуется комплексное преобразование Фурье. Эффективность первого на 40 % выше второго.
Если длина входной последовательности не является степенью числа 2, то применяется преобразование со смешанными основаниями, которые определяются как простые множители длины входной последовательности, которая при необходимости подвергается усечению.
Время расчета существенно зависит от значения длины последовательности. Если значение длины точно разлагается на простые множители, то вычисления для такой последовательности выполняются достаточно быстро; если же не все множители оказываются простыми, и даже их будет меньше, то время вычисления существенно возрастает.
Если сравнивать эффективность вычислений, то преобразование Фурье с основанием 2 действительной последовательности из 4096 точек занимает 2.1 с, а комплексной - 3.7 с. Обычное преобразование Фурье для последовательности из 4096 точек занимает 7 с, а для последовательности из 4098 точек - 58 с.
Сопутствующие функции: FFT2, IFFT2, FFTSHIFT, Signal Processing Toolbox [1].
Ссылки:
1. Signal Processing Toolbox User’s Guide. Natick: The MathWorks, Inc., 1993.
FFT2, IFFT2 - двумерное дискретное прямое и обратное преобразования Фурье
Синтаксис:
| Y = fft2(X) | X = ifft2(Y) | |
| Y = fft2(X, m, n) | X = ifft2(Y, m, n) |
Описание:
Функция Y = fft2(X) вычисляет для массива данных X двумерное дискретное преобразование Фурье. Если массив X двумерный, вычисляется дискретное преобразование для каждого столбца.
Функция Y = fft(X, n) вычисляет n-точечное дискретное преобразование Фурье. Если length(X) < n, то недостающие строки массива X заполняются нулями; если length(X) > n, то лишние строки удаляются.
Функция X = ifft(Y) вычисляет обратное преобразование Фурье для массива Y.
Функция X = ifft(Y, n) вычисляет n-точечное обратное преобразование Фурье для массива Y.
Примеры:
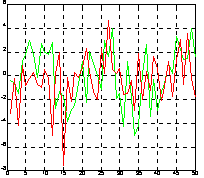
Рассмотрим тот же пример, что и для функции fft, но сформируем 2 входных последовательности (рис. а):
t = 0:0.001:0.6;
x = sin(2*pi*50*t) + sin(2*pi*120*t);
y1 = x + 2*randn(size(t));
y2 = x + 2*randn(size(t));
y = [y1; y2];
plot(y(1, 1:50)), hold on, plot(y(2, 1:50)), grid, hold off
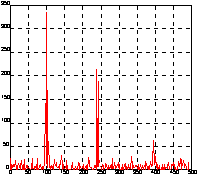
Применим двумерное преобразование Фурье для сигнала y на основе 512 точек и построим график спектральной плотности. Теперь можно выделить 2 частоты, на которых амплитуда спектра максимальна. Это частоты - 100/2Гц и 240/2Гц.
Y = fft2(y, 2, 512);
Pyy = Y.*conj(Y)/512;
f = 1000*(0:255)/512;
figure(2), plot(f, Pyy(1:256)), grid
 |
 |
| а) | б) |
Алгоритм:
Двумерное дискретное преобразование связано с одномерным дискретным преобразованием Фурье следующим образом:
fft2(X) = fft(fft(X).’).’
Сопутствующие функции: FFT, IFFT, FFTSHIFT, Signal Processing Toolbox.
Ссылки:
1. Signal Processing Toolbox User’s Guide. Natick: The MathWorks, Inc., 1993.
FFTSHIFT - перегруппировка выходных массивов преобразований Фурье
Синтаксис:
Y = fftshift(X)
Описание:
Функция Y = fftshift(X) перегруппировывает выходные массивы функций fft и fft2, размещая нулевую частоту в центре спектра.
Если v - одномерный массив, то выполняется циклическая перестановка правой и левой его половины:
| v | fftshift(v) |
| 1 2 3 4 5 | 4 5 1 2 3 |
Если X - двумерный массив, то меняются местами квадранты: I « IV и II « III:
X = [' I ' ' II ';...
' III ' ' IV ';]
fftshift(X)
| X | fftshift(X) | ||||||||
|
|
Пример:
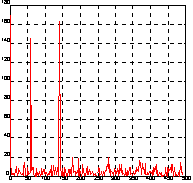
Рассмотрим тот же пример, который рассматривался и для функции fft, но введем постоянную составляющую с уровнем 0.3:
t = 0:0.001:0.6;
x = sin(2 * pi * 50 * t) + sin(2 * pi * 120 * t);
y = x + 2 * randn(size(t)) + 0.3;
plot(y(1:50)), grid
Применим одномерное преобразование Фурье для сигнала y и построим график спектральной плотности. Здесь можно выделить 3 частоты, на которых амплитуда спектра максимальна. Это частоты 0, 58.4 и 140.1 Гц (рис. а).
Y = fft(y);
Pyy = Y.*conj(Y)/512;
f = 1000 * (0:255)/512;
figure(1), plot(f, Pyy(1:256)), grid
ginput
| 58.4112 | 136.6337 | 140.1869 | 62.3762 | ||
| 58.4112 | 68.9109 | 140.1869 | 96.8317 |
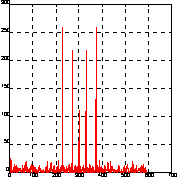
Выполним операции
Y = fftshift(Y);
Pyy = Y.*conj(Y)/512;
figure(2), plot(Pyy), grid
 |
 |
| а) | б) |
Из анализа рис. б) следует, что нулевая частота сместилась в середину спектра.
Сопутствующие функции: FFT, FFT2, Signal Processing Toolbox [1].
Ссылки:
1. Signal Processing Toolbox User’s Guide. Natick: The MathWorks, Inc., 1993.
Свертка и фильтрация
CONV, DECONV - свертка одномерных массивов
Синтаксис:
z = conv(x, y)
[q, r] = deconv(z, x)
Описание:
Если заданы одномерные массивы x и y длины соответственно m = length(x) и n = length(y), , то свертка z - это одномерный массив длины m + n -1, k-й элемент которого определяется по формуле
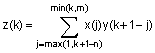 .
.
Функция z = conv(x, y) вычисляет свертку z двух одномерных массивов x и y.
Рассматривая эти массивы как выборки из двух сигналов, можно сформулировать теорему свертки в следующей форме:
Если X = fft([x zeros(1, length(y)-1]) и Y = fft([y zeros(1, length(x) - 1]) - согласованные по размерам преобразования Фурье сигналов x и y, то справедливо соотношение conv(x, y) = ifft(X.*Y).
Иначе говоря, свертка двух сигналов эквивалентна умножению преобразований Фурье этих сигналов.
Функция [q, r] = deconv(z, x) выполняет операцию, обратную операции свертки. Эта операция равносильна определению импульсной характеристики фильтра. Если справедливо соотношение z = conv(x, y), то q = y, r = 0.
Сопутствующие функции: Signal Processing Toolbox [1].
Ссылки:
1. Signal Processing Toolbox User’s Guide. Natick: The MathWorks, Inc., 1993.
CONV2 - свертка двумерных массивов
Синтаксис:
Z = conv2(X, Y)
Z = conv2(X, Y, ‘<опция>‘)
Описание:
Функция Z = conv2(X, Y) вычисляет свертку Z двумерных массивов X и Y. Если массивы имеют размеры соответственно mx х nx и my х ny, то размер массива Z равен (mx + my - 1) х (nx + ny - 1).
Функция Z = conv2(X, Y, ‘<опция>‘) имеет опцию для управления размером массива Z, которая может принимать следующие значения:
‘full’ - полноразмерная свертка (по умолчанию);
‘same’ - центральная часть размера mx х nx;
‘valid’ - центральная часть размера (mx-my+1) х (nx-ny+1) при условии, что (mx х nx) > (my х ny).
Процедура conv2 выполняется наиболее эффективно, если выполнено условие (mx х nx) > (my х ny), то есть количество элементов массива X превосходит количество элементов массива Y.
Пример:
Рассмотрим два массива X и Y.
| X | Y | |||||
| 8 | 1 | 6 | 1 | 1 | ||
| 3 | 5 | 7 | 1 | 1 | ||
| 4 | 9 | 2 |
И вычислим их свертку для различных значений опции.
| Z = conv2(X, Y) | Zs = conv2(X, Y, 'same') | Zv = conv2(X, Y, 'valid') | |||||||||||||||||||||||||||||
|
|
|
Сравнивая столбцы последней таблицы, можно понять назначение опций ‘full’, ‘same’, ‘valid’.
Сопутствующие функции: CONV, DECONV, FILTER2, Signal Processing Toolbox [1].
Ссылки:
1. Signal Processing Toolbox User’s Guide. Natick: The MathWorks, Inc., 1993.
FILTER - дискретная одномерная фильтрация
Синтаксис:
y = filter(b, a, x)
[y, Zf] = filter(b, a, x, Zi)
Описание:
Функция y = filter(b, a, x) фильтрует сигнал, заданный в виде одномерного массива x, используя дискретный фильтр, описываемый конечно-разностными уравнениями вида
y(n) = b(1) * x(n) + b(2) * x(n - 1) + ... + b(nb + 1) * x(n - nb)
- a(2) * y(n - 1) - ... - a(na + 1) * y(n - na),
при этом входной параметр b = [b(1) b(2) ... b(nb + 1)], а параметр a = [a(2) ... ... a(na+1)].
Функция [y, Zf] = filter(b, a, x, Zi) позволяет учесть запаздывания входного Zi и выходного Zf сигналов.
Сопутствующие функции: FILTER2, Signal Processing Toolbox [1].
Ссылки:
1. Signal Processing Toolbox User’s Guide. Natick: The MathWorks, Inc., 1993.
FILTER2 - дискретная двумерная фильтрация
Синтаксис:
Y = filter2(B, X)
Y = filter2(B, X, ‘<опция>‘)
Описание:
Функция Y = filter2(B, X) фильтрует сигнал, заданный в виде двумерного массива X, используя дискретный фильтр, описываемый матрицей B. Результат имеет те же размеры, которые имеет и массив X, и вычисляется с использованием двумерной свертки.
Функция Y = filter2(B, X, ‘<опция>‘) имеет опцию для управления размером массива Y, которая может принимать следующие значения:
| ‘same’ | size(Y) = size(X) (по умолчанию) |
| ‘valid’ | size(Y) < size(X) |
| ‘full’ | size(Y) > size(X) |
Пример:
Рассмотрим фильтр B и массив X.
| X | B | |||||
| 8 | 1 | 6 | 1 | 1 | ||
| 3 | 5 | 7 | 1 | 1 | ||
| 4 | 9 | 2 |
И вычислим их свертку для различных значений опции.
| Y = filter2(B, X) | Y = filter2(B, X, ‘valid’) | Zv = conv2(X, Y, 'full') | |||||||||||||||||||||||||||||
|
|
|
Сопутствующие функции: CONV2, FILTER, Signal Processing Toolbox [1].
Ссылки:
1. Signal Processing Toolbox User’s Guide. Natick: The MathWorks, Inc., 1993.
UNWRAP - корректировка фазовых углов
Синтаксис:
Q = unwrap(P)
Q = unwrap(P, cutoff)
Описание:
Функция Q = unwrap(P) корректирует фазовые углы элементов одномерного массива P при переходе через значение p, дополняя их значениями ±2p для того, чтобы убрать разрывы функции; если P - двумерный массив, то соответствующая функция применяется к столбцам.
Функция Q = unwrap(P, cutoff) позволяет пользователю изменить значение cutoff критического угла; по умолчанию cutoff = p .
Пример:
Рассмотрим непрерывный неминимально-фазовый фильтр, описываемый передаточной функцией
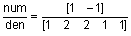 .
.
Вычислим частотную характеристику этого фильтра в диапазоне w = 0.1:0.01:10, используя функцию freqresp пакета Control System Toolbox [1].
w = 0.1:0.01:10;
g = freqresp(num, den, sqrt(-1) * w);
Вычислим фазовый угол частотной характеристики без использования и с использованием функции unwrap.
ph1 = (180./pi) * (atan2(imag(g), real(g)));
ph2 = (180./pi) * unwrap(atan2(imag(g), real(g)));
| w | ph1 | ph2 |
| 0.6000 | 126.7350 | 126.7350 |
| 0.7000 | 141.9270 | 141.9270 |
| 0.8000 | -158.7123 | 201.2877 |
| 0.9000 | -135.6888 | 224.3112 |
| 1.0000 | 135.0000 | -225.0000 |
| 1.1000 | -139.3435 | 220.6565 |
| 1.2000 | -145.0993 | 214.9007 |
| 1.3000 | -151.1794 | 208.8206 |
| 1.4000 | -157.1667 | 202.8333 |
| 1.5000 | -162.8839 | 197.1161 |
| 1.6000 | -168.2575 | 191.7425 |
| 1.7000 | -173.2642 | 186.7358 |
| 1.8000 | -177.9068 | 182.0932 |
| 1.9000 | 177.7986 | 177.7986 |
| 2.0000 | 173.8298 | 173.8298 |
Из таблицы следует, что при входе и выходе из диапазона частот 0.8-2.0 Гц фазовые углы ph1 при достижении критического угла p терпят разрывы, которые устраняются функцией unwrap.
Построим фазовые частотные характеристики ph1(w) и ph2(w)-360, которые подтверждают сделанные выводы.
semilogx(w, ph1), hold on, grid
semilogx(w, ph2-360, 'b')
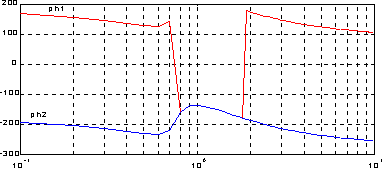
Сопутствующие функции: ANGLE, ABS, Control System Toolbox [1].
Ссылки:
1. Signal Processing Toolbox User’s Guide. Natick: The MathWorks, Inc., 1990
Комментарии