Справочник по MATLAB - Массивы, матрицы и операции с ними (В.Г.Потемкин)
Информация в данной статье относится к релизам программы MATLAB ранее 2016 года, и поэтому может содержать устаревшую информацию в связи с изменением функционала инструментов. С более актуальной информацией вы можете ознакомиться в разделе документация MATLAB на русском языке.
Массивы являются основными объектами в системе MATLAB: в версиях 4.х допускаются только одномерные массивы - векторы - и двумерные массивы - матрицы; в версии 5.0 возможно использование многомерных массивов - тензоров. Ниже описаны функции формирования массивов и матриц, операции над матрицами, специальные матрицы в рамках системы MATLAB версий 4.х.
Формирование массивов специального вида
- ZEROS - формирование массива нулей ⬇️
- ONES - формирование массива единиц ⬇️
- EYE - формирование единичной матрицы ⬇️
- RAND - формирование массива элементов, распределенных по равномерному закону ⬇️
- RANDN - формирование массива элементов, распределенных по нормальному закону ⬇️
- CROSS - векторное произведение ⬇️
- KRON - формирование тензорного произведения ⬇️
- LINSPACE - формирование линейного массива равноотстоящих узлов ⬇️
- LOGSPACE - формирование узлов логарифмичесокй сетки ⬇️
- MESHGRID - формирование узлов двумерной и трехмерной сеток ⬇️
- : - формирование векторов и подматриц ⬇️
Операции над матрицами
- DIAG - формирование или извлечение диагоналей матрицы ⬇️
- TRIL - формирование нижнетреугольной матрицы (массива) ⬇️
- TRIU - формирование верхнетреугольной матрицы (массива) ⬇️
- FLIPLR - поворот матрицы относительно вертикальной оси ⬇️
- FLIPUD - поворот матрицы относительно горизонтальной оси ⬇️
- ROT90 - поворот матрицы на 90 градусов ⬇️
- RESHAPE - преобразование размеров матрицы ⬇️
Специальные матрицы
- COMPAN - сопровождающая матрица характеристического многочлена ⬇️
- HADAMARD - матрица Адамара (Hadamard matrix) ⬇️
- HANKEL - матрица Ганкеля (Hankel matrix) ⬇️
- HILB, INVHILB - матрица Гильберта (Hilbert matrix) ⬇️
- MAGIC - магический квадрат ⬇️
- PASCAL - матрица Паскаля (Pascal matrix) ⬇️
- ROSSER - матрица Рессера (Rosser matrix) ⬇️
- TOEPLITZ - матрица Теплица (Toeplitz matrix) ⬇️
- VANDER - матрица Вандермонда (Vandermonde matrix) ⬇️
- WILKINSON - матрица Уилкинсона (Wilkinson matrix) ⬇️
Формирование массивов специального вида
ZEROS - формирование массива нулей
Синтаксис:
Y = zeros(n)
Y = zeros(m, n)
Y = zeros(size(A))
Описание:
Функция Y = zeros(n) формирует массив нулей размера n х n.
Функция Y = zeros(m, n) формирует массив нулей размера m х n.
Функция Y = zeros(size(A)) формирует массив нулей соразмерный с массивом A.
Примеры:
Формирование одномерного массива из 1000 элементов можно выполнить двумя способами:
- в виде цикла с n = 1000
for i = 1 : n, x(i) = 0; end ,
что требует для реализации около 1.05 с на PC AT/486 (50 МГц);
- в виде оператора присваивания
x = zeros(1, 1000);
что требует для реализации лишь 0.11 с на том же компьютере.
Сопутствующие функции: ONES, EYE, RAND, RANDN.
ONES - формирование массива единиц
Синтаксис:
Y = ones(n)
Y = ones(m, n)
Y = ones(size(A))
Описание:
Функция Y = ones(n) формирует массив единиц размера n х n.
Функция Y = ones(m, n) формирует массив единиц размера m х n.
Функция Y = ones(size(A)) формирует массив единиц соразмерный с массивом A.
Сопутствующие функции: ZEROS, EYE, RAND, RANDN.
EYE - формирование единичной матрицы
Синтаксис:
Y = eye(n)
Y = eye(m, n)
Y = eye(size(A))
Описание:
Функция Y = ones(n) формирует единичную матрицу размера n х n.
Функция Y = ones(m, n) формирует единичную матрицу размера m х n.
Функция Y = ones(size(A)) формирует единичную матрицу соразмерную с матрицей A.
Сопутствующие функции: ZEROS, ONES, RAND, RANDN.
RAND- формирование массива элементов, распределенных по равномерному закону
Синтаксис:
| X = rand(n) | rand | |
| X = rand(m, n) | rand(‘seed’) | |
| X = rand(size(A)) | rand(‘seed’, x0) |
Описание:
Функция X = rand(n) формирует массив размера n х n, элементами которого являются случайные величины, распределенные по равномерному закону в интервале (0, 1).
Функция X = rand(m, n) формирует массив размера m х n, элементами которого являются случайные величины, распределенные по равномерному закону в интервале (0, 1).
Функция X = rand(size(A)) формирует массив соразмерный с матрицей A, элементами которого являются случайные величины, распределенные по равномерному закону в интервале (0, 1).
Функция rand без аргументов формирует одно случайное число, подчиняющееся равномерному закону распределения в интервале (0, 1), которое изменяется при каждом последующем вызове.
Функция rand(‘seed’) возвращает текущее значение базы (начального значения) генератора случайных чисел.
Функция rand(‘seed’, x0) присваивает базе (начальному значению) генератора случайных чисел значение x0.
Алгоритм:
Алгоритм генерации равномерно распределенных случайных чисел основан на линейном конгруентном методе, описанном в работе [1]. Вычисление следующего случайного числа реализовано согласно соотношению
seed = (77 х seed) (mod(231 -1).
Примеры:
Обращение к генератору равномерно распределенных случайных чисел реализуется следующим образом
X = rand(3, 4)
X =
| 0.0579 | 0.0099 | 0.1987 | 0.1988 | |
| 0.3529 | 0.1389 | 0.6038 | 0.0153 | |
| 0.8132 | 0.2028 | 0.2722 | 0.7468 |
Этот результат может оказаться иным и зависит от версии системы и предыстории сеанса работы.
Сопутствующие функции: RANDN, SPRANDN.
Ссылки:
1. Park S. K., Miller K. W. Random Number Generators: Good ones are hard to find// Comm. ACM. N.10. Vol. 32, 1988, P. 1192-1201.
RANDN - формирование массива элементов, распределенных по нормальному закону
Синтаксис:
| X = randn(n) | randn | |
| X = randn(m, n) | randn(‘seed’) | |
| X = randn(size(A)) | randn(‘seed’, x0) |
Описание:
Функция X = randn(n) формирует массив размера n х n, элементами которого являются случайные величины, распределенные по нормальному закону с математическим ожиданием 0 и среднеквадратическим отклонением 1.
Функция X = randn(m, n) формирует массив размера m х n, элементами которого являются случайные величины, распределенные по нормальному закону с математическим ожиданием 0 и среднеквадратическим отклонением 1.
Функция X = randn(size(A)) формирует массив соразмерный с матрицей A, элементами которого являются случайные величины, распределенные по нормальному закону с математическим ожиданием 0 и среднеквадратическим отклонением 1.
Команда randn без аргументов формирует одно случайное число, распределенное по нормальному закону с математическим ожиданием 0 и среднеквадратическим отклонением 1, которое изменяется при каждом последующем вызове.
Команда randn(‘seed’) возвращает текущее значение базы (начального значения) генератора нормально распределенных случайных чисел.
Команда randn(‘seed’, x0) присваивает базе (начальному значению) генератора случайных чисел значение x0.
Алгоритм:
Алгоритм генерации нормально распределенных случайных чисел использует для формирования несколько значений равномерно распределенных случайных чисел, которые обрабатываются в соответствии с алгоритмом, описанным в работе [1].
Примеры:
Обращение к генератору нормально распределенных случайных чисел реализуется следующим образом
X = randn(3, 4)
X =
| -0.4326 | 0.2877 | 1.1892 | 0.1746 | |
| -1.6656 | -1.1465 | -0.0376 | -0.1867 | |
| 0.1253 | 1.1909 | 0.3273 | 0.7258 |
Этот результат может оказаться иным и зависит от версии системы и предыстории сеанса работы.
Сопутствующие функции: RAND.
Ссылки:
1. Forsythe G. E., Malcolm M. A., Moler C. B. Computer Methods for Mathematical Computations. Prentice-Hall, 1977.
CROSS - векторное произведение
Синтаксис:
c = cross(a, b)
Описание:
Функция c = cross(a, b) формирует векторное произведение двух векторов в трехмерном пространстве.
Результирующий вектор имеет следующее описание:
c = a x b = (aybz - azby)i + (azbx - axbz)j + (axby - aybx)k.
Сопутствующие функции: LINSPACE, KRON.
KRON - формирование тензорного произведения
Синтаксис:
K = kron(X, Y)
Описание:
Функция K = kron(X, Y) формирует тензорное произведение (произведение Кронекера) двух числовых массивов (матриц), так что результирующий массив (матрица) имеет вид
K = X х Y = [xij * Y] = 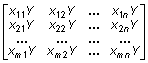
Его размер равен m * size(Y, 1) х n * size(Y, 2).
Сопутствующие функции: CROSS, LINSPACE, MESHGRID.
LINSPACE - формирование линейного массива равноотстоящих узлов
Синтаксис:
x = linspace(x1, x2)
x = linspace(x1, x2, n)
Описание:
Функция x = linspace(x1, x2) формирует линейный массив размера 1 х 100, начальным и конечным элементами которого являются точки x1 и x2.
Функция x = linspace(x1, x2, n) формирует линейный массив размера 1 х n, начальным и конечным элементами которого являются точки x1 и x2.
Сопутствующие функции: LOGSPACE, MESHGRID, :.
LOGSPACE - формирование узлов логарифмичесокй сетки
Синтаксис:
x = logspace(d1, d2)
x = logspace(d1, d2, n)
Описание:
Функция x = logspace(d1, d2) формирует вектор-строку, содержащую 50 равноотстоящих в логарифмическом масштабе точек, которые покрывают диапазон от 10d1 до 10d2.
Функция x = logspace(d1, d2, n) формирует вектор-строку, содержащую n равноотстоящих в логарифмическом масштабе точек, которые покрывают диапазон от 10d1 до 10d2.
Сопутствующие функции: LINSPACE, MESHGRID, :.
MESHGRID - формирование узлов двумерной и трехмерной сеток
Синтаксис:
[X, Y] = meshgrid(x, y)
[X, Y] = meshgrid(x)
[X, Y, Z] = meshgrid(x, y, z)
Описание:
Функция [X, Y] = meshgrid(x, y) формирует массивы X и Y, которые определяют координаты узлов прямоугольника, задаваемого векторами x и y. Этот прямоугольник задает область определения функции от двух переменных, которую можно построить в виде 3D-поверхности.
Функция [X, Y] = meshgrid(x) является сокращенной формой записи функции [X, Y] = meshgrid(x, x).
Функция [X, Y, Z] = meshgrid(x, y, z) формирует массивы X, Y и Z, которые определяют координаты узлов параллелепипеда, задаваемого векторами x, y и z. Этот параллелепипед задает область определения для вычисления функции от трех переменных и построения 3D-параметрических поверхностей.
Пример:
Для вычисления функции в области -2 < x < 2, -2 < y < 2 необходимо выполнить следующую последовательность операций:
[X, Y] = meshgrid(-2:.2:2, -2:.2:2);
Z = X.*exp(-X.^2 - Y.^2);
mesh(Z)
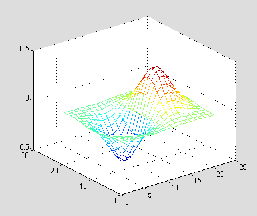
Сопутствующие функции: SURF, SLICE.
: - формирование векторов и подматриц
Синтаксис:
| j : k | A(i1 : i2, j1 : j2) | |
| j : i : k | A(n1 : n2) |
Описание:
Оператор : является очень полезным оператором языка MATLAB. Он применяется для формирования векторов и матриц или для выделения из них подвекторов, подматриц, подблоков массива.
Формирование векторов:
j : k
если j >= k, это вектор вида [j j+1 j+2 ... k];
если j < k, это пустой вектор;
j : i : k
если j >= k, это вектор вида [j j+i j+2i... k];
если i < 0 и j < k, или i > 0 и j>k, это пустой вектор.
Выделение подблоков:
A(i1 : i2, j1 : j2) - выделение подблока массива A со строками i1 : i2 и столбцами j1 : j2.
A(i, :) - i-я строка массива A;
A(:, j) - j-й столбец массива A.
Поскольку в языке MATLAB элементы массива упорядочены по столбцам, то допустимы операторы вида A(n1:n2), которые выделяют пронумерованные элементы с номера n1 до номера n2. Оператор A( : ) записывает все элементы массива A в виде столбца.
Сопутствующие функции: LINSPACE, LOGSPACE, MESHGRID.
Операции над матрицами
DIAG - формирование или извлечение диагоналей матрицы
Синтаксис:
| X = diag(v) | v = diag(X) | |
| X = diag(v, k) | v = diag(X, k) |
Описание:
Функция X = diag(v) формирует квадратную матрицу X с вектором v на главной диагонали.
Функция X = diag(v, k) формирует квадратную матрицу X порядка length(v)+abs(k) с вектором v на k-й диагонали.
Функция v = diag(X) извлекает из матрицы X главную диагональ.
Функция v = diag(X, k) извлекает из матрицы X диагональ с номером k; при k > 0 это номер k-й верхней диагонали, при k < 0 это номер k-й нижней диагонали.
Примеры:
diag(diag(X)) - диагональная матрица;
sum(diag(X)) - след матрицы X.
Оператор
diag(-m : m) + diag(ones(2*m, 1), 1) + diag(ones(2*m, 1), -1)
формирует трехдиагональную матрицу размера 2*m + 1.
Для m = 3 результирующая матрица имеет вид: m = 3;
diag(-m:m)+diag(ones(2*m,1),1)+diag(ones(2*m,1),-1)
ans =
| -3 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 1 | -2 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 1 | -1 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 2 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 3 |
Сопутствующие функции: TRIL, TRIU.
TRIL - формирование нижнетреугольной матрицы (массива)
Синтаксис:
L = tril(X)
L = tril(X, k)
Описание:
Функция L = tril(X) сохраняет нижнюю треугольную часть матрицы X.
Функция L = tril(X, k) сохраняет нижнюю треугольную часть матрицы X начиная с диагонали с номером k. При k > 0 это номер k-й верхней диагонали, при k < 0 это номер k-й нижней диагонали.
Пример:
Для массива X=[1 2 3; 4 5 6; 1 2 3; 4 5 6; 1 2 3; 4 5 6]
| X = | tril(X) = | tril(X, -2) = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Сопутствующие функции: DIAG, TRIU
TRIU - формирование верхнетреугольной матрицы (массива)
Синтаксис:
U = triu(X)
U = triu(X, k)
Описание:
Функция U = triu(X) сохраняет верхнюю треугольную часть матрицы (массива) X.
Функция U = triu(X, k) сохраняет верхнюю треугольную часть матрицы (массива) X начиная с диагонали с номером k. При k > 0 это номер k-й верхней диагонали, при k < 0 это номер k-й нижней диагонали.
Пример:
Для массива X=[1 2 3; 4 5 6; 1 2 3; 4 5 6; 1 2 3; 4 5 6]
| X = | triu(X) = | triu(X, -2) = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Сопутствующие функции: DIAG, TRIL.
FLIPLR - поворот матрицы относительно вертикальной оси
Синтаксис:
B = fliplr(A)
Описание:
Функция B = fliplr(A) переставляет столбцы массива A симметрично относительно вертикальной оси. Если массив A имеет нечетное число столбцов, то средний столбец остается на своем месте.
Пример:
Для массива A = [1 2 3 4; 1 2 3 4 ; 1 2 3 4]
| A = | fliplr(A) = | ||||||||||||||||||||||||||||||||
|
|
Сопутствующие функции: FLIPUD, ROT90
FLIPUD - поворот матрицы относительно горизонтальной оси
Синтаксис:
B = flipud(A)
Описание:
Функция B = flipud(A) переставляет строки массива A симметрично относительно горизонтальной оси. Если массив A имеет нечетное число строк, то средняя строка остается на своем месте.
Пример:
Для массива A = [1 1 1; 2 2 2; 3 3 3; 4 4 4]
| A = | flipud(A) = | ||||||||||||||||||||||||
|
|
Сопутствующие функции: FLIPLR, ROT90.
ROT90 - поворот матрицы на 90 градусов
Синтаксис:
B = rot90(A)
B = rot90(A, k)
Описание:
Функция B = rot90(A) осуществляет поворот массива A размером m х n на 90 градусов против часовой стрелки.
Функция B = rot90(A, k) осуществляет поворот массива A размером m х n на 90*k, где k = 1, -1, 2, -2,...
Пример:
Для массива A = [ 1 2 3; 4 5 6]
| A = | B = rot90(A) = | C = rot90(a, -2) = | ||||||||||||||||||
|
|
|
Сопутствующие функции: VIEW, FLIPUD, FLIPLR.
RESHAPE - преобразование размеров матрицы
Синтаксис:
B = reshape(A, m, n)
Описание:
Функция B = reshape(A, m, n) возвращает массив размером m х n, сформированный из элементов массива A путем их последовательной выборки по столбцам. Если число элементов массива A не равно произведению m * n, выводится сообщение об ошибке.
Алгоритм:
С помощью оператора ( : ) можно получить те же результаты, которые можно получить и с помощью функции reshape. Функция reshape выражается через оператор ( : ) следующим образом:
B = zeros(m, n);
B( : ) = A;
Пример:
Для массива A = [ 1 2 3 4; 1 2 3 4; 1 2 3 4]
| A = | reshape(A, 6, 2) = | reshape(A, 2, 6) = | ||||||||||||||||||||||||||||||||||||
|
|
|
Сопутствующие функции и операторы: FLIPLR, FLIPUD, ROT90.
Специальные матрицы
COMPAN - сопровождающая матрица характеристического многочлена
Синтаксис:
C = compan(p)
Описание:
Функция C = compan(p) формирует сопровождающую матрицу С для входного массива p, который состоит из коэффициентов некоторому многочлена степени n.
Пример:
Полиному (x-1)(x-2)(x-3) = x3 - 7x + 6 соответствует вектор коэффициентов p = [1 0 -7 6]; , для которого сопровождающая матрица имеет вид:
C = compan(p)
C =
| 0 | 7 | -6 | |
| 1 | 0 | 0 | |
| 0 | 1 | 0 |
Сопутствующие функции: POLY, POLYVAL, POLYVALM.
HADAMARD - матрица Адамара (Hadamard matrix)
Синтаксис:
H = hadamard(n)
Описание:
Функция H = hadamard(n) возвращает матрицу Адамара порядка n.
Матрицы Адамара встречаются в различных приложениях - комбинаторном и численном анализе, обработке сигналов [1, 2]. Это матрицы, составленные из 1 и -1, столбцы которых ортогональны, так что справедливо соотношение
H’ * H = n * I,
где [n, n] = size(H) и I = eye(n, n).
Матрица Адамара порядка n > 2 существует только тогда, когда n кратно 4. Данный алгоритм вычисляет матрицы Адамара для тех случаев, когда величины n, n/12, n/20 являются степенями по основанию 2 [3].
Пример:
H = hadamard(8)
H =
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | |
| 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | |
| 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | |
| 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | |
| 1 | -1 | 1 | -1 | -1 | 1 | -1 | 1 | |
| 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | |
| 1 | -1 | -1 | 1 | -1 | 1 | 1 | -1 |
Картина линий уровня для этой матрицы напоминает ковер
contour(hadamard(8))
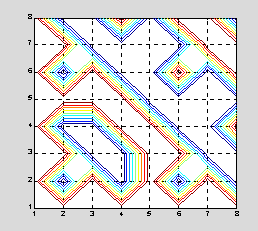
Сопутствующие функции: HANKEL, TOEPLITZ, COMPAN.
Ccылки:
- Ryser H. J. Combinatorial Mathematics. New York: John Wiley&Sons, 1963.
- Pratt W. K. Digital Signal Processing. New York: John Wiley&Sons, 1978.
- Golomb S. W., Baumert L. D. The search for Hadamard matrices//Amer. Math. Monthly. Vol. 70, 1963. P. 12-17.
HANKEL - матрица Ганкеля (Hankel matrix)
Синтаксис:
H = hankel(c)
H = hankel(c, r)
Описание:
Функция H = hankel(c) возвращает квадратную матрицу Ганкеля, первый столбец которой совпадает с вектором c, а все элементы H(i, j), i + j > n, лежащие ниже второй главной диагонали, равны нулю.
Функция H = hankel(c, r) возвращает матрицу Ганкеля, первый столбец которой совпадает с вектором c, а последняя строка с вектором r. Если последний элемент вектора c не равен первому элементу вектора r, то возникает конфликт на второй главной диагонали, когда предпочтение отдается элементу вектора c.
Примеры:
c = [1 2 3];
H = hankel(c)
H =
| 1 | 2 | 3 | |
| 1 | 2 | 0 | |
| 3 | 0 | 0 |
c = 1:3; r = 7:10; H = hankel(c, r)
Warning: Column wins anti-diagonal conflict.
> In d:\matlab5\toolbox\matlab\elmat\hankel.m at line 27
H =
| 1 | 2 | 3 | 8 | |
| 2 | 3 | 8 | 9 | |
| 3 | 8 | 9 | 0 |
Warning: Column wins anti-diagonal conflict.
> In d:\matlab5\toolbox\matlab\elmat\hankel.m at line 27
Столбец выигрывает конфликт на второй главной диагонали
> В d:\matlab5\toolbox\matlab\elmat\hankel.m в строке 27
Сопутствующие функции: TOEPLITZ, VANDER, HADAMARD.
HILB, INVHILB - матрица Гильберта (Hilbert matrix)
Синтаксис:
H = hilb(n)
H = invhilb(n)
Описание:
Функция H = hilb(n) формирует матрицу Гильберта порядка n. Элементы этой матрицы определяются следующим образом:
H(i, j) =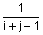 .
.
Матрица Гильберта - это пример очень плохо обусловленной по отношению к операции обращения матрицы [1].
Функция H = invhilb(n) формирует матрицу, обратную матрице Гильберта порядка n. Точная обратная матрица - это матрица, элементами которой являются целые числа. Точное представление такой матрицы в арифметике с плавающей точкой возможно только тогда, когда порядок матрицы не превышает 13. Для больших значений n функция invhilb(n) формирует только приближенную матрицу.
Сравнение функций invhilb(n) и inv(hilb(n)) позволяет выявить несколько источников ошибок:
- ошибки, вызванные функцией hilb(n);
- ошибки, связанные с процедурой обращения;
- ошибки, вызванные функцией invhilb(n).
Оказывается, что первый источник ошибок, связанный с представлением правильных дробей вида 1/3 или 1/5 в арифметике с плавающей точкой, наиболее существенный.
Пример:
Матрица Гильберта порядка 4 имеет число обусловленности 1.5514e+004.
Ее обратная матрица - это целочисленная матрица вида
invhilb(4)
ans =
| 16 | -120 | 240 | -140 | |
| -120 | 1200 | -2700 | 1680 | |
| 240 | -2700 | 6480 | -4200 | |
| -140 | 1680 | -4200 | 2800 |
а результат обращения в арифметике с плавающей точкой
format long e, inv(hilb(4))
1.0e+ 003*
ans =
| 0.0160 | -0.1200 | 0.2400 | -0.1400 | |
| -0.1200 | 1.2000 | -2.7000 | 1.6800 | |
| 0.2400 | -2.7000 | 6.4800 | -4.2000 | |
| -0.1400 | 1.6800 | -4.2000 | 2.8000 |
Ссылки:
1. Forsythe G. E., Moler C. B. Computer Solution of Linear Algebraic Systems. Prentice-Hall, 1967.
MAGIC - магический квадрат
Синтаксис:
M = magic(n)
Описание:
Функция M = magic(n) для n > 3 формирует специальную квадратную матрицу порядка n, элементами которой являются целые числа от 1 до n2, суммы элементов которой по строкам и столбцам равны. Эта функция магического квадрата была включена в состав системы MATLAB в 1993 году и подробно описана в работе [1]. Cумму элементов по строкам (столбцам) назовем инвариантом магического квадрата и обозначим mn. Значение инварианта зависит от n и равно
mn = n(n2 +1)/2.
Если матрицу магического квадрата отнормировать делением на ее инвариант, то получим дважды стохастическую матрицу, обладающую тем свойством, что ее матричная норма любого порядка равна 1 [2].
Ранг матрицы M зависит от n следующим образом [2]:
rank(magic(n)) = 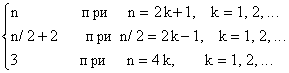
График функции rank(magic(n)) для 3 <= n< = 32 показан на рисунке:
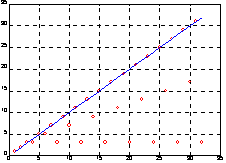
Сопутствующие функции: RAND, ONES.
Ссылки:
1. Moler C. B. MATLAB’s magical mystery tour//The MathWorks Newsletter. 1993. Vol. 7(1). 2. Higham N. J. The Test Matrix Toolbox for MATLAB (version 3.0)//Numerical Analysis Report. Manchester, 1995. Vol. 276.
PASCAL - матрица Паскаля (Pascal matrix)
Синтаксис:
P = pascal(n)
P = pascal(n, k)
Описание:
Функция P = pascal(n) формирует симметрическую положительно определенную квадратную матрицу порядка n, которая составлена из элементов треугольника Паскаля. Треугольник Паскаля представляет собой коэффициенты разложения бинома (1 + w)j, записанные в следующем виде:
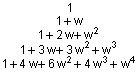 ,
,
а матрицы Паскаля порядка 3 и 4 имеют следующий вид:
| pascal(3) = | pascal(4) = | ||||||||||||||||||||||||||
|
|
Функция pascal(n, 0) равносильна функции pascal(n).
Матрица P = pascal(n, 1) - это нижняя треугольная матрица в разложении Холецкого для матрицы pascal(n) с точностью до знаков чисел в столбцах. Эта матрица обладает свойством P2 = I, где I - единичная матрица [1].
Матрица P = pascal(n, 2) - это матрица, полученная в результате транспонирования и перестановок в матрице pascal(n, 1). Эта матрица обладает свойством P3 = I, где I - единичная матрица [2-3].
Пример:
Сформируем матрицы pascal(3), pascal(3, 1) и pascal(3, 2): P = pascal(3)
| P=pascal(3) | P1=pascal(3,1) | P2=pascal(3,2) | |||||||||||||||||||||||||||
| P = | P1= | P2 = | |||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
| P1^2 | P2^2 | ||||||||||||||||||||||||||||
| ans = | ans = | ||||||||||||||||||||||||||||
|
|
Сопутствующие функции: Test Matrix Toolbox for MATLAB.
Ссылки:
- Higham N. J. The Test Matrix Toolbox for MATLAB (version 3.0)//Numerical Analysis Report. Manchester, 1995. Vol. 276.
- Higham N. J. Accuracy and Stability of Numerical Algorithms. Society for Industrial and Applied Mathematics, Philadelphia, 1996.
- Brawer R., Pirovino M. The linear algebra of the Pascal matrix//Linear Algebra and Appl. 1992. Vol. 174. P. 13-23.
ROSSER - матрица Рессера (Rosser matrix)
Синтаксис:
R = rosser
Описание:
Функция R = rosser формирует тестовую матрицу для классической симметрической проблемы собственных значений. Эта матрица служила камнем преткновения для многих алгоритмов вычисления собственных значений. Только QR-алгоритм Франсиса, усовершенствованный Уилкинсоном [1] и реализованный в пакете программ EISPACK и в системе MATLAB, позволяет справиться с указанной проблемой.
Матрица rosser - это матрица порядка 8 с целочисленными элементами, она обладает следующим спектром собственных значений:
- пара кратных значений;
- 3 близких собственных значения;
- нулевое собственное значение;
- малое ненулевое собственное значение.
Пример:
Матрица Рессера
R = rosser
R =
| 611 | 196 | -192 | 407 | -8 | -52 | -49 | 29 | |
| 196 | 899 | 113 | -192 | -71 | -43 | -8 | -44 | |
| -192 | 113 | 899 | 196 | 61 | 49 | 8 | 52 | |
| 407 | -192 | 196 | 611 | 8 | 44 | 59 | -23 | |
| -8 | -71 | 61 | 8 | 411 | -599 | 208 | 208 | |
| -52 | -43 | 49 | 44 | -599 | 411 | 208 | 208 | |
| -49 | -8 | 8 | 59 | 208 | 208 | 99 | -911 | |
| 29 | -44 | 52 | -23 | 208 | 208 | -911 | 99 |
имеет следующие точные собственные значения:
| 10(1 + sqrt(10201)) | |
| 1020 | |
| 510 + 100sqrt(26) | |
| 1000 | |
| 1000 | |
| 510 - 100sqrt(26) | |
| 0 | |
| -10(1 + sqrt(10201)) |
Сопутствующие функции: EIG, WILKINSON.
Ссылки:
1. Уилкинсон, Райнш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра: Пер. с англ. М.: Машиностроение, 1976. 390 с.
TOEPLITZ - матрица Теплица (Toeplitz matrix)
Синтаксис:
T = toeplitz(c)
T = toeplitz(c, r)
Описание:
Функция T = toeplitz(c) возвращает симметрическую матрицу Теплица, определяемую однозначно вектором c.
Функция T = toeplitz(c, r) возвращает несимметрическую матрицу Теплица, первый столбец которой совпадает с вектором c, а первая строка с вектором r. Если первый элемент вектора c не равен первому элементу вектора r, то возникает конфликт на главной диагонали, когда предпочтение отдается элементу вектора c.
Примеры:
c=1:4; T = toeplitz(c)
T =
| 1 | 2 | 3 | 4 | |
| 2 | 1 | 2 | 3 | |
| 3 | 2 | 1 | 1 | |
| 4 | 3 | 2 | 1 |
c=1:4; r=1.5:4.5; T=toeplitz(c,r)
Column wins diagonal conflict.
Столбец выигрывает конфликт на главной диагонали.
T =
| 1.0000 | 2.5000 | 3.5000 | 4.5000 | |
| 2.0000 | 1.0000 | 2.5000 | 3.5000 | |
| 3.0000 | 2.0000 | 1.0000 | 2.5000 | |
| 4.0000 | 3.0000 | 2.0000 | 1.0000 |
Сопутствующие функции: HANKEL, VANDER.
VANDER - матрица Вандермонда (Vandermonde matrix)
Синтаксис:
V = vander(x)
Описание:
Функция V = vander(x) возвращает матрицу Вандермонда порядка length(x), j-й столбец которой определяется соотношением
V(:, j) = x^(n - j).
Примеры:
x = [1 2 3 4];
V = vander(x)
V =
| 1 | 1 | 1 | 1 | |
| 8 | 4 | 2 | 1 | |
| 27 | 9 | 3 | 1 | |
| 64 | 16 | 4 | 1 |
Сопутствующие функции: POLYFIT, HANKEL, TOEPLITZ.
WILKINSON - матрица Уилкинсона (Wilkinson matrix)
Синтаксис:
W = wilkinson(n)
Описание: Функция W = wilkinson(n) формирует тестовую матрицу Уилкинсона для задачи на собственные значения. Это симметрическая трехдиагональная матрица, наибольшие собственные значения которой попарно близки, но не являются кратными.
Матрица Уилкинсона порядка 7 имеет следующий вид:
W = wilkinson(7)
W =
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 2 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 2 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 3 |
Обычно в качестве тестовой используется матрица 21-го порядка, имеющая следующие собственные значения:
eig(wilkinson(21))
ans =
| 1.074619418290340e+001 | |
| 1.074619418290332e+001 | |
| 9.210678647304920e+000 | |
| 9.210678647361334e+000 | |
| 8.038941115814275e+000 | |
| 8.038941122829025e+000 | |
| 7.003951798616376e+000 | |
| 7.003952209528676e+000 | |
| 6.000234031584169e+000 | |
| 6.000217522257100e+000 | |
| 5.000244425001915e+000 | |
| 4.999782477742904e+000 | |
| 4.004354023440856e+000 | |
| 3.996048201383625e+000 | |
| 3.043099292578824e+000 | |
| 2.961058884185728e+000 | |
| 2.130209219362503e+000 | |
| 1.789321352695079e+000 | |
| 9.475343675292900e-001 | |
| 2.538058170966714e-001 | |
| -1.125441522119984e+000 |
Сопутствующие функции: EIG, ROSSER, PASCAL.
Комментарии