Список функций Image Processing Toolbox
Информация в данной статье относится к релизам программы MATLAB ранее 2016 года, и поэтому может содержать устаревшую информацию в связи с изменением функционала инструментов. С более актуальной информацией вы можете ознакомиться в разделе документация MATLAB на русском языке.
В статье приведено описание основных функций Image Processing Toolbox
Оглавление
Форматы представления данных
-
xyz2uint16 - Преобразование цветовых данных из формата XYZ в uint16
-
xyz2double - преобразование данных в XYZ-значения в формате double
-
double - представление элементов массива в формате double
-
uint8 - представление элементов массива в формате uint8
-
im2double - представление изображения массивом в формате double
-
im2uint8 - представление изображения массивом в формате uint8
-
im2uint16 - представление изображения массивом в формате uint16
-
im2mis - представление изображений в Java MemoryImageSource
-
im2java2d - преобразование изображения в буферизованное изображение Java
-
im2java - преобразование данных в Java-изображение
-
lab2uint8 - преобразование данных из формата L*a*b* в uint8
-
lab2uint16 - преобразование данныхL*a*b* в формат uint16
-
lab2double - преобразование данных L*a*b* в формат double
-
iptnum2ordinal - преобразование положительных целых чисел в строку
Определение типа изображения
-
isbw - проверить, является ли изображение бинарным
-
isgray - проверить, является ли изображение полутоновым
-
isind - проверить, является ли изображение палитровым
-
isrgb - проверить, является ли изображение полноцветным
Работа с графическими форматами файлов
-
imfinfo - чтение из файла информации об изображении
-
imread - чтение изображения из файла
-
imwrite - запись изображения в файл
-
imageinfo - Создание информационных данных о изображении
-
imagemodel - Доступ к свойствам изображений с точки зрения их отображения
Установка и чтение глобальных переменных IPT
-
iptsetpref - установка глобальных переменных IPT
-
iptgetpref - чтение глобальных переменных IPT
-
getline - выбор ломаной линии с помощью мышки
-
getpts - выбор точек с помощью мышки
-
getrect - выбор прямоугольника с помощью мышки
-
ipticondir - возвращает название директории, содержащей IPT и MATLAB иконки
-
iptgetapi - доступ к прикладному программному интерфейсу
Вывод изображений на экран и захват их с экрана
-
imshow - вывод изображения на экран
-
truesize - установка размеров окна для отображения изображений
-
subimage - вывод нескольких изображений в одном окне
-
colorbar - вывод на экран палитры
-
imcontour - построение для изображения линий уровня
-
immovie - создание видеопоследовательности
-
montage - вывод на экран всех кадров многокадрового изображения
-
warp - наложение изображения на поверхность
-
zoom - масштабирование изображения в окне изображения
-
getimage - получение изображения из графического объекта
-
dicominfo - чтение метаданных из DICOM-файла
-
dicomread - чтение DICOM изображений
-
dicomwrite - запись изображений в DICOM-файл
-
dicomuid - Генерация идентификатора для DICOM-файлов
-
imview - Отображение изображений в Image Viewer
-
imgcf - получение последних отображаемых изображений
-
imgca - получение недавно обрабатываемых данных
-
imgetfile - отображение диалогового окна открытия изображений
-
imhandles - установка ручного управления изображениями
-
dicomanon - анонимность DICOM-файла
-
dicomdict - получение или установка активного словаря DICOM-данных
-
impositionrect - создание передвигаемого прямоугольника
-
imscrollpanel - панель прокрутки для интерактивного управления изображениями
-
analyze75info - считывание метаданных из установленного заголовка файла данных Analyze 7.5
-
analyze75read - считывание данных изображения из Analyze 7.5
Преобразования типов изображений
-
im2bw - бинаризация отсечением по порогу яркости
-
mat2gray - преобразование матрицы чисел в полутоновое изображение
-
rgb2gray - преобразование полноцветного изображения в полутоновое
-
ind2gray - преобразование палитрового изображения в полутоновое
-
gray2ind - преобразование полутонового изображения в палитровое
-
grayslice - преобразование полутонового изображения в палитровое отсечением по нескольким порогам
-
ind2rgb -преобразование палитрового изображения в полноценное
-
dither - диффузионное псевдосмешение цветов
-
rgb2ind - преобразование полноцветного изображения в палитровое
-
imapprox - уменьшение количества цветов палитрового изображения
-
cmunique - поиск палитры минимального размера
-
cmpermute - изменение порядка цветов в палитре
-
label2rgb - преобразование матрицы меток в RGB-изображение
Конвертирование цветовых систем
-
rgb2hsv - конвертирование из RGB в HSV
-
hsv2rgb - конвертирование из HSV в RGB
-
rgb2ntsc - конвертирование из RGB в YIQ
-
ntscc2rgb - конвертирование из YIQ в RGB
-
rgb2ycbcr - конвертирование из RGB в YCbCr
-
ycbcr2rgb - конвертирование из YCbCr в RGB
-
rgbplot - изображение компонентов RGB палитры (MATLAB Toolbox)
-
graythresh - вычисление глобального порога изображения с использованием метода Отса
-
iccread - считывание описания ICC
Геометрические преобразования изображений
-
imcrop - кадрирование изображений
-
imresize - изменение размеров изображения
-
imrotate - поворот изображения
-
checkerboard - создание шахматно-образных изображений
-
findbounds - определение границ при пространственных преобразованиях
-
imtransform - применение пространственных преобразований изображений
-
makeresampler - создание повторяющейся структуры
-
maketform - создание структуры пространственных преобразований (TFORM)
-
tformarray - применение пространственных преобразований для многомерных массивов
-
tformfwd - применение прямых пространственных преобразований
-
para2fan - вычисление веерно-лучевых проекций на основании параллельно-лучевых томографических данных
-
tforminv - применение обратных пространственных преобразований
-
fan2para - вычисление параллельно-лучевых проекций данных томографии с расходящимся пучком
-
fanbeam - вычисление веерно-лучевых преобразований
-
fliptform - перестановка исходных и результирующих данных в структуре TFORM
-
ifanbeam - вычисление инверсного веерно-лучевого преобразования
-
applycform - применение преобразования цветовых пространств
-
makecform - создание структуры преобразования цветовых значений
-
whitepoint - описание полноцветной белой точки в цветовом пространстве
-
immagbox - локальное увеличение с использованием панели прокрутки
Анализ изображений
-
imhist - построение гистограммы
-
improfile - построение профиля
-
impixel - определение значения пиксела
-
pixval - управление режимом отображения значений пикселов
-
mean2 - вычисление среднего значения элементов матрицы
-
std2 - вычисление среднеквадратического отклонения элементов матрицы
-
corr2 - вычисление коэффициентов корреляции между двумя матрицами
-
xcorr2 - вычисление двумерной взаимной корреляционной функции
-
imabsdiff - определение отличительных признаков двух изображений
-
imadd - суммирование двух изображений или суммирование изображения и константы
-
imcomplement - дополнение изображений
-
imdivide - разделение двух изображений или разделения изображения на константу
-
imlincomb - вычисление линейной комбинации двух изображений
-
immultiply - умножение двух изображений или умножение изображения на константу
-
imsubtract - вычитание двух изображений или вычитание константы из изображения
-
regionprops - определение свойств области изображения
-
cpstruct2pairs - конвертирование cpstruct в наиболее важные контрольные точки
-
cp2tform - вывод пространственных преобразований между парой контрольных точек
-
cpcorr - определение согласованных контрольных точек с использованием кросс-корреляции
-
cpselect - инструмент выбора контрольных точек
-
normxcorr2 - нормализация двумерной кросс-корреляции
-
deconvblind - улучшение изображений с использованием обратной свертки
-
deconvlucy - улучшение изображений с использованием метода Лаки-Ричардсона
-
deconvreg - улучшение изображений с использованием регуляризационной фильтрации
-
deconvwnr - улучшение изображений с использованием фильтра Винера
-
ippl - проверка наличия библиотеки функций (Intel Performance Primitives Library (IPPL))
-
getrangefromclass - получение динамического диапазона изображений на основе их формата
-
graycomatrix - полутоновая матрица смежности для изображений
-
graycoprops - свойства полутоновых матриц смежности
-
hough - преобразование Хо
-
houghlines - получение линий сегментации на основе преобразований Хо
-
houghpeaks - локализация пиков при преобразованиях Хо
-
imdisplayrange - отображение динамического диапазона яркостей изображения
-
entropy - энтропия интенсивности элементов изображения
-
entropyfilt - локальная энтропия интенсивностей элементов изображения
-
impixelinfoval - средства получения информации о пикселе без текстовых меток
-
getimagemodel - восстановление моделей объектов изображения на основе объектов изображения
-
impixelregion - средства просмотра локального массива пикселей
-
impixelregionpanel - панель инструментария отображения локального массива пикселей изображения
-
impixelinfo - средства получения информации о пикселях
Улучшение изображений
-
histeq - выравнивание гистограммы
-
imadjust - контрастирование с гамма–коррекцией
-
brighten - управление яркостью палитры
-
imnoise - добавление шума
-
roifill - заполнение областей интереса
-
stretchlim - поиск границ повышения контраста изображения
-
edgetaper - виделение краев с использованием функции протяженности точек
-
otf2psf - преобразование оптической функции в функцию протяженности точек
-
psf2otf - преобразование функции протяженности точек в оптическую функцию
-
adapthisteq - Выполнение контрастно ограниченной адаптивной эквализации гистограммы
-
decorrstretch - Применение декорреляционного растяжения многоканальных изображений
-
axes2pix - интерактивный методы регулирования контраста и яркости
-
imcontrast - средства усиления контраста изображения
Фильтрация изображений
-
conv2 - свертка изображений
-
convn - свертка N–мерных сигналов
-
convmtx2 - вычисление матрицы свертки
-
filter2 - двумерная линейная фильтрация
-
freqz2 - двумерная АЧХ
-
fspecial - задание маски предопределенного фильтра
-
fsamp2 - формирование маски линейного фильтра по желаемой АЧХ
-
ftrans2 - формирование маски линейного фильтра методом преобразования частот
-
fwind1 - формирование маски линейного фильтра по желаемой АЧХ с использованием одномерного окна
-
fwind2 - формирование маски линейного фильтра по желаемой АЧХ с использованием двумерного окна
-
blkproc - обработка блоков изображения
-
bestblk - определение размера блока
-
nlfilter - обобщенный нелинейный фильтр
-
colfilt - оптимизированная операция фильтрации
-
im2col - преобразование фрагментов изображения в столбцы
-
col2im - преобразование вспомагательного изображения
-
ordfilt2 - ранговая фильтрация
-
medfilt2 - медианная фильтрация
-
wiener2 - адаптивная винеровская фильтрация
-
roifilt2 - фильтрация областей интереса
-
imfilter - фильтрация двумерных и многомерных изображений
-
freqspace - определение отзыва в двумерной частотной области (MATLAB Toolbox)
Сегментация изображений
-
poly2mask - преобразование некоторой области в маску
-
qtdecomp - сегментация методом разделения
-
qtgetblk - получение блоков из квадро–дерева результатов сегментации
-
qtsetblk - замена блоков–результатов сегментации
-
edge - выделение границ
-
roipoly - задание области интереса с помощью полигона
-
roicolor - бинаризация по заданым цветам
-
watershed - Алгоритм маркерного водораздела
Морфологические операции над бинарным изображением
-
uintlut - вычисление новых значений массива на основе табличных преобразований
-
applylut - преобразование бинарного изображения с помощью таблицы перекодировки
-
bwboundaries - отслеживание локальных границ на бинарном изображении
-
bwmorph - морфологические операции над бинарным изображением
-
bwareaopen - открытие бинарных площадей (малых объектов)
-
bwdist - определение периода преобразования бинарных объектов
-
bwfill - заполнение областей фона
-
bwhitmiss - бинарные hit-miss операции
-
bwlabeln - установка метки связанных элементов в многомерных бинарных изображениях
-
bwpack - упаковка бинарных изображений
-
bwperim - выделение границ бинарных объектов
-
bwselect - выделение объектов
-
bwtraceboundary - oтслеживание контуров бинарных изображений
-
bwulterode - предельная эрозия
-
bwunpack - распаковка бинарных изображений
-
conndef - отсутствие связности
-
dilate - наращение бинарного объекта
-
erode - эрозия бинарного объекта
-
imbothat - выполнение низкочастотной фильтрации
-
imclearborder - подавление световой структуры связанной с краями изображения
-
imclose - закрыть изображение
-
imdilate - расширение изображения
-
imerode - эрозия изображения
-
imextendedmax - максимальная длительность преобразований
-
imextendedmin - минимальная длительность преобразований
-
imfill - заполнение областей изображения
-
imhmax - H-максимальные преобразования
-
imhmin - H-минимальные преобразования
-
imimposemin - установка минимума
-
imopen - открыть изображение
-
imreconstruct - морфологическое восстановление изображений
-
imregionalmax - максимум области
-
imregionalmin - минимум области
-
imtophat - выполнение высокочастотной фильтрации
-
makelut - формирование таблицы перекодировки
Поиск объектов и вычисление их признаков
-
bwlabel - поиск объектов
-
bwarea - вычисление площади объектов
-
bweuler - вычисление числа Эйлера
-
imfeature - вычисление признаков объектов
-
imattributes - получение информации об атрибутах изображения
Преобразования Фурье
-
fft2 - двумерное БПФ
-
fftn - n–мерное БПФ
-
ifft2 - обратное двумерное БПФ
-
ifftn - n–мерное обратное БПФ
-
fftshift - перегрупировка выходного массива преобразования Фурье
Дискретное косинусное преобразование
Преобразование Радона
-
radon - прямое преобразование Радона
-
iradon - обратное преобразование Радона
-
phantom - создание модельного изображения головы
Создание и обработка структурных элементов
-
getheight - создание вертикальных структурных элементов
-
getneighbors - определение местоположения соседних структурных элементов
-
getnhood - создание соседних структурных элементов
-
getsequence - создание последовательности разложенных структурных элементов
-
isflat - возвращение одинаковых структурных элементов
-
reflect - представление структурных элементов через их центр
-
strel - создание морфологических структурных элементов
-
translate - преобразование структурных элементов
Операции с массивами
-
padarray - пустой массив
Демонстрация
-
dctdemo - демонстрация сжатия изображений на основе двумерных дискретных косинусных преобразований
-
edgedemo - демонстрация выделения границ объектов изображения
-
firdemo - демонстрация двумерной фильтрации изображений и проектирования фильтров
-
imadjdemo - демонстрация корректировки яркостей и эквализации гистограммы изображений
-
landsatdemo - демонстрация сложноцветных изображений
-
nrfiltdemo - демонстрация фильтрации шумовой составляющей
-
qtdemo - демонстрация разложения квадродеревьев
-
roidemo - демонстрация обработки областей интереса
xyz2uint16 - Преобразование цветовых данных из формата XYZ в uint16
Синтаксис:
xyz16=xyz2uint16(xyz)
Описание:
Функция xyz16=xyz2uint16(xyz) выполняет преобразование массива значения цветов XYZ с размерностью Mx3 или MxNx3 в формат uint16. Обработанный массив xyz16 имеет тот же размер, что и xyz.
Описанные преобразования в пакете обработки изображений (Image Processing Toolbox) соответствуют установленным требованиям Международной комиссии по освещению о представлении массива в формате удвоенной точности. Элементы массива XYZ , согласно этим требованиям (ICC.1:2001-4, www.color.org), представляются 16-битовыми числами без знака. 8-битовое представление элементов массива не является стандартным. Преобразования, которые выполняются согласно этим требованиям, представлены в таблице.
Значения (X, Y и Z) uint16 значения 0.0 0 1.0 32768 1.0 + (32767/32768) 65535 Требования к исходным данным.
Данные xyz представляются неразреженным массивом вещественных чисел в формате uint16 или double. Массив xyz16 представляется в формате uint8.
xyz2double - преобразование данных в XYZ-значения в формате double
Синтаксис:
xyzd=xyz2double(XYZ)
Описание:
Функция xyxd=xyz2double(XYZ) преобразует массив с размерностью Mx3 или MxNx3 в XYZ-значения цвета в формате double. Размерность xyzd аналогична размерности XYZ.
Описанные преобразования в пакете Image Processing Toolbox выполняются в режиме удвоенной точности, согласно требованиям Международной комиссии по освещению от 1931 года. Массив XYZ , который представлен в формате uint16, согласно данным требованиям представляется 16-битными целыми числами без знака. Кодирование согласно этим требованиям представлено в таблице.
Значение (X, Y или Z) uint16 значение 0.0 0 1.0 32768 1.0 + (32767/32768) 65535 Требования к исходным данным
Данные xyz представляются неразреженным массивом вещественных чисел в формате uint16 или double. Массив xyzd представляется в формате double.
double - представление элементов массива в формате double
Синтаксис:
B=double(A)
Описание:
Функция double используется для преобразования элементов массива А в действительные числа удвоенной точности и помещает их в новый массив В. Если А является массивом чисел в формате double, то осуществляется копирование из массива А в В. Данная функция используется для преобразования данных матрицы изображения из формата uint8 в формат double.
uint8 - представление элементов массива в формате uint8
Синтаксис:
B=uint8(A)
Описание:
Функция uint8 используется для преобразования элементов массива А в целые неотрицательные числа в диапазоне [0, 255] и помещает их в новый массив В. Если А является массивом чисел в формате uint8, то осуществляется копирование из массива А в В. Данная функция используется для преобразования данных матрицы изображения из формата double в формат uint8.
При выполнении преобразования дробная часть отбрасывается. По этой причине рекомендуется предварительно округлять значения элементов массива до ближайшего целого с помощью функции round, например: B=uint8(round(A)). Для элементов массива А вне диапазона [0, 255] значения в массиве В не определены и могут быть различными для различных вычислительных платформ.
На платформе Intel при преобразовании из double в uint8 сначала действительное число преобразуется в целое число, а затем берется младший байт целочисленного представления числа в памяти ПК. Таким образом значение 256 из массива А будет преобразовано в 0, так как младший байт целочисленного представления числа 256 равен 0. Отрицательные целые числа хранятся в памяти ПК в дополнительном коде. Значение -1 из массива А будет преобразовано в 255, так как младший байт представления в дополнительном коде числа -1 равен 255.
Система MATLAB не осуществляет никакого контроля соответствия диапазонов, и обязанность следить за правильностью преобразований полностью возлагается на пользователя.
Пример.
% examp1.m
% Пример демонстрирует использование функции uint8.
x=[-10.3 -1.9 0.0 10.15 10.8 255.2 300.3 600.9];
y=uint8(x);
% Будет выведено:
% y=246 255 0 10 100 255 44 88
z=uint8(round(x))
% Будет выведено:
% z=246 254 0 10 101 255 44 89
im2double - представление изображения массивом в формате double
Синтаксис:
B=im2double(A)
YВ=im2double(XS, ‘indexed’)
Описание:
Функция im2double позволяет представить все пикселы матрицы изображения в виде действительных чисел двойной точности. При реализации этой функции, в отличии от функции double, осуществляется приведение значений пикселов к требуемому диапазону. Для бинарных, полутоновых и полноцветных изображений это диапазон [0,1], а для палитровых изображений – [1, N], где N – количество цветов в палитре.
Функция B=im2double(A) преобразует бинарное, полутоновое или полноцветное изображение А в формат double и помещает результат в новую матрицу В. Преобразования осуществляются в соответствии со следующими соотношениями:
Бинарное B=im2double(A) Полутоновое B=im2double(A)/255 Полноцветное B=im2double(A)/255 Функция YВ=im2double(XS, ‘indexed’) преобразует в формат double палитровое изображение XS и помещает результат в новую матрицу YВ. Преобразование описывается соотношением:
YВ=double(XS)+1
im2uint8 - представление изображения массивом в формате uint8
Синтаксис:
B=im2uint8(A)
YВ=im2uint8(XS, ‘indexed’)
Описание:
Функция im2double позволяет представить все пикселы матрицы изображения в виде целых неотрицательных чисел в диапазоне [0, 255]. При конвертировании, в отличие от функции uint8, осуществляется приведение значений пикселов к требуемому диапазону.
Функция B=im2uint8(A) преобразует в формат uint8 бинарное, полутоновое или полноцветное изображение А и помещает результат в новую матрицу В. Преобразования осуществляются в соответствии со следующими соотношениями:
Бинарное B=logical(uint8(A)) Полутоновое B=uint8(round(A*255)) Полноцветное B=uint8(round(A*255)) Функция YВ=im2uint8(XS, ‘indexed’) преобразует в формат uint8 палитровое изображение XS и помещает результат в новую матрицу YВ. Преобразование описывается соотношением:
YВ=double(XS)+1
im2uint16 - представление изображения массивом в формате uint16
Синтаксис:
I2=im2uint16(I1) RGB2=im2uint16(RGB1)
I=im2uint16(BW)
X2=im2uint16(X1, 'indexed')
Описание :
Функция im2uint16 использует изображение в качестве исходных данных и возвращает его вформате представления данных uint16. Если исходное изображение былопредставлено в формате uint16, тогда результирующее изображение будет емуидентично. Если исходное изображение было представлено в формате double илиuint8, тогда функция im2uint16 возвращает эквивалентное изображение в форматеuint16, проведя нужные яркостные преобразования (масштабирование).
Функция I2=im2uint16(I1) преобразует полутоновое изображение I1 в формат uint16,проведя соответствующие яркостные масштабирующие преобразования данных.
Функция RGB2=im2uint16(RGB1) преобразует цветное изображение RGB1 в формат uint16,проведя соответствующие яркостные масштабирующие преобразования данных.
Функция I=im2uint16(BW) преобразует бинарное изображение BW в яркостное (полутоновое)изображение в формате uint16.
Функция X2=im2uint16(X1, 'indexed') преобразует индексное изображение X1 в форматuint16, проведя соответствующие преобразования данных. Отметим, что подобныепреобразования реально касаются только тех изображений, для которых они возможны.Например, если изображение X1 представлено в формате double, тогда значенияинтенсивностей его элементов max(X1(:)) могут достигать 65536.
im2java2d - преобразование изображения в буферизованное изображение Java
Синтаксис:
jimage=im2java2d(I)jimage=im2java2d(X, MAP)
Описание:
Функция jimage=im2java2d(I) проводит преобразование изображения в отдельный класс Java-изображений java.awt.image.BufferedImage. Изображение I должно быть яркостным (полутоновым), RGB или бинарным изображением.
Функция jimage=im2java2d(X, MAP) также преобразует индексное изображение X с палитрой MAP в отдельный класс Java-изображений java.awt.image.BufferedImage.
Требования к исходным данным.
Исходное яркостное (полутоновое), индексное или RGB изображение должно быть представлено в формате uint8, uint16 или double. Если исходное изображение бинарное, то оно должно быть представлено в формате logical.
Пример.В этом примере считаем изображение в рабочее пространство MATLAB и с помощью функции im2java2d преобразуем его в Java-формат java.awt.image.BufferedImage.I=imread('moon.tif');javaImage=im2java2d(I);frame=javax.swing.JFrame;icon=javax.swing.ImageIcon(javaImage);label=javax.swing.JLabel(icon);frame.getContentPane.add(label);frame.packframe.show
im2java - преобразование данных в Java-изображение
Синтаксис:
jimage=im2java(I)jimage=im2java(X, MAP)jimage=im2java(RGB)
Описание:
При работе с изображениями в среде MATLAB возникает необходимость в их конвертации в класс Java, т.е. java.awt.Image.
Функция jimage=im2java(I) преобразует яркостное изображение в данные в формате java.awt.Image.
Функция jimage=im2java(X, MAP) преобразует индексное изображение X с палитрой MAP в формат java.awt.Image.
Функция jimage=im2java(RGB) преобразует RGB-изображение в формат Java.
Требования к исходным данным.
Исходное изображение может быть представлено в формате uint8, uint16 или double.
Примечание.
Для создания изображений в формате java.awt.Image необходимо, чтобы данные были представлены в формате uint8. Если исходные данные представлены в формате uint8, то после обработки функцией jimage получим те же данные в том же формате uint8. Если же исходные изображения были представлены в формате uint16, то функция im2javaпреобразует их в эквивалентное изображение в формате uint8 с дальнейшим преобразованием в формат java.awt.Image.
Пример.В этом примере считаем изображение из файла в рабочее пространство MATLAB и далее, применяя функцию im2java, преобразуем его в Java-изображение.I=imread('your_image.tif');javaImage=im2java(I);frame=javax.swing.JFrame;icon=javax.swing.ImageIcon(javaImage);label=javax.swing.JLabel(icon);frame.getContentPane.add(label);frame.packframe.show
lab2uint8 - преобразование данных из формата L*a*b* в uint8
Синтаксис:
lab8=lab2uint8(lab)
Описание:
Функция lab8=lab2uint8(lab) выполняет преобразование массива цветовых значений размерностью Mx3 или MxNx3 из формата L*a*b* в формат uint8. Размерность данных lab8 совпадает с размерностью исходных данных lab.
Форматы представления данных массивов удвоенной точности L*a*b* , которые используются в пакете Image Processing Toolbox, соответствуют общепринятым требованиям. Массив L*a*b* , который представлен в формате uint8 или uint16, соответствует требованиям ICC (ICC.1:2001-4, www.color.org). Некоторые особенности ICC-кодирования приведены в таблицах.
Значение (L*) Значение uint8 Значение uint16 0.0 0 0 100.0 255 65280 100.0 + (25500/65280) None 65535 Значение (a* или b*) Значение uint8 Значение uint16 -128.0 0 0 0.0 128 32768 127.0 255 65280 127.0 + (255/256) - 65535 Требования к исходным данным.
Исходные данные lab должны быть представлены не разреженным массивом вещественных чисел в формате uint8, uint16 или double. Результирующие данные представляются в формате uint8.
lab2uint16 - преобразование данныхL*a*b* в формат uint16
Синтаксис:
lab16=lab2uint16(lab)
Описание:
Функция lab16=lab2uint16(lab) реализует преобразование некоторого массива с размерностью Mx3 или MxNx3 в значения цвета L*a*b* , представленные в формате uint16. Массив lab16 имеет тот же формат, что и lab.
Аналогично как и в функции lab2double, а также в других функциях, преобразования в пакете Image Processing Toolbox реализованы согласно требованиям Международной комиссии по освещению от 1976 года, т.е. значения L*a*b* -массива представлены в формате удвоенной точности. Массивы L*a*b* , которые представлены в формате uint8 или uint16, преобразуются к виду ICC, описанному в ICC.1:2001-4 (www.color.org), для представления в формате целых чисел без знака. Примеры ICC-кодирования представлены в таблицах.
Значение (L*) uint8 значение uint16 значение 0.0 0 0 100.0 255 65280 100.0+(25500/65280) None 65535 Значение (a* or b*) uint8 значение uint16 значение -128.0 0 0 0.0 128 32768 127.0 255 65280 127.0+(255/256) None 65535 Требования к исходным данным.
Данные lab должны быть представлены неразреженным массивом вещественных чисел в формате uint8, uint16 или double. Массив lab16 имеет формат представления данных uint16.
lab2double - преобразование данных L*a*b* в формат double
Синтаксис:
labd=lab2double(lab)
Описание:
Функция labd=lab2double(lab) реализует преобразование некоторого массива с размерностью Mx3 или MxNx3 в значения цвета L*a*b* , представленные в формате double. Результирующий массив имеет ту же размерность что и lab.
Преобразования в пакете Image Processing Toolbox реализованы согласно требованиям Международной комиссии по освещению от 1976 года, т.е. значения L*a*b* -массива представлены в формате удвоенной точности. Массивы L*a*b* , которые представлены в формате uint8 или uint16, преобразуются к виду ICC, описанному в ICC.1:2001-4 (www.color.org), для представления в формате целых чисел без знака. Примеры ICC-кодирования представлены в таблицах.
Значение (L*) uint8 значение uint16 значение 0.0 0 0 100.0 255 65280 100.0+(25500/65280) None 65535 Значение (a* or b*) uint8 значение uint16 значение -128.0 0 0 0.0 128 32768 127.0 255 65280 127.0+(255/256) None 65535 Требования к исходным данным.
Данные lab должны быть представлены неразреженным массивом вещественных чисел в формате uint8, uint16 или double. Массив labd представляется в формате double.
iptnum2ordinal - преобразование положительных целых чисел в строку
Синтаксис:
string = iptnum2ordinal(number)
Описание:
Функция string = iptnum2ordinal(number) преобразовывает положительные целые числа в текстовую строку string.
Пример:
В следующем примере показано пример возвращения строки "четыре".
str = iptnum2ordinal(4)
Аналогичный пример.
str = iptnum2ordinal(23)
isbw - проверить, является ли изображение бинарным
Синтаксис:
flag=isbw(S)
Описание:
Функция isbw возвращает 1, если S является бинарным изображением, и 0 - в противном случае. Считается, что массив представляет собой бинарное изображение, если он удовлетворяет следующим условиям:
- является двумерным;
- имеет формат представления данных double, при этом все его элементы имеют значение либо 0, либо 1, или имеет формат представления данных uint8;
- для этого массива установлен логический флаг, который является некоторым атрибутом массивов MATLAB и может быть установлен функцией logical.
isgray - проверить, является ли изображение полутоновым
Синтаксис:
flag=isgray(S)
Описание:
Функция isgray возвращает 1, если S является полутоновым изображением, и 0 - в противном случае. Считается, что массив представляет собой полутоновое изображение, если он удовлетворяет следующим условиям:
- является двумерным;
- имеет формат представления данных double, при этом все его элементы имеют значение из диапазона [0, 1], или имеет формат представления данных uint8 вне зависимости от значения логического флага.
isind - проверить, является ли изображение палитровым
Синтаксис:
flag=isind(S)
Описание:
Функция isind возвращает 1, если S является палитровым изображением, и 0 - в противном случае. Считается, что массив представляет собой палитровое изображение, если он удовлетворяет следующим условиям:
- является двумерным;
- имеет формат представления данных double, при этом все его элементы являются целыми числами, большими 0, или имеет формат представления данных uint8 и логический флаг сброшен.
Пример.
Легко заметить, что существует некоторая неоднозначность при определении типа изображения с помощью функций isbw, isgray, isind. Один и тот же массив может одновременно считаться бинарным и полутоновым или палитровым и полутоновым изображением. Подобный подход не противоречит здравому смыслу. Например, бинарное изображение может рассматриваться как частный случай полутонового. Однако в ряде случаев необходимо учитывать особенности работы функций isbw, isgray, isind.
Рассмотрим работу функций isbw, isgray, isind для различных вариантов массива, состоящего только из нулей и единиц. Заметим, что для массивов, состоящих не только из нулей и единиц, результат будет иным.
% example.m
% Пример демонстрирует работу функций isbw, isgray, isind.
Im=[1 0 1 0 1];
% Массив в формате double, логический флаг сброшен.
isbw(Im);
ans
%Будет выведено:
%=0;
isgray(Im);
ans
%=1
isind(Im);
ans
%=0;
Im=logical(Im);
% Массив в формате double, логический флаг установлен.
isbw(Im);
ans
%= 1
isgray( Im);
ans
%=1
isind( Im);
ans
% =0
lm=[1 0 1 0 1];
Im = uint8( Im );
% Массив в формате uint8, логический флаг сброшен.
isbw(Im);
ans
%=0
isgray( Im);
ans
%=1
isind( Im);
ans
%=1
Im = logical(Im);
% Массив в формате uint8, логический флаг установлен.
isbw( Im);
ans
%=1
isgray(Im);
ans
%=1
isind(Im);
ans
%=0
isrgb - проверить, является ли изображение полноцветным
Синтаксис:
Flag=isrgb(S)
Описание:
Функция isrgb возвращает 1, если S является полноцветным изображением, и 0 - в противном случае. Считается, что массив представляет собой полноцветное изображение, если он удовлетворяет следующим условиям:
- является трехмерным массивом размера MxNx3, где М - число строк изображения, N - число столбцов;
- имеет формат представления данных double, при этом значения всех его элементов принадлежат диапазону [0, 1 ]; или имеет формат представления данных uint8;
- логический флаг сброшен.
imfinfo - чтение из файла информации об изображении
Синтаксис:
info=imfinfo(filemane, fmt)
info=imfinfo(filemane)
Описание:
Функции imfinfo(filemane, fmt) и imfinfo(filemane) в структуре info возвращают информацию об изображении и способе его хранения из файла с именем filemane. Первая функция позволяет кроме имени файла filemane задать его расширение - ftm. В этом случае если MATLAB не может найти файл с именем filemane, то ищется файл с именем filemane и расширением ftm.
Параметры filemane и ftm являются строками. Пакет ІРТ поддерживает работу со следующими графическими форматами файлов:
Значение параметра ftm Название формата ‘bmp’ Windows Bitmap (BMP) ‘tif’ или ‘tiff’ Tag Image File Format (TIFF) ‘jpg’ или ‘jpeg’ Joint Photographic Experts Group (JPEG) ‘pcx’ Windows Painbrush (PCX) ‘hdf’ Hierarchical Data Format (HDF) ‘xwd’ X Windows Dump (XWD) Информация об изображении и способе его хранения в данном файле возвращается в структуре info. Структуры для разных форматов отличаются друг от друга. Общими являются 9 полей структуры, по которым можно определить формат файла, тип и размеры изображения:
Имя поля Тип данных Описание Filename Строка Имя файла, если файл находится в текущей директории, или полный путь к файлу FileModDate Строка Дата и время последней модификации файла FileSize Число Размер файла в байтах Format Строка Формат файла, значение поля совпадает с трехбуквенным вариантом параметра fmt FormatVersion Строка или число Версия формата Width Число Ширина изображения в пикселах Height Число Высота изображения в пикселах BitDepth Число Глубина изображения в битах на пиксел ColorType Строка Тип изображения:
‘truecolor’ или ‘RGB’ для полноцветных изображений;
‘grayscale’ для полутоновых изображений;
‘indexed’ для палитровых изображенийВ файлах форматов TIFF и HDF может хранится несколько изображений. В этом случае info является массивом структур.
imread - чтение изображения из файла
Синтаксис:
D=imread(filename, fmt)
[X,map]=imread(filename, fmt)
[…]=imread(filename)
[…]=imread(…, idx)
[…]=imread(…, ref)
Описание:
Функция D=imread(filename, fmt) читает из файла с именем filename бинарное, полутоновое или полноцветное изображение и помещает его в массив D. Функция [X,map]=imread(filename, fmt) читает из файла с именем filename палитровое изображение X с палитрой map.
Если MATLAB не может найти файл с именем filename, то ищется файл с именем filename и расширением fmt. Параметры filename и fmt являются строками. Параметр fmt в вызове функции может быть опущен, в этом случае формат файла автоматически определяется из его содержимого. В таблице приведены типы изображений, которые могут быть прочитаны функцией imread.
Формат Глубина цвета Особенности BMP 1, 4, 8, 24 Несжатые файлы 4, 8 Файлы с RLE-сжатием TIFF 1, 8, 24 Несжатые файлы 1, 8, 24 Файлы, использующие Packbit-сжатие 1 Файлы, использующие ССITT-сжатие JPEG 8, 24 PCX 1, 8, 24 HDF 8, 24 XWD 1, 8 Функция […]=imread(…, idx) читает одно изображение из TIFF-файла, содержащего несколько изображений. Номер изображения по порядку в списке IFD указывается в параметре idx. Если параметр idx при вызове функции не указан, то читается первое по порядку изображение в файле.
Функция […]=imread(…, ref) читает одно изображение из HDF-файла, содержащего несколько изображений. Каждое изображение в HDF-файле имеет уникальный номер-описатель. Этот описатель указывается в параметре ref. Если параметр ref при вызове функции не указан, то читается первое по порядку изображение в файле.
Прочитанное из файла изображение имеет формат представления данных uint8.
imwrite - запись изображения в файл
Синтаксис:
imwrite(S, filename, fmt)
imwrite(X, map, filename, fmt)
imwrite(…, filename)
imwrite(…, Parameter, Value)
Описание:
Функция imwrite(S, filename, fmt) записывает в файл с именем filename бинарное, полутоновое или полноцветное изображение S. Функция imwrite(X, map, filename, fmt) записывает в файл с именем filename палитровое изображение X с палитрой map. Формат файла определяется параметром ftm. Параметры filename и ftm являются строками. Возможные значения параметра ftm приведены в описании функции iminfo.
Функция imwrite(…, filename) аналогична описанным функциям, но формат файла определяется по расширению filename.
В таблице 1 приведены типы изображений, которые могут быть прочитаны функцией imwrite.
Таблица 1.
Формат Тип изображений BMP 8 бит/пиксел - палитровые,
24 бит/пиксел - палитровыеTIFF Бинарные несжатые или с использованием Packbit- или CCITT-сжатия;
8 бит/пиксел - палитровые или полутоновые несжатые или с использованием Packbit-сжатия;
несжатые или с использованием Packbit-сжатияJPEG 8 бит/пиксел - полутоновые,
24 бит/пиксел - полноцветные;
палитровые конвертируются в полноцветныеPCX 8 бит/пиксел - полутоновые HDF 8 бит/пиксел - полутоновые и палитровые,
24 бит/пиксел - полноцветныеXWD 8 бит/пиксел-палитровые При записи изображений в файлы форматов TIFF, JPEG, HDF можно указать ряд дополнительных параметров, влияющих на способ сохранения изображений. Для этого в функции imwrite после параметров filename и ftm передается одна или несколько пар параметров Parameter, Value.
Если запись осуществляется в JPEG-файлы, то можно указывать показатель качества сжатого изображения. Для этого Parameter должен быть строкой ‘Quality’, а Value - число, которое определяет степень сжатия изображения. Этот показатель может принимать значения в диапазоне [0, 100]. Чем меньше значение этого показателя, тем выше степень сжатия, но хуже качество изображения.
При записи изображений в TIFF-файл можно использовать следующие дополнительные параметры (табл. 2):
Таблица 2.
Параметр Возможные значения Value Значение Value по умолчанию ‘Compression‘ ‘none’ - не использовать сжатие;
‘packbits’ - использовать метод сжатия Рackbits;
‘ccitt’ - использовать метод сжатия ССІТТ‘ccitt’ - для бинарных изображений;
‘packbits’ - для других типов изображений‘Description’ Любая строка. Эта строка находится в поле ImageDascription структуры, возвращаемой iminfo ‘’ ‘Resolution’ Разрешение в точках на дюйм 72 При записи изображений в HDF - файл можно использовать следующие дополнительные примеры (табл. 3):
Таблица 3.
Параметр Возможные значения Value Значение Value по умолчанию ‘Compression‘ ‘none’ - не использовать сжатие;
‘rle’ - использовать метод сжатия RLE;
‘jpeg’ - использовать метод сжатия JPEG‘rle’ ‘Quality’ Показатель качества при JPEG - сжатии, это число задается в диапазоне [0, 100] 75 ‘’WriteMode ‘overwrite’ - переписать существующий файл;
‘append’ - добавить изображение в существующий файл‘overwrite’ Если исходное изображение имеет формат представления данных double, то перед записью в файл данные изображения автоматически преобразуются в формат uint8.
imageinfo - Создание информационных данных о изображении
Синтаксис:
imageinfo
imageinfo(h)
imageinfo(filename)
imageinfo(info)
imageinfo(himage,filename)
imageinfo(himage,info)
hfig = imageinfo(...)
Описание:
Функция imageinfo создает информационные данные об изображении, которые связаны с изображением в текущем окне просмотра. Такой инструмент отображения разделяет информацию по основным атрибутам касательно рассматриваемого изображения. Функция imageinfo может также выдавать результат в зависимости от запрашиваемых данных.
В таблице приведен список основных составляющих информации об изображении. Отметим, что число информационных составляющих зависит от типа изображения.
Атрибуты имени Значение Width (columns) Число столбцов в изображении. Height (rows) Число строк в изображении. Class Тип данных зависит от изображения.
Примечание: Для single или int16 изображений функция imageinfo возвращает данные в формате double, поскольку объекты изображения преобразуются в этот формат.Image type Один из типов изображений, идентифицируемых приложением Image Processing Toolbox: 'intensity', 'truecolor', 'binary' или 'indexed'. Minimum intensity Для яркостных изображений это значение представляет наименьшее значение яркости некоторого пикселя.
Для индексных изображений это значение представляет наименьший индекс в палитре цветов.
Этот параметр отсутствует для изображений типа 'binary' или 'truecolor'.Maximum intensity Для яркостных изображений это значение представляет наибольшее значение яркости некоторого пикселя.
Для индексных изображений это значение представляет наибольший индекс в палитре цветов.
Этот параметр отсутствует для изображений типа 'binary' или 'truecolor'.Функция imageinfo(h) создает информационный инструмент для описания изображений с использованием параметра h, где h обеспечивает установку окна отображения, осей и объектов отображения.
Функция imageinfo(filename) создает информационный инструмент для описания изображений, содержащий метаданные изображений из графического файла. Изображение может не визуализироваться в окне отображения. Параметром filename может представляться файл любого типа, который регистрируется информационной функцией в реестре формата файлов imformats или может быть прочитан функцией imfinfo. Параметр filename может также представлять DICOM-файлы, информация о которых считывается функцией dicominfo.
Функция imageinfo(info) создает информационный инструмент для описания изображений, содержащий метаданные изображений в структуре info. info представляет структуру, возвращаемую функцией imfinfo или dicominfo.
Функция imageinfo(himage,filename) создает информационный инструмент для описания изображений, содержащий информацию относительно основных атрибутов изображения, описанных в himage и метаданные изображения из графического файла filename.
Функция imageinfo(himage,info) создает информационный инструмент для описания изображений, содержащий информацию относительно основных атрибутов изображения, описанных в himage и метаданные изображений в структуре info.
Функция hfig=imageinfo(...) возвращает отображение информационного инструментария изображений.
Пример:
imageinfo('peppers.png')
h = imshow('bag.png');
info = imfinfo('bag.png');
imageinfo(h,info);
imshow('trees.tif');
imageinfo;
imagemodel - Доступ к свойствам изображений с точки зрения их отображения
Синтаксис:
imgmodel = imagemodel(himage)
Описание:
Функция imgmodel = imagemodel(himage) создает объекты модели изображения для himage. Параметр himage представляет объект изображения или массив объектов изображения.
Функция imagemodel возвращает объект модели изображения или массив объектов модели изображения, когда himage является массивом объектов изображения.
Объекты модели изображения содержат информацию о таких характеристиках изображения как класс, тип, диапазон визуализации, значение минимальной и максимальной интенсивности.
Объекты модели изображений поддерживают методы, которые можно использовать для получения описанной выше информации, а также для получения информации о пикселях на изображении и о других аспектах. В таблице приведен список этих методов с коротким описанием. Используя функцию methods(imgmodel) можно получить методы моделирования изображений.
Метод Значение getClassType Возвращает строку, указывающую на класс изображений. str = getClassType(imgmodel),
где параметр imgmodel представляет модель изображения и str является текстовой строкой типа 'uint8'getDisplayRange Возвращает массив, содержащий минимальное и максимальное значения диапазона отображения для яркостного изображения. Для всех других типов изображений, кроме яркостного, возвращается пустой массив. disp_range = getDisplayRange(imgmodel)
где параметр imgmodel является действительной моделью изображения, а disp_range массивом в формате чисел удвоенной точности в диапазоне [0 255].getImageHeight Возвращает скаляр в формате чисел двойной точности, содержащий число строк. height = getImageHeight(imgmodel)
где параметр imgmodel является моделью изображения, а height скаляром в формате удвоенной точности.getImageType Возвращает текстовую строку, описывающую тип изображения. str = getImageType(imgmodel)
где imgmodel представляет модель изображения, а str представляет одну из текстовых строк 'intensity', 'truecolor', 'binary' или 'indexed'.getImageWidth Возвращает скаляр, содержащий число столбцов. width = getImageWidth(imgmodel)
где параметр imgmodel является моделью изображения, width скаляром в формате удвоенной точности.getMinIntensity Возвращает минимальное значение на изображении, вычисленное по формуле min(Image(:)). Для яркостных изображений, это значение представляет собой минимальную яркость. Для индексных изображений, это значение равно минимальному индексу. Для других типов изображений это значение представляется пустым массивом. minval = getMinIntensity(imgmodel)
где параметр imgmodel представляет модель изображения, а minval - числовое значение. Формат minval зависит от формата объекта изображения.getMaxIntensity Возвращает максимальное значение на изображении, вычисленное по формуле max(Image(:)). Для яркостных изображений это значение равно максимальной интенсивности. Для индексных изображений оно равно максимальному индексу. Для других типов изображений это значение представляется пустым массивом.
maxval = getMaxIntensity(imgmodel)
где imgmodel представляет модель изображения, а maxval - числовое значение. Формат maxval зависит от формата объекта изображения.getNumberFormatFcn Возвращает функцию преобразования числового значения в строку.
fun = getNumberFormatFcn(imgmodel)
где параметр imgmodel представляет действительную модель изображения. fun представляет функцию, которая захватывает числовые значения и возвращает их в виде текстовой строки. Например, ее можно использовать для преобразования числового значения getPixelValue в тестовую строку.
str = fun(getPixelValue(imgmodel,100,100))getPixelInfoString Возвращает текстовую строку, содержащую значение пикселя, расположение которого описано в виде строки и столбца.
str = getPixelInfoString(imgmodel,row,column)
где параметр imgmodel представляет действительную модель изображения, а row и column скаляры значений строк и столбцов. str представляется некоторым характерным массивом. Например, для RGB-изображений, возвращается текстовая строка типа '[66 35 60]'.getPixelRegionFormatFcn Возвращает некоторую функцию, конвертирующую значение пикселя в текстовую строку.
fun = getPixelRegionFormatFcn(imgmodel)
где параметр imgmodel представляет действительную модель изображения. fun представляет собой некоторую функцию, захватывающую информацию о расположении пикселя объекта изображения и возвращающую значение пикселя в виде строки описанного текстового формата. Например, при работе с RGB-изображением, функция возвращает текстовую строку в формате 'R:000 G:000 B:000', где 000 представляет действительное значение пикселя. str = fun(100,100)getPixelValue Возвращает значение пикселя, расположение которого описано через строку и столбец в виде числового массива.
val = getPixelValue(imgmodel,row, column)
где параметр imgmodel представляет действительную модель изображения, а row и column строки и столбцы в виде числовых скалярных значений. Формат параметра val зависит от формата объекта изображения.getDefaultPixelInfoString Возвращает текстовую строку, описывающую тип информации, возвращаемой информационной строкой о пикселе. Эта строка может использоваться в качестве информации о значении пикселя.
str = getDefaultPixelInfoString(imgmodel)
где параметр imgmodel представляет действительную модель изображения. В зависимости от типа изображения, str может быть одной из тестовых строк 'Intensity', '[R G B]', 'BW' или ' [R G B]'.getDefaultPixelRegionString Возвращает текстовую строку, указывающую на тип информации, отображаемой в Pixel Region tool для каждого типа изображения. Эта строка может использоваться для получения действительных значений пикселей.
str = getDefaultPixelRegionString(imgmodel)
где параметр imgmodel представляет действительную модель изображения. В зависимости от типа изображения, str может быть одной из текстовых строк '000', 'R:000 G:000 B:000]', '0' или '<000> R:0.00 G:0.00 B:0.00'.getScreenPixelRGBValue Возвращает отображаемые значения пикселей, расположение которых описывается параметрами ROW и COLUMN в виде массива в формате double.
val = getScreenPixelRGBValue(imgmodel,row, col)
где параметр imgmodel представляет действительную модель изображения, а row и column соответственно строки и столбцы в виде числовых скалярных значений. val представляется массивом в формате удвоенной точности, например, [0.2 0.5 0.3].Примечание:
Функция imagemodel работает через запрашиваемые объекты изображения CData. Для изображений в формате single или int16, объекты изображения преобразуются из CData в double. Например, в нашем случае h = imshow(int16(ones(10))), class(get(h,'CData')) возвращает 'double'. Поэтому, getClassType(imgmodel) возвращает 'double'.
Пример:
Рассмотрим пример использования функции imagemodel.
h = imshow('peppers.png');
im = imagemodel(h);
figure,subplot(1,2,1)
h1 = imshow('hestain.png');
subplot(1,2,2)
h2 = imshow('coins.png');
im = imagemodel([h1 h2]);
iptsetpref - установка глобальных переменных IPT
Синтаксис:
iptsetpref(prefname, value)
Описание:
Функция iptsetpref(prefname, value) присваивает глобальной переменной с именем prefname значение value. Имена глобальных переменных не зависят от регистра.
Установленные значения сохраняются в течение текущей сессии MATLAB либо пока не будут изменены последующим вызовом функции iptsetpref. Для того, чтобы сохранить значения между сессиями MATLAB, необходимо поместить соответствующие вызовы iptsetpref в файл startup.m.
В таблице ниже приведены возможные имена и значения глобальных переменных.
Параметр prefmane Возможные значения Описание 'ImshowBorder' 'loose' Изображение будет отображаться функцией imshow с отступом от края окна figure. Таким образом, в окне остается место для дополнительных надписей. Используется по умолчанию 'tight' Изображение будет отображаться функцией imshow так, чтобы оно занимало все окно figure 'ImshowAxesVisible' 'on' При выводе изображения функцией imshow в окне figure дополнительно будут выведены оси координат 'off' При выводе изображения функцией imshow в окне figure оси координат не выводятся. Используется по умолчанию 'ImshowTruesize' 'auto' Если в окне figure находится только изображение и его оси координат, то при выводе изображения функцией imshow автоматически вызывается функция truesize. Используется по умолчанию 'manual' При выводе изображения функцией imshow функция truesize не вызывается автоматически. Ее можно вызвать отдельно или передать соответствующий параметр функции imshow 'TruesizeWarning' 'on' При вызове функции truesize в окне интерпретатора MATLAB будет выводиться предупреждение в том случае, если размер выводимого изображения больше размеров окна. Используется по умолчанию 'off' Предупреждение функцией truesize не выводится iptgetpref - чтение глобальных переменных IPT
Синтаксис:
value=iptgetpref(prefname)
Описание:
Функция value=iptgetpref(prefname) возвращает значение глобальной переменной с именем prefname. Имена глобальных переменных не зависят от регистра.
Если вызвать функцию iptgetpref без входного параметра, то в value возвращается структура, содержащая значения всех глобальных переменных. Имена полей структуры совпадают с именами глобальных переменных.
getline - выбор ломаной линии с помощью мышки
Синтаксис:
[x, y]=getline(fig)[x, y]=getline(ax)[x, y]=getline[x, y]=getline(... , 'closed')
Описание:
Функция [x, y]=getline(fig) позволяет выбрать ломаную линию в текущем окне изображения fig с помощью мышки. Координаты ломаной линии помещаются в X и Y. Использование одного нажатия клавиши мышки приводит к прибавлению точки к ломаной кривой. Использование нажатия правой клавиши или удвоенного щелчка обозначает установку завершающей точки при выборе ломаной линии. Нажатие Return или Enter также приводит к установке последней точки при выборе ломаной линии. Нажатие Backspace или Delete возвращает к выбору предварительной точки ломаной линии.
[x, y]=getline(ax) - позволяет создать ломаную линию в системе координат, описанной в ax. [x, y]=getline - аналогично выражению [x, y]=getline(gcf). [x, y]=getline(..., 'closed') - динамика и возвращение результирующего полинома. getpts - выбор точек с помощью мышки
Синтаксис:
[x, y]=getpts(fig)
[x, y]=getpts(ax)
[x, y]=getpts
Описание:
Функция [x, y]=getpts(fig) позволяет выбрать точки в текущих координатах окна отображения fig с помощью мышки. Координаты выбранных точек помещаются в X и Y.
Использование левой клавиши мышки приводит в установке точки. Нажатие правой клавиши или двойной щелчок приводят к установке последней выбранной точки. Нажатие Return или Enter также приводит к установке последней выбранной точки. Нажатие Backspace или Delete приводит к выбору предварительной точки.
[x, y]=getpts(ax) - установка выбранной точки в координатах, описанных в ax. [x, y]=getpts - эквивалентное выражение [x, y]=getpts(gcf). getrect - выбор прямоугольника с помощью мышки
Синтаксис:
rect=getrect(fig)rect=getrect(ax)rect=getrect(fig)
Описание:
Функция rect=getrect(fig) позволяет установить прямоугольник в текущих координатах фигуры с использованием мышки. Координаты прямоугольника помещаются в X и Y.
Использование нажатия клавиш мышки и плавного ее передвижения приводит к созданию нужного прямоугольника. Параметр rect представляется четырехэлементным вектором в форме [xmin ymin width height].
Функция rect=getrect(ax) приводит к созданию прямоугольника в текущих координатах, описанных в ax.
ipticondir - возвращает название директории, содержащей IPT и MATLAB иконки
Синтаксис:
[D1 D2] = ipticondir
Описание:
Функция [D1, D2] = imicondir возвращает название директории, содержащей иконку приложения Image Processing Toolbox (D1) и иконку MATLAB (D2).
Примеры:
[iptdir, MATLABdir] = ipticondir
dir(iptdir)
iptgetapi - доступ к прикладному программному интерфейсу
Синтаксис:
API = iptgetapi(h)
Описание:
Функция API = iptgetapi(h) возвращает API-структуру, связанную с параметром h, в случае его существования. В других случаях, функция iptgetapi возвращает пустой массив.
Для более детальной информации см. функции immagbox, impositionrect или imscrollpanel.
Примеры:
hFig = figure('Toolbar','none',...
'Menubar','none');
hIm = imshow('tape.png');
hSP = imscrollpanel(hFig,hIm);
api = iptgetapi(hSP);
api.setMagnification(2) % 2X = 200%
imshow - вывод изображения на экран
Синтаксис:
imshow(l, n)
imshow(l, [low high])
imshow(BW)
imshow(X, map)
imshow(RGB)
imshow(...,display_option)
imshow(XData, YData, ...)
imshow filename
h=imshow(...)
Описание:
Функция imshow(I, n) выводит на экран полутоновое изображение I, используя при выводе n уровней серого. Если при вызове функции опустить параметр n, то когда MATLAB запущен в графическом режиме TrueColor, для вывода полутонового изображения используется 256 градаций серого или 64 градации серого, когда MATLAB запущен в графическом режиме с меньшим количеством цветов.
Функция imshow(I, [low high]) выводит на экран полутоновое изображение I, дополнительно контрастируя выводимое изображение. Пикселы изображения I, яркость которых меньше либо равна low, отображаются черным цветом. Пикселы, яркость которых больше либо равна high, отображаются белым цветом. Пикселы, яркость которых имеет значение между low и high, отображаются серым цветом. Все уровни серого равномерно распределены от low до high. Если вызвать функцию imshow(I, [ ]), указав вторым аргументом пустой массив, то low будет присвоено минимальное значение в I(low = min(I(:))), a high будет присвоено максимальное значение в I(max = max(I(:))).
Функция imshow(BW) выводит на экран бинарное изображение BW. Пикселы, значение которых равно 0, отображаются черным цветом. Пикселы, значение которых равно 1, отображаются белым цветом.
Функция imshow(X, map) выводит на экран палитровое изображение Х с палитрой mар.
Функция imshow(RGB) выводит па экран полноцветное изображение RGB.
Дополнительно в перечисленные функции можно передать параметр display_оption (imshow(...,display_ option)), который может принимать значения 'truesize' и 'notruesize'. Если параметр display_option равен 'truesize', то imshow будет автоматически вызывать функцию truesize. Если параметр display_option равен 'notruesize', то вызова функции truesizeпроисходить не будет. Когда параметр display_option не определен, вызов функции truesize зависит от значения глобальной переменной IPT 'ImshowTruesize'.
Кроме того, в перечисленные функции можно передать два двухэлементных вектора XData и YData, определяющих диапазон изменения значений по осям пространственной системы координат: imshow(XData, YData,...).
Функция imshow filename выводит на экран изображение из файла с именем filename. Для чтения файла imshow вызывает функцию imread.
Если для функций imshow определить выходной параметр h=imshow(...), то в h будет возвращен описатель (handler) выведенного изображения как объекта графического интерфейса MATLAB.
truesize - установка размеров окна для отображения изображений
Синтаксис:
truesize(fig, [mrows mcols])
truesize(fig)
Описание:
Функция truesize(fig, [mrows mcols]) устанавливает для окна с описателем fig размер в mrows пикселов по вертикали и mcols пикселов по горизонтали. Если в данное окно выводится изображение, то оно масштабируется до этих размеров.
Функция truesize(fig) устанавливает для окна с описателем fig размер, равный размерам изображения, выведенного в окне fig. В результате изображение выводится без масштабирования.
При вызове рассматриваемых функций можно опустить параметр fig. В этом случае размеры будут устанавливаться для текущего окна.
Когда глобальная переменная 'TruesizeWarning' имеет значение 'on' (включено), то в командном окне системы MATLAB выводится предупреждение, если размер выводимого изображения больше размера экрана.
subimage - вывод нескольких изображений в одном окне
Синтаксис:
subimage(S)
subimage(X,map)
subimage(XData, Ydata, …)
h= subimage(…)
Описание:
Функция subimage(S) в сочетании с функцией MATLAB subplot позволяет вывести в одно окно figure несколько полноцветных, полутоновых и бинарных изображений S. Аналогично для вывода палитровых изображений работает функция subimage(X,map). Заметим, что в одно окно могут выводиться изображения разного типа.
Функция subplot(m, n, p) разбивает текущее окно на
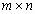 подокон и устанавливает текущим окно с номером p. Подокна нумеруются слева направо и сверху вниз, начиная от левого верхнего подокна, которое имеет номер 1. Функция subimageвыводит изображение в текущее подокно.
подокон и устанавливает текущим окно с номером p. Подокна нумеруются слева направо и сверху вниз, начиная от левого верхнего подокна, которое имеет номер 1. Функция subimageвыводит изображение в текущее подокно.Кроме того, в функцию subimage можно передать два двухэлементных вектора XData и Ydata, определяющих диапазон изменения значений по осям пространственной системы координат: subimage(XData, Ydata, …).
Если для функций subimage определить выходной параметр h=subimage(…), то в h будет возвращен описатель (handler) выведенного изображения как объекта графического интерфейса системы MATLAB.
Пример.
Функции subplot и subimage удобно использовать тогда, когда требуется для визуальной оценки полученных результатов в одно окно поместить исходное изображение и результат его обработки.
Программа демонстрирует чтение расфокусированного изображения и его фильтрацию с целью увеличения резкости. Исходное изображение и результат выводятся в одно окно (рис. 1).
%Пример демонстрирует фильтрацию изображения с целью повышения резкости
%и вывод исходного и получившегося изображения в одно окно.
%Чтение исходного файла
im=imread(‘lena.tif’);
im=im2double(im);
%Фильтрация с целью повышения резкости.
h=fspecial(‘unsharp’, 0.5);
imsharp=conv2(im, h);
imsharp=im2uint8(imsharp);
%Вывод исходного и полученного изображения в одно окно.
subplot(1,2,1), subimage(im);
subplot(1,2,2), subimage(imsharp);
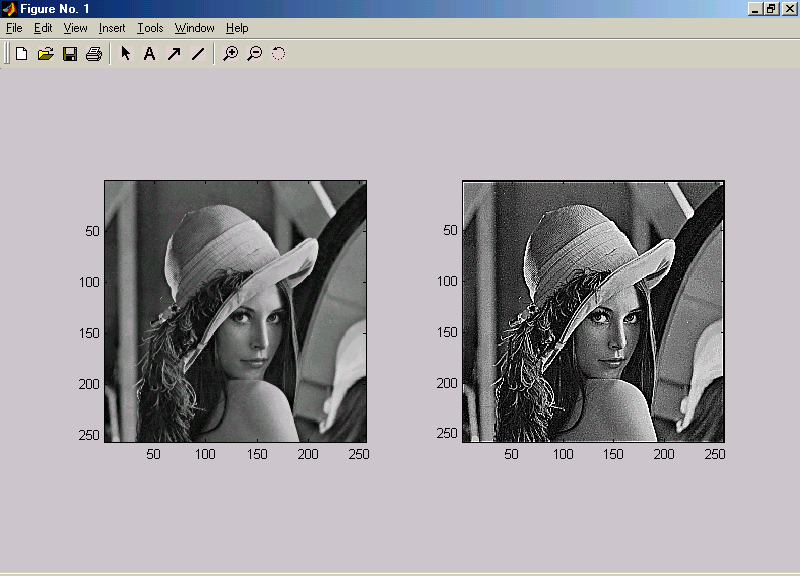
Рис. 1
colorbar - вывод на экран палитры
Синтаксис:
colorbar
colorbar(‘vert’)
colorbar(‘horiz’)
colorbar(h)
h=colorbar(…)
Описание:
Функция colorbar без параметров или функция colorbar(‘vert’) добавляет в текущее окно справа от изображения вертикальный прямоугольник с цветами текущей палитры. Функция colorbar(‘horiz’) добавляет в текущее окно снизу от изображения горизонтальный прямоугольник с цветами текущей палитры.
Функция colorbar(h) добавляет в окно с описателем h вертикальный прямоугольник с цветами текущей палитры.
Если для функции colorbar определить выходной параметр h=colorbar(…), то в h будет возвращен описатель (handler) нарисованной палитры как объекта графического интерфейса MATLAB.
imcontour - построение для изображения линий уровня
Синтаксис:
imcontour(I, n)
imcontour(I, v)
imcontour(XData, YData, …)
imcontour(…, LineSpec)
[C, h]=imcontour(…)
Описание:
Функция imcontour рассматривает полутоновое изображение I как трехмерную поверхность (x, y - пространственной системы координат и третья координата – яркость), строит для поверхности линии уровня аналогично функции MATLAB contour и выводит их на экран. Линии уровня образуются в результате пересечения плоскостей, перпендикулярных оси яркости и рассматриваемой поверхности. Линии уровня, соответствующие различным яркостям (лежащим в различных плоскостях), обозначаются разными цветами.
Функция imcontour(I, n) строит линии уровня для полутонового изображения I, используя n плоскостей, проходящих через значения, равномерно распределенные по оси яркости. Если в вызове функции параметр n опущен, то он выбирается автоматически.
Функция imcontour(I, v) строит линии уровня для полутонового изображения I, используя плоскости, проходящие через значения на оси яркости из вектора v.
Функция imcontour(XData, YData, …) в двухкомпонентных векторах XData и Ydata дополнительно определяет диапазон изменения значений по осям пространственной системы координат.
Функция imcontour(…, LineSpec) дополнительно определяет тип линии в параметре LineSpec. Существующие типы линий можно посмотреть в описании функции MATLAB plot.
Функция [C, h]=imcontour(…) возвращает массив С координат линий уровня и вектор h описателей графических объектов для изображений, соответствующих каждой линии уровня.
Пример.
Для полутонового изображения (рис. 1а) создается изображение с линиями уровня для трех уровней яркости (рис. 1б).
%Пример демонстрирует построение линий уровня
%для полутонового изображения
%Чтение изображения и вывод его на экран
I=imread(‘lena.tif’);
imshow(I);
%Вывод линий уровня для трех уровней яркости в новое окно.
figure, imcontour(I,3);

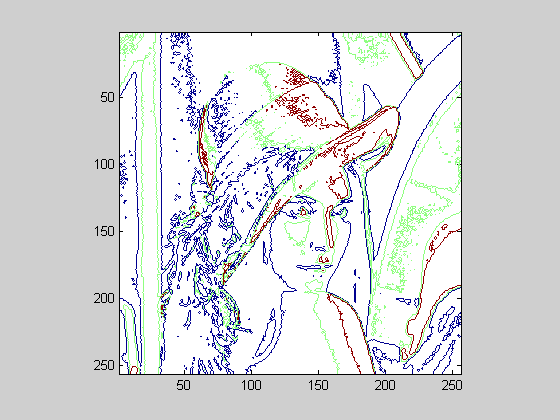
Рис. 1
immovie - создание видеопоследовательности
Синтаксис:
MovX=immovie(MX, map)
Описание:
Функция MovX=immovie(MX, map) формирует матрицу MovX из многокадрового палитрового изображения MX с палитрой map. Матрица MovX представляет собой видеопоследовательность, которая может быть показана на экране с помощью функции MATLAB movie.
Многокадровое палитровое изображение MX составляется из нескольких палитровых изображений одинакового размера
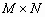 и использующих одинаковую палитру. MX является четырехмерным массивом
и использующих одинаковую палитру. MX является четырехмерным массивом 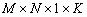 , где
, где 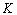 – количество кадров.
– количество кадров.Пример.
Имеется 4 полноцветных изображения. Требуется составить из этих кадров видеопоследовательность (маленький фильм) и показать его на экране.
%Пример демонстрирует создание видеопоследовательности.
%Чтение отдельных кадров из файлов.
f1=imread(‘frame1.bmp’);
f2=imread(‘frame2.bmp’);
f3=imread(‘frame3.bmp’);
f4=imread(‘frame4.bmp’);
%Преобразование полноцветных изображений в палитровые.
%Поскольку у всех кадров должна быть одинаковая палитра,
%то первое изображение преобразовываем с подбором оптимальной
%палитры map и применяем эту палитру к остальным изображениям.
[f1, map]=rgb2ind(f1, 200);
f2=rgb2ind(f2, map);
f3=rgb2ind(f3, map);
f4=rgb2ind(f4, map);
%Формируем многокадровое палитровое изображение
MX=cat(4, f1, f2, f3, f4);
%Формируем матрицу видеопоследовательности.
mov=immovie(MX, map);
%Выводим 10 раз видеопоследовательность на экран
%с частотой 8 кадров в секунду.
movie(mov, 10, 8);
montage - вывод на экран всех кадров многокадрового изображения
Синтаксис:
montage(MS);
montage(MX, map);
h=montage(…)
Описание:
Функция montage(MS) одновременно выводит на экран в текущее окно все кадры многокадрового полноцветного, полутонового или бинарного изображения MS. Многокадровое полутоновое или бинарное изображение составляется из нескольких соответственно полутоновых или бинарных изображений одинакового размера
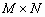 . Такое многокадровое изображение является четырехмерным массивом
. Такое многокадровое изображение является четырехмерным массивом .gif) , где
, где 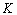 – количество кадров. Многокадровое полноцветное изображение составляется из нескольких полноцветных изображений одинакового размера
– количество кадров. Многокадровое полноцветное изображение составляется из нескольких полноцветных изображений одинакового размера .gif) . Полноцветное многокадровое изображение является четырехмерным массивом
. Полноцветное многокадровое изображение является четырехмерным массивом  , где
, где .gif) – количество кадров.
– количество кадров.Функция montage(MX, map) одновременно выводит на экран в текущее окно все кадры многокадрового палитрового изображения MX с палитрой map. Многокадровое палитровое изображение MX составляется из нескольких палитровых изображений одинакового размера
.gif) и использующих одинаковую палитру. MX является четырехмерным массивом
и использующих одинаковую палитру. MX является четырехмерным массивом .gif) , где
, где .gif) – количество кадров.
– количество кадров.Функция h=montage(…) возвращает описатель выведенного многокадрового изображения как объекта графического интерфейса системы MATLAB.
warp - наложение изображения на поверхность
Синтаксис:
warp(S)
warp(X, map)
warp(I, n)
warp(z,…)
warp(x,y,z,…)
h= warp(…)
Описание:
Функция warp(S) выводит в текущее окно плоскую прямоугольную поверхность, на которую наложено полноцветное или бинарное изображение S.
Функция warp(X, map) выводит в текущее окно плоскую прямоугольную поверхность, на которую наложено палитровое изображение X с палитрой map.
Функция warp(I, n) выводит в текущее окно плоскую прямоугольную поверхность, на которую наложено полутоновое изображение I. При выводе на экран используется n градаций яркости.
Функция warp(x, y, z) выводит в текущее окно поверхность, задаваемую вектором координат x, y, z, на которую наложено изображение.
Функция warp(z,…) выводит в текущее окно поверхность, задаваемую вектором координат z (координаты x, y подбираются автоматически), на которую наложено изображение.
Функция h= warp(…) возвращает описатель выведенной поверхности или объекта графического интерфейса MATLAB.
Пример.
Рассмотрим пример, в котором изображение накладывается на сферическую поверхность. На экран выводятся исходное изображение (рис.1 а) и сфера, на которую наложено изображение (рис.1. б).
%Пример демонстрирует наложение изображения
%на сферическую поверхность.
%Чтение исходного файла изображения и вывод его на экран.
I=imread(‘blood.tif’);
imshow(I);
%Создание сферической поверхности
% и наложение на нее изображения.
[x, y, z]=sphere;
figure, warp(x, y, x, I);
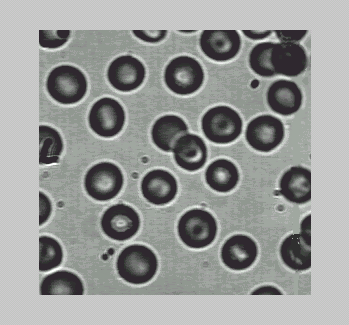

a) б)
Рис. 1.
zoom - масштабирование изображения в окне изображения
Синтаксис:
zoom on
zoom off
zoom out
zoom reset
zoom
zoom xon
zoom yon
zoom(factor)
zoom(fig, option)
Описание:
Команда zoom on включает режим интерактивного масштабирования для текущего окна (figure). В этом режиме щелчок клавиши мыши приводит к увеличению или уменьшению окна в factor раз. Курсор мыши должен находится в пределах изображения. Щелчок левой клавишей мыши приводит к увеличению окна, а щелчок правой клавишей - к уменьшению. Если перемещать курсор при нажатой левой клавише мыши, то можно указать прямоугольный фрагмент изображения, который следует увеличить до размеров всего окна.
Команда zoom out возвращает размер изображения к его первоначальному состоянию. Аналогичное действие производит двойной щелчок левой клавиши мыши, когда курсор находится в пределах изображения.
Команда zoom reset запоминает текущие размеры отображаемого фрагмента изображения как его первоначальные размеры. Позднее к этим размерам можно будет возвратиться с помощью команды zoom out.
Команда zoom off выключает режим интерактивного масштабирования.
Команда zoom переключает режим интерактивного масштабирования, то есть если режим был включен, то он выключается, а если был выключен, то включается.
Команда zoom xon и zoom yon включают режим интерактивного масштабирования отдельно по горизонтали или вертикали соответственно.
Функция zoom(factor) устанавливает значение коэффициента масштабирования. По умолчанию factor=2.
Функция zoom(fig, option) управляет режимом масштабирования для окна с описателем fig. Параметр option может принимать значения параметров описанных выше команд: on, off, xon, yon, reset, factor.
Необходимо отметить, что zoom конфликтует с другими функциями, которые включают режим интерактивного использования курсора, например с функцией pixval. Одновременно можно использовать только одну функцию подобного типа.
getimage - получение изображения из графического объекта
Синтаксис:
D=getimage(h)
[xData, yData, D]=getimage(h)
[…, D, flag]=getimage(h)
Описание:
Функция D=getimage(h) возвращает изображение D, содержащееся в графическом объекте MATLAB, например в окне figure, с описателем h. Если объект с описателем h не содержит изображения, то функция возвращает пустую матрицу.
Функция [xData, yData, D]=getimage(h) дополнительно возвращает два двухэлементных вектора xData и yData, содержащих диапазоны изменения координат по осям пространственной системы координат изображения D.
Функция […, D, flag]=getimage(h) дополнительно возвращает целочисленный параметр flag, который указывает тип изображения, содержащегося в графическом объекте с описателем h и, соответственно, помещенного в D.
Параметр flag может принимать следующие значения:
Флаг Тип изображения 0 Графический объект не содержит изображение. D – пустая матрица 1 D – полутоновое изображение со значениями яркости в стандартных диапазонах, т.е. [0, 1] – для формата представления данных double, [0,255] – для формата представления данных uint8 2 D – палитровое изображение 3 D – полутоновое изображение со значениями яркости вне стандартных диапазонов 4 D – полноцветное изображение dicominfo - чтение метаданных из DICOM-файла
Синтаксис:
info=dicominfo(filename)
info=dicominfo(filename,'dictionary', D)
Описание:
Функция info=dicominfo(filename) формирует метаданные, полученные из DICOM-файла (Digital Imaging and Communications in Medicine).
Функция info=dicominfo(filename, 'dictionary', D) использует словарные данные для считывания в массив D DICOM-сообщений. Системе MATLAB необходимо указать путь к записываемому файлу. По умолчанию этот файл называется dicom-dict.txt.
Пример:
info=dicominfo('CT-MONO2-16-ankle.dcm')
info=
Filename:[1x47 char]
FileModDate:'24-Dec-2000 19:54:47'
FileSize:525436
Format:'DICOM'
FormatVersion:3
Width:512
Height:512
BitDepth:16
ColorType:'grayscale'
… и т.д.
dicomread - чтение DICOM изображений
Синтаксис:
X=dicomread(filename)
X=dicomread(info)
[X, map]=dicomread(...)
[X, map, alpha]=dicomread(...)
[X, map, alpha, overlays]=dicomread(...)
Описание:
Функция X=dicomread(filename) считывает видеоинформацию, представленную файлом в формате “Цифровые изображения и коммуникации в медицине” (Digital Imaging and Communications in Medicine (DICOM)). В большинстве случаев, это массив полутонового изображения X с размерностью M
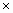 N или массив цветного изображения X с размерностью M
N или массив цветного изображения X с размерностью M.gif) N
N.gif) 3. Многомерные изображения могут представляться четырехмерным массивом.
3. Многомерные изображения могут представляться четырехмерным массивом.Функция X=dicomread(info) считывает справочные данные из DICOM-файла в структуру info, которая генерируется функцией dicominfo.
Функция [X, map]=dicomread(...) возвращает изображение X и палитру MAP. Когда массив X является полутоновым или цветным (true) изображением, параметр map пустой.
Функция [X, map, alpha]=dicomread(...) возвращает изображение X, палитру map и alpha канал для матрицы X. Значение параметра alpha равно 0, если пикселы темные, в других случаях равен индексам палитры. Значения RGB в палитре map при помощи alpha замещают значения массива X. Размерность alpha совпадает с размерностью массива X, а в многомерном случае – с размерностью мультифреймовых изображений.
Функция [X,map, alpha, overlays]=dicomread(...) также возвращает изображение X, палитру map, alpha канал для матрицы X и некоторые оверлейные данные из DICOM–файла. Эти данные представляют собой однобитные черно-белые изображения, размерность которых совпадает с размерностью X. Оверлейные данные могут представляться как многомерными массивами, так и быть пустыми в случае их отсутствия.
Синтаксис записи исходных параметров должен быть следующим:
[...]=dicomread(filename, param1, value1, param2, value2, ...)
[...]=dicomread(info, param1, value1, param2, value2, ...)
Параметры названия (names) и значения (values) должны быть следующими.
'Frames', V Функция dicomread считывает только фреймы в вектор V с изображений. V должен быть целым числом, вектором целых чисел или строчкой в формате 'all'. По умолчанию вектор V имеет формат представления данных 'all'. 'Dictionary', D Функция dicomread использует данные словарного файла, название которого отображено в D. По умолчанию это значение представлено в 'dicom-dict.txt'. 'Raw', TF Функция dicomread выполняет преобразование значений пикселов в зависимости от значения параметра TF. Если параметр TF равен 1 (по умолчанию), функция dicomread считывает пикселы из изображения и не проводит преобразование их значений. Если значение параметра TF равно 0, то проводятся преобразования с использованием динамических рангов, а цветные изображения конвертируются в цветовое пространство RGB.
Примечание 1: Поскольку цветовое пространство HSV не отвечает требованиям стандарта DICOM, функция dicomread не может автоматически конвертировать их в RGB.
Примечание 2: Функция dicomread никогда не проводит преобразований цветовых пространств изображений, содержащих печатные данные.
Примечание 3: Преобразование значений и цветовых систем не приводит к изменению метаданных.Пример 1:
При использовании функции dicomread для восстановления данных матрицы X и ее палитры map, необходимо сделать так:
[X, map]=dicomread('US-PAL-8-10x-echo.dcm');
montage(X, map);
Пример 2:
Для получения информации из DICOM–файла функция dicomread использует dicominfo. Отображаются изображения с помощью функции imshow.
info=dicominfo('CT-MONO2-16-ankle.dcm');
Y=dicomread(info);
imshow(Y, []);
dicomwrite - запись изображений в DICOM-файл
Синтаксис:
dicomwrite(X, filename)
dicomwrite(X, map, filename)
dicomwrite(..., param1, value1, param2, value2, ...)
dicomwrite(..., meta_struct, ...)
dicomwrite(..., info, ...)
status=dicomwrite(...)
Описание:
Функция dicomwrite(X, filename) записывает бинарное полутоновое или цветное изображение X в файл формата DICOM (Digital Imaging and Communications in Medicine).
Функция dicomwrite(X, map, filename) записывает индексное изображение X вместе с палитрой map.
Функция dicomwrite(..., param1, value1, param2, value2, ...) определяет дополнительные метаданные для записи DICOM–файлов. С помощью параметров (param1, param2 и т.д.) записываются другие атрибуты и опции DICOM–файлa. Каждый атрибут или опция соответствует некоторому значению (value1, value2 и т.д.).
Полный список названий атрибутов DICOM–файла содержится в словарном файле, который включен в Image Processing Toolbox.
В таблице приведен список опций, которые поддерживаются функцией dicomwrite.
Название опции Описание Значение 'Endian' Определяет байтовый порядок для файла. 'Little' [по умолчанию]
'Big''VR' Определяет двухзнаковый код представления значений, записанных в файле ('explicit') или возможных данных со словаря ('implicit'). 'Implicit' [по умолчанию]
'Explicit'
Примечание: Когда значение опции 'Endian' определено как 'Big', то опция 'VR' может принимать только значение 'Explicit'.'CompressionMode' Определяет метод сжатия для хранения изображений. 'None' [по умолчанию]
'JPEG lossy' (с потерями информации)
'RLE''TransferSyntax' Определяет синтаксис преобразований DICOM–файлов.
Примечание:
Когда определена опция 'TransferSyntax', функция dicomwrite игнорирует другие три опции, если они были определены.Синтаксис преобразований DICOM–файла определяет по умолчанию значения для опций 'Endian', 'VR' и 'CompressionMode'. Функция dicomwrite(..., meta_struct, ...) определяет метаданные в структуре meta_struct. Название структурных областей должно быть отображено в названиях атрибутов или опций DICOM–файла. Значения областей являются значениями атрибутов или опций.
Функция dicomwrite(..., info, ...) определяет метаданные в структуре info, которая генерирует функцию dicominfo. Для более детальной информации о структуре см. функцию dicominfo.
Функция status=dicomwrite(...) возвращает перечень трех типов метаданных, которые содержатся в dicomwrite. Этот синтаксис используется, когда определена структура info, создающая dicominfo в функции dicomwrite. В структуре info может быть определено много полей. Когда метаданные не определены, dicomwrite возвращает пустую матрицу ([]).
При использовании dicomwrite структура содержит три поля.
Поле Описание 'dicominfo_fields' Массив содержит названия метаданных, которые могут быть использованы при записи. 'wrong_IOD' Массив содержит названия атрибутов (IOD=Information Object Definition). 'not_modifiable' Массив содержит названия полей метаданных, которые не изменяются при использовании. Пример:
Этот пример демонстрирует использование dicominfo для восстановления информации о содержании простого DICOM–файла, который содержится в Image Processing Toolbox. Пример использует dicomread для считывания данных из файла и записи данных в новый DICOM–файл, содержащий метаданные исходного файла.
info=dicominfo('CT-MONO2-16-ankle.dcm');
Y=dicomread(info);
status=dicomwrite(Y, 'my_dicomfile.dcm', info);
status=
dicominfo_fields: {12x1 cell}
wrong_IOD: {21x1 cell}
not_modifiable: {23x1 cell}
status.dicominfo_fields
ans=
'BitDepth'
'ColorType'
'FileModDate'
'FileSize'
'FileStruct'
'Filename'
'Format'
'FormatVersion'
'Height'
'SelectedFrames'
'StartOfPixelData'
'Width'
dicomuid - Генерация идентификатора для DICOM-файлов
Синтаксис:
UID=dicomuid
Описание:
Функция UID=dicomuid создает строку UID, содержащую новый идентификатор для DICOM-файлов.
Вызов функции dicomuid формирует уникальный идентификатор. Следующий вызов функции dicomuid всегда приводит к формированию нового значения.
imview - Отображение изображений в Image Viewer
Синтаксис:
imview(I)imview(RGB)imview(X, map)imview(I, range)imview(filename)imview(..., 'InitialMagnification', initial_mag)h=imview(...)imview close all
Описание:
Функция imview(I) отображает полутоновое изображение I.
Функция imview(RGB) отображает RGB-изображение (true-color).
Функция imview(X, map) отображает индексное изображение X с палитрой map.
Функция imview(I, range) отображает полутоновое изображение I, где параметр range является двухэлементным вектором [LOW HIGH], который контролирует диапазон (полутоновый) яркостей в отображаемом изображении. Функция imview отображает значение LOW (или другие значения, которые меньше чем LOW) как черное и значение HIGH (или другие значения, которые больше чем HIGH) как белые. Промежуточные значения отображаются различными оттенками серого. Параметр range может быть также пустым ([]), в этом случае функция imview отображает минимальное значение изображения I черным, а максимальное значение - белым. Другими словами, функция imview(I,[]) эквивалентна выражению imview(I, [min(I(:)) max(I(:))]).
Функция imview(filename) отображает изображение, содержащиеся в файле с названием, описанным в filename. Файл должен содержать изображение, которое может быть прочитано функцией imread. Когда файл содержит много изображений, отображается только первое.
Применение функции imview без исходных аргументов открывает диалоговое окно, с помощью которого существует возможность интерактивного выбора изображений.
H=imview(...) возвращает ручное управление средствами просмотра. Функция close(H) закрывает средство просмотра изображений (image viewer).
Функция imview close закрывает все окна просмотра изображений (image viewers).
Функция imview(..., 'InitialMagnification', initial_mag) отображает изображение, которое описывается параметрами InitialMagnification, контролирующими начальное увеличение для отображения изображений. Параметр initial_mag может принимать одно из следующих значений.
Значение Описание 100 Отображается изображение в 100% увеличении; каждый элемент изображения отображается одним пикселем 'fit' Изображение помещается в окно Image Viewer. Требования к исходным данным.Исходное изображение может быть представлено данными в формате logical, uint8, uint16 или double.Пример.Это пример открытия и отображения файла, описанного текстовой строкой:imview('board.tif').Это пример открытия и отображения индексного изображения:[X, map]=imread('trees.tif');imview(X, map)Это пример ввода полутонового изображения в рабочее пространство MATLAB и его отображение:I=imread('cameraman.tif');imview(I)Это пример отображения изображения с описанием диапазона интенсивностей. Эта функция использует также управление Image Viewer:h=imview(I,[0 80]);close(h)Примечание.Управление многооконным Image Viewer.
В Image Viewer существует возможность одновременного просмотра нескольких изображений, также существует возможность их одновременного закрытия с помощью команды:
imview close all
Сделать такую же операцию, которая заключается в закрытии всех отрытых окон Image Viewer, можно с использованием кнопки Close All в Window-меню командного окна MATLAB.
В отдельных случаях Window-меню можно использовать и для открытия и управления окнами Image Viewer.
Управление памятью.
Для увеличения объема памяти, которая поступает в распоряжение Image Viewer, создается файл с названием 'java.opts' и помещается в исходную директорию MATLAB. По умолчанию, MATLAB использует память Virtual Machine объемом 64 MB.
Файл java.opts может использовать объем памяти до 128 MB:
-Xmx128m
С целью предупреждения перегрузок, опция -Xmx option устанавливается на уровне, не превышающем 66% от оперативной памяти.
Система UNIX создает файл java.opts в рабочей директории и заходит в эту директорию перед запуском MATLAB.
В системе Windows:
-
Создается файл java.opts в директории, откуда будет запущен MATLAB.
-
Создается ярлык MATLAB.
-
Нажатие правой клавиши приводит к выбору окна Properties (Свойства).
-
В окне Properties описано название директории, в которой создан файл java.opts; эта директория является стартовой для MATLAB.
-
-
MATLAB как и Image Viewer использует память Java Virtual Machine. Для просмотра больших изображений запускают MATLAB, а далее используют Image Viewer.
imgcf - получение последних отображаемых изображений
Синтаксис:
hfig = imgcf
Описание:
Функция hfig = imgcf возвращает последние отображаемые изображения. Изображения визуализируются в окне figure.
Если окно figure не было открыто, то функция imgcf создает новое окно figure.
Примечание:
Функция imgcf может быть полезна для получения окна Image Tool figure.
Пример:
imtool rice.png
cmap = copper(256);
set(imgcf,'Colormap',cmap)
imgca - получение недавно обрабатываемых данных
Синтаксис:
hax = imgca
hax = imgca(hfig)
Описание:
Функция hax = imgca возвращает недавно обрабатываемые данные, которые связаны с изображением. Эти данные могут представлять собой координатные оси в виде окна отображения или окна просмотра Image Tool window.
Когда окно просмотра не содержит этих данных, то функция imgca создает новые координатные оси.
Функция hax = imgca(hfig) возвращает координатные оси, которые содержат изображение в описанном окне просмотра.
Примечание:
Функция imgca может использоваться для получения осей в Image Tool.
Пример:
Считаем изображение из файла coins.png. Вычислим некоторые его характеристики и представим результаты с помощью функций imtool и imgca.
I = imread('coins.png');
figure, imshow(I)
bw = im2bw(I, graythresh(getimage));
figure, imshow(bw)
bw2 = imfill(bw,'holes');
L = bwlabel(bw2);
s = regionprops(L, 'centroid');
centroids = cat(1, s.Centroid);
Отобразим полученные результаты.
imtool(I)
hold(imgca,'on')
plot(imgca,centroids(:,1), centroids(:,2), 'r*')
hold(imgca,'off')
imgetfile - отображение диалогового окна открытия изображений
Синтаксис:
[filename, user_canceled] = imgetfile
Описание:
Функция [filename, user_canceled] = imgetfile отображает диалоговое окно открытия изображений, а также указывает полный путь к выбранному файлу. Если пользователь надавит кнопку Cancel, параметр user_canceled будет иметь значение TRUE. В противном случае, параметр user_canceled равен FALSE.
Диалоговое окно открытия изображения является прообразом интерактивной командной строки системы MATLAB. В imformats перечислены все типы файлов диалогового окна, включая DICOM.
imhandles - установка ручного управления изображениями
Синтаксис:
himage = imhandles(H)
Описание:
Функция himage = imhandles(H) через использование параметра h в качестве исходного, возвращает все предыдущие изображения. В свою очередь, h представляет собой массив параметров, описывающих оси, окно просмотра и другие установки.
Результат himage представляется в виде массива.
Примечание:
Функция imhandles может выдавать ошибку, если объекты изображения в himage не имеют предыдущей версии.
Примеры:
Пример демонстрирует ручное управление объектами изображения в данном окне отображения.
figure, imshow('moon.tif');
himage = imhandles(gcf)
В этом примере показано отображение двух изображений в окне просмотра с использованием функции imhandles.
subplot(1,2,1), imshow('autumn.tif');
subplot(1,2,2), imshow('glass.png');
himages = imhandles(gca)
dicomanon - анонимность DICOM-файла
Синтаксис:
dicomanon(file_in, file_out)
dicomanon(...,'keep',FIELDS)
dicomanon(...,'update',ATTRS)
Описание:
Функция dicomanon(file_in,file_out) перемещает конфиденциальную медицинскую информацию из DICOM-файла file_in и создает новый файл file_out с модифицируемыми значениями. Данные изображения и другие атрибуты не модифицируются.
Функция dicomanon(...,'keep',FIELDS) модифицирует все конфиденциальные данные, за исключением данных, перечисленных в FIELDS и представленных в виде массива с соответствующими названиями полей. Такой синтаксис удобен для хранения метаданных, которые могут идентифицировать пациента при диагностике (например, PatientAge, PatientSex и т.д.).
Примечание:
Хранение определенных полей может носить конфиденциальный характер.
Функция dicomanon(...,'update',ATTRS) модифицирует и частично обновляет конфиденциальные данные. Параметр ATTRS представляет собой структуру, названия полей которой совпадают с соответствующими атрибутами. Значения структур являются значениями атрибутов. Используется синтаксис иерархического хранения или специальных названий для более общих свойств.
Для более детальной информации о полях, которые подлежат модификации или переносу, см. DICOM Supplement 55 на сайте http://medical.nema.org/.
Примеры:
Перенос всех конфиденциальных метаданных из файла.
dicomanon('patient.dcm', 'anonymized.dcm')
Создание учебного файла.
dicomanon('tumor.dcm', 'tumor_anon.dcm', ...
'keep', {'PatientAge', 'PatientSex', 'StudyDescription'})
Анонимность серии изображений, которые хранятся иерархично.
values.StudyInstanceUID = dicomuid;
values.SeriesInstanceseriesUID = dicomuid;
d = dir('*.dcm');
for p = 1:numel(d)
dicomanon(d(p).name, sprintf('anon%d.dcm', p), ...
'update', values)
end
dicomdict - получение или установка активного словаря DICOM-данных
Синтаксис:
dicomdict('set', dictionary)
dictionary = dicomdict('get')
dictionary = dicomdict('factory')
Описание:
Функция dicomdict('set',dictionary) устанавливает словарь DICOM-данных для запоминания значений в виде строки, содержащей название файла. DICOM-зависимые функции, в большинстве случаев, используют словарь по умолчанию.
Функция dictionary = dicomdict('get') возвращает строку, содержащую название файла с запоминаемыми данными.
Функция dictionary = dicomdict('factory') восстанавливает данные DICOM-словаря, приводя первоначальное значение.
Примечание:
По умолчанию данные словаря хранятся в виде MAT-файла, dicom-dict.mat. Приложение также включает текстовую версию данных словаря dicom-dict.txt. Если есть необходимость создания своего DICOM-словаря, необходимо открыть файл dicom-dict.txt в текстовом редакторе, модифицировать его, а потом запомнить под другим именем.
Примеры:
dictionary = dicomdict('get')
dictionary =
dicom-dict.mat
impositionrect - создание передвигаемого прямоугольника
Синтаксис:
H = impositionrect(hparent,position)
Описание:
Функция H = impositionrect(hparent,position) создает прямоугольник на объекте с описанием hparent. Возвращаемая функция H управляет прямоугольником, который представлен объектом hggroup. Прямоугольник описывается четырехэлементным вектором [XMIN YMIN WIDTH HEIGHT].
Все измерения описываются свойством object. По умолчанию функция impositionrect использует вектор значений [0 0 1 1].
Примечание:
Месторасположение прямоугольника можно изменять, передвигая его с помощью мышки.
С прямоугольником связано контекстное меню, которое можно использовать для копирования в буфер, изменения цвета прямоугольника на экране монитора и др.
Синтаксис функции API:
Прямоугольник связан с функцией API, которая дает возможность управлять им. Для получения функции API используется функция iptgetapi.
API = iptgetapi(H)
В приведенном ниже списке описаны функции и их роль при размещении прямоугольника.
Функции Описание setPosition Установка прямоугольника на новую позицию.
api.setPosition(new_position),
где параметр new_position представляет четырехэлементный вектор, описывающий новое расположение.getPosition Возвращает информацию о текущем расположении прямоугольника.
position = api.getPosition()
Расположение описывается четырехэлементным вектором.delete Удаляет информацию о расположении прямоугольника, связанную с функцией API.
api.delete()setColor Установка цвета, который используется при прорисовке месторасположения прямоугольника.
api.setColor(new_color),
где параметр new_color представляет собой трехэлементный вектор, описывающий значения RGB изображения.addNewPositionCallback Добавляет функцию управления списком функций новых позиций.
id = api.addNewPositionCallback(fun)
При изменении позиции прямоугольника, каждая функция в прямоугольнике называется соответственно принятому синтаксису:
fun(position)
Возвращаемое значение id используется только с NewPositionCallback.removeNewPositionCallback Возвращает соответствующую функцию из списка новых позиций api.removeNewPositionCallback(id), где параметр id представляет собой идентификатор, возвращаемый api.addNewPositionCallback setDragConstraintCallback Установка функции принудительного передвижения описывается параметром fcn.
api.setDragConstraintCallback(fcn)
При каждом изменении расположения прямоугольника с помощью мышки, функция принудительного передвижения использует следующий синтаксис:
constrained_position = fcn(new_position),
где параметр new_position представляется в виде четырехэлементного вектора. Это позволяет пользователю контролировать размещение прямоугольника при передвижении.Пример:
Отобразим в командном окне размещение прямоугольника при передвижении.
close all, plot(1:10)
h = impositionrect(gca, [4 4 2 2]);
api = iptgetapi(h);
api.addNewPositionCallback(@(p) disp(p));
Заставим прямоугольник передвигаться только вверх и вниз.
close all, plot(1:10)
h = impositionrect(gca, [4 4 2 2]);
api = getappdata(h, 'API');
api.setDragConstraintCallback(@(p) [4 p(2:4)]);
Опишем цвет прямоугольника.
close all, plot(1:10)
h = impositionrect(gca, [4 4 2 2]);
api = iptgetapi(h, 'API');
api.setColor([1 0 0]);
Когда размещение прямоугольника занимает только пять пикселей на экране, то прямоугольник может увеличиваться.
close all, imshow cameraman.tif
h = impositionrect(gca, [100 100 10 10]);
imscrollpanel - панель прокрутки для интерактивного управления изображениями
Синтаксис:
hpanel = imscrollpanel(hparent, himage)
Описание:
Функция hpanel = imscrollpanel(hparent, himage) создает панель прокрутки, содержащую объекты изображения (для навигации). Параметр himage управляет этими объектами. Параметр hparent управляет окном отображения, которое содержит новую панель прокрутки. Параметр hpanel управляет панелью прокрутки, которая является объектом uipanel.
Панель прокрутки делает изображение прокручиваемым. Когда размер или увеличение изображения больше, чем может быть отображено в окне, панель прокрутки отображает изображение частями. Панель прокрутки добавляет горизонтальную и вертикальную прокрутку для удобства просмотра отображаемого изображения.
Функция imscrollpanel изменяет некоторые объекты изображения. Взамен привычной иерархии объектов figure->axes->image, функция imscrollpanel вставляет некоторые объекты uipanel и uicontrol между окном просмотра и осями объекта.
API функции.
Панель прокрутки содержит структуру управления функциями, названную API. С помощью этой структуры можно манипулировать панелью прокрутки. Для получения этой структуры используется функция iptgetapi. Приведем пример.
api = iptgetapi(hpanel)
В таблице приведен список API функций панели прокрутки в порядке их появления в этой структуре.
API функции панели прокрутки Описание setMagnification Установка увеличения.
mag = api.getMagnification(new_mag),
где параметр new_mag представляет собой коэффициент увеличения.getMagnification Возвращает текущий коэффициент увеличения.
mag = api.getMagnification()
Умножая параметр mag на 100 получим процентное представление. Например, если mag=2, тогда это эквивалентно 200% увеличению.setMagnificationAndCenter При изменении увеличения точки cx, cy будут показаны в центре панели прокрутки. Эта операция эквивалентна симуляции увеличения и смещению центра.
api.setMagnificationAndCenter(mag,cx,cy)findFitMag Возвращает коэффициент увеличения, который устанавливается для данного изображения в панели прокрутки.
mag = api.findFitMag()setVisibleLocation Перемещает изображение объекта в точку описанного расположения.
api.setVisibleLocation(xmin,ymin)
api.setVisibleLocation([xmin ymin])getVisibleLocation Возвращает описание текущего расположения объектов.
loc = api.getVisibleLocation(),
где параметр loc представляется вектором [xmin ymin].addNewMagnificationCallback Возвращает текущую видимую часть изображения.
r = api.getVisibleImageRect(),
где параметр r описывает прямоугольник [xmin ymin width height].removeNewMagnificationCallback Добавляет функцию управления fcn в список новых увеличений.
id = api.addNewMagnificationCallback(fcn)
При каждом изменении увеличения панели прокрутки, каждая функция в списке именуется в соответствии с синтаксисом:
fcn(mag),
где параметр mag представляет собой скаляр коэффициентов увеличения. Возвращаемое значение id используется в removeNewMagnificationCallback.addNewLocationCallback Перемещение соответствующей функции из списка новых увеличений.
api.removeNewMagnificationCallback(id),
где параметр id представляет собой идентификатор, возвращаемый addNewMagnificationCallback.removeNewLocationCallback Дополняет функцию управления fcn в список функций новых размещений.
id = api.addNewLocationCallback(fcn)
При каждом изменении панели прокрутки, каждая функция в списке именуется в соответствии с синтаксисом:
fcn(loc),
где параметр loc представляется в виде [xmin ymin].getVisibleImageRect Перемещает соответствующую функцию из списка новых месторасположений.
pi.removeNewLocationCallback(id),
где параметр id представляет собой идентификатор, возвращаемый функцией addNewLocationCallback.Пример:
В этом примере показано создание панели прокрутки с функцией увеличения.
1.Создание панели прокрутки
hFig = figure('Toolbar','none',...
'Menubar','none');
hIm = imshow('saturn.png');
hSP = imscrollpanel(hFig,hIm);
set(hSP,'Units','normalized',...
'Position',[0 .1 1 .9])
2.Добавление блока увеличения и средств общего просмотра.
hMagBox = immagbox(hFig,hIm);
pos = get(hMagBox,'Position');
set(hMagBox,'Position',[0 0 pos(3) pos(4)])
imoverview(hIm)
3.Управление панелью прокрутки API для контроля просмотра.
api = iptgetapi(hSP);
4.Получение данных о текущем увеличении и расположении.
mag = api.getMagnification()
r = api.getVisibleImageRect()
5.Просмотр верхнего левого угла изображения.
api.setVisibleLocation(0.5,0.5)
6.Изменение значения увеличения.
api.setMagnification(api.findFitMag())
7.Увеличение на 1600%.
api.setMagnificationAndCenter(16,306,800)
analyze75info - считывание метаданных из установленного заголовка файла данных Analyze 7.5
Синтаксис:
info = analyze75info(filename)
info = analyze75info(filename,'ByteOrder', endian)
Описание:
Функция info = analyze75info(filename) считывает заголовок файла filename Analyze 7.5. Функция возвращает параметр info, поля структуры которой содержат информацию об установленных данных.
Analyze 7.5 является продуктом, который реализует визуализацию и анализ 3-мерных биомедицинских изображений. Он был разработан группой по обработке биомедицинских изображений клиники Майо. Данные в Analyze 7.5 состоят фактически из двух файлов - файла заголовка и файла изображения. Файлы имеют одинаковые названия, но различные расширения. Файл заголовка имеет расширение .hdr и файл изображения имеет расширение .img.
Функция info = analyze75info(filename,'ByteOrder', endian) считывает заголовок файла Analyze 7.5, используя битовый порядок, описанный через параметр endian, который может принимать следующие значения:
Значение Описание 'ieee-le' Прямой порядок байтов (формат хранения и передачи двоичных данных, при котором сначала передается младший (наименее значимый) бит (байт)). 'ieee-be' Обратный порядок байтов (формат хранения и передачи двоичных данных, при котором сначала передается старший (наиболее значимый) бит (байт)). Примеры:
Считаем заголовок файла Analyze 7.5
info = analyze75info('CT_HAND.hdr');
Опишем байтовый порядок установленных данных.
info = analyze75info('CT_HAND', 'ByteOrder', 'ieee-be');
analyze75read - считывание данных изображения из Analyze 7.5
Синтаксис:
X = analyze75read(filename)
X = analyze75read(info)
Описание:
Функция X = analyze75read(filename) считывает данные изображения из Analyze 7.5 файла filename. Функция возвращает данные изображения в виде X. Для однофреймовых полутоновых изображений X представляет собой массив с размерностью mxn. analyze75read использует для X тип данных, который установлен в файле заголовка.
Analyze 7.5 представляет собой продукт, который предназначен для визуализации и анализа трехмерных биомедицинских изображений и был разработан группой по обработке биомедицинских изображений клиники Майо. Данные в Analyze 7.5 состоят фактически из двух файлов - файла заголовка и файла изображения. Файлы имеют одинаковые названия, но различные расширения. Файл заголовка имеет расширение .hdr и файл изображения имеет расширение .img.
Функция X = analyze75read(info) считывает данные изображения из файла, который описан параметром info.
Примечание:
Функция analyze75read возвращает данные в виде рентгенографической ориентации, по умолчанию используя формат Analyze 7.5.
Примеры:
Пример 1:
Считаем данные изображения из Analyze 7.5 файла изображения.
X = analyze75read('CT_HAND');
Поскольку формат Analyze 7.5 имеет радиологическую ориентацию, для корректного отображения в MATLAB изображение нужно перевернуть.
X = flipdim(X,1);
Выбор фреймов с 51 по 56 и использование функции reshape при создании массива для их монтажа.
Y = reshape(X(:,:,51:56),[size(X,1) size(X,2) 1 6]);
montage(Y);
Пример 2:
Получение данных из метафайла, содержащего файл заголовка, с помощью функции analyze75info.
info = analyze75info('CT_HAND.hdr');
X = analyze75read(info);
Требования к исходным данным.
Данные X должны быть представлены в виде массива в формате logical, uint8, int16, int32, single или double. Составные или данные типа RGB не поддерживаются.
im2bw - бинаризация отсечением по порогу яркости
Синтаксис:
BW=im2bw(S, threshold)
BW=im2bw(X, map, threshold)
Описание:
Группа функций imbw создает бинарное изображение, используя отсечение по порогу яркости. Для этой цели полноцветные и палитровые изображения конвертируются в полутоновые. Пикселы результирующего бинарного изображения BW принимают значения 0 (черный цвет), если яркость соответствующих пикселов исходного изображения меньше порога threshold, и значения 1 (белый цвет), если яркость соответствующих пикселов исходного изображения больше либо равна threshold. Порог threshold должен задаваться в диапазоне [0, 1]. Часто данную операцию называют бинаризацией по порогу.
Функция BW=im2bw(S, threshold) используется для преобразования полутонового или полноцветного изображения S в бинарное BW.
Функция BW=im2bw(X, map, threshold) используется для преобразования палитрового изображения X с палитрой map в бинарное BW.
Исходное изображение может иметь формат представления данных double или uint8. Результирующее изображение имеет формат uint8.
Пример.
Рассмотрим пример выделения на изображении черных круглых объектов на полутоновом изображении (рис. 1а). Если threshold установить равным 0.5, то образуется бинарное изображение BW, показанное на рис. 1б. Далее на этом изображении можно, например, подсчитать количество объектов интереса с помощью функции bwlabel(~BW).
%Пример демонстрирует бинаризацию полутонового изображения
%по порогу яркости.
%Чтение изображения и вывод его на экран.
I=imread(‘blood.tif’);
imshow(I);
%Бинаризация по порогу 0.5
%и вывод полученного бинарного изображения на экран.
BW=im2bw(I, 0.5);
figure, imshow(BW);

a) б)
Рис. 1.
На рисунке 1 приведен пример пороговой бинаризации изображения, объекты которого расположены на однородном фоне. На практике такие изображения встречаются реже. В большинстве случаев изображения имеют более сложное семантическое наполнение. Фон также не всегда является однородным. Его яркость в разных частях изображения существенно отличается. Поэтому, для обработки изображений со сложной структурой фона, целесообразно применять адаптивную бинаризацию, которая учитывает яркостные характеристики локальных участков изображения.
mat2gray - преобразование матрицы чисел в полутоновое изображение
Синтаксис:
I=mat2gray(M, [amin amax])
I=mat2gray(M)
Описание:
Функция mat2gray создает из матрицы чисел полутоновое изображение, осуществляя необходимые операции масштабирования для приведения к виду, принятому для полутоновых изображений.
Функция I=mat2gray(M, [amin amax]) создает из матрицы М полутоновое изображение I, масштабируя значения элементов матрицы М, находящиеся в диапазоне [amin, amax], к диапазону [0, 1] в соответствии со следующим алгоритмом:
если М(r, с)
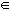 [amin, amax], то I(r, с)=(М(r, с)-amin)/(amax-amin);
[amin, amax], то I(r, с)=(М(r, с)-amin)/(amax-amin);если М(r, с)<amin, то I(r, с)=0;
если М(r, с)>amax, то I(r, с)=1.
Функция I=mat2gray(M) создает из матрицы М полутоновое изображение I, диапазон масштабирования задается минимальным и максимальным значениями в матрице М, т. е. amin=min( М(:)), amax=max(М(:)).
Исходная матрица должна иметь формат double. Результирующее изображение также будет представлено в формате double.
Необходимо отметить, что в результате применения некоторых функций обработки к полутоновым или полноцветным изображениям значения пикселов результирующего изображения выходят за пределы диапазона [0, 1]. В этом случае может потребоваться преобразовать результат с помощью функции mat2gray.
rgb2gray - преобразование полноцветного изображения в полутоновое
Синтаксис:
I=rgb2gray(RGB)
newmap=rgb2gray(map)
Описание:
Функция I=rgb2gray(RGB) создает полутоновое изображение I, преобразуя R-, G-, В-составляющие пикселов полноцветного изображения в соответствующие им значение яркости.
Функция newmap=rgb2gray(map) создает палитру newmap, состоящую из значений яркости (градаций серого), полученных преобразованием R-, G-, B-составляющих цветов исходной палитры mар.
Яркость полагают равной Y-составляющей цветовой системы YІQ. Для преобразования в цветовую систему YIQ функция rgb2gray вызывает функцию rgb2ntsc.
Форматы представления данных исходного RGB и результирующего I изображений совпадают.
ind2gray - преобразование палитрового изображения в полутоновое
Синтаксис:
I=ind2gray(X, map)
Описание:
Функция ind2gray создает полутоновое изображение I, преобразуя R-, G-, В-составляющие из палитры map, соответствующие индексам палитрового изображения X, в значения яркости.
Яркость полагают равной Y-составляющей цветовой системы YIQ. Для преобразования в цветовую систему YIQ внутри функции rgb2gray используется функция rgb2ntsc.
Форматы представления данных исходного Х и результирующего I изображений совпадают.
gray2ind - преобразование полутонового изображения в палитровое
Синтаксис:
[X, map]=gray2ind(I, n)
Описание:
Функция gray2ind создает палитровое изображение Х с палитрой mар, преобразуя полутоновое изображение I. Палитра mар содержит n градаций серого цвета равномерно распределенных в диапазоне [0, 1]. По умолчанию значение n равно 64.
Для создания палитры внутри функции gray2ind вызывается функция gray(n).
Если n меньше либо равно 256, то результирующее палитровое изображение X имеет формат представления данных uint8. В противном случае Х имеет формат double.
grayslice - преобразование полутонового изображения в палитровое отсечением по нескольким порогам
Синтаксис:
Х=grayslice(l, n)
Х=grayslice(l, v)
Описание:
Функция grayslice создает палитровое изображение Х из полутонового I, используя отсечение по нескольким порогам яркости Tl, T2, ..., Tk-l. В результате преобразования получается только матрица индексов X, но не формируется палитра. Для показа получившегося палитрового изображения можно воспользоваться функцией imshow(X, map), где map - любая палитра с размером, большим либо равным k.
Функция Х=grayslice(I, n) устанавливает пороги равными: Tl=1/n, T2=2/n, ..., Tk-1=(n-1)/n, где n - скалярное число, большее 1. При этом количество цветов результирующего изображения k = n+1.
Функция Х=grayslice(I, v) устанавливает пороги равными Tl=v(l). T2=v(2), ..., Tk-1=v(length(v)), где v - вектор. При этом количество цветов результирующего изображения k на единицу превышает количество элементов вектора v: k=length(v)+1.
Данные исходного изображения могут быть представлены в формате uint8, тем не менее пороги должны иметь значения в диапазоне от 0 до 1.
Матрица индексов результирующего изображения Х формируется в соответствии со следующими правилами:
если k больше 256, то результирующее палитровое изображение Х имеет формат double и выполняются соотношения
Х(r, с)=1, если I(г, с)<Т1;
Х(r, с)=2, если Tl < I(r, с)<T2;
…;
X(r,c)=k, ecли Tk-1<I(r,c);
если k меньше либо равно 256, то результирующее палитровое изображение Х имеет формат uint8 и выполняются соотношения
Х(r, с)=0,если I(r,с)<Т1;
Х(r, с)=1, если Tl<1(r, с)<T2;
…;
Х(r, с) = k-1, если Tk-1<I(r, с).
Пример.
Используем функцию grayslice для окрашивания полутонового изображения псевдоцветами. Рассмотрим изображение на рис. 1, а. Результирующее изображение Х с палитрой mар показано на рис. 1, б.
%examp.m
%Пример демонстрирует окрашивание полутонового изображения
%псевдоцветами.
%Создание палитры их трех цветов map=zeros(3,3);
%Темно-синий цвет
mар(1,1)=0; mар(1, 2)=0; mар(1, 3)=0.5;
% Зеленый цвет.
map(2,1)=0; map(2, 2) = 1; map(2, 3)=0;
% Белый цвет.
map(3,1)=1; map(3, 2)=1; map(3, 3)=1;
% Чтение исходного изображения. I=imread('rs.tif');
% Окрашивание псевдоцветами.
X=grayslice(l,[30 180]);
% Вывод изображения в псевдоцветах на экран.
imshow(X, map);
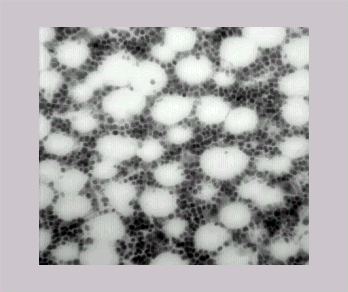

Рис. 1.
ind2rgb -преобразование палитрового изображения в полноценное
Синтаксис:
RGB=ind2rgb(X, map)
Описание:
Функция ind2rgb создает полноцветное изображение RGB из палитрового изображения Х с палитрой mар.
Исходное изображение Х может иметь формат uint8 или double, результирующее изображение RGB всегда имеет формат double.
dither - диффузионное псевдосмешение цветов
Синтаксис:
Х=dither(RGB, map, Qm, Qe)
BW=dither(I)
Описание:
Функция Х=dither(RGB, map, Qm, Qe) создает палитровое изображение X с палитрой map из полноцветного изображения RGB, используя алгоритм Флойда-Стенберга диффузионного псевдосмешения цветов. Параметры Qm и Qe определяют скорость и точность работы алгоритма. Qm задает число бит для представления каждой из цветовых составляющих во вспомогательной таблице преобразования цветов, а Qe определяет точность вычисления ошибки - разницы между действительным значением цвета пиксела и ближайшим цветом в палитре. Qm может изменяться в диапазоне [1, 10] и должно быть меньше Qe. Qe может изменяться в диапазоне [1,31]. Если Qe < Qm, то псевдосмешения цветов не происходит. При вызове функции параметры Qm, Qe можно не указывать. По умолчанию Qm=5, Qe=8.
Если размер палитры mар меньше либо равен 256, то результирующее изображение Х имеет формат uint8, в противном случае оно имеет формат double.
Функция BW=dither(I) создает бинарное изображение BW из полутонового I, используя диффузионное псевдосмешение цветов. Результирующее изображение имеет формат uint8. Алгоритм:
Псевдосмешение (dithering) создает впечатление, что на изображении присутствует большее количество различных цветов (или градаций серого цвета в случае полутоновых изображений), чем есть на самом деле. Требуемый визуальный эффект достигается за счет группирования в локальной области пикселов с цветами, представленными в палитре, смешение которых дало бы близкий к необходимому цвет.
При реализации функции dither используется хорошо известный алгоритм Флойда-Стенберга [1]. В этом алгоритме пиксел изображения заменяет свой цвет на ближайший в евклидовой метрике из имеющихся в палитре и вычисляет ошибки цветности для каждой из цветовых составляющих, вычитая значения RGB-цвета палитры и значения RGB-цвета исходного изображения. Для полутоновых изображений вычисляется ошибка яркости. Затем ошибки распространяются на соседние пикселы путем добавления некоторой доли ошибки к значениям соответствующих составляющих и происходит так называемая диффузия ошибки. По этой причине алгоритмы подобного типа еще называют рассеиванием или распределением ошибки (error diffusion). Ошибки распространяются на правые и нижние соседние пикселы в следующих соотношениях, определяемых матрицей
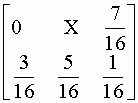 ,
,где X обозначает пиксел, ошибка которого распространяется. Алгоритм применяется рекурсивно ко всем пикселам изображения при обходе матрицы изображения слева направо и сверху вниз.
Использование псевдосмешения цветов позволяет улучшить цветовое восприятие за счет ухудшения разрешения и повышения уровня ВЧ шумов.
rgb2ind - преобразование полноцветного изображения в палитровое
Синтаксис:
[X, map]=rgb2ind(RGB)
[X, тар]=rgb2ind(RGB, n, dither_option)
[X, map]=rgb2ind(RGB, tol, dither_option)
X=rgb2ind(RGB, map, dither_option)
Описание:
Функция rgb2ind создает палитровое изображение из полноцветного, используя один из четырех способов: запись в виде палитрового изображения без уменьшения количества цветов, установка равномерной палитры, оптимальный подбор палитры, использование некоторой предопределенной палитры. Три последних способа преобразования могут также использовать диффузионное псевдосмешение цветов (dithering) с помощью алгоритма Флойда-Стенберга [1].
[X, map)=rgb2ind(RGB) создает палитровое изображение X из полноцветного RGB, составляя палитру mар из всех уникальных цветов, представленных в исходном изображении. Результирующая палитра mар может быть очень большого размера.
[X, mар]=rgb2ind(RGB, tol, dither_option), где tol - число в диапазоне (0,1), создает палитровое изображение Х из полноцветного RGB, устанавливая равномерную палитру mар из цветов, которые в диапазоне [0, 1] берутся с шагом tol по каждой из цветовых составляющих R, G, В. Цвета исходного изображения заменяются ближайшими из установленной палитры mар. Максимально возможное число цветов в палитре mар составляет (floor(l/tol) + 1)^3. Действительное число цветов в палитре может оказаться меньше максимального, так как из палитры удаляются все цвета, которые отсутствуют в изображении.
[X, map]=rgb2md( RGB, n, dither_option ), где n - число, большее 1, создает палитровое изображение Х из полноцветного RGB, используя для подбора палитры mар из n цветов один из способов оптимального подбора палитры. Цвета исходного изображения заменяются ближайшими из подобранной палитры mар. Действительное число цветов в палитре может оказаться меньше n, так как из палитры удаляются все цвета, которые отсутствуют в изображении.
Х=rgb2ind(RGB, map, dither_option) создает палитровое изображение Х из полноцветного RGB. Цвета исходного изображения заменяются ближайшими из заданной палитры mар.
Параметр dither_option позволяет при преобразованиях применять или отказываться от применения диффузионного псевдосмешения цветов. Этот параметр может быть равен одной из следующих строковых констант:
'dither' - использовать диффузионное псевдосмешение цветов;
'nodither' - не использовать диффузионное псевдосмешение цветов.
По умолчанию псевдосмешение цветов применяется, и параметр dither_option может быть опущен. Псевдосмешение цветов позволяет улучшить цветовое восприятие изображения за счет ухудшения его пространственного разрешения и повышения уровня ВЧ шумов.
Для всех способов преобразования, если размер палитры mар меньше либо равен 256, результирующее изображение Х имеет формат uint8, в противном случае оно имеет формат double.
Пример.
Рассмотрим пример преобразования полноцветного изображения (рис. 1) в палитровое, содержащее только 16 цветов.
%.examp.m
% Пример демонстрирует преобразование
% полноцветного изображения в палитровое из 16 цветов.
% Чтение исходного полноцветного изображения
% и вывод его на экран (рис. 1а).
RGB=imread( 'f2.bmp');
imshow(RGB);
%Преобразование в палитровое изображение
%с равномерной палитрой и без псевдосмешения цветов (рис. 1б).
[Х1 map1]=rgb2ind( RGB, 0.65, 'nodither');
%Вывод получившегося палитрового изображения на экран.
figure, imshow( Х1, map1 );
%Преобразование в палитровое изображение
%с оптимальной палитрой и с псевдосмешением цветов.
[Х2 map2]=rgb2ind( RGB, 16 );
% Вывод получившегося палитрового изображения на экран (рис. 1в).



Рис. 1.
imapprox - уменьшение количества цветов палитрового изображения
Синтаксис:
[Xd, newmap]=imapprox(Xs, map, tol, dither_option)
[Xd, newmap]=imapprox(Xs, map, n, dither_option)
Xd=imapprox(Xs, map, newmap, dither_option)
Описание:
Функция imapprox создает новое палитровое изображение Xd из исходного палитрового Xs, уменьшая количество используемых цветов.
Функция [Xd, newmap] = imapprox(Xs, map, to], dither_option ), где tol - число в диапазоне (0, 1), создает палитровое изображение Xd с палитрой newmap из палитрового Хs с палитрой map, устанавливая равномерную палитру newmap из цветов, которые в диапазоне [0, 1] берутся с шагом tol по каждой из цветовых составляющих R, G, В. Цвета исходного изображения заменяются ближайшими из установленной палитры newmap. Максимально возможное число цветов в палитре newmap составляет (floor(l/tol) + 1)^3. Действительное число цветов в палитре может оказаться меньше максимального, так как из палитры удаляются все цвета, которые отсутствуют в изображении.
Функция [Xd, newmap] = imapprox(Xs, map, n, dither_option), где n - число, большее 1, создает палитровое изображение Xd с палитрой newmap из палитрового Xs с палитрой map, используя для подбора палитры newmap из n цветов один из способов оптимального подбора палитры. Цвета исходного изображения заменяются ближайшими из подобранной палитры newmap. Действительное число цветов в палитре может оказаться меньше n, так как из палитры удаляются все цвета, которые отсутствуют в изображении.
Функция Xd = imapprox(Xs, map, newmap, dither_option) создает палитровое изображение Xd с палитрой newmap из палитрового Xs с палитрой map. Цвета исходного изображения заменяются ближайшими из заданной палитры newmap.
Параметр dither_option позволяет при преобразованиях применять или отказываться от применения диффузионного псевдосмешения цветов. Этот параметр может быть равен одной из следующих строковых констант:
'’dither’ -использовать диффузионное псевдосмешение цветов;
‘nodither’ - не использовать диффузионное псевдосмешение цветов.
По умолчанию псевдосмешение цветов применяется, и параметр dither_option может быть опущен. Псевдосмешение цветов позволяет улучшить цветовое восприятие изображения за счет ухудшения его пространственного разрешения и повышения уровня ВЧ шумов.
Для всех способов преобразования, если размер палитры map меньше либо равен 256, результирующее изображение Xd имеет формат uint8, в противном случае оно имеет формат double.
cmunique - поиск палитры минимального размера
Синтаксис:
[Xd, newmap]=cmunique(Xs, map)
[Xd, newmap]=cmunique(RGB)
[Xd, newmap]=cmunique(l)
Описание:
Функция [Xd, newmap]=cmunique(Xs, map) создает новое палитровое изображение Xd с палитрой newmap минимально возможного размера. При этом изображение Xd выглядит точно так же, как исходное палитровое изображение Xs с палитрой map. Уменьшение размера палитры достигается за счет исключения дублирования в палитре одинаковых цветов.
Функция [Xd, newmap]=cmunique(RGB) создает палитровое изображение Xd с палитрой newmap из полноцветного изображения RGB. Палитра newmap имеет минимально возможный размер, так как каждый из уникальных цветов изображения RGB включен в палитру newmap только 1 раз.
Функция [Xd, newmap]=cmunique(I) создает палитровое изображение Xd с палитрой newmap из полутонового изображения I. Палитра newmap имеет минимально возможный размер, так как каждый из уникальных уровней яркости из изображения I включен в палитру newmap только 1 раз.
Для всех функций cmunique, если размер палитры newmap меньше либо равен 256, результирующее изображение Xd имеет формат uint8, в противном случае оно имеет формат double.
cmpermute - изменение порядка цветов в палитре
Синтаксис:
[Xd, newmap]=cmpermute(Xs, map)
[Xd, newmap]=cmpemute(Xs, map, index)
Описание:
Функция [Xd, newmap]=cmpermute(Xs, map) создает новое палитровое изображение Xd с палитрой newmap, цвета которой совпадают с цветами палитры map, но их порядок случайным образом изменен. Результирующее Xd и исходное Xs изображения выглядят одинаково.
Функция [Xd, newmap]=cmpemute(Xs, map, index) для определения порядка цветов в новой палитре newmap использует матрицу индексов такую же, как второй параметр функции MATLAB sort.
Форматы представления данных исходного и результирующего изображений совпадают.
Пример.
Из некоторого палитрового изображения сформируем аналогичное ему новое палитровое изображение, в палитре которого цвета расположены в порядке возрастания яркости.
%Пример демонстрирует изменение расположения цветов палитры
%в порядке возрастания яркости.
%Чтение исходного полноцветного изображения и вывод его на экран.
RGB=imread(‘lena.bmp’);
%Преобразование в палитровое изображение
%с оптимальной палитрой и псевдосмешением цветов.
[XS map]=rgb2ind(RGB, 16);
%Изменение расположения цветов палитры
%в порядке возрастания яркости.
ntsc=rgb2ntsc(map);
[dum, index]=sort(ntsc(:,1));
[XD, newmap]=cmpermute(XS, map, index);
label2rgb - преобразование матрицы меток в RGB-изображение
Синтаксис:
RGB=label2rgb(L)RGB=label2rgb(L, map)RGB=label2rgb(L, map, zerocolor)RGB=label2rgb(L, map, zerocolor, order)
Описание:
Функция RGB=label2rgb(L) реализует преобразование матрицы меток L, которая, в свою очередь, была получена при использовании функций bwlabel или watershed, в цветное RGB-изображение с целью дальнейшей визуализации отмеченных областей. Функция label2rgb определяет цвет для каждого объекта на основе чисел, которые присвоены соответствующему объекту в матрице меток и в соответствии с диапазоном цветов в цветовой палитре. Функция label2rgb использует цвета из всего цветового диапазона.
Функция RGB=label2rgb(L, map) определяет цветовую палитру map для RGB-изображения. Параметр map должен содержать следующие составляющие:
- палитра с размерностью nx3 ;
- строка, содержащая название палитры в среде MATLAB (для более детальной информации см. функцию colormap).
- интерактивное управление функцией палитры.
Когда описание палитры не задано, то по умолчанию это значение равно 'jet'.
Функция RGB=label2rgb(L, map, zerocolor) определяет RGB-цвета элементов изображения, отмеченных 0 (нулями) в исходной матрице меток L. Когда этот элемент отмечен нулем в матрице меток, то он описывается с помощью трех цветов RGB или строки, значения которой перечислены в таблице.
Значение Цвет r 'b' Синий 'c' Голубой 'g' Зеленый 'k' Черный 'm' Яркокрасный 'r' Красный 'w' Белый 'y' Желтый В случае, когда элемент изображения не отмечен в матрице меток, то он отображается белым цветом [1 1 1].
Функция RGB=label2rgb(L, map, zerocolor, order) контролирует каким образом определяются цвета из палитры для данной области в матрице меток. Когда установлена опция 'noshuffle' (по умолчанию), тогда функция label2rgb устанавливает цвета палитры для матрицы меток в числовом порядке. Когда установлена опция 'shuffle', то функция label2rgb устанавливает цвета палитры псевдослучайным образом.
Требования к исходным данным.
Исходная матрица меток L должна быть представлена в неразреженном числовом формате. Она должна представлять собой массив положительных целых чисел в ограниченном диапазоне. Результат работы функции label2rgb представляется в формате uint8.
Пример.
I=imread('rice.png');figure, imshow(I), title('исходное изображение') BW=im2bw(I, graythresh(I)); L=bwlabel(BW); RGB=label2rgb(L); RGB2=label2rgb(L, 'spring', 'c', 'shuffle'); imview(RGB), imview(RGB2);


rgb2hsv - конвертирование из RGB в HSV
Синтаксис:
HSV=rgb2hsv(RGB)
hsvmap=rgb2hsv(rgbmap)
Описание:
Функция HSV=rgb2hsv(RGB) создает полноцветное изображение, значения пикселов которого представлены в цветовой системе HSV, из исходного полноцветного изображения в цветовой системе RGB. Результирующее изображение имеет формат представления данных double.
Функция hsvmap=rgb2hsv(rgbmap) создает палитру hsvmap, значения цвета в которой задаются в цветовой системе HSV, из исходной палитры rgbmap, хранящей цвета в цветовой системе RGB.
Алгоритм:
Широкое распространение в компьютерной графике и цифровой обработке изображений получила цветовая система HSV (hue - цветовой фон, saturation - насыщенность, volume - светлота) [1]. Часто для названия этой же системы используется аббревиатура HSB (hue, saturation, brightness - яркость).
Геометрическая модель системы HSV получается из следующих соображений. Если цветовой куб RGB спроецировать на плоскость, перпендикулярную диагонали, на которой в RGB-кубе расположены значения яркости (оттенки серого от черного до белого), то получается правильный шестиугольник с красным, желтым, зеленым, голубым, синим и пурпурным цветами в вершинах. При снижении насыщенности RGB цветов уменьшается размер и цветовой охват RGB-куба. При этом соответствующая шестиугольная проекция также будет меньше. Если проекции собрать вокруг оси яркости V, то получится перевернутый объемный шестигранный конус HSV, показанный на рис. 1 [1].
Яркость V изменяется от 0 в вершине конуса (черный цвет) до 1 в середине основания конуса (белый цвет). На оси V расположены ахроматические цвета - оттенки серого. Насыщенность S определяется расстоянием до оси V. На ней насыщенность равна нулю, а на сторонах конуса - единице. Цветовой тон H определяется углом поворота оси S против часовой стрелки относительно оси, проходящей через красный цвет.
Рис. 1.
Цветовая система HSV соответствует тому, как составляют цвета художники. Чистым цветам соответствуют значения V=1 и S=1, разбелам - цвета с увеличенным содержанием белого, т.е. с меньшими значениями S. Система HSV удобна для выбора цветов, поэтому ее относят к цветовым системам, приближенным к человеческому восприятию (perception).
Пример.
Большинство функций IPT по фильтрации и улучшению изображений предназначены для обработки полутоновых изображений. Рассмотрим, каким образом эти функции можно применять для обработки полноцветных изображений.
Известно, что зрение человека более чувствительно к изменениям яркости, чем к изменениям цвета. Этот факт делает целесообразным производить обработку отдельно для яркостной составляющей. Для этого полноцветное изображение из цветовой системы RGB следует преобразовать в систему, в которой одна из составляющих является сигналом яркости, а другие описывают цвет; например, таким требованиям отвечают системы HSV или YIQ.
Исходное полноцветное изображение (рис. 2 а) слишком темное и имеет низкий контраст. Данное изображение преобразуется в цветовую систему HSV, где V является яркостной составляющей. Для этой составляющей повышается контраст. Затем изображение преобразуется обратно в систему RGB. Полученное в результате изображение показано на рис. 2 б.
%Пример демонстрирует подход к фильтрации и контрастированию
%цветных изображений.
%Чтение исходного изображения и вывод его на экран.
RGB=imread(‘flowers.tif’);
imshow(RGB);
%Преобразование в цветовую систему HSV.
HSV=rgb2hsv(RGB);
%Контрастирование составляющей Н - яркости изображения.
HSV(:,:,3)=imadjust(HSV(:,:,3), [0.02 0.68], [], 0.7);
%Преобразование в цветовую систему RGB.
RGB=hsv2rgb(HSV);
%Вывод результатов на экран.
figure, imshow(RGB);
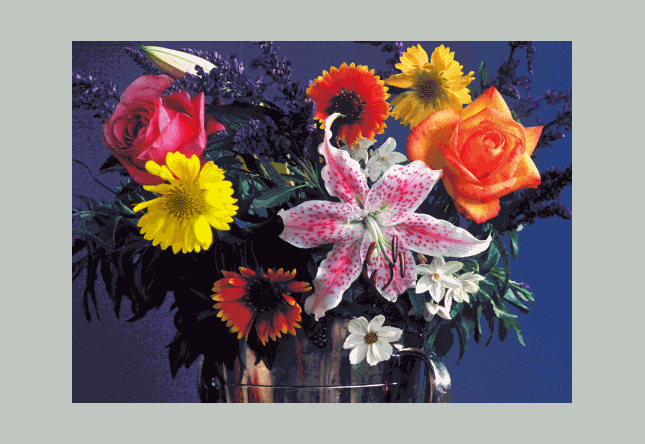
а)

б)
Рис. 2.
hsv2rgb - конвертирование из HSV в RGB
Синтаксис:
RGB=hsv2rgb(HSV)
rgbmap=hsv2rgb(hsvmap)
Описание:
Функция RGB=hsv2rgb(HSV) создает полноцветное изображение, значения пикселов которого представлены в цветовой системе RGB, из исходного полноцветного изображения в цветовой системе HSV. Исходное изображение должно иметь формат представления данных double. Результирующее изображение также имеет формат представления данных double.
Функция rgbmap=hsv2rgb(hsvmap) создает палитру rgbmap, значения цвета в которой задаются в цветовой системе RGB, из исходной палитры hsvmap, хранящей цвета в цветовой системе HSV.
rgb2ntsc - конвертирование из RGB в YIQ
Синтаксис:
YIQ=rgb2ntsc(RGB)
yiqmap=rgb2ntsc(rgbmap)
Описание:
Функция YIQ=rgb2ntsc(RGB) создает полноцветное изображение, значения пикселов которого представлены в цветовой системе YIQ, из исходного полноцветного изображения в цветовой системе RGB. Результирующее изображение имеет формат представления данных double.
Функция yiqmap=rgb2ntsc(rgbmap) создает палитру yiqmap, цвета в которой задаются в цветовой системе YIQ, из исходной rgbmap, хранящей цвета в цветовой системе RGB.
Алгоритм:
Цветовая система YIQ используется в телевизионной системе NTSC представления цветного телевизионного сигнала. Составляющая Y содержит информацию о яркости изображения, а составляющие I и Q - о его цветности. Преобразование из цветовой системы RGB в YIQ имеет вид [1]:
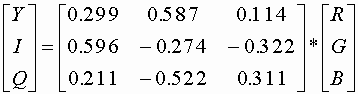
Обратное преобразование осуществляется с помощью следующего соотношения:
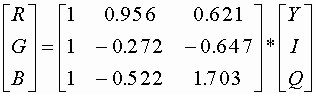
Иные системы телевидения, как аналоговые, так и цифровые, используют похожие цветовые системы. Их отличие от системы YIQ заключается, как правило, в коэффициентах, применяемых для формирования составляющих цветности.
ntscc2rgb - конвертирование из YIQ в RGB
Синтаксис:
RGB=ntsc2rgb(YIQ)
rgbmap=ntsc2rgb(yiqmap)
Описание:
Функция RGB=ntsc2rgb(HSV) создает полноцветное изображение, значения пикселов которого представлены в цветовой системе RGB, из исходного полноцветного изображения в цветовой системе YIQ. Исходное изображение должно иметь формат представления данных double. Результирующее изображение также имеет формат представления данных double.
Функция rgbmap = ntsc2rgb(yiqmap) создает палитру rgbmap, значение цвета в которой задаются в цветовой системе RGB, из исходной viqmap, хранящей цвета в цветовой системе Y1Q.
rgb2ycbcr - конвертирование из RGB в YCbCr
Синтаксис:
YCbCr=rgb2ycbcr(RGB)
ycbcrmap=rgb2ycbcr(rgbmap)
Описание:
Функция YCbCr=rgb2ycbcr(RGB) создает полноцветное изображение, значения пикселов которого представлены в цветовой системе YCbCr, из исходного полноцветного изображения в цветовой системе RGB. Формат представления данных исходного и результирующего изображений совпадают.
Функция ycbcrmap=rgb2ycbcr(rgbmap) создает палитру ycbcrmap, значения цвета в которой задаются в цветовой системе YCbCr, из исходной палитры rgbmap, хранящей цвета в цветовой системе RGB.
Алгоритм:
Цветовая система YCbCr широко используется в цифровом видео. Составляющая Y содержит информацию о яркости изображения, а составляющие Cb и Cr (так называемые цветоразностные составляющие) - о его цветности.
Преобразование из цветовой системы RGB, где составляющие принадлежат диапазону [0, 1], в систему YCbCr имеет вид:
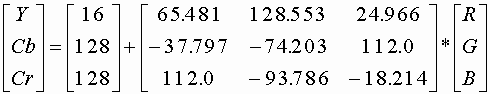
В результате данного преобразования составляющая Y принадлежит диапазону [16, 235], а составляющие Cb и Cr принадлежат диапазону [16, 240]. Оставшиеся допустимые значения вне указанных диапазонов ([0, 15] и [236, 255] для Y, [0, 15] и [241, 255] для Cb, Cr) используются для дополнительной информации (например, звука), которая передается вместе с видеопотоком.
ycbcr2rgb - конвертирование из YCbCr в RGB
Синтаксис:
RGB=ycbcr2rgb(YCbCr)
rgbrmap=ycbcr2rgb(ycbcrmap)
Описание:
Функция RGB=ycbcr2rgb(YCbCr) создает полноцветное изображение, значения пикселов которого представлены в цветовой системе RGB, из исходного полноцветного изображения в цветовой системе YCbCr. Формат представления данных исходного и результирующего изображений совпадают.
Функция rgbrmap=ycbcr2rgb(ycbcrmap) создает палитру rgbmap, значения цвета в которой задаются в цветовой системе RGB, из исходной палитры ycbcrmap, хранящей цвета в цветовой системе YCbCr.
graythresh - вычисление глобального порога изображения с использованием метода Отса
Синтаксис:
level=graythresh(I)
Описание:
Функция level=graythresh(I) вычисляет значение глобального порога, который используется для преобразования яркостей (интенсивностей) изображения в бинарное изображение в функции im2bw.
Значения нормализованных интенсивностей находятся в диапазоне [0, 1].
Функция graythresh использует метод Отсу, который выбирает порог путем минимизации различных вариантов черных и белых пикселов.
Многомерные массив автоматически преобразуется в двумерный с использованием функции reshape. Функция graythresh игнорирует все ненулевые мнимые части массива I.
Требования к исходным данным:
Исходное изображение I может быть представлено неразреженным массивом с форматом представления данных uint8, uint16 или double. Возвращаемое значение имеет формат представления данных double.
iccread - считывание описания ICC
Синтаксис:
P=iccread(filename)
Описание:
Функция P=iccread(filename) считывает описание данных цветов, предоставленное Международным цветовым консорциумом (International Color Consortium (ICC)). Функция iccread возвращает описание данных в структуре P.
ICC также предоставляет описание управления цветовыми системами с необходимой информацией относительно преобразования между цветовыми данными, заложенными в устройстве, а также описание управления устройствами с независимыми цветовыми пространствами (Profile Connection Space (PCS)).
Возвращаемое описание P имеет структуру массива, поля которого содержат данные, найденные в описании ICC.1:2001-04. Число полей P зависит от класса описания и выбора способа создания описания.
В таблице приведено перечень полей, которые находятся в структуре описания, генерируемой функцией iccread. Более детальная информация относительно описания ICC размещена на web-странице www.color.org.
Поле Тип данных Описание Filename Текстовая строка Название описания Header Массив с размерностью 1x1 Заголовок описания TagTable Массив с размерностью nx3 Описание tag-таблиц Copywright Текстовая строка Описание авторских прав Description Текстовая строка Описание MediaWhitepoint Массив в формате double XYZ трехцветные значения белых точек для медиаустройств PrivateTags Массив с размерностью mx2 Содержание всех персональных или не определенных полей в ICC.1:2001-04. Поле подписей содержится в первом столбце, содержание полей содержится в других полях. Кроме того, P может содержать одно или более правил редактирования данных.
Пример.Считаем описание цветового пространства sRGB.prof=iccread('sRGB.icm');prof= Filename: 'sRGB.icm' Header: [1x1 struct] TagTable: {17x3 cell} Copyright: 'Copyright (c) 1999 Hewlett-Packard Company' Description: 'sRGB IEC61966-2.1 991203' MediaWhitePoint: [0.9505 1 1.0891] MediaBlackPoint: [0 0 0] DeviceMfgDesc: 'IEC ' DeviceModelDesc: 'sRGB IEC 61966-2.1 sRGB 991203' ViewingCondDesc: 'Reference Viewing Condition in IEC61966-2.1' ViewingConditions: [1x1 struct] Luminance: [76.0365 80 87.1246] Measurement: [28x1 uint8] Technology: [4x1 uint8] MatTRC: [1x1 struct] PrivateTags: {} Для определения цветового пространства см. поле ColorSpace в структуре Header.prof.Header.ColorSpaceans=RGBДля определения описания PCS см. поле ConnectionSpace в структуре Header.prof.Header.ConnectionSpaceans=XYZ
imcrop - кадрирование изображений
Синтаксис:
D=imcrop(S)
Xd=imcrop(Xs, map)
D=imcrop(S, rect)
Xd=imcrop(Xs, map, rect)
[…]=imcrop(XData, YData,…)
[A, rect]=imcrop(…)
[XData, YData, A, rect]=imcrop(…)
Описание:
Функции D=imcrop(S) и Xd=imcrop(Xs, map) выводят на экран бинарное, полутоновое, полноцветное изображение S и палитровое изображение Xs и ожидают задания с помощью мыши прямоугольника, ограничивающего вырезаемый фрагмент. Для указания положения одного из углов ограничивающего прямоугольника следует нажать на левую кнопку мыши. Положение противоположного угла ограничивающего прямоугольника будет задано, если, не отпуская кнопку мыши, переместить курсор, а затем отпустить кнопку. Когда требуется задать квадратный фрагмент, следует при перемещении курсора мыши держать нажатой клавишу Shift.
Функция imcrop возвращает изображение, ограниченное заданным прямоугольником. Если выходные параметры не заданы, например imcrop(I), то результат отображается в новом графическом окне.
Если не определены входные параметры, например D=imcrop, то функция imcrop оперирует с изображением в текущем графическом окне.
Используя функции D=imcrop(S, rect) и Xd=imcrop(Xs, map, rect), можно явно определить ограничивающий прямоугольник, где rect - вектор из четырех элементов: [ xmin ymin w h], которые задают положение левого верхнего угла (xmin ymin) прямоугольника, а также его ширину (w) и высоту (h) в пространственных координатах.
Для задания произвольного масштаба по осям пространственной системы координат обрабатываемого изображения необходимо дополнительно передать два двухэлементных вектора XData и Ydata, определяющих диапазон изменения значений по осям координат: imcrop(XData, Ydata, …). Например, D=imcrop(XData, YData, S).
Если определить дополнительные выходные параметры, то функция [D, rect]=imcrop(…) возвратит координаты ограничивающего прямоугольника rect, а функция [XData, YData, D, rect]=imcrop(…) дополнительно возвратит диапазоны изменения значений по осям координат XData и YData.
Формат представления данных и тип результирующего изображения совпадает с форматом и типом исходного изображения.
Пример.
Изображение I читается из файла. Затем из него вырезается прямоугольный фрагмент и помещается в изображение I2. В используемой пространственной системе координат левый верхний угол ограничивающего прямоугольника является центром пиксела (20, 20), а правый нижний угол является центром пиксела (60,50). Оба эти пиксела помещаются в изображение I2. Таким образом, результирующее изображение имеет размеры 31 строка х 41 столбец.
%Пример демонстрирует кадрирование изображения.
%Чтение исходного изображения и вывод его на экран.
I=imread(‘valley.tif’);
imshow(I);
%Кадрирование и вывод получившегося фрагмента на экран.
I2=imcrop(I, [20 20 40 30]);
figure, imshow(I2);
imresize - изменение размеров изображения
Синтаксис:
D=imresize(S, m, method)
D=imresize(S, [mrows ncols], method)
D=imresize(…, method, n)
D=imresize(…, method, H)
Описание:
Функция imresize создает новое изображение, изменяя размеры исходного изображения любого типа. Для изменения размеров используется один из предопределенных методов интерполяции [1], который задается во входном параметре method в виде одной из следующих строк:
‘nearest’ - использовать значение ближайшего пиксела (установлен по умолчанию, и данный параметр может быть опущен при вызове функции);
‘bilinear’ - использовать интерполяцию по билинейной поверхности;
‘bicubic’ - использовать интерполяцию по бикубической поверхности;
Функция D=imresize(S, m, method) создает изображение D, размеры которого в m раз отличаются от размеров исходного изображения S. Если m принадлежит диапазону от 0 до 1, то D меньше S. Если m больше 1, то D больше S.
Функция D=imresize(S, [mrows ncols], method) создает изображение D с размерами mrows х ncols.
Когда размеры выходного изображения меньше, чем размеры входного, и при этом используется интерполяция по билинейной или бикубической поверхности, исходное изображение предварительно фильтруется ФНЧ с целью устранения эффекта ступенчатости. По умолчанию используется усредняющий фильтр с размером маски 11х11. Можно задать произвольный размер маски фильтра nxn, передав дополнительный параметр n в функцию: D=imresize(…, method, n). Если n равно 0, то предварительной фильтрации не производится.
Функция D=imresize(…, method, H) позволяет задать маску Н для предварительной фильтрации вместо усредняющего фильтра. Соответствующую матрицу возвращают функции ftrans2, fwind1, fwind2, fsamp2.
Тип и формат представления данных результирующего изображения совпадают с типом и форматом исходного изображения.
imrotate - поворот изображения
Синтаксис:
D=imrotate(S, angle, method)
D=imrotate(S, angle, method, crop)
Описание:
Функция D=imrotate(S, angle, method) создает изображение D, соответствующее повернутому исходному изображению S, используя один из предопределенных методов интерполяции [1], который задается во входном параметре method в виде одной из следующих строк:
''nearest' - использовать значение ближайшего пиксела (установлено по умолчанию, и данный параметр может быть опущен при вызове функции);
''bilinear' - использовать интерполяцию по билинейной поверхности;
''bicubic' - использовать интерполяцию по бикубической поверхности;
Угол поворота angle задается в градусах. Положительные значения данного параметра соответствуют повороту против часовой стрелки, а отрицательные - по часовой стрелке.
В общем случае количество пикселов результирующего изображения D больше либо равно количеству пикселов исходного изображения S. Значения пикселов изображения D, для которых отсутствуют соответствующие им пикселы в изображении S, устанавливаются в 0, что, например, для полутоновых изображений соответствует черному цвету. Функция D=imrotate(S, angle, method, crop) имеет дополнительный параметр 'crop', который указывает, что следует возвратить изображение с размерами, равными размерам S. В этом случае берется центральная часть повернутого изображения.
Тип и формат представления данных результирующего изображения совпадают с типом и форматом исходного.
Пример:
Полутоновое изображение читается из файла, поворачивается на 87° против часовой стрелки. При повороте используется интерполяция по билинейной поверхности. На экран выводятся исходное (рис. 1 а) и преобразованное изображение (рис. 1 б).
%Пример демонстрирует поворот изображения
%Чтение изображения из файла и вывод его на экран.
I1=imread('ic.tif');
Imshow(I1);
%Поворот изображения на 87° и вывод результата на экран.
I2=imrotate(I1, 87, 'bilinear');
figure, imshow(I2);
Сопутствующие функции: IMCROP, IMRESIZE.
Ссылки на литературу:
1. Адамс Дж. Математические основы машинной графики. М.: Машиностроение, 1980.
2. Яншин В., Калинин Г. Обработка изображений на языке С для IBM PC. М.: Мир, 1994.


а) б)
Рис. 1.
checkerboard - создание шахматно-образных изображений
Синтаксис:
I=checkerboard
I=checkerboard(N)
I=checkerboard(N, P, Q)
Описание:
Функция I=checkerboard создает изображение типа шахматной доски, которое включает четыре различных локальных окрестности площадью 8x8 элементов. Светлая “клетка” на левой половине шахматной доски является белой. Светлая “клетка” на правой половине шахматной доски – серая.
Функция I=checkerboard(N) создает изображение типа шахматной доски, где размер стороны каждой локальной площади равен N пикселам.
Функция I=checkerboard(N, P, Q) создает прямоугольное изображение шахматной доски, где параметры P и Q определяют соответственно число строчек и столбцов. Элементами строчек и столбцов являются “клетки” шахматной доски, размер стороны которых равен N пикселов, и определяются как:
TILE=[DARK LIGHT; LIGHT DARK]
Если не указывать параметр Q, тогда по умолчанию он будет равен P и изображение шахматной доски будет квадратным.
Пример:
Создать изображение шахматной доски, где размер стороны каждой площадки ("клетки") равен 20 пикселам.
I=checkerboard(20);
imshow(I)

Создать прямоугольное изображение шахматной доски с соотношением 2x3.
J=checkerboard(20, 2, 3);
figure, imshow(J)

Создать черно-белое изображение шахматной доски.
K=(checkerboard > 0.5);
figure, imshow(K)

findbounds - определение границ при пространственных преобразованиях
Синтаксис:
outbounds=findbounds(TFORM, inbounds)
Описание:
Функция outbounds=findbounds(TFORM, inbounds) оценивает результирующие границы, которые обусловлены соответственными пространственными преобразованиями и набором исходных изображений. Параметр TFORM, который формируется maketform, представляет собой структуру пространственных преобразований. Массив inbounds является матрицей с размерностью 2
 NUM_DIMS. Первая строка массива inbounds определяет нижнюю границу для каждой размерности, вторая строка определяет верхнюю границу. Параметр NUM_DIMS совмещается с полем ndims_in field в TFORM.
NUM_DIMS. Первая строка массива inbounds определяет нижнюю границу для каждой размерности, вторая строка определяет верхнюю границу. Параметр NUM_DIMS совмещается с полем ndims_in field в TFORM.Функция outbounds имеет ту же форму, что и inbounds. Оценка минимальной прямоугольной области целиком основывается на представленных минимальных границах, а оценка результирующих границ не основывается на преобразованиях исходного прямоугольника.
Когда TFORM содержит предварительные преобразования (непустое поле forward_fcn), тогда findbounds преобразует вертикальные исходные границы прямоугольника и представляет результат в виде минимального или максимального значения.
Когда TFORM не содержит предварительных преобразований, тогда findbounds оценивает результирующие границы используя критерий Nelder-Mead для оптимизации функции fminsearch. Когда вероятность оптимизации небольшая, тогда findbounds выдает предупреждение и возвращает outbounds=inbounds.
Пример:
inbounds=[0 0; 1 1]
tform=maketform('affine', [2 0 0; .5 3 0; 0 0 1])
outbounds=findbounds(tform, inbounds)
makeresampler - создание повторяющейся структуры
Синтаксис:
R=makeresampler(interpolant, padmethod)
Описание:
Функция R=makeresampler(interpolant, padmethod) создает отдельную повторяющуюся структуру для совместного использования с функциями tformarray и imtransform. Используется эта функция, в основном, для реализации геометрических преобразований изображений.
Интерполяционный аргумент interpolant описывает узлы интерполяции, которые используются при формировании повторений. Параметр interpolant может принимать одно из приведенных в таблице следующих значений, от которых зависит тип интерполяции.
Параметр Interpolant Описание 'cubic' Кубическая интерполяция 'linear' Линейная интерполяция 'nearest' Интерполяция по ближайшей окрестности Когда узлы интерполяции определяются обычным путем, тогда параметр interpolant можно интерпретировать как массив описания некоторых форм.
{half_width, positive_half} Параметр half_width представляет собой положительный скаляр, который служит для создания симметрических узлов интерполяции. Параметр positive_half является вектором, значения которого равномерно размещены в диапазоне [0 positive_half]. {half_width, interp_fcn} Параметр interp_fcn представляет собой функцию, определяющую значения узлов интерполяции, взятые из массива исходных значений на интервале [0 positive_half]. Метод интерполяции не зависит от направления и может быть создан комбинацией разных типов интерполяции. Число элементов в ячейках массива должно быть равно числу направлений преобразований. Например, когда параметр interpolant описан как
{'nearest', 'linear', {2 KERNEL_TABLE}},
тогда используется интерполяция по ближайшей окрестности вдоль первого направления, линейная интерполяция вдоль второго направления и табличная интерполяция вдоль третьего направления.Аргумент padmethod контролирует результат интерполяции. В таблице приведены все возможные значения padmethod.
Аргумент PadMethod Описание 'bound' Определяет значения для наполнения массива, которые, в свою очередь, зависят от типа интерполяции. 'circular' Наполнение массива круговым повторением элементов. Аналогично функции padarray. 'fill' Генерация результирующего массива с размытыми границами (кроме использования интерполяции по ближайшей окрестности). 'replicate' Наполнение массива повторением элементов границы. Аналогично функции padarray. 'symmetric' Наполнение массива зеркальным отражением самого себя. Аналогично функции padarray. В том случае, если установлены опции 'fill', 'replicate', 'circular' или 'symmetric', повторение осуществляется в два этапа с использованием функций tformarray или imtransform:
-
Наполнение массива A непрерывно до полного преобразования исходных данных.
-
Оценка свертки наполненного массива A с повторяющимися узлами результирующих точек, описанных в геометрической карте.
-
-
Традиционная выборка.
В синтаксисе описания алгоритма выборки используются отдельные функции пакета Image Processing Toolbox. Существует возможность создания структур более высокой сложности
R=makeresampler(PropertyName, PropertyValue, ...)
Функция makeresampler поддерживает следующие свойства.
Свойства Описание 'Type' Может принимать значения 'separable' или 'custom'. Когда опция 'Type' принимает значение 'separable', тогда это эквивалентно использованию синтаксиса makeresampler(interpolant, padmethod). Когда опция 'Type' принимает значение 'custom', тогда нужно определять также такие свойства как 'NDims', 'ResampleFcn' и 'CustomData'. 'PadMethod' Для более детальной информации см. аргумент padmethod. 'Interpolant' Для более детальной информации см. аргумент interpolant. 'NDims' Параметр 'NDims' представляется положительным целым числом и указывает в каком направлении будет производиться обработка. Значение Inf указывает на то, что направление не выбрано. Когда опция 'Type' принимает значение 'custom', тогда параметр NDims нужно указывать обязательно. 'ResampleFcn' Интерфейс пользователя и результат обработки во многом зависят от установленных параметров. Например,B=resample_fcn(A, M, TDIMS_A, TDIMS_B, FSIZE_A, FSIZE_B, F, R)Для более детальной информации об исходных параметрах A, TDIMS_A, TDIMS_B и F см. функцию tformarray. Аргумент M представляет собой массив, в котором отображены преобразования индексов данных B в данные A. Когда A имеет N направлений преобразований (N=length(TDIMS_A)) и B имеет P направлений преобразований (P=length(TDIMS_B)), тогда ndims(M)=P+1, когда N>1 или N==1, тогда size(M,P+1)=N. 'CustomData' Определяется пользователем. Пример.
Выполним преобразование (растяжение) размеров изображения. Для этого в различных направлениях будем использовать различные методы.
A=imread('moon.tif');
resamp=makeresampler({'nearest', 'cubic'}, 'fill');
stretch=maketform('affine', [1 0; 0 1.3; 0 0]);
B=imtransform(A, stretch, resamp);

maketform - создание структуры пространственных преобразований (TFORM)
Синтаксис:
T = maketform(transformtype,...)
Описание:
Функция T = maketform(transformtype,...) создает структуру многомерных пространственных преобразований (так называемую TFORM-структуру), которая используется при реализации функций tformfwd, tforminv, fliptform, imtransform или tformarray.
Функция transformtype может работать с одним из следующих типов пространственных преобразований. Синтаксис этих типов описан в таблице.
Тип преобразований Описание 'affine' Аффинные преобразования (двумерные или N-мерные) 'projective' Проекционные преобразования (двумерные или N-мерные) 'custom' Преобразования, которые определяются пользователем (двумерные или N-мерные) 'box' Независимые аффинные преобразования по каждой размерности (масштабирование и сдвиг) 'composite' Построение нескольких произвольных преобразований Типы преобразований
Аффинные преобразования
Функция T = maketform('affine',A) создает TFORM-структуру T, которая используется при N-мерных аффинных преобразованиях. A представляет собой невырожденную матрицу с размерностью (N+1)
 (N+1) или (N+1)
(N+1) или (N+1).gif) N. Когда размерность матрицы A равна (N+1)
N. Когда размерность матрицы A равна (N+1).gif) (N+1), тогда последний столбец равен [zeros(N,1);1]. В другом случае, матрица A автоматически дополняется так, чтобы последний столбец был равен [zeros(N,1);1]. В матрице A определены прямые преобразования, например tformfwd(U,T), где U представлено вектором с размерностью 1
(N+1), тогда последний столбец равен [zeros(N,1);1]. В другом случае, матрица A автоматически дополняется так, чтобы последний столбец был равен [zeros(N,1);1]. В матрице A определены прямые преобразования, например tformfwd(U,T), где U представлено вектором с размерностью 1.gif) N, а X возвращает вектор с размерностью 1
N, а X возвращает вектор с размерностью 1.gif) N - X=U*A(1:N,1:N)+A(N+1,1:N). Параметр T представляет прямые и инверсные преобразования.
N - X=U*A(1:N,1:N)+A(N+1,1:N). Параметр T представляет прямые и инверсные преобразования.Функция T = maketform('affine',U,X) создает TFORM-структуру T для двумерных аффинных преобразований, которые трансформируют каждую строку U в соответствующую строку X. Каждый из аргументов U и X имеет размерность 3
.gif) 2 и определяет углы исходных и результирующих треугольников. Углы не должны быть коллинеарными.
2 и определяет углы исходных и результирующих треугольников. Углы не должны быть коллинеарными.Проекционные преобразования
Функция T = maketform('projective',A) создает TFORM-структуру для N-мерных проекционных преобразований. A представляет собой невырожденную матрицу с размерностью (N+1)
.gif) (N+1). Значения A(N+1,N+1) равны нулю. В матрице A определены прямые преобразования, например, tformfwd(U,T), где параметр U представлен в виде вектора с размерностью 1
(N+1). Значения A(N+1,N+1) равны нулю. В матрице A определены прямые преобразования, например, tformfwd(U,T), где параметр U представлен в виде вектора с размерностью 1.gif) N. X определяется как X = W(1:N)/W(N+1), где W=[U 1]*A. Структура преобразований T используется как при прямых, так и при инверсных преобразованиях.
N. X определяется как X = W(1:N)/W(N+1), где W=[U 1]*A. Структура преобразований T используется как при прямых, так и при инверсных преобразованиях.Функция T = maketform('projective',U,X) создает TFORM-структуру T для реализации двумерных проекционных преобразований, которые отображают каждую строку U соответствующей строкой X. Аргументы U и X имеют размерность 4
.gif) 2 и определяют исходный и результирующий прямоугольник. Углы не должны быть коллинеарными.
2 и определяют исходный и результирующий прямоугольник. Углы не должны быть коллинеарными.Преобразования, которые определяются пользователем
Функция T = maketform('custom',NDIMS_IN,NDIMS_OUT,...FORWARD_FCN,INVERSE_FCN,TDATA) создает TFORM-структуру T на основе параметров, которые задаются пользователем. Параметры NDIMS_IN и NDIMS_OUT определяют число исходных и результирующих размерностей. С помощью FORWARD_FCN и INVERSE_FCN задается функция прямых и инверсных преобразований. Эти функции должны поддерживать следующий синтаксис:
Прямая функция: X = FORWARD_FCN(U,T) Инверсная функция: U = INVERSE_FCN(X,T), где параметр U представляет собой матрицу с размерностью P
.gif) NDIMS_IN. Строки представляют точки в исходном пространстве преобразований и X представляет собой матрицу с размерностью P
NDIMS_IN. Строки представляют точки в исходном пространстве преобразований и X представляет собой матрицу с размерностью P.gif) NDIMS_OUT, где строки представляют точки в результирующем пространстве преобразований. Аргумент TDATA представляет собой некоторый массив системы MATLAB и используется для хранения параметров преобразований. Для доступа к этому массиву используются функции FORWARD_FCN и INVERSE_FCN в поле "tdata" в T.
NDIMS_OUT, где строки представляют точки в результирующем пространстве преобразований. Аргумент TDATA представляет собой некоторый массив системы MATLAB и используется для хранения параметров преобразований. Для доступа к этому массиву используются функции FORWARD_FCN и INVERSE_FCN в поле "tdata" в T.Независимые аффинные преобразования по каждой размерности
Функция T = maketform('box',tsize,LOW,HIGH) или T = maketform('box',INBOUNDS, OUTBOUNDS) создает TFORM-структуру T для N-мерных аффинных преобразований. Аргумент tsize представляет собой N-элементный вектор положительных целых чисел. Параметры LOW и HIGH представляют собой также N-элементные векторы. Отображение преобразований производится с использованием параметров INBOUNDS и INBOUND.
Построение нескольких произвольных преобразований
Функция T = maketform('composite',T1,T2,...,TL) или T = maketform('composite', [T1 T2 ... TL]) создает TFORM-структуру T, где прямые и инверсные функции состоят из нескольких функций прямых и инверсных преобразований T1, T2, ..., TL.
Например, когда L = 3, тогда выражение tformfwd(U,T) аналогично tformfwd(tformfwd(tformfwd(U,T3),T2),T1).
Пример 1.
Сконструируем и применим аффинные преобразования.
T = maketform('affine',[.5 0 0; .5 2 0; 0 0 1]);
tformfwd([10 20],T)
I = imread('cameraman.tif');
figure, imshow(I);

I2 = imtransform(I,T);
imshow(I2)

T = maketform('projective',[.5 0 0; .5 1 0; 0 0 1]);
tformfwd([20 10],T)
I2 = imtransform(I,T);
imshow(I2)

Пример 2.
Приведем также другой пример использования функции maketform.
I = checkerboard(20,1,1);
imview(I)
T = maketform('projective',[1 1; 41 1; 41 41; 1 41],...
[5 5; 40 5; 35 30; -10 30]);
R = makeresampler('cubic','circular');
J = tformarray(I,T,R,[1 2],[2 1],[100 100],[],[]);
imview(J)
tformarray - применение пространственных преобразований для многомерных массивов
Синтаксис:
B=tformarray(A, T, R, TDIMS_A, TDIMS_B, TSIZE_B, TMAP_B, F)
Описание:
Функция B=tformarray(A, T, R, TDIMS_A, TDIMS_B, TSIZE_B, TMAP_B, F) применяется для пространственных преобразований массива A в массив B. По своим характеристикам функция tformarray похожа на функцию imtransform и реализует обработку многомерных массивов. В большинстве случаев эта функция используется вместе с такими функциями как maketform, makeresampler, findbounds и tformarray.
В таблице представлено краткое описание всех исходных аргументов.
Аргумент Описание A Исходный массив или изображение T Типичная структура пространственных преобразований, обозначаемая TFORM, создается с помощью функции maketform R Типичная повторяющаяся структура, которая создается с помощью функции makeresampler TDIMS_A Строчный вектор, в котором перечислены исходные данные преобразований TDIMS_B Строчный вектор, в котором перечислены результирующие данные преобразований TMAP_B Размерность результирующего массива с преобразованными данными TSIZE_B Массив точек результирующего пространства, который используется как альтернативный путь описания пространственных преобразований F Массив заполненных значений Данные в A должны быть представлены числовым неразреженным массивом вещественных или комплексных чисел.
Параметр T представляет структуру TFORM, которая определяет особенности пространственных преобразований. Для каждого элемента, который будет подвержен преобразованиям, описаны соответствующие данные для исходного и результирующего пространств. Эти данные будут используются функциями tformarray и tforminv для отображения особенностей пространственных преобразований.
Когда параметр T пустой, тогда функция tformarray работает аналогично функции повторения структуры для вычисления параметра R. Параметр R представляет собой структуру, которая определяет значения интерполяции исходного массива в описанных точках. В большинстве случаев параметр R создается с помощью функции makeresampler, которая позволяет проводить контроль интерполяции вдоль каждой размерности.
Параметры TDIMS_A и TDIMS_B указывают какие размерность исходного и результирующего массива задействованы в пространственных преобразованиях. Каждый элемент должен однозначно определяться и представляться положительным целым числом. Индексы элементов перечислены не в порядке возрастания, а в порядке поступления. Описание, которое точно отображает зависимости при преобразованиях между исходным A и результирующим B массивами, помещено в T. Значение length(TDIMS_A) должно быть равно T.ndims_in, а значение length(TDIMS_B) must - соответственно T.ndims_out.
Например, когда параметр T представляет двумерные преобразования (TDIMS_A=[2 1] и TDIMS_B=[1 2]), тогда размерность вдоль столбца и размерность вдоль строки массива A соответствует первому и второму направлению преобразований в исходном пространстве. Размерность вдоль строки и размерность вдоль столбца соответствует первому и второму направлению преобразований в результирующем пространстве.
Параметр TSIZE_B описывает размеры массива B после проведения преобразований. Отметим, что размеры B вдоль не преобразованных размерностей пропорциональны размерностям A вдоль тех же размерностей. Когда, например, параметр T представляет двумерные преобразования, тогда size(A)=[480 640 3 10], TDIMS_B=[2 1], TSIZE_B=[300 200] и size(B) равно [200 300 3].
Параметр TMAP_B представляет собой массив, в котором содержится альтернативный путь описания размещения элементов при преобразованиях. Параметр TMAP_B может быть использован, например, для вычисления деформации изображений в результирующем пространстве. Когда массив TMAP_B не пустой, тогда его размер определяется по формуле:
[D1 D2 D3 ... DN L]
где N равно length(TDIMS_B). Вектор [D1 D2 ... DN] используется в пространстве TSIZE_B.
Значение L зависит от того, пустой ли массив T. Когда массив T не пустой, тогда L равно T.ndims_out и каждая точка L-измерения в TMAP_B преобразует исходное пространство с использованием T. Когда массив T пустой, тогда L имеет размерность length(TDIMS_A) и каждая точка L-измерения в TMAP_B используется для локализации в исходном пространстве.
Параметр F представляется массивом удвоенной точности, содержащим наполненные значения. Значения массива F могут использоваться в трех ситуациях:
-
когда повторяющая структура создается с помощью функции makeresampler и опция padmethod установлена как 'fill' или 'bound'.
-
когда используется повторяющаяся структура и она поддерживает метод наполнения, который определяется опциями 'fill' или 'bound'.
-
когда отображаются преобразования данных B и A для некоторых точек.
-
-
Требования к исходным данным.
Параметр A может быть представлен любым неразреженным числовым массивом действительных или комплексных чисел. Также массив может быть представлен в формате logical.
Пример.
Создадим изображение шахматной доски 2
 2, что эквивалентно квадрату в 20 пикселей. Далее преобразуем это изображение с помощью проекционных преобразований. Для создания повторяющейся структуры используем метод наполнения 'circular'. Пусть размеры результирующего изображения будут 100
2, что эквивалентно квадрату в 20 пикселей. Далее преобразуем это изображение с помощью проекционных преобразований. Для создания повторяющейся структуры используем метод наполнения 'circular'. Пусть размеры результирующего изображения будут 100.gif) 100.
100. I=checkerboard(20, 1, 1);
figure; imshow(I)

T=maketform('projective', [1 1; 41 1; 41 41; 1 41],[5 5; 40 5; 35 30; -10 30]);R=makeresampler('cubic', 'circular');J=tformarray(I, T, R, [1 2], [2 1], [100 100], [], []);figure; imshow(J)

para2fan - вычисление веерно-лучевых проекций на основании параллельно-лучевых томографических данных
Синтаксис:
F=para2fan(P, D)I=para2fan(..., param1, val1, param2, val2, ...)[F, fan_positions, fan_rotation_angles]=fan2para(...)
Описание:
Функция F=para2fan(P, D) вычисляет веерно-лучевые данные (синограммы) F на основе параллельно-лучевых данных (синограмм) P. Каждый столбец P содержит выборку данных одного параллельно-лучевого сенсора, соответствующую некоторому повороту угла. Параметр D представляет собой расстояние в пикселях от центра поворота до центра датчика.
Предполагается, что датчики отображаются с помощью одного пикселя. Параллельно-лучевое угловое вращение возможно в пределах, эквивалентных [0,180] градусов. Веерно-лучевые угловые вращения вычисляются в диапазоне [0,360) аналогично как и параллельно-лучевые угловые вращения. Трансформации между веерно-лучевыми и параллельно-лучевыми проекциями проводятся с учетом пространственного размещения датчиков.
В функции I=para2fan(..., param1, val1, param2, val2, ...) используются параметры, которые контролируют различные аспекты para2fan-преобразований. Название параметров приведено в виде аббревиатуры, но от этого не меняется их суть. Значения параметров, которые используются по умолчанию, приведены в фигурных скобках: {по умолчанию}.
Параметр Описание 'FanCoverage' Строка, описывающая диапазон лучей при их повороте.Возможные значения: {'cycle'} или 'minimal'.Для более детальной информации см. описание функции ifanbeam. 'FanRotationIncrement' Положительный вещественный скаляр, описывающий приращение угла поворота в градусах при веерно-лучевых проекциях.
Когда параметр 'FanCoverage' принимает значение 'cycle', тогда 'FanRotationIncrement' должен быть равен 360.
Когда параметр 'FanRotationIncrement' не описан, то он устанавливается таким же, как и при параллельно-лучевых угловых поворотах.'FanSensorGeometry' Текстовая строка, описывающая расположение датчиков.
Возможные значения: {'arc'} или 'line'
Для более детальной информации см. описание функции fanbeam.'FanSensorSpacing' Положительный вещественный скаляр, описывающий распределение веерных лучей. Интерпретация значений зависит от установки опции 'FanSensorGeometry':
Когда опция 'FanSensorGeometry' установлена как 'arc', тогда это значение рассматривается как угловое пространство в градусах. По умолчанию это значение равно 1.
Когда опция 'FanSensorGeometry' установлена как 'line', тогда это значение интерпретируется как линейное пространство в пикселях.
В случае, если опция 'FanSensorSpacing' не определена, тогда по умолчанию устанавливается наименьшее значение 'ParallelSensorSpacing'.
Когда опция 'FanSensorGeometry' установлена как 'arc', тогда 'FanSensorSpacing' определяется как180/PI*ASIN(PSPACE/D)
где PSPACE равно значению параметра 'ParallelSensorSpacing'.
Когда опция 'FanSensorGeometry' установлена как'line', тогда 'FanSensorSpacing' принимает значениеD*ASIN(PSPACE/D)'Interpolation' Текстовая строка, описывающая тип интерполяции, который используется при преобразованиях между параллельно-лучевыми и веерно-лучевыми данными.
'nearest' - по ближайшей окрестности
{'linear'} - линейная
'spline' - кусочные кубические сплайны
'pchip' - кусочные кубические эрмитовские сплайны
'cubic' - аналогично 'pchip''ParallelCoverage' Текстовая строка, описывающая диапазон поворота.
'cycle' - параллельные данные покрывают 360 градусов
{'halfcycle'} - параллельные данные покрывают 180 градусов'ParallelRotationIncrement' Положительный вещественный скаляр, описывающий приращения при параллельно-лучевых угловых поворотах, измеренные в градусах. Угол поворота параллельных лучей вычисляется в диапазоне [0,180) градусов с приращением PAR_ROT_INC, где PAR_ROT_INC принимает значение 'ParallelRotationIncrement'. 180/PAR_ROT_INC должно быть целым числом.
Когда опция 'ParallelRotationIncrement' не определена, приращения устанавливаются аналогичными как и при веерно-лучевых угловых вращениях.'ParallelSensorSpacing' Положительный вещественный скаляр, описывающий пространственное расположение датчиков в пикселях. Диапазон размещения датчиков зависит от диапазона угла веера и вычисляется за выражением [D*sin(min(FAN_ANGLES)),D*sin(max(FAN_ANGLES))]
Когда опция 'ParallelSensorSpacing' не описана, расположение принимается равномерным и зависит от угла веера и его дискретизации.Если при использовании функции [F, fan_positions, fan_rotation_angles]=fan2para(...) опция 'FanSensorGeometry' принимает значение 'arc', тогда параметр fan_positions содержит веерно-лучевые датчики угла. Когда 'FanSensorGeometry' принимает значение 'line', когда параметр fan_positions содержит информацию о месторасположении веерно-лучевых датчиков вдоль линии. Параметр fan_rotation_angles содержит информацию о угловом вращении.
Требования к исходным данным.
Все исходные числовые аргументы должны иметь формат представления данных double. Результат также представляется в формате double.
Пример.Сгенерируем параллельно-лучевые проекции ph=phantom(128); theta=0:180; [P, xp]=radon(ph, theta); imshow(theta, xp, P, [], 'n'), axis normal title('Parallel-Beam Projections') xlabel('\theta (degrees)') ylabel('x''') colormap(hot), colorbar Преобразуем в веерно-лучевые проекции [F, Fpos, Fangles]=para2fan(P, 100); figure, imshow(Fangles, Fpos, F, [], 'n'), axis normal title('Fan-Beam Projections') xlabel('\theta (degrees)') ylabel('Sensor Locations (degrees)') colormap(hot), colorbar
fan2para - вычисление параллельно-лучевых проекций данных томографии с расходящимся пучком
Синтаксис:
P=fan2para(F, D)P=fan2para(..., param1, val1, param2, val2, ...)[P, parallel_locations, parallel_rotation_angles]=fan2para(...)
Описание:
Функция P=fan2para(F, D) вычисляет параллельно-лучевые проекции (синограммы) на основании данных томографии с расходящимся пучком F. Каждая строка F содержит данные о веерной протяженности углов и их перемещении. Параметр D является расстоянием от вершины веера до центра вращения.
Функция fan2para работает с проекциями протяженности углов и некоторыми приращениями исходных углов поворота. Исходные углы поворота являются ступенчатыми приращениями в диапазоне [0,360). Результирующие углы вычисляются в диапазоне [0,180) с аналогичными приращениями.
Функция P=fan2para(..., param1, val1, param2, val2, ...) описывает параметры, которые контролируют различные аспекты преобразования с помощью функции fan2para; их перечень приведен в таблице. Названия параметров могут быть сокращенными, однако это не влияет на суть. По умолчанию значение задается в фигурных скобках ({}).
Параметр Описание 'FanCoverage' Строка, описывающая ранг через поворот лучей.Возможные значения: {'cycle'} или 'minimal'
См. ifanbeam для более детальной информации.'FanRotationIncrement' Положительный вещественный скаляр, описывающий приращения угла поворота в лучевых проекциях, выраженный в количестве ступенек приращения.
По умолчанию это значение равно 1.'FanSensorGeometry' Строка, описывающая как размещены сенсоры.Возможные значения: {'arc'} или 'line'
См. fanbeam для более детальной информации.'FanSensorSpacing' Положительный вещественный скаляр, описывающий распределение пучка. Интерпретация значений зависит от установки 'FanSensorGeometry':
Когда 'FanSensorGeometry' равно 'arc', тогда значение определяет угловое ступенчатое пространство. По умолчанию равно 1.
Когда 'FanSensorGeometry' равно 'line', тогда значение определяет линейное пространство в пикселях.'Interpolation' Текстовая строка, описывающая тип используемой интерполяции между параллельно-лучевыми и точечно-лучевыми данными.
'nearest' - по ближайшей окрестности
{'linear'} - линейная
'spline' - кусочно-линейные кубические сплайны
'pchip' - кусочно-линейные эрмитовские кубические сплайны
'cubic' - идентично 'pchip''ParallelCoverage' Текстовая строка, описывающая ранг поворота.Возможные значения: 'cycle' или {'halfcycle'}.
См. para2fan для более детальной информации.'ParallelRotationIncrement' Положительный вещественный скаляр, описывающий приращения угла при параллельно-лучевом повороте, измеряемом в количестве приращений. Углы вычисляются в диапазоне [0,180) с приращениями PAR_ROT_INC, где PAR_ROT_INC является значением 'ParallelRotationIncrement'. Значение 180/PAR_ROT_INC должно быть целым.
Когда 'ParallelRotationIncrement' не определено, тогда приращения равны приращениям при точечно-лучевых углах поворота.'ParallelSensorSpacing' Положительный вещественный скаляр, описывающий размещение параллельно-лучевых сенсоров в пикселях. Порядок размещения сенсоров (датчиков) вытекает из порядка лучевых углов и устанавливается равным[D*sin(min(FAN_ANGLES)),D*sin(max(FAN_ANGLES))].
Когда 'ParallelSensorSpacing' не определено, тогда размещение будет равномерным и минимальное размещение вытекает из веера углов и указывает на ранг, который определяется на основании этих углов.Выражение [P, parallel_locations,parallel_rotation_angles]=fan2para(...) возвращает параллельно-лучевое размещение сенсоров в parallel_locations и поворот угла в parallel_rotation_angles.
Пример.Создадим искусственные данные параллельно-лучевых проекций и используем их для преобразования в точечно-параллельные данные.ph=phantom(128);theta=0:179;[Psynthetic, xp]=radon(ph, theta);imshow(theta, xp, Psynthetic, [], 'n'),title('Synthetic Parallel-Beam Data')xlabel('\theta (degrees)')ylabel('x''')colormap(hot), colorbarFsynthetic=para2fan(Psynthetic, 100, 'FanSensorSpacing', 1);Возвращение к параллельно-лучевым данным.[Precovered, Ploc, Pangles] = fan2para(Fsynthetic, 100, ... 'FanSensorSpacing', 1, ... 'ParallelSensorSpacing', 1);figure, imshow(Pangles, Ploc, Precovered, [], 'n'), axis normaltitle('Recovered Parallel-Beam Data')xlabel('Rotation Angles (degrees)')ylabel('Parallel Sensor Locations (pixels)')colormap(hot), colorbar
Требования к исходным данным.
Массив I должен иметь формат представления данных double, uint8, uint16 или logical. Все другие исходные и результирующие числовые значения должны быть представлены в формате double.
fanbeam - вычисление веерно-лучевых преобразований
Синтаксис:
F=fanbeam(I, D)F=fanbeam(..., param1, val1, param1, val2, ...)[F, sensor_positions, fan_rotation_angles]=fanbeam(...)
Описание:
Функция F=fanbeam(I, D) на основании изображения I вычисляет данные F веерно-лучевых преобразований (синограмм). D представляет собой расстояние в пикселях от вершины до центра вращения. Каждый столбец F содержит данные о веерно-лучевом воспринимающем элементе (сенсоре); эти данные соответствуют выборке элементарных вращений. Сенсор характеризует один шаг в угловом пространстве. Угловое вращение в пространстве эквивалентно следующему диапазону отсчетов [0:359].
Функция F=fanbeam(..., param1, val1, param1, val2, ...) описывает параметры, которые контролируют различные аспекты веерно-лучевых проекций; перечень этих параметров приведен в таблице. Название параметров может быть подано в виде аббревиатуры, но это не влияет на суть. Значения, которые используются по умолчанию, заключены в фигурные скобки ({}).
Параметр Описание 'FanRotationIncrement' Положительный вещественный скаляр, описывающий приращение угла поворота в веерно-лучевых проекциях.
По умолчанию это значение равно 1.'FanSensorGeometry' Текстовая строка, описывающая размещение сенсоров.
{'arc'} - сенсоры размещены по кругу на расстоянии D от центра поворота.
'line' - сенсоры размещены равномерно вдоль линии, замыкающая точка размещена на расстоянии D от центра поворота.'FanSensorSpacing' Положительный вещественный скаляр, описывающий размещение веера лучей. Интерпретация значений зависит от установок 'FanSensorGeometry'.
Когда параметр 'FanSensorGeometry' равен 'arc', значение определяется как отсчеты углового пространства. По умолчанию это 1.
Когда параметр 'FanSensorGeometry' установлен в 'line', значение определяется как линейное пространство в пикселях.Функция [F, sensor_positions, fan_rotation_angles]=fanbeam(...) возвращает информацию о размещении сенсоров и углов поворота. Когда опция 'FanSensorGeometry' равна 'arc', то sensor_positions содержит веерно-лучевой сенсор измерения углов, которые измеряются в количестве отсчетов. Когда опция 'FanSensorGeometry' равна 'line', тогда параметр sensor_positions содержит информацию о размещении веерно-лучевого сенсора, измеряемую в пикселях. Параметр fan_rotation_angles содержит углы поворота.
Требования к исходным данным.
Элементы массива I должны быть представлены в формате double, logical или другом формате целых чисел. Все другие исходные и результирующие числовые данные должны быть представлены в формате double. Исходные данные не должны быть разреженными.
Пример.ph=phantom(128);imview(ph)[F, Floc, Fangles]=fanbeam(ph, 250);imshow(Fangles, Floc, F, [], 'n'), axis normalxlabel('Rotation Angles (degrees)')ylabel('Sensor Positions (degrees)')colormap(hot), colorbar
fliptform - перестановка исходных и результирующих данных в структуре TFORM
Синтаксис:
TFLIP=fliptform(T)
Описание:
Функция TFLIP=fliptform(T) создает новую структуру пространственных преобразований TFORM путем перестановки исходных и результирующих данных в существующей структуре TFORM.
Пример.T=maketform('affine', [.5 0 0; .5 2 0; 0 0 1]);T2=fliptform(T)Это эквивалентно следующему выражению:x=tformfwd([-3 7], T)x=tforminv([-3 7], T2)
ifanbeam - вычисление инверсного веерно-лучевого преобразования
Синтаксис:
I=ifanbeam(F, D)I=ifanbeam(..., param1, val1, param2, val2, ...)[I, H]=ifanbeam(...)
Описание:
Функция I=ifanbeam(F, D) восстанавливает изображение I из проекций, которые заданы в двумерном массиве F. Каждый столбец массива F содержит данные веерно-лучевых проекций при повороте на один градус. В функции ifanbeam центр поворота является точкой центра проекций и определяется как ceil(size(F,1)/2).
Исходные углы вращения имеют одинаковые приращения и покрывают все [0:359] градусов. D является расстоянием от вершины до центра вращения.
Функция I=ifanbeam(..., param1, val1, param2, val2, ...) содержит описания параметров, которые контролируют различные аспекты ifanbeam-реконструкции; описания приведены в следующей таблице. Названия параметров могут быть поданы в виде аббревиатуры, однако это не влияет на суть. Значения, которые применяются по умолчанию заключаются в фигурные скобки ({}).
Параметр Описание 'FanCoverage' Строка, описывающая ранг (диапазон), который применяется при вращении лучей.
{'cycle'} - Вращение через полный диапазон [0,360).
'minimal' - Минимальный диапазон вращения, который необходим для представления объекта.'FanRotationIncrement' Положительный вещественный скаляр, описывающий приращения углов поворота веерно-лучевых проекций, измеряемые в градусах. Для более детальной информации см. функцию fanbeam. 'FanSensorGeometry' Строка, описывающая положение сенсоров. Для более детальной информации см. функцию fanbeam. 'FanSensorSpacing' Положительный вещественный скаляр, описывающий размещение веерно-лучевых сенсоров. Интерпретация этого значения зависит от установки опции 'FanSensorGeometry'. Для более детальной информации см. функцию fanbeam. 'Filter' Строка, описывающая название фильтра. Для более детальной информации см. функцию iradon. 'FrequencyScaling' Скаляр в диапазоне (0,1], который изменяет фильтр путем масштабирования частотной оси. Для более детальной информации см. функцию iradon. 'Interpolation' Строка, описывающая метод интерполяции. Для более детальной информации см. функцию iradon. 'OutputSize' Положительный скаляр, описывающий число сток и столбцов в реконструированном изображении.
Когда параметр 'OutputSize' не описывается, функция ifanbeam определяет размер автоматически.
Когда параметр 'OutputSize' описан, тогда функция ifanbeam реконструирует области изображения, не изменяя масштаб данных.
Примечание: Когда проекции вычислены с помощью функции fanbeam, реконструированное изображение не может иметь те же размеры, что и исходное изображение.[I, H]=ifanbeam(...) возвращает частоту отзыва фильтра в вектор H.
Примечание.
Функция ifanbeam преобразует веерно-лучевые данные в параллельно-лучевые проекции и использует их в алгоритме фильтрации обратных проекций для выполнения обратного преобразования Радона. Фильтр работает полностью в частотной области.
Требования к исходным данным.
Все исходные числовые аргументы должны быть представлены в формате double. Результирующие аргументы также будут представлены в формате double.
Пример.ph=phantom(128);d=100;F=fanbeam(ph, d);I=ifanbeam(F, d, 'FanSensorSpacing', 0.5);imview(ph); imview(I);
applycform - применение преобразования цветовых пространств
Синтаксис:
out=applycform(I, C)
Описание:
Функция out=applycform(I, C) преобразует значения интенсивностей цветов изображения I в то цветовое пространство, которое описано в структуре преобразования цветов C. Эта структура содержит описание различных параметров преобразования. Для более детальной информации см. функцию makecform.
Если I представляет собой двумерный массив, каждый элемент интерпретируется как цвет. Элементы типичного массива I зависят от исходного пространства цветов. Значения элементов выходного массива зависят от результирующего цветового пространства.
Если массив I трехмерный, каждое положение столбец-строка интерпретируется как цветовой вектор, который зависит от исходного цветового пространства. На выходе получаем число строк и столбцов соответствующее I и размер size(out, 3), который зависит от результирующего цветового пространства.
Требования к исходным данным.
Изображение I должно быть представлено конечным не разреженным вещественным массивом в формате представления данных uint8, uint16 или double. Формат представления данных и размеры результирующего массива аналогичны исходному изображению, за исключением случая, когда цветовым пространством является XYZ. Когда исходные данные представлены в цветовом пространстве XYZ и формате uint8, тогда результирующий массив будет представлен в формате uint16.
Пример.Считаем цветное изображение с использованием цветового пространства RGB.I=imread('peppers.png');Создадим структуру преобразования цветового пространства, которая определяет переход из RGB в XYZ.C=makecform('srgb2xyz');Теперь выполним преобразования с помощью функции applycform.I_xyz=applycform(I, C);
makecform - создание структуры преобразования цветовых значений
Синтаксис:
C=makecform(type)C=makecform(type, 'whitepoint', WP)C=makecform('icc', src_profile, dest_profile)C=makecform('icc', src_profile, dest_profile, 'SourceRenderingIntent', src_intent, 'DestRenderingIntent', dest_intent)C=makecform('clut', profile, LUTtype)C=makecform('mattrc', MatTrc, 'Direction', direction)
Описание:
Функция C=makecform(type) создает структуру C преобразования цветов, которая описывает типы преобразования цветовых пространств. Структура цветовых преобразований может использоваться в качестве аргумента в функции applycform.
Перечень возможных типов преобразований приведен в таблице. Функция makecform поддерживает преобразования между цветовыми пространствами, которые не зависят от устройства и отвечают требованиям Международной комиссии по освещению (CIE, Commission Internationale de l'Eclairage (International Commission on Illumination)). Дополнительно функция makecform поддерживает преобразования в стандарте sRGB. При перечне каждого цветового пространства используется аббревиатура пакета Image Processing Toolbox.
Тип Описание 'lab2lch' Преобразование из L*a*b* в цветовое пространство L*ch. 'lab2srgb'1 Преобразование из L*a*b* в цветовое пространство srgb. 'lab2xyz'1 Преобразование из L*a*b* в цветовое пространство XYZ. 'lch2lab' Преобразование из L*ch в цветовое пространство L*a*b*. 'srgb2lab'1 Преобразование из srgb в цветовое пространство L*a*b*. 'srgb2xyz' Преобразование из srgb в цветовое пространство XYZ. 'upvpl2xyz' Преобразование из u'v'L в цветовое пространство XYZ. 'uvl2xyz' Преобразование из uvL в цветовое пространство XYZ. 'xyl2xyz' Преобразование из xyY в цветовое пространство XYZ. 'xyz2lab'1 Преобразование из XYZ в цветовое пространство L*a*b*. 'xyz2srgb' Преобразование из XYZ в цветовое пространство srgb. 'xyz2upvpl' Преобразование из XYZ в цветовое пространство u'v'L. 'xyz2uvl' Преобразование из XYZ в цветовое пространство uvL. 'xyz2xyl' Преобразование из XYZ в цветовое пространство xyY. Для преобразований типа 'xyz2lab', 'lab2xyz', 'srgb2lab' и 'lab2srgb' существует возможность оптимального описания значений интенсивностей с использованием так называемых белых точек. Для этого используется синтаксис
C=makecform(type, 'WhitePoint', WP),
где WP представляет собой вектор XYZ-значений с размерностью 1x3 при единичном диапазоне Y. По умолчанию, в соответствии с требованиями Международной комиссии по освещению, иллюминент D50 описан в ICC.1:2001-04. Также существует возможность использования функции whitepoint для создания вектора WP.
Функция C=makecform('icc', src_profile, dest_profile) создает структуру преобразования цветов, которая базируется на двух ICC-описаниях. Параметры src_profile и dest_profile являются элементами ICC-описания, которые возвращаются функцией iccread.
Функция C=makecform('icc', src_profile, dest_profile, 'SourceRenderingIntent', src_intent, 'DestRenderingIntent', DEST_INTENT) создает структуру цветовых преобразований, которые также базируются на двух ICC-описаниях src_profile и dest_profile. Параметры src_profile и dest_profile раскрывают смысл аргументов src_intent и назначение описания dest_intent.
Предоставленные описания способов преобразования данных сгруппированы в зависимости от их содержания. Для многих устройств диапазон воспроизводимых цветов является больше или меньше чем диапазон цветов PCS. Гамма палитра зависит от интерпретации описания dest_intent. Перечень возможных значений приведен в таблице.
Значение Описание 'AbsoluteColorimetric' Палитра всей гаммы цветов ближайшей палитры, содержащей похожие оттенки исходной гаммы. Полное изложение всех цветовых данных является относительным, поскольку много цветов образуется путем диффузии существующих. 'Perceptual' (default) Результат работы технологии описания гаммы палитры для оптимизации диапазона воспроизводимых цветов во многом зависит от самого устройства. В действительности, если количество оттенков очень большое, то они могут не воспроизводиться устройством. 'RelativeColorimetric' Палитра всей гаммы оттенков цветов относительно исходной гаммы. Цветовые данные определяются относительно так называемой "белой точки" устройства. 'Saturation' Применение технологии создания палитры для максимизации насыщения цветов, которые воспроизводятся устройством. Здесь также используется так называемая "белая точка" устройства. Функция C=makecform('clut', profile, LUTtype) создает структуру преобразования цветов C, в основу которой положен метод табличных преобразований цветов (color lookup table (CLUT)), описание которого содержится в ICC. Описание ICC генерируется функцией iccread. Параметр LUTtype описывает какой метод CLUT используется. Описание этого параметра подано в таблице.
Тип LUT Описание 'AToB0' Содержит 16–битные и 8–битные компоненты LUTtag , которые преобразуют цвета устройств в PCS –цвета с использованием поэлементного представления. 'AToB1' Содержит 16–битные и 8–битные компоненты LUTtag , которые преобразуют цвета устройств в PCS –цвета с использованием свойств относительного представления. 'AToB2' Содержит 16–битные и 8–битные компоненты LUTtag , которые преобразуют цвета устройств в PCS –цвета с использованием свойств насыщенного представления. 'BToA0' Содержит 16–битные и 8–битные компоненты LUTtag , которые преобразуют PCS –цвета в цвета устройства с использованием свойств визуального восприятия. ' BToA1' Содержит 16–битные и 8–битные компоненты LUTtag , которые преобразуют PCS –цвета в цвета устройства с использованием свойств колориметрического восприятия. 'BToA2' Содержит 16–битные и 8–битные компоненты LUTtag , которые преобразуют PCS –цвета в цвета устройства с использованием свойств насыщенного представления. 'Gamut' Содержит 16–битные и 8–битные компоненты LUTtag , которые определяют какие PCS –цвета из данной гаммы являются приемлемыми для данного устройства. 'Preview0' Содержит 16–битные и 8–битные компоненты LUTtag , которые определяют такие PCS –цвета, которые доступны программе для поэлементного представления. 'Preview1' Содержит 16–битные и 8–битные компоненты LUTtag , которые определяют такие PCS –цвета, которые доступны программе для относительного колориметрического представления. 'Preview2' Содержит 16–битные и 8–битные компоненты LUTtag , которые определяют такие PCS –цвета, которые доступны программе для представления насыщенности. Функция C=makecform('mattrc', MatTrc, 'Direction', direction) создает структуру цветовых преобразований C, в основу которой положена матрично-градационная модель представление кривых, содержащаяся в ICC-описании цветов. Параметр direction может принимать одно из двух значений 'forward' или 'inverse' и описывает какая матрично-градационная модель применяется в прямом и инверсном направлении. Для более детальной информации см. раздел 6.3.1.2 в спецификации Международного консорциума цветов ICC.1:2001-04 (www.color.org).
Ремарка.
В пакете Image Processing Toolbox используется следующая аббревиатура для представления цветовых пространств.
Аббревиатура Описание Xyz 1931 CIE XYZ трехцветные значения Xyl 1931 CIE xyY хроматические значения Uvl 1960 CIE uvL значения Upvpl 1976 CIE u'v'L значения Lab 1976 CIE L*a*b* значения Lch Полярные преобразования CIE L*a*b* значений, где c=chroma и h=hue srgb Стандартные RGB-значения для компьютерных мониторов, (IEC 61966-2-1) Пример.
Преобразование RGB-изображения в L*a*b* , формат представления исходного изображения uint8.
rgb=imread('peppers.png');
cform=makecform('srgb2lab');
lab=applycform(rgb,cform);
whitepoint - описание полноцветной белой точки в цветовом пространстве
Синтаксис:
xyz=whitepointxyz=whitepoint(string)
Описание:
Функция xyz=whitepoint возвращает элемент xyz, который представляет собой трехэлементный вектор значений в единичном диапазоне.
Функция xyz=whitepoint(string) возвращает элемент xyz, который представляет собой трехэлементный вектор значений, которые описывают составляющие компоненты цвета. В таблице приведен перечень всех возможных значений этой строки. Значение, которое используется по умолчанию, заключено в фигурные скобки ({}).
Значение Описание 'a' CIE стандартный иллюминант A 'c' CIE стандартный иллюминант C 'd50' CIE стандартный иллюминант D50 'd55' CIE стандартный иллюминант D55 {'icc'} ICC стандартное описание связных иллюминантов пространства; 16-битная кусочная аппроксимация D50 Требования к исходным данным
Строка может содержать цифровой массив. Формат представления xyz double.
Пример.
В этом примере в цветовом пространстве XYZ представлены составляющие иллюминанты 'icc' белой точки.
wp_icc = whitepointwp_icc = 0.9642 1.0000 0.8249
immagbox - локальное увеличение с использованием панели прокрутки
Синтаксис:
hbox = immagbox(hparent,himage)
Описание:
Функция hbox = immagbox(hparent,himage) реализует локальное увеличение для изображений, отображаемых с использованием панели прокрутки через imscrollpanel. Параметр hparent задается вручную и описывает локальное увеличение. Функция immagbox возвращает результат в виде hbox, который представляет объекты локального увеличения.
Локальное увеличение представляется редактируемым текстовым блоком uicontrol, содержащим информацию об изображении. После введения нового значения локального увеличения, это приведет к изменениям на изображении в соответствии с этими установками. Когда изменения на изображении не будут иметь смысла, то блок локального увеличения скорректирует введенные значения.
API функции.
Блок увеличения содержит структуру в виде функции, названную API. Ее можно использовать для изменений в блоке увеличения. Для восстановления этой структуры используется функция iptgetapi.
api = iptgetapi(hbox)
Параметр API блока увеличения включает следующие функции.
Значение Описание setMagnification Установка попиксельного увеличения.
api.setMagnification(new_mag)
где new_mag представляет значение коэффициента усиления. Умножая значение параметра на 100, получим уровень увеличения в процентах. Например, выражение api.setMagnification(2) обозначает увеличение, которое можно представить в виде текстовой строки как '200%'.Пример
Рассмотрим пример добавления блока к прокручиваемому изображению. Инструмент прокрутки является стандартным инструментом системы MATLAB и реализован в окне просмотра.
hFig = figure(`Toolbar','none',...
'Menubar','none');
hIm = imshow('pears.png');
hSP = imscrollpanel(hFig,hIm);
set(hSP,'Units','normalized',...
'Position',[0 .1 1 .9])
hMagBox = immagbox(hFig,hIm);
pos = get(hMagBox,'Position');
set(hMagBox,'Position',[0 0 pos(3) pos(4)])
Для изменения увеличения изображения с использованием панели прокрутки применяется функция API с параметром setMagnification.
apiSP = iptgetapi(hSP);
apiSP.setMagnification(2)
imhist - построение гистограммы
Синтаксис:
imhist(I, n)
imhist(BW, n)
[h, cx]=imhist(I, n)
[h, cx]=imhist(BW, n)
[h, cx]=imhist(BW, map)
Описание:
Функции imhist(I, n) и imhist(BW, n) в текущем окне строят гистограммы яркостей пикселов соответственно полутонового и бинарного изображений. Гистограмма состоит из n столбцов. Значение n при вызове функции можно не указывать, в этом случае будут использованы значения по умолчанию: n=256 для полутонового изображения и n=2 для бинарного изображения. Под рисунком гистограммы выводится шкала яркостей.
Функция [h, cx]=imhist(BW, map) в текущем окне строит гистограмму индексов пикселов палитрового изображения Х. Под рисунком гистограммы выводится палитра map.
Функция [h, cx]=imhist(BW, map) возвращает вектор гистограммы h и вектор положения центров столбцов гистограммы сх на оси яркостей (для полутоновых и бинарных изображений) или на оси индексов (для палитровых изображений), что позволяет производить дальнейшую обработку гистограммы h или, например, построить огибающую гистограммы с помощью функции plot(cx, h).
Пример.
Для полутонового изображения I (рис. 1 а) строится гистограмма яркостей пикселов (рис. 1 б) и огибающая гистограммы в логарифмическом масштабе (рис. 1 в).
%Пример демонстрирует построение гистограммы изображения.
%Чтение изображения из файла.
I=imread(‘lena.tif’);
%Построение гистограммы яркостей пикселов и вывод ее на экран.
imhist(I);
%Получение гистограммы в логарифмическом масштабе
%и вывод ее на экран.
[h, cx]=imhist(I);
h=log10(h);
figure, plot(cx, h);
.gif)
а) б) в)
Рис. 1.
improfile - построение профиля
Синтаксис:
c=improfile
c=improfile(n)
c=improfile(S, xi, yi)
c=improfile(S, xi, yi, n)
[cx, cy, c]=improfile(…)
[cx, cy, c, xi, yi]=improfile(…)
[…]=improfile(XData, YData, S, xi, yi)
[…]=improfile(XData, YData, S, xi, yi, n)
[…]=improfile(…, method)
Описание:
Функция improfile вычисляет вдоль пути, состоящего из одного или нескольких отрезков прямой, значения яркости (так называемый профиль яркости) для полутоновых изображений или значения R-, G-, B-составляющих (профили цветовых составляющих) для полноцветных изображений.
Функции c=improfile и c=improfile(n) позволяют интерактивно задать путь, вдоль которого вычисляется профиль, для изображения в текущем окне. Параметр n задает количество точек, в которых вычисляются значения яркости или цвета пикселов. Эти n точек расположены вдоль пути на одинаковом расстоянии. Если параметр n не задан, то он устанавливается приблизительно равным числу пикселов, которые пересекает путь. Для полутоновых изображений выходной параметр с является одномерным массивом, в который помещаются n значений яркости, а для полноцветных изображений параметр с есть двумерный массив nx3.
Координаты отрезков, формирующих путь, задаются щелчком левой клавиши мыши. Нажатие на клавишу Backspace или Delete удаляет предыдущую заданную точку. Нажатие на правую клавишу мыши или двойной щелчок левой клавишей задает конечную точку последнего отрезка пути и завершает процесс выбора пикселов. Также завершить процесс выбора пикселов без указания последнего пиксела можно нажатием на клавишу Enter. Когда путь задан, в массив возвращается профиль.
Если параметр с при вызове функций improfile не указан, то профиль в виде графика выводится на экран в новое окно. При этом, если путь состоит из одного отрезка, то график - двумерный, координата Х которого совпадает с заданным отрезком. Если в пути более одного отрезка, то график - трехмерный, в осях X и Y которого указываются пространственные координаты изображения. Для полноцветных изображений в одних координатах одновременно выводятся 3 графика: красным, зеленым и синим цветом для R-, G-, B-составляющих соответственно.
В функциях c=improfile(S, xi, yi) и c=improfile(S, xi, yi, n) для полутонового или полноцветного изображения S путь задается явно с помощью векторов xi, yi одинаковой длины, содержащих значения координат конечных точек отрезков пути в пространственной системе координат.
Если для функций, рассмотренных выше, дополнительно определить два выходных параметра сх и су, то функции [cx, cy, c]=improfile(…) возвратят в них координаты в пространственной системе координат, в которых взяты значения яркости или цветовых составляющих. Можно также дополнительно определить еще два выходных параметра xi и yi: [cx, cy, c, xi, yi]=improfile(…), в которых будут возвращены координаты конечных точек отрезков пути.
Если требуется определить для изображения пространственную систему координат, отличную от системы координат по умолчанию, то следует воспользоваться функциями […]=improfile(XData, YData, S, xi, yi), […]=improfile(XData, YData, S, xi, yi, n), где двухэлементные векторы XData и YData определяют диапазон изменений значений по осям пространственной системы координат.
Для получения значений яркости или цвета в произвольной точке изображения используется интерполяция по значениям в соседних точках. Метод интерполяции задается во входном параметре method в виде одной из следующих строк:
‘nearest’ - использовать значение ближайшего пиксела (установлено по умолчанию, и данный параметр может быть опущен при вызове функции);
‘bilinear’ - использовать интерполяцию по билинейной поверхности;
‘bicubic’ - использовать интерполяцию по бикубической поверхности.
Пример.
Профиль яркости изображения (рис. 1 а) вдоль отрезка прямой от левого верхнего до правого нижнего угла изображения. Профиль показан на рис. 1 б.
%Пример демонстрирует построение профиля яркости изображения.
%Чтение изображения и вывод его на экран.
I=imread(‘cameraman.tif’);
imshow(I);
%Построение профиля яркости изображения вдоль прямой
%от левого верхнего до правого нижнего угла изображения.
[r c]=size(I);
figure, improfile(I, [1 c], [1 r], ‘bilinear’);

а)
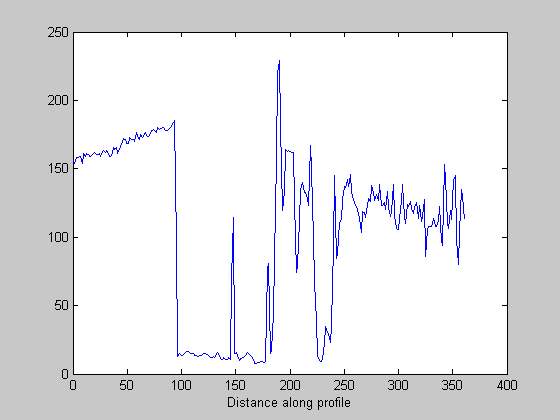
б)
Рис. 1.
impixel - определение значения пиксела
Синтаксис:
P=impixel()
P=impixel(I)
P=impixel(X, map)
P=impixel(RGB)
P=impixel(I, c, r)
P=impixel(X, map, c, r)
P=impixel(RGB, c, r)
[c, r, P]=impixel(…)
P=impixel(XData, YData, I, xi, yi)
P=impixel(XData, YData, X, map, xi, yi)
P=impixel(XData, YData, RGB, xi, yi)
[xi yi P]=impixel(XData, YData, …)
Описание:
Функция P=impixel() возвращает значения красной (R), зеленой (G) и синей (B) составляющих цвета для определенных пикселов изображения, находящегося в текущем окне. У полутоновых изображений значения составляющих совпадают. Пикселы необходимо определять интерактивно. Для выбора пиксела следует установить на него курсор и нажать на левую клавишу мыши. Таким образом можно выбрать несколько пикселов. На изображении они помечаются крестиками. Предыдущий выбранный пиксел можно удалить, если нажать на клавиши Backspace или Delete. Нажатие на правую клавишу мыши или двойной щелчок левой клавишей выбирает последний пиксел и завершает процесс выбора пикселов. Также завершить процесс выбора пикселов без указания последнего пиксела можно нажатием на клавишу Enter. Когда процесс выбора пикселов завершен, функция impixel возвращает в Р матрицу Nx3, в столбцах которой содержатся значения R-, G-, B-составляющих N выбранных пикселов.
Функции P=impixel(I), P=impixel(X, map), P=impixel(RGB) выводят на экран соответственно полутоновое изображение I, палитровое Х с палитрой map и полноцветное RGB и переходят в режим выбора пикселов. Далее работа осуществляется полностью аналогично функции impixel без параметров.
При вызове функции impixel можно явно (не интерактивно) задать координаты пикселов, значения составляющих которых требуется получить. Причем координаты могут быть заданы как в пиксельной, так и в пространственной системе координат.
Для задания координат в пиксельной системе координат для различных типов изображений следует воспользоваться одной из функций P=impixel(I, c, r), P=impixel(X, map, c, r), P=impixel(RGB, c, r), где c и r - векторы значений строк и столбцов требуемых пикселов. При этом в і-той строке матрицы Р будут находиться R-, G-, B-составляющие пиксела из c(i) столбца и r(i) строки.
Если для функций, рассмотренных выше, дополнительно определить два выходных параметра c и r, то функции [c, r, P]=impixel(…) возвратят в них пиксельные координаты выбранных пикселов.
Для задания координат в пространственной системе координат для различных типов изображений следует воспользоваться одной из функций P=impixel(XData, YData, I, xi, yi), P=impixel(XData, YData, X, map, xi, yi), P=impixel(XData, YData, RGB, xi, yi), где xi и yi - координаты, а двухэлементные векторы XData и YData определяют диапазон изменений значений по осям пространственной системы координат. Параметры XData и YData при вызове функций можно опустить. В этом случае будет использоваться пространственная система координат со значениями по осям по умолчанию.
Если для трех функций, работающих с пространственной системой координат, дополнительно определить два выходных параметра xi и yi, то функции [xi yi P]=impixel(XData, YData, …) возвратят в них значения координат выбранных пикселов.
pixval - управление режимом отображения значений пикселов
Синтаксис:
pixval on
pixval off
pixval
pixval(fig, option)
Описание:
Функция pixval on включает режим отображения значений пиксела для текущего окна. В этом режиме в нижней части окна выводятся строка, столбец и цветовые значения пиксела, над которым находится курсор мыши. Также в режиме отображения значений пиксела можно измерять евклидово расстояние между пикселами. Для этого нужно нажать на левую клавишу мыши и перемещать курсор. За курсором потянется прямая линия, а внизу окна будет отображаться расстояние между пикселом, на котором находился курсор, когда была нажата клавиша, и пикселом, на который указывает курсор. Когда клавиша мыши отпускается, то линия и значение расстояния пропадают.
Местоположение прямоугольника со значениями пиксела можно перемещать в пределах окна. Для этого нужно поместить курсор в прямоугольник, нажать левую клавишу мыши и переместить курсор в нужное место.
Функция pixval off выключает режим отображения значений пиксела для текущего окна. Также этот режим можно выключить, если нажать на кнопку в правой части прямоугольника со значениями пиксела.
Функция pixval переключает режим отображения значений пиксела, т.е. если режим был включен, то он выключается, а если был выключен, то включается.
Функция pixval(fig, option) управляет режимом отображения значений пиксела для окна с описателем fig. Параметр option может принимать значения ‘on’ (включить режим) и ’off’ (выключить режим).
Необходимо отметить, что pixval конфликтует с другими функциями, которые включают режим интерактивного использования курсора, например с функцией zoom. Одновременно можно использовать только одну функцию подобного типа.
mean2 - вычисление среднего значения элементов матрицы
Синтаксис:
m=mean2(S)
Описание:
Функция m=mean2(S) вычисляет среднее значение элементов матрицы S. Данная функция эквивалентна mean(S(:)).
std2 - вычисление среднеквадратического отклонения элементов матрицы
Синтаксис:
D=std2(S)
Описание:
Функция D=std2(S) вычисляет среднеквадратическое отклонение элементов матрицы S. Данная функция эквивалента std(S(:)).
corr2 - вычисление коэффициентов корреляции между двумя матрицами
Синтаксис:
k=corr2(A,B)
Описание:
Функция k=corr2(A,B) вычисляет коэффициент корреляции между матрицами А и В одинакового размера.
Алгоритм.
Коэффициент корреляции вычисляется с помощью следующего соотношения:
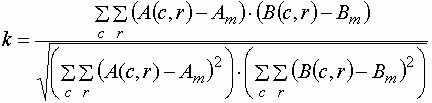 ,
,где
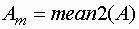 ,
, 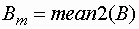 .
.xcorr2 - вычисление двумерной взаимной корреляционной функции
Синтаксис:
c=xcorr2(a, b)
c=xcorr2(a)
Описание:
Функция c=xcorr2(a, b) вычисляет двумерную взаимную корреляционную функцию с двух двумерных сигналов по выборкам, заданным в матрицах a и b.
Функция c=xcorr2(a) вычисляет автокорреляционную функцию и эквивалентна функции c=xcorr2(a, a).
imabsdiff - определение отличительных признаков двух изображений
Синтаксис:
Z=imabsdiff(X,Y)
Описание:
Функция Z=imabsdiff(X,Y) вычитает каждый элемент изображения Y из соответствующего элемента изображения X и помещает абсолютную разницу этих элементов в результирующий массив Z. Изображения X и Y должны представлять собой неразреженный числовой массив одного формата и размерности. Массив Z имеет тот же формат и размерность, что и X и Y. Когда изображения X и Y представляются массивом вещественных чисел, результирующие элементы усекаются, поскольку они превышают границы.
Когда массивы X и Y имеют формат представления данных double, то взамен этой функции можно использовать выражение abs(X-Y).
Пример:
В примере приводятся вычисления абсолютной разности между массивами формата uint8.
X=uint8([ 255 10 75; 44 225 100]);
Y=uint8([ 50 50 50; 50 50 50 ]);
Z=imabsdiff(X,Y)
Z=
205 40 25
6 175 50
Отображение абсолютных разностей между исходным и отфильтрованным изображениями.
I=imread('cameraman.tif');
J=uint8(filter2(fspecial('gaussian'), I));
K=imabsdiff(I, J);
imshow(K, []) % []=scale data automatically
imadd - суммирование двух изображений или суммирование изображения и константы
Синтаксис:
Z=imadd(X, Y)
Описание:
Функция Z=imadd(X, Y) суммирует каждый элемент массива X с соответствующим элементом массива Y и возвращает сумму соответственных элементов в результирующем массиве Z. X и Y представляют собой не разреженные числовые вещественные массивы одинакового размера и одинакового формата представления данных. Результирующий массив Z имеет тот же размер и формат представления данных, что и Y, когда Y скаляр формата double. В противном случае размерность и формат представления данных результирующего массива Z совпадает с массивом X.
Когда X и Y представляют собой массивы целых чисел и элементы результирующего массива превышают допустимый диапазон, то они усекаются или округляются.
Когда X и Y представляют собой массивы данных в формате double, тогда взамен данной функции используется выражение X+Y.
Пример:
Просуммировать два массива с форматом представления данных uint8. Применить усечение, когда значения элементов превышают 255.
X=uint8([ 255 0 75; 44 225 100]);
Y=uint8([ 50 50 50; 50 50 50 ]);
Z=imadd(X, Y)
Z=
255 50 125
94 255 150
Просуммировать два изображения и определить формат представления данных результирующего массива.
I=imread('rice.tif');
J=imread('cameraman.tif');
K=imadd(I, J, 'uint16');
imshow(K,[])
Просуммировать константу и изображение.
I=imread('rice.tif');
J=imadd(I, 50);
subplot(1, 2, 1), imshow(I)
subplot(1, 2, 2), imshow(J)
imcomplement - дополнение изображений
Синтаксис:
IM2=imcomplement(IM)
Описание:
Функция IM2=imcomplement(IM) вычисляет дополнение к изображению IM. IMдолжно быть бинарным, яркостным (полутоновым) или RGB изображением. Форматпредставления данных и размерность результирующего изображение IM2 те же, что иIM.
При дополнении бинарного изображения, нули дополняются единицами, аединицы нулями. Дополнение к полутоновому или цветному RGB изображениюнаходится так - каждое значение пиксела вычитается из максимально возможногозначения и разница представляется как значение пиксела результирующегоизображения. Таким образом темные области результирующего изображениядополняются соответственными светлыми областями исходного изображения, асветлые области результирующего изображения дополняются соответственнымитемными областями исходного изображения.
Примечание.
Когда IM является яркостным (полутоновым) или цветным (RGB) изображениемв формате double, можно взамен этой функции использовать выражение 1-IM. КогдаIM является бинарным изображением, взамен этой функции можно использоватьвыражение ~IM.
Пример.
Создать дополнение к массиву в формате uint8.
X=uint8([ 255 10 75; 44 225 100]);X2=imcomplement(X)X2=0 245 180211 30 155
На бинарном изображении 0 (черное) и 1 (белое) являются противоположнымии дополняемыми значениями.
bw=imread('text.tif');bw2=imcomplement(bw);subplot(1, 2, 1), imshow(bw)subplot(1, 2, 2), imshow(bw2)
Создать дополнение к яркостному (полутоновому) изображению.
I=imread('bonemarr.tif');J=imcomp(I);imshow(I), figure, imshow(J)
imdivide - разделение двух изображений или разделения изображения на константу
Синтаксис:
Z=imdivide(X,Y)
Описание:
Функция Z=imdivide(X, Y) делит каждый элемент массива X на соответствующий элемент в массиве Y и возвращаетрезультат в соответствующий элемент результирующего массива Z. X и Y являютсявещественными, неразреженными числовыми массивами с одинаковыми размерностями иформатами представления данных, или Y может быть представлен скаляром в форматеdouble. Размерность и формат представления данных массива Z совпадает сразмерностью и форматом представления данных массивов X и Y.
Когдаизображение X представлено массивом целых чисел, тогда элементы результирующегомассива, которые превышают допустимый диапазон (ранг целых чисел) , усекаются и округляются.
Когда X и Y представляются массивами в формате double, взамен этой функции можно использовать выражение X./Y.
Пример.
Разделить два изображения в формате uint8. Если значение дробной частибольше или равно 0.5, тогда его необходимо округлить к ближайшему целому.
X=uint8([ 255 10 75; 44 225 100]);Y=uint8([ 50 20 50; 50 50 50 ]);Z=imdivide(X,Y)Z=5 1 21 5 2
Оценка иразделение производятся на примере изображения риса (тонкоструктурноеизображение).
I=imread('rice.tif');blocks=blkproc(I, [32 32], 'min(x(:))');background=imresize(blocks, [256 256], 'bilinear');Ip=imdivide(I, background);imshow(Ip, []) % []=let imshow scale data automatically
Разделение изображения на постоянный коэффициент.
I=imread('rice.tif'); J=imdivide(I, 2);subplot(1, 2, 1), imshow(I)subplot(1, 2, 2), imshow(J)
imlincomb - вычисление линейной комбинации двух изображений
Синтаксис:
Z=imlincomb(K1, A1, K2, A2, ..., Kn, An)
Z=imlincomb(K1, A1, K2, A2, ..., Kn, An, K)
Z=imlincomb(..., output_class)
Описание:
Функция Z=imlincomb(K1, A1, K2, A2, ... , Kn, An) проводит следующие вычисления:
K1*A1+K2*A2+...+Kn*An ,
где K1, K2, …, Kn – вещественные скаляры в формате представления данных double и A1, A2, …, An – неразреженные числовые вещественные массивы той же размерности и формата. Размерность и формат представления данных результата вычислений Z совпадает с A1.
Функция Z=imlincomb(K1, A1, K2, A2, ... , Kn, An, K) проводит вычисления согласно выражению:
K1*A1+K2*A2+...+Kn*An+K ,
где функция imlincomb добавляет K (вещественный скаляр в формате представления данных double) к сумме K1, …, Kn и A1, …, An.
Функция Z=imlincomb(..., output_class) определяет формат представления данных Z. Параметр output_class имеет числовой формат.
Примечание. Когда выполняется серия арифметических операций на паре изображений, можно добиться лучшего результата если использовать функцию imlincomb. Для комбинации операций вычисления проводятся быстрее, чем при использовании функции imadd, что объясняется структурой используемого алгоритма.
Пример:
Преобразование исходного изображения с коэффициентом два.
I=imread('cameraman.tif');
J=imlincomb(2, I);
imshow(J)
Сдвиг разницы изображений на 128.
I=imread('cameraman.tif');
J=uint8(filter2(fspecial('gaussian'), I));
K=imlincomb(1, I, –1, J, 128); % K(r, c)=I(r, c)–J(r, c)+128
imshow(K)
Для иллюстрации выполнения функцией imlincomb всех арифметических операций с быстрым получением результата, сравним результат вычисления среднего двух массивов X и Y с использованием вложенных арифметических операций и с использованием функции imlincomb.
Рассмотрим значения строк и столбцов: 255 в X и 50 в Y. Функция imadd суммирует 255 и 50, и усекает результат до 255. Возвращаемое средние значение в Z(1,1) равно 128.
X=uint8([ 255 10 75; 44 225 100]);
Y=uint8([ 50 20 50; 50 50 50 ]);
Z=imdivide(imadd(X, Y), 2)
Z=
128 15 63
47 128 75
Функция imlincomb выполняет суммирование и деление в формате double с усечением к нужному диапазону результирующих данных. Средние значение в этом случае равно Z2(1, 1) is 153.
Z2=imlincomb(.5, X, .5, Y)
Z2=
153 15 63
47 138 75
Сдвиг разницы изображений на 128.
I=imread('cameraman.tif');
J=uint8(filter2(fspecial('gaussian'), I));
K=imlincomb(1, I, –1, J, 128);
% K(r, c)=I(r, c)–J(r, c)+128
imshow(K)
immultiply - умножение двух изображений или умножение изображения на константу
Синтаксис:
Z=immultiply(X, Y)
Описание:
Функция Z=immultiply(X, Y) выполняет умножение каждого элемента массива X на соответствующий ему элемент в массиве Y и помещает результат в массив Z.
Когда X и Y являются числовыми массивами вещественных чисел одинаковой размерности и формата представления данных, тогда размерность и формат результирующего массива совпадают с X. Когда изображение X представлено числовым массивом, а Y скаляром в формате double, тогда массив Z имеет ту же размерность и формат, что и X.
Когда изображение X представлено логическим, а изображение Y числовым массивом, тогда размерность и формат представления данных массива Z те же, что и в Y. Когда X числовой массив, а Y – логический, тогда размерность и формат представления данных массива Z совпадает с X.
Функция immultiply вычисляет каждый элемент Z в формате double с плавающей точкой. Когда X массив целых чисел, тогда элементы Z, превышающие допустимый диапазон, должны усекаться и округляться. Когда изображения X и Y являются массивами в формате double, тогда вместо этой функции можно использовать выражение X.*Y.
Пример:
Пример умножения изображения. Приведем также пример преобразования форматов представления данных из uint8 в uint16 перед выполнением операции умножения во избежание усечения результата.
I=imread('moon.tif');
I16=uint16(I);
J=immultiply(I16, I16);
imshow(I), figure, imshow(J)
Умножение изображения на константу:
I=imread('moon.tif');
J=immultiply(I, 0.5);
subplot(1, 2, 1), imshow(I)
subplot(1, 2, 2), imshow(J)
imsubtract - вычитание двух изображений или вычитание константы из изображения
Синтаксис:
Z=imsubtract(X,Y)
Описание:
Функция Z=imsubtract(X, Y) вычитает каждый элемент массива Y изсоответственного элемента в массиве X и возвращает результат вычитания врезультирующий массив Z. Изображения X и Y должны быть представлены неразреженнымимассивами вещественных чисел одинаковой размерности и формата представленияданных или Y должно быть представлено скаляром в формате double. Размерность иформат представления данных результирующего массива Z совпадает с массивом X.
Когда X представлено массивом целых чисел, тогда элементы результирующегомассива, которые превышают допустимый диапазон, отсекаются и округляются.
Когда изображения X и Y представлены массивами в формате double, тогдавзамен этой функции можно использовать выражение X-Y.
Пример.
Провести операцию вычитания для двух изображений в формате uint8.Отрицательные значения элементов округляются до 0.
X=uint8([ 255 10 75; 44 225 100]);Y=uint8([ 50 50 50; 50 50 50 ]);Z=imadd(X, Y)Z=205 0 250 175 50I=imread('rice.tif');blocks=blkproc(I, [32 32], 'min(x(:))');background=imresize(blocks, [256 256], 'bilinear');Ip=imsubtract(I, background);imshow(Ip, [])
Вычесть значение константы из изображения:
I=imread('rice.tif');Iq=imsubtract(I, 50);subplot(1, 2, 1), imshow(I)subplot(1, 2, 2), imshow(Iq)
regionprops - определение свойств области изображения
Синтаксис:
STATS=regionprops(L, properties)
Описание:
Функция STATS=regionprops(L, properties) измеряет набор характеристик для каждойобласти, отмеченной в матрице меток L. Положительные вещественные элементы Lсоответствуют разным областям. Например, набор элементов L равных 1соответствует 1-й области, набор элементов L равных 2 соответствует 2-й областии т.д. Результирующая переменная STATS имеет структуру в виде массива длинойmax(L(:)). Поля структурного массива обозначают различные измерения для каждогорегиона и определяют их характеристики.
Характеристикимогут перечисляться в виде строки, ячейка массива содержит строку единиц,строку 'all' или 'basic'. В таблице приведен список всех строковыххарактеристик. Характеристики могут существенно укорачиваться.
'Area' 'EquivDiameter' 'MajorAxisLength' 'BoundingBox' 'EulerNumber' 'MinorAxisLength' 'Centroid' 'Extent' 'Orientation' 'ConvexArea' 'Extrema' 'PixelIdxList' 'ConvexHull' 'FilledArea' 'PixelList' 'ConvexImage' 'FilledImage' 'Solidity' 'Eccentricity' 'Image' 'SubarrayIdx' Когдахарактеристики представлены строкой 'all', тогда вычисляются все перечисленныевыше измерения.
Когдахарактеристики не определены или определены опцией 'basic', тогда проводятсятакие измерения: 'Area', 'Centroid' и 'BoundingBox'.
Определения.
'Area' - скаляр;действительное число пикселей в обозначенной области. (Это значение можетнемного отличаться от значения, выдаваемого функцией bwarea.)
'Centroid' - векторс размерностью 1
 ndims(L);центр масс области. Отметим, что первым элементом характеристики Centroidявляется горизонтальная координата (или x-координата) центра масс, а вторымэлементом является вертикальная координата (или y-координата).
ndims(L);центр масс области. Отметим, что первым элементом характеристики Centroidявляется горизонтальная координата (или x-координата) центра масс, а вторымэлементом является вертикальная координата (или y-координата).'BoundingBox' -вектор 1
.gif) ndims(L)*2;минимальный прямоугольник, вмещающий рассматриваемую локальную область.BoundingBox является вектором [ul_corner width], где ul_corner представляется вформе [x y z ...] и описывает верхний-левый угол ограничивающегопрямоугольника; width представляется в форме [x_width y_width ...] и определяетширину вдоль каждой размерности.
ndims(L)*2;минимальный прямоугольник, вмещающий рассматриваемую локальную область.BoundingBox является вектором [ul_corner width], где ul_corner представляется вформе [x y z ...] и описывает верхний-левый угол ограничивающегопрямоугольника; width представляется в форме [x_width y_width ...] и определяетширину вдоль каждой размерности.Рисунок внизуиллюстрирует центр масс и ограничивающий прямоугольник. Область состоит избелых пикселей, зеленым отмечен ограничивающий прямоугольник и красным отмеченцентр масс.

'MajorAxisLength'- скаляр; длина (в пикселях) большой оси эллипса, который имеет тот же второй моментчто и рассматриваемая область. Эти свойства поддерживаются только для двумерныхисходных матриц меток.
'MinorAxisLength'- скаляр; длина (в пикселях) меньшей оси эллипса, который имеет тот же второй моментчто и рассматриваемая область. Эти свойства поддерживаются только для двумерныхисходных матриц меток.
'Eccentricity' -скаляр; эксцентриситет эллипса с главными моментами инерции, равными главныммоментам инерции объекта. Эксцентриситет - это отношение расстояний междуфокусом и большой осью эллипса. Это значение в диапазоне от 0 до 1. (0 и 1 длявырожденных случаев; когда эксцентриситет эллипса 0, тогда это круг, когда жеэксцентриситет эллипса 1, тогда это часть линии.) Эти свойства поддерживаютсятолько для двумерных исходных матриц меток.
'Orientation' -скаляр; угол (положение) между максимальной осью эллипса и x-осью. Эти свойстваподдерживаются только для двумерных исходных матриц меток.
Рисунок внизудемонстрирует оси и ориентацию эллипса. Левая сторона фигуры показывает наизображении область и соответствующий эллипс. Правая сторона показывает тот жеэллипс с характеристиками, которые отображены графически; сплошная синяя линияобозначает оси, красными пятнами отмечены фокусы и ориентация определяется какугол между горизонтальной пунктирной линией и главной осью.

'Image' -бинарное (логическое) изображение, размеры которого совпадают с размерамипрямоугольника, ограничивающего область; все пиксели вне региона удаляются.
'FilledImage' -бинарное (логическое) изображение, размеры которого совпадают с размерами прямоугольника, ограничивающего область (изображение объекта с "залитыми"дырами). Все отверстия в рассматриваемой области заполняются.
'FilledArea' -скаляр; полное число пикселей в FilledImage.
Этот рисунокдемонстрирует параметры 'Image' и `FilledImage'.
'ConvexHull' -матрица с размерностью p
.gif) 2;минимальный выпуклый многоугольник, который вмещает рассматриваемую область.Каждая строка матрицы содержит x- и y-координаты одной вершины многоугольника.Эти свойства поддерживаются только для двумерных исходных матриц меток.
2;минимальный выпуклый многоугольник, который вмещает рассматриваемую область.Каждая строка матрицы содержит x- и y-координаты одной вершины многоугольника.Эти свойства поддерживаются только для двумерных исходных матриц меток.'ConvexImage' -бинарное (логическое) изображение; выпуклый многоугольник со всеми наполняющимиего пикселями. (Для пикселей, лежащих на границе выпуклости, функция regionprops использует ту же логику для определения внутренних и внешнихпикселей, что и в функции roipoly. Изображение представляет собой область,ограниченную прямоугольником. Эти свойства поддерживаются только для двумернойматрицы меток.
'ConvexArea' -скаляр; число пикселей 'ConvexImage'. Эти свойства поддерживаются только длядвумерной матрицы меток.
'EulerNumber' -скаляр; равно числу объектов в области минус число отверстий. Эти свойстваподдерживаются только для двумерной матрицы меток.
'Extrema' -матрица размерностью 8
.gif) 2;экстремальные точки в области. Каждая строка матрицы описывает x- иy-координаты одной точки. Формат вектора следующий [верхний-левыйверхний-правый правый-верхний правый-нижний нижний-правый нижний-левыйлевый-нижний левый-верхний]. Эти свойства поддерживаются только для двумернойматрицы меток.
2;экстремальные точки в области. Каждая строка матрицы описывает x- иy-координаты одной точки. Формат вектора следующий [верхний-левыйверхний-правый правый-верхний правый-нижний нижний-правый нижний-левыйлевый-нижний левый-верхний]. Эти свойства поддерживаются только для двумернойматрицы меток.Рисунокиллюстрирует экстремум двух различных областей. В области слева, каждаяэкстремальная точка отдельна, в области справа, точно идентифицирована однаэкстремальная точка (например, верхняя-левая и левая-верхняя).
'EquivDiameter'- скаляр; диаметр окружности, площадь которой эквивалентна площадирассматриваемой области. Вычисляется как sqrt(4*Area/pi). Эти свойстваподдерживаются только для двумерной матрицы меток.
'Solidity' -скаляр; коэффициент выпуклости, равен отношению площади объекта к площадиограничивающего многоугольника. Вычисляется как Area/ConvexArea. Эти свойстваподдерживаются только для двумерной матрицы меток.
'Extent' -скаляр; коэффициент заполнения - равен отношению площади объекта к площадиограничивающего прямоугольника. Вычисляется как Area/(width*height). Этисвойства поддерживаются только для двумерной матрицы меток.
'PixelList' -матрица с размерностью p
.gif) ndims(L);фактическое число пикселей в области. Каждая строка матрицы имеет форму [x y z...] и определяет координаты пикселей области.
ndims(L);фактическое число пикселей в области. Каждая строка матрицы имеет форму [x y z...] и определяет координаты пикселей области.Требования к исходным данным.
Исходная матрицаметок L может иметь любой числовой формат представления данных.
Примечание.
Элементы массиваразделяются запятой, что очень удобно при работе с результатами regionprops.Например, для полей, содержащих скаляр, можно использовать синтаксис созданиявектора, содержащего значения полей для каждой области изображения.
Например, когдаполя массива заполняют некоторые статистические данные, тогда это эквивалентноследующему выражению.
stats(1).Area, stats(2).Area, ..., stats(end).Area
и
stats.Area
Поэтому, можно создать вектор, содержащий данные всех регионов изображения.
stats=regionprops(L, 'Area');allArea=[stats.Area];allArea является вектором, длина которого аналогична длине массива статистических данных.
Функция ismember пригодна для конъюнкции с функцией regionprops при выборе областей на основенекоторых критериев. Например, эта команда создает бинарное изображение,содержащее только те области в text.tif, чья площадь больше чем 80.
idx=find([stats.Area] > 80);BW2=ismember(L, idx);Такие преобразования не требуют больших затрат на вычисление и зависят от числа областей в L:'ConvexHull' 'ConvexImage' 'ConvexArea' 'FilledImage'
Пример.
BW=imread('text.tif');L=bwlabel(BW);stats=regionprops(L, 'all');stats(23)ans=Area: 89Centroid: [95.6742 192.9775]BoundingBox: [87.5000 184.5000 16 15]MajorAxisLength: 19.9127MinorAxisLength: 14.2953Eccentricity: 0.6961Orientation: 9.0845ConvexHull: [28x2 double]ConvexImage: [15x16 uint8 ]ConvexArea: 205Image: [15x16 uint8 ]FilledImage: [15x16 uint8 ]FilledArea: 122EulerNumber: 0Extrema: [ 8x2 double]EquivDiameter: 10.6451Solidity: 0.4341Extent: 0.3708PixelList: [89x2 double]
cpstruct2pairs - конвертирование cpstruct в наиболее важные контрольные точки
Синтаксис:
[input_points, base_points]=cpstruct2pairs(CPSTRUCT)
Описание:
Функция [input_points, base_points]=cpstruct2pairs(CPSTRUCT) на основе обработки CPSTRUCT возвращает массив координат пар контрольных точек в input_points и base_points. Функция cpstruct2pairs устраняет прогнозированные точки.
Пример:
Запустить Control Point Selection Tool, cpselect.
cpselect('lily.tif','flowers.tif')
Использование функции cpselect обозначает пики контрольных точек на изображении. Выбор Save To Workspace с File menu запоминает точки рабочего пространства. С помощью команды Save, можно создать файловую структуру со всеми контрольными исходными и основными точками.
С помощью команды cpstruct2pairs извлекаются исходные и основные точки с CPSTRUCT.
[input_points,base_points]=cpstruct2pairs(cpstruct).
cp2tform - вывод пространственных преобразований между парой контрольных точек
Синтаксис:
TFORM=cp2tform(input_points, base_points, transformtype)
TFORM=cp2tform(CPSTRUCT, transformtype)
TFORM=cp2tform(input_points, base_points, transformtype, parameter)
TFORM=cp2tform(CPSTRUCT, transformtype, parameter)
[TFORM, input_points, base_points]=cp2tform(CPSTRUCT, ...)
[TFORM, input_points, base_points, input_points_bad, base_points_bad]=cp2tform(..., 'piecewise linear')
Описание:
Функция TFORM=cp2tform(input_points, base_points, transformtype) выбирает пары контрольных точек и использует их для вывода пространственных преобразований изображения. Функция возвращает TFORM структуру, которая содержит в себе пространственные преобразования. input_points представляет собой матрицу формата double и размерности m2, содержащую координаты x и y контрольных точек изображения, которое будет подвержено преобразованию. base_points также является массивом формата double с размерностью m2, который содержит координаты x и y контрольных точек на основном изображении. Параметр transformtype определяет тип проводимых преобразований. Для более детальной информации о типах, смотрите “Типы преобразований” (Transform Type).
Функция TFORM=cp2tform(CPSTRUCT, transformtype) обрабатывает CPSTRUCT структуру, которая содержит массивы контрольных точек исходного и основного изображений. CPSTRUCT создается в Control Point Selection Tool, cpselect.
Функция [TFORM, input_points, base_points]=cp2tform(CPSTRUCT, ...) возвращает контрольные точки, которые используются в input_points и base_points. Некоторые из этих точек могут не использоваться. Для более детальной информации см. cpstruct2pairs.
Типы преобразований:
Параметр transformtype определяет тип пространственных преобразований. В таблице приведено все типы преобразований, которые поддерживаются функцией cp2tform. В таблице указывается минимальное число пар контрольных точек, которые необходимы при выборе конкретного типа преобразований. Для преобразований, указанных как 'lwm' и 'polynomial' возможно применение дополнительных оптимизирующих параметров. Для более подробной информации см. описание синтаксиса.
Типы преобразований Описание Минимум контрольных точек Примеры 'linear conformal' Это преобразование используется, когда форму исходного изображения нужно оставить без изменений, за исключением частей изображения искаженных некоторой комбинацией преобразований или вращением. Прямые линии остаются прямыми, а параллельные – параллельными. 2 пары 
'affine' Это преобразование используется, когда форму исходного изображения нужно представить срезанной. Прямые линии остаются прямыми, а параллельные – параллельными, прямоугольник превращается в параллелограмм. 3 пары 
'projective' Это преобразование используется, когда изображение необходимо наклонить. Прямые линии остаются прямыми, а параллельные сходятся в перспективе. 4 пары 
'polynomial' Это преобразование используется, когда объект изображения необходимо искривить. Чем выше полиномиальная степень, тем более искривленным получается результирующее изображение. 6 пар (степень 2)
10 пар (степень 3)
16 пар (степень 4)
'piecewise linear' Это преобразование используется, когда к различным частям исходного изображения применяются различные преобразования. 4 пары 
'lwm' Это преобразование (взвешенное локальное средние) используется, когда необходимо искривить различные локальные участки. 6 пар (12 пар рекомендуется) 
Когда параметр transformtype является 'linear conformal', 'affine', 'projective' или 'polynomial', а input_points и base_points (или CPSTRUCT) имеют минимальное число контрольных точек необходимых для специальных преобразований, то функция cp2tform однозначно определяет коэффициенты. Для более детальной информации см. mldivide.
TFORM=cp2tform(input_points, base_points, 'polynomial', ORDER);
TFORM=cp2tform(CPSTRUCT, 'polynomial', order) .
Когда в типе преобразований указан параметр 'polynomial', можно использовать оптимальное определение полинома. Степень может быть скалярной величиной – 2, 3 или 4. Если не указывать степень, то по умолчанию она равна 3.
TFORM=cp2tform(input_points, base_points, 'lwm', N);
TFORM=cp2tform(CPSTRUCT, 'lwm',N) .
Когда в типе преобразований указан параметр 'lwm', можно оптимально определить число точек N, используемых для каждого полинома. Радиус действия значительно увеличивается, если контрольные точки используют этот полином. N соседних точек используется полиномом степени 2 для каждой пары контрольных точек. Если не указать число N, то по умолчанию оно равно 12. N может быть меньше 6, что уменьшает возможность генерации неверного полинома.
[TFORM,input_points,base_points,input_points_bad,base_points_bad]=
cp2tform(input_points,base_points,'piecewise linear');
[TFORM,input_points,base_points,input_points_bad,base_points_bad]=
cp2tform(CPSTRUCT,'piecewise linear') .
Когда в типе преобразований указан параметр 'lwm', то функция cp2tform возвращает оптимальные контрольные точки, которые используются в input_points и base_points, а также возвращает два массива input_points_bad и base_points_bad, которые содержат устраненные контрольные точки.
Алгоритм:
Функция cp2tform использует следующие основные процедуры:
1. Использование пар контрольных точек для вывода пространственных преобразований.
2. Возвращение TFORM структуры, содержащей пространственные преобразования.
Процедуры изменяются в зависимости от типа преобразований “transformtype”.
Линейные конформные преобразования.
Линейные конформные преобразования содержат в себе вращение, масштабирование и перемещение. Форма и углы сохраняются. Параллельные линии остаются параллельными. Прямые линии остаются прямыми.
sc=scale*cos(angle);
ss=scale*sin(angle);
[u v]=[x y 1]*[ sc –ss ss sc tx ty] .
Для sc, ss, tx, ty найдем:
t_lc=cp2tform(input_points, base_points, 'linear conformal') .
Коэффициенты инверсного представления хранятся в t_lc.tdata.Tinv. Линейные конформные преобразования являются частным случаем аффинных преобразований t_lc.forward_fcn в @affine_fwd и t_lc.inverse_fcn в @affine_inv. При минимальных двух парах контрольных точек необходимо найти четыре неизвестных коэффициента.
Аффинные преобразования.
В аффинных преобразованиях, размерности x и y независимо масштабируются и далее с ними проводятся последующие преобразования. Параллельные линии остаются параллельными. Прямые линии остаются прямыми. Линейные конформные преобразования являются частным случаем аффинных преобразований.
Для аффинных преобразований:
[u v]=[x y 1]*Tinv .
Tinv является матрицей размерности 32 . Найти для 6 элементов массив Tinv.
t_affine=cp2tform(input_points, base_points, 'affine') .
Коэффициенты инверсных преобразований хранятся в t_affine.tdata.Tinv. Для минимальных 3 пар контрольных точек необходимо найти 6 неизвестных коэффициентов.
Преобразование проекций (Projective).
При проекционных преобразованиях четырехугольник представляется четырехугольником. Прямые линии преобразуются в прямые. Аффинные преобразования являются подмножеством проекционных преобразований.
Для проекционных преобразований:
[up vp wp]=[x y w]*Tinv ,
где
u=up/wp;
v=vp/wp .
Tinv является матрицей с размерностью 33.
Исходные данные
Tinv=[ A D G;B E H;C F I ];
u=(Ax+By+C)/(Gx+Hy+I);
v=(Dx+Ey+F)/(Gx+Hy+I) .
Найти для 9 элементов Tinv.
t_proj=cp2tform(input_points, base_points, 'projective') .
Коэффициенты инверсных преобразований содержатся в t_proj.tdata.Tinv. При минимальных 4 парах контрольных точек находятся 9 неизвестных коэффициентов.
Полиномиальные преобразования (Polynomial).
При полиномиальных преобразованиях, полиномиальная функция от x и y является детерминированной.
Второй порядок полинома
Для полиномиальных преобразований второго порядка:
[u v]=[1 x y x*y x^2 y^2]*Tinv .
u и v являются полиномами второго порядка от x и y. Каждый полином второго порядка имеет шесть термов. При определении всех коэффициентов размерность Tinv равна 62.
t_poly_ord2=cp2tform(input_points, base_points, 'polynomial') .
Коэффициенты инверсных преобразований хранятся в t_poly_ord2.tdata. Для минимальных 6 пар контрольных точек необходимо определить 12 неизвестных коэффициентов.
Третий порядок полинома
Для полиномиальных преобразований третьего порядка:
[u v]=[1 x y x*y x^2 y^2 y*x^2 x*y^2 x^3 y^3]*Tinv .
u и v являются полиномами третьего порядка от x и y. Каждый полином третьего порядка имеет десять термов. При определении всех коэффициентов размерность Tinv равна 102.
t_poly_ord3=cp2tform(input_points, base_points, 'polynomial',3) .
Коэффициенты инверсных преобразований хранятся в t_poly_ord3.tdata. Для минимальных 10 пар контрольных точек необходимо определить 20 неизвестных коэффициентов.
Четвертый порядок полинома
Для полиномиальных преобразований четвертого порядка:
[u v]=[1 x y x*y x^2 y^2 y*x^2 x*y^2 x^3 y^3]*Tinv .
u и v являются полиномами четвертого порядка от x и y. Каждый полином четвертого порядка имеет пятнадцать термов. При определении всех коэффициентов размерность Tinv равна 152.
t_poly_ord4=cp2tform(input_points, base_points, 'polynomial',4) .
Коэффициенты инверсных преобразований хранятся в t_poly_ord4.tdata. Для минимальных 15 пар контрольных точек необходимо определить 30 неизвестных коэффициентов.
Кусочно–линейные преобразования.
При кусочно–линейных преобразованиях линейные аффинные преобразования применяются отдельно к каждому участку изображения [1]. Для этого необходимо:
1. Найти триангуляционную свертку для основных контрольных точек.
2. Использовать три вертикали для каждой триангуляции и вывода аффинных преобразований основных исходных координат.
Локальное взвешенное средние.
Для каждой контрольной точки в in base_points необходимо:
1.Найти N близких контрольных точек.
2.Использовать эти N точек и соответствующие им точки в input_points для вывода полинома второго порядка.
3.Вычислить радиус воздействия этого полинома как расстояние от центра контрольной точки к самой дальней точке, использовав выведенный полином (используя base_points) [2].
Пример:
I=checkerboard;
J=imrotate(I, 30);
base_points=[11 11; 41 71];
input_points=[14 44; 70 81];
cpselect(J, I, input_points, base_points);
t=cp2tform(input_points, base_points, 'linear conformal') .
Для обратного получения углов и масштабов:
ss=t.tdata.Tinv(2,1); %ss=scale*sin(angle);
sc=t.tdata.Tinv(1,1); % sc=scale*cos(angle);
angle=atan2(ss,sc)*180/pi;
scale=sqrt(ss*ss+sc*sc) .
cpcorr - определение согласованных контрольных точек с использованием кросс-корреляции
Синтаксис:
input_points=cpcorr(input_points_in, base_points_in, input, base)
Описание:
Функция input_points=cpcorr(input_points_in, base_points_in, input, base) использует нормированную кросс-корреляцию для установки каждой пары контрольных точек, обозначив их как input_points_in и base_points_in. Матрица input_points_in с размерностью M
 2 и форматом представления данных double содержит координаты контрольных точек на исходном изображении. Матрица input_points_in с размерностью M
2 и форматом представления данных double содержит координаты контрольных точек на исходном изображении. Матрица input_points_in с размерностью M.gif) 2 и форматом представления данных double содержит координаты контрольных точек на основном (базисном) изображении.
2 и форматом представления данных double содержит координаты контрольных точек на основном (базисном) изображении.Функция cpcorr возвращает установленные контрольные точки в матрице input_points, которая по размерности совпадает с матрицей input_points_in и имеет формат представления данных double.
Функция cpcorr имеет возможность изменять позиции контрольных точек. Установка координат является точной для одной десятой части пикселов. Функция cpcorr создает подэлементы изображения только на основе изображения и очень приблизительно выбирает контрольные точки.
Для повышения эффективности функции cpcorr исходное и основное изображения должны иметь одинаковую размерность.
Функция cpcorr не может устанавливать точки, когда выполняется одно из следующих условий:
1) точки находятся очень близко к краю обоих изображений;
2) локальная окрестность содержит в себе элементы со значением Inf или NaN;
3) среднеквадратическое отклонение значений элементов локальной окрестности равно нулю;
4) значения элементов локальной окрестности плохо коррелированны.
Требования к исходным данным:
Исходное и основное изображения должны иметь формат представления данных logical, uint8, uint16 или double. Пары контрольных точек должны быть класса double.
Алгоритм:
Функция cpcorr использует следующие основные процедуры.
Для каждой пары контрольных точек необходимо:
1.Определить окрестность 11
 11 для исходных контрольных точек и окрестность 21
11 для исходных контрольных точек и окрестность 21.gif) 21 для основных контрольных точек.
21 для основных контрольных точек.2.Вычислить нормированную кросс-корреляцию для этих окрестностей.
3.Найти абсолютный максимум матрицы кросс-корреляции.
4.Использовать расположение максимумов для установки координат исходных контрольных точек.
Пример:
В примере рассмотрено использование функции cpcorr для поиска согласованных контрольных точек на изображении. Записываются эти параметры в матрицы input_points matrix и the input_points_adj соответственно.
input=imread('lily.tif');
base=imread('flowers.tif');
input_points=[127 93; 74 59];
base_points=[323 195; 269 161];
input_points_adj = cpcorr(input_points,base_points,...
input(:,:,1),base(:,:,1))
input_points_adj=
126.0000 94.0000
72.1000 60.0000
cpselect - инструмент выбора контрольных точек
Синтаксис:
cpselect(input, base)
cpselect(input, base, CPSTRUCT_IN )
cpselect(input, base, XYINPUT_IN, XYBASE_IN)
H=cpselect(input, base, ...)
Описание:
Функция cpselect(input, base) запускает пакет Control Point Selection Tool, графический интерфейс которого дает возможность выбора контрольных точек на двух похожих изображениях. Исходным является изображение, которое необходимо трансформировать и преобразовать в координатную систему основного изображения. Исходные или основные данные могут быть представлены в виде изображения или последовательности цифр, взятых из файла, содержащего полутоновое изображение. Пакет Control Point Selection Tool возвращает контрольные точки в виде структуры CPSTRUCT.
Функция cpselect(input, base, CPSTRUCT_IN) запускает cpselect и помещает набор контрольных точек в CPSTRUCT_IN. Этот синтаксис позволяет перезапускать функцию cpselect с состояния предварительного запоминания контрольных точек в CPSTRUCT_IN.
Функция cpselect(input, base, xyinput_in, xybase_in) запускает cpselect с наборами пар контрольных точек. Данные xyinput_in и xybase_in являются матрицами размерности m2, которые содержат исходные и основные координаты соответственно.
Функция H=cpselect(input, base, ...) предоставляет ручное управление пакетом с помощью параметра H. Для того, чтобы закрыть пакет с командной строки нужно использовать dispose(H) или H.dispose синтаксис.
Требования к исходным данным.
Исходные изображения должны иметь формат представления данных uint8, uint16, double или logical.
Алгоритм:
Функция cpselect использует следующие основные процедуры для прогноза контрольных точек:
1. Определение всех действительных контрольных точек.
2. Определение пространственных преобразований между исходными и основными контрольными точками с использованием метода который зависит от числа пар контрольных точек следующим образом:
2 пары Линейные конформные преобразования 3 пары Аффинные преобразования 4 пары Преобразование проекций 3. Использование пространственных преобразований для новых точек, сгенерированных на основе предсказанных.
4. Отображение предсказанных точек.
Пример:
Запускаем пакет с запоминанием изображений.
aerial=imread('westconcordaerial.png');
cpselect(aerial(:, :, 1), 'westconcordorthophoto.png')
Запускаем пакет с рабочим пространством изображений и точек.
I=checkerboard;
J=imrotate(I, 30);
base_points=[11 11; 41 71];
input_points=[14 44; 70 81];
cpselect(J, I, input_points, base_points);
normxcorr2 - нормализация двумерной кросс-корреляции
Синтаксис:
C=normxcorr2(TEMPLATE, A)
Описание:
Функция C=normxcorr2(TEMPLATE, A) вычисляет нормированную взаимную корреляцию матриц TEMPLATE и A. Матрица A должна быть больше матрицы TEMPLATE. Значения TEMPLATE не должны быть все одинаковыми. Результирующая матрица C содержит корреляционные коэффициенты, которые представляют собой числа в диапазоне от -1.0 до 1.0.
Требования к исходным данным.
Исходные матрицы должны быть представлены в формате uint8, uint16 или double.
Алгоритм.
Функция normxcorr2 использует следующие основные процедуры:
-
Вычисление взаимной корреляции в пространственной или частотной областях, что зависит от размеров изображения.
-
Вычисление локальных сумм на стадии предобработки. [1]
-
Использование локальных сумм для нормализации взаимной корреляции и получения корреляционных коэффициентов. [2]
-
-
Пример.
T=.2*ones(11); % Формирование светло-серой области на фоне темно-серого фона.T(6, 3:9)=.6;T(3:9, 6)=.6;BW=T>0.5; % Формирование белого и темного фона.imshow(BW)figure, imshow(T)% Формирование нового изображения.T_offset=.2*ones(21);offset=[3 5];T_offset((1:size(T, 1))+offset(1), (1:size(T, 2))+offset(2))=T;figure, imshow(T_offset)% Взаимная корреляция массивов BW и T_offsetcc=normxcorr2(BW, T_offset);[max_cc, imax]=max(abs(cc(:)));[ypeak, xpeak]=ind2sub(size(cc), imax(1));corr_offset=[(ypeak-size(T, 1)) (xpeak-size(T, 2)) ];isequal(corr_offset, offset)
deconvblind - улучшение изображений с использованием обратной свертки
Синтаксис:
[J, PSF]=deconvblind(I, INITPSF)
[J, PSF]=deconvblind(I, INITPSF, NUMIT)
[J, PSF]=deconvblind(I, INITPSF, NUMIT, DAMPAR)
[J, PSF]=deconvblind(I, INITPSF, NUMIT, DAMPAR, WEIGHT)
[J, PSF]=deconvblind(I, INITPSF, NUMIT, DAMPAR, WEIGHT, READOUT)
[J, PSF]=deconvblind(... , FUN, P1, P2, ... , PN)
Описание:
Функция [J, PSF]=deconvblind(I, INITPSF) вычисляет обратное преобразование свертки для изображения I, используя алгоритм максимума вероятности, и возвращает восстановленное изображение J и восстановленную функцию протяженности PSF. Исходные массивы I, PSF и INITPSF могут быть числовыми массивами или массивами в виде ячеек. Восстановленная функция протяженности PSF является положительным массивом, который имеет такую же размерность как INITPSF.
Для улучшения восстановления, нужно оптимизировать некоторые параметры свертки, которые будут описаны ниже.
Функция [J, PSF]=deconvblind(I, INITPSF, NUMIT) определяет число итераций (по умолчанию 10).
Функция [J, PSF]=deconvblind(I, INITPSF, NUMIT, DAMPAR) определяет порог отклонения результирующего изображения от исходного I (в терминах среднеквадратического отклонения пуассоновского шума). Итерации прекращаются для пикселов, которые отклоняются на величину, не более чем DAMPAR, от их начального значения. Это приводит к уменьшению генерации шума на таких изображениях, и сохранению мелких деталей.
Функция [J, PSF]=deconvblind(I, INITPSF, NUMIT, DAMPAR, WEIGHT) определяет пикселы исходного изображения I, которые будут подвержены восстановлению. По умолчанию, параметр WEIGHT является единичным массивом, размеры которого совпадают с размерами исходного изображения. Также есть возможность определять элементы массива WEIGHT, значение которых должно быть в пределах между 0 и 1. Значение элементов массива WEIGHT определяется пикселами, которые находятся на позициях соответствующих описанию. Например, исключить из рассмотрения элементы, соответственные пикселы которых в массиве WEIGHT, равны 0. Существует возможность улучшить весовые значения, задавая каждому пикселу соответственно корректирующие значения.
В команде [J, PSF]=deconvblind(I, INITPSF, NUMIT, DAMPAR, WEIGHT, READOUT) параметр READOUT является массивом (или значением), которое соответствует добавленному шуму (фон, передний план) и может быть одним из вариантов шума, вносимого телевизионной камерой. READOUT может иметь размерность исходного изображения.
В функции [J, PSF]=deconvblind(..., FUN, P1, P2, ..., PN) FUN является функцией, описывающей дополнительные ограничения для PSF.
Функция FUN вызывается в конце каждой итерации и должна принимать значение PSF в качестве первого аргумента, также может принимать дополнительные параметры P1, P2,..., PN. Функция может возвратить один аргумент PSF, размеры которого совпадают с размерами исходного параметра PSF и который удовлетворяет дополнительным условиям.
Обратное преобразование свертки.
Сначала выполняется свертка с произвольными параметрами. Далее особенности выходного изображения I будут использоваться при выборе параметров PSF, INITPSF. Функция свертки возвращает результирующее изображение J и восстановленные точки функции протяженности PSF могут использоваться в следующих операциях свертки. Выходной массив J содержит четыре элемента:
J{1} – содержит массив I, исходное изображение;
J{2} – содержит результат предпоследний итерации;
J{3} – содержит результат последний итерации;
J{4} – массив, который генерирует итерационный алгоритм.
Требования к исходным данным.
Массив I должен иметь формат представления данных uint8, uint16 или double. Аргументы DAMPAR и READOUT имеют тот же формат представления данных что и исходное изображение. Другие параметры должны иметь формат представления данных double. Результирующее изображение J или первый массив результирующего массива имеют тот же формат представления данных, что и исходное изображение.
Пример:
I=checkerboard(8);
PSF=fspecial('gaussian', 7, 10);
V=.0001;
BlurredNoisy=imnoise(imfilter(I, PSF), 'gaussian', 0, V);
WT=zeros(size(I));
WT(5:end-4, 5:end-4)=1;
INITPSF=ones(size(PSF));
FUN=inline('PSF+P1', 'PSF', 'P1');
[J P]=deconvblind(BlurredNoisy, INITPSF, 20, 10*sqrt(V), WT, FUN, 0);
subplot(221); imshow(BlurredNoisy);
title('A=Blurred and Noisy');
subplot(222); imshow(PSF, []);
title('True PSF');
subplot(223); imshow(J);
title('Deblured Image');
subplot(224);imshow(P,[]);
title('Recovered PSF');
deconvlucy - улучшение изображений с использованием метода Лаки-Ричардсона
Синтаксис:
J=deconvlucy(I, PSF)
J=deconvlucy(I, PSF, NUMIT)
J=deconvlucy(I, PSF, NUMIT, DAMPAR)
J=deconvlucy(I, PSF, NUMIT, DAMPAR, READOUT)
J=deconvlucy(I, PSF, NUMIT, DAMPAR, READOUT, WEIGHT)
deconvlucy(I, PSF, NUMIT, DAMPAR, READOUT, WEIGHT, SUBSMPL)
Описание:
Функция J=deconvlucy(I, PSF) восстанавливает изображение I, размытое сверткой с функцией протяженности точки PSF и возможным добавлением шума. Алгоритм основывается на максимизации вероятностных характеристик результирующего изображения J, полученного на основании исходного изображения I. Исходный массив I должен быть числовым массивом.
Улучшение восстановления возможно на основе оптимизации параметров свертки. Пустой вектор [] используется как место для хранения неопределенных промежуточных параметров.
Функция J=deconvlucy(I, PSF, NUMIT) определяет число итераций выполнения функции свертки. Если это значение не определено, то по умолчанию оно равно 10.
Функция J=deconvlucy(I, PSF, NUMIT, DAMPAR) определяет порог отклонения результирующего изображения от изображения I (в терминах стандартного отклонения пуассоновского шума). Итерации прекращаются для пикселов, значения которых отклоняются от исходных значений на величину больше DAMPAR. Такое подавление генерации шума в этих пикселах позволяет сохранить детальность изображений. По умолчанию это значение равно 0.
Функция J=deconvlucy(I, PSF, NUMIT, DAMPAR, WEIGHT) определяет весовое значение каждого пиксела, на основании чего можно говорить о качестве камеры. Испорченные пикселы удаляются из растра путем присвоения им нулевого веса. Вместо этого пиксела берется соседний пиксел с скорректированным весом. По умолчанию размерность массива J совпадает с размерностью исходного изображения I.
Функция J=deconvlucy(I, PSF, NUMIT, DAMPAR, WEIGHT, READOUT) определяет значение соответственного добавленного шума (например, фон или шум переднего плана), который может являться шумом считывания камеры. Параметр READOUT может быть представлен в виде изображения. По умолчанию его значение равно 0.
Восстанавливающая свертка.
Если исходное изображение I представляет собой массив пикселов, то результат представляет собой массив J с размерами 1х4, где
J{1} содержит массив I, исходное изображение;
J{2} содержит результат предпоследний итерации;
J{3} содержит результат последний итерации;
J{4} массив, который генерируется итерационным алгоритмом.
Исходные данные представляются одним числовым массивом (размытое изображение) или четырьмя числовыми массивам, когда там представлены и результаты предыдущих сверток.
Требования к исходным данным.
Исходный массив I должен иметь формат представления данных uint8, uint16 или double. Параметры DAMPAR и READOUT имеют формат представления данных тот же, что и исходное изображение. Другие исходные данные имеют формат представления данных double. Формат представления данных результирующего изображения совпадает с форматом исходного изображения.
Пример:
I=checkerboard(8);
PSF=fspecial('gaussian', 7, 10);
V=.0001;
BlurredNoisy=imnoise(imfilter(I, PSF), 'gaussian', 0, V);
WT=zeros(size(I));
WT(5:end–4,5:end–4)=1;
J1=deconvlucy(BlurredNoisy, PSF);
J2=deconvlucy(BlurredNoisy, PSF, 20, sqrt(V));
J3=deconvlucy(BlurredNoisy, PSF, 20, sqrt(V), [], WT);
subplot(221); imshow(BlurredNoisy);
title('A=Blurred and Noisy');
subplot(222); imshow(J1);
title('deconvlucy(A, PSF)');
subplot(223); imshow(J2);
title('deconvlucy(A,PSF,NI,DP)');
subplot(224); imshow(J3);
title('deconvlucy(A, PSF, NI, DP, [], WT)');
deconvreg - улучшение изображений с использованием регуляризационной фильтрации
Синтаксис:
J=deconvreg(I, PSF)
J=deconvreg(I, PSF, NOISEPOWER)
J=deconvreg(I, PSF, NOISEPOWER, LRANGE)
J=deconvreg(I, PSF, NOISEPOWER, LRANGE, REGOP)
[J, LAGRA]=deconvreg(I, PSF, ...)
Описание:
Функция J=deconvreg(I, PSF) восстанавливает изображение I с помощью свертки и функции протяженности PSF с возможным прибавлением шума. Алгоритм является оптимальным в сенсе минимальной квадратической ошибки между расчетным и действительным изображением при его сглаживании.
В функции J=deconvreg(I, PSF, NOISEPOWER) NOISEPOWER является параметром добавленного шума. По умолчанию это значение равно 0.
В функции J=deconvreg(I, PSF, NOISEPOWER, LRANGE) параметр LRANGE является вектором, задающий ранг для поиска оптимального разрешения. Алгоритм ищет оптимальный коэффициент Лагранжа LAGRA в пределах ранга LRANGE. Когда параметр LRANGE скаляр, алгоритм присваивает параметру LAGRA значение равное LRANGE. По умолчанию ранг находится в пределах [1e-9 и 1e9].
В функции J=deconvreg(I, PSF, NOISEPOWER, LRANGE, REGOP) параметр REGOP является регуляризационным оператором, который описывает свертку. По умолчанию регуляризационный оператор является лапласианом, который подвергает изображение операции усреднения. Размерность массива REGOP не должна превышать размерность изображения.
Результирующие значение функции [J, LAGRA]=deconvreg(I, PSF, ...) в виде коэффициента Лагранжа, прибавляется к восстановленному изображению J.
Требования к исходным данным.
Изображение I должно иметь формат представления данных uint8, uint16 или double. Другие параметры должны иметь формат представления данных double. Массив J имеет тот же формат представления данных что и I.
Пример:
I=checkerboard(8);
PSF=fspecial('gaussian', 7, 10);
V=.01;
BlurredNoisy=imnoise(imfilter(I, PSF), 'gaussian', 0, V);
NOISEPOWER=V*prod(size(I));
[J LAGRA]=deconvreg(BlurredNoisy, PSF, NOISEPOWER);
subplot(221); imshow(BlurredNoisy);
title('A=Blurred and Noisy');
subplot(222); imshow(J);
title('[J LAGRA]=deconvreg(A, PSF, NP)');
subplot(223); imshow(deconvreg(BlurredNoisy, PSF, [], LAGRA/10));
title('deconvreg(A, PSF, [], 0.1*LAGRA)');
subplot(224); imshow(deconvreg(BlurredNoisy, PSF, [], LAGRA*10));
title('deconvreg(A, PSF, [], 10*LAGRA)');
deconvwnr - улучшение изображений с использованием фильтра Винера
Синтаксис:
J=deconvwnr(I, PSF)
J=deconvwnr(I, PSF, NSR)
J=deconvwnr(I, PSF, NCORR, ICORR)
Описание:
Функция J=deconvwnr(I, PSF) восстанавливает изображение I, которое было испорчено сверткой с функцией протяженности точки PSF и возможным дополнением шума. Алгоритм оптимизируется с точки зрения наименьшей среднеквадратической ошибки между вычисляемым и исходным изображениями и использует матрицу корреляции изображения и шума. При отсутствии шумовой составляющей, фильтр Винера превращается в идеальный инверсный фильтр.
В функции J=deconvwnr(I, PSF, NSR) параметр NSR указывает на соотношение сигнал/шум. Величина NSR является скаляром или массивом, размерность которого такая же как I. По умолчанию это значение равно 0.
В функции J=deconvwnr(I, PSF, NCORR, ICORR) параметры NCORR и ICORR являются автокорреляционными функциями шума и исходного изображения соответственно. Размерность NCORR и ICORR не должна превышать размерность исходного изображения. Векторы NCORR или ICORR представляют автокорреляционную функцию с такой же размерностью как и PSF. Если PSF является массивом, одномерная автокорреляционная функция экстраполируется суммированием всех неединичных размерностей PSF.
Требования к исходным данным.
Исходный массив I должен иметь формат представления данных uint8, uint16 или double. Другие исходные данные должны иметь формат представления данных double. Формат представления данных массива J такой же как и массива I.
Пример:
I=checkerboard(8);
noise=0.1*randn(size(I));
PSF=fspecial('motion', 21, 11);
Blurred=imfilter(I, PSF, 'circular');
BlurredNoisy=im2uint8(Blurred+noise);
NSR=sum(noise(:).^2)/sum(I(:).^2);% шумовая составляющая
NP=abs(fftn(noise)).^2;
NPOW=sum(NP(:))/prod(size(noise));
NCORR=fftshift(real(ifftn(NP)));% центрированная автокорреляционная функция шума
IP=abs(fftn(I)).^2;
IPOW=sum(IP(:))/prod(size(I));
ICORR=fftshift(real(ifftn(IP)));% центрированная автокорреляционная функция изображения
ICORR1=ICORR(:, ceil(size(I, 1)/2));
NSR=NPOW/IPOW;
subplot(221); imshow(BlurredNoisy, []);
title('A=Blurred and Noisy');
subplot(222); imshow(deconvwnr(BlurredNoisy, PSF, NSR), []);
title('deconvwnr(A, PSF, NSR)');
subplot(223); imshow(deconvwnr(BlurredNoisy, PSF, NCORR, ICORR), []);
title('deconvwnr(A, PSF, NCORR, ICORR)');
subplot(224); imshow(deconvwnr(BlurredNoisy, PSF, NPOW, ICORR1), []);
title('deconvwnr(A, PSF, NPOW, ICORR_1_D)');
ippl - проверка наличия библиотеки функций (Intel Performance Primitives Library (IPPL))
Синтаксис:
TF=ippl
[TF B]=ippl
Описание:
Библиотека функций (IPPL) содержит коллекцию основных функций (методов), которые используются при обработке сигналов и изображений. В основу большинства этих методов положены принципы параллельной обработки, а также другие современные технологии. Эта концепция является основой архитектуры процессоров Intel. Библиотека методов IPPL используется также некоторыми функциями Image Processing Toolbox для ускорения вычислений.
Выражение TF=ippl возвращает единицу 1 (true), когда библиотека методов IPPL является доступной и 0 (false) в других случаях.
Функция [TF B]=ippl возвращает массив B. Каждая строка B содержит описание специальных модулей библиотеки IPPL.
Когда библиотека методов IPPL является доступной, то функции арифметической обработки изображений пакета Image Processing Toolbox (imabsdiff, imadd, imsubtract, imdivide, immultiply и imlincomb) и функция imfilter работают с повышенным быстродействием. Это придает им большое преимущество.
Примечание.
Библиотека функций IPPL в зависимости от условий работает только с некоторыми типами данных. Более детальная информация размещена в описании функций в главе Помощь (help sections), которая станет доступной при активации библиотеки методов IPPL.
Библиотека методов IPPL может изменятся.
getrangefromclass - получение динамического диапазона изображений на основе их формата
Синтаксис:
range = getrangefromclass(I)
Описание:
Функция range = getrangefromclass(I) на основе знаний о типе формата возвращает динамический диапазон изображения I. range представляет собой двухэлементный вектор, описывающий динамический диапазон.
Если окно figure не было открыто, то функция imgcf создает новое окно figure.
Требования к исходным данным:
Массив изображения I должен быть представлен в формате uint8, uint16, int16, logical, single или double. Результат range представляется в формате double.
Примечание:
Для данных, представленных в формате single и double, функция getrangefromclass возвращает диапазон [0 1]. Для целочисленных данных функция getrangefromclass возвращает диапазон соответственно их формату. Например, если данные представлены в формате uint8, динамический диапазон равен [0 255].
Пример:
Рассмотрим пример считывания 16-битного DICOM-изображения и определение его диапазона.
CT = dicomread('CT-MONO2-16-ankle.dcm'); r = getrangefromclass(CT)
graycomatrix - полутоновая матрица смежности для изображений
Синтаксис:
glcm = graycomatrix(I)
glcms = graycomatrix(I,param1,val1,param2,val2,...)
[glcms,SI] = graycomatrix(...)
Описание:
Функция glcms = graycomatrix(I) создает полутоновую матрицу смежности (gray-level co-occurrence matrix (GLCM)) для изображения I. Функция graycomatrix создает GLCM на основе вычислений того, как часто пиксель со значением интенсивности i встречается по горизонтали с пикселем со значением интенсивности j. (Также можно описать их пространственное взаиморасположение с использованием параметра 'Offsets'.) Каждый элемент (i,j) в матрице смежности glcm описывает число случаев, когда пиксель со значением i встречается с пикселем со значением j.
Для определения динамического диапазона изображения на основе матрицы смежности GLCM требуется дополнительная обработка, поскольку функция graycomatrix масштабирует значения в I. Когда I представляет собой бинарное изображение, функция graycomatrix масштабирует изображение до двух значений. Когда I представляет собой яркостное изображение, то функция graycomatrix масштабирует его до восьми значений. Число полутоновых значений определяет размерность GLCM. Также существует возможность описания уровней серого в матрице смежности GLCM с помощью параметра 'NumLevels' и путем, которым функция graycomatrix масштабирует значения с использованием параметра 'GrayLimits'.
На рисунке показано как функция graycomatrix вычисляет значение элемента матрицы смежности glcm(1,1). Этот элемент содержит значение 1, потому что есть только один случай совместного появления в горизонтальном расположении двух пикселей со значением 1. Как показано на рисунке элемент glcm(1,2) принимает значение 2, поскольку в данном примере два раза встречается совместное появление пикселей со значениями 1 и 2 в горизонтальном размещении.
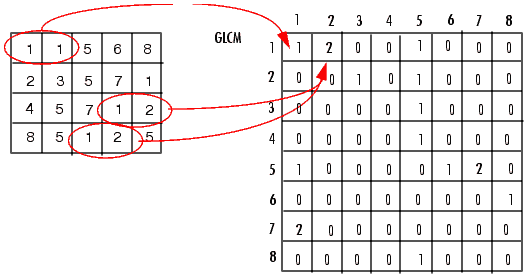
Функция glcms = graycomatrix(I,param1,val1,param2,val2,...) возвращает одну или больше полутоновых матриц смежности, что зависит от значений пар параметр/значение. Название параметра задается в виде аббревиатуры, что не влияет на его сущность.
Параметры:
В таблице приведен список параметров в алфавитном порядке.
Параметр Описание По умолчанию GrayLimits Двухэлементный вектор [low high], который описывает значения уровней серого в I и используется при их линейном масштабировании. Уровни серого, которые меньше или равны значению low приравниваются 1. Значения серого, которые больше или равны high приравниваются к NumLevels. Когда graylimits установлен в виде [], то функция graycomatrix использует минимальное и максимальное значение уровня серого в качестве границ [min(I(:)) max(I(:))]. Минимум и максимум зависит от формата, например, для формата double диапазон равен [0 1], а для формата int16 - [-32768 32767] NumLevels При описании уровней серого в виде целых чисел могут использоваться масштабированные значения I. Например, когда NumLevels равно 8, то функция graycomatrix вычисляет целые значения в I между 1 и 8. Число уровней серого определяет размерность матрицы смежности (glcm). 8 (числовые)
2 (бинарные)Offset Массив целых чисел с размерностью px2, описывающий расстояние между пикселем интереса и окрестностью. Каждая строка в массиве представляется двухэлементным вектором [row_offset, col_offset], который описывает отношение пары пикселей. Параметр row_offset представляет собой число строк между пикселем интереса и окрестностью. Также это можно представить в так называемом угловом представлении.
Приведем пример.
Угол Направление 0 [0 D] 45 [-D D] 90 [-D 0] 135 [-D -D]
На рисунке проиллюстрировано массив offset = [0 1; -1 1; -1 0; -1 -1]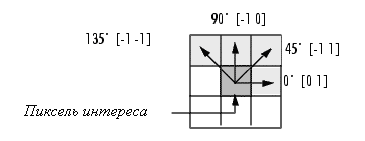
[0 1] Функция [glcm, SI] = graycomatrix(...) возвращает масштабированное изображение SI, используя вычисления уровней серого матрицы смежности. Значения в SI находятся между 1 и NumLevels.
Требования к исходным данным:
Массив I может быть представлен двумерным числовым или логическим не разреженным массивом действительных чисел. SI представляет собой матрицу в формате double, размерность которой совпадает с I. Матрица смежности glcms представляет собой массив в формате double с размерностью 'NumLevels' 'NumLevels' P, где P определяется из 'Offset'.
Примечание:
Полутоновую матрицу смежности называют еще полутоновой матрицей пространственных зависимостей.
Функция graycomatrix игнорирует пары пикселей, если они содержат значение NaN.
Функция graycomatrix заменяет положительные значения элементов Infs на значения NumLevels, а также отрицательные Infs на значения 1.
Функция graycomatrix игнорирует крайние пиксели изображения.
Пример:
Вычислим уровни серого матрицы смежности и сформируем масштабированную версию изображения SI, используя функцию graycomatrix для генерации GLCM.
I = [ 1 1 5 6 8 8; 2 3 5 7 0 2; 0 2 3 5 6 7];
[glcm,SI] = graycomatrix(I,'NumLevels',9,'G',[])
Вычислим уровни серого матрицы смежности для полутонового изображения circuit.tif.
I = imread('circuit.tif');
glcm = graycomatrix(I,'Offset',[2 0]);
graycoprops - свойства полутоновых матриц смежности
Синтаксис:
stats = graycoprops(glcm, properties)
Описание:
Функция stats = graycoprops(glcm, properties) вычисляет статистическое описание в виде свойств полутоновой матрицы смежности glcm. Эта матрица представляет собой массив с размерностью mxnxp. Если матрица смежности glcm является частью иного массива GLCM, тогда результат stats является статистическим массивом для каждой матрицы смежности glcm.
Функция graycoprops нормирует уровни серого матрицы смежности (GLCM). Каждый элемент (r,c) в нормированной матрице GLCM характеризует местонахождение пикселей, определяя пространственное отношение уровней серого r и c на изображении. Функция graycoprops использует нормированную матрицу GLCM для вычисления значений ее свойств.
Свойства могут быть записаны в виде строки через запятую или в другом виде, например, массиве. В таблице приведено более детальное описание.
Параметр Описание Формула 'Contrast' Возвращает меру контраста интенсивностей между пикселем и окрестностью или целым изображением.
Range = [0 (size(GLCM,1)-1)^2]
Если контраст равен нулю, то изображение представляется в виде матрицы с одинаковым уровнем яркости всех элементов..gif)
'Correlation' Возвращает меру корреляции между пикселем и окрестностью или целым изображением.
Range = [-1 1]
Если корреляция равна 1 или -1, то это говорит о наилучшей положительной или отрицательной корреляции изображений. Если корреляция равна NaN, то изображение представляется в виде матрицы с одинаковым уровнем яркости всех элементов.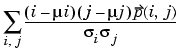
'Energy' Возвращает сумму квадратов элементов в GLCM.
Range = [0 1]
Такие действия аналогичны вычислению энергии элементов изображения и если она равна 1, то изображение представляется в виде матрицы с одинаковым уровнем яркости всех элементов.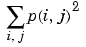
'Homogeneity' Возвращает значение, которое характеризует плотность распределения элементов в матрице смежности GLCM относительно ее диагонали.
Range = [0 1]
Гомогенность равна 1 для диагонали GLCM.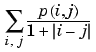
Результат представляется в виде структуры, поля которой описывают соответствующие свойства. Каждое поле представляется в виде массива с размерностью 1xp, где p является числом уровней серого в матрице смежности в GLCM. Например, когда GLCM представляется массивом с размерностью 8x8x3, то свойство 'Energy', которое в stats представлено в поле Energy, содержит массив с размерностью 1x3.
Параметры:
Такое свойство как энергия можно интерпретировать также как монотонность или второй угловой момент. А контраст известен еще также как мера различия или инерция.
Требования к исходным данным:
Массив glcm должен быть представлен логическим или числовым массивом, содержащим действительные неотрицательные целые числа из ограниченного диапазона.
Пример:
GLCM = [0 1 2 3;1 1 2 3;1 0 2 0;0 0 0 3];
stats = graycoprops(GLCM)
I = imread('circuit.tif');
GLCM2 = graycomatrix(I,'Offset',[2 0;0 2]);
stats = graycoprops(GLCM2,{'contrast','homogeneity'})
Сопутствующие функции: GRAYCOMATRIX.
hough - преобразование Хо
Синтаксис:
[H, theta, rho] = hough(bw)
Описание:
Функция [H, theta, rho] = hough(BW) реализует стандартное преобразование Хо (Standard Hough Transform (SHT)) бинарного изображения BW. Также функцию hough можно использовать для детектирования линий на изображении. Результат работы функции представляется в виде матрицы преобразования Хо H. Параметры theta (в градусах) и rho представляют массивы значений rho и theta, на основе которых генерируется матрица преобразований Хо.
Функция [H, theta, rho] = hough(BW,param1,val1,param2,val2) описывает пары параметр/значение, приведенные в таблице. Название параметров поданы в виде аббревиатуры, что не влияет на их суть.
Параметр Описание 'ThetaResolution' Скаляр вещественных чисел между 0 и 90, описывающий пространственные (в градусах) преобразования Хо вдоль оси theta. По умолчанию это значение равно 1. 'RhoResolution' Скаляр вещественных чисел между 0 и norm(size(BW)), который описывает пространственные преобразования Хо вдоль оси rho. По умолчанию это значение равно 1. Примечание:
Функция hough является инструментом для реализации стандартного преобразования Хо (SHT). При этом преобразовании используется параметрическое представление линии:
rho = x*cos(theta) + y*sin(theta)
Переменная rho является расстоянием от начала координат до линии вдоль вектора, перпендикулярного к ней. theta представляет собой угол между осью x и этим вектором. Функция hough генерирует параметры пространственной матрицы, где строка и столбец представляют соответственно параметры rho и theta. Пиковое значение в этом пространстве представляет потенциальную линию на исходном изображении.
Размерность матрицы преобразований Хо H равна NRHO NTHETA, где NRHO = 2*ceil(norm(size(BW))/RhoResolution)-1, а NTHETA = 2*ceil(90/ThetaResolution). Значение угла Theta находится в диапазоне [-90, 90) градусов, а значение rho - в диапазоне от -DIAGONAL до DIAGONAL, где DIAGONAL = RhoResolution*ceil(norm(size(BW))/RhoResolution). Отметим, что если 90/DTHETA не целое число, фактический угол в пространстве равен 90/ceil(90/DTHETA).
Требования к исходным данным:
Изображение BW должно быть представлено в виде двумерного не разреженного логического, числового вещественного массива.
Пример:
Проведем вычисления и визуализируем преобразования Хо для изображения.
RGB = imread('gantrycrane.png');
I = rgb2gray(RGB); % Преобразование в яркостное изображение
BW = edge(I,'canny'); % Выделение границ
[H,T,R] = hough(BW,'RhoResolution',0.5,'ThetaResolution',0.5);
% Отображение исходного изображения
subplot(2,1,1);
imshow(RGB);
title('gantrycrane.png');
% Отображение матрицы преобразований Хо
subplot(2,1,2);
imshow(imadjust(mat2gray(H)),'XData',T,'YData',R,...
'InitialMagnification','fit');
title('Hough transform of gantrycrane.png');
xlabel('\theta'), ylabel('\rho');
axis on, axis normal, hold on;
colormap(hot);
houghpeaks - локализация пиков при преобразованиях Хо
Синтаксис:
peaks = houghpeaks(H,numpeaks)
Описание:
Функция peaks = houghpeaks(H,numpeaks) локализирует пики матрицы преобразований Хо H, генерируемой функцией hough. Параметр numpeaks описывает максимальное число локализированных пиков.
Функция возвращает данные о пиках в виде матрицы с размерностью Qx2, где Q принимает значение от 0 до numpeaks. В параметре Q содержатся данные о координатах пиков. Если параметр numpeaks упущен, то по умолчанию он принимает значение 1.
Функция peaks = houghpeaks(...,param1,val1,param2,val2) описывает пары параметр/значение, перечисленные в следующей таблице. Название параметров поданы в виде аббревиатуры, что не влияет на их суть.
Параметр Описание 'Threshold' Неотрицательный скаляр, значения которого описывают значение порога по отношению к их пикам. Значение порога может изменяться в диапазоне от 0 до Inf. По умолчанию этот параметр принимает значение 0.5*max(H(:)). 'NHoodSize' Двухэлементный вектор положительных непарных целых чисел: [M N]. Параметр 'NHoodSize' учитывает влияние окрестности. По умолчанию: наименьшее нечетное значение больше или равно size(H)/50. Требования к исходным данным:
H представляет собой результат работы функции hough. Параметр numpeaks представлен положительным скаляром целых чисел.
Пример:
Приведем пример локализации и отобразим два пика при преобразованиях Хо для изображения circuit.tif.
I = imread('circuit.tif');
BW = edge(imrotate(I,50,'crop'),'canny');
[H,T,R] = hough(BW);
P = houghpeaks(H,2);
imshow(H,[],'XData',T,'YData',R,'InitialMagnification','fit');
xlabel('\theta'), ylabel('\rho');
axis on, axis normal, hold on;
plot(T(P(:,2)),R(P(:,1)),'s','color','white');
imdisplayrange - отображение динамического диапазона яркостей изображения
Синтаксис:
imdisplayrange
imdisplayrange(h)
imdisplayrange(hparent,himage)
hpanel=imdisplayrange(...)
Описание:
Функция imdisplayrange выдает информацию о динамическом диапазоне яркостей изображения в текущем окне отображения. Эта информация касается изображений в текущем окне отображения.
Информация отображается при помощи объекта uipanel, размещенного в нижнем правом углу изображения. Она содержит текстовую строку "Display range:", которая показывает значения диапазона яркостей элементов изображения, представленного в данном окне отображения.
Для индексных, полноцветных или бинарных изображений не всегда применяется понятие отображаемого диапазона. Поэтому результат может быть представлен в виде пустого массива ([]).
Функция imdisplayrange(h) формирует инструментарий отображения диапазона в окне figure через описание h, где hуказывает на некоторые параметры изображения. Эти параметры должны содержать описание как минимум одного объекта изображения.
Функция imdisplayrange(hparent, himage) формирует инструментарий отображения диапазона через параметр hparent, который отображает диапазон визуализации через himage.
Примечание.
Инструментарий отображения диапазона может работать с многослойными (типа RGB) изображениями. Когда курсор находится не на изображении в окне отображения, тогда диапазон отображения представляется в виде текстовой строки [black white].
Пример:
Визуализируем изображение и применим инструментарий отображения диапазона.
imshow('bag.png');
imdisplayrange;
Внесем 16-битное DICOM-изображение и визуализируем его. Диапазон отображения будет установлен по умолчанию.
dcm = dicomread('CT-MONO2-16-ankle.dcm');
subplot(1,2,1), imshow(dcm);
subplot(1,2,2), imshow(dcm,[]);
imdisplayrange;
entropy - энтропия интенсивности элементов изображения
Синтаксис:
E = entropy(I)
Описание:
Функция E = entropy(I) возвращает параметр E, скалярное значение которого представляет энтропию интенсивности элементов изображения I. Энтропия является статистической мерой неопределенности, которая используется для характеристики текстуры исходного изображения. Энтропия определяется как
-sum(p.*log(p)),
где p содержит отсчеты гистограммы, возвращаемые функцией imhist. По умолчанию, энтропия использует 2 отсчета для бинарных изображений и 256 для изображений, представленных массивом в формате uint8, uint16 или double.
Исходный массив I может представлять и многомерные изображения. Когда I имеет больше, чем две размерности, функция энтропии имеет свои особенности, как для многомерных изображений, так и для RGB изображений.
Требования к исходным данным.
Исходное изображение может представляться в виде непустого, неразреженного массива действительных чисел в формате logical, uint8, uint16 или double.
Пример:
I = imread('circuit.tif');
J = entropy(I)
entropyfilt - локальная энтропия интенсивностей элементов изображения
Синтаксис:
J = entropyfilt(I)
J = entropyfilt(I,NHOOD)
Описание:
Функция J = entropyfilt(I) возвращает массив J, где каждый пиксель содержит значение энтропии локальной окрестности с размерами 9х9 элементов с центром в соответствующем пикселе исходного изображения I. Массив I может быть произвольной размерности. Когда массив I имеет больше, чем две размерности, функция entropyfilt интерпретирует его как многомерное яркостное изображение. Результат, который представлен в виде массива J, имеет ту же размерность, что и массив исходного изображения I.
Для пикселей, расположенных на краю изображения I, функция entropyfilt использует симметрическое дополнение. При симметрическом дополнении, значения дополненных пикселей зеркально отражаются от крайнего пикселя изображения I.
Функция J = entropyfilt(I,NHOOD) выполняет фильтрацию исходного изображения I на основе энтропии, где локальная окрестность описывается параметром NHOOD. Параметр NHOOD может представляться многомерным массивом нулей и единиц, где ненулевые элементы характеризуют окрестность. Размер NHOOD's должен быть непарным по каждой размерности.
Например, функция entropyfilt использует локальную окрестность 9х9. Тогда центр этой локальной окрестности будет определен как floor((size(NHOOD) + 1)/2). Для описания различной формы локальных окрестностей (например, в виде диска) используется функция strel для создания структурного элемента объекта и дальнейшего его использования в функции getnhood при формировании окрестности на основе этого структурного элемента.
Требования к исходным данным.
Исходное изображение может представляться в виде неразреженного массива действительных чисел в формате logical, uint8, uint16 или double. Параметр NHOOD должен быть логическим или цифровым и содержать нули или единицы. Результирующий массив J имеет формат представления данных double.
Пример:
I = imread('circuit.tif');
J = entropyfilt(I);
imshow(I), figure, imshow(J,[]);
impixelinfoval - средства получения информации о пикселе без текстовых меток
Синтаксис:
hcontrol = impixelinfoval(hparent,himage)
Описание:
Функция hcontrol = impixelinfoval(hparent,himage) создает инструментарий получения информации о пикселе посредством параметра hparent, который доставляет информацию о пикселе изображения, описанном в himage. Параметр hparent вводиться вручную в окне отображения или объекте uipanel.
Средства получения информации отображают данные о пикселе на изображении, где был помещен курсор. Этот инструмент позволяет получать информацию о пикселях для всех изображений в окне отображения.
При создании объекта impixelinfo используется объект uipanel, размещенный в левом нижнем угле окна отображения. Он содержит текстовую метку "Pixel Info:", далее размещены значения координат пикселей вдоль соответствующих осей x и y.
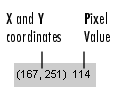
Отображаемая информация зависит также от типа представленного изображения. Для более детальной информации см. функцию impixelinfo.
Для копирования значения пикселя в буфер используется контекстное меню Copy pixel info.
Пример:
Добавление инструментария отображения информации о пикселе в окно отображения. Отметим также, что существует возможность изменения стиля и размера шрифта отображения значений при помощи стандартных команд.
ankle = dicomread('CT-MONO2-16-ankle.dcm');
h = imshow(ankle,[]);
hText = impixelinfoval(gcf,h);
set(hText,'FontWeight','bold')
set(hText,'FontSize',10)
getimagemodel - восстановление моделей объектов изображения на основе объектов изображения
Синтаксис:
imgmodel = getimagemodel(himage)
Описание:
Функция imgmodel = getimagemodel(himage) возвращает модель объектов изображения, ассоциированных с himage. Параметр himage может управлять объектом изображения или массивом объектов изображения.
Возвращаемые функцией imgmodel значения описывают модель объектов изображения. Если параметр himageпредставлен массивом управления объектами изображения, то результат imgmodel представляет массив моделей объектов изображения.
Если параметр himage не связан с моделью объекта изображения, тогда функция создает его.
Пример:
h = imshow('bag.png');
imgmodel = getimagemodel(h);
impixelregion - средства просмотра локального массива пикселей
Синтаксис:
impixelregion
impixelregion(h)
hfig = impixelregion(...)
Описание:
Функция impixelregion создает средства отображения локального массива пикселей изображения, представленного в текущем окне просмотра.
Средства просмотра локального массива пикселей открывают отдельное окно, которое содержит значения пикселей некоторой локальной окрестности данного изображения. Другими словами, числовые значения пикселей наложены на каждый отдельный пиксель. Существует также возможность просмотра пикселей из различных областей изображения.
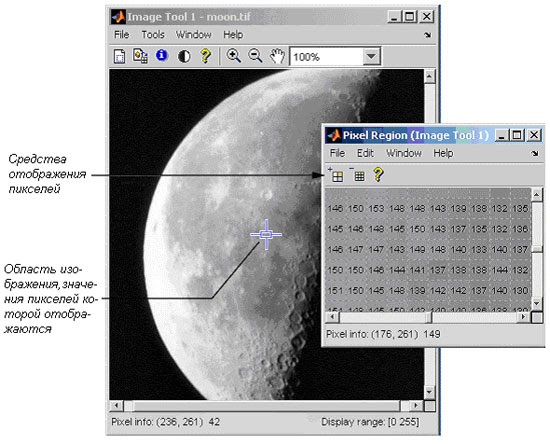
Функция impixelregion(h) создает средства отображения локального массива пикселей изображения, связанных с объектом, описанным параметром h. Параметр h может описывать окно просмотра, оси, а также другие объекты изображения. Если параметр h описывает оси или окно просмотра, то функция impixelregion ассоциируется с первым изображением, размещенным в текущем окне просмотра.
Функция hfig=impixelregion(...) возвращает значение hfig, которое управляет диалоговым окном средств отображения локального массива пикселей изображения.
Примечание:
Для создания инструментария отображения локального массива пикселей изображения, который может быть встроен в существующее окно просмотра или uipanel, используется функция impixelregionpanel.
Пример:
Приведем пример отображения и последующего создания инструментария отображения локального массива пикселей, связанного с данным изображением.
imshow peppers.png
impixelregion
impixelregionpanel - панель инструментария отображения локального массива пикселей изображения
Синтаксис:
hpanel = impixelregionpanel(hparent,himage)
Описание:
Функция hpanel = impixelregionpanel(hparent,himage) создает панель инструментария отображения локального массива пикселей, связанного с изображением, описанным параметром himage. Пиксели этого изображения будут отображаться. Параметр hparent управляет окном просмотра или объектом uipanel, который связан со средствами просмотра локального массива пикселей.
Инструмент отображения локального массива пикселей представляется объектом uipanel, который содержит небольшую часть изображения в виде значений пикселей. Другими словами, значения пикселей накладываются на каждый пиксель рассматриваемого изображения. Рассматриваемая часть изображения представляет собой прямоугольную область. Для просмотра пикселей из различных областей изображения, необходимо нажать на прямоугольник, размещенный на изображении и перетянуть его в соответствующую область.
Примечание:
Для создания средств отображения локального массива пикселей в отдельном окне используется функция impixelregion.
Пример:
himage = imshow('peppers.png');
hfigure = figure;
hpanel = impixelregionpanel(hfigure, himage);
Установка размещения позиции в нижнем левом углу окна просмотра.
set(hpanel, 'Position', [0 0 .5 .5])
impixelinfo - средства получения информации о пикселях
Синтаксис:
impixelinfo
impixelinfo(h)
impixelinfo(hparent,himage)
hpanel = impixelinfo(...)
Описание:
Функция impixelinfo создает средства получения информации о пикселях изображения в текущем окне просмотра. С помощью этих средств информация о пикселе отображается в том месте изображения, где указывает курсор. Средства отображения информации о пикселях работают со всеми изображениями, размещенными в окне просмотра.
Эти средства представляются объектом uipanel, который размещен в нижнем левом углу изображения. Он содержит текстовую строку "Pixel info:" с соответствующими координатами пикселя и значением, которое он принимает на этой позиции изображения.
Содержание отображаемой информации зависит от типа изображения. В таблице приведена информация о способе отображения данных в зависимости от типа изображения. Если курсор размещен в окне просмотра, но вне поля изображения, то информация о пикселях отображает некоторую информацию по умолчанию.
Тип изображения Информация о пикселях, которая выдается по умолчанию Пример Яркостное (X,Y) Яркость (13,30) 82 Яркостное (X,Y) <индекс> [R G B] (2.6) <4> [0.29 0.05 0.32] Бинарное (X,Y) BW (12,1) 0 Полноцветное (X,Y) [R G B] (19,10) [15 255 10] При необходимости отображения информации вне метки "Pixel Info", используется функция impixelinfoval.
Функция impixelinfo(h) создает средства отображения информации о пикселях в окне просмотра, описанном через h, где параметр h описывает объекты изображения. Такие объекты как оси, uipanel или окно отображения должны содержать как минимум один объект.
Функция impixelinfo(hparent,himage) создает средства отображения информации о пикселях в hparent, которое поставляет информацию о пикселях в himage. Параметр himage служит для описания изображений. А параметр hparent описывает окно просмотра или объект uipanel, который содержит средства описания пикселей изображений.
Функция hpanel=impixelinfo(...) передает управление средствами описания пикселями объекту uipanel.
Примечание:
Для копирования информации о пикселях в буфер, следует навести курсор на нужный пиксель и нажать правую кнопку мыши. Отобразиться контекстное окно, в котором следует выбрать пункт Copy pixel info.
Пример:
Приведем пример отображения изображения и добавления средств получения информации о пикселях в окно просмотра. В примере показано также возможность изменения размещения этих средств в окне просмотра с использованием свойств объекта uipanel.
h = imshow('hestain.png');
hp = impixelinfo;
set(hp,'Position',[150 290 300 20]);
Средства отображения информации о пикселях могут работать также в окне просмотра, содержащем многослойные изображения разных типов.
figure
subplot(1,2,1), imshow('liftingbody.png');
subplot(1,2,2), imshow('autumn.tif');
impixelinfo;
histeq - выравнивание гистограммы
Синтаксис:
Id=histeq(Is, hgram)
[Id, T]=histeq(Is, hgram)
Id=histed(Is, n)
[Id, T]=histeq(Is, n)
newmap=histeq(X, map, hgram)
[newmap, T]=histeq(X, map, hgram)
newmap=histeq(X, map)
[newmap, T]=histeq(X, map)
Описание:
Функция histeq улучшает контраст изображения с помощью преобразования значений пикселов исходного изображения таким образом, чтобы гистограмма яркостей пикселов результирующего изображения приблизительно соответствовала некоторой предопределенной гистограмме [1,2]. Данная функция предназначена для преобразования полутоновых изображений или палитровых изображений.
Функция histeq(Is, hgram) преобразует исходное полутоновое изображение Is таким образом, чтобы гистограмма яркостей пикселов результирующего полутонового изображения Id приблизительно соответствовала гистограмме, задаваемой вектором hgram. Количество элементов в hgram задает число столбцов гистограммы, а значение каждого элемента - относительную высоту каждого столбца. Значение элементов вектора hgram должно быть в диапазоне [0, 1]. Функция hgram автоматически масштабирует значения элементов hgram так, чтобы сумма значений элементов в гистограмме была равна количеству пикселов изображения, т.е. sum(hgram)=prod(size(Is)). Гистограмма результирующего изображения Id будет лучше соответствовать заданной гистограмме hgram в том случае, когда количество столбцов hgram (length(hgram)) много меньше количества градаций яркости исходного изображения Is.
Функция Id=histeq(Is, n) преобразует исходное полутоновое изображение Is таким образом, чтобы результирующее полутоновое изображение Id имело гистограмму яркостей пикселов, близкую к равномерной. Равномерная гистограмма hgram создается из n столбцов как hgram=ones(1, n)*prod(size(Is))/n. Чем меньше n по сравнению с количеством градаций яркости в изображении Is, тем более равномерной получается гистограмма яркостей пикселов результирующего изображения Id. По умолчанию значение n равно 64, и данный параметр можно не указывать при вызове функции. Формат результирующего изображения Id совпадает с форматом исходного Is.
Функция [Id, T]=histeq(Is, n) дополнительно возвращает вектор T, задающий характеристику передачи уровней яркости исходного изображения Is в уровни яркости результирующего изображения Id.
Функция newmap=histeq(X, map, hgram) преобразует палитру map, связанную с палитровым изображением Х, таким образом, чтобы гистограмма яркостей пикселов изображения Х с палитрой newmap приблизительно соответствовала гистограмме hgram. Для получения значений яркости из палитры map используется функция rgb2ntsc. Количество элементов вектора hgram должно быть равно размеру палитры map.
Функция newmap=histeq(X, map, hgram) преобразует палитру map, связанную с палитровым изображением Х, таким образом, чтобы гистограмма яркостей пикселов изображения Х с палитрой newmap была близка к равномерной.
Функция [newmap, T]=histeq(X, …) дополнительно возвращает вектор Т, задающий характеристику передачи уровней яркости из исходной палитры map в уровни яркости результирующей палитры newmap.
Существуют также другие, более сложные подходы к решению задачи улучшения изображений путем гистограммных преобразований. Они базируются не только на анализе гистограммы распределения яркостей элементов изображения в целом, но и ее отдельных компонент. Также существует ряд методов, основанных на анализе локальных гистограмм отдельных участков изображения. Существование большого количества методов гистограммных преобразований объясняется их относительной простотой и высокой эффективностью.
Алгоритм:
Характеристика передачи уровней яркости Т выбирается путем минимизации функции F(k)=|c1(T(k))-c0(k)|, где c0 - сумма всех пикселов полутонового изображения I с яркостью, меньше либо равной k; c1 - сумма значений заданной гистограммы hgram для всех дискретных уровней яркости, меньших либо равных k. При минимизации на функцию Т накладывают следующие ограничения: Т должна быть монотонной и c1(T(k)) не должно превышать c0(a) более, чем на половину количества точек с яркостью а.
Пример.
Полутоновое изображение I читается из файла и выводится на экран (рис. 1 а). Строится гистограмма яркостей пикселов исходного изображения (рис. 1 б). Функция histeq выравнивает гистограмму изображения I. Результат преобразования и гистограмма яркостей его пикселов выводятся на экран (соответственно рис. 1 в и рис. 1 г).
%Пример демонстрирует повышение контраста изображения
%с помощью выравнивания гистограммы.
%Чтение исходного изображения и вывод его на экран.
I=imread(‘image1.tif’);
imshow(I);
%Построение гистограммы исходного изображения.
figure, imhist(I);
%Выравнивание гистограммы.
I=histeq(I, 80);
%Вывод преобразованного изображения на экран.
Figure, imshow(I);
%Вывод гистограммы преобразованного изображения.
figure, imhist(I);
Сопутствующие функции: BRIGHTEN, IMADJUST, IMHIST, RGB2NTSC.
Ссылки на литературу:
1. Прэтт У. Цифровая обработка изображений: В 2 т. М.: Мир, 1982.
2. Павлидис Т. Алгоритмы машинной графики и обработки изображений. М.: Радио и связь, 1986.

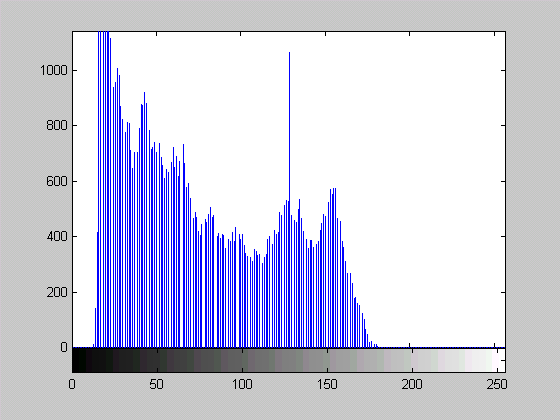
а) б)

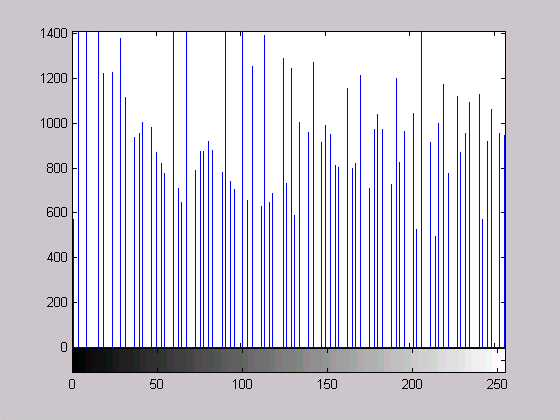
в) г)
Рис. 1.
imadjust - контрастирование с гамма–коррекцией
Синтаксис:
Id=imadjust(Is, [low high], [boton top], gamma)
newmap=imadjust(map, [low high], [boton top], gamma)
newmap=(map, [IR hR; IG hG; IB hB], [bR tR; bG tG; bB tB], [gR gG gB])
RGBd=imadjust(RGBs, [low high], [botton top], gamma)
RGBD=(RGBS, [IR hR; IG hG; IB hB], [bR tR; bG tG; bB tB], [gR gG gB])
Описание:
Функция Id=imadjust(Is, [low high], [bottom top], gamma) создает полутоновое изображение Id путем контрастирования исходного полутонового изображения Is. Значения яркости в диапазоне [low high] преобразуются в значения яркости в диапазоне [bottom top]. Значения яркости, меньшие low, принимают значение bottom, а значения яркости, большие high, принимают значение top. Значения top, bottom, low, high должны принадлежать диапазону [0,1]. Если в качестве второго ([low high]) или третьего ([bottom top]) параметров передать пустой вектор [], то по умолчанию будет использован вектор [0,1]. С помощью показателя gamma можно дополнительно осуществлять преобразование, называемое гамма - коррекцией. Параметр gamma определяет форму кривой характеристики передачи уровней яркости. Если gamma меньше 1, то характеристика передачи уровней будет выпуклой и результирующее изображение будет светлее, чем исходное. Если gamma больше 1, то характеристика передачи уровней будет вогнутой и результирующее изображение будет темнее, чем исходное. По умолчанию параметр gamma равен 1, что соответствует линейной характеристике передачи уровней и отсутствию гамма - коррекции. При вызове функции показатель gamma можно опустить.
Характеристики передачи уровней для различных значений gamma приведены на рис. 1.
.gif)
а)
.gif)
б)
.gif)
с)
Рис. 1. Характеристика передачи уровней для различных значений gamma
Функция newmap=imadjust(map, [low high], [boton top], gamma) создает новую палитру newmap путем контрастирования исходной палитры map. Преобразование осуществляется аналогично преобразованию полутонового изображения отдельно для каждой R-, G-, B-составляющих. Диапазоны преобразования интенсивностей составляющих [low high] и [boton top], а также показатель gamma задаются одинаковыми для всех составляющих. Различные диапазоны преобразования интенсивностей и показатель gamma для R-, G-, B-составляющих можно задать с помощью функции newmap=(map, [IR hR; IG hG; IB hB], [bR tR; bG tG; bB tB], [gR gG gB]).
Функция RGBd=imadjust(RGBs, [low high], [botton top], gamma) создает полноцветное изображение RGBd путем контрастирования исходного полноцветного изображения RGBs. Преобразование осуществляется аналогично преобразованию полутонового изображения отдельно для каждой из R-, G-, B-составляющих. Диапазоны преобразования интенсивностей составляющих [low high] и [botton top], а также показатель gamma задаются одинаковыми для всех составляющих. Различные диапазоны преобразования интенсивностей и показатель gamma для R-, G-, B-составляющих можно задать с помощью функции RGBD=(RGBS, [IR hR; IG hG; IB hB], [bR tR; bG tG; bB tB], [gR gG gB]).
Однако существуют классы изображений, для которых линейное или нелинейное преобразование яркостных диапазонов не всегда эффективно. В первую очередь это касается изображений, градации яркостей которого занимают максимально возможный диапазон, а яркостной диапазон потенциально информативных участков изображения - небольшую часть диапазона. Для таких изображений рекомендуется применять метод кусочно-линейных или кусочно-нелинейных преобразований яркостных диапазонов. Этот метод позволяет максимально сберечь визуальную информацию на изображениях при их преобразованиях. Следует отметить, что известные методы трансформации яркостных диапазонов являются частным случаем метода кусочно-линейных (нелинейных) преобразований градационных характеристик изображения.
Форматы представления данных исходного и результирующего изображения совпадают.
Пример.
Полутоновое изображение I читается из файла и отображается на экране (рис. 2 а). Для анализа диапазона яркостей исходного изображения I строится гистограмма яркостей пикселов с помощью функции imhist(I) (рис.2 б). По гистограмме видно, что пикселы изображения I имеют яркости в диапазоне [0, 75], изображение I недостаточно контрастное. Функция imadjust “растягивает” исходный диапазон яркостей на диапазон от минимально возможной яркости до максимально возможной. Результат преобразования выводится на экран в новое окно (рис. 2 в). Гистограмма яркостей пикселов результирующего изображения показана на рис. 2 г. Результирующее изображение контрастнее, чем исходное.
%Пример демонстрирует контрастирование изображения.
%Чтение исходного изображения и вывод его на экран.
I=imread(‘gory.tif’);
imshow(I);
%Построение гистограммы исходного изображения.
figure, imhist(I);
%Контрастирование исходного изображения.
I=imadjust(I, [0 75]/255, [ ], 1);
%Вывод преобразованного изображения на экран.
figure, imshow(I);
%Вывод гистограммы преобразованного изображения.
figure, imhist(I);

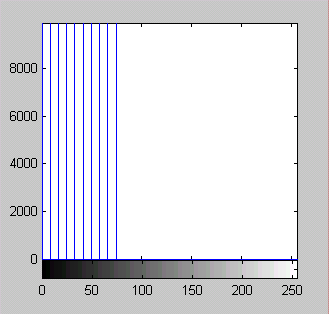
а) б)

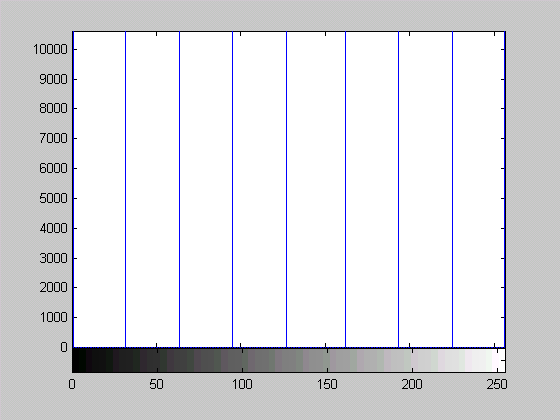
г) д)
Рис. 2.
brighten - управление яркостью палитры
Синтаксис:
brighten(beta)
newmap=brighten(beta)
newmap=brighten(map, beta)
brighten(fig, beta)
Описание:
Функция brighten(beta) заменяет текущую палитру, используемую для отображения рисунков в текущем окне figure, на более яркую или более темную в зависимости от значения параметра beta. Для вывода изображения в текущее окно figure будет использоваться новая палитра. Текущая палитра будет ярче, если beta принадлежит диапазону (0, 1], и темнее, если beta принадлежит диапазону [-1, 0). Необходимо отметить, что в результате действия функции brightenизменяется только яркость цветов палитры, значение цветового тона остается неизменным. Последовательное применение функции brighten с параметром beta и -beta оставляет палитру без изменений.
Функция newmap=brighten(beta) возвращает палитру, полученную преобразованием текущей палитры, но не меняет текущую палитру. Таким образом, цвета при отображении изображения в текущем окне не изменяются.
Функция newmap=brighten(map, beta) возвращает палитру, полученную преобразованием палитры map, но не меняет текущую палитру. Цвета при отображении изображения в текущем окне не изменяются.
Функция brighten(fig, beta) изменяет яркость палитры, используемой для окна с описателем fig.
imnoise - добавление шума
Синтаксис:
Id=imnoise(Is, type, params)
Описание:
Функция imnoise создает новое изображение Id путем добавления шума к исходному полутоновому изображению Is. В основном данная функция предназначена для создания тестовых изображений, используемых при выборе методов фильтрации шума, однако может применяться и для придания фотореалистичности искусственно синтезированным изображениям.
Функция imnoise может добавлять шум трех типов. Тип шума задается строковой константой type, которая может принимать одно из следующих значений:
- ‘gaussian’ - для гауссова белого шума;
- ‘salt&pepper’ - для импульсного шума (шум типа “соль и перец”);
- ‘speckle’ - для мультипликативного шума.
Количество и смысл параметров params определяются выбранным типом шума. Если параметры не указаны, то будут использованы значения по умолчанию.
Id=imnoise(Is, ‘gaussian’, m, v) добавляет к изображению Is гауссов белый шум с математическим ожиданием m и дисперсией v. По умолчанию математическое ожидание равно 0, а дисперсия - 0.01.
Id=imnoise(Is, ‘salt&pepper’, d) добавляет к изображению Is импульсный шум. Параметр d определяет плотность шума и равен доле искаженных пикселов. По умолчанию d=0.05.
Id=imnoise(Is, ‘speckle’, v) добавляет к изображению Is мультипликативный шум Id=Is+n*Is, где n - равномерно распределенный случайный шум с математическим ожиданием 0 и дисперсией v. По умолчанию v=0.04.
Форматы представления данных исходного и результирующего изображений совпадают.
roifill - заполнение областей интереса
Синтаксис:
Id=roifill(Is)
Id=roifill(Is, c, r)
Id=roifill(Is, BW)
Id=roifill(XData, YData, Is, xi, yi)
[Id, BW]=roifill(…)
[XData, YData, Id, BW, xi, yi]=roifill(…)
Описание:
Функция roifill предназначена для устранения небольших по площади дефектов полутоновых изображений. Она заполняет задаваемые области плавными переходами яркости, используя интерполяцию по значениям яркости граничных пикселов области.
Функция Id=roifill(Is) позволяет интерактивно задать область на исходном полутоновом изображении Is и создает новое полутоновое изображение Id, которое отличается от исходного изображения Is тем, что заданная область заполнена. Данная функция выводит изображение Is в окно и ожидает от пользователя задания области интереса, предназначенной для заполнения. Область интереса должна быть заключена в полигон (многоугольник), вершины которого задаются однократным нажатием левой клавиши мыши. Предыдущую заданную вершину можно удалить, если нажать на клавиши Backspace или Delete. Нажатие на правую клавишу мыши или двойной щелчок левой клавишей задает последнюю вершину полигона. Также завершить процесс задания вершин без указания последней можно нажатием на клавишу Enter. Для определения точек, лежащих внутри полигона, используется правило Non-Zero Winding. Если при вызове функции параметр Is опущен, то изображение берется из текущего окна.
Функция Id=roifill(Is, c, r) позволяет явно задать координаты вершин полигона, ограничивающего заполняемую область, в векторах r (номера строк) и c (номера столбцов) одинаковой длины.
Функция Id=roifill(XData, YData, Is, xi, yi) аналогична предыдущей, но в ней координаты полигона, передаваемые в векторах xi и yi, задаются в пространственной системе координат. Двухэлементные векторы XData и YData определяют диапазон изменения значений по осям пространственной системы координат.
Области, которые необходимо заполнить, могут быть заданы с помощью бинарного изображения BW. В этом случае используется функция Id=roifill(Is, BW). Изображения Is и BW имеют одинаковый размер. Пикселы изображения BW, относящиеся к областям, предназначенным для заполнения, должны быть равны 1.
Для рассмотренных функций можно дополнительно определить 4 выходных параметра: [XData, YData, Id, BW, xi, yi]=roifill(…). Тогда в параметрах xi и yi будут возвращены координаты вершин полигона, ограничивающего заполненную область, а в XData и YData будут возвращены диапазоны значений по осям пространственной системы координат, которая использовалась для изображения Is.
Если функцию roifill задавать без выходных параметров, то результирующее изображение выводится на экран в новом окне.
Форматы представления данных исходного Is и результирующего Id изображений совпадают.
Пример.
Рассмотрим использование функции roifill для устранения небольших дефектов полутонового изображения. На рис. 1 а показано исходное изображение с искусственным белым прямоугольником, который симулирует некоторый дефект на изображении. Уберем этот небольшой дефект, расположенный в центре изображения. Для этого с помощью функции roipoly интерактивно создадим бинарное изображение, задающее область интереса, а затем воспользуемся функцией roifill.
% Пример демонстрирует устранение на изображении малых по площади дефектов.
%Чтение исходного изображения и вывод его на экран.
I=imread('shot1.tif');
Imshow(I);
%Задание области интереса (интерактивно).
BW=roipoly;
%Заполнение области интереса.
I=roifill(I,BW);
%Вывод результата на экран.
figure, imshow(I);


а) б)
Рис. 1.
stretchlim - поиск границ повышения контраста изображения
Синтаксис:
LOW_HIGH=stretchlim(I, TOL)LOW_HIGH=stretchlim(RGB, TOL)
Описание:
Функция LOW_HIGH=stretchlim(I, TOL) возвращает пару значений яркостей, которые могут использоваться функцией imadjust для увеличения контраста изображения.
Параметр TOL=[LOW_FRACT HIGH_FRACT] описывает часть изображения с точки зрения минимальной и максимальной яркости.
Когда параметр TOL представлен скаляром, тогда значения TOL=LOW_FRACT и HIGH_FRACT=1 - LOW_FRACT применяют к похожим частям изображения.
Когда аргумент упущен, тогда, по умолчанию, TOL равно [0.01 0.99].
Когда параметр TOL равен 0, тогда LOW_HIGH=[min(I(:)) max(I(:))].
Функция LOW_HIGH=stretchlim(RGB, TOL) возвращает матрицу интенсивностей с размерностью 2x3 для повышения контрастности каждой составляющей RGB-изображений. Параметр TOL описывает параметры преобразования для каждой составляющей.
Требования к исходным данным.
Исходное изображение должно быть представлено в формате uint8, uint16 или double. Результирующие интенсивности LOW_HIGH должны быть представлены в формате double и находится в диапазоне между 0 и 1.
Пример.
I=imread('pout.tif');
J=imadjust(I, stretchlim(I), []);
imshow(I), figure, imshow(J)

edgetaper - виделение краев с использованием функции протяженности точек
Синтаксис:
J=edgetaper(I, PSF)
Описание:
Функция J=edgetaper(I, PSF) размывает контуры исходного изображения I, используя функцию протяженности точки PSF. Результирующее изображение J представляет собой взвешенную сумму исходного изображения и его размытой версии. Массив весов определяется автокорреляционной функцией от PSF, массив J соответствует массиву I в центре области и равен размытой версии I около контуров.
Функция edgetaper очень эффективно используется в методах для преобразования размытых изображений, которые используют дискретное преобразование Фурье, например, deconvwnr, deconvreg и deconvlucy.
Примечание. Размерность функции PSF не может превышать половины любой размерности изображения.
Требования к исходным данным.
Массив I и PSF должны иметь формат представления данных uint8, uint16 или double. Массив J имеет формат представления данных тот же, что и I.
Пример:
I=imread('cameraman.tif');
PSF=fspecial('gaussian', 60, 10);
J=edgetaper(I, PSF);
subplot(1, 2, 1); imshow(I, []); title('original image');
subplot(1, 2, 2); imshow(J, []); title('edges tapered');
otf2psf - преобразование оптической функции в функцию протяженности точек
Синтаксис:
PSF=otf2psf(OTF)PSF=otf2psf(OTF, OUTSIZE)
Описание:
Функция PSF=otf2psf(OTF) вычисляет обратное быстрое преобразование Фурье (ОБПФ) массива оптической функции и создает функцию протяженности точки с тем же центром. По умолчанию, функция протяженности точки имеет ту же размерность, что и оптическая функция.
Функция PSF=otf2psf(OTF, OUTSIZE) выполняет преобразование оптической функции в массив функции протяженности точки, а параметр OUTSIZE описывает размер результирующей функции протяженности точки. Отметим, что размер результирующего массива не должен превышать размер оптической функции.
Рассмотренные функции используются при реализации операций конволюции и деконволюции изображений.
Требования к исходным данным.
Функция оптического преобразования должна быть представлена неразреженным числовым массивом. Функция протяженности точки имеет формат представления данных double.
Пример.
PSF=fspecial('gaussian', 13, 1);OTF=psf2otf(PSF, [31 31]); % PSF-->OTFPSF2=otf2psf(OTF,size(PSF)); % OTF-->PSF2subplot(1, 2, 1); surf(abs(OTF)); title('|OTF|');axis square; axis tightsubplot(1, 2, 2); surf(PSF2); title('соответствует PSF');axis square; axis tight
adapthisteq - Выполнение контрастно ограниченной адаптивной эквализации гистограммы
Синтаксис:
J=adapthisteq(I)J=adapthisteq(I, param1, val1, param2, val2...)
Описание:
Функция J=adapthisteq(I) улучшает контраст полутонового изображения I путем преобразования значений его элементов методом контрастно ограниченной адаптивной эквализации гистограммы (CLAHE).
Метод CLAHE более эффективный при работе с небольшими локальными окрестностями изображений, чем с полными изображениями. При улучшении контраста локальных окрестностей используется описание гистограммы, которое определяется с помощью параметра 'Distribution'. Во избежание появления ложных границ при обработке локальных окрестностей используются также соседние окрестности, которые объединяются с помощью билинейной интерполяции. Контраст, особенно на однородных окрестностях, должен быть ограниченным во избежание усиления шумовой составляющей.
Функция J=adapthisteq(I, param1, val1, param2, val2...) определяет несколько дополнительных пар параметров (значений), описание которых приведено в таблице. Названия некоторых параметров приведены в сокращенном виде.
Параметр Значение 'NumTiles' Двухэлементный вектор целых чисел, описывающих число локальных окрестностей [M N]. Оба параметра M и N должны быть кратны 2. Общее число областей эквивалентно M*N. По умолчанию: [8 8] 'ClipLimit' Вещественный скаляр в диапазоне [0 1], который определяет границу усиления контраста. Большее число соответствует большему контрасту.По умолчанию: 0.01 'NBins' Положительный целый скаляр, определяющий число значений гистограммы, которая используется при трансформациях изображений с целью улучшения контраста. Большее число соответствует большему динамическому диапазону, однако приводит к уменьшению быстродействия.По умолчанию: 256 'Range' Строка, описывающая ранг (диапазон) данных результирующего изображения.
'original' - ранг, ограниченный диапазоном исходного изображения [min(I(:)) max(I(:))].
'full' - полный ранг (диапазон) для результирующего изображения. Например, для изображения в формате uint8, диапазон равен [0 255].
По умолчанию: 'full''Distribution' Строка, определяющая желательную форму гистограммы для окрестностей изображения:
'uniform' - равномерная гистограмма
'rayleigh' - колоколообразная гистограмма
'exponential' - экспоненциальная гистограмма
По умолчанию: 'uniform''Alpha' Неотрицательный вещественный скаляр, описывающий параметр распределения.По умолчанию: 0.4
Примечание: Используется, когда параметр 'Distribution' принимает значения 'rayleigh' или 'exponential'.Требования к исходным данным.
Полутоновое изображение I может иметь формат представления данных uint8, uint16 или double. Результирующее изображение J имеет формат представления данных тот же, что и I.
Пример 1.Обработаем изображение методом контрастно ограниченной адаптивной эквализации гистограммы и визуализируем результат.I=imread('tire.tif');A=adapthisteq(I, 'clipLimit', 0.02, 'Distribution', 'rayleigh');imview(I);imview(A);Пример 2.Обработаем цветное фотографическое изображение методом контрастно ограниченной адаптивной эквализации гистограммы.[I MAP]=imread('shadow.tif');RGB=ind2rgb(I, MAP);YIQ=rgb2ntsc(RGB); %преобразование в YIQ-изображениеY=YIQ(:, :, 1);YIQ(:, :, 1)=adapthisteq(Y, 'Divisions', [8 8], 'ClipLimit', 0.005);J=ntsc2rgb(YIQ); %преобразование обратно в RGB-изображениеimview(RGB); %отображение результата
decorrstretch - Применение декорреляционного растяжения многоканальных изображений
Синтаксис:
S=decorrstretch(I)S=decorrstretch(I, TOL)
Функция S=decorrstretch(I) применяется для декорреляционного растяжения многоканального изображения I и возвращает результат в S. Размерность и формат представления данных массива S совпадают с исходным массивом I.
Функция S=decorrstretch(I, TOL) при декорреляционном растяжении использует информацию о контрасте. Преобразование контраста контролируется параметром TOL: TOL=[LOW_FRACT HIGH_FRACT], который определяет диапазон интенсивностей для локальных окрестностей изображения.
Когда TOL представляет собой скаляр, то LOW_FRACT=TOL и HIGH_FRACT=1-TOL.
Примечание.
Декорреляционное растяжение обычно применяется для трехмерных изображений (обычных RGB или многоспектральных искусственных RGB изображений).
Главной целью применения метода декорелляционного растяжения является решение задачи улучшения качества визуального восприятия изображений. Небольшая коррекция параметра TOL может привести к весьма заметным изменениям в результирующем изображении.
Требования к исходным данным.
Исходное изображение должно иметь формат представления данных uint8, uint16 или double.
Пример.
[I col]=imread('forest.tif');
S=decorrstretch(ind2rgb(I, col));
subplot(2, 1, 1), imshow(I, col)
subplot(2,1,2), imshow(S)
axes2pix - интерактивный методы регулирования контраста и яркости
Синтаксис:
pixelx = axes2pix(DIM, XDATA, AXESX)
Описание:
Функция pixelx = axes2pix(DIM, XDATA, AXESX) выполняет преобразование axes-координат в пиксельные координаты. Например, когда pt = get(gca,'CurrentPoint'), тогда AXESX будет равно pt(1,1) или pt(1,2). Параметр AXESX выражается в пиксельных координатах. Параметр XDATA представляет собой двухэлементный вектор, возвращаемый функцией get(image_handle, 'XData') или get(image_handle,'YData'). Параметр DIM представляет число столбцов для x-координаты или число строк для у-координаты.
Если окно figure не было открыто, то функция imgcf создает новое окно figure.
Требования к исходным данным:
Параметры DIM, XDATA и AXESX должны быть представлены в формате double. Результат представляется также в формате double.
Примечание:
Функция axes2pix выполняет минимальную проверку соответствия данных AXESX, DIM и XDATA. Например, функция axes2pix возвращает отрицательные координаты, когда AXESX меньше, чем XDATA(1). Функция axes2pix отвечает за ошибочный контроль.
Примеры:
Пример с параметрами XData и Ydata, заданными по умолчанию.
h = imshow('pout.tif');
[nrows,ncols] = size(get(h,'CData'));
xdata = get(h,'XData')
ydata = get(h,'YData')
px = axes2pix(ncols,xdata,30)
py = axes2pix(nrows,ydata,30)
Пример с параметрами XData и Ydata, которые не задаются по умолчанию.
xdata = [10 100]
ydata = [20 90]
px = axes2pix(ncols,xdata,30)
py = axes2pix(nrows,ydata,30)
imcontrast - средства усиления контраста изображения
Синтаксис:
imcontrast
imcontrast(h)
hfigure = imcontrast(h)
Описание:
Функция imcontrast создает инструментарий усиления контраста изображения, связанный с полутоновым изображением в текущем окне просмотра и названный объектом изображения. Когда окно просмотра содержит многослойное изображение, объектом является первое полутоновое изображение в окне просмотра (созданное последним). Функция imcontrast создает этот инструментарий в отдельном окне просмотра.
Инструмент усиления контраста (Adjust Contrast tool) реализует интерактивное регулирование контраста и яркостного диапазона изображения, представленного в текущем окне просмотра. Этот подход можно использовать, в частности, при работе с топографическими картами при представлении их в виде изображений. Описанная обработка приводит к изменению свойств изображений.
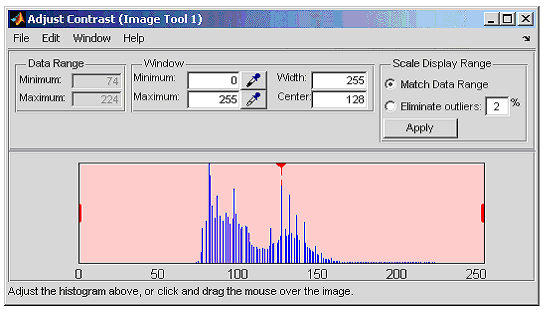
Примечание:
Инструментарий усиления контраста может работать с полутоновыми изображениями, представленными в формате double и single.
Функция imcontrast(h) создает средства усиления контраста изображения, связанные с изображениями, описанными через параметр h. Параметр h может управлять окном просмотра, осями, объектами изображения. Когда параметр h содержит описание окна просмотра или осей, тогда функция imcontrast применяет инструмент повышения контраста к первому изображению, размещенному в окне отображения.
Функция hfigure = imcontrast(...) возвращает управление средствами усиления контраста в окне просмотра.
Примечание:
В основу инструментария усиления контраста положено масштабирование гистограммы распределения значений яркости элементов изображения. Один из вариантов состоит в выравнивании гистограммы изображения, т.е. равномерном представлении пикселей с одинаковым значением яркости. Использование красной метки слева приводит к изменению гистограммы в сторону меньших значений. Минимальные значение и значения меньше минимума, отображаются как черные. Использование красной метки справа приводит к изменению гистограммы в сторону больших значений. Максимальные значение и значения больше максимума, отображаются как белые. Все промежуточные значения принимают различные оттенки серого.
Вместе минимальные и максимальные значения создаю так называемое "окно". Растяжение окна приводит к уменьшению контраста. Сжатие окна приводит к повышению контраста. Изменение центра окна приводит к изменению яркостей изображения. Возможным является также ручной ввод значений минимума, максимума, размерности и центра окна. Изменение этих значений автоматически влияет на изменение значений других элементов изображения.
Совместные параметры окно/значение:
После создания средств регулировки контраста, автоматически активируется иконка окно/значение в окне просмотра. Значения этого окна можно изменять с помощью курсора. С помощью курсора можно также изменять контраст и яркость изображения. Перемещение мышки горизонтально слева направо приводит к изменению размера окна (т.е. контраста). Перемещение мышки вертикально сверху вниз приводит к изменению центра окна (т.е. яркости). Удерживание клавиши Ctrl приводит к усилению изменений, а удерживание клавиши Shift - к ослаблению изменений.
Пример:
imshow('pout.tif')
imcontrast(gca)
conv2 - свертка изображений
Синтаксис:
Z=conv2(X, Y)
Z=conv2(hcol, hrow, X)
Z=conv2(…, shape)
Описание:
Функция Z=conv2(X, Y) вычисляет свертку Z двух изображений [1], представленных в виде двумерных массивов X и Y. Если эти массивы соответственно имеют размеры mx*my, то размер массива Z равен (mx+my-1)*(nx+ny-1).
Функция Z=conv2(hcol, hrow, X) выполняет свертку двумерного массива X с вектором-столбцом hcol и вектором-строкой hrow.
Функция Z=conv2(…, shape) с помощью параметра shape управляет размером массива Z. Параметр shape может принимать следующие значения:
- ‘full’ - полноразмерная свертка;
- ‘same’ - центральная часть размера mx*my;
- ‘valid’ - центральная часть размера (mx-my+1)*(nx-ny+1) при условии, что (mx*my)>(my*ny).
При использовании значений ‘same’ и ‘valid’ изображение необходимо задавать в параметре X, а коэффициенты фильтра (маску) - в параметре Y. Если используется значение ‘full’, то порядок задания параметров может быть произвольным.
Процедура conv2 выполняется наиболее эффективно при условии, что (mx*my)>(my*ny), т.е. если количество элементов массива X превосходит количество элементов массива Y.
Результирующий массив Z имеет формат представления данных double.
convn - свертка N–мерных сигналов
Синтаксис:
Z=convn(X, Y)
Z=convn(X, Y, shape)
Описание:
Функция Z=convn(X, Y) вычисляет свертку Z многомерных массивов X и Y. Если эти массивы соответственно имеют размеры size(X) и size(Y), то размер массива Z равен size(X)+size(Y)-1.
Функция Z=convn(X, Y, shape) с помощью параметра shape управляет размером массива Z. Параметр shape может принимать следующие значения:
- 'full' - полноразмерная свертка (по умолчанию);
-''same' - центральный фрагмент размера size(Z);
- ''valid' - фрагмент полной свертки, при вычислении которого не использованы части входного массива Х, дополненные нулями.
Результирующий массив Z имеет формат представления данных double.
convmtx2 - вычисление матрицы свертки
Синтаксис:
T=convmtx2(H, m, n)
T=convmtx2(H, [m n])
Описание:
Функции T=convmtx2(H, m, n) и T=convmtx2(H, [m n]) возвращают матрицу свертки Т для матрицы Н. Если Х - матрица размера mxn, то conv2(X, H) эквивалентно reshape(T*X(:), size(H)*m*n).
Исходные массивы должны иметь формат представления данных double. Результирующая матрица Т является разреженным массивом (sparse). Число ненулевых элементов матрицы Т не превышает prod(size(H)*m*n).
filter2 - двумерная линейная фильтрация
Синтаксис:
D=filter2(h, S)
D=filter2(h, S, shape)
Описание:
Функция D=filter2(h, S) выполняет фильтрацию данных, заданных в двумерном массиве S, двумерным КИХ-фильтром, коэффициенты которого сведены в матрицу h, называемую также маской фильтра. Как правило, S и D являются полутоновыми изображениями. Результат фильтрации, возвращаемый в матрице D, вычисляется как двумерная свертка, выполняемая с помощью функции conv2. Матрица D имеет тот же размер, что и S. Для этого при проведении вычислений исходная матрица временно дополняется необходимым количеством нулевых строк и столбцов.
Результат выполнения функции D=filter2(h, S, shape) зависит от значения параметра shape. Если параметру присвоено значение ‘same’, то в D возвращается центральная часть свертки, размер которой равен размеру исходных данных - S. Это параметр используется по умолчанию. Если параметру присвоено значение ’full’, возвращается весь результат свертки. При этом size(D)>size(S). Если параметру присвоено значение valid, возвращается только та часть свертки, при вычислении которой использовались краевые части исходных данных, дополненные нулями. При этом size(D)>size(S).
Результат D имеет формат представления данных double.
Алгоритм:
В функции filter2 для выполнения двумерной свертки исходных данных с маской фильтра используется функция conv2. Для передачи в функцию conv2 маска h поворачивается на 1800: conv2(S, rot90(h, 2), shape).
freqz2 - двумерная АЧХ
Синтаксис:
[h, f1, f2]=freqz2(h, n1, n2)
[h, f1, f2]=freqz2(h, [n1 n2])
[H, f1, f2]=freqz2(h, f1, f2)
[…]=freq2(h, n1, n2, [dx dy])
[…]=freq2(h, n1, n2, dx)
[…]=freq2(h, f1, f2, [dx dy])
[…]=freq2(h, f1, f2, dx)
freq2(…)
Описание:
Функция [h, f1, f2]=freqz2(h, n1, n2) формирует матрицу Н размера n1
 n2, которая является АЧХ на частотах, содержащихся в векторах f1 и f2 линейного двумерного КИХ-фильтра с маской h. В векторы f1 и f2 функция помещает равномерно распределенные нормализованные значения частот в диапазоне [-1, 1], где 1 соответствует половине частоты дискретизации (частоте Найквиста). Вектор f1 содержит n1 значений частоты, а вектор f2 содержит n2 значений частоты. Если при вызове функции параметры n1 и n2 опущены, то они берутся равными n1=n2=64.
n2, которая является АЧХ на частотах, содержащихся в векторах f1 и f2 линейного двумерного КИХ-фильтра с маской h. В векторы f1 и f2 функция помещает равномерно распределенные нормализованные значения частот в диапазоне [-1, 1], где 1 соответствует половине частоты дискретизации (частоте Найквиста). Вектор f1 содержит n1 значений частоты, а вектор f2 содержит n2 значений частоты. Если при вызове функции параметры n1 и n2 опущены, то они берутся равными n1=n2=64.Функция [H, f1, f2]=freqz2(h, [n1 n2]) полностью аналогична функции [H, f1, f2]=freqz2(h, n1, n2).
Функция [H, f1, f2]=freqz2(h, f1, f2) формирует матрицу Н, которая является АЧХ на частотах f1 и f2 линейного двумерного КИХ-фильтра с маской h. В векторы f1 и f2 должны быть помещены нормализованные значения частот в диапазоне [-1, 1]. Матрица Н имеет размер length(f1)
.gif) length(f2).
length(f2).В функциях […]=freq2(h, n1, n2, [dx dy]) и […]=freq2(h, f1, f2, [dx dy]) параметры dx и dy задают диапазоны изменения значений по осям частот как [-1/(2*dx), 1/(2dx)] для оси абсцисс и [-1/(2*dy), 1/(2dy)] для оси ординат. Например, если dx равно 1, то нормализованные частоты по оси абсцисс принадлежат диапазону [-0.5, 0.5], а если dx равно 5, то нормализованные частоты по оси абсцисс принадлежат диапазону [-0.1, 0.1].
В функциях […]=freq2(h, n1, n2, dx) и […]=freq2(h, f1, f2, dx) параметр dx задает одинаковые диапазоны изменения значений по осям частот: [-1/(2*dx, 1/(2*dx))].
Функция freq2(…) без выходных параметров выводит в текущее окно на экране двумерную АЧХ.
fspecial - задание маски предопределенного фильтра
Синтаксис:
h=fspecial(type, P1, P2)
Описание:
Функция h=fspecial(type, P1, P2) возвращает маску h предопределенного двумерного линейного фильтра, задаваемого строкой type. Маска h предназначена для передачи в функции filter2 или conv2, выполняющих двумерную линейную фильтрацию. В зависимости от типа фильтра для него могут быть определены один или два дополнительных параметра Р1, Р2. Ниже будут рассмотрены возможные варианты функции fspecial.
Функция h=fspecial(‘gausian’, n, sigma) возвращает маску h фильтра нижних частот Гаусса. Размер маски определяет параметр n. Если n - двухкомпонентный вектор, то размер маски n(1)
.gif) n(2). Если n скаляр, то размер маски n
n(2). Если n скаляр, то размер маски n.gif) n. Параметр sigma задает среднеквадратическое отклонение распределения Гаусса, которое используется при формировании маски h. Если при вызове функции параметры n и sigma опущены, то размер маски устанавливается равным 3
n. Параметр sigma задает среднеквадратическое отклонение распределения Гаусса, которое используется при формировании маски h. Если при вызове функции параметры n и sigma опущены, то размер маски устанавливается равным 3.gif) 3, а среднеквадратическое отклонение 0.5.
3, а среднеквадратическое отклонение 0.5.Функция h=fspecial(‘sobel’) возвращает маску фильтра Собеля для выделения горизонтальных границ:
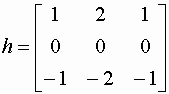 .
.Для выделения вертикальных границ достаточно транспонировать данную маску h.
Функция h=fspecial(‘prewitt’) возвращает маску фильтра Превита для выделения горизонтальных границ:
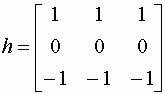 .
.Для выделения вертикальных границ достаточно транспонировать данную маску h.
Функция h=fspecial(‘laplasian’, a) возвращает маску h ВЧ фильтра Лапласа. Размер маски 3
.gif) 3. Параметр а управляет соотношением между центральным и граничными элементами маски. Данный параметр должен устанавливаться в диапазоне [0, 1]. По умолчанию а=0.2.
3. Параметр а управляет соотношением между центральным и граничными элементами маски. Данный параметр должен устанавливаться в диапазоне [0, 1]. По умолчанию а=0.2.Функция h=fspecial(‘log’, n, sigma) возвращает маску h фильтра, аналогичного последовательному применению фильтров Гаусса и Лапласа, так называемого лапласиана-гауссиана. Размер маски определяет параметр n. Если n - двухкомпонентный вектор, то размер маски n(1)
.gif) n(2). Если n - скаляр, то размер маски n
n(2). Если n - скаляр, то размер маски n.gif) n. Параметр sigma задает среднеквадратическое отклонение Гаусса, которое используется при формировании маски h. Если при вызове функции параметры n и sigma опущены, то размер маски устанавливается равным 5
n. Параметр sigma задает среднеквадратическое отклонение Гаусса, которое используется при формировании маски h. Если при вызове функции параметры n и sigma опущены, то размер маски устанавливается равным 5.gif) 5, а среднеквадратическое отклонение 0.5.
5, а среднеквадратическое отклонение 0.5.Функция h=fspecial(‘average’, n) возвращает маску h усредняющего НЧ фильтра. Размер маски определяет параметр n. Если n - двухкомпонентный вектор, то размер маски n(1)
.gif) n(2). Если n - скаляр, то размер маски n
n(2). Если n - скаляр, то размер маски n.gif) n. Если при вызове функции параметр n опущен, то размер маски устанавливается равным 3
n. Если при вызове функции параметр n опущен, то размер маски устанавливается равным 3.gif) 3.
3.Функция h=fspecial(‘unsharp’, a) возвращает маску h фильтра, повышающего резкость изображения. Размер маски 3
.gif) 3. Параметр а управляет соотношением между центральным и граничными элементами маски. Данный параметр должен устанавливаться в диапазоне [0, 1]. По умолчанию а=0.2.
3. Параметр а управляет соотношением между центральным и граничными элементами маски. Данный параметр должен устанавливаться в диапазоне [0, 1]. По умолчанию а=0.2.Алгоритмы:
Усредняющий фильтр относится к фильтрам нижних частот. Он предназначен для фильтрации высокочастотного шума, и его работа сопровождается размытием изображения. Каждый элемент маски равен 1/MN, где М и N - размеры маски (количество строк и столбцов).
Фильтр Гаусса также относится к НЧ фильтрам. В отличие от усредняющего фильтра он в меньшей мере размывает обрабатываемое изображение [1]. Маска фильтра такова, что центральный элемент маски имеет наибольшее значение, он соответствует пику распределения Гаусса. Значения остальных элементов уменьшаются по мере удаления от центрального элемента. Уменьшение происходит в соответствии с распределением Гаусса. Маска формируется с использованием следующих соотношений:
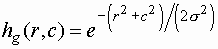 ;
;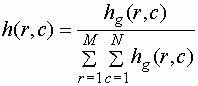 ,
,где M и N - размеры маски;
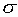 - среднеквадратическое отклонение распределения Гаусса.
- среднеквадратическое отклонение распределения Гаусса.Фильтр Лапласа относится к ВЧ фильтрам и предназначен для выделения границ (перепадов) во всех направлениях [1]. Маска фильтра конструируется следующим образом:
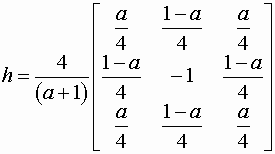 ,
,где
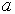 - параметр в диапазоне [0,1], передаваемый в функцию fspecial.
- параметр в диапазоне [0,1], передаваемый в функцию fspecial.Лапласиан-гауссиан также относится к ВЧ фильтрам, но в отличие от фильтра Лапласа выделяет более резкие перепады. Маска фильтра создается по формуле
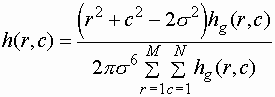 ,
,где M и N - размеры маски;
.gif) - среднеквадратическое отклонение распределения Гаусса.
- среднеквадратическое отклонение распределения Гаусса.Формула для вычисления
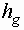 выведена выше.
выведена выше.Маска фильтра, повышающего резкость изображения, создается следующим образом:
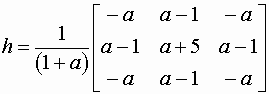 ,
,где
.gif) - параметр в диапазоне [0,1], передаваемый в функцию fspecial.
- параметр в диапазоне [0,1], передаваемый в функцию fspecial.Пример:
Рассмотрим, каким образом влияет среднеквадратическое отклонение распределения Гаусса на элементы маски фильтра Гаусса, возвращаемые функцией fspecial. Получим значения маски фильтра Гаусса размера 5
.gif) 5 для среднеквадратического отклонения 0.5 и 0.7. На рис. 1 а приведена частотная характеристика фильтра Гаусса с маской h05, а на рис. 1 б - частотная характеристика фильтра Гаусса с маской h07.
5 для среднеквадратического отклонения 0.5 и 0.7. На рис. 1 а приведена частотная характеристика фильтра Гаусса с маской h05, а на рис. 1 б - частотная характеристика фильтра Гаусса с маской h07.%Пример демонстрирует формирование маски фильтра Гаусса
%с помощью функции fspecial.
%Создание маски для фильтра Гаусса размера 5
.gif) 5
5%и со среднеквадратическим отклонением 0.5.
h05=fspecial(‘gaussian’, 5, 0.5)
%Будет выведено:
%h05 =
% 0.0000 0.0000 0.0002 0.0000 0.0000
% 0.0000 0.0113 0.0837 0.0113 0.0000
% 0.0002 0.0837 0.6187 0.0837 0.0002
% 0.0000 0.0113 0.0837 0.0113 0.0000
% 0.0000 0.0000 0.0002 0.0000 0.0000
%Создание маски для фильтра Гаусса размера 5
.gif) 5
5%и со среднеквадратическим отклонением 0.7.
h07=fspecial(‘gaussian’, 5, 0.7)
%Будет выведено:
%h07 =
% 0.0001 0.0020 0.0055 0.0020 0.0001
% 0.0020 0.0422 0.1171 0.0422 0.0020
% 0.0055 0.1171 0.3248 0.1171 0.0055
% 0.0020 0.0422 0.1171 0.0422 0.0020
% 0.0001 0.0020 0.0055 0.0020 0.0001
%Вывод на экран частотных характеристики линейных фильтров
%с масками h05 и h07.
freqz2(h05, [32 32]);
figure, freqz2(h07, [32 32]);
а)
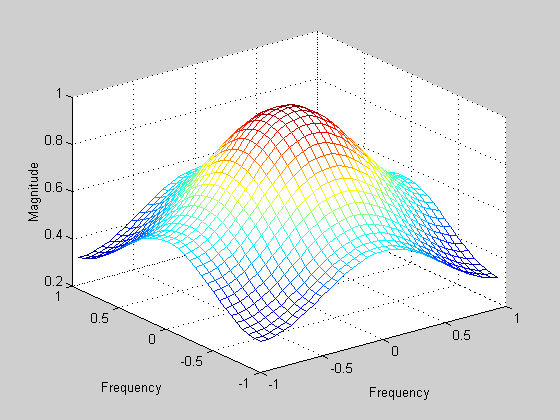
б)
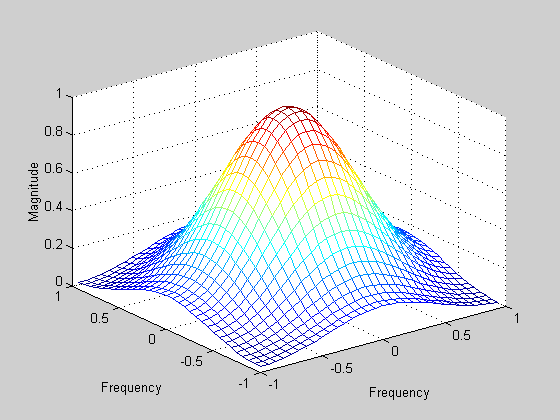
Рис. 1.
fsamp2 - формирование маски линейного фильтра по желаемой АЧХ
Синтаксис:
h=fsamp2(H)
h=fsamp2(f1, f2, H, [m n])
Описание:
Задача линейной фильтрации связана с применением линейной системы для извлечения сигнала из суммы сигнала и шума. С точки зрения векторного пространства задачей линейной фильтрации можно считать определение такого линейного преобразования в векторном пространстве, которое сводит длину или норму вектора ошибки к минимуму. Обобщение понятия линейной фильтрации может производиться при фильтрации сигнала и шума, которые комбинируются неаддитивно, лишь при условии, что правило их комбинирования удовлетворяет алгебраическим постулатам векторного сложения. Далее рассмотрим возможности функции fsamp2.
Функция h=fsamp2(H) формирует маску с линейного двумерного КИХ-фильтра, основываясь на желаемой АЧХ двумерного фильтра, передаваемой в матрице Н. Маска h предназначена для передачи в функции filter2 или conv2, которые выполняют двумерную линейную фильтрацию. Размер маски h совпадает с размером матрицы Н. Значения АЧХ в матрице Н соответствуют частотам по осям абсцисс и ординат, равномерно распределенным в диапазоне [-1, 1], где 1 соответствует половине частоты дискретизации (частоте Найквиста).
.gif)
При формировании матрицы Н для получения более точного результата рекомендуется использовать отсчеты частоты, возвращаемые функцией freqspace.
Функция h=fsamp2(f1, f2, H, [m n]) формирует маску h размера mxn линейного двумерного КИХ-фильтра, основываясь на желаемой АЧХ двумерного фильтра Н, для частот, передаваемых в векторах f1 и f2. Векторы f1 и f2 содержат нормализированные значения частот в диапазоне [-1, 1], где 1 соответствует половине частоты дискретизации. Для получения маски фильтра h размера mxn используется аппроксимация по методу наименьших квадратов. Требуется, чтобы длина вектора f1 была не менее, чем n, а длина вектора f2 - не менее, чем m.
Алгоритм.
Для вычисления маски фильтра h функция fsamp2 выполняет обратное ДПФ желаемой АЧХ [1, 2]:
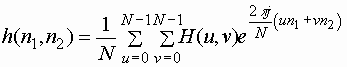
Пример.
Рассмотрим пример, демонстрирующий формирование маски двумерного линейного фильтра, повышающего резкость изображения. АЧХ такого фильтра должна быть равна 0 в начале координат и увеличиваться по мере удаления от начала координат. Один из возможных вариантов желаемой частотной характеристики приведен на рис. 1, а. По данной АЧХ fsamp2 создает маску h линейного фильтра, АЧХ которого приведена на рис. 1, б.
Исходное изображение с рис. 1, в фильтруется линейным фильтром с маской h. Результат фильтрации дополнительно контрастируется. Получившееся в итоге изображение показано на рис. 1, г.
%Пример демонстрирует повышение резкости изображения
%с помощью линейного КИХ-фильтра, сформированного по желаемой АЧХ.
%Получение нормализированных значений частот.
[f1 f2]=freqspace(15, 'meshgrid');
%Формирование желаемой АЧХ, как функции расстояния от начала координат.
%Для вычисления расстояния используется так называемая метрика городских кварталов.
dist=abs(f1)+abs(f2);
H=dist/max(dist(:));
%Вывод на экран желаемой АЧХ.
mesh(f1,f2,H), colormap(cool(32));
%Формирование маски КИХ-фильтра.
h=fsamp2(f1, f2, H, [5 5])
%Будет выведено:
%h =
% 0.0000 0.0000 -0.0012 0.0000 -0.0000
% -0.0000 0.0000 -0.1090 0.0000 -0.0000
% -0.0012 -0.1090 0.5333 -0.1090 -0.0012
% -0.0000 0.0000 -0.1090 -0.0000 -0.0000
% 0.0000 0.0000 -0.0012 -0.0000 0.0000
%Вывод на экран получившейся АЧХ.
figure, colormap(cool(32)), freqz2(h);
%Чтение исходного изображения и вывод его на экран.
i=imread('cameraman.tif');
figure, imshow(i);
%Фильтрация изображения.
i=mat2gray(filter2(h, im2double(i)));
%Контрастирование результата фильтрации.
i=imadjust(i, [0 0.8], []);
%Вывод результирующего изображения на экран.
figure, imshow(i);
а)
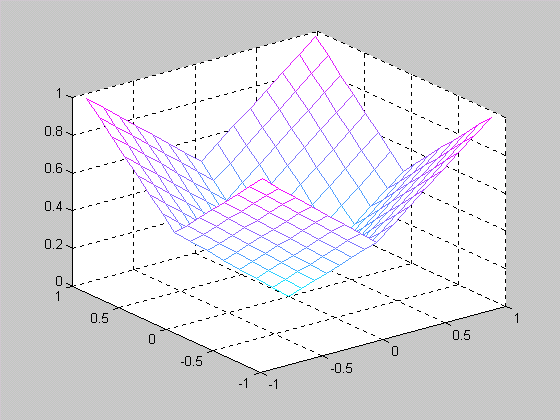
б)
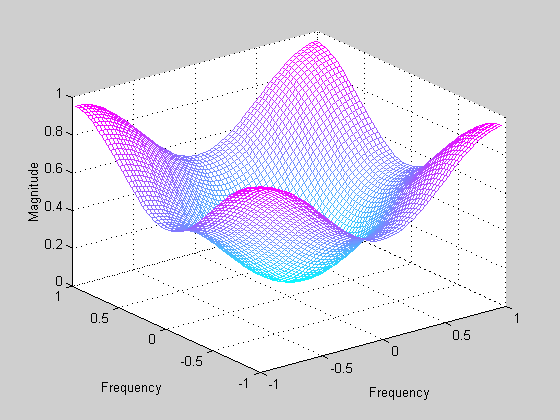


в) г)
Рис. 1.
ftrans2 - формирование маски линейного фильтра методом преобразования частот
Синтаксис:
h=ftrans2(b)
h=ftrans2(b, t)
Описание:
Функция h=ftrans2(b) формирует маску h линейного двумерного КИХ-фильтра, используя метод преобразования частот для трансформации одномерного КИХ-фильтра с коэффициентом b. Вектор b коэффициентов фильтра возвращают функции fir1, fir2, remez из Signal Processing Toolbox. Метод преобразования частот трансформирует одномерный КИХ-фильтр в двумерный [5]. Для преобразования частот используется специальная матрица трансформации t. По умолчанию применяется матрица Мак-Клеллана:
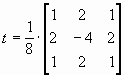 .
.В функции h=ftrans2(b, t) можно указать иную матрицу трансформации t.
Маска h предназначена для передачи в функции filter2 или conv2, которые выполняют двумерную линейную фильтрацию.
Алгоритм:
Метод преобразования частот [2-4] заключается в том, что АЧХ двумерного фильтра формируется как
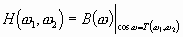 ,
,где
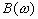 - ДПФ одномерного фильтра b:
- ДПФ одномерного фильтра b: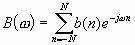 ;
;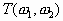 - двумерное ДПФ матрицы трансформации t:
- двумерное ДПФ матрицы трансформации t: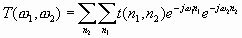 .
.Для вычисления маски фильтра h выполняется обратное ПФ АЧХ
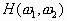 [1]:
[1]: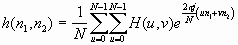 .
.Пример:
Рассмотрим, как формируется двумерный ФНЧ по одномерному с помощью метода преобразования частот. Создадим одномерный КИХ ФНЧ 14-го порядка с частотой среза 0.2. АЧХ и ФНЧ такого фильтра приведены на рис. 1, а. С помощью функции ftrans2 одномерный ФНЧ трансформируется в двумерный. АЧХ двумерного ФНЧ приведена на рис. 1, б.
На рис. 1, в показано исходное изображение, полученное в результате сканирования полиграфической иллюстрации. Данное изображение имеет характерный дефект - паразитную регулярную структуру, которая возникает в результате сканирования. Подобные дефекты называют муаром. Для подавления муара исходное изображение необходимо размыть. Это можно сделать с помощью созданного двумерного ФНЧ. Результат фильтрации показан на рис. 1, г.
%Пример демонстрирует размытие изображения
%с целью подавления муара.
%Размытие выполняется с помощью линейного двумерного КИХ ФНЧ,
%сформированного из одномерного ФНЧ
%методом преобразования частот.
%Создание одномерного КИХ ФНЧ 14-го порядка
%с частотой среза 0.2.
b=fir1(14, 0.2);
%Вывод на экран АЧХ и ФНЧ созданного одномерного фильтра.
freqz(b, 1, 256);
%Формирование двумерного фильтра из одномерного.
h=ftrans2(b);
%Вывод на экран АЧХ двумерного фильтра.
figure, freqz2(h);
%Чтение исходного изображения из файла и вывод его на экран.
I=imread(‘image1.bmp’);
I=im2double(I);
figure, imshow(I);
%Фильтрация изображения и вывод на экран результата фильтрации.
I=filter2(h,I);
figure, imshow(I);
а) 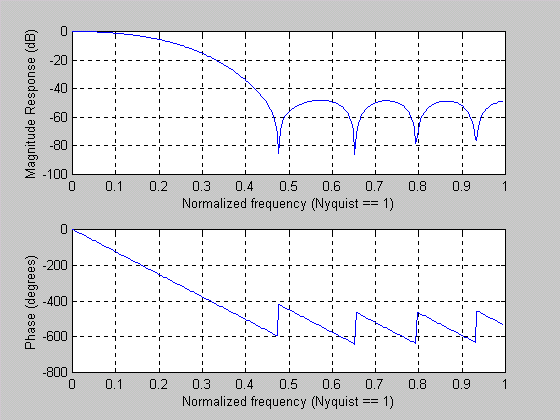
б) 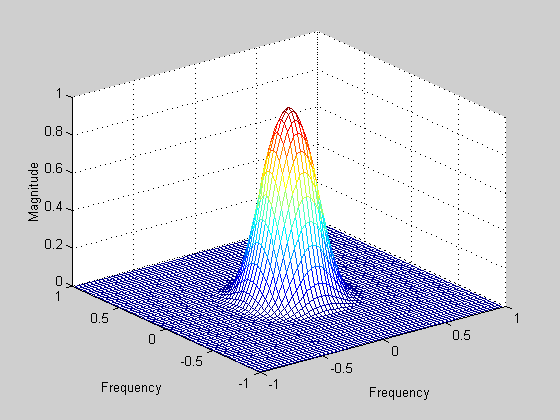


в) г) Рис.1.
fwind1 - формирование маски линейного фильтра по желаемой АЧХ с использованием одномерного окна
Синтаксис:
h=fwind1(H, win)
h=fwind1(H, win1, win2)
h=fwind1(f1, f2, H, …)
Описание:
Функция h=fwind1(H, win) формирует маску h линейного двумерного КИХ-фильтра, основываясь на желаемой АЧХ двумерного фильтра, передаваемой в матрице Н. Значения АЧХ в матрице Н соответствуют частотам по осям абсцисс и ординат, равномерно распределенным в диапазоне [-1, 1], где 1 соответствует половине частоты дискретизации (частоте Найквиста). При формировании матрицы Н для получения более точного результата рекомендуется использовать отсчеты частоты возвращаемой функцией freqspace.
В параметре win передается одномерное окно. Получить различные виды окон можно с помощью функций SPT: boxcar, hammimg, hanning, bartlett, blackman, kaiser, chebwin. Для формирования двумерного окна из одномерного используется метод Хуанга (см. ниже). Для вычисления маски фильтра h выполняется обратное ДПФ желаемой АЧХ и умножение на матрицу двумерного окна.
Маска h предназначена для передачи в функции filter2 или conv2, которые выполняют двумерную линейную фильтрацию. Размер маски h равен length(win)
.gif) length(win).
length(win).Функция h=fwind1(H, win1, win2) формирует маску h линейного двумерного КИХ-фильтра, основываясь на Н - желаемой АЧХ двумерного фильтра и двумерном окне, созданном по двум одномерным win1 и win2. Размер маски h равен length(win1)
.gif) length(win2).
length(win2).Функция h=fwind1(f1, f2, H, …) формирует маску h линейного двумерного КИХ-фильтра, основываясь на желаемой АЧХ двумерного фильтра Н для частот, передаваемых в векторах f1 и f2. Векторы f1 и f2 содержат нормированные значения частот в диапазоне [-1, 1], где 1 соответствует половине частоты дискретизации. Размер маски h определяется размером окон, как это описано выше.
Алгоритм:
В методе Хуанга радиально-симметричное двумерное окно
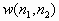 создается из одномерного окна
создается из одномерного окна 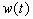 как
как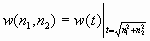 .
.При задании двух одномерных окон
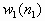 и
и 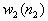 двумерное окно
двумерное окно 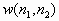 создается как их произведение:
создается как их произведение: 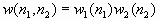 .
.Для вычисления маски фильтра h выполняет обратное преобразование Фурье желаемой АЧХ и умножение на матрицу двумерного окна:
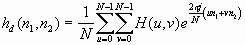 ;
;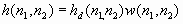 .
.fwind2 - формирование маски линейного фильтра по желаемой АЧХ с использованием двумерного окна
Синтаксис:
h=fwind2(H, win2)
h=fwind2(f1, f2, H, win2)
Описание:
Функция h=fwind2(H, win2) формирует маску h линейного двумерного КИХ-фильтра, используя двумерное окно win2 и основываясь на желаемой АЧХ двумерного фильтра, передаваемой в матрице Н. Значения АЧХ в матрице Н соответствуют частотам по осям абсцисс и ординат, равномерно распределенным в диапазоне [-1, 1], где 1 соответствует половине частоты дискретизации. При формировании матрицы Н для получения более точного результата рекомендуется использовать отсчеты частоты, возвращаемые функцией freqspase.
Маска h предназначена для передачи в функции filter2 или conv2, которые выполняют двумерную линейную фильтрацию. Размер маски h равен размеру двумерного окна win2.
Функция h=fwind2(f1, f2, H, win2) формирует маску h линейного двумерного КИХ-фильтра, используя двумерное окно win2 и основываясь на желаемой АЧХ двумерного фильтра Н для частот, передаваемых в векторах f1 и f2. Векторы f1 и f2 содержат нормализованные значения частот в диапазоне [-1, 1], где 1 соответствует половине частоты дискретизации. Размер маски h также равен размеру двумерного окна win2.
Алгоритм:
Для вычисления маски фильтра h данная функция выполняет обратное преобразование Фурье желаемой АЧХ и умножение на матрицу двумерного окна
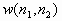 :
: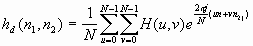 ;
;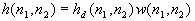 .
.blkproc - обработка блоков изображения
Синтаксис:
D=blkproc(S, [m n], fun)
D=blkproc(S, [m n], fun, P1, P2, …)
D=blkproc(S, [m n], [mborder nborder], fun, …)
D=blkproc(S, ‘indexed’, …)
Описание:
Функция D=blkproc(S, [m n], fun) формирует новое изображение D, пиксели которого являются результатом обработки функцией fun каждого из неперекрывающихся блоков размера
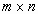 исходного изображения S. Данная функция предназначена для обработки бинарных или полутоновых изображений. Исходное изображение S разбивается на неперекрывающиеся блоки
исходного изображения S. Данная функция предназначена для обработки бинарных или полутоновых изображений. Исходное изображение S разбивается на неперекрывающиеся блоки .gif) пикселей. Блоки располагаются вплотную друг к другу, начиная с левого верхнего угла изображения. При проведении вычислений исходное изображение временно дополняется столбцами нулей справа и строками нулей снизу так, чтобы размеры изображений были кратны соответствующим размерам блока. Например, на рис. 1 исходное изображение имеет 10 строк и 9 столбцов. Если для обработки использовать блок [3 4], то изображение дополняется двумя строками и тремя столбцами нулевых пикселей.
пикселей. Блоки располагаются вплотную друг к другу, начиная с левого верхнего угла изображения. При проведении вычислений исходное изображение временно дополняется столбцами нулей справа и строками нулей снизу так, чтобы размеры изображений были кратны соответствующим размерам блока. Например, на рис. 1 исходное изображение имеет 10 строк и 9 столбцов. Если для обработки использовать блок [3 4], то изображение дополняется двумя строками и тремя столбцами нулевых пикселей.
Рис. 1.
Существует 3 варианта задания параметра fun. Имя х является условным обозначением обрабатываемого блока изображения.
Параметр fun Пример Комментарий Строка - имя функции D=blkproc(S, [m n], ‘myfunc’); Предварительно должна быть реализована функция myfunc, которая получает в качестве параметра блок х и возвращает матрицу или скаляр y: y=myfunc(x). Строка - выражение языка D=blkproc(S, [m n], ‘mean2(x)*ones(size(x))’); В строку помещается выражение, допустимое синтаксисом MATLAB. Это выражение интерпретируется при выполнении каждого блока. inline - функция f=inline(‘std2(x)*ones(size(x))’);
D=blkproc(S, [m n], f);В качестве параметра функции inlineуказывается строка - выражение языка MATLAB. Оно компилируется и создается так называемая функция inline - функция, которая вызывается при обработке каждого блока. Использование inline - функций предпочтительнее по временным затратам. В результате обработки каждого блока создается матрица, вектор или скаляр, из которых формируется результирующее изображение D. Таким образом, размеры исходного и результирующего изображения, как правило, различаются.
Функция D=blkproc(S, [m n], fun, P1, P2, …) формирует изображение D, передавая в функцию fun дополнительные параметры Р1, Р2 и т.д.
Функция D=blkproc(S, [m n], [mborder nborder], fun, …) формирует изображение D, пиксели которого являются результатом обработки функцией fun частично перекрывающихся блоков размера
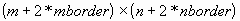 исходного изображения S. Каждый блок размера
исходного изображения S. Каждый блок размера .gif) расширяется вверх и вниз на mborder строк, а также вправо и влево на nborder столбцов. При этом центральные части размера
расширяется вверх и вниз на mborder строк, а также вправо и влево на nborder столбцов. При этом центральные части размера .gif) (ядра) расширенных блоков не перекрываются друг с другом и располагаются, как и в предыдущем рассмотренном случае, последовательно начиная от левого верхнего угла изображения. В этом случае при проведении вычислений исходное изображение временно дополняется столбцами нулей справа и строками нулей снизу, чтобы размеры изображений были кратны соответствующим размерам блока
(ядра) расширенных блоков не перекрываются друг с другом и располагаются, как и в предыдущем рассмотренном случае, последовательно начиная от левого верхнего угла изображения. В этом случае при проведении вычислений исходное изображение временно дополняется столбцами нулей справа и строками нулей снизу, чтобы размеры изображений были кратны соответствующим размерам блока .gif) , и дополнительно на mborder строк вверх и вниз и на nborder столбцов вправо и влево. Рис. 2 демонстрирует расположение двух соседних по диагонали блоков с размерами ядра 3х4 и mborder=1 nborder=2 на изображении, имеющем 10 строк и 9 столбцов. При вычислении изображение будет расширено на 3 строки вниз, 1 строку вверх, 5 столбцов вправо и 2 столбца влево.
, и дополнительно на mborder строк вверх и вниз и на nborder столбцов вправо и влево. Рис. 2 демонстрирует расположение двух соседних по диагонали блоков с размерами ядра 3х4 и mborder=1 nborder=2 на изображении, имеющем 10 строк и 9 столбцов. При вычислении изображение будет расширено на 3 строки вниз, 1 строку вверх, 5 столбцов вправо и 2 столбца влево.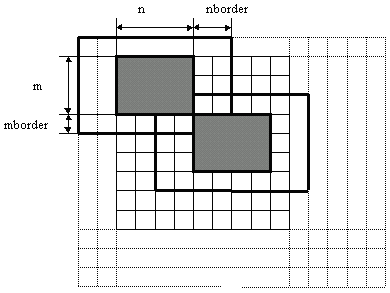
Рис. 2.
Формат представления данных изображений S и D определяется реализацией функции fun.
Функция D=blkproc(S, ‘indexed’, …) аналогична рассмотренным выше, но предназначена для обработки палитровых изображений. При проведении вычислений исходное изображение временно дополняется либо единицами при формате представления данных Xs-double, либо нулями при формате представления данных Xs-uint8.
Повысить эффективность обработки блоков можно с помощью функции colfilt, которая предварительно преобразует блоки в столбцы.
Пример:
Рассмотрим выравнивание фона изображения с использованием функции blkproc. Неравномерный фон является серьезным дефектом изображений, который ухудшает визуальное восприятие и мешает выделению объектов с помощью порогового ограничения.
Исходное биомедицинское изображение показано на рис. 3,а. Это изображение характеризуется значительной неравномерностью фона. С помощью функции blkproc оценим яркость фона как среднее значение яркостей пикселей в блоках 25х25 пикселей. В результате работы blkproc получается изображение с размером в 25 раз меньшим, чем исходное. Для того чтобы изображение фона и исходное изображение были одинакового размера, изображение фона увеличивается с помощью функции imresize. Полученная оценка фона показана на рис. 3,б.
Если вычесть изображение фона из исходного изображения, то получится изображение с равномерным фоном. Добавление константы 0.5 необходимо для того, чтобы значения пикселей получившегося изображения были в диапазоне [0, 1]. Функцией imadjast результирующее изображение дополнительно контрастируется. Получившийся результат показан на рис. 3,в.
%Пример демонстрирует выравнивание фона.
%Чтение изображения.
I=imresd(‘image03.tif’);
I=im2double(I);
%Вывод на экран.
imshow(I);
%Получение оценки фона изображения как среднего
%в блоках 25х25 пикселей.
F=inline(‘mean2(x)’);
fon=blkproc(I, [25 25],f);
fon=imresize(fon, size(I), ‘bicubic’);
figure, imshow(fon);
%Вычитаем фон и контрастируем получившееся изображение.
I=I-fon+0.5;
I=imadjust(I, [0.2 0.7], 1);
% Вывод на экран результата.
figure, imshow(I);
а) 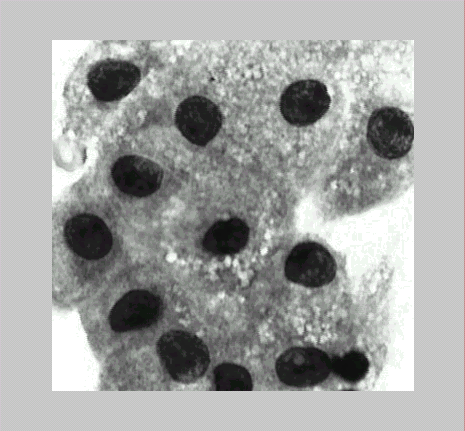
б) 
в) 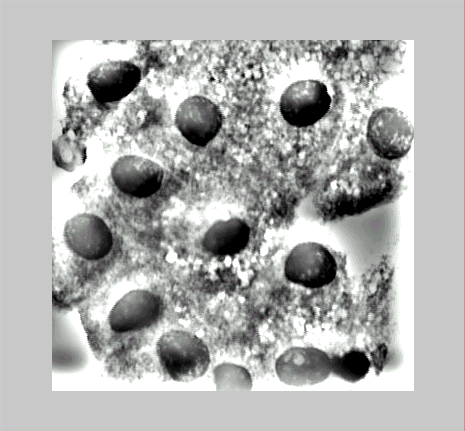
Рис. 3.
bestblk - определение размера блока
Синтаксис:
siz=bestblk([m n], k)
[mb, nb]=bestblk([m n], k)
Описание:
Функция siz=bestblk([m n], k) возвращает для изображения размера m
.gif) n оптимальный размер блока для обработки с помощью функции blkproc. Возвращаемый параметр siz является двухэлементным вектором, который содержит количество строк и столбцов в блоке. Параметр k определяет максимально возможное количество строк и столбцов в блоке. Если при вызове функции параметр k опущен, то ему присваивается значение 100.
n оптимальный размер блока для обработки с помощью функции blkproc. Возвращаемый параметр siz является двухэлементным вектором, который содержит количество строк и столбцов в блоке. Параметр k определяет максимально возможное количество строк и столбцов в блоке. Если при вызове функции параметр k опущен, то ему присваивается значение 100.Функция [mb, nb]=bestblk([m n], k) возвращает в mb количество строк, а в nb - количество столбцов блока.
Алгоритм:
Если
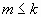 , то количество строк блока берется равным m. Иначе рассматриваются все значения в диапазоне [min(m/10, k/2), k] и выбирается количество строк блока, обеспечивающее наименьшее количество добавляемых к исходному изображению в функции blkproc нулевых строк.
, то количество строк блока берется равным m. Иначе рассматриваются все значения в диапазоне [min(m/10, k/2), k] и выбирается количество строк блока, обеспечивающее наименьшее количество добавляемых к исходному изображению в функции blkproc нулевых строк.Алгоритм для выбора количества столбцов блока аналогичен.
nlfilter - обобщенный нелинейный фильтр
Синтаксис:
D=nlfilter(S, [m n], fun)
D=nlfilter(S, [m n], fun, P1, P2)
Xd=nlfilter(Xs, ‘indexed’,…)
Описание:
Функция D=nlfilter(S, [m n], fun) формирует новое изображение D, пиксели которого являются результатом обработки функцией fun пикселей исходного изображения S, соответствующих положению маски фильтра размера mxn. Операция применяется нерекурсивно для всех положений маски. При проведении вычислений исходное изображение временно дополняется n/2 столбцами нулевых пикселей справа и слева, и m/2 строками нулевых пикселей сверху и снизу.
Данная функция предназначена для обработки бинарных или полутоновых изображений.
Существует 3 варианта задания параметра fun. Они приведены в таблице в описании функции blkproc. Через х должна быть обозначена матрица пикселей исходного изображения, соответствующих положению маски фильтра.
Функция D=nlfilter(S, [m n], fun, P1, P2) формирует изображение D, передавая в функцию fun дополнительные параметры Р1, Р2.
Формат представления данных изображений S и D определяется реализацией функции fun.
Функция Xd=nlfilter(Xs, ‘indexed’,…) аналогична рассмотренным выше, но предназначена для обработки палитровых изображений. При проведении вычислений исходное изображение временно дополняется либо единицами при формате представления данных Xs-double, либо нулями при формате представления данных Xs-uint8.
Повысить скорость осуществления нелинейной фильтрации можно с помощью функции colfilt, которая предварительно преобразует пиксели окна в столбцы.
Пример:
Реализуем с помощью функции nlfilter операцию усреднения с порогом. Данная операция предназначена для фильтрации импульсного шума. Смысл операции усреднения с порогом состоит в том, что центральному пикселю в пределах окна присваивается среднее значение яркости всех пикселей в пределах окна только в том случае, если разница между исходным значением центрального пикселя и средним больше некоторого порогового значения. В результате импульсная помеха отфильтровывается, а изображение не размывается так сильно, как при простой усредняющей фильтрации [1].
На рис. 1,а приведено исходное изображение, поврежденное импульсным шумом. На рис. 1,б - результат фильтрации.
%Пример демонстрирует работу усредняющего фильтра с порогом.
%Чтение исходного изображения и вывод его на экран.
I=imread(‘bacteria.tif’);
I=im2double(I);
imshow(I);
%Усредняющая фильтрация с порогом.
I=nlfilter(I, [3 3], ‘AverageWithTh’, 0.2);
%Вывод на экран результата фильтрации.
figure, imshow(I);
%AverageWithTh.m
%Функция усреднения с порогом.
function R=AverageWithTh(x, Th);
%Определяем размер маски.
[r c]=size(x);
n=r*c;
%Определяем координаты центрального пиксела окна.
r=floor((r+1)/2);
c=floor((c+1)/2);
%Результат усреднения.
s=sum(x(:))/n;
%Если разница центрального пиксела окна и среднего больше порога, то заменяем значение центрального
%пиксела на среднее.
if (abs(x(r, c)-s))>Th
R=s;
%Иначе значение текущего пиксела не изменяется.
else
R=x(r, c);
end;
end;
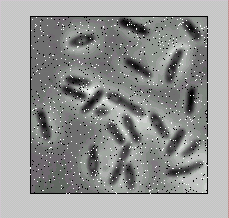
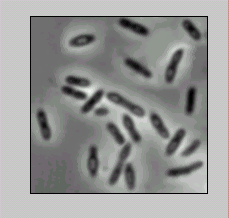
а) б) Рис. 1.
colfilt - оптимизированная операция фильтрации
Синтаксис:
D=colfilt(S, [m n], block_type, fun)
D=colfilt(S, [m n], block_type, fun, P1, P2, …)
Xd=colfilt(Xs, ‘indexed’, …)
Описание:
Функция D=colfilt(S, [m n], block_type, fun) выполняет операции фильтрации, полностью аналогичные выполняемым функциям blkproc или nlfilter, но значительно быстрее. Она предназначена для обработки полутоновых и бинарных изображений. Увеличение скорости обработки достигается за счет того, что обработке подвергается вспомогательное изображение, в котором каждый столбец представляет собой фрагмент исходного изображения S, передаваемый в функцию fun. Такой подход позволяет существенно уменьшить количество операций по чтению и записи отдельных пикселей изображения. Кроме того, каждый столбец может обрабатываться независимо от соседних. Для преобразования исходного изображения во вспомогательное и обратно в функции colfilt используются соответственно функции im2col и col2im.
Режим работы функции colfilt определяется значением параметра block_type:
-
Функция D=colfilt(S, [m n], block_type, fun, P1, P2, …) позволяет передавать дополнительные параметры Р1, Р2 и так далее при вызове функции fun.
Формат представления данных изображений S и D определяется реализацией функции fun.
Аналогично функциям blkproc и nlfilter с параметром ‘indexed’ функция Xd=colfilt(Xs, ‘indexed’, …) предназначена для обработки палитровых изображений и при проведении вычислений дополняет изображение либо единицами при формате представления данных Xs-double, либо нулями при формате представления данных Xs-uint8.
ordfilt2 - ранговая фильтрация
Синтаксис:
D=ordfilt2(S, order, domain);
D=ordfilt2(S, order, domain, S);
Описание:
Функция D=ordfilt2(S, order, domain) создает полутоновое изображение D, каждый пиксель которого формируется следующим образом. Пиксели исходного полутонового изображения S, соответствующие ненулевым элементам маски фильтра domain, сортируются по возрастанию. Пикселю изображения D, соответствующему центральному элементу маски, присваивается значение с номером order в отсортированном множестве. Операция применяется нерекурсивно для всех положений маски. Фильтрацию такого вида называют порядковой или ранговой [1].
Для того чтобы размеры изображений S и D были одинаковыми, при проведении вычислений изображение S временно дополняется необходимым количеством строк и столбцов нулевых пикселей. Формат представления данных результирующего изображения D совпадает с форматом исходного изображения S.
Функция D=ordfilt2(S, order, domain, S) работает аналогично функции ordfilt2(S, order, domain, A), за исключением того, что перед сортировкой к значениям пикселей, соответствующих ненулевым элементам маски фильтра domain, прибавляются значения из матрицы А. Матрицы domain и А должны быть одинакового размера. Матрица А имеет формат представления данных double. Соответственно формат представления данных результирующего изображения D - также double.
Пример:
С помощью функции рангового фильтра можно осуществить морфологические операции эрозии и наращения над полутоновым изображением. Эрозии соответствует замена значения центрального пикселя на минимальное из значений пикселей в пределах маски фильтра. Наращению соответствует замена значения центрального пикселя на максимальное из значений пикселей в пределах маски фильтра.
На рис. 2,а приведено исходное изображение, на рис. 2,б и 2,в - соответственно результаты эрозии и наращивания фона с маской из единиц размера 3х3. Так как фон данного изображения серый, то эрозия приводит к уменьшению фона, а наращивание - к его увеличению.
%Пример демонстрирует операции эрозии и наращения
%над полутоновым изображением.
%Чтение исходного изображения и вывод его на экран.
I=imread(‘image.tif’);
imshow(I);
%Эрозия полутонового изображения.
I_er=ordfilt2(I, 1, ones(3, 3));
figure, imshow(I_er);
%Наращение полутонового изображения.
I_dil=ordfilt2(I, 9, ones(3, 3));
figure, imshow(I_dil);
а)
б)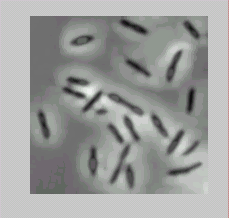
в)Рис. 2.
medfilt2 - медианная фильтрация
Синтаксис:
D=medfilt2(S, [m n])
Xd=medfilt2(Xs, ‘indexed’,...)
Описание:
Медианная фильтрация является частным случаем ранговой фильтрации.
Функция D=medfilt2(S, [m n]) создает полутоновое изображение D, каждый пиксель которого формируется следующим образом. Пиксели исходного полутонового изображения S, соответствующие всем элементам маски фильтра размера m
.gif) n, составляют упорядоченную последовательность А. Пикселю D(r, с), где r и с – координаты текущего положения центрального элемента маски, присваивается значение медианы последовательности А. Операция применяется нерекурсивно для всех положений маски.
n, составляют упорядоченную последовательность А. Пикселю D(r, с), где r и с – координаты текущего положения центрального элемента маски, присваивается значение медианы последовательности А. Операция применяется нерекурсивно для всех положений маски.Медианой упорядоченной последовательности A(i), где i=1...N, называется величина A((N + 1)/2), если N - нечетное, и (A(N/2) + A((N+2)/2))/2, если N - четное.
Для того чтобы размеры изображений S и D были одинаковыми, при проведении вычислений изображение S временно дополняется необходимым количеством строк и столбцов нулевых пикселей. Формат представления данных результирующего изображения D совпадает с форматом исходного изображения S.
Если вектор [m n] при вызове функции D=medfilt2(S) не задан, то в качестве маски фильтра используется маска размера 3
.gif) 3.
3.Функция Xd=medfilt2(Xs, 'indexed', ...) аналогична рассмотренной выше, но предназначена для обработки палитровых изображений. При проведении вычислений исходное изображение временно дополняется либо единицами при формате представления данных Xs–double, либо нулями при формате представления данных Xs–uint8.
Пример:
Медианная фильтрация может эффективно применяться для устранения импульсного шума [1, 2]. На рис. 1 б приведен результат медианной фильтрации с маской 3
.gif) 3 изображения на рис. 1,а.
3 изображения на рис. 1,а.% Пример демонстрирует работу медианного фильтра.
% Чтение исходного изображения и вывод его на экран.
I=imread('bacteria.tif');
imshow(l);
% Медианная фильтрация.
I=medfilt2(I);
% Вывод на экран результата фильтрации.
figure, imshow(I);
.gif)
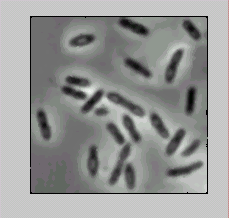
а) б) Рис.1.
wiener2 - адаптивная винеровская фильтрация
Синтаксис:
Id=wiener2(ls, [m n], noise)
[Id, noise]=wiener2(ls, [m n])
Описание:
Функция Id=wiener2(Is, [m n], noise) формирует полутоновое изображение Id, которое является результатом адаптивной фильтрации Винера исходного полутонового изображения Is. Параметры m иn задают размеры скользящего окна, в пределах которого оцениваются среднее и среднеквадратичное отклонение значений яркости. Если при вызове функции параметры m и n опущены, то размер окна устанавливается равным 3
.gif) 3.
3.Параметр noise устанавливает мощность гауссова белого шума, которым повреждено изображение. Этот параметр должен быть определен из каких–либо априорных сведений об изображении. Если это сделать не удается, то при вызове функции wiener2 параметр noise можно опустить. В этом случае мощность шума будет оцениваться автоматически.
Функция [Id, noise]=wiener2(Is, [m n]) работает аналогично описанной выше и дополнительно возвращает оценку мощности гауссова белого шума.
Форматы представления данных исходного и результирующего изображений совпадают.
Алгоритм:
Функция wiener2 использует алгоритм адаптивной винеровской фильтрации для подавления аддитивного гауссова белого шума. Данный алгоритм основан на статистических оценках фрагментов изображения в пределах скользящего окна размера n
.gif) m пикселей [1, 2].
m пикселей [1, 2].Для всех положений скользящего окна с центральным пикселем и координатами (r, с) вычисляются:
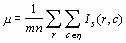 – средние значение яркости;
– средние значение яркости;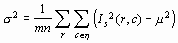 – дисперсия.
– дисперсия.Данная формула применяется нерекурсивно для всех положений скользящего окна.
Если мощность гауссова белого шума не задана, то она оценивается как среднее из всех
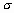 .
.roifilt2 - фильтрация областей интереса
Синтаксис:
Id=roifilt2(h, ls, BW)
Id=roifilt2(ls, BW, fun)
Id=roifilt2(ls, BW, fun, P1, P2, ...)
Описание:
Функция roifilt2 предназначена для фильтрации отдельных фрагментов полутоновых изображений. Эти фрагменты – области интереса (regions of interest) - задаются с помощью бинарного изображения BW. Размеры BW и исходного полутонового изображения Is должны совпадать. Единичные значения в BW указывают на то, что пиксели исходного изображения с такими же координатами принадлежат области интереса. Таким образом, если BW(r, с) равно 1, то Id(r, с) равно значению пикселя с координатами (r, с), полученного в результате фильтрации исходного изображения Is. Если BW(r, с) равно 0, то Id(r, с) равно Is(r, с), т. е. изменение изображения происходит только в областях интереса.
Функция Id=roifilt2(h, Is, BW) создает изображение Id как результат фильтрации областей интереса BW исходного изображения Is линейным фильтром с маской h. Для фильтрации функция roifilt2 вызывает функцию filter2. Результирующее изображение Id имеет формат представления данных double.
Функция Id =roifilt2(Is, BW, fun) создает изображение Id как результат фильтрации областей интереса BW исходного изображения Is с помощью функции fun. Существует 3 варианта задания параметра fun. Они приведены в таблице в описании функции blkproc. Именем X должно быть обозначено обрабатываемое полутоновое изображение Is. Возвращаемое функцией fun результирующее изображение у должно иметь размеры, равные размерам изображения X.
Функция Id=roifilt2(Is, BW, fun, PI, P2,. .) формирует изображение Id, передавая в функцию fun дополнительные параметры PI, P2, ...
Формат представления данных изображений Is и id определяется реализацией функции fun.
Пример:
Рассмотрим фильтрацию области интереса (в данном случае произвольной области) на примере изображения на рис. 1,а.
Использование фильтрации повышает контраст в области интереса. Результат фильтрации показан на рис. 1,б.
% Пример демонстрирует фильтрацию области интереса.
% Чтение изображения и вывод его на экран.
I=imread(‘bacteria.tif');
imshow(l);
% Создаем область интереса в середине исходного изображения.
[n m]=size(l);
BW=zeros(n,m);
BW(n/4 : 3*n/4, m/4 : 3*m/4) = 1;
% Устанавливаем маску для фильтрации.
h = [–1 –2–1 353–1 –2–1;
–1 –2–1353–1 –2–1;
–1 –2–1353–1 –2–1;
–1 –2–1353–1 –2–1;
–1 –2–1353–1 –2–1]/15;
% Фильтрация области интереса.
I2=roifilt2(h, I, BW);
% Вывод результата фильтрации на экран.
figure, imshow(I2).


а) б) Рис. 1.
imfilter - фильтрация двумерных и многомерных изображений
Синтаксис:
B=imfilter(A,H)
B=imfilter(A, H, option1, option2, ...)
Описание:
Функция B=imfilter(A, H) фильтрует многомерный массив A многомерным фильтром H. МассивA должен быть неразреженным числовым массивом любого формата и размерности.Результирующий массив B имеет ту же размерность и формат представления данных,что и массив A.
Каждый элементрезультирующего массива B вычисляется с использованием чисел удвоенной точностис плавающей точкой. Если A представляет собой массив целых чисел, тогдаэлементы результирующего массива, превышающие допустимый диапазон, усекаются иокругляются.
Функция B=imfilter(A, H, option1, option2, ...) выполняет многомерную фильтрацию всоответствии с заданными опциями. Аргументы опции могут принимать следующиезначения.
Граничныеопции.
Опция Описание Х Значения элементов внешних границ исходного массива принимают значения массива Х. Когда граничные опции не определены, функция imfilter использует значение X=0. 'symmetric' Значения элементов внешних границ исходного массива вычисляются как зеркальное отражение края этого массива. 'replicate' Значения элементов внешних границ исходного массива допускаются равными по значениям ближайшим элементам края массива. 'circular' Значения элементов внешних границ исходного массива вычисляются как периодическая структура исходного массива. Опциирезультирующих размеров.
Опция Описание 'same' Размеры результирующего массива совпадают с размерами исходного. Это свойство применяется по умолчанию, когда не указаны опции результирующих размеров. 'full' Результирующий массив содержит полный результат фильтрации. Его размеры больше, чем у исходного массива. Опциикорреляции и конволюции.
Опция Описание 'corr' Функция imfilter выполняет многомерную фильтрацию с использованием корреляции. Эта операция аналогична фильтрации, которая выполняется функцией filter2. Когда определены опции корреляции или конволюции, тогда функция imfilter использует корреляцию. 'conv' Функция imfilter выполняет многомерную фильтрацию с использованием конволюции. N-D конволюцияотносительно N-D корреляции является отражением матрицы фильтрации.
Пример.
Этот примердемонстрирует считывание трехмерного изображения в формате uint8(rgb-изображение). С помощью функции imshow осуществляется визуализацияизображения.
rgb=imread('flowers.tif');
imshow(rgb), title('Original')
Далее создаетсяфильтр h, который используется для аппроксимации линейного движения камеры.После применения функции imfilter к обработке трехмерного RGB изображения,создается новое изображение rgb2.
h=fspecial('motion', 50, 45);
rgb2=imfilter(rgb, h);
figure, imshow(rgb2), title('Filtered')
Отметим, что в функции imfilter память используется более эффективно, чем при других операцияхфильтрации, в которых результирующий массив имеет тот же формат представленияданных, что и исходный массив. В этом примере, формат представления данныхрезультирующего массива uint8.
whos rgb2Name Size Bytes Classrgb2 362x500x3 543000 uint8 array
Рассмотрим еще один пример фильтрации.
rgb3=imfilter(rgb, h, 'replicate');figure, imshow(rgb3), title('Filtered with boundary replication')
poly2mask - преобразование некоторой области в маску
Синтаксис:
BW=poly2mask(x, y, m, n)
Описание:
Функция BW=poly2mask(x, y, m, n) проводит вычисления бинарной маски области интереса BW на основе анализа этой же локальной области, представляя ее в виде векторов x и y. Размерность результата обработки BW равна mxn. Пиксели в BW, которые находятся внутри многоугольника (x, y), равны 1; пиксели вне этой области равны 0. Данные BW представляются в логическом формате.
Функция poly2mask проводит автоматическое закрытие области многоугольника.Пример.x=[63 186 54 190 63];y=[60 60 209 204 60];bw=poly2mask(x, y, 256, 256);imshow(bw)hold onplot(x, y, 'b', 'LineWidth', 2)hold offСоздание маски с использованием случайных точек.x=256*rand(1, 4);y=256*rand(1, 4);x(end+1)=x(1);y(end+1)=y(1);bw=poly2mask(x, y, 256, 256);imshow(bw)hold onplot(x, y, 'b', 'LineWidth', 2)hold off
qtdecomp - сегментация методом разделения
Синтаксис:
А=qtdecomp(l)
А=qtdecomp(l, threshold)
А=qtdecompO, threshold, mindim)
A=qtdecomp(l, threshold, [mindim maxdim])
A=qtdecomp(l, fun)
A=qtdecomp(l, fun, P1, P2, ...)
Описание:
Функция qtdecomp осуществляет сегментацию полутоновых изображений методом разделения. Суть метода заключается в следующем [1]. Изображение разбивается на неперекрывающиеся блоки. Каждый блок с помощью некоторого критерия проверяется на однородность. Если блок неоднороден, то он разбивается на блоки меньшего размера, каждый из которых, в свою очередь, проверяется на однородность. Процесс завершается тогда, когда ни один из блоков не может быть разделен, т. е. либо блоки однородны, либо их размеры достигли предельно малых величин. В результате работы алгоритма получается набор однородных блоков различного размера.
В функции qtdecomp каждый блок разбивается на 4 неперекрывающихся блока одинакового размера. На первом шаге алгоритма блоком считается все изображение. Мельчайшим по размерам является блок, который нельзя разделить на 4 блока одинакового размера, т. е. такой блок, у которого число строк или число столбцов нечетное. Таким образом, в функции qtdecomp рекомендуется использовать изображения с размерами, равными степеням двух. В этом случае мельчайший блок будет состоять из одного пикселя. При реализации алгоритма разделения используются структуры данных, основанные на квадро-деревьях. По этой причине данный алгоритм часто называют декомпозицией или разделением с помощью квадро-деревьев.
Функция А=qtdecomp(I) осуществляет сегментацию полутонового изображения I методом разделения и помещает результат в разреженный массив А (тип данных sparse MATLAB). Разреженный массив А конструируется следующим образом. Элементам матрицы А(r, с), соответствующим координатам левых верхних углов блоков на исходном изображении I, присваиваются значения, определяющие размеры каждого блока. Таким образом, большинство элементов матрицы равно нулю. И поэтому для хранения квадро-дерева применяется разреженный массив, который эффективно использует память, когда большинство элементов массива равно нулю. Для данной функции критерием однородности блока является равенство всех пикселей блока друг другу.
Функция А=qtdecomp(I, threshold) работает аналогично описанной выше, но в ней блок считается однородным, если разница между максимальным и минимальным значением пикселей блока меньше параметра threshold.
В функции А=qtdecomp(I, threshold, mindim) параметр mindim определяет минимальный размер блока. Неоднородный блок не разделяется, если в результате разделения получаются блоки размером менее mindim.
В функции А=qtdecomp(I, threshold, [mindim maxdim]) параметр mindim определяет минимальный, а параметр maxdim - максимальный размер блока. Неоднородный блок не разделяется, если в результате разделения получаются блоки размером менее mindim. Блок, превышающий размером maxdim, разделяется, даже если он однородный. Отношение параметров maxdim/mindim должно быть равно степени двух.
Функция А=qtdecomp(I, fun) позволяет для определения однородности блока передать вторым параметром собственную функцию fun. Существует 3 варианта задания параметра fun. Они приведены в таблице в описании функции blkproc. В функцию fun передается массив В из всех текущих блоков размера m
.gif) m, т. е. массив m
m, т. е. массив m.gif) m
m.gif) k, где k - количество блоков. В результате работы функции fun возвращается вектор Z длиной k элементов, состоящий из 0 и 1. Единица указывает на то, что соответствующий блок должен быть разделен, а нуль - на то, что блок не следует далее разделять, т. е. если Z(i) = 1, то блок В(:,:, i) должен быть разделен.
k, где k - количество блоков. В результате работы функции fun возвращается вектор Z длиной k элементов, состоящий из 0 и 1. Единица указывает на то, что соответствующий блок должен быть разделен, а нуль - на то, что блок не следует далее разделять, т. е. если Z(i) = 1, то блок В(:,:, i) должен быть разделен.Функция А=qtdecomp(I, fun, PI, P2, ...) позволяет передать в функцию fun дополнительные параметры PI, P2,...
Пример:
Рассмотрим работу функции qtdecomp совместно с функциями qtgetblk и qtsetblk для полутонового изображения размера 8
.gif) 8 пикселей. Формат представления данных изображения - uint8. Будем считать, что блок изображения является однородным, если величина разброса яркостей пикселей в блоке не превышает 10 градаций яркости. Минимально возможный размер блока установим равным двум.
8 пикселей. Формат представления данных изображения - uint8. Будем считать, что блок изображения является однородным, если величина разброса яркостей пикселей в блоке не превышает 10 градаций яркости. Минимально возможный размер блока установим равным двум.Будем считать, что к объекту относятся блоки, средняя яркость которых не превышает 50. Требуется изменить исходное изображение так, чтобы пикселям блоков, относящихся к объекту, было присвоено значение 1, а пикселям блоков, не относящихся к объекту, - 0.
% Пример демонстрирует сегментацию небольшого тестового
% изображения методом разделения.
% Исходное изображение.
I= [ 10 11 10 15 20 25 47 51
11 14 17 13 27 29 52 55
12 13 11 10 24 47 56 60
13 14 11 13 49 54 74 77
15 16 43 48 79 82 87 86
17 18 45 50 85 80 80 84
29 51 50 59 80 83 83 85
59 61 58 61 81 85 86 88 ];
% Сегментация методом разделения: размер минимального блока 2
.gif) 2,
2,% блок однородный, если в его пределах яркость изменяется
% менее чем на 10 градаций.
А=qtdecomp(l, 10, 2);
% Для контроля выведем квадро-дерево с результатами сегментации
% на экран. Для удобства визуального анализа предварительно
% преобразуем разреженную матрицу А в обычную матрицу М
% с помощью функции full.
М=full(A)
% Будет выведено:
% 4 0 0 0 2 0 2 0
% 0 0 0 0 0 0 0 0
% 0 0 0 0 2 0 2 0
% 0 0 0 0 0 0 0 0
% 2 0 2 0 4 0 0 0
% 0 0 0 0 0 0 0 0
% 2 0 2 0 0 0 0 0
% 0 0 0 0 0 0 0 0
% В результате сегментации получилось 2 блока размера 4
.gif) 4
4% (левая верхняя и правая нижняя части изображения)
% и 8 блоков размера 2
.gif) 2.
2.% Переберем в цикле все возможные размеры блоков: 8, 4, 2.
dim=8;
while dim >= 2
% Получить в blocks все блоки размера dim.
[blocks, idx]=qtgetblk(l, A, dim);
[xy n] = size(blocks);
% Если блоки такого размера есть в квадро-дереве,
if n >0
% то перебираем все блоки размера dim.
for j=1:n
% Если среднее значение яркости пикселей
% в пределах блока меньше 50,
if ( mean2(blocks(:,:,j)) < 50 )
% то заменяем значения всех пикселей блока на 1,
blocks(:,:,j)=ones(dim,dim);
else
% иначе заменяем значения всех пикселей блока на 0.
blocks(:,:,j)=zeros(dim,dim);
end;
end %end for
% Устанавливаем новые значения для пикселей блоков размера
% dim в изображении I.
I=qtsetblk(l, A, dim, blocks);
end; %end if
dim = dim/2;
end; %end while
% Для контроля выведем получившееся изображение I.
I=
%1 1 1 1 1 1 0 0
%1 1 1 1 1 1 0 0
%1 1 1 1 1 1 0 0
%1 1 1 1 1 1 0 0
%1 1 1 1 1 1 0 0
%1 1 1 1 0 0 0 0
%1 1 1 1 0 0 0 0
% 0 0 0 0 0 0 0 0
% 0 0 0 0 0 0 0 0
qtgetblk - получение блоков из квадро–дерева результатов сегментации
Синтаксис:
[vals, r, с]=qtgetblk(l, A, dim)
[vals, idx]=qtgetblk(l, A, dim)
Описание:
Функция [vals, r, c]=qtgetblk(I, A, dim) возвращает в массив vals все блоки размера dim, получившиеся в результате сегментации полутонового изображения I с помощью функции qtdecomp. В параметре А передается разреженный массив, описывающий квадро-дерево с результатами сегментации. В векторы r и с помещаются соответственно номера строк и столбцов левых верхних углов блоков изображения, помещенных в массив vals. Если ни одного блока размера dim нет, то всем возвращаемым параметрам присваиваются значения пустых матриц.
Функция [vals, idx]=qtgetblk(I, A, dim) работает аналогично описанной выше, но координаты левых верхних углов блоков, помещенных в массив vals, передает в векторе idx. Координату (r, с) пикселя по значению idx(k) можно вычислить с помощью следующих соотношений:
с=fix( (idx(k) + rows - 1) / rows);
г=idx(k) - rows * (с - 1),
где rows - количество строк в исходном изображении; k - номер блока.
qtsetblk - замена блоков–результатов сегментации
Синтаксис:
Id=qtsetblk(Is, A, dim, vals)
Описание:
Функция Id=qtsetblk(Is, A, dim, vals) создает новое полутоновое изображение Id, заменяя в исходном полутоновом изображении Is все блоки размера dim, полученные в результате сегментации с помощью функции qtdecomp, на блоки из массива vals. В параметре А передается разреженный массив, описывающий квадро-дерево с результатами сегментации. Массив vals должен содержать столько же блоков размера dim, сколько их хранится в квадро-дереве А.
Данная функция используется для преобразования изображения в соответствии с результатами сегментации методом разделения. Форматы представления данных исходного и результирующего изображения совпадают.
edge - выделение границ
Синтаксис:
BW=edge(l, method)
BW=edge(l, method, thresh)
BW=edge(l, method, thresh, P)
[BW, thresh]=edge(l, method, ...)
Описание:
Для сегментации на изображениях часто необходимо обнаружить границы объектов - участки изображения, в которых есть перепад яркости.
Функция BW=edge(I, method) предназначена для выделения границ на исходном полутоновом изображении I. Данная функция возвращает бинарное изображение BW такого же размера, как исходное I. Пиксель BW(r, с) равен 1, если пиксель I(r, с) принадлежит границе. Для обнаружения границ может использоваться несколько методов. Применяемый метод задается в параметре method в виде одной из следующих строк: 'sobel', 'prewitt', 'roberts', 'log', 'zerocross', 'canny'. Если параметр method при вызове функции опущен, то по умолчанию он полагается равным 'sobel'.
Для каждого из методов определения границ можно задать дополнительные параметры. Для этого используется одна из функций BW=edge(I, method, thresh), BW=edge(I, method, thresh, P), где параметр thresh задает порог для определения того, принадлежит ли пиксель к границе, а в параметре Р передаются настройки, специфичные для каждого из методов.
Если при вызове функции параметр thresh опущен, то значение порога выбирается автоматически. Получить значение порога можно, дополнительно определив выходной параметр thresh: [BW, thresh]=edge(I, method,...).
Рассмотрим использование функции edge для каждого из методов выделения границ.
Функция BW=edge(I, 'sobel', thresh) для определения границ использует фильтрацию исходного изображения I фильтром Собеля [1, 3]; пиксель считается относящимся к границе, если соответствующий ему пиксель результата фильтрации имеет значение, большее thresh. Для данного метода можно указать дополнительный параметр direction: BW=edge(I, 'sobel', thresh, direction), который определяет, какие границы будут обнаруживаться. Параметр direction может принимать значения:
-
'horizontal' - выделение горизонтальных границ;
-
'vertical' - выделение вертикальных границ;
-
'both' - выделение границ во всех направлениях (данное значение используется по умолчанию, когда параметр direction не определен).
Функция BW=edge(I, 'prewitt', thresh) для определения границ использует фильтрацию исходного изображения I фильтром Превита [1,3]; пиксель считается относящимся к границе, если соответствующий ему пиксель результата фильтрации имеет значение, большее thresh. Для данного метода можно указать дополнительный параметр direction: BW=edge(I, 'prewitt', thresh, direction), который определяет, какие границы будут обнаруживаться. Возможные значения параметра direction описаны выше.
Функция BW=edge(I, 'roberts', thresh) для определения границ использует фильтрацию исходного изображения I фильтром Робертса; пиксель считается относящимся к границе, если соответствующий ему пиксель результата фильтрации имеет значение, большее thresh.
Функция BW=edge(I, 'log', thresh) для определения границ использует фильтрацию исходного изображения I фильтром лапласиан–гауссиана [1, 2]; пиксель считается относящимся к границе, если соответствующий ему пиксель результата фильтрации имеет значение, большее thresh. Для формирования маски фильтра используется функция fspecial с параметрами sigma=2 (среднеквадратичное отклонение) и n=ceil(sigma*3)*2+1 (размер маски). Параметр sigma можно задать в параметре функции edge: BW=edge(I, 'log', thresh, sigma).
Функция BW=edge(I, 'zerocross', thresh, h) для определения границ использует фильтрацию исходного изображения I линейным фильтром с маской h; пиксель считается относящимся к границе, если соответствующий ему пиксель результата фильтрации имеет значение, большее thresh.
Функция BW=edge(I, 'canny', thresh) использует для определения границ метод Канни. Это достаточно сложный метод, состоящий из большого числа этапов [4]. Суть метода состоит в поиске локальных участков с перепадами яркости. Перепады яркости ищутся с помощью фильтрации по каждой из осей одномерным фильтром лапласиан–гауссиана (см. функцию fspecial). В методе Канни для классификации перепадов на "слабые" и "сильные" используется два порога - нижний и верхний. "Слабые" границы отмечаются в результирующем изображении, только если они соединены с "сильными". Для зашумленных изображений данный метод обеспечивает наилучшее обнаружение границ по сравнению с остальными методами функции edge, но требует существенно большего времени.
Параметр thresh может являться двухэлементным вектором. В этом случае первый элемент вектора задает значение нижнего порога, а второй элемент - значение верхнего порога. Если параметр thresh является скалярным значением, то thresh задает значение верхнего порога, а для нижнего порога используется значение 0.4*thresh. Если параметр thresh при вызове функции опущен или в качестве thresh передан пустой массив ([ ]), то значения порогов определяются автоматически.
В функцию BW=edge(I, 'canny', thresh, sigma) дополнительно передается параметр sigma, задающий среднеквадратичное отклонение распределения Гаусса, которое используется при формировании маски фильтра, выделяющего перепады яркости.
Пример:
Рассмотрим выделение границ методом Собеля. Исходное изображение показано на рис. 1,а. Результирующее изображение, на котором отмечены границы, показано на рис. 1,б.
% Пример демонстрирует выделение границ методом Собеля.
% Чтение исходного изображения и вывод его на экран.
I=imread(‘lena.bmp’);
imshow(l);
% Выделение границ методом Собеля и вывод результата на экран.
BW=edge(l, ‘sobel’, 0.09);
figure, imshow(BW);


а)
б)
Рис. 1.
roipoly - задание области интереса с помощью полигона
Синтаксис:
BW=roipoly(S)
BW=roipoly(S, с, r)
BW=roipoly(XData, YData, S, xi, yi)
[BW, xi, yi]=roipoly(...)
[XData, YData, BW, xi, yi]=roipoly(...)
Описание:
Функция BW=roipoly(S) позволяет интерактивно задать область интереса на исходном изображении S любого типа и поместить результат в бинарное изображение BW. Полученное бинарное изображение BW можно использовать в качестве области интереса для функции roifilt2 или для задания положения объектов и их последующего поиска с помощью функции bwlabel.
Данная функция выводит изображение S в окно и ожидает от пользователя определения области интереса. Если при вызове функции параметр S опущен, то изображение берется из текущего окна. Интересующая область изображения должна быть обведена полигоном, вершины которого задаются однократным нажатием левой клавиши мыши. Предыдущую заданную вершину можно удалить, если нажать на клавиши Backspace или Delete. Нажатие на правую клавишу мыши или двойной щелчок левой клавишей задает последнюю вершину полигона. Также завершить процесс задания вершин без указания последней можно нажатием на клавишу Enter.
Изображения BW и S имеют одинаковый размер. Пикселю бинарного изображения BW(r, с) присваивается значение 1, если пиксель S(r, с) находится внутри полигона. В противном случае BW(r, с) равно 0. Для определения точек, лежащих внутри полигона, используется правило Non-Zero Winding.
Функция BW=roipoly(S, с, r) позволяет явно задать координаты вершин полигона, ограничивающего область интереса, в векторах r (номера строк) и с (номера столбцов) одинаковой длины.
Функция BW=roipoly(XData, YData, S, xi, yi) аналогична предыдущей, но в ней координаты полигона, передаваемые в векторах xi и yi, задаются в пространственной системе координат. Двухэлементные векторы XData и YData определяют диапазон изменения значений по осям пространственной системы координат.
Если для рассмотренных функций дополнительно определить два выходных параметра xi и yi: [BW, xi, yi]=roipoly(...), то в них будут возвращены координаты вершин полигона в пространственной системе координат. Если же дополнительно определить еще два выходных параметра XData и YData: [XData, YData, BW, xi, yi]=roipoly(...), то в них будут возвращены диапазоны значений по осям пространственной системы координат, которая использовалась для изображения S.
Если функцию roipoly вызвать без выходных параметров, то результирующее бинарное изображение выводится на экран в новом окне. В любой из рассмотренных функций можно заменить параметр S (исходное изображение) на два параметра m и n, которые определяют размер исходного изображения. Например, если вызвать функцию BW=roipoly(100, 200), то на экран будет выведено черное изображение в 100 строк и 200 столбцов и функция будет ожидать от пользователя интерактивного задания вершин полигона. Результирующее изображение BW имеет формат представления данных uint8.
Пример приведен в описании функции roifill.
roicolor - бинаризация по заданым цветам
Синтаксис:
BW=roicolor(S, low, high)
BW =roicolor(S, v)
Описание:
Функция BW=roicolor(S, low, high) помещает результат бинаризации исходного полутонового или палитрового изображения S в бинарное изображение BW. Изображения BW и S имеют одинаковый размер. Пикселю бинарного изображения ВW(r, с) присваивается значение 1, если яркость пикселя S(r, с) исходного полутонового изображения или индекс S(r, с) палитрового изображения принадлежит диапазону [low, high]. В противном случае BW(r, с) присваивается значение 0.
Полученное бинарное изображение BW можно использовать в качестве области интереса для функции roifilt2 или для задания диапазона яркостей объектов и их последующего поиска с помощью функции bwlabel.
Функция BW=roicolor(S, v) помещает результат бинаризации исходного и полутонового или палитрового изображения S в бинарное изображение BW. Пикселю бинарного изображения BW(r, с) присваивается значение 1, если значение пикселя S(r, с) равно любому из значений вектора v. В противном случае BW(r, с) присваивается значение 0.
Результирующее изображение BW имеет формат представления данных uintS.
watershed - Алгоритм маркерного водораздела
Синтаксис:
L=watershed(A)
L=watershed(A,CONN)
Описание:
Функция L=watershed(A) вычисляет матрицу меток, которая идентифицирует области водораздела исходной матрицы A. Матрица А может быть любой размерности. Элементы матрицы L – это целые числа, которые больше или равны 0. Элементы, помеченные нулями не принадлежат никакой области водораздела. Они называются пикселами водораздела. Элементы помеченные единицами принадлежат области водораздела, элементы помеченные двойкой принадлежат другой области водораздела и т.д.
По умолчанию, реализованный алгоритм маркерного водораздела использует 8-связные окрестности для двумерных и 26-связные окрестности для трехмерных изображений. Для
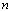 –мерных изображений, алгоритм маркерного водораздела использует связность, которая определяется как conndef(ndims(A),'maximal').
–мерных изображений, алгоритм маркерного водораздела использует связность, которая определяется как conndef(ndims(A),'maximal').Функция L=watershed(A,CONN) определяет связность для использования в алгоритме маркерного водораздела. Параметр CONN принимает одно из приведенных ниже значений.
Значение параметра
CONN
Описание
Двумерная связность
4
4–связная окрестность
8
8–связная окрестность
Трехмерная связность
6
6–связная окрестность
18
18–связная окрестность
26
26–связная окрестность
Связность может быть определена, в большинстве случаев, для любой размерности при использовании для параметра CONN матрицы нулей и единиц размерности 3х3х...х3. Значение 1 определяет местоположение окрестности относительно центрального элемента CONN. Запись значений параметра CONN должна быть симметрична относительно центрального элемента.
Требования к исходным данным.
Массив A может быть числовым или логическим массивом любой размерности. Также он должен быть не разреженным. Выходной массив L принадлежит классу double.
Примеры:
Пример для двумерных массивов:
1.Создать бинарное изображение, содержащее два перекрывающихся круглых объекта.
center1=-10;
center2=-center1;
dist=sqrt(2*(2*center1)^2);
radius=dist/2*1.4;
lims=[floor(center1-1.2*radius) ceil(center2+1.2*radius)];
[x,y]=meshgrid(lims(1):lims(2));
bw1=sqrt((x-center1).^2+(y-center1).^2)<=radius;
bw2=sqrt((x-center2).^2+(y-center2).^2)<=radius;
bw=bw1|bw2;
figure, imshow(bw,'n'), title('bw')
2.Вычисление преобразования расстояний в дополнение к бинарному изображению.
D=bwdist(~bw);
figure, imshow(D,[],'n'), title('Distance transform of ~bw')
3.Дополнительное преобразование расстояний и обработка пикселов, которые принадлежат объектам и имеют значение -Inf.
D=-D;
D(~bw)=-Inf;
4.Вычисление алгоритма маркерного водораздела и визуализация результата в виде индексного изображения.
L=watershed(D);
rgb=label2rgb(L,'jet',[.5 .5 .5]);
figure, imshow(rgb,'n'), title('Watershed transfrom of D');
Пример для трехмерных массивов:
1.Создать трехмерное бинарное изображение, которое содержит две перекрывающиеся сферы.
center1=-10;
center2=-center1;
dist=sqrt(3*(2*center1)^2);
radius=dist/2*1.4;
lims=[floor(center1-1.2*radius) ceil(center2+1.2*radius)];
[x,y,z]=meshgrid(lims(1):lims(2));
bw1=sqrt((x-center1).^2+(y-center1).^2 + ...
(z-center1).^2)<=radius;
bw2=sqrt((x-center2).^2+(y-center2).^2 + ...
(z-center2).^2)<=radius;
bw=bw1|bw2;
figure, isosurface(x,y,z,bw,0.5), axis equal, title('BW')
xlabel x, ylabel y, zlabel z
xlim(lims), ylim(lims), zlim(lims)
view(3), camlight, lighting gouraud
2.Вычисление преобразования расстояний.
D=bwdist(~bw);
figure, isosurface(x,y,z,D,radius/2), axis equal
title('Isosurface of distance transform')
xlabel x, ylabel y, zlabel z
xlim(lims), ylim(lims), zlim(lims)
view(3), camlight, lighting gouraud
3.Дополнительное преобразование расстояний и обработка пикселов, которые не принадлежат объектам и имеют значение -Inf, вычисление алгоритма маркерного водораздела.
D=-D;
D(~bw)=-Inf;
L=watershed(D);
figure, isosurface(x,y,z,L==2,0.5), axis equal
title('Segmented object')
xlabel x, ylabel y, zlabel z
xlim(lims), ylim(lims), zlim(lims)
view(3), camlight, lighting gouraud
figure, isosurface(x,y,z,L==3,0.5), axis equal
title('Segmented object')
xlabel x, ylabel y, zlabel z
xlim(lims), ylim(lims), zlim(lims)
view(3), camlight, lighting gouraud
Алгоритм
маркерного водораздела использует разновидность алгоритма Vincent-Soille [1]. Для более детальной информации смотрите toolbox/images/images/private/watershed_vs.h.
uintlut - вычисление новых значений массива на основе табличных преобразований
Синтаксис:
B=uintlut(A, LUT)
Описание:
Функция uintlut(A, LUT) создает массив, содержащий новые значения A, на основе табличных преобразований (lookup table (LUT)). Например, когда A представляет собой вектор, в котором k-й элемент эквивалентный alpha, то B(k)эквивалентно соответствующему значению из табличных преобразований, LUT(alpha+1).
Требования к исходным данным
Массив A представляется в формате uint8 или uint16. Когда массив A представлен в формате uint8, тогда табличные преобразования проводятся над 256-элементным вектором в формате uint8. Когда массив A представлен в формате uint16, тогда табличные преобразования поводятся над вектором, состоящим из 65536 элементов. Данные в B имеют ту же размерность и формат представления данных, что и массив A.
Пример:
A=uint8([1 2 3 4; 5 6 7 8; 9 10 11 12]);LUT=repmat(uint8([0 150 200 255]), 1, 64);B=uintlut(A, LUT);imview(A),imview(B);
applylut - преобразование бинарного изображения с помощью таблицы перекодировки
Синтаксис:
D=applylift( BW, lut)
Описание:
Функция D=applylut(BW, lut) создает изображение D из бинарного изображения BW, используя таблицу перекодировки lut. Вектор lut является вектором, содержащим либо 16 либо 512 элементов. Подобный вектор формируется функцией makelut. Вектор lut содержит выходные значения для всех возможных конфигураций соседей пикселя бинарного изображения в квадрате 2x2 или 3x3 пикселя.
Тип и формат представления данных изображения D зависит от значений в lut. Если lut содержит только 0 и 1, то D является бинарным изображением в формате uint8. В противном случае D - полутоновое изображение. Оно имеет формат представления данных uint8, если значения в lut принадлежат диапазону [0, 255], и double в противном случае.
Чаще всего функция applylut используется для выполнения морфологических операций над бинарным изображением. Возможные размеры структурного элемента 2x2 и 3x3.
Алгоритм:
В функции applylut новое изображение создается из значений в таблице перекодировки.
Для получения матрицы индексов, содержащей индексы для обращения к таблице перекодировки, производятся следующие действия. Выполняется свертка исходного бинарного изображения с матрицей
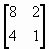 , если длина таблицы перекодировки равна 16, или матрицей
, если длина таблицы перекодировки равна 16, или матрицей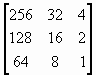 , если длина равна 512.
, если длина равна 512. Затем к результатам свертки добавляется 1. Это гарантирует, что значения в получившейся матрице индексов находятся в диапазоне [1, 16], если длина таблицы перекодировки равна 16, и в диапазоне [1, 512], если длина равна 512.
Результирующее изображение образуется в результате получения значений из таблицы перекодировки по индексам из матрицы индексов.
Пример:
Сконструируем с помощью makelut и applylut морфологическую операцию эрозии и наращения по преобладанию в окрестности пикселей фона или объекта, аналогичную операции 'majority' (см. функцию bwmorph), но с пороговым значением 4. То есть необходимо каждый пиксель изображения обработать следующим образом: если в окрестности пикселя размера 3x3 находится 4 или более пикселей объекта, то рассматриваемый пиксель устанавливается в 1, в противном случае он приравнивается к 0.
Исходное изображение и получившийся результат показаны на рис. 1а и 1б.
% Пример демонстрирует реализацию операции эрозии и наращения
% по преобладанию в окрестности пикселов фона или объекта.
% Чтение исходного изображения и вывод его на экран.
BW1=imread('objl.bmp');
imshow(BWI);
% Формирование соответствующей таблицы перекодировки.
lut=makelut('sum(x(:))>=4', 3);
% Применение эрозии и наращения по преобладанию.
BW2=applylut(BW1, lut);
% Вывод результата на экран.
figure, imshow(BW2);
а)
б)Рис. 1.
bwboundaries - отслеживание локальных границ на бинарном изображении
Синтаксис:
B=bwboundaries(BW)B=bwboundaries(BW, CONN)B=bwboundaries(BW, CONN, options)[B L]=bwboundaries(...)[B L N A]=bwboundaries()
Описание:
Функция B=bwboundaries(BW) отслеживает наружные границы объекта на бинарном изображении BW. Функция bwboundaries позволяет обрабатывать различные объекты, в том числе объекты, которые являются включенными в другие объекты. Исходный массив BW должен быть бинарным изображением, где ненулевые пиксели соответствуют объекту, а нулевые - фону. Рисунок внизу демонстрирует возможные варианты расположения объектов.

Функция bwboundaries возвращает массив B с размерностью Px1, где P является числом объектов и отверстий. Каждый элемент массива содержит матрицу с размерностью Qx2. Каждая строка этой матрицы содержит координаты строки и столбца граничного пикселя. Q является числом граничных пикселей соответствующей области.
Функция B=bwboundaries(BW, CONN) для определения границ объектов, которые находятся внутри других объектов, использует описание связности. Параметр связности CONN может принимать следующие скалярные значения.
CONN Описание 4 4-связная окрестность 8 8-связная окрестность. Устанавливается по умолчанию. Функция B=bwboundaries(BW, CONN, options) при обработке использует аргумент options, который может принимать одно из следующих значений.
option Описание 'holes' Поиск для обоих объектов и границ отверстий. 'noholes' Поиск только границ объекта (внешнего и внутреннего). Этот параметр обеспечивает улучшенную обработку. Функция [B, L]=bwboundaries(...) возвращает матрицу меток L в качестве второго дополнительного аргумента. Объекты и отверстия являются мечеными. Параметр L представляет собой двумерный массив неотрицательных целых чисел, которые отображают соседние окрестности. Число объектов и отверстий, представленных в L равно max(L(:)). Нулевые значения элементов соответствуют фону.
Функция [B, L, N, A]=bwboundaries(...) возвращает N - число используемых объектов, A - смежные матрицы. Первые N элементов в B являются границами объекта. Массив A описывает объект, вложенный в объект. A - это квадратная разреженная логическая матрица со стороной длиною max(L(:)), чьи строки и столбцы описывают позиции границ, хранящихся в B.
Закрытые границы B{m} могут быть найдены с использованием A следующим образом:
enclosing_boundary=find(A(m,:));
enclosed_boundaries=find(A(:,m));
Требования к исходным данным.
BW должен быть не разреженным двумерным логическим или числовым массивом вещественных чисел. Данные L и N имеют формат представления данных double. Массив A является логическим и разреженным.
Примеры.
Пример 1.
Считаем и обработаем методом пороговой бинаризации полутоновое изображение. Отобразим отмеченные объекты с использованием colormap, на сером фоне белым отображены границы.
I=imread('rice.png');BW=im2bw(I, graythresh(I));[B, L]=bwboundaries(BW, 'noholes');imshow(label2rgb(L, @jet, [.5 .5 .5]))hold onfor k=1:length(B) boundary = B{k}; plot(boundary(:, 2), boundary(:, 1), 'w', 'LineWidth', 2)endПример 2.
Считаем и отобразим на мониторе бинарное изображение. Поверх изображения отобразим контуры объектов. Отобразим также текст, показывая номер области (на основании матрицы меток). Дополнительно отобразим смежные матрицы с использованием функций MATLAB.
Часто изображения отображают с использованием инструмента zoom и считывания индивидуальных меток.
BW=imread('blobs.png');[B, L, N, A]=bwboundaries(BW);imshow(BW); hold on;colors=['b' 'g' 'r' 'c' 'm' 'y'];for k=1:length(B), boundary=B{k}; cidx=mod(k, length(colors))+1; plot(boundary(:, 2), boundary(:, 1), colors(cidx), 'LineWidth',2); %randomize text position for better visibility rndRow=ceil(length(boundary)/(mod(rand*k, 7)+1)); col=boundary(rndRow, 2); row=boundary(rndRow, 1); h=text(col+1, row-1, num2str(L(row,col))); set(h, 'Color', colors(cidx), 'FontSize', 14, 'FontWeight', 'bold');endfigure; spy(A);Пример 3.Отобразим границы объекта красным, а отверстий зеленым цветом.BW=imread('blobs.png');[B, L, N]=bwboundaries(BW);imshow(BW); hold on;for k=1:length(B), boundary = B{k}; if(k > N) plot(boundary(:,2), boundary(:,1), 'g','LineWidth',2); else plot(boundary(:,2), boundary(:,1), 'r','LineWidth',2); endendПример 4.Отобразим границы внешнего объекта красным (пустая строка смежной матрицы соответствует объекту) и его отверстия зеленым цветом.BW=imread('blobs.png');[B, L, N, A]=bwboundaries(BW);imshow(BW); hold on;for k=1:length(B), if(~sum(A(k, :))) boundary=B{k}; plot(boundary(:,2), boundary(:,1), 'r','LineWidth',2); for l=find(A(:,k))' boundary = B{l}; plot(boundary(:,2), boundary(:,1), 'g','LineWidth',2); end endend
bwmorph - морфологические операции над бинарным изображением
Синтаксис:
BWd=bwmorph(BWs, operation)
BWd=bwmorph(BWs, operation, n)
Описание:
Функция BWd=bwmorph(BWd, operation) создает бинарное изображение BWd, подвергая обработке морфологическим фильтром исходное бинарное изображение BWs. Тип используемого морфологического фильтра определяется параметром operation. Морфологические операции (их также называют морфологическими фильтрами) представляют собой нелинейный способ обработки изображений. Их применяют с целью изменения формы объектов. Рассматривая морфологические операции, будем называть связные области, значения пикселей которых равны единице, объектами, а области изображения, значения пикселей которых равны нулю, фоном.
Параметр operation может принимать одно из следующих значений:
"erode" Эрозия объекта. Приводит к замене значений граничных пикселей объекта на 0. Однократное применение эрозии приводит к удалению слоя границы толщиной в 1 пиксель (рис. 16). "dilate" Наращение объекта. Приводит к замене значений пикселей фона, граничащих с объектом, на 1. Однократное применение наращения приводит к добавлению к объекту слоя толщиной в 1 пиксель (рис. 1в). "open" Открытие. Представляет собой последовательное применение эрозии и наращения. Приводит к соединению областей фона, ранее разъединенных узкими участками пикселей объектов (рис. 1г). "close" Закрытие. Представляет собой последовательное применение наращения и эрозии. Приводит к удалению небольших по площади фрагментов фона внутри объектов, например "дыр" (замкнутых областей фона внутри объекта) (рис. 1д). "tophat" Преобразование типа "верх шляпы ". Соответствует вычитанию из исходного изображения результата его открытия (рис. 1е). "bothat" Преобразование типа "низ шляпы". Соответствует вычитанию исходного изображения из результата его закрытия (рис. 1ж). "clean" Удаление изолированных пикселей объектов. Пиксели равные l, все 8 соседей которых равны 0, заменяются на 0. "fill" Заполнение изолированных пикселей фона. Пиксели, равные 0, все 8 соседей которых равны 1, заменяются на 1. "diag" Уничтожение 8-связности фона. Осуществляется добавлением необходимого количества единиц во фрагменты объектов, связанных только по диагонали. Например, фрагмент изображения  заменяется на
заменяется на 
"bridge" Соединение пикселей объекта, разъединенных фрагментом фона толщиной в 1 пиксель. Например, фрагмент изображения  заменяется на
заменяется на 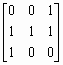
"hbreak" Удаление центрального пикселя в конфигурациях, похожих на букву "Н": 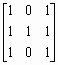 и
и 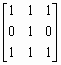 заменятся соответственно на
заменятся соответственно на 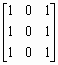 и
и 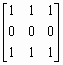
"remove" Удаление внутренних пикселей объектов. Для этого в 0 устанавливаются пиксели объекта, у которых 4 соседних по горизонтали и вертикали пикселя были равны 1, т.е. тоже являлись пикселями объекта. В результате применения этого морфологического фильтра не сброшенными останутся только пиксели границы объекта (рис. 1б). "majority" Эрозия и наращение по преобладанию в окрестности пикселей фона или объекта. Осуществляется следующим образом: если в окрестности пикселя размера 3x3 находится 5 или более пикселей объекта, то рассматриваемый пиксель устанавливается в 1, в противном случае – в 0. "skel" Построение остова (скелета) объекта. Операция выполняет эрозию объекта с учетом ряда условий для сохранения 8-связности остова. В результате последовательного применения данной операции можно построить остов, представляющий собой связную линию толщиной в 1 пиксель, проходящую по середине объекта (рис. 1в). "shrink" Сжатие объекта. Операция выполняет эрозию объекта с учетом ряда условий для сохранения 8-связности замкнутых участков остова. В результате последовательного применения данной операции объекты, не содержащие дыр, превращаются в точку, а объекты с дырами "сжимаются" в 8-связные замкнутые участки остова, проходящие посередине и по внешней границе объекта (рис. 1г). "thin" Утоньшение объекта. Операция выполняет эрозию объекта с учетом ряда условий для сохранения 8-связности участков остова. В результате последовательного применения данной операции объекты, не содержащие дыр, превращаются в одну или несколько связных линий с минимальным количеством разветвлении остова по сравнению с остовом, получаемым с помощью оператора 'skel", а объекты с дырами сжимаются в 8-связные замкнутые участки остова, проходящие посередине между границами дыр и внешней границей объекта (рис. 1д). "thicken" Утолщение объекта. Операция выполняет наращение объекта с учетом ряда условий для сохранения 4-связности участков фона. Данная операция может рассматриваться как построение остова фона и является по смыслу обратной операции 'thin'. Результат данной операции будет незначительно отличаться от результатов применения оператора 'thin' к инвертированному изображению (рис. 1е). "spur" Удаление ответвлений объекта толщиной в 1 пиксель, т. е. удаление пикселей, у которых только один из соседних пикселей установлен в 1, а остальные - в 0.
Например, фрагмент изображения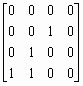 заменяется на
заменяется на 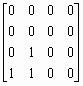 .
.
В результате последовательного применения данной операции к изображению остова на изображении остаются только замкнутые участки остова.На рис. 1, б-ж показаны результаты применения одной итерации эрозии, наращения, открытия, закрытия, операций 'tophat' и 'bothat' соответственно к бинарному объекту, изображенному на рис. 1а. Изображения показаны в инверсных цветах относительно того, как они воспроизводятся в MATLAB.

а) исходное изображение
б) эрозия
в) наращение
г) открытие
д) закрытие
е) операция "tophat"
ж) операция "bothat"Рис. 1.
Функция BWd=bwmorph(BWs, operation, n) создает бинарное изображение BWd, подвергая BWs морфологической фильтрации n раз. Параметр n может быть равен Inf, в этом случае обработка продолжается до тех пор, пока результаты двух последовательных итераций не совпадут.
Параметр n=Inf имеет смысл использовать для операций построения остова: 'shrink', 'skel', 'thicken', 'thin', удаления ответвлений 'spur'. Заметим, что в результате применения данных операций при построении остова для изображения не изменяется число Эйлера (см. описание функции bweuler).
На рис. 2, б-е показаны результаты применения операций 'shrink', 'skel', 'thicken', 'thin', 'remove' при n=Inf к бинарному изображению, приведенному на рис. 2а. Изображения показаны в инверсных цветах относительно того, как они воспроизводятся в MATLAB.

а) исходное изображение
б) операция "remove"
в) операция "skel"
г) операция "shrink"
д) операция "thin"
е) операция "thicken"Рис. 2.
Результирующее изображение BWd имеет формат представления данных uint8.
Алгоритмы:
Эрозия и наращение являются базовыми операциями морфологической обработки. Рассмотрим алгоритмы их выполнения. Для обеих операций задается структурный элемент, который называют маской морфологического фильтра. Ненулевые значения в маске определяют, какие из соседних пикселей следует учитывать при осуществлении операции [1, 2, 3].
При эрозии бинарного изображения пиксель исходного изображения сбрасывается на 0, если хотя бы один из пикселей окрестности, соответствующий ненулевому элементу маски, равен 0. При наращении бинарного изображения пиксель исходного изображения устанавливается равным 1, если хотя бы один из пикселей окрестности, соответствующий ненулевому элементу маски, равен 1.
В функции bwmorph в операциях эрозии и наращения, а также в производных от них операциях (открытие, закрытие и т. д.) используется структурный элемент 3x3 вида:
 .
.Данные правила применяются нерекурсивно ко всем пикселям изображения.
Для осуществления ряда морфологических операций в функции bwmorph используется функция applylut с предопределенными таблицами перекодировки.
Пример:
Рассмотрим подход к разъединению слипшихся объектов круглой формы с помощью морфологических операций.
Исходное полутоновое изображение I читается из файла (рис. 3a). Пиксели объектов имеют значения яркости меньше 150, поэтому для выделения объектов можно воспользоваться бинаризацией по порогу 150: BW1=I<150. Однако на бинарном изображении BW1 объекты слипаются (рис. 36).
Для разделения объектов можно использовать следующий подход. Сначала изображение подвергают эрозии до тех пор, пока не исчезнет слипание объектов. При этом объекты не должны в результате эрозии совсем исчезнуть. В рассматриваемом случае необходимо 6 итераций эрозии. Результат эрозии помещается в изображение BW2 (рис. 3в).
Затем для BW2 "утолщаются" объекты (строится остов фона) (рис. 3г). Результат логического "И" изображений BW1 & BW2 дает изображение с пикселями фона в местах слипания объектов (рис. 3д). Таким образом, объекты удалось разделить.
Далее для выделения объектов и подсчета их числа можно воспользоваться функцией bwlabel.
% Пример разделение слипшихся объектов с помощью
% морфологических операций.
% Чтение исходного изображения и вывод его на экран.
I=imread('split.bmp');
imshow(I);
% Бинаризация по порогу яркости.
BW1=I<150;
figure, imshow(BW1);
% Эрозия бинарного изображения.
BW2=bwmorph(BW1, 'erode', 6);
figure, imshow(BW2);
% Утолщение объектов.
BW2=bwmorph(BW2, 'thicken', Inf);
figure, imshow(BW2);
% Логическое И изображений результата утолщения
% и исходного бинарного.
BW1=BW1&BW2;
figure, imshow(BWI);

а)
б)
в)
г)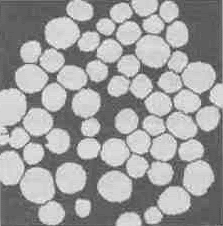
д)Рис. 3.
bwareaopen - открытие бинарных площадей (малых объектов)
Синтаксис:
BW2=bwareaopen(BW,P)
BW2=bwareaopen(BW,P,CONN)
Описание:
Функция BW2=bwareaopen(BW,P) удаляет с бинарного изображения все связные компоненты (объекты), площадь которых меньше P пикселов, и помещает результат обработки в изображение BW2. По умолчанию связными являются 8 элементов для двух измерений, 26 – для трех измерений и conndef(ndims(BW),'maximal') – для больших измерений.
В функции BW2=bwareaopen(BW,P,CONN) дополнительно указывается параметр связности. Параметр CONN может принимать любое из приведенных ниже значений.
Значение параметра
CONNОписание Двумерная связность 4 4–связная окрестность 8 8–связная окрестность Трехмерная связность 6 6–связная окрестность 18 18–связная окрестность 26 26–связная окрестность Связность может быть определена и для других измерений с помощью параметра CONN. Следует отметить, что связность должна быть симметричной или иметь центральный элемент.
Требования к исходным данным.
Исходное изображения должно быть представлено логическим или числовым неразреженным массивом. Результат обработки, который помещается в изображение BW2, является логическим массивом.
Алгоритм:
Основные шаги:
1. Определение связных компонент.
L=bwlabeln(BW, CONN);
2. Вычисление площади каждого компонента.
S=regionprops(L, 'Area');
3. Удаление (перемещение) небольших объектов.
bw2=ismember(L, find([S.Area]>=P));
Пример:
Необходимо удалить все объекты изображения, которые занимают эквивалентную площадь меньше 40 пикселов.
1. Считывание и визуализация исходного изображения.
bw=imread('text.tif');
imshow(bw)
.gif)
2. Удаление всех объектов меньше 40 пикселов.
bw2=bwareaopen(bw,40);
figure, imshow(bw2)
.gif)
В результате обработки было удалено несколько объектов (букв), площадь которых меньше 40 пикселов.
bwdist - определение периода преобразования бинарных объектов
Синтаксис:
D=bwdist(BW)
[D,L]=bwdist(BW)
[D,L]=bwdist(BW, METHOD)
Описание:
Функция D=bwdist(BW) осуществляет вычисление евклидовых расстояний на бинарном изображении BW. Для каждого пиксела на изображении BW результат вычислений определяется числом, которое является расстоянием между текущим пикселом и ближайшим ненулевым пикселом изображения BW. Функция bwdist использует метрику евклидового пространства по умолчанию. Изображение BW может иметь произвольную размерность. Размерность массива D совпадает с размерностью массива BW.
Функция [D,L]=bwdist(BW) также осуществляет вычисления для ближайших соседних пикселов и возвращает результат в матрицу меток L, размерность которой совпадает с размерностями массивов BW и D. Каждый элемент матрицы L содержит в себе линейные индексы ближайших ненулевых пикселов BW.
Функция [D,L]=bwdist(BW,METHOD) осуществляет вычисление расстояний, где параметр METHOD определяет переменную метрическую дистанцию. Параметр METHOD может принимать следующие значения:
'chessboard' В двумерном измерении, расстояние типа “шахматной доски” (chessboard) между пикселами (x1,y1) и (x2,y2) определяется как: 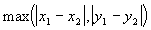
'cityblock' В двумерном измерении, расстояние типа “городских кварталов” (cityblock) между пикселами (x1,y1) и (x2,y2) определяется как: 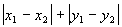
'euclidean' В двумерном измерении, евклидово расстояние между пикселами (x1,y1) и (x2,y2) определяется как: 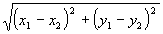
Это значение параметра устанавливается по умолчанию.'quasi-euclidean' В двумерном измерении, квазиевклидово расстояние между пикселами (x1,y1) и (x2,y2) определяется как: 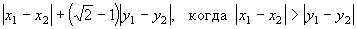 ,
, 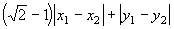 , в других случаях.
, в других случаях.Параметр METHOD может не указываться.
Функция bwdist использует устойчивый алгоритм вычисления евклидового расстояния, который определен для двумерных массивов. Другие подходы базируются на обоснованных аналогиях этого метода. Однако, для альтернативных вычислений расстояний иногда используют ускорители обработки многомерных изображений, особенно если они (изображения) содержат много ненулевых элементов.
Требования к исходным данным.
Исходное изображение BW должно быть числовым или логическим неразреженным массивом. D и L дублирующиеся матрицы, размерность которых равна размерности BW.
Пример:
Здесь приведен пример вычисления евклидового расстояния.
bw=zeros(5,5); bw(2,2)=1; bw(4,4)=1
bw=
0 0 0 0 0
0 1 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 0 0
[D,L]=bwdist(bw)
D=
1.4142 1.0000 1.4142 2.2361 3.1623
1.0000 0 1.0000 2.0000 2.2361
1.4142 1.0000 1.4142 1.0000 1.4142
2.2361 2.0000 1.0000 0 1.0000
3.1623 2.2361 1.4142 1.0000 1.4142
L=
7 7 7 7 7
7 7 7 7 19
7 7 7 19 19
7 7 19 19 19
7 19 19 19 19
В матрице L значения 7 и 19 представляют позиции ненулевых элементов, используя матричную линейную индексацию.
Приведем пример двумерных вычислений (преобразований) расстояний. Для сравнения, на рисунке 1 приведены также другие примеры метода вычислений расстояний.
bw=zeros(200,200); bw(50,50)=1; bw(50,150)=1;
bw(150,100)=1;
D1=bwdist(bw,'euclidean');
D2=bwdist(bw,'cityblock');
D3=bwdist(bw,'chessboard');
D4=bwdist(bw,'quasi-euclidean');
figure
subplot(2,2,1), subimage(mat2gray(D1)), title('Euclidean')
hold on, imcontour(D1)
subplot(2,2,2), subimage(mat2gray(D2)), title('City block')
hold on, imcontour(D2)
subplot(2,2,3), subimage(mat2gray(D3)), title('Chessboard')
hold on, imcontour(D3)
subplot(2,2,4), subimage(mat2gray(D4)), title('Quasi-Euclidean')
hold on, imcontour(D4)
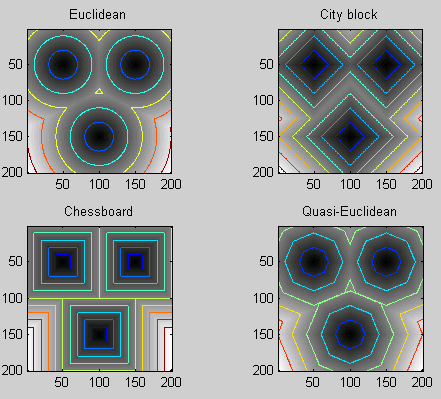
Рис. 1.
Следующий пример демонстрирует вычисление (преобразование) расстояний для трехмерных измерений, которые содержат в центре несколько ненулевых элементов (рис. 2).
bw=zeros(50,50,50); bw(25,25,25)=1;
D1=bwdist(bw);
D2=bwdist(bw,'cityblock');
D3=bwdist(bw,'chessboard');
D4=bwdist(bw,'quasi-euclidean');
figure
subplot(2,2,1), isosurface(D1,15), axis equal, view(3)
camlight, lighting gouraud, title('Euclidean')
subplot(2,2,2), isosurface(D2,15), axis equal, view(3)
camlight, lighting gouraud, title('City block')
subplot(2,2,3), isosurface(D3,15), axis equal, view(3)
camlight, lighting gouraud, title('Chessboard')
subplot(2,2,4), isosurface(D4,15), axis equal, view(3)
camlight, lighting gouraud, title('Quasi-Euclidean')
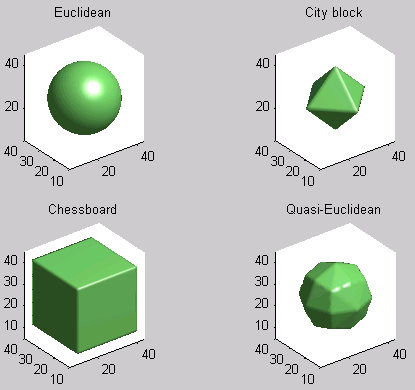
Рис. 2.
Алгоритм.
Для двумерных вычислений (преобразований) евклидового расстояния функция bwdist использует алгоритм, описанный в:
Heinz Breu, Joseph Gil, David Kirkpatrick, and Michael Werman, "Linear Time Euclidean Distance Transform Algorithms," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 17, no. 5 May 1995, pp. 529-533.
Для многомерных вычислений (преобразований) евклидового расстояния функция bwdist использует алгоритм, описанный в:
Jerome H. Friedman, Jon Louis Bentley, and Raphael Ari Finkel, "An Algorithm for Finding Best Matches in Logarithmic Expected Time," ACM Transactions on Mathematics Software, vol. 3, no. 3, September 1997, pp. 209-226.
Для вычислений (преобразований) евклидовых расстояний типа “городских кварталов”, “шахматной доски” и квазиевклидовых преобразований функция bwdist использует двухпроходной, с последовательным сканированием алгоритм, описанный в:
A. Rosenfeld and J. Pfaltz, "Sequential operations in digital picture processing," Journal of the Association for Computing Machinery, vol. 13, no. 4, 1966, pp. 471-494.
Другие виды дистанционных измерений описаны в:
David Paglieroni, "Distance Transforms: Properties and Machine Vision Applications," Computer Vision, Graphics, and Image Processing: Graphical Models and Image Processing, vol. 54, no. 1, January 1992, pp. 57-58.
bwfill - заполнение областей фона
Синтаксис:
BWd=bwfill(BWs, с, r, n)
BWd=bwfill(BWs, n)
[BWd, idx]=bwfill(...)
BWd=bwfill(x, y, BWs, xi, yi, n)
[x, y, BWd, idx, xi, yi]=bwfill(...)
BWd=bwfill(BWs, 'holes', n)
[BWd, idx]=bwfill(BWs, 'holes', n)
Описание:
Функция BWd=bwfill(BWs, c, r, n) создает бинарное изображение BWd, отличающееся от изображения BWs связной областью фона, включающей пиксель с координатами (r, с), которая в BWd будет заполнена пикселями объекта. Пиксель, с которого начинается заполнение, называют затравочным. Если параметры r и с являются векторами одинаковой длины, то заполняются все области фона с затравочными пикселями (r(k), c(k)).
Параметр n для всех рассматриваемых функций bwfill задает критерий связности для пикселей объекта. Этот параметр может принимать значения 4 или 8 (значение по умолчанию). Следует помнить, что критерий связности для пикселей фона противоположен критерию связности для пикселей объекта, т.е. если объекты 8-связные, то фон 4-связный, и наоборот.
Функция BWd=bwfill(BWs, n) выводит изображение BWs на экран и предоставляет пользователю возможность интерактивно задать координаты затравочных пикселей. Бинарное изображение BWd создается из исходного изображения BWs, у которого заполнены связные области фона, включающие затравочные пиксели. Координаты затравочных пикселей задаются однократным щелчком левой клавиши мыши. Предыдущий заданный затравочный пиксель можно удалить, если нажать клавишу Backspace или Delete. Последний затравочный пиксель задается двойным щелчком левой клавиши мыши или однократным щелчком правой клавиши мыши. Нажатие клавиши Enter завершает процесс выделения затравочных пикселей без добавления еще одного затравочного пикселя. Сразу после нажатия клавиши Enter или указания последней затравочной точки начинается заполнение соответствующих пикселей фона.
Если при вызове функции параметр BWs опущен, то функция использует изображение из текущего окна.
Функция [BWd, idx]=bwfill(...) дополнительно возвращает вектор idx, позволяющий определить координаты всех заполненных пикселей. Координату (r, с) пикселя по значению idx(k) можно вычислить с помощью следующих соотношений:
с=fix((idx(k)+rows-l)/rows);
r=idx(k)-rows*(с-1), где rows - количество строк в исходном изображении.
Функция BWd=bwfill(x, у, BWS, xi, yi, n) создает новое бинарное изображение BWd из исходного изображения BWs, у которого связная область фона, включающая пиксели с координатами из векторов xi и yi, заданными в пространственной системе координат, заполнена пикселями объекта. Диапазоны изменения координат пространственной системы координат устанавливаются для изображения ВWd двухкомпонентными векторами х и у.
Функция [х, у, BWd, idx, xi, yi]=bwfill(...) дополнительно возвращает векторы координат xi и yi, соответствующих координатам заполненных пикселей в пространственной системе координат. Диапазоны изменения координат пространственной системы координат, установленные для исходного изображения, возвращаются в двухкомпонентных векторах х и у.
Функция BWd=bwfill(BWs, 'holes', n) создает новое бинарное изображение BWd, у которого пикселами объекта заполнены дыры в объектах исходного изображения BWd.
Если функция bwfill используется без выходных параметров, например bwfill(BWs, 'holes'), то получившееся в результате изображение отображается на экране в новом окне.
Результирующее изображение имеет формат представления данных uint8.
Пример:
Рассмотрим заполнение областей фона с использованием различных критериев связности. Сначала критерий связности пикселей объектов равен 3. При этом критерий связности пикселей фона равен 4 и заполняется только 4-связная область в левом верхнем углу. Затем критерий связности пикселей объектов равен 4, т.е. критерий связности пикселей фона равен 8. Заполняются все 8-связные пиксели фона.
% Пример демонстрирует работу функции bwfill.
% Исходное бинарное изображение
BW=[ 0 0 0 1 1 0,
1 0 1 0 1 1,
0 1 1 1 0 1];
% Заполнение области с пикселем, имеющим координаты (2, 2).
% Используется критерий 8-связности.
BW1=bwfill(BW, 2, 2, 8)
% Результат работы bwfill.
% BW1=
% 1 1 1 1 1 0
% 1 1 1 0 1 1
% 0 1 1 1 0 1
% Заполнение области с пикселей, имеющим координаты (2, 2).
% Используется критерий 4-связности.
BW2=bwfill(BW, 2, 2, 4)
% Результат работы bwfill.
% BW2=
% 1 1 1 1 1 0
% 1 1 1 1 1 1
% 1 1 1 1 1 1
bwhitmiss - бинарные hit-miss операции
Синтаксис:
BW2=bwhitmiss(BW1, SE1, SE2)
BW2=bwhitmiss(BW1, INTERVAL)
Описание:
Функция BW2=bwhitmiss(BW1, SE1, SE2) выполняет операции типа “hit-and-miss” с использованием структурных элементов SE1 и SE2. Операции типа “hit-and-miss” определяют те пикселы, окрестности которых совпадают по форме с структурным элементом SE1 и не совпадают по очертаниям с структурным элементом SE2. Структурные элементы SE1 и SE2 могут быть представлены в виде объекта из плоских структурных элементов, созданного на основе других структурных элементов или массива окрестности. Окрестности SE1 и SE2 не должны иметь перекрывающихся элементов. Синтаксис функции bwhitmiss(BW1, SE1, SE2) является эквивалентом выражения imerode(BW1,SE1) & imerode(~BW1,SE2).
Функция BW2=bwhitmiss(BW1,INTERVAL) выполняет операции типа “hit-and-miss” с использованием одиночных массивов. Элементы массива могут быть равными 1, 0 или -1. 1 – значения элементов, которые составляют область SE1; -1 – значения элементов, которые составляют область SE2; и 0 – значения элементов, которые игнорируются. Синтаксически функция bwhitmiss(INTERVAL) является эквивалентом функции bwhitmiss(BW1,INTERVAL==1, INTERVAL==-1).
Требования к исходным данным:
BW1 должен быть логическим или цифровым массивом любой размерности, также он должен быть не разреженным. BW2 – это всегда логический массив того же размера, что и BW1. SE1 и SE2 должны быть плоскими структурными элементами (STREL objects), логическими или цифровыми массивами, содержащими элементы 1 или 0. INTERVAL представляет собой массив, содержащий элементы 1, 0 или -1.
Пример:
Этот пример демонстрирует выполнение операций типа “hit-and-miss” на бинарном изображении с использованием интервалов.
bw= [0 0 0 0 0 0
0 0 1 1 0 0
0 1 1 1 1 0
0 1 1 1 1 0
0 0 1 1 0 0
0 0 1 0 0 0]
interval=[0 -1 -1
1 1 -1
0 1 0];
bw2=bwhitmiss(bw,interval)
bw2=
0 0 0 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
bwlabeln - установка метки связанных элементов в многомерных бинарных изображениях
Синтаксис:
L=bwlabeln(BW)
[L, NUM]=bwlabeln(BW)
[L, NUM]=bwlabeln(BW, CONN)
Описание:
Функция L=bwlabeln(BW) возвращает матрицу меток L, содержащую метки связных компонентов на бинарном изображении BW. Изображение BW может быть любой размерности; размерность матрицы меток L совпадает с размерностью изображения BW. Элементы матрицы L представляют собой целые числа больше или равны 0. Пикселы, отмеченные нулями, являются фоном. Пикселы, отмеченные 1, указывают на первый объект; пикселы, отмеченные 2, указывают на второй объект, и т.д. По умолчанию связными являются 8 элементов для двух измерений, 26 – для трех измерений и conndef(ndims(BW),'maximal') – для больших измерений.
Функция [L, NUM]=bwlabeln(BW) возвращает в параметре NUM число связных объектов, найденных на основе анализа бинарного изображения BW.
Функция [L, NUM]=bwlabeln(BW,CONN) определяет компоненты требуемой связности. Параметр CONN может принимать любое из приведенных ниже значений.
Значение параметра
CONNОписание Двумерная связность 4 4–связная окрестность 8 8–связная окрестность Трехмерная связность 6 6–связная окрестность 18 18–связная окрестность 26 26–связная окрестность Связность может быть определена и для других измерений с помощью параметра CONN. Следует отметить, что связность должна быть симметричной или иметь центральный элемент.
Функция bwlabel работает только с двумерными исходными изображениями. Для обработки многомерных изображений следует использовать функцию bwlabeln. В некоторых случаях, можно отдать предпочтение функции bwlabeln, поскольку она отличается более высоким быстродействием. Если объекты исходного двумерного изображения являются относительно крупными по вертикали, в этом случае рекомендуется использовать функцию bwlabel, в других случаях, с целью увеличения быстродействия, следует использовать функцию bwlabeln.
Требования к исходным данным.
BW1 может быть логическим или цифровым массивом любой размерности, также он должен быть не разреженным. Матрица меток L имеет формат представления данных double.
Пример:
BW=cat(3,[1 1 0; 0 0 0; 1 0 0],...
[0 1 0; 0 0 0; 0 1 0],...
[0 1 1; 0 0 0; 0 0 1])
bwlabeln(BW)
ans(:,:,1)=
1 1 0
0 0 0
2 0 0
ans(:,:,2) =
0 1 0
0 0 0
0 2 0
ans(:,:,3) =
0 1 1
0 0 0
0 0 2
Алгоритм:
Функция bwlabeln использует следующие основные процедуры:
1. Сканирование всех пикселов изображения, установка предварительных меток ненулевым пикселам и запись эквивалентных меток в единую таблицу.
2. Принятие решений по эквивалентным классам с использованием алгоритма [1].
3. Смена меток пикселов на основе принятия решений по эквивалентным классам.
bwpack - упаковка бинарных изображений
Синтаксис:
BWP=bwpack(BW)
Описание:
Функция BWP=bwpack(BW) упаковывает бинарное изображение BW (uint8) в массив BWP (uint32), который будет представлять упакованное бинарное изображение (packed binary image). Поскольку значение каждого 8-битного пиксела бинарного изображения 1 или 0, функция bwpack может палитру каждого пиксела в упакованном результирующем изображении представить одним битом.
Функция bwpack обрабатывает по столбцам пикселы изображения, представляя палитровые группы 32 пикселов в битах как некоторое число в формате uint32. Первый пиксел в первой строчке соответствует наименьшему значению бита первого элемента (uint32) результирующего (преобразованного) массива. Первый пиксел в 32-й исходной строчке соответствует значению 32-го бита этого же элемента. Первый пиксел 33-й строчки соответствует наименьшему значению бита второго результирующего элемента, и так далее. Если размеры бинарного изображения BW M-на-N, тогда размерность BWP определяется как ceil(M/32)-by-N. Схема внизу иллюстрирует как упаковываются бинарные изображения с помощью функции bwpack на основе преобразования палитры пикселов бинарного изображения.
.gif)
Упаковка бинарных изображений используется для ускорения некоторых бинарных морфологических операций, типа наращивания (dilation) и эрозии (erosion). Если в качестве исходного в функциях imdilate или imerode применить упакованное бинарное изображение, это приведет к увеличению быстродействия обработки.
Функция bwunpack реализует распаковку бинарного объекта.
Требования к исходным данным:
BW может быть логическим или цифровым двумерным массивом, также он должен быть не разреженным, а его элементы вещественными числами. BWP имеет формат представления данных uint32.
Пример:
Провести операции упаковки, наращивания и распаковки бинарного изображения:
bw=imread('text.tif');
bwp=bwpack(bw);
bwp_dilated=imdilate(bwp,ones(3,3),'ispacked');
bw_dilated = bwunpack(bwp_dilated, size(bw,1));
bwperim - выделение границ бинарных объектов
Синтаксис:
BWd=bwperim(BWs, n)
Описание:
Функция BWd=bwperim(BWs, n) создает бинарное изображение BWd, у которого значения различных пикселей объектов исходного изображения установлены в 1, а значения остальных пикселей результирующего изображения установлены в 0. Пиксель считается граничным, если он равен 1 и хотя бы один из его n соседей равен 0. Параметр n для всех рассматриваемых функций bwperim задает критерий связности для пикселей границы и может принимать значения 4 или 8. Если при вызове функции bwperim параметр n опущен, то проверяются на равенство нулю все 8 соседей пикселя.
Результирующее изображение BWd имеет формат представления данных uint8.
Данная функция незначительно отличается от вызова функции bwmorph(BW, 'remove', Inf).
bwselect - выделение объектов
Синтаксис:
BWd=bwselect(BWs, с, r, n)
BWd=bwselect(BWs, n)
[BWd, idx]=bwselect(...)
BWd=bwselect(x, y, BWs, xi, yi, n)
[x, y, BWd, idx, xi, yi]=bwselect(...)
Описание:
Функция BWd=bwselect(BWs, с, r, n) создает новое бинарное изображение BWd, содержащее объект исходного изображения BWs, который включает в себя пиксел с координатами (r, с). Пиксел, с которого начинается выделение объекта, называют затравочным. Если параметры r и с являются векторами одинаковой длины, то с изображения BWs на изображение BWd переносятся все объекты с координатами затравочных пикселов (r(k), c(k)).
Параметр n для всех рассматриваемых функций bwselect задает критерий связности для пикселов объекта. Этот параметр может принимать значения 4 или 8 (значение по умолчанию).
Функция BWd=bwselect(BWs, n) выводит изображение BWs на экран и предоставляет пользователю возможность интерактивно отметить затравочные пикселы. Все объекты, которые содержат хотя бы один из отмеченных пикселов, переносятся с изображения BWs на изображение BWd. Координаты затравочных пикселов задаются однократным щелчком левой клавиши мыши. Предыдущий заданный затравочный пиксел можно удалить, если нажать клавишу Backspace или Delete. Последний затравочный пиксел задается двойным щелчком левой клавиши мыши или однократным щелчком правой клавиши мыши. Нажатие клавиши Enter завершает процесс выделения затравочных пикселов без добавления еще одного затравочного пиксела. Сразу после нажатия клавиши Enter или выбора последнего затравочного пиксела создается новое бинарное изображение BWd.
Функция [BWd, idx]=bwselect(...) дополнительно возвращает вектор idx, позволяющий определить координаты всех пикселов всех объектов изображения BWd. Координату (r, с) пиксела по значению idx(k) можно вычислить с помощью следующих соотношений:
с=fix((idx(k)+rows-l)/rows);
r=idx(k)-rows*(с-1), где rows – количество строк в исходном изображении.
Функция BWd=bwselect(x, у, BWs, xi, yi, n) создает новое бинарное изображение BWd, содержащее те объекты исходного изображения BWs, которые включают в себя затравочные пикселы с координатами, передаваемыми в векторах xi и yi. Координаты в xi и yi указываются в пространственной системе координат. Диапазоны изменения координат пространственной системы координат устанавливаются для изображения BWd двухкомпонентными векторами х и у.
Функция [х, у, BWd, idx, xi, yi]=bwselect(...) дополнительно возвращает векторы координат xi и yi, соответствующих координатам центров пикселов объектов с изображения BWd. Диапазоны изменения координат пространственной системы координат, установленные для исходного изображения, возвращаются в двухкомпонентных векторах х и у.
Если функция bwselect используется без выходных параметров, например bwselect(BWs, 10,30), то получившееся в результате изображение отображается на экране в новом окне.
Результирующее изображение имеет формат представления данных uint8.
Пример:
Предположим, на бинарном изображении, содержащем 6 объектов, требуется оставить только два из них. Это делается путем передачи в функцию bwselect координат двух пикселов, каждый из которых принадлежит одному из выбираемых объектов.
Исходное изображение и получившийся результат показаны соответственно на рис. 1, а и 1, б.
% Пример демонстрирует работу функции bwselect.
% Чтение исходного изображения и вывод его на экран.
BW=imread('circles.bmp');
imshow(BW);
% Выбор двух объектов.
BW=bwselect(BW, [83 168], [161 51], 8);
% Вывод результата на экран.
figure, imshow(BW)

а)
б)Рис. 1.
bwtraceboundary - oтслеживание контуров бинарных изображений
Синтаксис:
B=bwtraceboundary(BW, P, fstep)B=bwtraceboundary(BW, P, fstep, CONN)B=bwtraceboundary(..., N, dir)
Описание:
Функция B=bwtraceboundary(BW, P, fstep) отслеживает контуры объекта на бинарном изображении BW. Ненулевые пиксели принадлежат объекту, а нулевые фону. P является двухэлементным вектором, который определяет координаты строки и столбца точки на границе объекта. Параметр fstep является строкой, определяющей начальное направление поиска для пикселей объекта, связанных с P. Используются такие обозначения направления поиска 'N' - север, 'NE' - северо-восток. На рисунке внизу представлены все возможные значения параметра fstep.
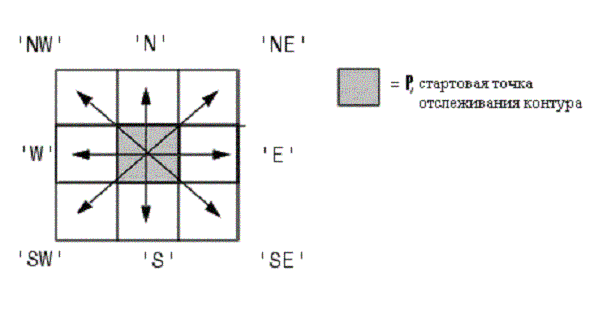
Результаты работы функции bwtraceboundary содержатся в матрице B. Размерность B равна Qx2, где Q является числом контурных пикселей исследуемого объекта в данной локальной области. Параметр B содержит координаты строк и столбцов пикселей контура.
В функции B=bwtraceboundary(bw, P, fstep, CONN) для отслеживания границ используется описание связности. Параметр CONN может принимать следующие скалярные значения.
CONN Описание 4 4-связная окрестность.
Примечание: При таком значении параметра связности CONN,
fstep может принимать следующие значения: 'N', 'E', 'S' и 'W'.8 8-связная окрестность. Этот параметр устанавливается по умолчанию. Одним из параметров функции B=bwtraceboundary(..., N, dir) является N - максимальное число определяемых граничных пикселей. Второй параметр dir описывает направления, согласно которым происходит отслеживание контуров. По умолчанию параметр N принимает значение Inf (бесконечность), в этом случае алгоритм определяет все граничные пиксели. Параметр dir может принимать следующие значения.
dir Описание 'clockwise' Поиск контура по направлению движения часовой стрелки. Это значение устанавливается по умолчанию. 'counterclockwise' Поиск направлений обратно движению часовой стрелки. Требование к исходным данным.
BW должен быть двумерным не разреженным логическим или числовым массивом вещественных чисел. Параметры B, P, CONN и N имеют формат представления данных double, а параметры dir и fstep - строковые переменные.
Пример.
Считаем и отобразим бинарное изображение. Обработку начинаем с верхнего левого пикселя и проходим изображение до первого ненулевого пикселя. Используем те локальные окрестности, где пиксели являются стартовыми точками отслеживания границ. Включая стартовые пиксели, получим 50 пикселей контура и наложим их на изображение. Отметим стартовые точки зеленым 'x'.
BW=imread('blobs.png');imshow(BW,[]);s=size(BW);for row=2:55:s(1) for col=1:s(2) if BW(row, col), break; end endcontour=bwtraceboundary(BW, [row, col], 'W', 8, 50, 'counterclockwise'); if(~isempty(contour)) hold on; plot(contour(:,2),contour(:,1),'g','LineWidth',2); hold on; plot(col, row,'gx','LineWidth',2); else hold on; plot(col, row,'rx','LineWidth',2); endend
bwulterode - предельная эрозия
Синтаксис:
BW2=bwulterode(BW)
BW2=bwulterode(BW, METHOD, CONN)
Описание:
Функция BW2=bwulterode(BW) проводит операцию эрозии над бинарным изображением BW. Операция максимальной эрозии изображения BW заключается в преобразовании локального максимума евклидового расстояния на изображении. По умолчанию связными для вычисления локальных максимумов являются 8 элементов для двух измерений, 26 – для трех измерений и conndef(ndims(BW),'maximal') – для больших измерений.
Функция BW2=bwulterode(BW, METHOD, CONN) позволяет связать методы пространственных преобразований и локальных максимумов. Параметр METHOD может принимать значение 'euclidean', 'cityblock',
'chessboard' или 'quasi-euclidean'.
CONN может принимать любое из приведенных ниже значений.
Значение параметра
CONNОписание Двумерная связность 4 4–связная окрестность 8 8–связная окрестность Трехмерная связность 6 6–связная окрестность 18 18–связная окрестность 26 26–связная окрестность Связность может быть определена и для других измерений с помощью параметра CONN. Следует отметить, что связность должна быть симметричной или иметь центральный элемент.
Требования к исходным данным.
Изображение BW может быть числовым или логическим массивом произвольной размерности. Этот массив также должен быть не разреженным. Результирующий массив BW2 является всегда логическим.
Пример:
bw=imread('circles.tif');
imshow(bw), title('Original')
bw2=bwulterode(bw);
figure, imshow(bw2), title('Ultimate erosion')
bwunpack - распаковка бинарных изображений
Синтаксис:
BW=bwunpack(BWP,M)
Описание:
Функция BW=bwunpack(BWP, M) распаковывает упакованное бинарное изображение BWP. Формат представления данных массива BWP uint32. Когда BWP является упакованным изображением, функция bwunpack первому пикселу первой строки BW присваивает значение наименьшего бита числа первой строчки BWP. Наибольшее значение бита первого элемента присваивается первому элементу 32-й строчки BW и т.д. Массив BW имеет размерность M
.gif) N, где N число столбцов массива BWP. Значение M можно определить за выражением 32*size(BWP,1).
N, где N число столбцов массива BWP. Значение M можно определить за выражением 32*size(BWP,1).Упаковка бинарных изображений используется для ускорения некоторых бинарных морфологических операций, например, наращивания и эрозии. Если в качестве исходного в функциях imdilate или imerode применить упакованное бинарное изображение, это приведет к увеличению быстродействия обработки.
Функция bwpack используется для создания упакованных бинарных изображений.
Требования к исходным данным.
Массив BWP имеет формат представления данных uint32. Он должен быть двумерным массивом вещественных чисел, а также быть не разреженным. Массив результирующего изображения имеет формат представления данных uint8.
Пример:
Упаковать, нарастить и распаковать бинарное изображение.
bw=imread('text.tif');
bwp=bwpack(bw);
bwp_dilated=imdilate(bwp, ones(3,3), 'ispacked');
bw_dilated=bwunpack(bwp_dilated, size(bw,1));
conndef - отсутствие связности
Синтаксис:
CONN=conndef(NUM_DIMS, TYPE)
Описание:
Функция CONN=conndef(NUM_DIMS, TYPE) возвращает массив связности, определенный через TYPE для NUM_DIMS размерности. TYPE может принимать одно из значений, представленных в таблице.
'minimal' Определение окрестностей, соседних относительно центрального элемента, на (N-1)-мерной поверхности, для N-мерного случая.
См. пример для иллюстрации.'maximal' Определение окрестностей, включая соседние относительно центрального элемента, другим путем ones(repmat(3,1,NUM_DIMS)).
См. пример для иллюстрации.Несколько функций пакета Image Processing Toolbox используют conndef для определения связности исходных компонент.
Пример:
Массив минимальной связности для двумерного случая, включая соседние относительно центрального элемента (‘line’):
conn1=conndef(2,'minimal')
conn1=
0 1 0
1 1 1
0 1 0
Массив минимальной связности для двумерного случая, включая соседние относительно центрального элемента (‘face’):
conndef(3,'minimal')
ans(:,:,1)=
0 0 0
0 1 0
0 0 0
ans(:,:,2)=
0 1 0
1 1 1
0 1 0
ans(:,:,3)=
0 0 0
0 1 0
0 0 0
Массив максимальной связности для двумерного случая, включая соседние относительно центрального элемента (‘in any way’):
conn2=conndef(2,'maximal')
conn2=
1 1 1
1 1 1
1 1 1
imbothat - выполнение низкочастотной фильтрации
Синтаксис:
IM2=imbothat(IM, SE)
IM2=imbothat(IM, NHOOD)
Описание:
Функция IM2=imbothat(IM, SE) выполняет морфологическую “bottom-hat”–фильтрацию исходного полутонового или бинарного изображения IM, возвращая обработанное изображение IM2. Аргумент SE представляет собой структурный элемент, который возвращается функцией strel. SE должен быть объектом единичных структурных элементов.
Функция IM2=imbothat(IM, NHOOD) выполняет морфологическую “bottom-hat”–фильтрацию, где параметр NHOOD является массивом нулей и единиц, которые описывают размер и форму структурных элементов. Это эквивалентно выражению imbothat(IM, strel(NHOOD)).
Требования к исходным данным:
IM должен быть числовым или логическим не разреженным массивом. Результирующее изображение имеет тот же формат представления данных, что и исходное изображение. Когда исходное изображение бинарное (логическое), тогда структурные элементы должны быть плоскими.
Пример:
Для повышения контрастности изображений высокочастотная и низкочастотная фильтрация должны использоваться одновременно.
1.Считываем изображение в рабочую область MATLAB.
I=imread('pout.tif');
imshow(I), title('Original')

2. Прибавляем исходное изображение к обработанному с помощью “top-hat”–фильтра и вычитаем изображение, обработанное “bottom-hat”–фильтром.
se=strel('disk', 3);
J=imsubtract(imadd(I, imtophat(I, se)), imbothat(I, se));
figure, imshow(J), title('Contrast filtered')

imclearborder - подавление световой структуры связанной с краями изображения
Синтаксис:
IM2=imclearborder(IM)
IM2=imclearborder(IM, CONN)
Описание:
Функция IM2=imclearborder(IM) выполняет операцию подавления световойструктуры, окрестности которой связаны с краями изображения. Массив IM долженпредставлять собой яркостное (полутоновое) или бинарное изображение. Поэтомурезультирующее изображение IM2 представляет собой соответственно яркостное(полутоновое) или бинарное изображение. По умолчанию используется 8-связнаяокрестность для двумерных изображений, 26-связная окрестность для трехмерныхизображений и conndef(ndims(BW),'maximal') для размерностей высших порядков.
Примечание.
Для яркостных (полутоновых) изображений функция imclearborder имееттенденцию к тотальному ослаблению яркостных значений вместе с подавлениемкраевой структуры.
В функции IM2=imclearborder(IM, CONN) определяется нужная связность.Параметр CONN может принимать следующие скалярные значения.
Значение параметра CONN Описание Двумерная связность 4 4 - связная окрестность 8 8 - связная окрестность Трехмерная связность 6 6 - связная окрестность 18 18 - связная окрестность 26 26 - связная окрестность Связность может быть определена иным путем для любой размерности сиспользованием CONN в виде матрицы нулей и единиц с размерностью 33...
 3. Единичноезначение элемента определяет соседнюю окрестность относительно центральногоэлемента CONN. Объект CONN должен быть симметричным относительно центральногоэлемента.
3. Единичноезначение элемента определяет соседнюю окрестность относительно центральногоэлемента CONN. Объект CONN должен быть симметричным относительно центральногоэлемента.Примечание.
Пикселы на краю исходного изображения могут не рассматриваться какграничные, когда определена связность. Например, когда conn=[0 0 0; 1 1 1; 0 0 0],то элементы в первой и последней строке не рассматриваются как граничные пикселы,потому что определена соответственная связность, которая не связывает областивнешней части изображения.
Требования к исходным данным.
Изображение IM должно быть представлено неразреженным числовым илилогическим массивом вещественных чисел произвольной размерности. ИзображениеIM2 имеет тот же формат представления данных, что и IM.
Пример.
В примере для иллюстрации работы функции imclearborder с заданиемсвязности используется единичное бинарное изображение.
BW=
0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 01 0 0 1 1 1 0 0 00 1 0 1 1 1 0 0 00 0 0 1 1 1 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0
При использовании 4-связной окрестности, пиксел с координатами (5, 2) нерассматривается связанным с краевым пикселом (4, 1), поэтому не удаляется.
BWc1=imclearborder(BW,4)
BWc1=
0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 1 1 1 0 0 00 1 0 1 1 1 0 0 00 0 0 1 1 1 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0
При использовании 8-связной окрестности, пиксел с координатами (5, 2)рассматривается связанным с пикселом (4, 1), поэтому удаляется.
BWc2=imclearborder(BW,8)
BWc2=
0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 1 1 1 0 0 00 0 0 1 1 1 0 0 00 0 0 1 1 1 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0
Алгоритм.
Функция imclearborder использует морфологическую реконструкцию, где:
- маскированное(нечеткое) изображение является исходным изображением;
- маркированноеизображение является нулевым всегда, за исключением элементов края, значениякоторых аналогичны исходному изображению.
imclose - закрыть изображение
Синтаксис:
IM2=imclose(IM, SE)
IM2=imclose(IM, NHOOD)
Описание:
Функция IM2=imclose(IM, SE) выполняет морфологическое закрытие полутонового или бинарного изображения IM, возвращая результат в массиве IM2. Структурный элемент SE, в отличии от массива объектов, должен быть единичным структурным элементом.
Функция IM2=imclose(IM, NHOOD) выполняет операцию закрытия с структурным элементом strel(NHOOD), где параметр NHOOD представляет собой массив нулей и единиц, описывающий соседние структурные элементы.
Требования к исходным данным:
Изображение IM должно представляться числовым или логическим не разреженным массивом произвольной размерности. Формат представления данных массива IM2 совпадает с форматом представления данных массива IM.
Пример:
Этот пример демонстрирует основные особенности функции закрытия изображений.
1.Считывание изображения в рабочее пространство MATLAB и выполнение операции порогового разделения.
I=imread('pearlite.tif');
bw=~im2bw(I, graythresh(I));
figure, imshow(bw), title('Step 1: threshold')

2.Закрытие изображений с использованием структурных элементов в виде диска.
se=strel('disk', 6);
bw2=imclose(bw, se);
figure, imshow(bw2), title('Step 2: closing')

3.Открытие изображений с некоторыми структурными элементами.
bw3=imopen(bw2, se);
figure, imshow(bw3), title('Step 3: opening')

imdilate - расширение изображения
Синтаксис:
IM2=imdilate(IM, SE)
IM2=imdilate(IM, NHOOD)
IM2=imdilate(IM, SE, PACKOPT)
IM2=imdilate(..., PADOPT)
Описание:
Функция IM2=imdilate(IM, SE) выполняет операцию наращения полутонового, бинарного или упакованного бинарного изображения IM, возвращая результат в виде изображения IM2. Аргумент SE представляет структурный элемент объекта или массив структурных элементов объекта, возвращаемый функцией strel.
Когда массив IM логический, а структурные элементы плоские, функция imdilate выполняет бинарное наращение; в других случаях выполняется полутоновое наращение. Когда SE является массивом структурных элементов объекта, функция imdilate выполняет многократное наращение исходного изображения, используя последовательно каждый структурный элемент SE.
Функция IM2=imdilate(IM, NHOOD) выполняет операцию наращения изображения IM, где NHOOD является матрицей нулей и единиц, описывающей окрестность структурных элементов. Синтаксически это эквивалентно выражению imdilate(IM, strel(NHOOD)). Функция imdilate определяет центральный элемент окрестности за выражением floor((size(NHOOD)+1)/2).
Функции IM2=imdilate(IM, SE, PACKOPT) или imdilate(IM, NHOOD, PACKOPT) дополнительно определяют какой массив IM является упакованным бинарным изображением. Параметр PACKOPT может принимать следующие значения.
'ispacked' Массив IM обрабатывается как упакованное бинарное изображение, полученное в результате применения функции bwpack. IM должен быть двумерным массивом с форматом представления данных uint32 и плоскими двумерными структурными элементами SE. Когда PACKOPT принимает значение 'ispacked', тогда параметр PADOPT должен принимать значение 'same'. 'notpacked' IM обрабатывается как нормальный массив. Это значение принимается по умолчанию. Функция IM2=imdilate(..., PADOPT) дополнительно определяет размерность результирующего изображения. Параметр PADOPT может принимать следующие значения.
'same' Сделать размерность результирующего изображения такой же как и размерность исходного. Это значение принимается по умолчанию. Когда значение PACKOPT – 'ispacked', то параметр PADOPT должен принимать значение 'same'. 'full' Вычисление полного наращения. Параметр PADOPT аналогичен аргументу SHAPE в функциях conv2 и filter2.
Требования к исходным данным:
Изображение IM должно представляться логическим или цифровым неразреженным массивом вещественных чисел. Допускается любая размерность. Когда IM представлено логическим массивом, параметр SE должен быть плоским. Результат представляется в том же формате данных, что и исходное изображение. Когда исходные данные представляются упакованным бинарным изображением, то результат обработки также должен быть представлен упакованным бинарным изображением.
Пример:
Пример наращения бинарного изображения с вертикальными структурными элементами.
bw=imread('text.tif');
se=strel('line', 11, 90);
bw2=imdilate(bw, se);
imshow(bw), title('Original')
figure, imshow(bw2), title('Dilated')

Далее приведем пример наращения полутонового изображения с волнообразными структурными элементами.
I=imread('cameraman.tif');
se=strel('ball', 5, 5);
I2=imdilate(I, se);
imshow(I), title('Original')
figure, imshow(I2), title('Dilated')

Области соединения двух плоских структурных элементов подвергаются наращению последовательно двумя структурными элементами с использованием опции 'full'.
se1=strel('line', 3, 0)
se1=
Плоский объект STREL содержит в себе 3 соседа.
Окрестность:
1 1 1
se2=strel('line', 3, 90)
se2=
Плоский объект STREL содержит в себе 3 соседа.
Окрестность:
1
1
1
composition=imdilate(1, [se1 se2], 'full')
composition=
1 1 1
1 1 1
1 1 1
Алгоритм:
Функция imdilate автоматически принимает все преимущества декомпозиции структурных элементов объекта (если он существует). Итак, когда выполняется бинарное наращивание с структурными элементами объекта путем их декомпозиции, функция imdilate автоматически использует процедуру упаковки бинарных изображений для ускорения операции наращения.
Более детально операция наращения упакованных изображений описана в [2].
imerode - эрозия изображения
Синтаксис:
IM2=imerode(IM, SE)
IM2=imerode(IM, NHOOD)
IM2=imerode(IM, SE, PACKOPT, M)
IM2=imerode(..., PADOPT)
Описание:
Функция IM2=imerode(IM, SE) проводит операцию утончения полутоновых, бинарных или упакованных бинарных изображений IM, возвращая утонченное изображение IM2. Аргумент SE является структурным элементом объекта или массивом структурных элементов, возвращаемым функцией strel.
Когда IM является логическим или структурным плоским элементом, функция imerode выполняет бинарное наращивание; в других случаях полутоновое утончение. Когда SE является массивом структурных элементов объекта, функция imerode выполняет многократное утончение исходного изображения, используя каждый структурный элемент из последовательности SE.
Функция IM2=imerode(IM, NHOOD) выполняет операцию утончения изображения IM, где NHOOD представляет собой массив нулей и единиц, описывающий структурные элементы окрестности. Синтаксически эта функция эквивалентна выражению imerode(IM, strel(NHOOD)). Функция imerode определяет центральный элемент окрестности за выражением floor((size(NHOOD)+1)/2).
Функции IM2=imerode(IM, SE, PACKOPT, M) или imerode(IM, NHOOD, PACKOPT, M) определяют какой массив IM представляет собой бинарное изображение и проводит преобразование его размерностей M к виду исходного распакованного изображения. Параметр PACKOPT может принимать следующие значения.
'ispacked' Массив IM обработан как упакованное бинарное изображение с помощью функции bwpack. Изображение IM должно быть двумерным массивом с форматом представления данных uint32. Параметр SE также должен быть плоским двумерным структурным элементом. 'notpacked' IM обработан как нормальный массив. Это значение принимается по умолчанию. Когда параметр PACKOPT принимает значение 'ispacked', необходимо точно определить значение M.
Функция IM2=imerode(..., PADOPT) определяет размер результирующего изображения. Параметр PADOPT может принимать одно из следующих значений.
'same' Размерность результирующего изображения совпадает с размерностью исходного изображения. Это значение принимается по умолчанию. Когда параметр PACKOPT принимает значение 'ispacked', тогда PADOPT должен принимать значение 'same'. 'full' Вычисление полного утончения (эрозии). Параметр PADOPT является аналогом SHAPE, который является исходным параметром функций CONV2 и FILTER2.
Требования к исходным данным:
Изображение IM должно быть представлено числовым или логическим массивом любой размерности. Когда массив IM логический, тогда структурные элементы SE плоские. Формат представления данных результирующего изображения совпадает с форматом исходного изображения. Когда исходное изображение упакованное, тогда результирующее изображение будет также упакованным.
Пример:
Пример утончения бинарного изображения с вертикальными линиями.
bw=imread('text.tif');
se=strel('line', 11, 90);
bw2=imerode(bw, se);
imshow(bw), title('Original')
figure, imshow(bw2), title('Eroded')

Этот пример демонстрирует операцию утончения полутонового изображения с волновыми линиями.
I=imread('cameraman.tif');
se=strel('ball', 5, 5);
I2=imerode(I, se);
imshow(I), title('Original')
figure, imshow(I2), title('Eroded')

Примечание к алгоритму:
Функция imerode автоматически принимает на себя преимущества декомпозиции структурных элементов объекта (когда декомпозиция возможна). Итак, когда выполняется наращивание с структурными элементами в виде их декомпозиции, функция imerode автоматически использует бинарное упакованное изображение для ускорения наращивания.
Утончение с использованием упаковки описано в [2].
imextendedmax - максимальная длительность преобразований
Синтаксис:
BW=imextendedmax(I, H)
Описание:
Функция BW=imextendedmax(I, H) вычисляет максимальную продолжительность преобразований, которые, в свою очередь, основываются на преобразованиях локальных максимумов от H-максимальных преобразований. Параметр H представлен неотрицательным скаляром.
Локальные максимумы являются связными компонентами пикселов с одинаковыми значениями яркостей I, чьи внешние границы состоят из пикселов, значения которых меньше чем I.
По умолчанию, функция imextendedmax использует 8-связные соседние элементы для двухмерных изображений и 26-связные для трехмерных изображений. Для многомерных изображений функция imextendedmax использует выражение conndef(ndims(I), 'maximal').
Функция BW=imextendedmax(I, H, CONN) вычисляет максимальную продолжительность преобразований, где параметр CONN определяет связность. CONN может принимать одно из следующих значений.
Значение параметра CONN Описание Двумерная связность 4 4 – связная окрестность 8 8 – связная окрестность Трехмерная связность 6 6 – связная окрестность 18 18 – связная окрестность 26 26 – связная окрестность Связность может быть определена иным путем для любой размерности с использованием CONN в виде матрицы нулей и единиц с размерностью 3
 3
3.gif) ...
....gif) 3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.
3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.Требования к исходным данным:
Параметр I должен быть неразреженным числовым массивом произвольной размерности. Массив BW всегда логический и имеет тот же размер, что и I.
Пример:
I=imread('bonemarr.tif');
BW=imextendedmax(I, 40);
imshow(I), figure, imshow(BW)
imextendedmin - минимальная длительность преобразований
Синтаксис:
BW=imextendedmin(I, h)
Описание:
Функция BW=imextendedmin(I, h) вычисляет минимальную продолжительность преобразований, которые, в свою очередь, основываются на преобразованиях локальных минимумов от H-минимальных преобразований. Параметр H представлен неотрицательным скаляром.
Локальные минимумы являются связными компонентами пикселов с одинаковыми значениями яркостей I, чьи внешние границы состоят из пикселов, значения которых больше чем I.
По умолчанию, функция imextendedmin использует 8-связные соседние элементы для двухмерных изображений и 26-связные для трехмерных изображений. Для многомерных изображений функция imextendedmin использует выражение conndef(ndims(I), 'maximal').
Функция BW=imextendedmin(I, h, CONN) вычисляет минимальную продолжительность преобразований, где параметр CONN определяет связность. CONN может принимать одно из следующих значений.
Значение параметра CONN Описание Двумерная связность 4 4 – связная окрестность 8 8 – связная окрестность Трехмерная связность 6 6 – связная окрестность 18 18 – связная окрестность 26 26 – связная окрестность Связность может быть определена иным путем для любой размерности с использованием CONN в виде матрицы нулей и единиц с размерностью 3
 3
3.gif) ...
....gif) 3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.
3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.Требования к исходным данным:
Параметр I должен быть неразреженным числовым массивом произвольной размерности. Массив BW всегда логический и имеет тот же размер, что и I.
Пример:
I=imread('bonemarr.tif');
BW=imextendedmin(I, 10);
imshow(I), figure, imshow(BW)
imfill - заполнение областей изображения
Синтаксис:
BW2=imfill(BW)
[BW2, LOCATIONS]=imfill(BW)
BW2=imfill(BW, LOCATIONS)
BW2=imfill(BW, LOCATIONS, CONN)
BW2=imfill(BW, 'holes')
BW2=imfill(BW, CONN, 'holes')
I2=imfill(I, 'holes')
I2=imfill(I, CONN, 'holes')
Описание:
Функция BW2=imfill(BW, LOCATIONS) выполняет операцию заливки фоновыми пикселами исходного изображения BW, начиная из точек, определенных параметром LOCATIONS. Параметр LOCATIONS должен быть вектором с размерностью P
 1, в котором содержатся линейные индексы начальных точек. Параметр LOCATIONS может быть также матрицей P
1, в котором содержатся линейные индексы начальных точек. Параметр LOCATIONS может быть также матрицей P.gif) ndims(BW), в которой содержатся массивы индексов начальных элементов.
ndims(BW), в которой содержатся массивы индексов начальных элементов.Функция BW2=imfill(BW, 'holes') заполняет отверстия на исходном бинарном изображении.
Функция I2=imfill(I, 'holes') заполняет отверстия на исходном яркостном изображении I.
Интерактивная обработка:
Функция BW2=imfill(BW) визуализует бинарное изображение BW, на котором можно интерактивно с помощью мышки выбрать стартовые точки. Нажатие клавиши мышки прибавляет одну начальную точку. Нажатие клавиш <BackSpace> или <Delete> перемещает курсор на предыдущую точку. Комбинация клавиш shift-click, right-click или double-click позволяет выбрать последнюю стартовую точку и начать операцию заполнения; команда <Return> свидетельствует о завершении выбора стартовых точек. Интерактивный выбор стартовых точек поддерживается только для двумерных изображений.
Синтаксис [BW2, LOCATIONS]=imfill(BW) может использоваться для начала выбора стартовых точек с помощью мышки. Исходный параметр LOCATIONS представляет собой вектор линейных индексов на исходном изображении.
Определение связности:
По умолчанию функция imfill использует 4-связные фоновые окрестности для двумерных и 6-связные фоновые окрестности для трехмерных исходных изображений. Для более высоких размерностей по умолчанию связность фона определяется с использованием CONNDEF(NUM_DIMS, 'minimal').
BW2=imfill(BW, LOCATIONS, CONN)
BW2=imfill(BW, CONN, 'holes')
I2=imfill(I, CONN, 'holes')
Синтаксис интерактивного определения стартовых точек следующий:
BW2=imfill(BW, 0, CONN)
Параметр CONN может принимать одно из следующих скалярных значений.
Значение параметра CONN Описание Двумерная связность 4 4 – связная окрестность 8 8 – связная окрестность Трехмерная связность 6 6 – связная окрестность 18 18 – связная окрестность 26 26 – связная окрестность Связность может быть определена иным путем для любой размерности с использованием CONN в виде матрицы нулей и единиц с размерностью 3
.gif) 3...
3....gif) 3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.
3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.Требования к исходным данным:
Исходное изображение должно быть представлено числовым или логическим неразреженным массивом вещественных чисел. Массив может быть любой размерности. Результирующее изображение имеет формат представления данных тот же, что и исходное изображение.
Примеры:
Заполнение фона бинарного изображения с определением стартовых точек:
BW1=[1 0 0 0 0 0 0 0
1 1 1 1 1 0 0 0
1 0 0 0 1 0 1 0
1 0 0 0 1 1 1 0
1 1 1 1 0 1 1 1
1 0 0 1 1 0 1 0
1 0 0 0 1 0 1 0
1 0 0 0 1 1 1 0]
BW2=imfill(BW1, [3 3], 8)
Заполнение отверстий бинарного изображения:
BW4=~im2bw(imread('blood1.tif'));
BW5=imfill(BW4, 'holes');
imshow(BW4), figure, imshow(BW5)
Заполнение отверстий яркостного изображения:
I=imread('enamel.tif');
I2=imcomplement(imfill(imcomplement(I), 'holes'));
imshow(I), figure, imshow(I2)
Алгоритм:
Функция imfill использует алгоритм на основе морфологической реконструкции [1].
imhmax - H-максимальные преобразования
Синтаксис:
I2=imhmax(I, h)
Описание:
Функция I2=imhmax(I, h) подавляет все максимумы на яркостном (полутоновом) изображении I, значения которых больше чем h, где h является скаляром.
Локальный максимум является связной компонентой пикселей с одинаковыми значениями яркостей t, чьи все внешние граничные пиксели имеют значения меньше чем t.
По умолчанию функция imhmax использует 8-связную окрестность для двумерных изображений и 26-связную окрестность для трехмерных изображений. Для более высоких размерностей функция imhmax использует выражение conndef(ndims(I),'maximal').
Функция I2=imhmax(I, h, CONN) вычисляет H-максимальные преобразования, где параметр CONN определяет связность. Параметр CONN может принимать одно из следующих скалярных значений.
Значение параметра CONN Описание Двумерная связность 4 4 - связная окрестность 8 8 - связная окрестность Трехмерная связность 6 6 - связная окрестность 18 18 - связная окрестность 26 26 - связная окрестность Связность может быть определена иным путем для любой размерности с использованием CONN в виде матрицы нулей и единиц с размерностью 3x3...x3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.
Требования к исходным данным
Массив I должен быть неразреженным числовым массивом произвольной размерности. Размерность и формат представления данных массива I2 аналогичны с I.
Пример:
a=zeros(10, 10);a(2:4,2:4)=3; % минимум 7 больше чем окрестностиa(6:8,6:8)=8; % минимум 2 больше чем окрестностиb=imhmax(a, 4);
imhmin - H-минимальные преобразования
Синтаксис:
I2=imhmin(I, h)
Описание:
Функция I2=imhmin(I, h) подавляет все минимумы на яркостном (полутоновом) изображении I, чьи значения меньше чем h, где h является скаляром.
Локальный минимум является связным компонентом пикселей с одинаковыми значениями яркостей t, чьи все внешние граничные пиксели имеют значения меньше чем t.
По умолчанию функция imhmax использует 8-связную окрестность для двумерных изображений и 26-связную окрестность для трехмерных изображений. Для более высоких размерностей функция imhmax использует выражение conndef(ndims(I),'maximal').
Функция I2=imhmin(I,h,CONN) вычисляет H-минимальные преобразования, где CONN определяет параметр связности. Параметр CONN может принимать одно из следующих скалярных значений.
Значение параметра CONN Описание Двумерная связность 4 4 - связная окрестность 8 8 - связная окрестность Трехмерная связность 6 6 - связная окрестность 18 18 - связная окрестность 26 26 - связная окрестность Связность может быть определена иным путем для любой размерности с использованием CONN в виде матрицы нулей и единиц с размерностью 3x3...x3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.
Требования к исходным данным.
Массив I должен быть неразреженным числовым массивом произвольной размерности. Размерность и формат представления данных массива I2 аналогичны с I.
Пример:
a=10*ones(10,10);a(2:4,2:4)=7; % минимум 7 ниже чем окрестностьa(6:8,6:8)=2; % минимум 2 ниже чем окрестностьb=imhmin(a,4);
imimposemin - установка минимума
Синтаксис:
I2=imimposemin(I, BW)
Описание:
Функция I2=imimposemin(I, BW) проводит преобразование яркостей изображения I с использованием метода морфологического восстановления таким образом, чтобы все локальные минимумы BW были отличны от нуля. Результирующий массив BW является бинарным изображением, размерность которого совпадает с размерностью исходного изображения I.
По умолчанию, функция imimposemin использует 8–связную окрестность для двумерных изображений и 26–связную окрестность для трехмерных изображений. Для размерностей высших порядков, функция imimposemin использует выражение CONNDEF(ndims(I), 'mimimum').
Функция I2=imimposemin(I, H, CONN) определяется связностью, где параметр CONN может принимать следующие значения.
Значение параметра CONN Описание Двумерная связность 4 4 – связная окрестность 8 8 – связная окрестность Трехмерная связность 6 6 – связная окрестность 18 18 – связная окрестность 26 26 – связная окрестность Связность может быть определена иным путем для любой размерности с использованием CONN в виде матрицы нулей и единиц с размерностью 3
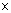 3...
3....gif) 3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.
3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.Требования к исходным данным:
Исходное изображение I может быть представлено неразреженным числовым массивом произвольной размерности в любом формате представления данных. Изображение BW представляет собой неразреженный числовой массив, размерность которого совпадает с размерностью исходного изображения I. Размерность и формат представления изображения I2 также совпадает с исходным изображением I.
Пример:
Преобразование изображения bonemarr.tif на основе локальных минимумов.
1. Сначала считывается и визуализируется исходное изображение и выбирается маска.
I=imread('bonemarr.tif');
imshow(I)
2. Создадим маркер изображения, который используется при дальнейшей обработке. Далее создадим бинарное изображение, совпадающее по размерах с исходным и состоящее из нулей. Также создадим некоторую локальную маску из единиц.
bw=zeros(size(I));
bw(98:102,101:105)=1;
Покажем какие пикселы исходного изображения выпали, вследствие наложения маски. Маркер представляет собой небольшое прямоугольное пятно.
J=I;
J(bw~=0)=255;
figure, imshow(J)
3. Установим минимум на исходном изображении, выполняя морфологическое восстановление изображения в локальной окрестности маркера. Отметим, что темная область исходного изображения, отмеченная маркером, стала светлее.
K=imimposemin(I, bw);
figure, imshow(K)

При выполнении операции преобразования минимумов исходного изображения используется функция IMREGIONALMINдля поиска всех локальных минимумов на изображении.
bw2=IMREGIONALMIN(K);
figure, imshow(bw2)

Алгоритм:
Функция imimposemin использует технологию, которая базируется на морфологической реконструкции.
imopen - открыть изображение
Синтаксис:
IM2=imopen(IM, SE)
IM2=imopen(IM, NHOOD)
Описание :
Функция IM2=imopen(IM, SE) выполняет морфологическую операцию открытия полутонового илибинарного изображения IM с структурным элементом SE. Аргумент SE должен быть единичнымструктурным элементом объекта, противоположным массиву объектов.
Функция IM2=imopen(IM, NHOOD) выполняет операцию открытия с структурным элементомstrel(NHOOD), где NHOOD является массивом нулей и единиц, который определяетэлементы окрестности.
Требования к исходным данным.
IM должен бытьлюбым числовым или логическим неразреженным массивом любой размерности. Когдамассив IM логический, тогда SE должны быть плоскими. Формат представленияданных массива IM2 тот же, что и в IM.
Пример.
Этот примериспользует операцию imopen для фильтрации небольших объектов на изображении.
1. Считываем изображение в рабочеепространство MATLAB и используем к нему некоторый порог.
I=imread('nodules1.tif');bw=~im2bw(I, graythresh(I));imshow(bw), title('Thresholded Image')

2. Создание дискообразногоструктурного элемента и открытие изображения.
se=strel('disk', 5);bw2=imopen(bw, se);figure, imshow(bw2), title('After opening')

imreconstruct - морфологическое восстановление изображений
Синтаксис:
IM=imreconstruct(MARKER,MASK)
IM=imreconstruct(MARKER, MASK, CONN)
Описание:
Функция IM=imreconstruct(MARKER, MASK) выполняет морфологическую реконструкциюизображения под изображение MASK. MARKER и MASK должны быть двумя полутоновымиили бинарными изображениями одинаковых размеров. Возвращаемое изображение IMтакже является полутоновым или бинарным изображением соответственно. Элементымассива MARKER должны быть меньшими или равными соответствующих элементовмассива MASK.
По умолчанию,функция imreconstruct использует 8-связную окрестность для двумерныхизображений и 26-связную для трехмерных изображений. Для больших размерностей,функция imreconstruct использует выражение conndef(ndims(I),'maximal').
Функция IM=imreconstruct(MARKER, MASK, CONN) выполняет морфологическую реконструкцию,для которой задается опция связности. Параметр CONN может принимать одно изследующих скалярных значений.
Значение параметра CONN Описание Двумерная связность 4 4 - связная окрестность 8 8 - связная окрестность Трехмерная связность 6 6 - связная окрестность 18 18 - связная окрестность 26 26 - связная окрестность Связность можетбыть определена иным путем для любой размерности с использованием CONN в видематрицы нулей и единиц с размерностью 3
 3...
3....gif) 3. Единичное значение элементаопределяет соседнюю окрестность относительно центрального элемента CONN. ОбъектCONN должен быть симметричным относительно центрального элемента.
3. Единичное значение элементаопределяет соседнюю окрестность относительно центрального элемента CONN. ОбъектCONN должен быть симметричным относительно центрального элемента.Морфологическаяреконструкция является алгоритмической базой многих других функций ImageProcessing Toolbox, в том числе including imclearborder, imextendedmax,imextendedmin, imfill, imhmax, imhmin и imimposemin.
Требования кисходным данным.
ИзображенияMARKER и MASK должны быть представлены неразреженными числовыми или логическимимассивами одинаковой размерности и формата представления данных. Форматпредставления данных массива IM совпадает с форматами MARKER и MASK.
Алгоритм.
Функция imreconstruct использует алгоритм "быстрого гибридного полутоновоговосстановления", описанный в [1].
imregionalmax - максимум области
Синтаксис:
BW=imregionalmax(I)BW=imregionalmax(I, CONN)
Описание:
Функция BW=imregionalmax(I) определяет локальные максимумы массива I. Результат работы функции imregionalmax представляется в виде бинарного изображения BW, размерность которого совпадает с I и на котором представлены локальные максимумы массива I. В массиве BW пиксели, которые обозначают локальные максимумы равны 1; все другие равны 0.
Локальные максимумы являются связными компонентами пикселей с одинаковыми значениями интенсивности t, чьи внешние пиксели имеют значения меньше чем t.
По умолчанию, функция imregionalmax использует 8-связную окрестность для двумерных изображений и 26-мерную окрестность для трехмерных изображений. Для больших размерностей, функция imregionalmax использует выражение conndef(ndims(I), 'maximal').
Функция BW=imregionalmax(I, CONN) при вычислении локальных максимумов использует определение связности. Параметр CONN может принимать следующие скалярные значения:
CONN Описание Двумерная связность 4 4-связная окрестность 8 8-связная окрестность. Трехмерная связность 6 6-связная окрестность 18 18-связная окрестность 26 26-связная окрестность Связность может быть определена иным путем для любой размерности с использованием CONN в виде матрицы нулей и единиц с размерностью 3x3...x3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.
Требования к исходным данным.
Изображение I должно быть представлено не разреженным числовым массивом произвольной размерности. Массив BW является логическим.
Пример.A=10*ones(10, 10);A(2:4, 2:4)=22; % максимум 22 больше, чем значения элементов окрестностиA(6:8, 6:8)=33; % максимум 33 больше, чем значения элементов окрестностиA(2, 7)=44;A(3, 8)=45;A(4, 9)=44;A=10 10 10 10 10 10 10 10 10 1010 22 22 22 10 10 44 10 10 1010 22 22 22 10 10 10 45 10 1010 22 22 22 10 10 10 10 44 1010 10 10 10 10 10 10 10 10 1010 10 10 10 10 33 33 33 10 1010 10 10 10 10 33 33 33 10 1010 10 10 10 10 33 33 33 10 1010 10 10 10 10 10 10 10 10 1010 10 10 10 10 10 10 10 10 10regmax=imregionalmax(A)regmax=0 0 0 0 0 0 0 0 0 00 1 1 1 0 0 0 0 0 00 1 1 1 0 0 0 1 0 00 1 1 1 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 1 1 1 0 00 0 0 0 0 1 1 1 0 00 0 0 0 0 1 1 1 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0
imregionalmin - минимум области
Синтаксис:
BW=imregionalmin(I)BW=imregionalmin(I, CONN)
Описание:
Функция BW=imregionalmin(I) вычисляет локальные минимумы массива I. На результирующем бинарном изображении BW значения 1 соответствуют тем пикселям изображения I, которые являются локальными минимумами. Размерность массива BW совпадает с размерностью I.
Локальные минимумы являются связными компонентами пикселей с одинаковыми значениями интенсивности t, чьи внешние пиксели имеют значения больше чем t.
По умолчанию, функция imregionalmin использует 8-связную окрестность для двумерных изображений и 26-мерную окрестность для трехмерных изображений. Для больших размерностей, функция imregionalmin использует выражение conndef(ndims(I), 'maximal').
Функция BW=imregionalmin(I, CONN) при вычислении локальных минимумов использует определение связности. Параметр CONN может принимать следующие скалярные значения.
CONN Описание Двумерная связность 4 4-связная окрестность 8 8-связная окрестность. Трехмерная связность 6 6-связная окрестность 18 18-связная окрестность 26 26-связная окрестность Связность может быть определена иным путем для любой размерности с использованием CONN в виде матрицы нулей и единиц с размерностью 3x3...x3. Единичное значение элемента определяет соседнюю окрестность относительно центрального элемента CONN. Объект CONN должен быть симметричным относительно центрального элемента.
Требования к исходным данным.
Изображение I должно быть представлено не разреженным числовым массивом произвольной размерности. Массив BW является логическим.
Пример.A=10*ones(10, 10);A(2:4, 2:4)=3; % минимум 3 меньше, чем значения элементов окрестностиA(6:8, 6:8)=8; % минимум 8 меньше, чем значения элементов окрестностиA=10 10 10 10 10 10 10 10 10 1010 7 7 7 10 10 10 10 10 1010 7 7 7 10 10 10 10 10 1010 7 7 7 10 10 10 10 10 1010 10 10 10 10 10 10 10 10 1010 10 10 10 10 2 2 2 10 1010 10 10 10 10 2 2 2 10 1010 10 10 10 10 2 2 2 10 1010 10 10 10 10 10 10 10 10 1010 10 10 10 10 10 10 10 10 10B=imregionalmin(A)B=0 0 0 0 0 0 0 0 0 00 1 1 1 0 0 0 0 0 00 1 1 1 0 0 0 0 0 00 1 1 1 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 1 1 1 0 00 0 0 0 0 1 1 1 0 00 0 0 0 0 1 1 1 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0
imtophat - выполнение высокочастотной фильтрации
Синтаксис:
IM2=imtophat(IM, SE)IM2 =imtophat(IM, NHOOD)
Описание:
Функция IM2=imtophat(IM, SE) выполняет морфологическую фильтрацию типа "верх шляпы" на полутоновом или бинарном исходном изображении IM с помощью структурного элемента SE, который образуется функцией strel. Массив SE должен иметь элементы единичной несложной структуры.
В функции IM2=imtophat(IM, NHOOD) параметр NHOOD является массивом нулей и единиц, который описывает размер и форму структурных элементов; эта функция аналогична выражению imptophat(IM,strel(NHOOD)).
Требования к исходным данным.
Изображение IM должно быть представлено числовым или логическим не разреженным массивом. Результирующее изображение IM2 имеет тот же формат представления данных, что и исходное изображение. Когда исходное изображение является бинарным (логическим), тогда структурные элементы должны быть плоскими.
Пример.
Используем фильтрацию типа "верх шляпы" для коррекции некоторого изображения. Для примера использования фильтрации типа "верх шляпы" с дискообразными структурными элементами воспользуемся изображением rice.tif.
-
-
Считаем изображение в рабочее пространство MATLAB.
I=imread('rice.tif');
imshow(I)
-
Создадим структурный элемент и применим его при фильтрации типа "верх шляпы".
se=strel('disk', 12);
J=imtophat(I, se);
figure, imshow(J)
-
Используем функции imadjust и stretchlim для улучшения визуального восприятия результирующего изображения.
K=imadjust(J, stretchlim(J));
figure, imshow(K)
-
-
makelut - формирование таблицы перекодировки
Синтаксис:
lut=makelut(fun, n)
lut=makelut(fun, n, P1, P2,...)
Описание:
Функция lut=makelut(fun, n) формирует вектор lut, который представляет собой таблицу перекодировки для использования в функции applylut. Смысл таблицы перекодировки заключается в том, чтобы каждому варианту конфигурации соседей пикселя бинарного изображения в квадрате 2x2 или 3x3 поставить в соответствие некоторое значение. Применение различных таблиц перекодировки в функции applylut позволяет реализовывать разнообразные морфологические операции.
Параметр fun определяет правило формирования таблицы перекодировки и является либо именем функции, либо inlme-функцией. В результате работы функция fun должна возвращать скалярное значение, соответствующее определенной конфигурации соседей пикселя. Функция makelut последовательно передает в fun все возможные конфигурации соседей пикселя и заносит возвращаемые fun значения в таблицу перекодировки. Параметр n может принимать значения 2 или 3 и означает размер матрицы из 0 и 1, соответственно 2x2 или 3x3, которую функция fun получает в качестве входного параметра.
При n=2 число возможных конфигураций соседей пикселя равно 16, а при n=3 - равно 512. Соответственно длина вектора lut также равна либо 16 при n=2, либо 512 при n=3. Индекс в таблице перекодировки получается в результате свертки матрицы конфигурации соседей пикселя с матрицей
.gif) при
при 
.gif) при
при 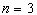 и добавления 1 к результату свертки.
и добавления 1 к результату свертки.В случае, когда необходимо передать дополнительные параметры в функцию fun, можно указать их при вызове makelut после параметра n, например, вызов lut=makelut(fun, n, P1, P2) приводит к передаче в fun в дополнение к матрице из конфигурации соседей пикселя двух параметров Р1 и Р2.
bwlabel - поиск объектов
Синтаксис:
L=bwlabei(BW, n)
[L, num]=bwlabel(BW, n)
Описание:
Функция L=bwlabel(BW, n) ищет на бинарном изображении BW связные области пикселов объектов и создает матрицу L, каждый элемент которой равен номеру объекта, которому принадлежит соответствующий пиксел изображения BW. Размер матрицы номеров объектов L равен размеру BW. Объекты нумеруются по порядку начиная с 1. Элементы, имеющие значение 1, относятся к первому объекту, имеющие значение 2 относятся ко второму объекту и т. д. Если элемент в матрице L равен 0, то это означает, что соответствующий пиксел исходного изображения относится к фону. Параметр n указывает критерий связности, используемый для нахождения связных областей - объектов. Параметр n может принимать значения 4 или 8 (значение по умолчанию).
Функция [L, num]=bwlabel(BW, n) дополнительно в параметр num возвращает количество объектов, найденных на изображении BW.
Матрица L имеет формат представления данных double.
Матрицу номеров объектов L удобно отображать на экране как палитровое изображение. Для этого следует вместе с L использовать палитру с количеством цветов больше либо равным num+1. Если палитра содержит различные цвета, то каждый объект будет окрашен в уникальный цвет.
imfeature - вычисление признаков объектов
Синтаксис:
feats=imfeature(L, measurements, n)
Описание:
Функция feats=imfeature(L, measurements, n) вычисляет признаки всех объектов, отмеченных в матрице номеров объектов L. Элементы матрицы L, имеющие значение 1, относятся к первому объекту, имеющие значение 2 относятся ко второму объекту и т.д. Если элемент в матрице L равен 0, то он относится к фону.
Значения признаков возвращаются в массиве структур feats. Количество элементов массива feats равно максимальному элементу матрицы L(mах(L(:))) и, следовательно, количеству объектов на изображении. Каждая структура содержит признаки для одного объекта. Какие именно признаки входят в структуру feats, определяется параметром measurements. Если в качестве параметра measurements указать строку "all", то будут вычислены все перечисленные ниже признаки. Если параметр measurements опущен или является строкой "‘basic", то вычисляются признаки "Area", "Centroid" и "BoundingBox". Вместо параметра measurements можно через запятую перечислить те признаки, которые необходимо вычислить. Имена полей структур из массива feats совпадают с именами вычисляемых признаков.
Вычисляемые признаки можно условно разбить на 5 групп: различные типы изображений объекта, габариты объекта, различные варианты определения площади объекта, коэффициенты формы и все оставшиеся признаки. Рассмотрим отдельно каждую группу.
Изображения объектов чаще всего необходимы для дальнейшей обработки или используются для визуализации объектов.
Параметр measurements Описание Тип данных "Image" Изображение объекта Бинарное изображение, использующее формат представления данных uint8 "Filledlmage" Изображение объекта с "залитыми" дырами Бинарное изображение, использующее формат представления данных uint8 "Convexlmage" Изображение "залитого" пикселями объекта выпуклого многоугольника, в который вписан объект Бинарное изображение, использующее формат представления данных uint8 Проиллюстрируем разницу между различными типами изображений объекта. На рис. 1а показано исходное изображение, на рис. 1б - изображение, возвращаемое в поле Image, на рис. 1в - изображение, возвращаемое в поле Filledlmage, на рис. 1г - изображение, возвращаемое в поле Convexlmage.

а)
б)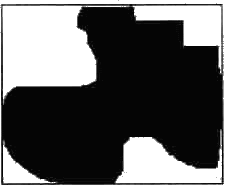
в)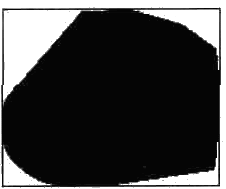
г)Рис. 1.
Часто бывает необходимо определить местоположение в поле зрения объекта в целом или местоположение его отдельных пикселей. Для этих целей могут служить различные способы описания объекта:
Параметр measurements Описание Тип данных ‘BoundingBox’ Ограничивающий прямоугольник Массив [х у width height], где (х, у) - координаты левого верхнего угла прямоугольника, width - ширина, height - высота прямоугольника 'ConvexHull' Выпуклый многоугольник, в который вписан объект Матрица Мх2, каждая строка матрицы содержит (х, у) координаты вершин многоугольника 'Extrema' Экстремальные координаты объекта Матрица 8x2 [top-left top-right right-top right-bottom bottom-right bottom-left left-bottom left-top] содержит экстремальные координаты объекта 'PixelList' Список всех пикселей объекта Nx2 матрица, каждая строка содержит (х, у) координаты центров всех пикселей объекта У всех перечисленных признаков координаты указываются в пространственной системе координат. На рис. 2 показаны ограничивающий прямоугольник и экстремальные координаты объекта.
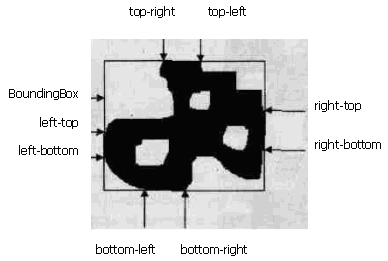
Рис. 2.
Рассматриваемые ниже признаки используются, как правило, для статистического оценивания формы или величины объектов на изображении или классификации объектов. Иногда их называют морфометрическими признаками.
Площадь является одним из основных морфометрических признаков. Она широко используется для описания объектов и вычисления коэффициентов формы. Различные варианты вычисления площади объекта связаны с рассмотренными типами представления изображения объекта:
Параметр measurements Описание Тип данных "Area" Площадь: количество пикселей объекта Число "FilledArea" Полная площадь: количество пикселей объекта плюс количество дыр в объекте. Число "ConvexArea" Выпуклая площадь: площадь выпуклого многоугольника, в который вписан объект. Соответствует площади изображения ConvexImage. Число К основным морфометрическим признакам также относятся следующие признаки:
Параметр measurements Описание Тип данных "Centroid" Центр масс объекта Двухэлементный массив, [x y] - координаты центра масс в пространственной системе координат "EquivDiameter" Эквивалентный диаметр: диаметр круга с площадью Area, равен sqrt(4*Area/pi) Число "Major Axis-Length" Длина максимальной оси инерции Число "Minor Axis-Length" Длина минимальной оси инерции Число "Orientation" Ориентация: угол в градусах между максимальной осью инерции и осью X Число "EulerNumber" Число Эйлера: количество объектов с одинаковым индексом в матрице L минус количество дыр в этих объектах Число Коэффициенты формы необходимы для того, чтобы математически описать форму объекта. Можно предложить достаточно много способов определения коэффициента формы, каждый из которых предназначен для решения определенного круга задач. Функция imfeature может вычислить 3 типа коэффициентов формы:
Параметр measurements Описание Тип данных "Solidity" Коэффициент выпуклости: равен отношению площади к выпуклой площади объекта 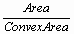
Число в диапазоне (0, 1] "Extent" Коэффициент заполнения: равен отношению площади объекта к площади ограничивающего прямоугольника 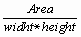
Число в диапазоне (0, 1] "Eccentricity" Эксцентриситет эллипса с главными моментами инерции, равными главным моментам инерции объекта Число в диапазоне [0, 1] Рассмотрим разницу между различными коэффициентами формы. На рис. 3, a-е приведены изображения объектов различной формы, а в таблице ниже - коэффициенты, соответствующие объектам с этих изображений.

а)
б)
в)
г)
д)
е)Рис. 3.
Изображение Solidity Extent Eccentricity а) Круг 0.9781 0.7822 0 б) Эллипс 0.9665 0.6602 0.8769 в) Квадрат 0.9669 0.6905 0.0501 г) Прямоугольник с отношением сторон 1:3 0.9495 0.4861 0.9454 д) Прямоугольник с отношением сторон 1:12 0.8816 0.2071 0.9971 е) S-образный объект 0.4595 0.4208 0.8728 При вычислении некоторых признаков, например, числа Эйлера, используется критерий связности. Он передается в параметре n и может принимать значения 4 или 8 (значение по умолчанию).
Алгоритм:
При вычислении ряда морфометрических признаков используются понятия механики твердого тела. В частности, это относится к длинам осей инерции объекта. Направления в теле, совпадающие с полуосями эллипсоида инерции, называют главными осями инерции. Для нахождения главных осей инерции, лежащих в плоскости объекта, в функции imfeature используются следующие соотношения [1, 2, 3].
Пусть N - количество пикселей, относящихся к объекту. Все множество пикселей р(х, у), относящихся к объекту, обозначим Q. Тогда координаты центра масс объекта вычисляются как
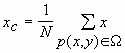 ,
, 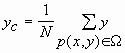
Вычислим несколько вспомогательных величин:
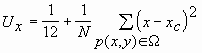 ;
;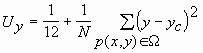 ;
;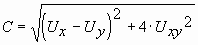 .
.Тогда длины максимальной
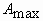 и минимальной
и минимальной 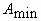 осей инерции вычисляются как:
осей инерции вычисляются как: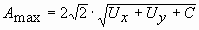 ;
;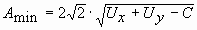 .
.Длины главных осей инерции используются для вычисления эксцентриситета и ориентации объекта.
Эксцентриситет определяется с помощью соотношения
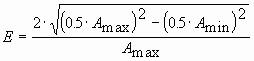 .
.Ориентация определяется как угол в градусах между максимальной осью инерции и осью X. Если
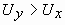 , то ориентация О вычисляется с помощью формулы
, то ориентация О вычисляется с помощью формулы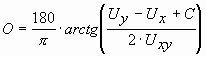 ,
,в противном случае О вычисляется как
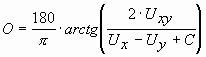 .
.Пример:
Построим гистограмму площадей объектов изображения. Предположим, что нас интересуют только объекты округлой формы, не касающиеся границы изображения. Пусть в результате бинаризации и морфологических операций сформировано бинарное изображение BW1, показанное на рис. 4а.
На этом изображении выделяются объекты. Вычисляются их площади и координаты центров масс. Затем исключаются из рассмотрения объекты, имеющие маленькую площадь или расположенные около границ изображения. Результат этих операций показан на рис. 4б. После этого операция поиска объектов повторяется, при этом формируется матрица L, которая отображается на экране как палитровое изображение, на котором каждый объект окрашен уникальным цветом (рис. 4в). В заключение вычисляются площади объектов и строится гистограмма площадей (рис. 4г).
% Пример демонстрирует построение гистограммы площадей объектов, не касающихся границ изображения.
% Чтение исходного изображения и вывод его на экран.
BW1=imread(split_bw.tif);
imshow(BWI);
% Поиск объектов.
[L num]=bwlabel(BW1, 8);
% Вычисление признаков объектов:
% площадей и координат центров масс.
feats=imfeature(L, ‘Area’, ‘Centroid’, 8);
% Переписывание значений признаков
% из массива структур feats в отдельные массивы.
Areas=zeros(num);
CentX=zeros(num);
CentY=zeros(num);
for i=1:1:num
Areas(i)=feats(l).Area;
CentX(i)=feats(i).Centroid(1);
CentY(i)=feats(i).Centroid(2);
end;
% Формирование бинарного изображения с объектами,
% площадь которых более 30 пикселов, а центр масс объекта удален
% от границ изображения более чем на 20 пикселов.
[rows cols]=size(BW1);
idx=find(Areas>30&CentX>20&CentY>20...
&CentX<(cols-20)&CentY<(rows-20));
BW1=ismember(Lidx);
figure, imshow(BW1);
% Снова поиск объектов.
[L num]=bwlabel(BW1, 8);
figure, imshow(L+1, jet(num+1));
% Вычисление площадей объектов.
feats=imfeature(L, 'Area', 8);
% Построение гистограммы площадей объектов.
figure, hist([feats, Area]);
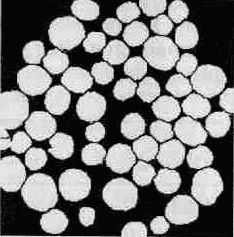
а)
б)
в)
г)Рис. 4.
imattributes - получение информации об атрибутах изображения
Синтаксис:
attrs = imattributes
attrs = imattributes(himage)
attrs = imattributes(imgmodel)
Описание:
Функция attrs = imattributes возвращает информацию об изображении в текущем окне отображения. Когда текущее окно отображения не содержит изображения, функция imattributes возвращает пустой массив.
Функция attrs = imattributes(himage) возвращает информацию об изображении, описанном через himage. Функция imattributes работает с атрибутами изображения через запрос соответствующих объектов изображения CData.
Функция imattributes возвращает информацию об атрибутах изображения в виде параметра attrs, который представляет собой массив с размерностью 4x2 или 6x2 и который зависит от типа изображения. Первый столбец массива содержит название атрибута в виде текстовой строки. Второй столбец содержит значение атрибута, которое также представляется в виде текстовой строки. В таблице приведен список атрибутов в порядке их размещения в массиве.
Название атрибута Значение 'Width (columns)' Число столбцов в изображении 'Height (rows)' Число строк в изображении 'Class' Тип данных, используемых в изображении. Например, uint8.
Примечание: Для изображений, представленных в формате single или int16, функция imattributes возвращает значение параметра 'Class' в формате double, потому что объекты изображения преобразованы в этот формат.'Image type' Один из типов изображений, идентифицированных приложением Image Processing Toolbox: 'intensity', 'truecolor', 'binary' или 'indexed'. 'Minimum intensity' Для яркостных изображений это значение представляет наименьшее значение пикселя. Для индексных изображений это значение представляет наименьшее значение индекса в палитре цветов. Этот параметр не применяется для изображений в формате 'binary' или 'truecolor'. 'Maximum intensity' Для яркостных изображений это значение представляет наибольшее значение пикселя. Для индексных изображений это значение представляет наибольшее значение индекса в палитре цветов. Этот параметр не применяется для изображений в формате 'binary' или 'truecolor'. Функция attrs = imattributes(imgmodel) возвращает информацию об изображении с помощью функции imgmodel.
Пример:
Получение атрибутов яркостного изображения.
h = imshow('liftingbody.png');
attrs = imattributes(h)
attrs =
'Width (columns)' '512'
'Height (rows)' '512'
'Class' 'uint8'
'Image type' 'intensity'
'Minimum intensity' '0'
'Maximum intensity' '255'
Создадим модель объектов truecolor-изображения и далее получим атрибуты для данных объектов.
h = imshow('gantrycrane.png');
im = imagemodel(h);
attrs = imattributes(im)
attrs =
'Width (columns)' '400'
'Height (rows)' '264'
'Class' 'uint8'
'Image type' 'truecolor'
fft2 - двумерное БПФ
Синтаксис:
Y=fft2(X)
Y=fft2(X, m, n)
Описание:
Функция Y=fft2(X) вычисляет двумерное ДПФ, возвращая результат в матрице комплексных чисел Y, имеющей тот же размер, что и матрица X; X может быть вектором, в этом случае возвращается вектор Y, имеющий такую же ориентацию, что и вектор X.
Функция Y=fft2(X, m, n) вычисляет двумерное преобразование Фурье матрицы mxn, при необходимости дополняя нулями или усекая исходную матрицу X. Возвращается матрица Y размера mxn.
Массив Y имеет формат представления данных double.
Алгоритм:
Двумерное преобразование Фурье вычисляется выполнением двух одномерных преобразований fft(fft(x).').'; сначала вычисляется ДПФ каждого столбца, а затем каждой строки результата [1, 2].
Пример:
Сформируем двумерный сигнал, являющийся суммой двух пространственных волн. Выведем его на экран в виде полутонового изображения (рис. 1, а) и трехмерной поверхности (1, в). Затем вычислим спектр сигнала и выведем его на экран (рис. 1, д). Так как спектр симметричен, 4 отчетливых пика на рис. 1, д соответствуют двум частотам волн, из которых сформировано исходное изображение.
Удалим из спектра пики, соответствующие одной из частот (рис. 1, е). Восстановим с помощью обратного преобразования Фурье из отредактированного спектра двумерный сигнал. Результат восстановления выводится на экран в виде полутонового изображения (рис. 1, 6) и трехмерной поверхности (рис. 1, г).
% Пример демонстрирует двумерное
% прямое и обратное преобразования Фурье.,
% Формирование исходного изображения,
[х, у]=meshgrid(1:32);
I=sin(2*pi*x/8)+sin(2*pi*y/16);
% Вывод исходного изображения на экран.
imshow(mat2gray(I));
% Вывод исходного изображения в виде 3D-поверхности.
figure, mesh(x,y, I);
% Прямое преобразование Фурье.
h=fft2(l);
% Вывод на экран спектра исходного изображения.
figure, mesh(x,y, abs(h));
% Обнуление части спектра.
h(1:32,1:2)=0;
% Вывод на экран получившегося спектра.
figure, mesh(x,y, abs(h));
% Обратное преобразование Фурье.
I=iffi2(abs(h));
% Вывод на экран результирующего изображения.
figure, imshow(mat2gray(l));
% Вывод на экран результирующего изображения в виде 3D-поверхности.
figure, mesh(x, y, abs(I));

а)
б)
в)
г).gif)
д).gif)
е)Рис. 2.
fftn - n–мерное БПФ
Синтаксис:
Y=fftn(X)
Y=fftn(X, siz)
Описание:
Функция Y=fftn(X) вычисляет N-мерное БПФ, возвращая результат в массиве Y, имеющем тот же размер, что и массив X.
Функция Y=fftn(X, siz) вычисляет N-мерное БПФ в виде многомерного массива размера siz, при необходимости дополняя нулями массив X или отбрасывая лишние строки и столбцы.
Массив Y имеет формат представления данных double.
Алгоритм:
N-мерное преобразование Фурье может быть вычислено последовательным применением одномерных преобразований:
Y=X;
for p=1:length(size(X))
Y=fft(Y,[],P);
end
Время, требуемое для вычислений, зависит от возможности разложения на простые множители размера входного массива. В том случае, если количество строк и столбцов является степенью двух, скорость вычислений максимальна.
ifft2 - обратное двумерное БПФ
Синтаксис:
Y=ifft2(X)
Y=ifft2(X, m, n)
Описание:
Функция Y=ifft2(X) вычисляет обратное двумерное ДПФ, возвращая результат в матрице Y, имеющей тот же размер, что и матрица X; X может быть вектором, в этом случае возвращается вектор Y, имеющий такую же ориентацию, что и вектор X.
Функция Y=ifft2(X, m, n) вычисляет двумерное преобразование Фурье матрицы mxn, при необходимости дополняя нулями или усекая исходную матрицу X. Возвращается матрица Y размера mxn.
С точностью, определяющейся ошибками округления, ifft2(fft2(X))=X, однако, если X содержит только действительные элементы, ifft2(fft2(X)) может содержать комплексные элементы с малыми по величине комплексными частями.
Массив Y имеет формат представления данных double.
Алгоритм:
Обратное двумерное преобразование Фурье вычисляется по тому же принципу, который реализован в функции fft2, т. е. двумерное преобразование выполняется с помощью двух последовательных одномерных обратных преобразований Фурье для строк и столбцов. Время расчетов минимально, если m иn являются степенями числа 2. Если m и n, простые числа – время расчетов максимально.
ifftn - n–мерное обратное БПФ
Синтаксис:
Y=ifftn(X)
Y=ifftn(X, siz)
Описание:
Функция Y=ifftn(X) вычисляет N-мерное обратное БПФ, возвращая результат в массиве Y, имеющем тот же размер, что и массив X.
Функция Y=ifftn(X, siz) вычисляет N-мерное обратное БПФ в виде многомерного массива размера siz, при необходимости дополняя нулями массив X или отбрасывая лишние строки и столбцы.
Массив Y имеет формат представления данных double.
Алгоритм:
N-мерное обратное преобразование Фурье может быть вычислено последовательным применением одномерных преобразований:
Y=X;
for р=1 :length(size(X));
Y=ifft(Y, [], р);
end.
dct2 - двумерное ДКП
Синтаксис:
D=dct2(S)
D=dct2(S, M, N)
D=dct2(S, [M N])
Описание:
Функция D=dct2(S) осуществляет двумерное ДКП матрицы S и помещает результат в матрицу D. Матрицы S и D имеют одинаковый размер.
Функции D=dcl2(S, M, N) и D=dct2(S, [M N]) осуществляют двумерное дискретное косинусное преобразование матрицы S размера MxN и помещают результат в матрицу D. При этом, если размеры матрицы S меньше, чем М и N, матрица S предварительно дополняется столбцами и строками нулей до размера MxN. А если размеры матрицы S больше, чем М и N, то у S справа и снизу отбрасываются лишние столбцы и строки.
Возвращаемая матрица D имеет формат представления данных double.
Алгоритм:
Дискретное косинусное преобразование ДКП (discrete cosine transform - DCT) довольно схоже с ДПФ. Оно также является разделимым линейным преобразованием, т. е. двумерное преобразование эквивалентно двум одномерным, произведенным последовательно по каждой из осей [1]. Двумерное ДКП осуществляется в соответствии со следующей формулой:
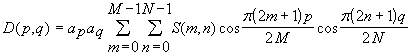
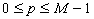 ,
, 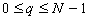 ,
,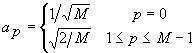 ,
,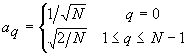 .
.где M и N - соответственно количество строк и столбцов исходного изображения S.
dctmtx - вычисление матрицы коэффициентов ДКП
Синтаксис:
А=dctmtx(n)
Описание:
Функция А=dctmtx(n) возвращает матрицу размера nхn, содержащую коэффициенты преобразования дискретного косинусного преобразования. Возвращаемая матрица А имеет формат представления данных double.
Для изображения S размера nхn матричное произведение D=A*S представляет собой дискретное косинусное преобразование столбцов S, а матричное произведение транспонированной матрицы S=A'*D представляет собой обратное дискретное косинусное преобразование столбцов D. Двумерное дискретное косинусное преобразование S можно выполнить как A*S*A'. Это существенно быстрее, чем использовать функцию dct2, особенно если требуется вычислять много преобразований маленьких блоков изображения, так как матрица А вычисляется только 1 раз. Например, такой подход эффективно применять при реализации сжатия JPEG, где двумерное дискретное косинусное преобразование выполняется над блоками изображения 8x8 пикселов.
radon - прямое преобразование Радона
Синтаксис:
R=radon(l, theta)
R=radon(l, theta, n)
[R, xp]=radon(...)
Описание:
Функция R=radon(I, theta) выполняет преобразование Радона полутонового изображения I и помещает результат в матрицу проекций R. Преобразование Радона представляет собой вычисление проекций изображения на оси, задаваемые углами в градусах относительно горизонтали против часовой стрелки. Эти углы передаются в параметре theta. Если theta - скаляр, то R является вектор-столбцом, содержащим преобразование Радона для угла theta. Если theta - вектор, то R представляет собой матрицу, в которой каждый столбец является преобразованием Радона для одного из углов, содержащихся в векторе theta. Если при вызове функции параметр theta опущен, то в theta записываются значения углов от 0 до 179 с шагом в 1°.
Функция R=radon(I, theta, n) выполняет преобразование Радона полутонового изображения I. Значения каждой проекции вычисляются в n точках, и матрица R имеет n строк. Если при вызове функции параметр n опущен, то он устанавливается равным
2*ceil(norm(size(I) - floor((size(I) - 1)/2) - 1)) + 3.
Если дополнительно определить выходной параметр xp: [R, xp]=radon(...), то в него помещаются значения координат, в которых вычислялись значения проекции. Значения в k-й строке R соответствуют координате xp(k).
Матрица проекций R может рассматриваться как полутоновое или палитровое изображение и имеет формат представления данных double.
Алгоритм:
Функция radon вычисляет проекции изображения вдоль определенных направлений. Проекция двумерной функции f(x, у) на ось х' представляет собой линейный интеграл [1]:
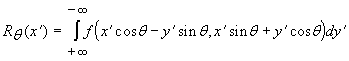 ,
,где оси х' и у' задаются поворотом на угол
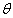 против часовой стрелки:
против часовой стрелки: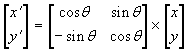
Исходное полутоновое изображение I рассматривается как двумерная функция. Начало координат в системе х'у' соответствует центральному пикселу изображения I в пиксельной системе координат. Центральный пиксел I можно определить как floor((size(I) + l)/2).
Пример:
Рассмотрим, каким образом в преобразовании Радона вычисляются проекции. Для этого сформируем небольшое тестовое изображение, состоящее из трех прямоугольников различной яркости (рис. 1, а). Проекции данного изображения на ось X, на ось под углом в 45° и на ось Y приведены соответственно на рис. 1, б, в, г. На рис. 1, д в виде полутонового изображения показана матрица проекций.
% Пример демонстрирует преобразование Радона.
% Формирование изображения.
I=zeros(100, 100);
I(20:80,20:80)=0.4;
I(30:70,45:55)=0.6;
I(45:55,45:55)=1;
imshow(I);
% Прямое преобразование Радона.
[R, xp]=radon(I, 0:179);
% Вывод на экран проекций на оси X, Y и
% под углом в 45°.
figure, plot(xp,R(:,1));
figure, plot(xp,R(:,46));
figure, plot(xp,R(:,91));
% Вывод на экран матрицы проекций.
iptsetpref(‘ImShowAxesVisible', 'on');
figure, imshow(0:179, xp, R, []);

а)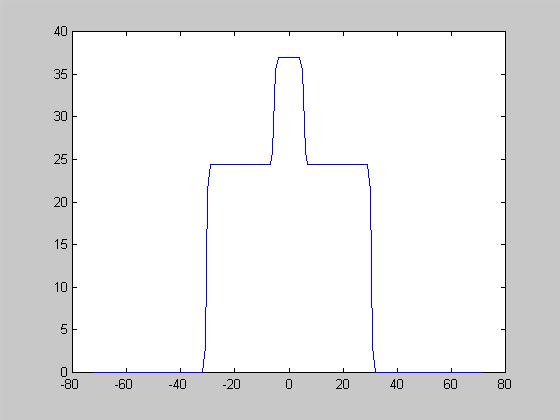
б)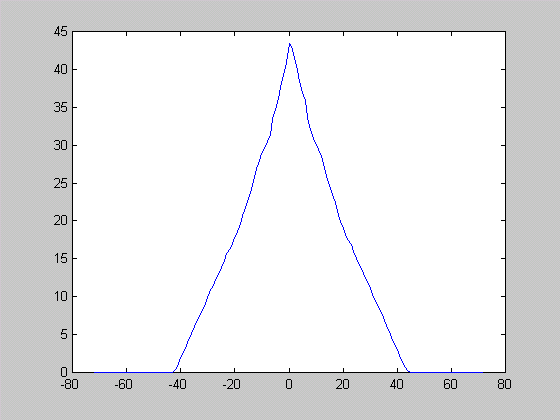
в)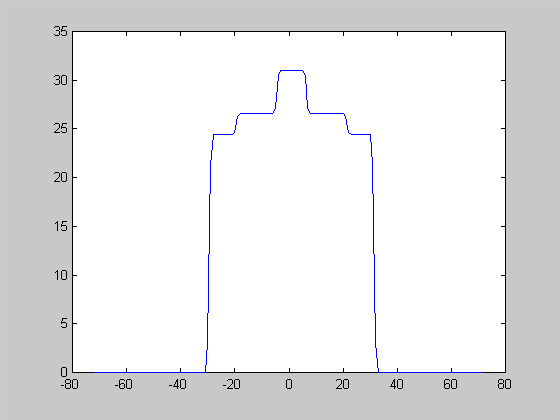
г)
д)Рис.1.
iradon - обратное преобразование Радона
Синтаксис:
I=iradon(P, theta)I=iradon(P, theta, interp, filter, d, n)[I, h]=iradon(...)
Описание:
Функция I=iradon(P, theta) выполняет реконструкцию изображения I по его проекционным данным, которые содержатся в массиве P. Строки P являются данными параллельно-лучевых проекций. В функции iradon центр вращения является центральной точкой проекций и определяется по выражению ceil(size(P, 1)/2).
Параметр theta описывает углы (в градусах), под которыми получена каждая проекция. Этот параметр может представлять собой вектор, содержащий углы или скаляр, описывающий угол между проекциями D_theta. Когда theta представлен вектором, тогда он должен содержать углы с равномерной разбивкой. Когда theta представлен скаляром, описывающим D_theta, тогда проекции берут согласно углам theta=m*D_theta, где m=0, 1, 2, ... , size(P, 2)-1. Когда исходными данными является пустая матрица ([]), тогда параметр D_theta по умолчанию равен 180/size(P, 2).
Функция iradon использует алгоритм фильтрации обратных проекций для выполнения инверсного преобразования Радона. Фильтр проектируется непосредственно в частотной области и умножается на функцию преобразования Фурье проекций. Для ускорения вычислений функции преобразования Фурье проводятся специальные преобразования над проекциями.
Функция I=iradon(P, theta, interp, filter, d, n) содержит описание параметров, которые используются при инверсных преобразованиях Фурье. Существует также возможность точного определения некоторых комбинаций последних четырех аргументов. Для упущенных параметров функция iradon по умолчанию устанавливает некоторые значения.
Параметр interp определяет тип интерполяции, который используется в backprojection. Приведем список доступных опций:
'nearest' - интерполяция по ближайшей окрестности;
'linear' - линейная интерполяция (по умолчанию);
'spline' - сплайновая интерполяция.
Параметр filter описывает какой тип фильтра используется для частотной фильтрации. Параметр filter представляет собой строку, в которой описаны несколько стандартных фильтров:
'Ram-Lak' - усеченный фильтр Рама-Лака (устанавливается по умолчанию). Частотный отзыв этого фильтра равен | f |. Одним из недостатков фильтра Рама-Лака является то, что он чувствительный к шуму на проекциях. Поэтому он используется в комбинациях с другими фильтрами.
'Shepp-Logan' - фильтр Шепа-Логана, умноженный на фильтр Рама-Лака через фазовую функцию.
'Cosine' - косинусный фильтр, умноженный на фильтр Рама-Лака через косинусную функцию.
'Hamming' - фильтр Хэмминга, умноженный на фильтр Рама-Лака через окно Хэмминга.
'Hann' - фильтр Ханна, умноженный на фильтр Рама-Лака через окно Ханна.
Параметр d представляет собой скаляр в диапазоне (0, 1] и служит для модификации фильтра в плане масштабирования по частотной оси. По умолчанию он равен 1. Когда d меньше 1, тогда фильтр сжимает частотный диапазон до [0, d], нормирует частоты; все частоты, которые больше значения d, приравниваются к 0.
Параметр n представляет собой скаляр, описывающий число строк и столбцов в восстановленном изображении. Когда параметр n не описан, тогда размеры определяются исходя из длины проекций.
n=2*floor(size(P, 1)/(2*sqrt(2)))
После определения параметра n, функция iradon восстанавливает изображение, не изменяя масштаб данных. Когда проекции были вычислены с помощью функции radon, тогда размеры восстановленного и исходного изображений могут не совпадать.
Функция [I, h]=iradon(...) возвращает частотный отклик фильтра в вектор h.
Требования к исходным данным.
Все исходные и результирующие аргументы должны быть представлены в формате double.
Пример.
P=phantom(128);R=radon(P, 0:179);I=iradon(R, 0:179, 'nearest', 'Hann');imshow(P)figure, imshow(I)

Алгоритм.
Функция iradon использует алгоритм фильтрации обратных проекций для реализации обратного преобразования Радона. Фильтр проектируется для работы в частотной области и далее умножается на функцию преобразования Фурье проекционных данных. Для ускорения Фурье преобразования с проекционными данными проводится некоторая предобработка.
phantom - создание модельного изображения головы
Синтаксис:
P=phantom(def, n)P=phantom(E, n)[P, E]=phantom(...)
Описание:
Функция P=phantom(def, n) создает изображение головы, которое может быть использовано в качестве тестового числового массива в таких алгоритмах двумерной реконструкции как radon, iradon или другие. Массив P представляет собой полутоновое яркостное изображение, которое состоит из одного продолговатого эллипса (симулирующего мозг) и нескольких меньших эллипсов (симулирующих особенности мозга).Параметр def является строковой величиной, которая определяет тип генерации фантома головы. Он может принимать следующие значения:
'Shepp-Logan' - тестовое изображение, которое широко используется при томографических исследованиях.'Modified Shepp-Logan' (по умолчанию) - вариант фантома Шеппа-Логана (Shepp-Logan) с повышенным контрастом для лучшего визуального восприятия.
Параметр n является скаляром и определяет число строк и столбцов в P. Если этот параметр отсутствует, по умолчанию он равен 256.
Функция P=phantom(E, n) создает фантом головы, параметры которого определяются пользователем и где каждая строка матрицы E определяет эллипс на изображении. E содержит шесть строк, каждая из которых содержит различные параметры эллипса. В таблице описаны столбцы матрицы.
Столбцы Параметр Значение Столбец 1 A Прибавление значения интенсивности эллипса Столбец 2 A Длина горизонтальной полуоси эллипса Столбец 3 B Длина вертикальной полуоси эллипса Столбец 4 x0 x-координата центра эллипса Столбец 5 y0 y-координата центра эллипса Столбец 6 Phi Угол (положение) между горизонтальной полуосью эллипса и x-осью изображения Пример.P=phantom('Modified Shepp-Logan', 200);imshow(P)

getheight - создание вертикальных структурных элементов
Синтаксис:
H=getheight(SE)
Описание:
Функция H=getheight(SE) возвращает массив, размерность которого совпадает с getnhood(SE), который содержит значения соседних элементов, связанных с каждым структурным элементом. Параметр H является полностью нулевым для плоских структурных элементов.
Требования к исходным данным.
Структурные элементы являются объектами типа STREL. Параметр H имеет формат представления данных double.
Пример:
se=strel(ones(3, 3), magic(3));
getheight(se).
getneighbors - определение местоположения соседних структурных элементов
Синтаксис:
[offsets, heights]=getneighbors(SE)
Описание:
Функция [offsets, heights]=getneighbors(SE) возвращает местоположение и соответственное значение для каждого соседнего элемента относительно структурного элемента SE.
Параметр offsets представляет собой массив размерностью P
 N, где P число соседей для структурного элемента и N размерность структурного элемента. Каждая строчка offsets содержит местоположение соответствующего соседнего элемента относительно центра структурного элемента.
N, где P число соседей для структурного элемента и N размерность структурного элемента. Каждая строчка offsets содержит местоположение соответствующего соседнего элемента относительно центра структурного элемента.Параметр heights представляет собой P-элементный вектор, содержащий значение (интенсивность) каждого структурного элемента.
Требования к исходным данным.
SE является объектом типа STREL. Массивы параметров offsets и heights имеют формат представления данных double.
Пример:
se=strel([1 0 1], [5 0 -5])
[offsets, heights]=getneighbors(se)
se=
Неплоские STREL–объекты, содержащие 2 соседних элемента.
Окрестность:
1 0 1
Значение:
5 0 -5
offsets=
0 1
heights=
5 -5
getnhood - создание соседних структурных элементов
Синтаксис:
nhood=getnhood(SE)
Описание:
Функция nhood=getnhood(SE) возвращает окрестность, связанную с структурным элементом SE.
Требования к исходным данным:
Структурные элементы являются объектами типа STREL. Параметр nhood представляет собой логический массив.
Пример:
se=strel(eye(5));
nhood=getnhood(se)
getsequence - создание последовательности разложенных структурных элементов
Определение последовательности разложенных структурных элементов
Синтаксис:
SEQ=getsequence(SE)
Описание:
Функция SEQ=getsequence(SE), где параметр SE является массивом структурных элементов, возвращает еще один массив структурных элементов SEQ, содержащий отдельные структурные элементы, которые являются разложением SE. Массив SEQ эквивалентный массиву SE, за исключением не разложенных элементов SEQ.
Требования к исходным данным:
Массивы SE и SEQ являются массивами типа STREL.
Пример:
Функция strel использует разложение для квадратных структурных элементов, размерность которых больше чем 3
 3. Функция getsequence извлекает разложение структурных элементов.
3. Функция getsequence извлекает разложение структурных элементов.se=strel('square', 5)
seq=getsequence(se)
se=
Плоские STREL – объекты содержат 25 соседних. Разложение: 2 STREL – объекта содержат около 10 соседей.
Окрестность:
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
seq=
Массив STREL – объектов размерностью 2x1.
Использование функции imdilate с опцией 'full' используется для расширения последовательности разложенных структурных элементов с площадью 5
 5:
5:imdilate(1, seq, 'full')
isflat - возвращение одинаковых структурных элементов
Синтаксис:
TF=isflat(SE)
Описание:
Функция TF=isflat(SE) возвращает значение "истина" (true (1)), когда структурный элемент SE является плоским; и значение "ложь" (false (0)) - в противоположном случае. Когда SE представлен массивом STREL-объектов, тогда массив TF имеет ту же размерность, что и SE.
Требования к исходным данным.
Параметр SE представлен STREL-объектом. Данные TF представляются значениями удвоенной точности.
reflect - представление структурных элементов через их центр
Синтаксис:
SE2=reflect(SE)
Описание:
Функция SE2=reflect(SE) отражает структурные элементы относительно их центра. Этого же эффекта можно достигнуть, если повернуть область структурных элементов на 180 градусов вокруг центра (для двумерных структурных элементов). Когда SE представляет собой структурный элемент объекта, тогда reflect(SE) отражает каждый элемент SE и SE2 имеет тот же размер, что и SE.
Требования к исходным данным.
Данные SE и SE2 являются объектами типа STREL.Пример.se=strel([0 0 1; 0 0 0; 0 0 0])se2=reflect(se)se=Плоский объект STREL содержит соседнюю 1.Окрестность: 0 0 1 0 0 0 0 0 0se2=Плоский объект STREL содержит соседнюю 1.Окрестность: 0 0 0 0 0 0 1 0 0 Сопутствующие функции: STREL.
strel - создание морфологических структурных элементов
Синтаксис:
SE=strel(shape, parameters)
Описание:
Функция SE=strel(shape, parameters) создает структурный элемент SE, тип которого описывается в параметре shape. В таблице перечислены все типы поддерживаемых форм структурных элементов. В зависимости от параметра формы shape, структурный элемент strel может иметь ряд дополнительных параметров. Синтаксис написания функции зависит от формы структурного элемента.
Плоские структурные элементы 'arbitrary' 'pair' 'diamond' 'periodicline' 'disk' 'rectangle' 'line' 'square' 'octagon' Неплоские структурные элементы 'arbitrary' 'ball' Функция SE=strel('arbitrary', NHOOD) создает плоский структурный элемент, где параметр NHOOD описывает окрестность. NHOOD представляет собой матрицу, состоящую из нулей и единиц; расположение единиц в окрестности зависит от морфологической операции. Центром NHOOD является центральный элемент, который определяется из выражения floor((size(NHOOD)+1)/2). Параметр 'arbitrary' можно опустить и вместо него использовать strel(NHOOD).
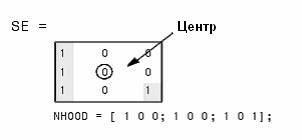
Функция SE=strel('arbitrary', NHOOD, HEIGHT) создает неплоский структурный элемент, где параметр NHOOD описывает окрестность. HEIGHT представляет собой матрицу той же размерности, что и NHOOD, содержащую значения, связанные с каждым ненулевым элементом в NHOOD. Матрица HEIGHT состоит из вещественных конечных значений. Параметр 'arbitrary' можно упустить и использовать выражение strel(NHOOD, HEIGHT).
Функция SE=strel('ball', R, H, N) создает неплоские, "шарообразные" (точнее эллиплообразные) структурные элементы с радиусом R в плоскости X-Y и высотой H. Отметим, что R должно выражаться положительным целым числом, H представляется вещественным скаляром, а N положительным целым числом. Когда N является больше 0, тогда шарообразные структурные элементы аппроксимируются последовательностью из N неплоских линейных структурных элементов. Когда N равно 0, аппроксимация не используется и структурные элементы формируются из всех пикселей, удаленных не более чем на от R от центра. Соответствующие значения определяются по формуле, которая выражает зависимость в эллипсе между R и H. Когда N не определено, тогда по умолчанию это значение равно 8.
Примечание. Морфологические операции работают значительно быстрее, если структурные элементы аппроксимируются (N>0).
Функция SE=strel('diamond', R) создает плоский ромбообразный структурный элемент, где R описывает расстояние от центра структурного элемента до точки ромба. R должно представляться неотрицательными целыми числами.
.jpg)
Функция SE=strel('disk', R, N) создает плоские, дискообразные структурные элементы, где параметр R описывает радиус. R должно быть неотрицательным вещественным числом. Параметр N должен принимать значения 0, 4, 6 или 8. Когда N больше 0, тогда дискообразный структурный элемент аппроксимируется последовательностью N периодично-линейных структурных элементов. Когда N равно 0, аппроксимация не используется и структурные элементы формируются из всех пикселей, удаленных не более чем на от R от центра. Кода N не определено, тогда по умолчанию это значение равно 4.
Примечание. Морфологические операции работают значительно быстрее, когда структурные элементы используют аппроксимацию (N>0). Однако, структурные элементы, которые не используют аппроксимацию (N=0) являются непригодными при решении задач гранулометрии. Иногда для формирования структурного элемента необходимо использовать аппроксимацию различных линейных структурных элементов. В этом случае число составных структурных элементов равно N+2.
.jpg)
Функция SE=strel('line', LEN, DEG) создает плоский линейный структурный элемент, где параметр LEN описывает длину, а параметр DEG описывает угол (в градусах) линии, измеренный в направлении против часовой стрелки относительно горизонтальной оси. Параметр LEN характеризует дистанцию между центрами структурных элементов, расположенных на противоположных концах линии.
.jpg)
Функция SE=strel('octagon', R) создает плоские восьмиугольные структурные элементы, где R описывает расстояние между центром структурного элемента и стороной восьмиугольника, измеренное вдоль горизонтальной или вертикальной оси. Параметр R должен представляться неотрицательной трехэлементной составляющей.
.jpg)
Функция SE=strel('pair', OFFSET) создает плоский структурный элемент, состоящий из двух частей. Одна часть расположена в центре. Расположение второй части зависит от описания, которое содержится в векторе OFFSET. OFFSET представляет собой двухэлементный вектор целых чисел.
.jpg)
Функция SE=strel('periodicline', P, V) создает плоский структурный элемент, состоящий из 2*P+1 частей. Параметр V является двухэлементным вектором, который содержит целочисленные значения строк и столбцов структурного элемента. Одна часть структурного элемента расположена в центре. Другие элементы расположены в 1*V, -1*V, 2*V, -2*V, ..., P*V, -P*V.
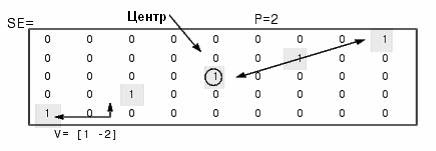
Функция SE=strel('rectangle', MN) создает плоский прямоугольный структурный элемент, где параметр MN описывает его размер. MN представляется двухэлементным вектором неотрицательных целых чисел. Первый элемент MN описывает число строк структурных элементов; второй элемент описывает число столбцов.
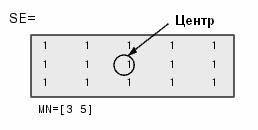
Функция SE=strel('square', W) создает структурные элементы в виде квадрата, размеры которого задаются параметром W. W должен представляться неотрицательными целыми числами.
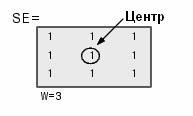
Примечание. Для всех форм за исключением, представленной параметром 'arbitrary', структурные элементы создаются с помощью семейства технологий известных под общим названием декомпозиция структурных элементов. Принципиально то, что морфологические операции расширения для больших структурных элементов объектов выполняются быстрее, чем для последовательности небольших структурных элементов.
Метод.
В таблице перечислены методы, которые поддерживают STREL-объекты.
getheight Получение высоты структурного элемента getneighbors Получение информации об окрестных элементах. getnhood Получение информации об окрестности. getsequence Получение последовательности составляющих структурного элемента. isflat Возвращение структурных элементов. reflect Отражение структурных элементов. translate Преобразование структурных элементов. Пример.
se1=strel('square', 11) % квадрат с размерами 11
 11se2=strel('line', 10, 45) % линия, длина 10, угол 45 градусовse3=strel('disk', 15) % диск, радиус 15se4=strel('ball', 15, 5) % шар, радиус 15, высота 5
11se2=strel('line', 10, 45) % линия, длина 10, угол 45 градусовse3=strel('disk', 15) % диск, радиус 15se4=strel('ball', 15, 5) % шар, радиус 15, высота 5Алгоритм.
Метод, который использует декомпозицию ромбообразных структурных элементов, известен под названием "логарифмическая декомпозиция" [1]. Метод, который использует декомпозицию дискообразных структурных элементов, базируется на "радиальной декомпозиции с использованием периодических линий" [2], [3]. Для более детальной информации см. toolbox/images/images/@strel/strel.m.
Метод, использующий шарообразные структурные элементы, известен как технология "радиальных составляющих сферы" [2].
translate - преобразование структурных элементов
Синтаксис:
SE2=translate(SE, V)
Описание:
Функция SE2=reflect(SE, V) перемещает структурный элемент SE в N-D пространстве. Параметр V представляет собой N-элементный вектор, содержащий начальные перемещения по каждой размерности.
Требования к исходным данным.
Переменные SE и SE2 являются объектами типа STREL; вектор V представляет собой вектор значений удвоенной точности.
Пример.
Морфологическая операция раскрытия с использованием структурного элемента strel(1) применяется для перемещения исходного изображения в пространстве. Приведем пример перемещения изображения cameraman.tif вниз и вправо на 25 пикселей.
I=imread('cameraman.tif'); se=translate(strel(1), [25 25]); J=imdilate(I, se); imshow(I), title('Original') figure, imshow(J), title('Translated');

padarray - пустой массив
Синтаксис:
B=padarray(A, padsize, method, direction)
Описание:
Функция B=padarray(A, padsize, method, direction) наполняет массив A в соответствии с параметром padsize некоторым числом элементов вдоль каждого направления, используя описанный метод и направление наполнения. N-й элемент вектора padsize описывает размер наполнения для N-ого направления массива A.
Параметр method может быть числовым скаляром, в этом случае он описывает значения для всех элементов. Кроме числового скаляра, этот параметр может быть представлен одним значением, определяющим метод наполнения значений. По умолчанию, method устанавливает значение наполнения 0.
Значение Описание 'circular' Наполнение с круговым повторением элементов в данном направлении. 'replicate' Наполнение с повторением граничных элементов массива. 'symmetric' Наполнение массива с зеркальным отражением самого себя. Параметр direction описывает вдоль какого направления наполняется массив. По умолчанию этот параметр задан как 'post'.
Значение Описание 'pre' Наполнение впереди первого элемента по каждому направлению. 'post' Наполнение позади последнего элемента вдоль каждого направления.
Это значение устанавливается по умолчанию.'both' Наполнение впереди первого и позади последнего элементов вдоль каждого направления. Требования к исходным данным.
Когда выполняется наполнение константами, тогда массив A должен быть числовым или логическим. Когда производится наполнение с использованием методов 'circular', 'replicate' или 'symmetric', тогда массив A может быть представлен в произвольном формате. Массив B имеет тот же формат, что и A.
Пример.
Присоединим три элемента к следующему некоторому вектору. Наполняющие элементы содержат зеркальные копии массива.
b=padarray([1 2 3 4], 3, 'symmetric', 'pre')
b=
3 2 1 1 2 3 4
Присоединим три элемента, наполняя окончание массива в одном направлении и присоединяя два элемента в другом направлении. В качестве наполняющих используем крайние элементы массива.
B=padarray([1 2; 3 4], [3 2], 'replicate', 'post')B= 1 2 2 2 3 4 4 4 3 4 4 4 3 4 4 4 3 4 4 4 Присоединим три элемента, наполняя в каждом направлении трехмерный массив. Каждый наполняющий элемент содержит значение 0.A=[ 1 2; 3 4];B=[ 5 6; 7 8];C=cat(3, A, B)C(:, :, 1)= 1 2 3 4C(:, :, 2)= 5 6 7 8D=padarray(C, [3 3], 0, 'both')D(:, :, 1)= 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 0 0 0 0 0 0 3 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0D(:, :, 2)= 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 6 0 0 0 0 0 0 7 8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Комментарии