Краткий курс теории обработки изображений
Информация в данной статье относится к релизам программы MATLAB ранее 2016 года, и поэтому может содержать устаревшую информацию в связи с изменением функционала инструментов. С более актуальной информацией вы можете ознакомиться в разделе документация MATLAB на русском языке.
Краткий курс теории обработки изображений. Автор - И.М.Журавель.
Содержание:
- Свойства зрительной системы человека
- Возможности цифровой обработки изображений в Matlab
- Типы изображений
- Бинарные изображения: геометрические характеристики
- Бинарные изображения: топологические характеристики - Формирование и обработка цифровых изображений
- Локально-адаптивная обработка изображений
- Адаптивное повышение контрастности изображений
- Энтропия изображения. Использование среднеквадратического отклонения значений яркостей элементов окрестности в методах контрастирования изображений. Нелинейное растяжение локальных контрастов.
- Анализ некоторых характеристик локальных окрестностей
- Статистическое определение локального контраста
- Локально-адаптивное улучшение качества изображений - Фильтрация изображений
- Алгоритмы сглаживания изображений
- Двумерное сглаживание изображений
- Обобщенная линейная фильтрация
- Градиентный метод выделение контуров объектов на цветных изображениях
- Пространственная фильтрация - Деконволюция
- Предварительная обработка изображений - Расширение границ изображений. Сверхразрешение
- - Реконструкция размытых изображений в MATLABСтруктурное распознавание на основе меры схожести символьных строк
- Границы изображений
- Края и их обнаружение - Оптимизация палитры изображений
- Кодирование и сжатие изображений
- задачи кодирования
- основные методы кодирования - Некоторые области практического применения методов обработки изображений и распознавания образов (геофизические наблюдения, применение в биологии, применение на транспорте)
- Распознавание рукописных знаков
- Коррекция неравномерной засветки изображения.
- Сегментация цветных изображений на основе кластеризации по методу k-средних.
- Сегментация цветных изображений на основе цветового пространства L*a*b*
- Уменьшение количества градаций цветных изображений
- Обнаружение вращений и масштабных искажений на изображении
- Регистрация изображений с помощью нормированной кросс-корреляции
- Наложение двух изображений
- Технология повышения контрастности изображений.
- Улучшение мультиспектральных цветных изображений
- Регистрация аэрофотографий на ортофотоснимках
- Пространственные преобразования изображений
- Исследование конформных преобразований
- Создание обивочных материалов с использованием изображений
- Извлечение данных из трехмерных магниторезонансных изображений
- Поиск длины маятника в движении
- Гранулометрия
- Идентификация округлых предметов
- Измерение углов пересечения
- Измерение радиуса части мотка ленты
- Обнаружение объектов с помощью сегментации изображений
- Реконструкция изображений по их проекционным данным
- Сегментация методом управляемого водораздела
- Восстановление изображений методом слепой деконволюции
- Реконструкция изображений с использованием регуляризационного фильтра
- Восстановление изображений с использованием метода Лаки-Ричардсона
- Некоторые подходы к улучшению визуального качества изображений с затемненными участками
- Реализация некоторых методов видоизменения гистограмм в системе Matlab
- Подавление шумов на изображениях
- Текстурная сегментация с использованием текстурных фильтров
- Поиск растительности на мультиспектральных изображениях
- Распознавание объектов на основе вычисления их признаков
- Распознавание объектов на основе вычисления коэффициента корреляции
- Анализ признаков объектов
- Некоторые аспекты задачи распознавания номерных знаков автомобилей
- Анализ серии изображений с распределенной обработкой данных
- Сглаживание цветных изображений
- Построение гистограмм
- Видоизменение гистограмм
Визуализация объектов - Применение методов улучшения изображений при разработке системы видеонаблюдения
- Улучшение изображений с яркостными искажениями
- Некоторые алгоритмы повышения визуального качества изображений
- Пороговая обработка цветных изображений
- Формирование ночного изображения на основе дневного и наоборот
- Обнаружение лиц на основе цвета
- Метод управления яркостью изображения
Свойства зрительной системы человека
Большое количество информации представляется в виде статических или динамических изображений. Поскольку далее эти изображения рассматриваются и анализируются человеком, то важно знать механизмы зрительного восприятия. Эти знания являются мощным инструментом при разработке различных систем обработки изображений.
Отметим, что психофизические аспекты восприятия света изучены не полностью. Однако существует большое количество различных методов и подходов, объясняющих законы и свойства зрительного восприятия света человеком.
Глаз человека является уникальным механизмом, обеспечивающим адаптивную настройку в соответствии с внешними условиями.
Рассмотрим некоторые основные свойства зрительной системы человека. Важной характеристикой зрительной системы является чувствительность, т.е. способность реагировать на внешние изменения. Чувствительность характеризуется верхним и нижним абсолютными порогами.
Существует несколько различных видов чувствительности. Световая чувствительность характеризует свойство глаза реагировать на максимально малый световой поток. Однако здесь следует отметить, что вероятность распознавания максимально малого светового потока зависит также и от других факторов, например угла зрения.
Зрительная система по-разному реагирует на излучения, которые равны по мощности, но излучаемые из различных диапазонов спектра. Такая чувствительность называется спектральной.
Способность глаза различать минимальные различия яркости смежных областей изображения характеризуется контрастной чувствительностью. Также зрительная система характеризуется различной чувствительностью к цветовому тону, т.е. к излучениям из различных участков спектра. Зрительная система характеризуется еще чувствительностью к насыщенности цвета.
Приведенные выше типы чувствительности зрительной системы не являются постоянными, а зависят от многих факторов, в частности, условий освещения. Например, при переходе из темной комнаты в светлую, нужно некоторое время для восстановления светочувствительности глаза. Этот процесс называется яркостной адаптацией глаза.
Цветоощущение характеризуется тремя основными характеристиками – светлота, цветовой тон и насыщенность. Для классификации цветов используются цветовые пространства.
На основе свойств и характеристик зрительных систем создаются различные модели цветового зрения. Среди них следует выделить модель цветового зрения, предложенную Фреем. Особенностью этой модели является то, что зрительная система представлена тремя каналами, два из которых характеризуют цветность, а третий – яркость. Эта модель наиболее удачно согласуется со многими свойствами цветного зрения.
Возможности цифровой обработки изображений в Matlab
На сегодняшний день система Matlab, в частности пакет прикладных программ Image Processing Toolbox, является наиболее мощным инструментом для моделирования и исследования методов обработки изображений. Он включает большое количество встроенных функций, реализующих наиболее распространенные методы обработки изображений. Рассмотрим основные возможности пакета Image Processing Toolbox.
Геометрические преобразования изображений
К наиболее распространенным функциям геометрических преобразований относится кадрирование изображений (imcrop), изменение размеров (imresize) и поворот изображения (imrotate).
Суть кадрирования состоит в том, что функция imcrop позволяет с помощью мыши в интерактивном режиме вырезать часть изображения и поместить ее в новое окно просмотра.
L=imread('cameraman.tif');
imshow(L);
imcrop;
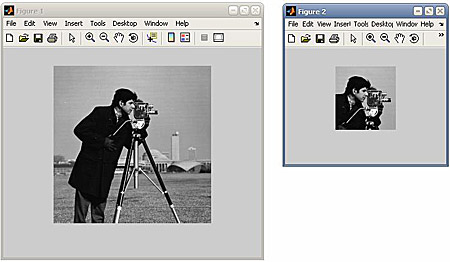
Функция изменения размеров изображения imresize позволяет, используя специальные методы интерполяции, изменять размер любого типа изображения.
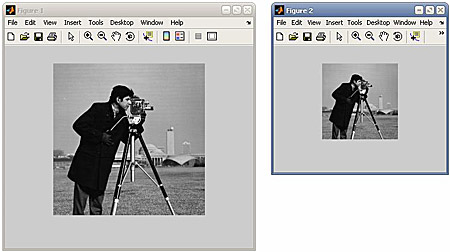
В пакете Image Processing Toolbox существует функция imrotate, которая осуществляет поворот изображения на заданный угол.
L1=imrotate(L,35,'bicubic'); figure,imshow(L1)

Таким образом, приведенные выше функции позволяют поворачивать, вырезать части, масштабировать, т.е. работать с целым массивом изображения.
Анализ изображений
Для работы с отдельными элементами изображений используются такие функции как imhist, impixel, mean2, corr2 и другие.
Одной из наиболее важных характеристик является гистограмма распределения значений интенсивностей пикселей изображения, которую можно построить с помощью функции imhist.
L=imread('cameraman.tif');
figure, imshow(L);
figure, imhist(L);
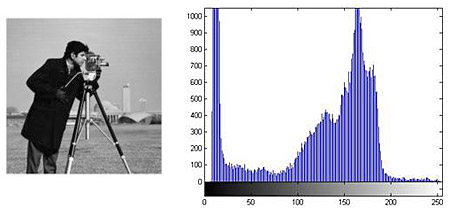
Довольно часто при проведении анализа изображений возникает необходимость определить значения интенсивностей некоторых пикселей. Для этого в интерактивном режиме можно использовать функцию impixel.
>> impixel
ans =
173 173 173
169 169 169
163 163 163
39 39 39
Следует отметить, что функция impixel по своим возможностям в некоторой степени повторяет опцию Data Cursor, пример использования которой при веден на изображении внизу.
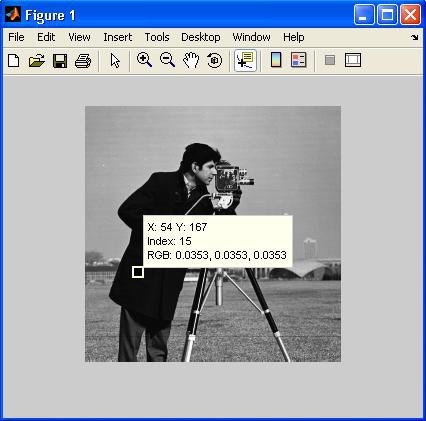
Еще одной широко применяемой функцией является функция mean2 – она вычисляет среднее значение элементов матрицы.
Функция corr2 вычисляет коэффициент корреляции между двумя матрицами. Другими словами, с помощью функции corr2 можно сказать насколько две матрицы или изображения похожи между собой. Эта функция широко применяется при решении задач распознавания.
Улучшение изображений
Среди встроенных функций, которые реализуют наиболее известные методы улучшения изображений, выделим следующие – histeq, imadjust та imfilter(fspecial).
Как уже отмечалось ранее, гистограмма изображения является одной из наиболее информативных характеристик. На основе анализа гистограммы можно судить о яркостных искажениях изображения, т.е. сказать о том, является ли изображение затемненным или засветленным. Известно, что в идеале на цифровом изображении в равном количестве должны присутствовать пиксели со всеми значениями яркостей, т.е. гистограмма должна быть равномерной. Перераспределение яркостей пикселей на изображении с целью получения равномерной гистограммы выполняет метод эквализации, который в системе Matlab реализован в виде функции histeq.
L=imread('cameraman.tif');
figure, imshow(L);
L1=histeq(L);
Figure, imsow(L1);

Исходное изображение

Изображение после эквализации гистограммы
Довольно часто при формировании изображений не используется весь диапазон значений интенсивностей, что отрицательно отражается на качестве визуальных данных. Для коррекции динамического диапазона сформированных изображений используется функция imadjust.
L=imread('cameraman.tif');
figure, imshow(L);
L1=imadjust(L);
figure, imshow(L1);
figure, imhist(L);
figure, imhist(L1);

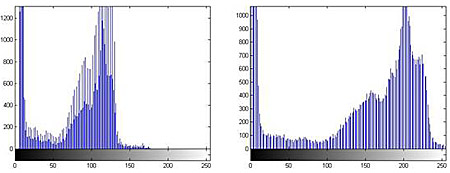
Также при решении задач улучшения изображений используется функция imfilter в паре с функцией fspecial. Функция fspecial позволяет задавать различные типы масок фильтра. Рассмотрим пример использования маски фильтра, повышающего резкость изображения.
L=imread('cameraman.tif');
figure, imshow(L);
H = fspecial('unsharp');
L1 = imfilter(L,H,'replicate');
figure, imshow(L1);

Фильтрация изображений
Пакет Image Processing Toolbox обладает очень мощным инструментарием по фильтрации изображений. Среди множества встроенных функций, которые решают задачи фильтрации изображений, особо следует выделить fspecial, ordfilt2, medfilt2.
Функция fspecial является функцией задания маски предопределенного фильтра. Эта функция позволяет формировать маски:
- высокочастотного фильтра Лапласа;
- фильтра, аналогичного последовательному применению фильтров Гаусса и Лапласа, так называемого лапласиана-гауссиана;
- усредняющего низкочастотного фильтра;
- фильтра, повышающего резкость изображения.
Рассмотрим примеры применения названных выше фильтров:
L=imread('cameraman.tif');
figure, imshow(L);
h=fspecial('laplasian',.5);
L1 = imfilter(L,h,'replicate');
figure, imshow(L1);

h=fspecial('log', 3, .5);
L1 = imfilter(L,h,'replicate');
figure, imshow(L1);

h=fspecial('average', 3);
L1 = imfilter(L,h,'replicate');
figure, imshow(L1);

h=fspecial('unsharp', .5);
L1 = imfilter(L,h,'replicate');
figure, imshow(L1);

Сегментация изображений
Среди встроенных функций пакета Image Processing Toolbox, которые применяются при решении задач сегментации изображений, следует выделить qtdecomp, edge и roicolor.
Функция qtdecomp выполняет сегментацию изображения методом разделения и анализа однородности не перекрывающихся блоков изображения.
I = imread('cameraman.tif');
S = qtdecomp(I,.27);
blocks = repmat(uint8(0),size(S));
for dim = [512 256 128 64 32 16 8 4 2 1];
numblocks = length(find(S==dim));
if (numblocks > 0)
values = repmat(uint8(1),[dim dim numblocks]);
values(2:dim,2:dim,:) = 0;
blocks = qtsetblk(blocks,S,dim,values);
end
end
blocks(end,1:end) = 1;
blocks(1:end,end) = 1;
imshow(I), figure, imshow(blocks,[])

Одной из наиболее часто применяемых является функция выделения границ edge, которая реализует такие встроенные методы – Собела, Превит, Робертса, лапласиан-гауссиана, Канни и др.
Приведем примеры реализации функции edge с использованием различных фильтров.
clear;
I = imread('cameraman.tif');
BW1=edge(I,'sobel');
figure,imshow(BW1);title('sobel');
BW2=edge(I,'prewitt');
figure,imshow(BW2);title('prewitt');
BW3=edge(I,'roberts');
figure,imshow(BW3);title('roberts');
BW4=edge(I,'log');
figure,imshow(BW4);title('log');
BW5=edge(I,'zerocross');
figure,imshow(BW5);title('zerocross');
BW6=edge(I,'canny');
figure,imshow(BW6);title('canny');
 |
 |
 |
 |
 |
 |
Еще одной функцией, которая применяется для бинаризации по заданным цветам, является функция roicolor. Приведем пример ее использования.
I = imread('cameraman.tif');
figure, imshow(I);
BW = roicolor(I,128,255);
imshow(I);
figure, imshow(BW);

Морфологические операции над бинарными изображениями
Система Matlab владеет довольно мощным инструментарием морфологической обработки бинарных изображений. Среди основных операций выделим следующие – эрозия, наращивание, открытие, закрытие, удаление изолированных пикселей, построение скелета изображения и т.п.
В качестве примера приведем решение задачи разделения слипшихся объектов с помощью морфологических операций.
clear;
L=imread('circles.bmp');
L=L(:,:,1);
imshow(L);
BW1=L<150;
figure,imshow(BW1);
BW2=bwmorph(BW1,'erode',12);
figure,imshow(BW2);
BW2=bwmorph(BW2,'thicken',Inf);
figure,imshow(BW2);
BW1=BW1&BW2;
figure,imshow(BW1);

Исходное изображение
 Бинарное изображение |
 Эрозия бинарного изображения |
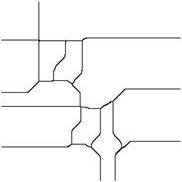 Утолщение объектов |
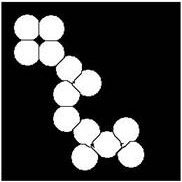 Результат разделения слипшихся объектов |
Кроме перечисленных возможностей, пакет прикладных программ Image Processing Toolbox владеет широкими возможностями при решении задач анализа изображений, в частности, при поиске объектов и вычислении их признаков.
Из представленного материала видно, что пакет прикладных программ Image Processing Toolbox обладает мощным инструментарием для обработки и анализа цифровых изображений. Это приложение является очень удобной средой для разработки и моделирования различных методов. Возможности каждой из приведенных выше, а также других, функций будут детально рассмотрены в последующих материалах.
Типы изображений
Интегрированные среды для моделирования и исполнения программ цифровой обработки изображений и сигналов содержат мощные средства для инженерно–научных расчетов и визуализации данных. Большинство современных пакетов поддерживает визуальное программирование на основе блок–схем. Это позволяет создавать программы специалистам, не владеющим техникой программирования. К таким пакетам относится Image Processing Toolbox системы MATLAB, разработанный фирмой MathWorks. Этот пакет владеет мощными средствами для обработки изображений. Они имеют открытую архитектуру и позволяют организовывать взаимодействие с аппаратурой цифровой обработки сигналов, а также подключать стандартные драйвера.
Система MATLAB и пакет прикладных програм Image Processing Toolbox (IPT) является хорошим инструментом разработки, исследования и моделирования методов и алгоритмов обработки изображений. При решении задач обработки изображений пакет IPT позволяет идти двумя путями. Первый из них состоит в самостоятельной программной реализации методов и алгоритмов. Другой путь позволяет моделировать решение задачи с помощью готовых функций, которые реализуют наиболее известные методы и алгоритмы обработки изображений. И тот, и другой способ оправдан. Но все же для исследователей и разработчиков методов и алгоритмов обработки изображений предпочтительным является второй путь.
Это объясняется гибкостью таких программ, возможностью изменения всех параметров, что очень актуально при исследовании, разработке, определении параметром регуляризации и т.д. Прежде чем использовать для решения каких-либо задач обработки изображений стандартные функции пакета IPT, разработчик должен в совершенстве их исследовать. Для этого он должен точно знать, какой метод и с какими параметрами реализует та или иная функция.
В том и другом подходе к решению задачи обработки видеоданных объектом исследования является изображение. Для этого рассмотрим коротко особенности представления изображений в IPT.
Изображения бывают векторными и растровыми. Векторным называется изображение, описанное в виде набора графических примитивов. Растровые же изображения представляют собой двумерный массив, элементы которого (пикселы) содержат информацию о цвете. В цифровой обработке используются растровые изображения. Они в свою очередь делятся на типы - бинарные, полутоновые, палитровые, полноцветные.
Элементы бинарного изображения могут принимать только два значения - 0 или 1. Природа происхождения таких изображений может быть самой разнообразной. Но в большинстве случаев, они получаются в результате обработки полутоновых, палитровых или полноцветных изображений методами бинаризации с фиксированным или адаптивным порогом. Бинарные изображения имеют то преимущество, что они очень удобны при передаче данных.
Полутоновое
изображение состоит из элементов, которые могут принимать одно из значений интенсивности какого-либо одного цвета. Это один из наиболее распространенных типов изображений, который применяется при различного рода исследованиях. В большинстве случаев используется глубина цвета 8 бит на элемент изображения.
В палитровых
изображениях значение пикселов является ссылкой на ячейку карты цветов (палитру). Палитра представляет собой двумерный массив, в столбцах которого расположены интенсивности цветовых составляющих одного цвета.
В отличии от палитровых, элементы полноцветных изображений непосредственно хранят информацию о яркостях цветовых составляющих.
Выбор типа изображения зависит от решаемой задачи, от того, насколько полно и без потерь нужная информация может быть представлена с заданной глубиной цвета. Также следует учесть, что использование полноцветных изображений требует больших вычислительных затрат.
В зависимости от типа изображения они по-разному представляются в разных форматах. Этот момент будет очень важным при создании программ в среде IPT. Наиболее удобно зависимость способов представления элементов изображения (диапазон их значений) от типа и формата представить в виде таблицы.
| Тип изображения | double | uint8 |
| Бинарное | 0 и 1 | 0 и 1 |
| Полутоновое | [0, 1] | [0, 255] |
| Палитровое | [1, размер палитры],
где 1 - первая строка палитры |
[0, 255],
где 0 - первая строка палитры.* |
| Полноцветное | [0, 1] | [0, 255] |
*
Примечание. При программной реализации лучше избегать использования такой индексации строк. MATLAB корректно воспринимает индексацию с первой, а не нулевой строки.
В дальнейшем, при рассмотрении методов обработки изображений, будем считать, что изображение представляется матрицей чисел (размер матрицы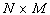 ), где значение каждого элемента отвечает определенному уровню квантования его энергетической характеристики (яркости). Это так называемая пиксельная система координат. Она применяется в большинстве функций пакета IPT. Существует также пространственная система координат, где изображение представляется непрерывным числовым полем квадратов с единичной величиной. Количество квадратов совпадает с числом пикселов. Значение интенсивности элемента в центре квадрата совпадает со значением соответствующего пиксела в пиксельной системе координат. При решении практических задач, связанных с измерениями реальных геометрических размеров объектов на изображении, удобно использовать пространственную систему координат, так как она позволяет учитывать разрешение (количество пикселов на метр) системы.
), где значение каждого элемента отвечает определенному уровню квантования его энергетической характеристики (яркости). Это так называемая пиксельная система координат. Она применяется в большинстве функций пакета IPT. Существует также пространственная система координат, где изображение представляется непрерывным числовым полем квадратов с единичной величиной. Количество квадратов совпадает с числом пикселов. Значение интенсивности элемента в центре квадрата совпадает со значением соответствующего пиксела в пиксельной системе координат. При решении практических задач, связанных с измерениями реальных геометрических размеров объектов на изображении, удобно использовать пространственную систему координат, так как она позволяет учитывать разрешение (количество пикселов на метр) системы.
Маска фильтра (или скользящее окно, или апертура) представляет собой матрицу размера 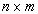 . Она накладывается на изображение и осуществляется умножением элементов маски фильтра и соответствующих элементов изображения с последующей обработкой результата. Когда маска передвигается к границе изображения, возникает так называемое явление краевого эффекта. Во избежание этого нежелательного эффекта необходимо, когда маска вышла за пределы исходного изображения, дополнить его не нулевыми элементами (как советует большинство книг по Matlab), а элементами изображения, симметричными относительно его краев.
. Она накладывается на изображение и осуществляется умножением элементов маски фильтра и соответствующих элементов изображения с последующей обработкой результата. Когда маска передвигается к границе изображения, возникает так называемое явление краевого эффекта. Во избежание этого нежелательного эффекта необходимо, когда маска вышла за пределы исходного изображения, дополнить его не нулевыми элементами (как советует большинство книг по Matlab), а элементами изображения, симметричными относительно его краев.
Обработка изображений осуществляется рекурсивными и нерекурсивными методами. Рекурсивные методы используют результат обработки предыдущего пиксела, нерекурсивные - не используют. В большинстве случаев используются нерекурсивные алгоритмы обработки изображений.
Бинарные изображения: геометрические характеристики
В этой работе рассматриваются черно–белые (бинарные) изображения [1]. Их легче получать, хранить и обрабатывать, чем изображения, в которых имеется много уровней яркости. Однако, поскольку в бинарных изображениях кодируется информация лишь о силуэте объекта, область их применения ограничена. В дальнейшем будут сформулированы условия, необходимые для успешного использования методов обработки бинарных изображений. Здесь же внимание акцентируется на таких простых геометрических характеристиках изображений, как площадь объекта, его положение и ориентация. Подобные величины могут использоваться, например, в процессе управления механическим манипулятором при его работе с деталями.
Поскольку изображения содержат большой объем информации, важную роль начинают играть вопросы ее представления. Покажем, что интересующие нас геометрические характеристики можно извлечь из проекций бинарных изображений. Проекции гораздо легче хранить и обрабатывать. Также рассмотрим непрерывные бинарные изображения, характеристическая функция которых равна нулю или единице в каждой точке плоскости изображения. Это упрощает анализ, однако при использовании ЭВМ изображение необходимо разбить на дискретные элементы.
Бинарные изображения
Начнем со случая, когда в поле зрения находится объект, а все остальное считается “фоном”. Если объект оказывается заметно темнее (или светлее), чем фон, то легко определить характеристическую функцию ![]() , которая равна нулю для всех точек изображения, соответствующих фону, и единице для точек на объекте (рис.1) или наоборот.
, которая равна нулю для всех точек изображения, соответствующих фону, и единице для точек на объекте (рис.1) или наоборот.
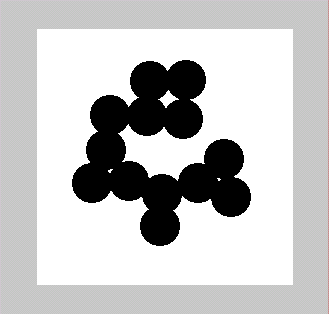
Рис. 1. Бинарное изображение, определяемое характеристической функцией ![]() , которая принимает значение “нуль” и “единица”.
, которая принимает значение “нуль” и “единица”.
Часто бинарное изображение получают пороговым разделением обычного изображения. К нему также можно прийти путем порогового разделения расстояния на “изображении”, полученном на основе измерений расстояний.
Такую функцию, принимающую два значения и называемую бинарным изображением, можно получить пороговым разделением полутонового изображения. Операция порогового разделения заключается в том, что характеристическая функция полагается равной нулю в точках, где яркость больше некоторого порогового значения, и единице, где она не превосходит его (или наоборот).
Иногда бывает удобно компоненты изображения, а также отверстия в них рассматривать как множества точек. Это позволяет комбинировать изображения с помощью теоретико–множественных операций, например, объединение и пересечение. В других случаях удобно поточечно использовать булевые операции. На самом деле это лишь два различных способа описания одних и тех же действий над изображениями.
Поскольку количество информации, содержащиеся в бинарном изображении, на порядок меньше, чем в совпадающем с ним по размерам полутоновом изображении, бинарное изображение легче обрабатывать, хранить и пересылать. Естественно, определенная часть информации при переходе к бинарным изображениям теряется, и, кроме того, сужается круг методов обработки таких изображений. В настоящее время существует достаточно полная теория того, что можно и чего нельзя делать с бинарными изображениями, чего, к сожалению, нельзя сказать о полутоновых изображениях.
Прежде всего мы можем вычислить различные геометрические характеристики изображения, например, размер и положение объекта. Если в поле зрения находится более одного объекта, то можно определить топологические характеристики имеющейся совокупности объектов: например, разность между числом объектов и числом отверстий (число Эйлера).
Пример:
Этой операции соответствует функция BWEULER – вычисление чисел Эйлера в пакете Image Processing Toolbox:
L=imread('test.bmp');
L=double(L);
imshow(L);

e=bweuler(L(:,:,1), 4)
e =
1; % На объекте действительно одно отверстие.
Нетрудно также пометить отдельные объекты и вычислить геометрические характеристики для каждого из них в отдельности. Наконец, перед дальнейшей обработкой изображение можно упростить, постепенно модифицируя его итеративным образом.
Обработка бинарных изображений хорошо понятна, и ее нетрудно приспособить под быструю аппаратную реализацию, но при этом нужно помнить об ограничениях. Мы уже упоминали о необходимости высокой степени контраста между объектом и фоном. Кроме того, интересующий нас образ должен быть существенно двумерным. Ведь все, чем мы располагаем, — лишь очертания или силуэт объекта. По такой информации трудно судить о его форме или пространственном положении.
Характеристическая функция ![]() определена в каждой точке изображения. Такое изображение будем называть непрерывным. Позже мы рассмотрим дискретные бинарные изображения, получаемые путем подходящего разбиения поля изображения на элементы.
определена в каждой точке изображения. Такое изображение будем называть непрерывным. Позже мы рассмотрим дискретные бинарные изображения, получаемые путем подходящего разбиения поля изображения на элементы.
Простые геометрические характеристики
Допустим снова, что в поле зрения находится лишь один объект. Если известна характеристическая функция ![]() , то площадь объекта вычисляется следующим образом:
, то площадь объекта вычисляется следующим образом:
![]() ,
,
где интегрирование осуществляется по всему изображению I. При наличии более одного объекта эта формула дает возможность определить их суммарную площадь.
Пример:
В системе Matlab этой операции соответствует функция BWAREA – вычисление площади объектов.
L=imread('test.bmp');
L=double(L);
imshow(L);

S=bwarea(L(:,:,1))
e =
24926; %Площадь объекта в пикселах (размер изображения 236х236).
Площадь и положение
Как определить положение объекта на изображении? Поскольку объект, как правило, состоит не из одной единственной точки, мы должны четко определить смысл термина “положение”. Обычно в качестве характерной точки объекта выбирают его геометрический центр (рис. 2).

Рис. 2. Положение области на бинарном изображении, которое можно определить ее геометрическим центром. Последний представляет собой центр масс тонкого листа материала той же формы.
Геометрический центр — это центр масс однородной фигуры той же формы. В свою очередь центр масс определяется точкой, в которой можно сконцентрировать всю массу объекта без изменения его первого момента относительно любой оси. В двумерном случае первый момент относительно оси ![]() рассчитывается по формуле
рассчитывается по формуле
![]() ,
,
а относительно оси ![]() — по формуле
— по формуле
![]() ,
,
где ![]() — координаты геометрического центра. Интегралы в левой части приведенных соотношений — не что иное, как площадь
— координаты геометрического центра. Интегралы в левой части приведенных соотношений — не что иное, как площадь![]() , о которой речь шла выше. Чтобы найти величины
, о которой речь шла выше. Чтобы найти величины ![]() и
и ![]() , необходимо предположить, что величина
, необходимо предположить, что величина ![]() не равна нулю. Заметим попутно, что величина
не равна нулю. Заметим попутно, что величина ![]() представляет собой момент нулевого порядка функции
представляет собой момент нулевого порядка функции ![]() .
.
Ориентация
Мы также хотим определить, как расположен объект в поле зрения, т. е. его ориентацию. Сделать это несколько сложнее. Допустим, что объект немного вытянут вдоль некоторой оси; тогда ее ориентацию можно принять за ориентацию объекта. Как точно определить ось, вдоль которой вытянут объект? Обычно выбирают ось минимального второго момента. Она представляет собой двумерный аналог оси наименьшей инерции. Нам необходимо найти прямую, для которой интеграл от квадратов расстояний до точек объекта минимален; этот интеграл имеет вид
![]() ,
,
где ![]() — расстояние вдоль перпендикуляра от точки с координатами
— расстояние вдоль перпендикуляра от точки с координатами ![]() до искомой прямой.
до искомой прямой.
Иной путь решения проблемы состоит в попытке найти угол поворота ![]() , при котором матрица вторых моментов размера 2x2 имеет диагональный вид.
, при котором матрица вторых моментов размера 2x2 имеет диагональный вид.
(В пакете Matlab операции определения центра масс, ориентации а также другие морфометрические признаки вычисляются с помощью функции IMFEATURE.)
Проекции
Для вычисления положения и ориентации объекта достаточно знать первые и вторые моменты. (При этом остается двузначность в выборе направления на оси.) Чтобы найти их значения, нет необходимости в исходном изображении: достаточно знать его проекции. Указанный факт представляет интерес, поскольку проекции описываются более компактно и приводят к гораздо более быстрым алгоритмам.
Дискретные бинарные изображения
До сих пор мы рассматривали непрерывные бинарные изображения, определенные во всех точках плоскости. Должно быть очевидным, что при переходе к дискретным изображениям интегралы становятся суммами. Например, площадь вычисляется (в единицах площади элемента изображения) в виде суммы
![]() ,
,
где ![]() — значение бинарного изображения в точке, находящейся в
— значение бинарного изображения в точке, находящейся в ![]() –й строке и
–й строке и ![]() –м столбце. Здесь мы полагали, что поле изображения разбито на квадратную решетку с т столбцами и п строками.
–м столбце. Здесь мы полагали, что поле изображения разбито на квадратную решетку с т столбцами и п строками.
Часто изображение просматривается строка за строкой в той же самой последовательности, в какой телевизионный луч бежит по экрану (если не учитывать того, что четные строки считываются вслед за нечетными). Как только считано значение очередного элемента изображения, проверяем равенство ![]() . Если оно выполняется, добавляем 1,
. Если оно выполняется, добавляем 1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() к накапливаемым значениям площади, первых моментов и вторых моментов. По окончании цикла сканирования с помощью этих значений легко найти площадь, положение и ориентацию.
к накапливаемым значениям площади, первых моментов и вторых моментов. По окончании цикла сканирования с помощью этих значений легко найти площадь, положение и ориентацию.
Кодирование с переменной длиной
Существует несколько способов кодирования, позволяющих еще больше сжать информацию о бинарных изображениях. Одним из широко распространенных является кодирование с переменной длиной кодовой последовательности. Этот метод основан на том, что вдоль любой просматриваемой в данный момент строки обычно обнаруживаются длинные цепочки нулей и единиц. Поэтому вместо передачи отдельных битов информации мы можем посылать длины подобных цепочек. Код с переменной длиной есть просто ![]() .
.
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
Для обозначения начала каждой строки нужно ввести специальный признак. Кроме того, принимается соглашение относительно того, с чего начинается строка (с нуля или единицы). Если строка начинается с противоположного символа, то первым символом кода устанавливается нуль.
Другой подход к обработке изображений описан в книге [2]. Книга [3] содержит сведения о некоторых работах в области обработки бинарных изображений. Много интересных бинарных изображений, полученных художниками, можно найти в книге [4].
Кодирование с переменной длиной кодовой последовательности основывается на избыточности лишь в одном измерении. В целях уменьшения затрат на передачу и хранение данных было предпринято несколько попыток использовать пространственную взаимосвязь между элементами изображения в обоих направлениях. Быть может наиболее удачной среди схем такого рода является схема, разработанная фирмой IBM и описанная в отчете [5].
В системе Matlab также рассматривается один из видов кодирования, который содержится в описании функции BWPACK.
Литература
- Хорн Б.К.П. Зрение роботов: Пер. с англ. – М.: Мир, 1989. – 487 с., ил. ISBN 5–03–000570–6.
- Rosenfeld A., Kak A.C., Digital Picture Processing, Vols. 1, 2, Second Edition, Academic Press, New York, 1982.
- Stoffel J.C. (ed.), Graphical and Binary Image Processing and Applications, Artech House, Inc., Massachusetts, 1982.
- Grafton C.B. (ed.), Silhouettes – A Pictorial Archive of Varied Illustrations, Dover Publications, New York, 1979.
- Mitchell J.L., Goertzel G., Two–Dimensional Facsimile Coding Scheme, IBM Reserch Report RC 7499, Jan., 1979.
Бинарные изображения: топологические характеристики
Рассмотрим некоторые методы восстановления информации по бинарным изображениям. Для этого необходимо тщательно определить, что подразумевается под связностью двух элементов изображения. Нужно изучить этот вопрос для различных способов разбиения плоскости изображения и исследовать средства, позволяющие помечать различные компоненты изображения при последовательном его просмотре.
Изображения содержат большой объем информации. Один из путей ее обработки за приемлемое время состоит в широком использовании распараллеливания процессов. Существуют два изящных класса методов параллельной обработки бинарных изображений – локальные методы и методы итеративной модификации. Для понимания того, какие величины можно вычислить в результате их применения, вводится свойство аддитивности.
Приведенные здесь методы могут найти применение в задачах визуальной инспекции, обнаружения и распознавания объектов.
Сложные объекты
Иногда в поле зрения попадает более одного объекта (рис. 1). В этом случае вычисление площади, геометрического центра и ориентации приведет к значениям, “усредненным” по всем компонентам бинарного изображения. Как правило, это не то, что требуется. Желательно как-то пометить отдельные компоненты изображения и вычислить значения площади, первых и вторых моментов для каждой компоненты в отдельности.
Разметка компонент
Будем считать две точки изображения связанными, если существует путь между ними, вдоль которого характеристическая функция постоянна. Так, на рис. 1 точка А связана с точкой В, но не связана с точкой С. Связная компонента бинарного изображения есть максимальное множество связанных точек, т. е. множество, состоящее из всех тех точек, между любыми двумя из которых существует связывающий их путь.
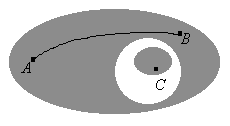
Рис. 1. Изображение, состоящее из нескольких областей, для каждой из которых необходимо проводить расчет положения и ориентации.
Элементы изображения необходимо пометить таким образом, чтобы принадлежащие одной области были отличимы от остальных Для этого нам необходимо решить, какие точки принадлежат одной и той же области. На рисунке 1 точка А считается связанной с точкой В, поскольку мы можем найти непрерывную кривую, целиком лежащую в затененной области и соединяющую указанные точки. Ясно, что точка А не связана с точкой С, так как в этом случае подобной кривой найти нельзя.
Один из способов разметки объектов на дискретном бинарном изображении состоит в выборе произвольной точки, в которой ![]() , и приписывании метки этой точке и ее соседям. На следующем шаге помечаются соседи этих соседей (кроме уже помеченных) и т. д. По завершении этой рекурсивной процедуры одна компонента будет полностью помечена, и процесс можно будет продолжить, выбрав новую начальную точку. Чтобы ее отыскать, достаточно каким-либо систематическим образом перемещаться по изображению до тех пор, пока не встретится первая еще непомеченная точка, в которой
, и приписывании метки этой точке и ее соседям. На следующем шаге помечаются соседи этих соседей (кроме уже помеченных) и т. д. По завершении этой рекурсивной процедуры одна компонента будет полностью помечена, и процесс можно будет продолжить, выбрав новую начальную точку. Чтобы ее отыскать, достаточно каким-либо систематическим образом перемещаться по изображению до тех пор, пока не встретится первая еще непомеченная точка, в которой ![]() . Когда на этом этапе не останется ни одного такого элемента, все объекты изображения окажутся размеченными.
. Когда на этом этапе не останется ни одного такого элемента, все объекты изображения окажутся размеченными.
Ясно, что “фон” также можно разбить на связные компоненты, поскольку объекты могут иметь отверстия. Их можно пометить с помощью той же процедуры, но при этом необходимо обращать внимание не на единицы, а на нули.
Связность
Теперь нужно аккуратно рассмотреть смысл термина сосед. Если мы имеем дело с квадратным растром, то, по-видимому, соседями следует считать четыре элемента изображения, касающиеся сторон данного элемента. Но как быть с теми, которые касаются его в углах? Существуют две возможности:
— четырехсвязность – соседями считаются только элементы, примыкающие к сторонам;
— восьмисвязность – элементы, касающиеся в углах, также считаются соседями. Указанные возможности приведены на следующих диаграммах:
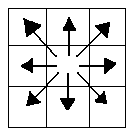
Оказывается, ни одна из этих схем не является полностью удовлетворительной. В этом можно убедиться, если вспомнить, что фон также можно разбить на несколько связных компонент. Здесь нам хотелось бы применить наши интуитивные представления о связности областей на непрерывном бинарном изображении. Так, например, простая замкнутая кривая должна разделять изображение на две связные области (рис. 2). Это так называемая теорема Жордана о кривой.
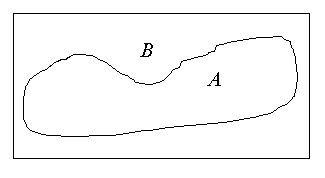
Рис. 2. Простая замкнутая кривая, разбивающая плоскость на две связные области.
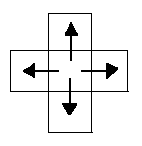
Теперь рассмотрим простое изображение, содержащее четыре элемента со значением “единица”, которые примыкают к центральному элементу со значением “нуль”:

Это — крест с выброшенным центром. Если принять соглашение о четырехсвязности, то на изображении окажутся четыре различные компоненты (![]() ,
,![]() ,
,![]() и
и ![]() ):
):
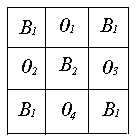
Они, естественно, не образуют замкнутой кривой, хотя центральный элемент, относящийся к фону, и не связан с остальным фоном. Несмотря на отсутствие какой-либо замкнутой кривой, у нас образовались две фоновые области. Если принять соглашение о восьмисвязности, то, наоборот, четыре элемента растра станут образовывать замкнутую кривую, и в то же время центральный элемент окажется связанным с остальным фоном:
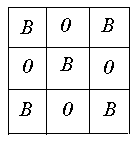
Итак, мы получили замкнутую кривую и только одну связную компоненту фона.
Одно из решений возникшей проблемы состоит в выборе четырехсвязности для объекта и восьмисвязности для фона (или наоборот). Подобная асимметрия в трактовке объекта и фона часто нежелательна, и ее можно избежать путем введения другого типа асимметрии. Будем считать соседями четыре элемента изображения, примыкающие к данному по сторонам, а также два из четырех элементов, касающихся в углах:
 или
или 
Для обеспечения симметричности отношения связности два угловых элемента должны находиться на одной и той же диагонали: если элемент А — сосед элемента В, то элемент В должен быть соседом элемента А. В дальнейшем мы будем пользоваться первым из двух возможных вариантов, приведенных выше, считая соседями элементы в направлениях N, E, SE, S, W и NW. С помощью шестисвязности как объект, так и фон можно трактовать единообразно без каких-либо дальнейших неувязок. Для изображений на квадратном растре мы примем именно такое соглашение.
На гексагональном растре рассуждения проще. Все шесть элементов растра, касающиеся данного центрального элемента, являются соседями, так что неопределенности не возникает. Наши предыдущие действия можно рассматривать как простой перекос квадратной решетки и превращение ее в гексагональную. Чтобы в этом убедиться, зафиксируем произвольный элемент и сдвинем ряд, находящийся над ним, на половину ширины элемента вправо, а ряд, находящийся под ним, — на ту же величину влево:

Теперь выбранный элемент касается шести других, и они в точности такие, которые мы выбрали при определении шестисвязности.
Локальные вычисления и итеративная модификация
До сих пор основное внимание уделялось последовательной обработке информации, содержащейся в бинарном изображении. Чтобы повысить скорость обработки и использовать возможности больших интегральных схем (БИС), необходимо также рассмотреть, какие результаты можно получить с помощью параллельно выполняемых локальных операций. Под локальной мы понимаем то, что на вход каждой такой операции поступает информация лишь с небольшого участка изображения.
Имеются два типа вычислений, выполнимых таким образом. Мы можем скомбинировать (сложить) результаты всех локальных операций и завершить тем самым работу в один шаг (рис. 5) или создать новое изображение на основе этих результатов.
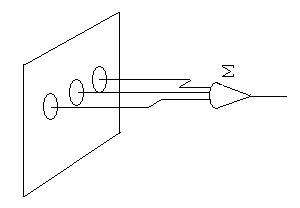
Рис. 5. Методы локальных вычислений. Комбинируются выходы отдельных вычислительных ячеек, каждая из которых соединена с несколькими элементами изображения, лежащими вблизи нее.
Локальные вычисления.
Рассмотрим очень простой случай. Каждый из локальных операторов обращается к одному элементу изображения и выдает его значение. После сложения всех таких выходов в качестве результата получим суммарную площадь объектов, находящихся в поле зрения. Таким образом, параллельный способ вычисления площади требует всего одного шага (проблему суммирования всех нулей и единиц мы здесь не рассматриваем).
Какие другие характеристики представимы в виде суммы результатов локальных операций? Например, периметр: достаточно просто подсчитать количество участков на изображении, где рядом с нулями стоят единицы. Имеются два типа локальных операторов (рис. 6): операторы одного типа просматривают два соседних элемента, расположенных в одной строке, а операторы другого типа — два соседних элемента, расположенных в одном столбце. В обоих случаях результат есть ИСКЛЮЧАЮЩЕЕ ИЛИ (аÄb) двух значений на входе. Сумма всех получаемых выходов представляет собой оценку периметра.
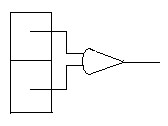
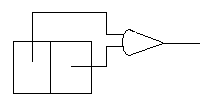
Рис. 6. Возможность использования операции ИСКЛЮЧАЮЩЕЕ ИЛИ к двум соседним элементам изображения для выделения участков, находящихся на границе областей.
Каждый из двух типов операторов реагирует на два типа шаблонных ситуаций. Здесь показаны два случая, включающие горизонтальный и вертикальный детекторы.
|
|
|
Вычисленный периметр представляет собой лишь приблизительную оценку, поскольку, как правило, дискретное бинарное изображение строится на основе непрерывного, и при этом границы объектов становятся более изрезанными. Например, оценка длины диагональной прямой в ![]() раз больше “истинной”:
раз больше “истинной”:
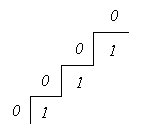
Усреднение по всем углам наклона дает среднее значение коэффициента, показывающего, во сколько раз увеличено полученное значение. Оно составляет 4/![]() =1,273.... Разделив на это число, можно улучшить оценку периметра.
=1,273.... Разделив на это число, можно улучшить оценку периметра.
Кроме площади и периметра с помощью локальных методов можно вычислить число Эйлера, которое определяется как разность между количеством объектов и количеством отверстий.
Бинарные изображения можно комбинировать разными путями. Можно осуществить операцию ИЛИ. В результате мы объединим два изображения в одно. Можно осуществить операцию И. В этом случае мы получим пересечение объектов. Большой интерес представляет то, как характеристики получаемых подобными способами изображений соотносятся с характеристиками исходных изображений. Одна из причин такого интереса связана с надеждой разбить изображение на большое число частей, одновременно обработать все эти части и затем объединить результат.
Если обозначить исходные изображения через ![]() и
и ![]() , то логические операции ИЛИ и И над
, то логические операции ИЛИ и И над ![]() и
и ![]() обозначаются соответственно
обозначаются соответственно ![]() и
и ![]() . Площади удовлетворяют соотношению
. Площади удовлетворяют соотношению ![]() , поскольку сумма площадей
, поскольку сумма площадей ![]() и
и ![]() равна площади их объединения плюс площадь тех частей, где они перекрываются. О любой числовой характеристике бинарного изображения, удовлетворяющей этому условию говорят, что она обладает свойством аддитивности.
равна площади их объединения плюс площадь тех частей, где они перекрываются. О любой числовой характеристике бинарного изображения, удовлетворяющей этому условию говорят, что она обладает свойством аддитивности.
Итеративная модификация
Значение каждого элемента нового изображения можно определить как результат локальной операции над соответствующим элементом исходного изображения. Полученное бинарное изображение можно снова подвергнуть обработке в следующем цикле вычислений. Это процесс, называемый итеративной модификацией, весьма полезен, поскольку позволяет постепенно перевести трудное для обработки изображение в такое, которое поддается ранее описанным методам.
В пакете Image Processing Toolbox системы Matlab существует много функций, осуществляющих обработку бинарных изображений, в частности, морфологические операции. Среди них – BWMORPH, DILATE, ERODE, BWPERIM, MAKELUT, BWFILL, BWSELECT, IMFEATURE и другие.
Существует огромное количество трудов по обработке бинарных изображений. Вот некоторые из содержательных работ на эту тему:
- Arcelli C., Pattern Thinning by Contour Tracing, Computer Graphics and Image Processing, 17, № 3, 130 – 144 (1981).
- Dyer C.R., Rosenfeld A., Thinning Algorithms for Gray–Scale Picture, IEEE Trans. on Pattern Analysis and Machine Intelligence, 1, №1, 88 – 89 (1979).
- Stefanelli R., Some Parallel Thinning Algorithms for Digital Pictures, Jornal of the ACM, 18, № 2, 255–264 (1971).
- Хорн Б.К.П. Зрение роботов: Пер. с англ. – М.: Мир, 1989. – 487 с., ил. ISBN 5–03–000570–6.
Формирование и обработка цифровых изображений
Изображение служит для представления информации в визуальном виде. Эффективность восприятия этой информации человеком зависит от многих факторов. Максимальный учет влияния этих факторов возможен при условии изучения целого ряда вопросов, связанных со способами получения, свойствами зрительного восприятия и обработкой изображений.
Методы получения цифровых изображений
На современном этапе развитие технической и медицинской диагностики неразрывно связано с визуализацией внутренних структур объекта [1]. Существует много различных видов визуализации. Возникают новые методы, но они не заменяют уже существующие, а лишь дополняют их. Разные методы визуализации основываются на разнообразных физических взаимодействиях электромагнитного излучения с материалами, средами, биотканями и, как следствие, обеспечивают измерение разных физических свойств этих объектов. Рассмотрим несколько основных методов получения изображений, которые представляют интерес для технической и медицинской диагностики.
Системы получения рентгенографических изображений
Рентгеновское излучение активно используется для получения изображений с момента его открытия в 1895 г. Изображение формируется в результате взаимодействия квантов рентгеновского излучения с приемником и представляет собой распределение квантов, которые прошли через объект диагностики и были зарегистрированы детектором (рис. 1). Последние делятся на первичные, т.е. те, которые прошли через объект
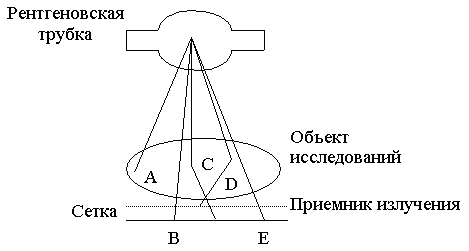
Рис. 1. Компоненты системы для получения рентгеновских изображений. B и E - кванты, которые прошли через исследуемый объект без взаимодействия; C и D - рассеянные кванты. Квант D отсеивается сеткой, которая препятствует рассеянному излучению, а квант A - поглощается в объекте.
без взаимодействия с его материалом, и на вторичные кванты, которые получаются в результате взаимодействия с материалом объекта. Вторичные кванты, как правило, отклоняются от направления своего начального движения и несут мало полезной информации. Полезную информацию несут первичные кванты. Они дают информацию о том, что квант проходит через материал объекта без взаимодействия.
Установлено, что контраст рентгенографического изображения резко уменьшается с увеличением энергии квантов, поэтому для получения большого контраста необходимо использовать излучение низкой энергии. Но это означает высокую дозу облучения, и потому должен быть найден некоторый компромисс между достаточным контрастом и наименьшей дозой облучения.
Даже если система получения изображений имеет высокую контрастность и хорошую дискретность, в случае высокого уровня шумов, перед рентгенологами возникают серьезные проблемы, связанные с идентификацией больших структур. Уровень шумов можно понизить за счет увеличения числа квантов, которые формируют изображение. Но при этом возрастает также доза облучения, поэтому необходимо принимать во внимание соотношения между двумя этими величинами.
Стандартные аналоговые системы осуществляют формирование и отображение информации аналоговым путем. Тем не менее, аналоговые системы имеют очень жесткие ограничения на экспозицию через маленький динамический диапазон, а также довольно скромные возможности по обработке изображений. В отличие от аналоговых, цифровые рентгенографические системы разрешают получать изображение при любой необходимой дозе и дают широкие возможности относительно их обработки.
Блок-схема типичной цифровой рентгенографической системы представлена на рис. 2.

Рис. 2. Элементы цифровой системы получения рентгеновских изображений.
Рентгеновский аппарат и приемник изображения связаны с компьютером, а полученное изображение запоминается и отображается (в цифровой форме) на телеэкране.
В цифровой рентгенографии используют такие приемники изображения как усилитель изображения, ионографическая камера и устройство с вынужденной люминесценцией. Эти приемники могут непосредственно формировать цифровые изображения без промежуточной регистрации. Усилители изображения не имеют наилучшей пространственной разрешающей способности или контраста, но имеют высокое быстродействие. Аналогово-цифровое преобразование флюорограммы с числом точек на изображении 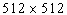 может занимать время меньшее, чем
может занимать время меньшее, чем ![]() с. Даже при числе точек на изображении
с. Даже при числе точек на изображении 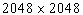 время его превращения в цифровую форму составляет всего несколько секунд. Время считывания из пластины с люминесценцией или с ионографической камеры значительно больше, хотя здесь лучшая разрешающая способность и динамический диапазон.
время его превращения в цифровую форму составляет всего несколько секунд. Время считывания из пластины с люминесценцией или с ионографической камеры значительно больше, хотя здесь лучшая разрешающая способность и динамический диапазон.
Записанное на фотопленке изображение можно перевести в цифровую форму с помощью сканирующего микроденситометра, но любая информация, зафиксированная на фотопленке с очень маленькой или очень высокой оптической плотностью, будет обезображена влиянием характеристик пленки. В цифровую форму можно превратить и ксерорентгенограмму также с помощью сканирующего денситометра, который работает в отраженном свете, но недостатком полученного изображения является наличие уже усиленных контуров.
К преимуществам цифровых рентгенографических систем относятся следующие факторы: цифровое отображение информации; низкая доза облучения; цифровая обработка изображений и улучшения качества. Рассмотрим эти преимущества более подробно [1-3].
Первое преимущество связано с отображением цифровой информации. Разложение изображения на уровни яркости на телеэкране или по плотности на фотопленке в цифровом виде становится в полной мере доступным для пользователя. Например, любую фотопленку, зарегистрированную с помощью цифровой обработки изображения, можно правильно экспонировать и получить характеристику, которая согласуется с соответствующими действительности значениями интенсивностей элементов изображения. И наоборот, весь диапазон оптических плотностей или яркостей может быть использован для отображения лишь одного участка диапазона яркостей изображения, которое приводит к повышению контраста в потенциально информативной области. В распоряжении оператора имеются алгоритмы для аналоговой обработки изображений с целью оптимального использования возможностей систем отображения. Метод гистограммной коррекции разрешает так обработать цифровое изображение на дисплее, что любому уровню яркости (или оптической плотности) в аналоговом изображении будут отвечать одинаковые числа ячеек яркости в цифровом отображении.
Второе преимущество цифровой рентгенологии - возможность снижения дозы облучения. Если в обычной рентгенологии доза облучения зависит от чувствительности приемника и динамического диапазона пленки, то в цифровой рентгенологии эти показатели могут оказаться несущественными.
Третье преимущество цифровой рентгенологии - это возможность цифровой обработки изображений. Рентгенолог должен обнаружить аномальные образования на осложненной фоном нормальной структуре объекта. Он может не заметить мелких деталей или пропустить слабоконтрастную структуру на фоне шумов изображения. Поэтому очень важной является возможность повышения визуального качества потенциально информативных участков для увеличения вероятности принятия правильных решений.
Получение изображений с помощью радиоизотопов
Метод, который рассматривается ниже, получил очень широкое применение в медицине. В последние десятилетия значительно развилась клиническая диагностика заболеваний человека с помощью введения в его организм радиоизотопов в индикаторном количестве. Визуализация с помощью радиоизотопов включает в себя ряд методов получения изображений, которые отражают распределение в организме меченных радионуклидами веществ. Эти вещества называются радиофармпрепаратами и предназначены для наблюдения и оценки физиологических функций отдельных внутренних органов. Характер распределения радиофармпрепаратов в организме определяется способами его введения, а также такими факторами, как величина кровотока объема циркулирующей крови и наличием того ли другого метаболического процесса.
Радиоизотопные изображения позволяют получать ценную диагностическую информацию. Наиболее распространенным методом этого класса является статическая изотопная визуализация в плоскости, которая называется планарной сцинтиграфией. Планарные сцинтиграммы представляют собой двумерные распределения, а именно проекции трехмерного распределения активности изотопов, которые находятся в поле зрения детектора. Томографические исследования с применением системы многоракурсного сбора информации об объекте разрешают преодолеть большинство проблем, связанных с наложением информации при одноракурсном способе сбора данных. Прогресс компьютерных технологий привел к применению компьютеров при исследованиях с помощью радиоизотопов, где важную роль играет томографическая и динамическая информация. Использование компьютерной техники повышает качество изображения и дает возможность при радиоизотопной визуализации получать количественную информацию об исследуемых объектах.
Ультразвуковая диагностика
Ультразвуковые методы визуализации широко применяются при разных диапазонах частот - от подводной локации и биоэхолокации (частоты до 300 КГц) до акустической микроскопии (от 12 МГц до 1ГГц и выше). Промежуточное расположение по частотам занимают ультразвуковая диагностика и терапия, а также неразрушающий контроль в промышленности. Информация о структуре исследуемого объекта закодирована в лучах, которые прошли через него и в рассеянном излучении. Задача системы визуализации состоит в расшифровке этой информации. В отличие от рентгеновских лучей, ультразвуковые волны преломляются и отбиваются на границах раздела сред с разными акустическими показателями преломления. Эти эффекты могут быть довольно заметными, что разрешает создать фокусирующие системы.
С точки зрения выбора конкретного способа построения систем визуализации, в зависимости от вида излучения между ультразвуком и рентгеновским излучением есть существенные различия. Ультразвуковые волны распространяются довольно медленно, поэтому при характерных размерах исследуемого объекта легко измерять соответствующее время распространения, которое разрешает использовать эхо-импульсные методы для формирования акустических изображений. С другой стороны, скорость ультразвуковых волн достаточно большая для того, чтобы накапливать и реконструировать всю информацию о виде полного кадра изображения за время 80 мс. Другими словами, появляется возможность наблюдать движение объектов в динамике. Ультразвуковые приборы отличаются один от другого лишь деталями.
Использование эффекта ядерного магнитного резонанса (ЯМР) для получения изображений
Несмотря на то, что во многих больших исследовательских центрах ЯМР-визуализация является одним из важных диагностических средств, сам метод еще находится на относительно ранней стадии своего развития. Само явление ядерного магнитного резонанса было открыто в 1946 году независимо Блохом и Парселлом с Паундом. Этот метод с помощью небольших изменений резонансной частоты (через наличие околомолекулярной электронной тучи) позволяет идентифицировать ядра в разном химическом окружении. Сначала ЯМР-методы с высокой разрешающей способностью разрабатывались как универсальное средство изучения химического состава и структуры твердого тела и жидкостей, а далее нашли свое применение и в других областях, в частности, медицине. Рядом с развитием ЯМР-спектроскопии развивались и методы визуализации - это и точечные методы, методы "быстрой" визуализации и прочие. Роль центрального процессора в современных ЯМР-системах выполняет мощный миникомпьютер, который обеспечивает канал связи с оператором и контроль функций узлов системы. Компьютер также обеспечивает запоминание и архивирование информации, отображение результатов исследований и во многих случаях соединяется с устройством быстрой обработки типа матричного процессора.
Пример обработки рентгеновских биомедицинских изображений с использованием системы MATLAB
Довольно часто рентгеновские биомедицинские изображения не отвечают тем критериям качества, которые необходимы для их достоверного анализа. Также не всегда существует возможность сделать повторный снимок. Это приводит к необходимости цифровой обработки такой информации [2, 3].
Основными недостатками рентгеновских изображений, в большинстве случаев, являются искаженные яркостные характеристики и низкая контрастность. Рассмотрим пример обработки одного из таких изображений с помощью системы MATLAB.
Недостаток исходного биомедицинского изображения (рис. 3а) состоит в том, что это изображение низкоконтрастное, что затрудняет анализ мелких деталей. Поэтому сначала выполняется операция растяжения гистограммы изображения на максимально допустимый диапазон (рис. 3б). Далее осуществляется контрастирование исследуемого изображения (рис. 3в). Это приводит к улучшению визуального качества рентгеновских изображений. На практике, конечно, применяются также и другие более сложные методы и алгоритмы обработки изображений такого рода.
%Пример программы обработки биомедицинских изображений в среде MATLAB
L=imread('cardial.bmp');
figure, imshow(L);
L1=imadjust(L,[min(min(L)) max(max(L))]/255,[],1);
figure, imshow(L1);
L=L1(:,:,1);
L=double(L);
Filter=[1 1 1,1 1 1,1 1 1];
Lser=filter2(Filter,L(:,:,1),'same')./9;
C=abs(L(:,:,1)-Lser)./(L(:,:,1)+Lser);
C=C.^.55;
[N M]=size(L);
for i=1:N;
disp(i);
for j=1:M;
if L(i,j,1)>Lser(i,j);
Lvyh(i,j)=Lser(i,j)*(1+C(i,j))/(1-C(i,j));
else
Lvyh(i,j)=Lser(i,j)*(1-C(i,j))/(1+C(i,j));
end;
end;
end;
figure, imshow(Lvyh/255);
|
|
|
|
Рис. 3.
- Физика визуализации изображений в медицине: в 2–х томах. Т. 2: Пер. С англ. / Под ред. С. Уэбба. – М.: Мир, 1991. – 408 с., ил.
- Беликова Т.П. Моделирование линейных фильтров для обработки рентгеновских изображений в задачах медицинской диагностики // Цифровая оптика. Обработка изображений и полей в экспериментальных исследованиях / Под ред. В.И.Сифорова и Л.П.Ярославского. – М.: Наука, 1990. – 176 с.
- Н.Н. Блинов, Е.М. Жуков, Э.Б. Козловский, А.И. Мазуров. Телевизионные методы обработки рентгеновских и гамма–изображений. М.: Энергоатоиздат, 1982. – 200 с.
Адаптивное повышение контрастности изображений
Одной из наиболее удобных форм представления информации при диагностировании материалов и изделий в неразрушающем контроле, органов человека в медицине и иных областях является изображение. Это приводит к необходимости развития способов диагностики с использованием разнообразных методов. Однако одним из существенных недостатков этих методов является то, что в большинстве своем они обеспечивают формирование низкоконтрастных изображений. Поэтому основная цель методов улучшения состоит в преобразовании изображений к такому виду, что делает их более контрастными и, соответственно, более информативнее [1]. Довольно часто на изображении присутствуют искажения в определенных локальных окрестностях, которые вызваны дифракцией света, недостатками оптических систем или розфокусировкой. Это приводит к необходимости выполнения локальных преобразований на изображении. Иными словами, такой адаптивный подход дает возможность выделить информативные участки на изображении и соответствующим образом их обработать. Изложенным требованиям отвечают методы адаптивного преобразования локального контраста [2]. Методы этого класса можно представить обобщенной структурной схемой (рис. 1), где использованы такие обозначения:
![]() - исходное изображение и его элемент с координатами
- исходное изображение и его элемент с координатами ![]() соответственно;
соответственно;
![]() - контраст элемента изображения с координатами
- контраст элемента изображения с координатами ![]() ;
;
![]() - преобразованное значение контраста
- преобразованное значение контраста ![]() ;
;
![]() - характеристики локальных окрестностей (
- характеристики локальных окрестностей (![]() - энтропия,
- энтропия, ![]() - среднеквадратичное отклонение,
- среднеквадратичное отклонение, ![]() - функция протяженности гистограммы);
- функция протяженности гистограммы);
![]() - элемент обработанного изображения с координатами
- элемент обработанного изображения с координатами ![]() .
.
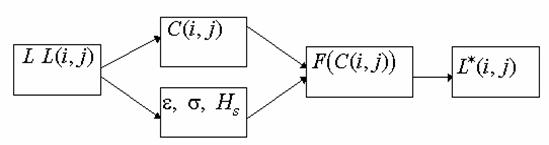
Рис. 1. Обобщенная структурная схема методов улучшения изображений с использованием адаптивного преобразования локальных контрастов.
Основные шаги реализации методов адаптивного преобразования локальных контрастов такие:
Шаг 1. Для каждого элемента изображения ![]() вычисляют значение локального контраста
вычисляют значение локального контраста ![]() в текущей окрестности
в текущей окрестности ![]() с центром в элементе с координатами
с центром в элементе с координатами ![]() .
.
Шаг 2. Вычисляют локальную статистику для текущей скользящей окрестности ![]() .
.
Шаг 3. Преобразуют (усиливают) локальный контраст ![]() , употребляя для этого нелинейные функции и учитывая локальную статистику текущей скользящей окрестности
, употребляя для этого нелинейные функции и учитывая локальную статистику текущей скользящей окрестности ![]() .
.
Шаг 4. Восстанавливают значение яркости изображения ![]() с усиленным локальным контрастом.
с усиленным локальным контрастом.
Шаги 1 и 2 могут выполняться в различной последовательности или параллельно.
Проанализируем более детально реализацию шага 3 вышеупомянутого метода. Его суть состоит в том, что для преобразования локальных контрастов используют нелинейные монотонные функции, а для формирования адаптивной функции преобразования локального контраста выбирают степенную функцию и задают минимальное ![]() и максимальное
и максимальное ![]() значения показателя степени
значения показателя степени ![]() . Адаптация состоит в формировании дополнительного слагаемого к
. Адаптация состоит в формировании дополнительного слагаемого к ![]() путем его определения на основе локальных статистик в скользящих окрестностях. В качестве параметров, которые будут характеризовать скользящие окрестности, используются функция протяженности гистограммы
путем его определения на основе локальных статистик в скользящих окрестностях. В качестве параметров, которые будут характеризовать скользящие окрестности, используются функция протяженности гистограммы ![]() , энтропия
, энтропия ![]() и среднеквадратическое отклонение
и среднеквадратическое отклонение ![]() значений яркостей элементов скользящей окрестности. Поэтому, в зависимости от поставленной задачи, методы данного класса могут отличаться как функцией преобразования локального контраста, так и характеристикой скользящей окрестности.
значений яркостей элементов скользящей окрестности. Поэтому, в зависимости от поставленной задачи, методы данного класса могут отличаться как функцией преобразования локального контраста, так и характеристикой скользящей окрестности.
Рассмотрим более детально предложенные локально-адаптивные методы улучшения изображений, проанализируем использование характеристик локальных окрестностей в выражениях преобразования локальных контрастов и обоснуем их выбор.
Использование функции протяженности гистограммы
Рассмотрим метод повышения качества изображения, который базируется на адаптивном преобразовании локального контраста. Адаптация в данном методе осуществляется на основании анализа такой характеристики как функция протяженности гистограммы элементов локальной скользящей окрестности. Для примера будем считать, что элементы изображения представлены 8-разрядными целыми числами, то есть ![]() .
.
Основные шаги реализации этого метода такие.
Шаг 1. Вычисляем локальный контраст элемента.
Шаг 2. Определяем характеристику локальной скользящей окрестности, используя функцию протяженности гистограммы
| (1) |
где ![]() ,
, ![]() - соответственно максимальное и минимальное значения яркостей элементов скользящей окрестности с центром в элементе с координатами
- соответственно максимальное и минимальное значения яркостей элементов скользящей окрестности с центром в элементе с координатами ![]() ;
; ![]() - максимальное значение гистограммы уровней яркости элементов окрестности с центром в элементе с координатами
- максимальное значение гистограммы уровней яркости элементов окрестности с центром в элементе с координатами ![]() .
.
Шаг 3. Вычисляем степенное преобразование локального контраста, которое благодаря использованию функции протяженности гистограммы скользящей окрестности, имеет адаптивный характер:
| (2) |
где
![]() ,
,
![]() ,
, ![]() - соответственно максимальное и минимальное значения функции протяженности гистограммы для окрестности с центром в элементе с координатами
- соответственно максимальное и минимальное значения функции протяженности гистограммы для окрестности с центром в элементе с координатами ![]() .
.
Шаг 4. Восстанавливаем элемент преобразованного изображения с усиленным контрастом.
Рассмотрим более детально реализацию шагов 2 и 3 известного метода. В частности, оценим возможные значения функции протяженности гистограммы ![]() скользящей окрестности
скользящей окрестности ![]() , подразумевая, что изображениям присущи три характерные типа окрестностей.
, подразумевая, что изображениям присущи три характерные типа окрестностей.
Первый тип - это однородный участок изображения, который характеризуется примерно одинаковыми уровнями яркостей элементов; гистограмма такой окрестности показана на рис. 2.
С рис. 2 видно, что ![]() , а следовательно , согласно выражению (1), функция протяженности гистограммы локальной окрестности
, а следовательно , согласно выражению (1), функция протяженности гистограммы локальной окрестности ![]() будет равна нулю.
будет равна нулю.
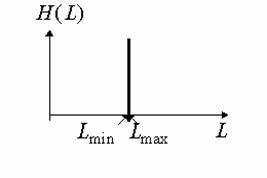
Рис. 2. Гистограмма распределения яркостей элементов однородной окрестности.
Локальные контрасты таких участков изображения усиливать не нужно, поскольку это приведет к возникновению дополнительных искажений, обусловленных усилением шумовой составляющей изображения.
Для бинарных участков изображения с примерно одинаковым количественным соотношением элементов ![]() и
и ![]() в скользящей окрестности
в скользящей окрестности ![]() , характерна гистограмма яркостей, которая представлена на рис. 3.
, характерна гистограмма яркостей, которая представлена на рис. 3.
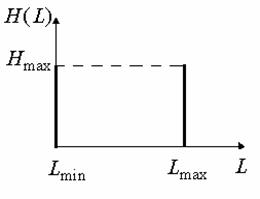
Рис. 3. Гистограмма распределения яркостей элементов бинарной окрестности.
Предполагая, что для темных и светлых элементов бинарной окрестности с примерно равным количественным соотношением максимальное значение гистограммы будет равно
| (3) |
где ![]() и
и ![]() - размеры скользящей окрестности
- размеры скользящей окрестности ![]() , выражение (1) будет иметь вид
, выражение (1) будет иметь вид
| (4) |
Если ![]() ,
, ![]() , а размеры
, а размеры ![]() локальной окрестности такие, что допускают присутствие элементов со всеми возможными уровнями яркостей
локальной окрестности такие, что допускают присутствие элементов со всеми возможными уровнями яркостей ![]() [0,255], например
[0,255], например ![]() элементов, тогда функция протяженности гистограммы в соответствии с выражением (4) примет значение
элементов, тогда функция протяженности гистограммы в соответствии с выражением (4) примет значение ![]() .
.
Третьим характерным типом возможной локальной окрестности является такая окрестность, где в примерно одинаковой мере присутствуют элементы со всеми возможными яркостями с диапазона [0,255]. Такие окрестности характеризуются гистограммой равномерного распределения яркостей, которая показана на рис. 4. Тогда согласно изложенных предположений относительно размера локальной окрестности и характера его гистограммы получим, что ![]() ,
, ![]()
![]() . В этом случае функция протяженности гистограммы примет значение
. В этом случае функция протяженности гистограммы примет значение ![]() . Для такой окрестности будем считать, что она высококонтрастна и не нуждается в усилении контраста.
. Для такой окрестности будем считать, что она высококонтрастна и не нуждается в усилении контраста.
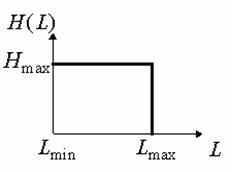
Рис. 4. Гистограмма скользящей окрестности с равномерно распределенными яркостями элементов.
Выше были рассмотрены граничные случаи локальных окрестностей. Все другие окрестности характеризуются такими значениями функций протяженности гистограммы, которые находятся в диапазоне [0,255].
На основании анализа рассмотренных типов окрестностей и соответствующих им значений функций протяженности гистограммы, можно более объективно подойти к формированию степенной функции преобразования локального контраста. Наиболее удобно такой анализ проводить с помощью графического представления функции преобразования локального контраста (рис. 5 , прямая 1). Укажем при этом, что ![]() и уменьшение
и уменьшение ![]() отвечает более высокому усилению локального контраста, а увеличение - более слабому его усилению.
отвечает более высокому усилению локального контраста, а увеличение - более слабому его усилению.
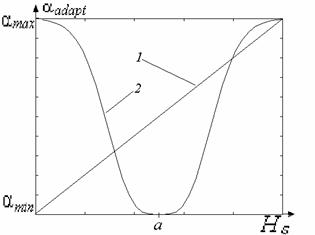
Рис. 5. Зависимость показателя степени ![]() преобразования локального контраста от функции протяженности гистограммы
преобразования локального контраста от функции протяженности гистограммы ![]() : 1 - в известном подходе [1], 2 - в предложенном методе.
: 1 - в известном подходе [1], 2 - в предложенном методе.
С рис. 5 (прямая 1) видно, что максимальное усиление локального контраста испытывают однородные участки изображения (![]() ), что не всегда желательно. Ведь однородные участки очень чувствительны к помехам, поэтому чрезмерное усиление их контраста приведет к значительным искажениям. Экспериментальные исследования показывают, что максимальному усилению (
), что не всегда желательно. Ведь однородные участки очень чувствительны к помехам, поэтому чрезмерное усиление их контраста приведет к значительным искажениям. Экспериментальные исследования показывают, что максимальному усилению (![]() ) должны подвергаться локальные контрасты в таких скользящих окрестностях, для которых функция протяженности гистограммы приобретает значения с середины диапазона
) должны подвергаться локальные контрасты в таких скользящих окрестностях, для которых функция протяженности гистограммы приобретает значения с середины диапазона ![]() .
.
В соответствии с изложенными требованиями нами предложено использовать степенную функцию преобразования локального контраста, характер изменения показателя степени которой отвечает представленному на рис. 5 (кривая 2).
Выражение для определения ![]() (рис. 5 , кривая 2) такое:
(рис. 5 , кривая 2) такое:
| (5) |
где ![]() - значение функции протяженности гистограммы, которое отвечает наиболее информативным участкам изображения
- значение функции протяженности гистограммы, которое отвечает наиболее информативным участкам изображения ![]() ;
; ![]() - постоянный коэффициент (
- постоянный коэффициент (![]() ).
).
Предложенное выражение (5) для модифицированного степенного преобразования позволяет более четко идентифицировать различные типы локальных окрестностей изображения и адаптивно усиливать их контраст в зависимости от значений локальных характеристик этих окрестностей.
Метод усиления контраста с использованием функции протяженности гистограммы эффективно используется в обработке широкого класса изображений. Учитывая характеристики скользящих окрестностей удается идентифицировать участки изображения по уровню контрастности и соответствующим образом на них реагировать. Благодаря этому достигается более тонкая обработка мелких деталей. Однако изображения должны отвечать двум требованиям. Они не должны содержать большого количества импульсных выбросов и темные или светлые участки большой площади. Ведь в первом случае это может привести к неадекватному вычислению функции протяженности гистограммы, а во втором - к неэффективному усилению контраста. Поэтому, если изображение не отвечает указанным выше требованиям, следует провести его фильтрацию или (и) градационную коррекцию.
%Программа, реализующая метод повышения контрастности изображения
%с использованием функции протяженности гистограммы
%=======Считывание данных======
clear;
L=imread('test.bmp');%Исходное изображение полутоновое, поэтому L(:,:,1)=L(:,:,2)=L(:,:,3);
L=L(:,:,1);
L=im2double(L);
m=15;n=m;n1=fix(n/2);m1=fix(m/2); %Определение размеров локальных окрестностей
%=======Преобразование матрицы яркостей изображения для устранения краевого эффекта=======
%=======В новых версиях системы Matlab существуют функции, которые реализуют эту процедуру=======
a=L(1,1);b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1;
for j=1:m1;
L1(i,j)=a; L3(i,j)=b; L6(i,j)=c; L8(i,j)=d;
end;
end;
L2=L(1,1:M); L02=L2;
for i=1:n1-1;
L2=[L2;L02];
end;
L7=L(N,1:M); L07=L7;
for i=1:n1-1;
L7=[L7;L07];
end;
L4=L(1:N,1); L4=L4'; L04=L4;
for i=1:m1-1;
L4=[L4;L04];
end;
L4=L4'; L5=L(1:N,M); L5=L5'; L05=L5;
for i=1:m1-1;
L5=[L5;L05];
end;
L5=L5'; L1=[L1;L4]; L1=[L1;L6]; L1=L1'; L2=[L2;L]; L2=[L2;L7]; L2=L2';
L3=[L3;L5]; L3=[L3;L8]; L3=L3'; L1=[L1;L2]; L1=[L1;L3];
Lr=L1';
clear L2;clear L3;clear L4;clear L5;clear L6;
clear L7;clear L8;clear L02;clear L04;clear L05;
clear L07;clear L1;clear L;
%=======Определение параметров локальной окрестности (функции протяженности гистограммы)=======
HP=zeros(N+2*n1,M+2*m1);
for i=1+n1:N+n1;
disp(i)
for j=1+m1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=Lr(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
D(n1+1+a,m+1)=Lr(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
LMIN=min(min(D)); LMAX=max(max(D));
H_lokal=hist(D(:)+1,LMAX-LMIN+1);
H_lokal_max=max(H_lokal);
clear H_lokal;
HP(i,j)=(LMAX-LMIN)/H_lokal_max;
clear LMIN; clear LMAX; clear H_lokal_max;
end;
end;
n_filter=3;m_filter=n_filter;
F=ones(n_filter,m_filter);
Lser=filter2(F,Lroshyrena,'same')/(n_filter*m_filter);
clear n_filter;clear m_filter;
amax=.7;amin=.5;
%=======Определение и преобразование локального контраста с учетом локальных характеристик=======
C=(Lr-Lser)./(Lr+Lser+eps);
C=abs(C);
for i=1+n1:N+n1;
disp(i)
for j=1+m1:M+m1;
if j==1+m1;
TM=0;
for a=-n1:n1;
for b=-m1:m1;
TM(n1+1+a,m1+1+b)=HP(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
TM(n1+1+a,m+1)=HP(i+a,j+m1);
end;
TM=TM(1:n,2:m+1);
end;
HP_MIN=min(min(TM));
HP_MAX=max(max(TM));
C(i,j)=C(i,j)^(amin+(amax-amin)*(HP(i,j)-HP_MIN)/(HP_MAX-HP_MIN));
if Lroshyrena(i,j)>Lser(i,j);
Lvyh(i,j)=Lser(i,j)*(1+C(i,j))/(1-C(i,j));
else
Lvyh(i,j)=Lser(i,j)*(1-C(i,j))/(1+C(i,j));
end;
if Lvyh(i,j)>=255;
Lvyh(i,j)=255;
end;
if Lvyh(i,j)<=0;
Lvyh(i,j)=0;
end;
end;
end;
Lvyh=round(Lvyh);
Lvyh=Lvyh(1+n1:N+n1,1+m1:M+m1);
L=Lr(1+n1:N+n1,1+m1:M+m1);
%=======Визуализация=======
colormap(gray(255));
subplot(221);image(L');axis('image');
subplot(222);image(Lvyh');axis('image');
Результат работы приведенной программы, реализующей метод повышения контрастности изображений с использованием функции протяженности гистограммы, приведен на рис. 1.
 |
 |
| а) | б) |
 |
 |
| в) | г) |
Рис. 1. Обработка изображения методом нелинейного преобразования локальных контрастов с использованием функции протяженности гистограммы: а) исходное аэрокосмическое изображение (в скобках указано количественная оценка визуального качества изображения) - 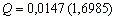 ; б) изображение а, обработанное известным методом -
; б) изображение а, обработанное известным методом - 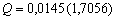 ; в) изображение а после выполнения градационной коррекции -
; в) изображение а после выполнения градационной коррекции - 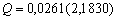 ; г) изображение а, обработанное предложенным методом -
; г) изображение а, обработанное предложенным методом - 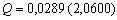 .
.
Литература.
- Dhawan A.P., Buelloni G., Gordon R. Enhancement of mammographic features by optimal adaptive neighbourhvod image processing // IEEE Trans. Med. Imaging. - 1986. - v.5. - P.8-15.
- 2. Gordon R., Rangayyan R.M. Feature enhancement of film mammograms using fixed and adaptive neighbourhood // Applied optics. - 1984. - v.23. - P. 560-564.
Энтропия изображения. Использование среднеквадратического отклонения значений яркостей элементов окрестности в методах контрастирования изображений. Нелинейное растяжение локальных контрастов.
Существует метод адаптивного преобразования локальных контрастов, в котором за параметр, характеризирующий скользящую окрестность, используется аналог энтропии [1]. С помощью энтропии можно характеризовать гладкость локальных окрестностей. Поэтому на основании меры априорной неопределенности значений яркостей элементов окрестности формируется функция преобразования локального контраста. Основные шаги реализации метода такие.
Шаг 1. Вычисляем локальный контраст элемента изображения ![]() .
.
Шаг 2. Для определения локальной энтропии изображения в скользящей окрестности ![]() с размерностью
с размерностью ![]() элементов и значениями
элементов и значениями ![]() используем выражение
используем выражение
| (1) |
где
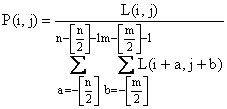 . . |
(2) |
Шаг 3. Вычисляем степенное преобразование локального контраста, которое в связи с использованием локальной энтропии приобретает адаптивный характер:
| (3) |
где ![]() ,
, ![]() - максимальное и минимальное значения энтропии скользящей окрестности
- максимальное и минимальное значения энтропии скользящей окрестности ![]() размером
размером ![]() элементов.
элементов.
Шаг 4. Восстанавливаем изображение за выражением, которое определяется из выражения определения локального контраста.
Отметим, что энтропия локальной окрестности изображения определяется как сумма произведений вероятностей элементов окрестности с различными значениями яркостей на логарифм этих вероятностей, взятая с противоположным знаком.
Согласно выражению (2) значение яркости ![]() следует воспринимать как вероятность яркости
следует воспринимать как вероятность яркости ![]() -го элемента окрестности. При таком подходе формула (1) для определения энтропии окрестности не отвечает общепринятому определению вероятностной энтропии, а является одной из разновидностей невероятностной энтропии. Согласно выражению (1), локальную окрестность следует рассматривать как некоторую сложную систему, состоящую с простых подсистем - элементов окрестности, и уже с этих позиций искать энтропию окрестности. Кроме того, такой подход для определения энтропии локальной окрестности требует значительных вычислительных затрат.
-го элемента окрестности. При таком подходе формула (1) для определения энтропии окрестности не отвечает общепринятому определению вероятностной энтропии, а является одной из разновидностей невероятностной энтропии. Согласно выражению (1), локальную окрестность следует рассматривать как некоторую сложную систему, состоящую с простых подсистем - элементов окрестности, и уже с этих позиций искать энтропию окрестности. Кроме того, такой подход для определения энтропии локальной окрестности требует значительных вычислительных затрат.
Для повышения эффективности описанного метода предложено использовать классический вероятностный подход к определению энтропии. Тогда в описанном выше алгоритме шаг 2 будет состоять в вычислении ![]() за выражением (1), но с вычислением вероятностей
за выражением (1), но с вычислением вероятностей ![]() как
как
| (4) |
где ![]() - значение гистограммы для элемента с значением яркости
- значение гистограммы для элемента с значением яркости ![]() .
.
Кроме этого нами предложено выражение преобразования локального контраста для модификации шага 3 известного подхода
| (5) |
где ![]() - параметр нелинейного усиления контраста.
- параметр нелинейного усиления контраста.
Предложенный метод обработки максимально эффективный для изображений, которые имеют равномерную гистограмму распределения яркостей и не содержат шума. На основании визуального и количественного анализа результатов экспериментальных исследований отметим, что предложенный метод является более эффективным в сравнении с известными методами этого класса.
Использование среднеквадратического отклонения значений яркостей элементов окрестности в методах контрастирования изображений
Выше была рассмотрена известная трехэтапная технология повышения контрастности изображения. Однако она недостаточно учитывает адаптацию к локальным особенностям изображения. Для устранения этого недостатка предложено использовать адаптивное определение показателя степени в классе степенных функций нелинейного преобразования локальных контрастов изображения. Однако и в этом случае эффективность метода недостаточна. Для ее увеличения предлагается дополнительно оценивать локальные окрестности ![]() изображения с учетом среднеквадратических отклонений относительно яркости центрального элемента
изображения с учетом среднеквадратических отклонений относительно яркости центрального элемента ![]() и на том основании формировать функцию нелинейного преобразования локальных контрастов яркостей элементов изображения.
и на том основании формировать функцию нелинейного преобразования локальных контрастов яркостей элементов изображения.
Определим величину показателя степени ![]() так:
так:
| (6) |
где ![]() - нормирующий коэффициент,
- нормирующий коэффициент, ![]() ,
, ![]() - среднеарифметическое значение яркости исходного изображения
- среднеарифметическое значение яркости исходного изображения
| (7) |
![]() ,
,![]() - размеры изображения (
- размеры изображения (![]() ,
, ![]() ),
),
![]() - среднеквадратическое отклонение значений яркостей элементов изображения в скользящей окрестности
- среднеквадратическое отклонение значений яркостей элементов изображения в скользящей окрестности ![]() , которое определяется выражением
, которое определяется выражением
 . . |
(8) |
Отметим, что при программной реализации предложенного метода учитывают случай, когда ![]() , задавая некоторое предельное минимальное значение
, задавая некоторое предельное минимальное значение ![]() . То есть текущему среднеквадратическому отклонению значений яркостей элементов изображения
. То есть текущему среднеквадратическому отклонению значений яркостей элементов изображения ![]() присваивают
присваивают ![]() в том случае, когда
в том случае, когда ![]() .
.
Для выражения (8) характерным является то, что когда элементы изображения, которые попадают в скользящую окрестность ![]() , мало отличаются по значению от центрального элемента окрестности
, мало отличаются по значению от центрального элемента окрестности ![]() , то это приводит к малым значениям среднеквадратического отклонения
, то это приводит к малым значениям среднеквадратического отклонения ![]() . В результате получаем значительное уменьшение коэффициента
. В результате получаем значительное уменьшение коэффициента ![]() от
от ![]() в выражении (6), что адекватно увеличению усиления контраста. Если же элементы изображения в скользящей окрестности
в выражении (6), что адекватно увеличению усиления контраста. Если же элементы изображения в скользящей окрестности ![]() значительно отличаются от центрального элемента окрестности
значительно отличаются от центрального элемента окрестности ![]() , то это приводит к большим значениям среднеквадратического отклонения
, то это приводит к большим значениям среднеквадратического отклонения ![]() . Поэтому значение степени
. Поэтому значение степени ![]() будет тем меньше отличаться от
будет тем меньше отличаться от ![]() , чем больше
, чем больше ![]() и, соответственно, контраст
и, соответственно, контраст ![]() будет усиливаться меньше. Следует отметить, что параметр
будет усиливаться меньше. Следует отметить, что параметр ![]() должен удовлетворять условию
должен удовлетворять условию ![]() .
.
Отметим также, что значение нормирующего коэффициента ![]() нужно выбирать исходя из анализа значений
нужно выбирать исходя из анализа значений ![]() , придерживаясь того, что
, придерживаясь того, что ![]() . Выбор значения
. Выбор значения ![]() существенно влияет на эффективность метода. Использование же глобального среднеарифметического значения яркости
существенно влияет на эффективность метода. Использование же глобального среднеарифметического значения яркости ![]() позволяет адаптировать обобщенный алгоритм преобразования к конкретному изображению, поскольку значение
позволяет адаптировать обобщенный алгоритм преобразования к конкретному изображению, поскольку значение ![]() отображает уровень адаптации за яркостью зрительной системы человека при восприятии изображения. Следовательно, употребляя среднеквадратическое отклонение
отображает уровень адаптации за яркостью зрительной системы человека при восприятии изображения. Следовательно, употребляя среднеквадратическое отклонение ![]() в качестве количественной оценки гладкости изображения в скользящей окрестности
в качестве количественной оценки гладкости изображения в скользящей окрестности ![]() , получаем непосредственную зависимость степени
, получаем непосредственную зависимость степени ![]() от
от ![]() . Это позволяет в целом реализовать адаптивное усиление локальных контрастов при их степенных преобразованиях.
. Это позволяет в целом реализовать адаптивное усиление локальных контрастов при их степенных преобразованиях.
Нелинейное растяжение локальных контрастов
Усиление контраста - одна из важных задач обработки изображений, распознавания образов и машинного зрения. Решение этой задачи непосредственно связано с повышением вероятности правильного восприятия изображения. В последнее время разработаны методы улучшения изображений, которые базируются на нелинейных преобразованиях локальных контрастов с учетом особенностей человеческого зрения. Реализация этих методов состоит в выполнении трех основных шагов:
Шаг 1. Определение количественной меры локального контраста.
Шаг 2. Увеличение по определенному закону некоторой количественной меры локального контраста.
Шаг 3. Восстановление элемента преобразованного изображения с усиленным локальным контрастом.
Такие преобразования выполняются для каждого элемента изображения.
Предлагается новый подход к повышению контраста изображения, который базируется на преобразовании гистограммы локальных контрастов.
Рассмотрев гистограммы распределения значений локальных контрастов реальных изображений отметим, что в большинстве случаев они имеют небольшие значения и занимают примерно треть допустимого диапазона (рис. 1).
Следовательно, реальные изображения характеризуются, в основном, небольшими значениями локальных контрастов. Гистограмма распределения значений локальных контрастов изображения, которое было обработано некоторым методом усиление контраста, будет иметь вид, представленный на рис. 2.
Анализируя гистограммы распределения значений локальных контрастов исходного и обработанного изображений, можно предположить, что гистограмма на рис. 2 получена вследствие нелинейного растяжения гистограммы на рис. 1.
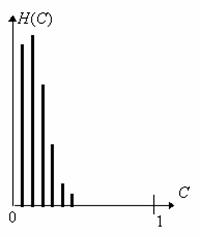
Рис. 1. Типичная гистограмма распределения значений локальных контрастов исходного изображения.
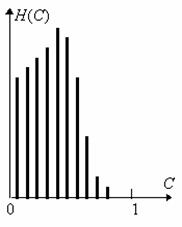
Рис. 2. Гистограмма распределения значений локальных контрастов изображения, обработанного некоторым методом повышения контрастности.
Рассмотрим метод повышения контрастности изображений с использованием предложенного подхода. Основные этапы реализации данного метода будут аналогичны к вышеупомянутой трехэтапной схеме [2], за исключением этапа нелинейного преобразования локальных контрастов, который рассмотрим более детально.
Для нелинейного преобразования локального контраста используем следующее выражение:
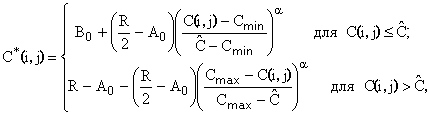 |
(9) |
где ![]() - значение локального контраста элемента исходного изображения с координатами
- значение локального контраста элемента исходного изображения с координатами ![]() ,
,
![]() - усиленное значение локального контраста элемента изображения с координатами
- усиленное значение локального контраста элемента изображения с координатами ![]() ;
;
![]() - максимально возможное значение локального контраста
- максимально возможное значение локального контраста ![]() ;
;
![]() ,
, ![]() - максимальное и минимальное значения локального контраста исходного изображения,
- максимальное и минимальное значения локального контраста исходного изображения,
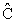 - оценка математического ожидания значений локального контраста (например, среднеарифметическое значение локальных контрастов элементов изображения),
- оценка математического ожидания значений локального контраста (например, среднеарифметическое значение локальных контрастов элементов изображения),
![]() ,
, ![]() - коэффициенты постоянного смещения;
- коэффициенты постоянного смещения;
![]() - показатель степени
- показатель степени ![]() .
.
Проанализируем функцию преобразования локального контраста (9). Для этого рассмотрим графики двух функций - степенного преобразования и предложенной функции (9), которые представленные на рис. 3. Функция степенного преобразования локального контраста вычисляется за выражением типа ![]() , где
, где ![]() .
.
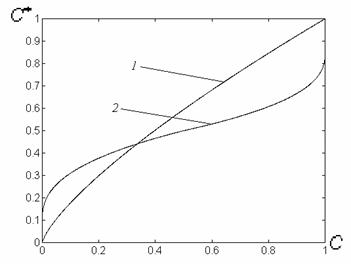
Рис. 3. Графики функций преобразования локального контраста (1 - степенная функция, 2 - за выражением (9)).
Из рис. 3 видно, что предложенная функция обеспечивает лучшее усиление для небольших значений локального контраста. Значения локальных контрастов для реальных изображений имеют как раз такой уровень. Тем не менее при практической реализации используют частный случай выражения (9). Он состоит в проведении преобразований лишь для таких локальных контрастов, которые удовлетворяют условию  . В целом предложенный метод позволяет проводить эффективное усиление контрастности изображений.
. В целом предложенный метод позволяет проводить эффективное усиление контрастности изображений.
%Программа, реализующая метод повышения контрастности изображений
%с использованием энтропии
clear;
%=====Считывание исходных данных=====
L=imread('image1.tif');
[N M]=size(L);
m=15;n=15;n1=fix(n/2);m1=fix(m/2);
%=====Преобразование матрицы элементов изображения для избежания краевого эффекта=====
a=L(1,1);b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1; for j=1:m1;
L1(i,j)=a; L3(i,j)=b; L6(i,j)=c; L8(i,j)=d;
end;end;
L2=L(1,1:M); L02=L2;
for i=1:n1-1;
L2=[L2;L02];
end;
L7=L(N,1:M); L07=L7;
for i=1:n1-1;
L7=[L7;L07];
end;
L4=L(1:N,1); L4=L4'; L04=L4;
for i=1:m1-1;
L4=[L4;L04];
end;
L4=L4'; L5=L(1:N,M); L5=L5'; L05=L5;
for i=1:m1-1;
L5=[L5;L05];
end;
L5=L5'; L1=[L1;L4]; L1=[L1;L6]; L1=L1'; L2=[L2;L]; L2=[L2;L7]; L2=L2';
L3=[L3;L5]; L3=[L3;L8]; L3=L3'; L1=[L1;L2]; L1=[L1;L3];
Lr=L1';
clear L2;clear L3;clear L4;clear L5;clear L6;clear L7;clear L8;clear L02;
clear L04;clear L05;clear L07;clear L1;clear L;
%=====Определение параметров локальной окрестности=====
Entropia=ones(N+2*n1,M+2*m1);
for i=1+n1:N+n1;
disp(i)
for j=1+n1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=Lr(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
D(n1+1+a,m+1)=Lr(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
Pk_vektor=hist(D(:),max(max(D))-min(min(D))+1)/(n*m);
for ind=1:length(Pk_vektor);
if Pk_vektor(ind)==0;
Pk_vektor(ind)=1;
end;
end;
Entropia(i,j)=-sum(Pk_vektor.*log(Pk_vektor));
end;
end;
n_filter=3;m_filter=n_filter;F=ones(n_filter,m_filter);
Lser=filter2(F,Lr,'same')/(n_filter*m_filter);
clear n_filter;clear m_filter;clear F;
amax=.7;amin=.5;
%=====Определение локальных контрастов и функции их преобразования=====
C=abs(Lr-Lser)./(Lr+Lser+eps);
alfa=amin+.2.*(1-exp(-((Entropia./max(max(Entropia))-.5).^2) ./(2*.14^2))).^3;
C=C.^alfa;
for i=1+n1:N+n1;
for j=1+n1:M+m1;
if Lr(i,j)>=Lser(i,j);
Lvyh(i,j)=Lser(i,j)*(1+C(i,j))/(1-C(i,j)+eps);
else
Lvyh(i,j)=Lser(i,j)*(1-C(i,j))/(1+C(i,j));
end;
%=====Проверка корректности диапазона=====
if Lvyh(i,j)>=255; Lvyh(i,j)=255; end;
if Lvyh(i,j)<=0; Lvyh(i,j)=0; end;
end;
end;
Lvyh=Lvyh(n1+1:N+n1,m1+1:M+m1);
Lvyh=round(Lvyh);
L=Lr(n1+1:N+n1,m1+1:M+m1);
%=====Визуализация результатов обработки=====
colormap(gray(255));
subplot(221);image(L');axis('image');
subplot(222);image(Lvyh');axis('image');
Результаты работы программы представлены на рис.
 |
 |
| а) | б) |
 |
 |
| в) | г) |
Рис. Локально-адаптивный метод повышения визуального качества изображений с использованием энтропии: а) исходное изображение; б) изображение а, обработанное известным методом с использованием энтропии; в) изображение а, обработанное известным методом с использованием классического подхода к определению энтропии; г) изображение а, обработанное предложенным методом.
%Программа, реализующая метод контрастирования изображений с использованием
%среднеквадратических отклонений значений яркостей элементов локальной окрестности.
clear;
%=====Считывание исходных данных=====
L=imread('image2.tif');
[N M]=size(L);
m=15;n=15;n1=fix(n/2);m1=fix(m/2);
%=====Преобразование матрицы элементов изображения для избежания краевого эффекта=====
a=L(1,1);b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1; for j=1:m1;
L1(i,j)=a; L3(i,j)=b; L6(i,j)=c; L8(i,j)=d;
end;end;
L2=L(1,1:M); L02=L2;
for i=1:n1-1;
L2=[L2;L02];
end;
L7=L(N,1:M); L07=L7;
for i=1:n1-1;
L7=[L7;L07];
end;
L4=L(1:N,1); L4=L4'; L04=L4;
for i=1:m1-1;
L4=[L4;L04];
end;
L4=L4'; L5=L(1:N,M); L5=L5'; L05=L5;
for i=1:m1-1;
L5=[L5;L05];
end;
L5=L5'; L1=[L1;L4]; L1=[L1;L6]; L1=L1';
L2=[L2;L]; L2=[L2;L7]; L2=L2';
L3=[L3;L5]; L3=[L3;L8]; L3=L3'; L1=[L1;L2];
L1=[L1;L3]; Lr=L1';
clear L2;clear L3;clear L4;clear L5;clear L6;clear L7;clear L8;
clear L02;clear L04;clear L05;clear L07;clear L1;clear L;
%====Определение среднеквадратических отклонений значений яркостей элементов локальной окрестности====
SV=zeros(N+2*n1,M+2*m1);
for i=1+n1:N+n1;
for j=1+m1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=Lr(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
D(n1+1+a,m+1)=Lr(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
D=D(:);
SV(i,j)=std(D);
end;
end;
%=====Определение массива усредненных значений элементов изображения=====
n_filter=3;m_filter=n_filter;
F=ones(n_filter,m_filter);
Lser=filter2(F,Lr,'same')/(n_filter*m_filter);
amin=.35;amax=.95;
C=(Lr-Lser)./(Lr+Lser+eps);
C=abs(C);
for i=1+n1:N+n1;
disp(i)
for j=1+m1:M+m1;
if SV(i,j)<=1;
SV(i,j)=1;
end;
if j==1+m1;
TM=0;
for a=-n1:n1;
for b=-m1:m1;
TM(n1+1+a,m1+1+b)=SV(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
TM(n1+1+a,m+1)=SV(i+a,j+m1);
end;
TM=TM(1:n,2:m+1);
end;
SV_MIN=min(min(TM));
SV_MAX=max(max(TM));
C(i,j)=C(i,j)^(amin+(amax-amin)*(SV(i,j)-SV_MIN)/(SV_MAX-SV_MIN));
if Lroshyrena(i,j)>=Lser(i,j);
Lvyh(i,j)=Lser(i,j)*(1+C(i,j))/(1-C(i,j));
else
Lvyh(i,j)=Lser(i,j)*(1-C(i,j))/(1+C(i,j));
end;
%=====Проверка корректности диапазона=====
if Lvyh(i,j)>=255; Lvyh(i,j)=255; end;
if Lvyh(i,j)<=0; Lvyh(i,j)=0; end;
end;
end;
Lvyh=Lvyh(n1+1:N+n1,m1+1:M+m1);
Lvyh=round(Lvyh);
L=Lroshyrena(n1+1:N+n1,m1+1:M+m1);
%=====Визуализация результатов=====
colormap(gray(255));
subplot(221);image(L);axis('image');
subplot(222);image(Lvyh);axis('image');
Результаты работы программы представлены на рис.
 |
 |
 |
| а) | б) | в) |
Рис. Локально-адаптивний метод улучшения визуального качества изображений с использованием среднеквадратических отклонений значений яркостей элементов локальной окрестности: а) исходное изображение; б) изображение а, обработанное известным методом; в) изображение а, обработанное предложенным методом.
%Программа, реализующая метод нелинейного (степенного) преобразования (растяжения)
%локальных контрастов (глобальная реализация)
clear;
%=====Считывание исходных данных=====
L=imread('im.tif');
[N M]=size(L);
%=====Задание параметров локальных окрестностей=====
m=5;n=m;n1=fix(n/2);m1=fix(m/2);
R=255;
%=====Преобразование матрицы интенсивностей с целью избежания краевого эффекта=====
a=L(1,1);b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1;
for j=1:m1;
L1(i,j)=a; L3(i,j)=b; L6(i,j)=c; L8(i,j)=d;
end;
end;
L2=L(1,1:M); L02=L2;
for i=1:n1-1;
L2=[L2;L02];
end;
L7=L(N,1:M); L07=L7;
for i=1:n1-1;
L7=[L7;L07];
end;
L4=L(1:N,1); L4=L4'; L04=L4;
for i=1:m1-1;
L4=[L4;L04];
end;
L4=L4'; L5=L(1:N,M); L5=L5'; L05=L5;
for i=1:m1-1;
L5=[L5;L05];
end;
L5=L5'; L1=[L1;L4]; L1=[L1;L6]; L1=L1';
L2=[L2;L]; L2=[L2;L7]; L2=L2';
L3=[L3;L5]; L3=[L3;L8]; L3=L3';
L1=[L1;L2]; L1=[L1;L3];
Lr=L1';
clear L2;clear L3;clear L4;clear L5;clear L6;
clear L7;clear L8;clear L02;clear L04;
clear L05;clear L07;clear L1;clear L;
%=====Определение усредненного локального среднего изображения=====
F=ones(n,m);
Lser=filter2(F,Lr,'same')/(n*m);
С=abs(Lr-Lser)/(Lr+Lser);
CMIN=min(min(C));
CMAX=max(max(C));
alfa=.9;
%=====Параметр нелинейного преобразования=====
%=====Нелинейное (при a>1 или a<1) растяжение локальных контрастов=====
C=((C-CMIN)./(CMAX-CMIN)).^alfa;
%=====Восстановление яркостей результирующего изображения=====
for i=1+n1:N+n1;
disp(i)
for j=1+m1:M+m1;
if Lr(i,j)>=Lser(i,j);
Lvyh(i,j)=Lser(i,j)*(1+C(i,j))/(1-C(i,j));
else
Lvyh(i,j)=Lser(i,j)*(1-C(i,j))/(1+C(i,j));
end;
if Lvyh(i,j)>=R; Lvyh(i,j)=R; end;
if Lvyh(i,j)<=0; Lvyh(i,j)=0; end;
end;
end;
Lvyh=Lvyh(n1+1:N+n1,m1+1:M+m1);
Lvyh=round(Lvyh);
L=Lroshyrena(n1+1:N+n1,m1+1:M+m1);
%=====Визуализация результатов=====
subplot(221);imshow(L');axis('image');
subplot(222);imshow(Lvyh');axis('image');
 |
 |
| а) исходное изображение | б) изображение а, обработанное методом Гордона |
 |
 |
| в) метод нелинейного преобразования локальных контрастов (глобальный) | г) метод нелинейного преобразования локальных контрастов (скользящий) |
Рис. Обработка изображений методом нелинейного растяжения локальных контрастов.
Как было сказано выше этот метод может быть реализован в скользящем варианте, в котором преобразование локальных контрастов выполняется с учетом характеристик локальных окрестностей.
%Программа, реализующая метод нелинейного (степенного) преобразования (растяжения)
%локальных контрастов (скользящая реализация)
clear;
%=====Считывание исходных данных=====
L=imread('im1.bmp');
L=L(:,:,1);
L=double(L)./255;
[N M]=size(L);
%=====Задание параметров локальных окрестностей=====
m=17;n=m;n1=fix(n/2);m1=fix(m/2);
R=255/255;
%=====Преобразование матрицы интенсивностей с целью избежания краевого эффекта=====
a=L(1,1);b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1;
for j=1:m1;
L1(i,j)=a; L3(i,j)=b; L6(i,j)=c; L8(i,j)=d;
end;
end;
L2=L(1,1:M); L02=L2;
for i=1:n1-1;
L2=[L2;L02];
end;
L7=L(N,1:M); L07=L7;
for i=1:n1-1;
L7=[L7;L07];
end;
L4=L(1:N,1); L4=L4'; L04=L4;
for i=1:m1-1;
L4=[L4;L04];
end;
L4=L4'; L5=L(1:N,M); L5=L5'; L05=L5;
for i=1:m1-1;
L5=[L5;L05];
end;
L5=L5'; L1=[L1;L4]; L1=[L1;L6]; L1=L1';
L2=[L2;L]; L2=[L2;L7]; L2=L2';
L3=[L3;L5]; L3=[L3;L8]; L3=L3';
L1=[L1;L2]; L1=[L1;L3];
Lr=L1';
clear L2;clear L3;clear L4;clear L5;clear L6;
clear L7;clear L8;clear L02;clear L04;
clear L05;clear L07;clear L1;clear L;
alfa=5;
%=====Параметр нелинейного преобразования=====
%=====Восстановление яркостей результирующего изображения=====
C=zeros(N+n+1,M+m+1);
C1=zeros(N+n+1,M+m+1);
for i=1+n1:N+n1;
disp(i)
for j=1+m1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=Lr(i+a,j+b);
end;
end;
end;
if j>(1+m1);
for a=-n1:n1;
D(n1+1+a,m+1)=Lr(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
Lser(i,j)=sum(sum(D))/(n*m);
C(i,j)=abs((Lr(i,j)-Lser(i,j))/(Lr(i,j)+Lser(i,j)));
end;
end;
for i=1+n1:N+n1;
disp(i)
for j=1+m1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=C(i+a,j+b);
end;
end;
end;
if j>(1+m1);
for a=-n1:n1;
D(n1+1+a,m+1)=C(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
CMIN(i,j)=min(min(D));
CMAX(i,j)=max(max(D));
C1(i,j)=((C(i,j)-CMIN(i,j))/(CMAX(i,j)-CMIN(i,j)))^alfa;
if C1(i,j)>1; C1(i,j)=1; end;
if C1(i,j)<0; C1(i,j)=0; end;
if Lr(i,j)>=Lser(i,j);
Lvyh(i,j)=Lser(i,j)*(1+C1(i,j))/(1-C1(i,j)+eps);
else
Lvyh(i,j)=Lser(i,j)*(1-C1(i,j))/(1+C1(i,j));
end;
if Lvyh(i,j)>R; Lvyh(i,j)=R; end;
if Lvyh(i,j)<0; Lvyh(i,j)=0; end;
end;
end;
Lvyh=Lvyh(n1+1:N+n1,m1+1:M+m1);
L=Lr(n1+1:N+n1,m1+1:M+m1);
%=====Визуализация результатов=====
subplot(221);imshow(L');axis('image');
subplot(222);imshow(Lvyh');axis('image');
Литература.
- Dash L., Chatterji B.N. Adaptive contrast enhancement and de-enhancement // Pattern Recognition, 1992. - V. 24, № 4. - P.289 - 302.
- Воробель Р.А. Цифровая обработка изображений на основе теории контрастности: Дис… докт. техн. наук: 05.13.06. - Львов, 1999. - 369 с.
Анализ некоторых характеристик локальных окрестностей
Аналитическим выражением, описывающим количественное определение реакции зрительной системы на световое возбуждение, является его контраст. Вид этого выражения определяется свойствами конкретной зрительной системы восприятия [1, 2]. То есть изменение выражения определения контраста отвечает изменению типа зрительной системы или ее параметров. Это создает возможности адаптации зрительной системы путем изменения выражения для определения локального контраста. Разумеется, что при этом аналитическое выражение должно обеспечивать сохранение основных предельных свойств. Эти свойства заключаются в том, что локальный контраст ![]() приобретает максимальное значение только тогда, когда его компоненты имеют значения, которые лежат на противоположных краях диапазона, и равный нулю - в случае равенства этих компонентов по величине. Критерием оценки выражений контраста является эффективность их применения при цифровой обработке изображений. Следовательно, удачный выбор того или иного выражения определения контраста существенно влияет на дальнейшее применение метода.
приобретает максимальное значение только тогда, когда его компоненты имеют значения, которые лежат на противоположных краях диапазона, и равный нулю - в случае равенства этих компонентов по величине. Критерием оценки выражений контраста является эффективность их применения при цифровой обработке изображений. Следовательно, удачный выбор того или иного выражения определения контраста существенно влияет на дальнейшее применение метода.
Вторым важным фактором эффективного применения адаптивных методов является правильный выбор функции адаптивного преобразования локальных контрастов. В данной работе рассматриваются только степенные функции преобразования типа ![]() . Далее будем более детально рассматривать только степень преобразования локальных контрастов
. Далее будем более детально рассматривать только степень преобразования локальных контрастов ![]() . При формировании таких функций задают минимальное (
. При формировании таких функций задают минимальное (![]() ) и максимальное (
) и максимальное (![]() ) значения степени
) значения степени ![]() , причем
, причем ![]() ,
, ![]() . А сама адаптация состоит в формировании дополнительного слагаемого к
. А сама адаптация состоит в формировании дополнительного слагаемого к ![]() на основе некоторой локальной статистики (энтропия, функция протяженности гистограммы, среднеквадратическое отклонение). Функции преобразования должны удовлетворять условиям:
на основе некоторой локальной статистики (энтропия, функция протяженности гистограммы, среднеквадратическое отклонение). Функции преобразования должны удовлетворять условиям:
![]() ,
, ![]() ,
, ![]() .
.
Отметим, что выбор той или иной функции преобразования зависит от того, какая статистика используется для характеристики гладкости локальной окрестности ![]() .
.
Рассмотрим несколько окрестностей, которым присуща различная степень гладкости: а) локальная окрестность с одинаковыми уровнями яркостей (однородная окрестность); б) локальная окрестность, элементы которой имеют значения яркостей, находящиеся на противоположных концах диапазона (условно бинарная окрестность); в) локальная окрестность, которая содержит элементы, значения яркостей которых не являются одинаковыми и не находятся на краях диапазона.
Приведенные выше типы окрестностей будут характеризоваться различными значениями локальных характеристик. Рассмотрим это более детально на примере энтропии, функции протяженности гистограммы и среднеквадратичного отклонения. Для определения энтропии в скользящей локальной окрестности размерами ![]() используется выражение:
используется выражение:
| (1) |
где ![]() - вычисляется за выражением
- вычисляется за выражением
![]() ,
,
![]() - значение гистограммы локальной окрестности
- значение гистограммы локальной окрестности ![]() (количество элементов с яркостью
(количество элементов с яркостью ![]() в окрестности
в окрестности ![]() ) для величины яркости элемента с координатами
) для величины яркости элемента с координатами ![]() .
.
Согласно выражению (1), энтропия приобретает максимальное значение на однородных участках, а минимальное - на участках с элементами, значения яркостей которых находятся на противоположных краях диапазона.
Второй статистикой, используемой для характеристик локальных окрестностей, является функция протяженности гистограммы, которая вычисляется по выражению:
| (2) |
где ![]() ,
, ![]() - минимальное и максимальное значения яркости в скользящей окрестности
- минимальное и максимальное значения яркости в скользящей окрестности ![]() с центром в элементе с координатами
с центром в элементе с координатами ![]() ;
;
![]() - максимальное значение гистограммы скользящей локальной окрестности
- максимальное значение гистограммы скользящей локальной окрестности ![]() с центром в элементе с координатами
с центром в элементе с координатами ![]() .
.
Эта характеристика локальной окрестности приобретает минимальные значения на однородных участках, и максимальные - на бинарных участках.
Следующей характеристикой гладкости локальных окрестностей является среднеквадратическое отклонение значений яркостей элементов скользящей окрестности ![]() , которое вычисляется за выражением:
, которое вычисляется за выражением:
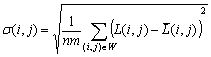 , , |
(3) |
где ![]() - среднеарифметическое значение яркостей элементов локальной окрестности
- среднеарифметическое значение яркостей элементов локальной окрестности ![]() с центром в элементе
с центром в элементе ![]() с координатами
с координатами ![]() .
.
Выражение (3) равно нулю для однородных окрестностей и возрастает с увеличением неоднородности. Более наглядно характер изменения значений локальных характеристик в зависимости от типа окрестности демонстрирует рис. 1.
Теперь, когда известен характер изменения значений локальных статистик в скользящих окрестностях различного типа, рассмотрим процедуру формирования функции преобразования локальных контрастов. Важная проблема, которая стоит перед исследователем при формировании этой функции, заключается в том, насколько нужно увеличить локальные контрасты на том или ином участке изображения. Характер изменения усиления определяется локальными статистиками, но границы изменения (![]() ) задаются исследователем. Это связано с тем, что пока не существует теоретического решения
) задаются исследователем. Это связано с тем, что пока не существует теоретического решения
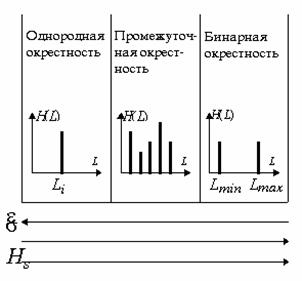
Рис. 1. Схематическое отображение изменения значений локальных характеристик в зависимости от типа скользящей окрестности (стрелками указано направление возрастания значения локальной статистики для различных типов скользящих окрестностей).
проблемы оптимальности преобразования локального контраста. Поэтому, исходя из опыта и знаний исследователя, функцию преобразования формируют таким образом, чтобы она обеспечивала максимальную контрастность изображения при минимуме искажений, вызванных чрезмерным усилением локальных контрастов.
Отметим, что вид функции преобразования в первую очередь зависит от конкретной задачи обработки изображения. Иными словами, формируя данную функцию, существует возможность регулировать степень преобразования локальных контрастов на различных типах окрестностей. При этом придерживаются следующих утверждений:
- на однородных окрестностях
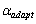 должна приобретать максимальное значение, что приведет к минимальному усилению локальных контрастов, поскольку в обратном случае это может привести к усилению шумовой составляющей сигнала. Исключение составляют только те однородные участки, которые являются потенциально информативными;
должна приобретать максимальное значение, что приведет к минимальному усилению локальных контрастов, поскольку в обратном случае это может привести к усилению шумовой составляющей сигнала. Исключение составляют только те однородные участки, которые являются потенциально информативными; - на локальных окрестностях, которые характеризуются высокой контрастностью,
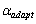 должно также принимать максимальное значение, что обеспечивает минимальное усиление локального контраста. Чрезмерное усиление высококонтрастных участков может привести к их искажениям;
должно также принимать максимальное значение, что обеспечивает минимальное усиление локального контраста. Чрезмерное усиление высококонтрастных участков может привести к их искажениям; - на остальных окрестностях
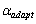 должно обеспечивать близкое к максимальному усиление контраста, поэтому должно принимать минимальное значение.
должно обеспечивать близкое к максимальному усиление контраста, поэтому должно принимать минимальное значение.
Следует отметить, что ![]() должно описываться относительно простыми выражениями, поскольку это влияет на вычислительную сложность метода.
должно описываться относительно простыми выражениями, поскольку это влияет на вычислительную сложность метода.
С учетом приведенных выше утверждений в роботе предложено несколько выражений для выбора показателя степени ![]() в степенном преобразовании локальных контрастов (табл. 1).
в степенном преобразовании локальных контрастов (табл. 1).
Таблица 1.
| № п/п |
Степень преобразования локальных контрастов |
Типичные виды зависимостей |
|
1 |
|
|
|
2 |
где |
|
|
3 |
где |
|
|
4 |
где
|
|
Выбор того или иного выражения ![]() обусловлен задачей корректировки реакции восприятия света конкретным пользователем [2].
обусловлен задачей корректировки реакции восприятия света конкретным пользователем [2].
Таким образом, когда известны значения локальных контрастов потенциально информативных участков, тогда, употребляя описанный выше подход, можно повышать контрастность указанных участков более эффективно.
Следовательно, предложенные принципы построения степенных функций преобразования обеспечивают широкие возможности относительно создания эффективных методов усиления локальных контрастов. При построении функций ![]() существует возможность учитывать особенности конкретных изображений, их информативных участков, что предоставляет дополнительные преимущества методам адаптивного преобразования локальных контрастов.
существует возможность учитывать особенности конкретных изображений, их информативных участков, что предоставляет дополнительные преимущества методам адаптивного преобразования локальных контрастов.
Литература
- Dash L., Chatterji B.N. Adaptive contrast enhancement and de-enhancement // Pattern Recognition, 1992. - V. 24, № 4. - P.289 - 302.
- Воробель Р.А. Цифровая обработка изображений на основе теории контрастности: Дис… докт. техн. наук: 05.13.06. - Львов, 1999. - 369 с.
Статистическое определение локального контраста
Рассмотрим оригинальную технологию повышения качества изображений путем усиления локальных контрастов. Ее суть состоит в определении числового значения локального контраста для определенного элемента изображения, нелинейном его усилении и восстановлении этого же элемента изображения с измененной яркостью, что обеспечивает в сравнении с исходным изображением усиление локального контраста. Структурно процедура усиления локального контраста состоит из трех основных этапов и используется для каждого элемента ![]() с координатами
с координатами ![]() исходного изображения
исходного изображения ![]() ,
, ![]() .
.
Однако использование описанного метода показывает, что его эффективность недостаточна для обработки изображений, которые содержат мелкие детали. Причина заключается в том, что локальный контраст определяется по формуле, где его значение пропорционально мере отличия центрального элемента изображения от окружающего фона по значению яркости. Составными элементами этой формулы являются непосредственные значения элементов или их усредненные значения, что приводит к неполному описанию текстуры локальной области.
Наиболее полно такие характеристики текстуры как однородность, шершавость и зернистость описываются статистическими методами.
Одним из наиболее простых методов описания текстуры является использование моментов гистограммы интенсивностей элементов изображения. Пусть ![]() - случайная величина, которая определяет дискретную интенсивность изображения,
- случайная величина, которая определяет дискретную интенсивность изображения, ![]() - соответствующие значения гистограммы. Известно, что
- соответствующие значения гистограммы. Известно, что ![]() -й момент
-й момент ![]() относительно среднего значения определяется формулой
относительно среднего значения определяется формулой
| (1) |
где ![]() - среднее значение яркостей элементов локальной окрестности
- среднее значение яркостей элементов локальной окрестности ![]() .
.
Из выражения (1) следует, что ![]() , а
, а ![]() . Второй момент, который называется дисперсией и обозначается как
. Второй момент, который называется дисперсией и обозначается как ![]() , служит для описания текстуры. Он является также мерой контраста интенсивности и применяется для описания однородности поверхностей. В некоторых работах в качестве меры контраста текстуры предложено использовать выражение
, служит для описания текстуры. Он является также мерой контраста интенсивности и применяется для описания однородности поверхностей. В некоторых работах в качестве меры контраста текстуры предложено использовать выражение
| (2) |
где ![]() - дисперсия в окрестности
- дисперсия в окрестности ![]() , k=0,8 - коэффициент нормирования.
, k=0,8 - коэффициент нормирования. ![]() согласно выражению (2) равно нулю для окрестностей с постоянной интенсивностью и единице - для больших значений
согласно выражению (2) равно нулю для окрестностей с постоянной интенсивностью и единице - для больших значений ![]() . Это свойство выражения (2) полностью отвечает требованиям определения локального контраста. Поэтому по аналогии с описанным известным подходом будем использовать в нем меру контраста, которая определяется за выражением (2).
. Это свойство выражения (2) полностью отвечает требованиям определения локального контраста. Поэтому по аналогии с описанным известным подходом будем использовать в нем меру контраста, которая определяется за выражением (2).
Следовательно, в предложенном методе на его первом этапе для каждого элемента изображения вычисляем локальный контраст, используя выражение (2).
На втором этапе осуществляем нелинейное преобразование локального контраста ![]() .
.
На третьем этапе восстанавливаем изображение путем определения нового значения яркости ![]() элемента с координатами
элемента с координатами ![]() . Для этого используем выражение, которое определяется из формулы (2):
. Для этого используем выражение, которое определяется из формулы (2):
![]()
![]()
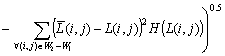 . . |
(3) |
Описанную процедуру повторяем для каждого элемента изображения.
В предложенном методе используется статистическое определение локальных контрастов, благодаря чему учитываются такие характеристики текстуры как однородность, шершавость и зернистость. Поэтому данный метод рекомендуется применять для обработки изображений, которые содержат мелкие детали.
%Программа, реализующая метод контрастирования изображений
%с использованием статистического определения локальных контрастов
clear;
%Считывание исходного изображения
L=imread('lena.tif');
L=double(L);
L=L(:,:,1)./255; %Поскольку изображение полутоновое, то L(:,:,1)=L(:,:,2)=L(:,:,3)
[N M]=size(L);
m=5;n=m;n1=fix(n/2);m1=fix(m/2); %Размеры локальной области
Lmax=max(L(:));Lmin=min(L(:));
H=imhist(L,256);
figure, imshow(L);
%Преобразование матрицы значений яркостей исходного изображения
%с целью избежания краевого эффекта
a=L(1,1);b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1;for j=1:m1;
L1(i,j)=a; L3(i,j)=b; L6(i,j)=c; L8(i,j)=d;
end;end;
L2=L(1,1:M); L02=L2;
for i=1:n1-1;
L2=[L2;L02];
end;
L7=L(N,1:M); L07=L7;
for i=1:n1-1;
L7=[L7;L07];
end;
L4=L(1:N,1); L4=L4'; L04=L4;
for i=1:m1-1;
L4=[L4;L04];
end;
L4=L4'; L5=L(1:N,M); L5=L5'; L05=L5;
for i=1:m1-1;
L5=[L5;L05];
end;
L5=L5'; L1=[L1;L4]; L1=[L1;L6]; L1=L1'; L2=[L2;L];
L2=[L2;L7]; L2=L2'; L3=[L3;L5]; L3=[L3;L8]; L3=L3';
L1=[L1;L2]; L1=[L1;L3]; L1=L1';
clear L2;clear L3;clear L4;clear L5;clear L6;
clear L7;clear L8;clear L02; clear L04;clear L05;clear L07;clear L;
F=ones(n,m);
Lser=filter2(F,L1,'same')/(n*m);
alfa=1;
P=3; %Параметр нормирования
for i=n1+1:n1+N;
disp(i);
for j=m1+1:m1+M;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=(Lser(i+a,j+b)-L1(i+a,j+b))^2*H(round(255*L1(i,j))+1);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
D(n1+1+a,m+1)=(Lser(i+a,j+m1)-L1(i+a,j+m1))^2*H(round(255*L1(i,j))+1);
end;
D=D(1:n,2:m+1);
end;
Dyspers(i,j)=(1/(n*m))*sum(sum(D));
C(i,j)=1-1/(Dyspers(i,j)/P+1);
C(i,j)=C(i,j)^.67;
suma(i,j)=sum(sum(D))-D(n1+1,m1+1);
DRD(i,j)=sqrt(n*m*C(i,j)/(1-C(i,j)+eps)-suma(i,j));
if L1(i,j)>=Lser(i,j);
Lvyh(i,j)=Lser(i,j)+alfa*DRD(i,j);
else
Lvyh(i,j)=Lser(i,j)-alfa*DRD(i,j);
end;
if Lvyh(i,j)>1;
Lvyh(i,j)=1;
end;
if Lvyh(i,j)<0;
Lvyh(i,j)=0;
end;
end;
end;
Lvyh=Lvyh(1+n1:n1+N,1+m1:m1+M);
figure, imshow(abs(Lvyh)); %Визуализация результата
|
а) исходное изображение |
|
|
б) изображение а), обработанное методом контрастирования с использованием известного выражения определения локального контраста |
|
|
в) изображение а), обработанное методом контрастирования с использованием предложенного выражения для статистического определения локального контраста |
|
Рис. 1. Обработка изображений методом степенного преобразования локальных контрастов с использованием известного ( б) ) и статистического ( в) ) выражений их определения (![]() - количественная оценка качества изображений).
- количественная оценка качества изображений).
Локально-адаптивное улучшение качества изображений
Качество изображения на локальных участках можно улучшать, используя такие параметры интенсивностей пикселей как среднее значение интенсивности и изменение интенсивности (или стандартное среднеквадратическое отклонение интенсивностей элементов локальной окрестности изображения). Среднее значение - это мера средней яркости. Вычисляя и анализируя среднюю яркость элементов изображения существует возможность ее коррекции, т.е. затемненные участки изображения делать более светлыми, а слишком светлые участки изображения затемнять. Однако, в случае, если на изображении присутствуют темные и светлые области, то такой подход только ухудшит его визуальное восприятие. Поэтому целесообразно использовать еще один параметр, который бы характеризовал распределение яркостей элементов изображения в некоторой локальной окрестности. Другими словами этот параметр характеризовал бы изменения интенсивностей или меру контрастности изображения.
Типичное локальное преобразование, основанное на этих параметрах, переводит интенсивность исходного изображения Lin в интенсивность нового изображения Lout путем осуществления следующей операции над расположением (i,j) каждого пикселя:
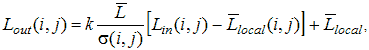
где
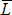 - среднее значение интенсивностей элементов всего изображения Lin;
- среднее значение интенсивностей элементов всего изображения Lin;
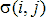 - среднеквадратическое отклонение интенсивностей элементов локальной окрестности изображения в точке с координатами (i,j);
- среднеквадратическое отклонение интенсивностей элементов локальной окрестности изображения в точке с координатами (i,j);
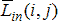 - среднее значение интенсивности для окрестности с центром в точке (i,j);
- среднее значение интенсивности для окрестности с центром в точке (i,j);
k - некоторая константа, 0 < k < 1.
Следует отметить, что значения параметров 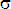 и и |
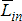 |
зависят от заданной окрестности точки | 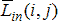 |
, что делает |
этот метод адаптивным. Локальные изменения увеличиваются за счет умножения разности между значением
| интенсивности пикселя исходного изображения Lin(i,j) и локальным средним | 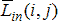 |
на |
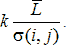 .
.
Среднеквадратическое отклонение будет принимать меньшие значения в малоконтрастных окрестностях и более
| высокие значения в окрестностях с более высокой контрастностью. Учитывая это, а также то, что | 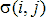 |
находится |
в знаменателе, участки с низкой контрастностью будут иметь большее усиление, чем участки с большей контрастностью. Среднее значение подставляется для восстановления среднего уровня интенсивности изображения на локальном участке. На практике целесообразно ограничивать диапазон значений множителя
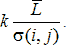
во избежание больших отклонений интенсивностей на отдельных участках.
% Метод повышения визуального качества изображений.
clear;
L=imread('krepost.bmp'); % считывание исходных данных изображения
L=L(:,:,:);
L=double(L)./(256);
figure, imshow(L); title('Input image');
[N M s]=size(L); %визуализация исходных данных
m=15; % размер локального окна
n=m;n1=fix(n/2); m1=fix(m/2);
Ltemp=L;
for r=1:s;
L=Ltemp(:,:,r);
% Предварительна обработка матрицы исходного изображения
% для устранения краевого эффекта
a=L(1,1);b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1; for j=1:m1;
L1(i,j)=a; L3(i,j)=b; L6(i,j)=c; L8(i,j)=d;
end;end;
L2=L(1,1:M); L02=L2;
for i=1:n1-1; L2=[L2;L02]; end;
L7=L(N,1:M); L07=L7;
for i=1:n1-1; L7=[L7;L07]; end;
L4=L(1:N,1); L4=L4'; L04=L4;
for i=1:m1-1; L4=[L4;L04]; end;
L4=L4'; L5=L(1:N,M); L5=L5'; L05=L5;
for i=1:m1-1; L5=[L5;L05]; end;
L5=L5'; L1=[L1;L4]; L1=[L1;L6]; L1=L1'; L2=[L2;L]; L2=[L2;L7]; L2=L2';
L3=[L3;L5]; L3=[L3;L8]; L3=L3'; L1=[L1;L2]; L1=[L1;L3]; Lr=L1';
clear L2;clear L3;clear L4;clear L5;clear L6;clear L7;clear L8;
clear L02;clear L04;clear L05;clear L07;clear L1;clear L;
Lser=mean(mean(Lr));
k=.4;
for i=1+n1:N+n1;
disp(i)
for j=1+m1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=Lr(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
D(n1+1+a,m+1)=Lr(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
LS=mean(mean(D));
sigma=std2(D)+eps;
Lvyh(i,j)=(k*Lser/sigma)*(Lr(i,j)-LS)+LS;
end;
end;
Lvyh(Lvyh>1)=1;
Lvyh(Lvyh<0)=0;
Lvyh=Lvyh(n1+1:N+n1,m1+1:M+m1);
Ltemp(:,:,s)=Lvyh;
end;
figure, imshow(Ltemp);
Результаты компьютерного моделирования рассмотренного метода представлены на рис. 1-4.

Рис. 1. Исходное изображение.

Рис. 2. Обработанное изображение при m=35 и k=0.7.

Рис. 3. Обработанное изображение при m=35 и k=0.3.

Рис. 4. Обработанное изображение при m=15 и k=0.7.
Проанализируем результаты моделирования. В методе есть два основных параметра, которые существенно влияют на результат обработки - размер локальной окрестности m и коэффициент k. Рассмотрим два изображения, которые представлены соответственно на рис. 2 и рис. 4, которые представляют результат обработки при одинаковом коэффициенте k, но разных размерах локальных окон m. Из этих изображений видно, что уменьшение размера локального окна приводит к увеличению детальности обработки. Для анализа влияния коэффициента k при одинаковых размерах локальной окрестности m рассмотрим два других изображения, которые представлены на рис. 2 и рис. 3. Уменьшение коэффициента k приводит к устранению резких перепадов на изображении и понижению его контрастности. Таким образом, используя различные значения параметров m и k, можно управлять уровнем контрастности и детальности обработки изображений.
Литература:
- Прэтт У. Цифровая обработка изображений - М.: Мир, 1982. - 790 с.
Фильтрация изображений: алгоритмы сглаживания изображений
Понятие сглаживания изображений имеет двоякий смысл. При коррекции искажений сигнала, внесенных изображающей системой, сглаживание – это подавление помех, связанных с несовершенством изображающей системы: аддитивных, флуктуационных, импульсных и др. При препарировании изображений сглаживание – это устранение деталей (обычно малоразмерных), мешающих восприятию нужных объектов на изображениях (так называемая генерализация изображения).
При коррекции искажений, вызванных изображающей системой, сглаживанию подвергается изображение на выходе изображающей системы. При препарировании сглаживание может применяться к изображению на любой стадии препарирования как один из его этапов.
Понятие сглаживания всегда подразумевает некоторое представление об "идеально гладком" сигнале. Такой сигнал – цель сглаживания.
Для изображений таким "идеально гладким" можно считать сигнал, описываемый кусочно-постоянной моделью, т. е. "лоскутное" изображение с пятнами–деталями, имеющими постоянное значение сигнала в пределах каждого пятна. Действительно, представление изображения в виде кусочно-постоянной модели есть не что иное, как сегментация изображений, являющаяся конечной целью анализа изображений для построения их описания. На первый взгляд может показаться, что оно применимо только к "детальным" изображениям. Но это справедливо и для "текстурных" изображений, только в этом случае оно относится не к первичному видеосигналу, а к его признаку, характеризующему текстуру.
Понятие сглаживания подразумевает также представление о том, что должно быть подавлено при сглаживании. Будем называть подавляемую часть сигнала шумом. Рассмотрим ранговые алгоритмы сглаживания для двух наиболее характерных моделей шума – аддитивной и импульсной.
Сглаживание для аддитивной модели
Аддитивная модель шума предполагает, что наблюдаемый сигнал представляет собой сумму полезного сигнала и шума. Ранговые алгоритмы сглаживания аддитивного шума проще всего обосновывать с позиций кусочно-постоянной модели изображения. При таком подходе, сглаживание можно определить как оценку параметра кластера, к которому принадлежит данный элемент. Для того чтобы найти эту оценку, необходимо определить границы кластера. Можно предложить два способа определения границ кластера: адаптивное квантование мод [1, 2] и "выращивание" кластера.
Адаптивное квантование мод заключается в том, что анализируется гистограмма распределения значений сигнала изображения (это может быть сигнал значений яркости изображения, плотности фотонегатива или значений того или иного скалярного признака, измеренного на изображении) и в ней отыскиваются границы между локальными максимумами. Эти границы рассматриваются как границы интервалов квантования, и все значения сигнала на изображении, попавшие в тот или иной интервал, заменяются значением, равным положению максимума (моды) гистограммы в этом интервале (рис. 1).
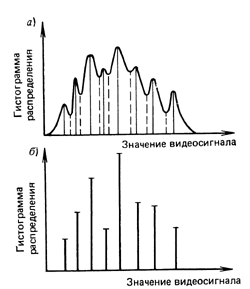
Рис. 1. Адаптивное квантирование мод: а – исходная гистограмма распределения значений видеосигнала; б – гистограмма после адаптивного квантирования.
Качество адаптивного квантования мод зависит от того, насколько хорошо разделяются моды гистограммы. Степень "размытия" мод определяется степенью однородности объектов на изображении по выбранному для анализа признаку, т. е. степенью соответствия изображения кусочно-постоянной модели, а также наличием искажений изображения: шумом датчика видеосигнала, дефокусировкой и т.п.
Для улучшения разделимости мод и повышения достоверности адаптивного квантования его целесообразно производить по отдельным фрагментам, размер которых выбирается так, чтобы они содержали небольшое число деталей изображения (т.е. чтобы в гистограмме было небольшое число мод). Кроме того, хорошие результаты дает использование условной гистограммы распределения, которая строится по значениям видеосигнала только в тех элементах изображения, где эти значения незначительно отличаются от значений в соседних элементах [3]. Степень допустимого отличия может задаваться априори или определяться автоматически в зависимости от локальной дисперсии видеосигнала на изображении.
При адаптивном квантовании мод может оказаться, что выделяются моды, площадь которых, т.е. количество элементов изображения, ей принадлежащих, относительно невелико. На изображении такие моды проявляются обычно в виде разбросанных точек, которые разбивают границы деталей изображения, образующих более мощные моды. Поэтому адаптивное квантирование мод целесообразно сочетать с отбраковкой выделяемых мод по их мощности. Если площадь моды в гистограмме (ее мощность) меньше заданной пороговой величины, эта мода объединяется с соседней более мощной.
При адаптивном квантировании мод определяются границы всех кластеров гистограммы изображения или его фрагментов. При скользящей обработке, когда нужно принять решение о принадлежности к тому или иному кластеру только одного, центрального элемента анализируемого фрагмента, определять границы всех кластеров гистограммы – слишком трудоемкая задача. В этих случаях применяют другие, более простые методы, например, метод "выращивания" кластера.
Сглаживание для модели импульсных помех
Модель импульсных помех предполагает, что с некоторой вероятностью элемент сигнала заменяется случайной величиной. Сглаживание импульсного шума, очевидно, требует обнаружения искаженных элементов сигнала и последующего оценивания их значений по значениям неискаженных элементов. Вообще говоря, алгоритмы сглаживания импульсных помех должны быть двухпроходовыми с разметкой искаженных элементов на первом проходе и оценкой их сглаженных значений на втором проходе. Но для упрощения можно сделать алгоритм однопроходовым, совмещая операции обнаружения и оценивания в одном проходе.
Разметка элементов изображения на искаженные шумом и не искаженные (обнаружение выбросов шума) может быть выполнена на основании проверки гипотезы о принадлежности центрального элемента некоторой локальной окрестности 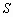 той же выборке, что и заданное большинство остальных элементов окрестности, или выпадения ее из этой выборки. Это достаточно типичная задача математической статистики, для решения которой обычно рекомендуются алгоритмы, основанные на ранговых статистиках [3].
той же выборке, что и заданное большинство остальных элементов окрестности, или выпадения ее из этой выборки. Это достаточно типичная задача математической статистики, для решения которой обычно рекомендуются алгоритмы, основанные на ранговых статистиках [3].
Наиболее простым ранговым способом проверки гипотезы о принадлежности центрального элемента 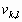 заданной локальной окрестности
заданной локальной окрестности 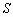 к выборке из большинства остальных элементов окрестности является голосование, т.е. проверка попадания ранга
к выборке из большинства остальных элементов окрестности является голосование, т.е. проверка попадания ранга 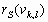 в
в 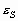 –окрестность медианы, задаваемой в зависимости от вероятности появления импульсных помех на элемент изображения.
–окрестность медианы, задаваемой в зависимости от вероятности появления импульсных помех на элемент изображения.
Если
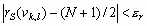 ,
,
то принимается решение об отсутствии помехи, в противном случае элемент (k, l) помечается как искаженный помехой. Такой способ обнаружения помехи предполагает, что импульсная помеха, как правило, принимает экстремальные значения. Отметим, что ранг как критерий проверки гипотезы о принадлежности элемента к данной выборке является частным случаем критерия Вилкоксона, проверяющего наличие сдвига между двумя выборками с одинаковым законом распределения.
Проверку гипотезы о наличии или отсутствии выброса помехи в центральном элементе S–окрестности можно производить также путем сравнения не по его рангу, а по его значению.
Порог 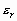 может быть выбран сразу для всего изображения, но его можно и адаптивно подстраивать в зависимости от локального разброса значений сигнала. В качестве оценки локального разброса можно использовать, например, квазиразмах по
может быть выбран сразу для всего изображения, но его можно и адаптивно подстраивать в зависимости от локального разброса значений сигнала. В качестве оценки локального разброса можно использовать, например, квазиразмах по 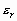 –окрестности:
–окрестности:
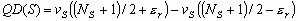 ,
,
являющийся, как известно, устойчивой к распределению оценкой разброса значений в выборке.
После этапа обнаружения элементы изображения, отмеченные как выбросы импульсного шума, должны быть заменены их оценкой. В качестве оценки можно использовать значения, полученные тем или иным сглаживанием по окрестности этих элементов, причем из этой окрестности исключаются элементы, отмеченные при обнаружении выбросов шума.
Таким образом, алгоритм сглаживания импульсного шума может быть представлен в виде:
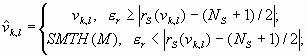
где SMTH(M) означает сглаживание по некоторой окрестности М, из которой исключены точки, подлежащие исправлению.
Характерными при сглаживании импульсных помех являются ошибки ложного обнаружения, которые приводят к нежелательному сглаживанию деталей изображения, и ошибки пропуска, из–за которых на изображении могут остаться несглаженные выбросы помех. Доля этих ошибок зависит от порогов: с увеличением порогов доля ложных обнаружений падает, а доля пропусков возрастает. Следует учитывать, что число ложных обнаружений и пропусков возрастает также из–за возможного наличия в S–окрестности не одного, а нескольких больших выбросов помех. Поэтому для повышения качества сглаживания импульсных помех его целесообразно проводить итеративно, начиная с больших значений порогов, и, по мере удаления больших выбросов помех, понижая пороги на каждой итерации.
Увеличение детальности изображений
Увеличение детальности изображений – понятие, противоположное сглаживанию. Если при сглаживании стираются различия деталей изображения, то при увеличении детальности они должны, наоборот, усиливаться. Поэтому увеличение детальности изображений называют также повышением локальных контрастов. Это, по существу, основная операция при препарировании изображений.
Повышение локальных контрастов достигается путем измерения отличий значения сигнала в каждом элементе изображения от его значений в элементах, окружающих данный, и усиления этих отличий.
Наиболее известный и очевидный метод определения и усиления отличий – так называемая нерезкая маска. При этом вычисляется разность между значениями элементов изображения и усредненными значениями по окрестности этих элементов, эта разность усиливается и добавляется к усредненному изображению:
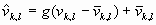 ,
,
где 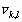 — сумма элементов локальной окрестности, взятых с некоторыми весами; g – коэффициент усиления.
— сумма элементов локальной окрестности, взятых с некоторыми весами; g – коэффициент усиления.
Отметим, что из этой формулы вытекает возможность обобщения метода нерезкой маски на использование ранговых алгоритмов. Она заключается в том, чтобы вместо взвешенного среднего по локальной окрестности (величины 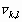 ) использовать сглаженное значение SMTH(M) сигнала, полученное с помощью ранговых алгоритмов сглаживания:
) использовать сглаженное значение SMTH(M) сигнала, полученное с помощью ранговых алгоритмов сглаживания:
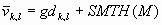 ,
,
где 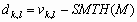 .
.
Преимущества нерезкого маскирования с ранговым сглаживанием вместо линейного – адаптивность и меньшая пространственная инерционность – вытекают из преимуществ рангового сглаживания.
Обнаружение деталей и их границ
Связь алгоритмов повышения локальных контрастов и выделения деталей со статистиками ранговых критериев, а также очевидная их аналогия с алгоритмами обнаружения выбросов импульсных помех, проливает новый свет на смысл этих алгоритмов. Эти алгоритмы можно трактовать как алгоритмы проверки гипотезы о несоответствии центрального элемента S–окрестности выборке, определяемой некоторым подмножеством, а вычисляемую ими оценку сигнала как критерий верности этой гипотезы, распределение значений которого по площади обрабатываемого изображения представляется пользователю как изображение–препарат.
Такая трактовка ведет к обобщению алгоритмов выделения деталей для задачи обнаружения деталей и их границ. В описанных алгоритмах использовались простейшие точечные критерии несоответствия элемента изображения заданной выборке: в разностных алгоритмах – разность между значением центрального элемента S–окрестности и оценкой среднего значения заданной выборки; в ранговых алгоритмах – количество элементов заданной выборки, не превышающих по своему значению значение центрального элемента, т.е. ранг центрального элемента в заданной выборке. Степень несоответствия трактовалась как контраст детали.
Для рангового обнаружения деталей изображения и их границ нужно измерять степень статистического несоответствия распределения значений элементов анализируемой окрестности заданному распределению значений сигнала в пределах деталей. При этом размер окрестности выбирают порядка размеров деталей, которые необходимо обнаруживать, или соответственно порядка размеров окрестности границ деталей. Для измерения степени несоответствия можно использовать известные в математической статистике критерии согласия.
Само по себе обнаружение состоит в сравнении измеренной степени соответствия с порогом. При препарировании изображений имеет смысл также предъявлять для визуализации саму величину соответствия, а не только бинарный результат сравнения с порогом. При этом обнаружение осуществляется оператором визуально [2].
Ранговые алгоритмы обнаружения, основанные на сравнении гистограмм значений сигнала, нечувствительны к пространственному "перепутыванию" элементов изображения. Но пространственное "перепутывание" не входит, как правило, в число возможных искажений изображений в оптических и аналогичных изображающих системах, и поэтому опасность спутать при обнаружении деталь с последовательностью независимых отсчетов, имеющих то же распределение значений, что и распределение значений отсчетов сигнала на детали, маловероятна. В то же время ранговые алгоритмы устойчивы к таким распространенным искажениям сигнала, как монотонные изменения их значений при амплитудных искажениях, засорение распределений, изменения ориентации.
Применения ранговых алгоритмов
Кроме применений для сглаживания, усиления детальности, выделения деталей изображений и границ деталей, ранговые алгоритмы могут употребляться также для решения многих других более частных задач обработки изображений. Из них можно упомянуть диагностику искажений видеосигнала и определение их статистических характеристик, стандартизацию изображений, определение статистических характеристик самого видеосигнала и измерение текстурных признаков.
Автоматическая диагностика параметров помех и искажений видеосигнала.
Она может основываться на принципе обнаружения и измерения аномалий в статистических характеристиках видеосигнала. Для обнаружения аномалий можно использовать ранговые алгоритмы, такие как алгоритм голосования проверки принадлежности анализируемого элемента выборки к заданному числу крайних (наибольших или наименьших) значений упорядоченной выборки.
Стандартизация изображений.
Стандартизация – это приведение характеристик изображений к некоторым заданным. С помощью ранговых алгоритмов может быть достаточно просто осуществлена стандартизация гистограмм, т. е. преобразование видеосигнала, делающее гистограмму распределения его значений заданной. В зависимости от задачи могут использоваться глобальная и локальная стандартизация гистограмм. В качестве •стандартной может использоваться не вся гистограмма стандартного изображения или его локальные гистограммы, а соответствующие гистограммы по локальным окрестностям.
Определение статистических характеристик видеосигнала и измерение текстурных признаков.
Адаптивные свойства ранговых алгоритмов делают их удобным инструментом для измерения локальных статистических характеристик изображений: локального среднего, локальной дисперсии и других моментов распределения. Очевидно, что эти и другие подобные характеристики гистограмм являются также текстурными характеристиками изображений.
Ранговые алгоритмы могут служить для оценки не только гистограммных текстурных признаков, но и для оценки текстурных признаков, связанных с локальными пространственными статистическими характеристиками изображений. Одним из простейших признаков такого рода является число локальных экстремумов S–окрестности обрабатываемого элемента. Ряд текстурных признаков связан с характеристиками пространственного распределения локальных экстремумов, т.е. среднего расстояния между ними, дисперсии расстояний между ними и т.д. Более общими являются признаки, характеризующие пространственное распределение рангов в обрабатываемом фрагменте. В частности, текстурным признаком является число перемен знака первой производной по фрагменту эквализованного изображения в заданном направлении сканирования. Ряд текстурных признаков можно рассматривать как параметры пространственного распределения элементов, принадлежащих локальным окрестностям, в частности, моменты распределения взаимных расстояний между ними.
Кодирование изображений.
Возможность применения ранговых алгоритмов для кодирования изображений связана с использованием алгоритмов адаптивного квантования мод в режиме пофрагментной обработки. В этом случае анализируется гистограмма распределения значений элементов изображения в пределах фрагмента (или, как принято говорить в кодировании, блока), находятся границы кластеров, которые выбираются в качестве границ интервалов квантования, и производится квантование всех отсчетов фрагмента в соответствии с найденными границами. Как правило, если размеры фрагмента не слишком велики, количество уровней квантования Qs отсчетов фрагмента намного меньше количества Q уровней квантования, выбираемого из условия качественного воспроизведения всего изображения. Нетрудно подсчитать, что количество бит, требуемых для передачи значений NB отсчетов фрагмента, будет равно сумме Qs log2Q бит на передачу таблицы квантования и Nslog2Qs бит на передачу номера уровня квантования, т.е. на один отсчет изображения требуется в среднем Iog2Qs+(Qslog2Q)/Ns бит вместо log2Q безадаптивного квантования по фрагментам. Отсюда вытекает, что площадь фрагментов целесообразно увеличивать до тех пор, пока количество уровней квантования Qs не превысит нескольких единиц. Опыты, проведенные по пофрагментному квантованию мод, показывают, что это возможно при размерах фрагмента до 30х30 элементов. Следовательно, оценкой потенциальных возможностей кодирования изображений этим методом является величина порядка 1–2 бит на элемент.
- Rosenfeld A., Troy E.B. Visual Texture Analysis // Conference Record of the Symposium on Feature Extraction and Selection in Pattern Recognition. – IEEE Publ. – 1970. – 70C51 – C.
- Ярославский Л.П. Цифровая обработка сигналов в оптике и голографии: Введение в цифровую оптику – М.: Радио и связь. – 1987. – 296 с.: ил.
- Беликова Т.П., Ярославский Л.П. Использование адаптивных амплитудных преобразований для препарирования изображений // Вопросы радиоэлектроники. Сер. Общетехн. – 1974. – Вып. 14.
Двумерное сглаживание изображений
Довольно часто развитие вычислительной техники и информационных технологий приводит к необходимости модификации известных алгоритмов обработки изображений. Рассмотрим один из таких методов - двумерное сглаживание изображений.
Сглаживание изображений - ослабление искажений, вызванных действием шумов системы воспроизведения изображений (фотографической, телевизионной и т. п.), представляет собой практически важную задачу.
Возможность сглаживания обусловлена различием свойств изображения и шума [1]. При статистическом подходе к сглаживанию эффективность получаемого алгоритма зависит от полноты используемого статистического описания изображения и шума. Обычно шумы отличаются простой статистической структурой, и их свойства либо известны, либо могут быть получены в результате несложных измерений. Для изображений же измерение достаточно полных статистических характеристик является сложной задачей, которую можно облегчить, используя конструктивную модель изображения.
В задаче сглаживания одномерных сигналов часто используют гауссовскую модель сигналов, которая приводит к винеровскому [2] алгоритму линейного сглаживания, обеспечивающему минимальное среднеквадратическое отклонение (СКО) сглаженного сигнала от исходного. Такое сглаживание осуществляется фильтром с частотной характеристикой
| (1) |
где ![]() ,
, ![]() - винеровские (энергетические) спектры сигнала и шума,
- винеровские (энергетические) спектры сигнала и шума, ![]() - частота. Теория винеровского сглаживания может быть легко обобщена на случай
- частота. Теория винеровского сглаживания может быть легко обобщена на случай ![]() -мерных сигналов, причем оптимальная частотная характеристика сглаживающего фильтра будет по-прежнему описываться выражением (1), в котором
-мерных сигналов, причем оптимальная частотная характеристика сглаживающего фильтра будет по-прежнему описываться выражением (1), в котором ![]() есть теперь
есть теперь ![]() -мерная частота.
-мерная частота.
Применение винеровского линейного сглаживания к изображению не всегда приводит к улучшению его качества, оцениваемого визуально. Это объясняется тем, что шум, как правило, имеет интенсивные составляющие мощности, вплоть до самых высоких пространственных частот, тогда как мощность изображений в основном сосредоточена на низких пространственных частотах, и величина ![]() быстро падает на высоких частотах. Поэтому в силу (1) сглаживающий фильтр подавит высокочастотные составляющие изображения, несущие важную информацию о краях и мелких деталях изображенных объектов. Сглаженное изображение станет нерезким.
быстро падает на высоких частотах. Поэтому в силу (1) сглаживающий фильтр подавит высокочастотные составляющие изображения, несущие важную информацию о краях и мелких деталях изображенных объектов. Сглаженное изображение станет нерезким.
Как указал Д. Габор [3], спектральное описание статистических свойств изображения оказывается недостаточным, так как оно не отражает его локально-анизотропную (но изотропную в целом) структуру.
Для описания такой структуры в статье предлагается "составная" модель фрагмента изображения. Эта модель используется для синтеза алгоритма сглаживания, дающего оценку элементов изображения с минимальным СКО.
"Составная" модель фрагмента изображения. Одноцветное неподвижное изображение может быть описано как распределение яркости ![]() , где
, где ![]() - пара чисел - координаты точек плоскости изображения. Будем рассматривать далее только дискретизированные изображения с целочисленными координатами.
- пара чисел - координаты точек плоскости изображения. Будем рассматривать далее только дискретизированные изображения с целочисленными координатами.
Ансамбль изображений представляет собой случайное поле. Вероятностное описание такого поля дается величиной ![]() -
- ![]() -мерной совместной плотностью вероятности фрагмента изображения
-мерной совместной плотностью вероятности фрагмента изображения ![]() , состоящего из
, состоящего из ![]() элементов.
элементов.
Допустим, что имеется ![]() классов фрагментов, которые отличаются характером корреляционных связей между элементами определяющими его структуру.
классов фрагментов, которые отличаются характером корреляционных связей между элементами определяющими его структуру.
Одни классы образованы фрагментами с изотропной структурой (без преобладания связей в каком-либо направлении на плоскости изображения), другие - фрагментами с той или иной анизотропией. Пусть - ![]() -
-![]() -мерная плотность вероятности фрагмента
-мерная плотность вероятности фрагмента ![]() при условии, что фрагмент принадлежит классу
при условии, что фрагмент принадлежит классу ![]() (
(![]() , а
, а ![]() - распределение вероятностей классов
- распределение вероятностей классов ![]() . Тогда
. Тогда
| (2) |
Выражение (2) есть разложение плотности ![]() по системе плотностей
по системе плотностей ![]()
![]() 1,…,M .Такое представление особенно полезно, когда
1,…,M .Такое представление особенно полезно, когда ![]() хорошо аппроксимируется с помощью небольшого набора гауссовских распределений:
хорошо аппроксимируется с помощью небольшого набора гауссовских распределений:
| (3) |
где ![]() - матрица, обратная ковариационной матрице
- матрица, обратная ковариационной матрице ![]() , соответствующей классу
, соответствующей классу ![]() , штрих обозначает транспонирование.
, штрих обозначает транспонирование.
Результаты статистических измерений фрагментов реальных изображений показывают, что хорошее описание их может быть получено с помощью модели, имеющей всего пять классов. Четыре из них соответствуют преобладающим корреляционным связям в одном из четырех направлений, составляющих углы 0°, 45°, 90° и 135° с горизонталью (выбор направлений обусловлен наличием квадратной решетки, на которой задано изображение). Пятый класс описывает фрагменты с "изотропной" структурой. Для нескольких изображений были измерены матрицы ![]() и распределение вероятностей
и распределение вероятностей ![]() ,
, ![]()
Алгоритм сглаживания. Пусть наблюдается изображение с аддитивно наложенным на него независимым от изображения шумом с известной плотностью вероятности. Требуется найти оптимальную (в смысле минимума СКО) оценку ![]() элемента изображения
элемента изображения ![]() по
по ![]() -элементному фрагменту наблюдаемого изображения
-элементному фрагменту наблюдаемого изображения ![]() , где
, где ![]() - заданные точки, лежащие в окрестности точки
- заданные точки, лежащие в окрестности точки ![]() .
.
Известно, что оптимальной оценкой элемента ![]() является апостериорное условное среднее значение
является апостериорное условное среднее значение
| (4) |
где
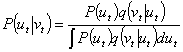 . . |
(5) |
В этих выражениях ![]() обозначает
обозначает ![]() ;
; ![]() и
и ![]() есть условная плотность наблюдаемого фрагмента
есть условная плотность наблюдаемого фрагмента ![]() при заданном фрагменте
при заданном фрагменте ![]() . Используя (2), перепишем (5) в следующем виде:
. Используя (2), перепишем (5) в следующем виде:
| (6) |
где
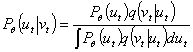 |
(7) |
и
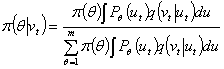 . . |
(8) |
Подставив (6) в (4), получим:
| (9) |
где
| (10) |
Величина ![]() есть условная оценка
есть условная оценка ![]() при заданном классе фрагмента. Оценка
при заданном классе фрагмента. Оценка ![]() есть взвешенная сумма условных оценок. Вес каждой условной оценки есть апостериорная вероятность (8) класса
есть взвешенная сумма условных оценок. Вес каждой условной оценки есть апостериорная вероятность (8) класса ![]() при данном фрагменте
при данном фрагменте ![]() .
.
Пусть шум имеет гауссовское распределение с известной ковариационной матрицей N. Тогда
| (11) |
Подставив (11) и (3) в (7), получим затем из (10) известную формулу Винера [2]
| (12) |
где ![]() - элемент матрицы
- элемент матрицы ![]() .
.
В этом случае апостериорная вероятность состояния (8) переходит в
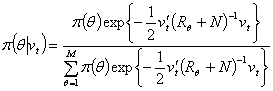 . . |
(13) |
Как показывает выражение (12), условная оценка ![]() может быть найдена с помощью линейного фильтра. При замене
может быть найдена с помощью линейного фильтра. При замене ![]()
![]() , т.е. при сдвиге наблюдаемого фрагмента на выходе фильтра, получим оценку
, т.е. при сдвиге наблюдаемого фрагмента на выходе фильтра, получим оценку ![]() .
.
Для реализации алгоритма (9) нужно построить ![]() линейных фильтров и
линейных фильтров и ![]() устройств для вычисления
устройств для вычисления ![]() . Выходит, что
. Выходит, что ![]() каждого фильтра надо умножить на соответствующую величину
каждого фильтра надо умножить на соответствующую величину ![]() и сложить все произведения.
и сложить все произведения.
Алгоритм (9) может быть интерпретирован следующим образом. Для каждого класса фрагментов применяется специфический режим сглаживания, осуществляемый соответствующим линейным фильтром. Если, например, при некотором ![]() матрица
матрица ![]() описывает только горизонтальные корреляционные связи, то оценка
описывает только горизонтальные корреляционные связи, то оценка ![]() должна получаться сглаживанием только в горизонтальном направлении.
должна получаться сглаживанием только в горизонтальном направлении.
Реализация алгоритма. На основе теоретического материала было проведено компьютерное моделирование предложенного в [1] алгоритма.
 |
|
| Рис. 1. | |
 |
 |
| Рис. 2. | Рис. 3. |
Для моделирования зашумленного изображения на оригинал накладывался белый гауссовский шум [4]. Наблюдаемый фрагмент содержал 5x5 элементов, причем оцениваемый элемент находился в центре фрагмента. Предполагалось, что имеется пять классов фрагментов, и использовались пять матриц ![]() , одна из которых соответствовала "изотропным" корреляционным связям и четыре были анизотропными. Эти матрицы соответствовали связям только вдоль одной из четырех прямых, проходящих через центр (вертикальной, горизонтальной и составляющей угол + 45° с горизонталью). Таким образом, имелось пять режимов сглаживания: по всему фрагменту из 25 элементов и по отрезкам прямых, содержащих по пять элементов. Пять оценок, получаемых в результате пяти процедур сглаживания, суммировались с весами, равными вычисленным апостериорным вероятностям. На рис. 1 показан оригинал с наложенным на него шумом, среднеквадратическая величина которого составляла 5% от диапазона яркостей изображения. На рис. 2 приведено изображение, полученное в результате сглаживания с зашумленного изображения в соответствии с алгоритмом (9). На рис. 3 показан результат винеровского сглаживания. Сравнение рис. 2 и 3 показывает, что описанный выше алгоритм (9) приводит к меньшей нерезкости изображения, чем алгоритм Винера, и, следовательно, использованная модель более адекватна структуре изображения, чем гауссовская.
, одна из которых соответствовала "изотропным" корреляционным связям и четыре были анизотропными. Эти матрицы соответствовали связям только вдоль одной из четырех прямых, проходящих через центр (вертикальной, горизонтальной и составляющей угол + 45° с горизонталью). Таким образом, имелось пять режимов сглаживания: по всему фрагменту из 25 элементов и по отрезкам прямых, содержащих по пять элементов. Пять оценок, получаемых в результате пяти процедур сглаживания, суммировались с весами, равными вычисленным апостериорным вероятностям. На рис. 1 показан оригинал с наложенным на него шумом, среднеквадратическая величина которого составляла 5% от диапазона яркостей изображения. На рис. 2 приведено изображение, полученное в результате сглаживания с зашумленного изображения в соответствии с алгоритмом (9). На рис. 3 показан результат винеровского сглаживания. Сравнение рис. 2 и 3 показывает, что описанный выше алгоритм (9) приводит к меньшей нерезкости изображения, чем алгоритм Винера, и, следовательно, использованная модель более адекватна структуре изображения, чем гауссовская.
Литература
- Лебедев Д.С., Миркин Л.И. Двумерное сглаживание с использованием "составной" модели фрагмента. Сб. "Иконика. Цифровая голография. Обработка изображений". М., "Наука", 1975.
- W. Wiener. The Interpolation, Extrapolation and Smoothing of Stationary Time Series. N.Y., 1949.
- D.Gabor. The Smoothing and Filtering of Two-Dimensional Images. - "Progress in Biocybernetics", v. 2. Amsterdam, 1965.
- D.Gabor. The Smoothing and Filtering of Two-Dimensional Images. - "Progress in Biocybernetics", v. 2. Amsterdam, 1965.
- R.E.Graham. Snow Removal - A noise -Stripping Process for picture Signals. - IRE Transaction on Information Theiry, 1962. V.IT - IT-8, № 2.
- Г. Г. Вайнштейн. Пространственная фильтрация изображений средствами аналоговой вычислительной техники.- В сб. "Иконика. Пространственная фильтрация изображений. Фотографические системы". М., "Наука", 1970.
Обобщенная линейная фильтрация
При проектировании фильтров или, в более общем случае, систем для обработки сигналов, линейные системы играют существенную роль. Когда производится проектирование линейной части системы обработки сигналов, в большинстве случаев можно обосновать принятые решения и вести проектирование с помощью формальных расчетных процедур. С другой стороны, при расчете нелинейной части чаще всего приходится руководствоваться интуицией и эмпирическими суждениями.
Понятие обобщенной суперпозиции дает возможность, по крайней мере в некоторых случаях, применить к классу задач нелинейной фильтрации формальный метод, который является расширением формального подхода, лежащего в основе линейной фильтрации [2].
Задача линейной фильтрации как это констатируется, связана с применением линейной системы для извлечения сигнала из суммы сигнала и шума. С точки зрения векторного пространства задачей линейной фильтрации можно считать определение такого линейного преобразования в векторном пространстве, которое сводит длину или норму вектора ошибки к минимуму. Норма для данного векторного пространства определяет используемый критерий ошибки. Во многих случаях, когда сигнал суммируется с шумом, линейная система не является лучшей системой. Рассмотрим, например, квантованный сигнал с уровнями квантования 1, 2, 3,..., и допустим, что к нему добавились шумы с пиковыми значениями ±0,25. Ясно, что сигнал может быть точно восстановлен с помощью квантизатора, хотя его нельзя формально обосновать как оптимальный нелинейный фильтр. В менее очевидных случаях могут существовать одновременно формальные обоснования как для "лучшего" линейного фильтра, так и для «лучшего» нелинейного фильтра из некоторого класса, но при этом не всегда может быть проведено полное и точное сравнение этих фильтров, хотя бы из-за того, что они часто используют различную информацию о входных сигналах.
Обобщение понятия линейной фильтрации может производиться при фильтрации сигнала и шума, которые комбинируются неаддитивно, лишь при условии, что правило их комбинирования удовлетворяет алгебраическим постулатам векторного сложения. Например, если нужно восстановить сигнал s(t) после такого воздействия шума n(t), что принятым сигналом является s(t)On(t), то необходимо связать s(t) и n(t) с векторами в векторном пространстве, а операцию О с векторным сложением. Тогда класс линейных преобразований в этом векторном пространстве окажется связанным с классом гомоморфных систем, для которых операция О является входной и выходной операцией. Таким образом, при обобщении проблемы линейной фильтрации получают задачу гомоморфной фильтрации. Здесь класс фильтров, из которого должен быть выбран оптимальный, будет классом таких гомоморфных систем, входные и выходные операции которых производятся по правилу, согласно которому объединены выделяемые сигналы.
Если x1 и х2 обозначают два сигнала, которые объединяются с помощью операции О, то каноническая форма для класса гомоморфных фильтров, которые можно было бы использовать для восстановления x1 или х2, имеет вид, приведенный на рис. 1.

Рис. 1. Каноническая форма класса гомоморфных фильтров, используемых для разделения сигналов, объединенных с помощью операции О.
Система 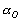 и обратная ей являются характеристическими для этого класса, и, следовательно, при выборе системы из класса необходимо определить только линейную систему
и обратная ей являются характеристическими для этого класса, и, следовательно, при выборе системы из класса необходимо определить только линейную систему 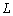 . Кроме того, мы видим что, поскольку система
. Кроме того, мы видим что, поскольку система 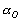 гомоморфна с входной операцией O и выходной операцией +, то входным сигналом линейной системы
гомоморфна с входной операцией O и выходной операцией +, то входным сигналом линейной системы 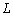 является
является 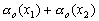 . Так как выходной сигнал линейного фильтра затем преобразуется с помощью обращения
. Так как выходной сигнал линейного фильтра затем преобразуется с помощью обращения 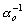 и так как сигнал
и так как сигнал 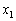 должен быть восстановлен из комбинации
должен быть восстановлен из комбинации 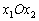 , то требуемым выходным сигналом линейной системы является
, то требуемым выходным сигналом линейной системы является 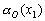 . Следовательно, задача сводится к линейной фильтрации, и может полностью применяться формальный аппарат.
. Следовательно, задача сводится к линейной фильтрации, и может полностью применяться формальный аппарат.
Следует подчеркнуть, что подход к нелинейной фильтрации, основанный на обобщенной суперпозиции, является лишь одним из многих возможных подходов. Основное его ценное качество состоит в том, что так же, как и при линейной фильтрации просуммированных сигналов, он удобен с точки зрения анализа и фактически сводится к проблеме линейной фильтрации. Хотя на практике при решении большинства задач линейной фильтрации для оптимального выбора фильтра обычно не выполняются формальные расчеты, критерием ошибки, получившим самое широкое распространение, является среднеквадратическая ошибка (или интегральная квадратическая ошибка для апериодических сигналов). При рассмотрении критерия ошибки для гомоморфных фильтров естественно было бы выбрать такой тип критерия, который позволяет выбирать линейный фильтр на основе среднеквадратической ошибки. Этот выбор может быть обоснован формально, но в любом случае естественно считать, что система оптимизируется, если оптимизируется линейный фильтр.
К двум типам задач, где оказалась полезной идея гомоморфной фильтрации, относятся фильтрация перемноженных сигналов и фильтрация свернутых сигналов.
Применение гомоморфной фильтрации
Рассмотрим некоторые специфические случаи применения гомоморфной фильтрации и фильтрации перемноженных и свернутых сигналов. Ограничимся рассмотрением только двух примеров применения, а именно сжатия динамического диапазона и усиления контрастности изображений.
Гомоморфная обработка изображений
Как показал Стокхэм [1], образование изображения является преимущественно мультипликативным процессом. В естественных условиях наблюдаемая яркость, запечатленная на сетчатке глаза или на фотографической пленке, может рассматриваться как произведение двух составляющих: функции освещенности и функции отражательной способности. Функция освещенности описывает освещенность спектра в различных точках, и ее можно считать независимой от предметов, расположенных на этой сцене. Функция отражательной способности характеризует детали сцены и может считаться независимой от освещенности. Таким образом, изображение может быть представлено как двумерный пространственный сигнал, выраженный в форме
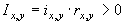 ,
,
где 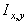 — изображение,
— изображение, 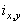 — составляющая освещенности, a
— составляющая освещенности, a 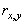 — составляющая отражательной способности. Отрицательные значения яркости по физическим причинам исключаются, а нулевая яркость исключается по практическим соображениям.
— составляющая отражательной способности. Отрицательные значения яркости по физическим причинам исключаются, а нулевая яркость исключается по практическим соображениям.
При обработке изображения часто возникают две задачи — сжатие динамического диапазона и усиление контрастности. Первая из их вызвана тем, что часто встречаются сцены с чрезмерными отношениями уровня светлого к уровню темного, что приводит к слишком большому динамическому диапазону по сравнению с возможностями имеющегося приемника, например фотографической пленки. Решение состоит в записи модифицированной интенсивности 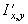 , связанной с
, связанной с 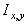 в следующем виде:
в следующем виде:
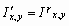 (1)
(1)
Параметр 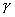 хорошо известен фотографам, которые выбором фотоматериалов и изменением времени проявления регулируют численное значение
хорошо известен фотографам, которые выбором фотоматериалов и изменением времени проявления регулируют численное значение 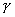 . Когда
. Когда 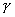 выбрано положительным, но меньшим единицы, происходит сжатие динамического диапазона.
выбрано положительным, но меньшим единицы, происходит сжатие динамического диапазона.
Другая задача состоит в такой обработке изображения, которая увеличивала бы контрастность, придавая большую четкость краям предметов. Это усиление контрастности часто достигается модификацией картины распределения пространственной яркости в соответствии с (1) при 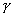 , выбранном больше единицы.
, выбранном больше единицы.
Ясно, что при таком специфическом подходе сжатие динамического диапазона и усиление контрастности являются противоречивыми задачами. Сжатие динамического диапазона, достигаемое при использовании 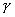 , меньшего единицы, вызывает уменьшение контрастности и может дать темное или размытое изображение. Усиление контрастности, достигнутое применением
, меньшего единицы, вызывает уменьшение контрастности и может дать темное или размытое изображение. Усиление контрастности, достигнутое применением 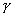 , большего единицы, увеличивает динамический диапазон изображения, причем в результате этого часто еще более затрудняется возможность передачи этого диапазона.
, большего единицы, увеличивает динамический диапазон изображения, причем в результате этого часто еще более затрудняется возможность передачи этого диапазона.
Для получения приемлемой аппроксимации сжатие динамического диапазона можно рассматривать как проблему, сосредоточенную на функции освещенности 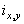 , а усиление контрастности — как проблему, сосредоточенную на функции отражательной способности
, а усиление контрастности — как проблему, сосредоточенную на функции отражательной способности 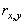 , т.е. считать, что большие динамические диапазоны, встречающиеся в естественных изображениях, обусловлены главным образом большим изменением освещенности, в то время как очертания краев предметов связаны только с составляющей отражательной способности. Таким образом, можно отдельно ввести функции отражательной способности и освещенности, модифицировать каждую из них различными показателями степени и затем восстановить их для того, чтобы сформировать модифицированное изображение. При таком подходе модифицированная яркость
, т.е. считать, что большие динамические диапазоны, встречающиеся в естественных изображениях, обусловлены главным образом большим изменением освещенности, в то время как очертания краев предметов связаны только с составляющей отражательной способности. Таким образом, можно отдельно ввести функции отражательной способности и освещенности, модифицировать каждую из них различными показателями степени и затем восстановить их для того, чтобы сформировать модифицированное изображение. При таком подходе модифицированная яркость 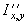
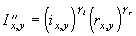 ,
,
где 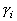 меньше единицы для сжатия динамического диапазона и
меньше единицы для сжатия динамического диапазона и 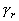 больше единицы для усиления контрастности.
больше единицы для усиления контрастности.
Имея перед собой эту задачу, можно говорить об обработке изображения с помощью гомоморфного фильтра, т.е. о раздельной обработке составляющих освещенности и отражательной способности. Такое устройство обработки изображения могло бы иметь вид, показанный на рис. 2. Функция освещенности обычно изменяется медленно, в то время как отражательная способность часто (но не всегда) изменяется быстро, так как предметы изменяют структуру и размеры и почти всегда имеют хорошо очерненные края. Если бы 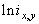 и
и 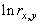 имели частотные составляющие, занимающие отдельные области пространственных частот, то их можно было бы обработать по отдельности в соответствии с рис. 2.
имели частотные составляющие, занимающие отдельные области пространственных частот, то их можно было бы обработать по отдельности в соответствии с рис. 2.
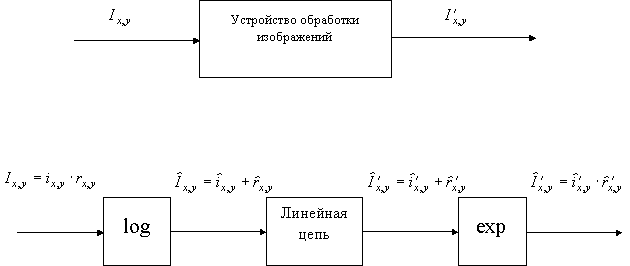
Рис. 2. Каноническая форма устройства обработки изображения, производящего раздельное изменение компонент освещенности и отражательной способности исходного изображения.
Целесообразно предположить, что 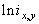 содержит главным образом низкие пространственные частоты. Быстрые изменения в
содержит главным образом низкие пространственные частоты. Быстрые изменения в 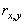 способствуют появлению высоких пространственных частот в
способствуют появлению высоких пространственных частот в 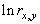 , хотя отражательная способность вносит некоторый вклад и в низкие пространственные частоты. Таким образом, возможна только частично независимая обработка. Тем не менее на практике оказалось полезным связать низкие пространственные частоты с
, хотя отражательная способность вносит некоторый вклад и в низкие пространственные частоты. Таким образом, возможна только частично независимая обработка. Тем не менее на практике оказалось полезным связать низкие пространственные частоты с 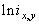 , а высокие пространственные частоты — с
, а высокие пространственные частоты — с 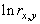 . При таком предположении линейный фильтр (рис. 3) выбирался так, чтобы он производил умножение низких пространственных частот на
. При таком предположении линейный фильтр (рис. 3) выбирался так, чтобы он производил умножение низких пространственных частот на 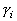 и высоких пространственных частот на
и высоких пространственных частот на 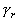 .
.
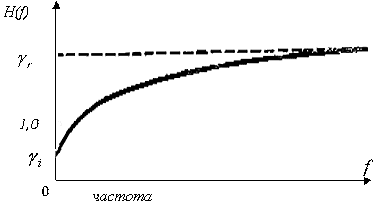
Рис. 3. Частотная характеристика линейного фильтра (рис. 2) для одновременного сжатия динамического диапазона и усиления контрастности.
При выполнении этой обработки частотная характеристика фильтра выбиралась так, чтобы она имела общий вид, как на рис. 3, и была изотропной с нулевой фазой. Линейная обработка проводилась с применением методов высокоскоростной свертки, выполняемых в двух измерениях. На рис. 4 приведены два примера изображений, обработанных таким образом для одновременного изменения динамического диапазона и усиления контрастности.
|
|
|
|
|
|
Рис. 4. Изображения а) и в) после обработки с целью одновременного изменения (растяжения или сжатия) динамического диапазона и усиления контрастности. Результаты обработки представлены на рис. 4 б) и г) соответственно.
- Blackman R.B., Tukey Y.W., "The Measurement of Power Spectra from the Point of View of Communication Engineering", Dover, 1959.
- Голд Б., Рэйдер Ч. Цифровая обработка сигналов. Пер. с англ., под ред. А.М.Трахтмана. М., "Сов. радио", 1973, 368 с.
Градиентный метод выделение контуров объектов на цветных изображениях
Если изображение представить двумерной функцией I = ƒ(x,y), то модуль градиента вычисляется за выражением
Одним из свойств градиента является то, что он всегда направлен в сторону возрастания функции в точке с координатами (x,y).
При практической реализации этого подхода производные аппроксимируются разностями значений пикселей. Представим некоторую локальную окрестность в виде
| z1 | z2 | z3 |
| z4 | z5 | z6 |
| z7 | z8 | z9 |
Тогда производная по представляется в виде
Тогда производная по представляется в виде
Для вычисления производных и по полю изображения используется встроенная функция imfilter. В качестве примера при вычислении производных использовались маски Собела, которые также могут быть формированы с помощью встроенной функции fspecial.
Пример. Представим реализацию рассмотренного выше подхода для выделения выделение контуров объектов. Считаем и визуализируем некоторое изображение.
I=imread('zhaba.bmp');
Выделим только одну цветовую компоненту, поскольку рассмотренный выше подход работает с полутоновыми изображениями, которые представлены одной цветовой плоскостью.
I=I(:,:,1);
I=double(I)./255;
figure,imshow(I);
Исходное изображение
Сформируем маску фильтра для выделения контуров объектов изображения.
f=fspecial('sobel')
f =
1 2 1
0 0 0
-1 -2 -1
Вычислим производную по направлению во всех точках изображения с помощью функции imfilter.
I_filtered_x=imfilter(I,f,'replicate');
figure,imshow(I_filtered_x);
Визуализация градиента по направлению без коррекции динамического диапазона
Полученное изображение I_filtered_x выходит за пределы динамического диапазона, поэтому его можно скорректировать.
I_filtered_x=I_filtered_x+min(min(I_filtered_x));
MN=min(min(I_filtered_x));
MX=max(max(I_filtered_x));
I_filtered_x=(I_filtered_x-MN)/(MX-MN);
figure,imshow(I_filtered_x);
Визуализация градиента по направлению y c коррекцией динамического диапазона
Полученное изображение I_filtered_y выходит за пределы динамического диапазона, поэтому его можно скорректировать.
MN=min(min(I_filtered_y));
MX=max(max(I_filtered_y));
I_filtered_y=(I_filtered_y-MN)/(MX-MN);
figure,imshow(I_filtered_y);
Визуализация градиента по направлению c коррекцией динамического диапазона
Далее сформируем градиент изображения на основе вычисленных градиентов по направлению x и y.
I_filtered=sqrt(I_filtered_x.^2+I_filtered_y.^2);
figure,imshow(I_filtered);
Градиент изображения без коррекции динамического диапазона
Полученное изображение I_filtered также выходит за пределы динамического диапазона, поэтому его можно скорректировать.
I_filtered=I_filtered+min(min(I_filtered));
MN=min(min(I_filtered));
MX=max(max(I_filtered));
I_filtered=(I_filtered-MN)/(MX-MN);
figure,imshow(I_filtered);
Градиент изображения с коррекцией динамического диапазона
Рассмотренный нами метод выделения контуров объектов может применяться для обработки полутоновых изображений.
Рассмотрим вопрос вычисления градиента изображений в цветовом пространстве RGB. Считаем и визуализируем исходное изображение.
L=imread('peppers.bmp');
L=double(L)./255;
figure,imshow(L);
Выполним фильтрацию по отдельным цветовым компонентам и сформируем из них результат в виде RGB изображения.
Итак, сначала выделим отдельные цветовые компоненты исходного изображения.
L_R=L(:,:,1); figure, imshow(L_R);
L_G=L(:,:,2);
figure, imshow(L_G);
L_B=L(:,:,3);
figure, imshow(L_B);
Градиент изображения без коррекции динамического диапазона
Полученное изображение I_filtered также выходит за пределы динамического диапазона, поэтому его можно скорректировать.
I_filtered=I_filtered+min(min(I_filtered));
MN=min(min(I_filtered));
MX=max(max(I_filtered));
I_filtered=(I_filtered-MN)/(MX-MN);
figure,imshow(I_filtered);
Градиент изображения с коррекцией динамического диапазона
Рассмотренный нами метод выделения контуров объектов может применяться для обработки полутоновых изображений.
Рассмотрим вопрос вычисления градиента изображений в цветовом пространстве RGB. Считаем и визуализируем исходное изображение
L=imread('peppers.bmp');
L=double(L)./255;
figure,imshow(L);
Выполним фильтрацию по отдельным цветовым компонентам и сформируем из них результат в виде RGB изображения. Итак, сначала выделим отдельные цветовые компоненты исходного изображения.
L_R=L(:,:,1);
figure, imshow(L_R);
L_G=L(:,:,2);
figure, imshow(L_G);
L_B=L(:,:,3);
figure, imshow(L_B);
Фильтрация по цветовой компоненте B изображения
L_B_filtered_x=imfilter(L_B,f,'replicate');%фильтрация по направлению х
L_B_filtered_y=imfilter(L_B,f','replicate');%фильтрация по направлению у
L_B_filtered=sqrt(L_B_filtered_x.^2+L_B_filtered_y.^2);
figure,imshow(L_B_filtered);%визуализация отфильтрированной цветовой
%компоненты изображения
Результат объединения отдельных отфильтрированных цветовых компонент в одно RGB-изображение представлен на изображении внизу.
Выше была рассмотрена задача обнаружения контуров путем вычисления градиентов отдельных цветовых составляющих. Теперь же решим эту задачу через нахождение градиента непосредственно в цветовом пространстве RGB. Для этого используется функция colorgrad.
[VG, A, PPG]=colorgrad(L, T);
где L – исходное RGB изображение; Т – порог; VG – модуль RGB градиента; A – матрица углов; PPG – градиент, который получен сложением двух одномерных градиентов по отдельным цветовым составляющим.
Из проведенных выше экспериментов можно сделать следующий вывод. Метод обработки отдельных цветовых компонент проводит только грубое выделение контуров. Для получения более детальной обработки нужно использовать векторный метод.
Сегментация RGB изображений
Задача сегментации состоит в том, что на изображении необходимо выделить объект, цвет которого лежит в определенном диапазоне. Один из подходов к решению данной задачи состоит в том, что сначала необходимо указать область, содержащую цвета этого диапазона, который будет использоваться при сегментации. Далее каждый пиксель изображения классифицируется на основе вычисления расстояния от данного пикселя к.заданному диапазону в пространстве RGB.
Рассмотрим решение этой задачи на конкретном примере.
Для этого считаем и визуализируем некоторое исходное изображение.
L=imread('peppers.bmp');
figure,imshow(L);
Для получения диапазона цветов, на основе которых будем выполняться сегментация, необходимо выделить область интереса.
mask=roipoly(L);
red=immultiply(mask,L(:,:,1));
green=immultiply(mask,L(:,:,2));
blue=immultiply(mask,L(:,:,3));
g=cat(3,red, green,blue);
figure,imshow(g);
Далее проводится анализ выделенной области на предмет получения среднеквадратических отклонений всех цветовых составляющих sd, которые будут использоваться для установки порога.
[M, N, K]=size(g);
I=reshape(g, M*N, 3);
idx=find(mask);
I=double(I(idx,1:3));
[C,m]=covmatrix(I);
d=diag(C);
sd=mean(sqrt(d));
После этого можно приступить к выполнению сегментации с помощью встроенной функции colorseg при разных порогах – sd,3*sd и при 5*sd.
E25=colorseg('euclidean',L,sd,m);
figure,imshow(E25);
E25=colorseg('euclidean',L,3*sd,m);
figure,imshow(E25);
E25=colorseg('euclidean',L,5*sd,m); figure,imshow(E25);
В функции colorseg в качестве меры сходства цветов использовалось евклидово расстояние. Однако для оценки сходства цветов можно использовать также и другие меры, например, расстояние Махаланобиса. Рассмотрим результаты, которые получены при использовании этой меры.
E25=colorseg('mahalanobis',L,sd,m);
figure,imshow(E25);
E25=colorseg('mahalanobis',L,3*sd,m);
figure,imshow(E25);
E25=colorseg('mahalanobis',L,5*sd,m);
figure,imshow(E25);
Выбор различных мер сходства цветов (евклидово расстояние или расстояние Махаланобиса) определяет методики отслеживания цветовых данных. А выбор порога (sd,3*sd и 5*sd) влияет на уровень выделения областей.
Литература.
Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде Matlab. Москва: Техносфера, 206. – 616 с.
Пространственная фильтрация
Как уже не раз отмечалось, методы обработки изображений с точки зрения реализации делятся на два основных класса – локальные и глобальные. Каждый из них имеет свои преимущества и недостатки. Преимущество методов при глобальной реализации заключается в простоте их исполнения и быстродействии. Локальные методы владеют более широкими функциональными возможностями, в частности, они могут учитывать характеристики локальных областей, т.е. быть адаптивными.
В этом материале рассмотрим некоторые методы пространственной фильтрации. Большинство из них относится к локальным методам. Реализация этих методов состоит из четырех основных этапов:
- формирование локальной окрестности и ее центральной точки;
- проведение операции на пикселями данной локальной окрестности;
- присвоение результата операции (п. 2) центральной точке окрестности;
- повторение операций, описанных в п.п. 1 – 3, для каждой точки изображения.
Далее приведем примеры применения некоторых видов пространственных фильтров.
Сначала считаем исходное изображение
L=imread('leo1.bmp');
Для лучшего понимания сути приведем реализацию метода для одной цветовой составляющей.
L=L(:,:,1); figure, imshow(L);

Рис. 1. Исходное изображение.
Испортим исходное изображение шумом типа ”соль и перец”.
L=imnoise(L,'salt & pepper',0.01); figure, imshow(L);

Рис. 2.
Далее применим к этому зашумленному изображению различные виды пространственных фильтров и проанализируем результат обработки.
Прежде чем приступать к реализации локальных методов, необходимо расширить границы исходного изображения. Размеры расширения зависят от размеров маски фильтра. Если проводить фильтрацию с помощью встроенной функции imfilter, то параметры расширения можно задавать с помощью опций:
– ‘P’ – границы изображения расширяются значением Р. По умолчанию значение Р=0;
– ‘replicate’ – размер изображения увеличивается повторением величин на его боковых границах;
– ‘symmetric’ – размер изображения увеличивается путем зеркального отражения через границы;
– ‘circular’ – размер изображения увеличивается периодическим повторением двумерной функции;
В этом примере будем использовать не встроенную функцию imfilter и опции расширения, а приведем детальное описание работы нескольких пространственных фильтров. Размер изображения увеличим путем зеркального отражения через границы.
%n, m – размеры локальной окрестности
n1=fix(n/2);m1=fix(m/2);
a=L(1,1);b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1;
for j=1:m1;
L1(i,j)=a;
L3(i,j)=b;
L6(i,j)=c;
L8(i,j)=d;
end;
end;
L2=L(1,1:M);
L02=L2;
for i=1:n1-1;
L2=[L2;L02];
end;
L7=L(N,1:M);
L07=L7;
for i=1:n1-1;
L7=[L7;L07];
end;
L4=L(1:N,1);
L4=L4';
L04=L4;
for i=1:m1-1;
L4=[L4;L04];
end;
L4=L4';
L5=L(1:N,M);
L5=L5';
L05=L5;
for i=1:m1-1;
L5=[L5;L05];
end;
L5=L5'; L1=[L1;L4]; L1=[L1;L6]; L1=L1'; L2=[L2;L]; L2=[L2;L7];
L2=L2'; L3=[L3;L5]; L3=[L3;L8]; L3=L3'; L1=[L1;L2]; L1=[L1;L3];
Lr=L1';
Приведем программную реализацию непосредственно самих методов
for i=1+n1:N+n1;
disp(i);
for j=1+m1:M+m1;
% Формирование локальной окрестности D
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=Lr(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
D(n1+1+a,m+1)=Lr(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
% Формирование результата обработки
% Контргармоническое среднее
Lout1(i,j)=sum(sum(D.^(q+1)))/sum(sum(D.^q+eps));
% Арифметическое среднее
Lout2(i,j)=sum(sum(D))./(m*n);
% Геометрическое среднее
Lout3(i,j)=prod(prod(D)).^(1/(m*n));
% Гармоническое среднее
Lout4(i,j)=(m*n)/sum(sum(1./(D+eps)));
% Медиана
Lout5(i,j)=median(median(D));
% Максимум по окрестности
Lout6(i,j)=max(D(:));
% Минимум по окрестности
Lout7(i,j)=min(D(:));
% Срединная точка
Lout8(i,j)=0.5*(max(D(:))+min(D(:)));
end;
end;
% а–усеченное среднее
d=6;
Dus=sort(D(:));
Dus=Dus(d/2+1:end-d/2);
Lout9(i,j)=mean(Dus);
Поскольку вначале проводилось расширение исходного изображения, то теперь все результирующие изображения необходимо привести к исходным размерам.
Lout1=Lout1(n1+1:N+n1,m1+1:M+m1); Lout2=Lout2(n1+1:N+n1,m1+1:M+m1); Lout3=Lout3(n1+1:N+n1,m1+1:M+m1); Lout4=Lout4(n1+1:N+n1,m1+1:M+m1); Lout5=Lout5(n1+1:N+n1,m1+1:M+m1); Lout6=Lout6(n1+1:N+n1,m1+1:M+m1); Lout7=Lout7(n1+1:N+n1,m1+1:M+m1); Lout8=Lout8(n1+1:N+n1,m1+1:M+m1); Lout9=Lout9(n1+1:N+n1,m1+1:M+m1);
Визуализируем полученные результаты.
figure, imshow(Lout1);
title('Контргармоническое среднее');
Контргармоническое среднее
Рис. 3. Контргармоническое среднее при q=1,5.
Контргармоническое среднее
Рис. 4. Контргармоническое среднее при q=-1,5.
Уравнение контргармонического фильтра можно представить следующим выражением:
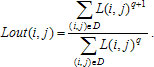 (1)
(1)
В зависимости от значения параметра q в выражении (1) метод приводит к удалению белых или темных импульсных выбросов (см. рис. 3).
figure, imshow(Lout2);
title('Арифметическое среднее');
Арифметическое среднее
Рис. 5. Арифметическое среднее при размере локального окна 3 3.
3.
Арифметическое среднее
Рис. 6. Арифметическое среднее при размере локального окна 9 9.
9.
При использовании фильтра типа арифметическое среднее качество устранения шума зависит от размеров локального окна. Увеличение размеров локального окна приводит к более качественному устранению шумовой составляющей. Недостаток этого фильтра состоит в том, что его применение приводит не только к устранению шумовой составляющей, но и размывает границы объектов, т.е. понижает качество визуального восприятия таких изображений.
figure, imshow(Lout3);
title('Геометрическое среднее');
Геометрическое среднее
Рис. 7. Геометрическое среднее при размере локального окна 3 3.
3.
Геометрическое среднее
Рис. 8. Геометрическое среднее при размере локального окна 9 9.
9.
Фильтр типа геометрическое среднее можно представить следующим выражением:
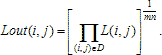 (2)
(2)
На основе выражения (2) можно предположить, что результат обработки будет существенно зависеть от размеров локальной апертуры. Это подтверждают обработанные этим методом изображения, которые представлены на рис. 7 и 8.
figure, imshow(Lout4);
title('Гармоническое среднее');
Гармоническое среднее
Рис. 9. Гармоническое среднее при размере локального окна 3 3.
3.
Гармоническое среднее
Рис. 10. Гармоническое среднее при размере локального окна 9 9.
9.
Исходя из выражения фильтра гармонического среднего
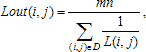 (3)
(3)
можно предположить, что результат обработки, как и в предыдущем случае, будет существенно зависеть от размеров локальной апертуры. Подтверждением тому являются изображения, которые обработаны с использованием фильтра гармонического среднего при различных размерах локальной апертуры (см. рис. 9, 10).
figure, imshow(Lout5);
title('Медиана');
Медиана
Рис. 11. Медиана при размере локального окна 3 3.
3.
Медиана
Рис. 12. Медиана при размере локального окна 9 9.
9.
Для устранения данного вида шума (‘соль и перец’) медианная фильтрация является одним из наиболее простых и эффективных методов. Размер локальной апертуры влияет на результат обработки, но не в такой степени как в других рассмотренных нами методах. Одно из основных преимуществ медианной фильтрации состоит в том, что она приводит к устранению импульсных выбросов, не размывая границ объектов (см. рис. 11, 12).
figure, imshow(Lout6);
title('Максимум по окрестности');
Максимум по окрестности
Рис. 13. Максимум по окрестности при размере локального окна 3 3.
3.
Максимум по окрестности
Рис. 14. Максимум по окрестности при размере локального окна 9 9.
9.
figure, imshow(Lout7);
title('Минимум по окрестности');
Минимум по окрестности
Рис. 15. Минимум по окрестности при размере локального окна 3 3.
3.
Минимум по окрестности
Рис. 16. Минимум по окрестности при размере локального окна 9 9.
9.
На рисунках 13–16 приведены результаты обработки изображений с помощью фильтра типа максимум (рис. 13, 14) и минимум (рис. 15, 16) по окрестности. Конечно, результаты такой обработки существенно зависят от размеров локальной апертуры.
figure, imshow(Lout8);
title('Срединная точка');
Срединная точка
Рис. 17. Срединная точка при размере локального окна 3 3.
3.
Срединная точка
Рис. 18. Срединная точка при размере локального окна 9 9.
9.
Фильтр типа срединная точка может быть представлен выражением
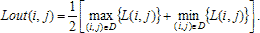 (4)
(4)
Обработка изображений данным методом показывает его неэффективность к устранению шума типа “соль и перец”. Также из представленных на рис. 17 и 18 результатов можно сделать вывод, что работа фильтра типа срединная точка зависит от размеров локальной окрестности.
figure, imshow(Lout9);
title('a-усеченное среднее');
a-усеченное среднее
Рис. 19. a –усеченное среднее при размере локального окна 3 3.
3.
a-усеченное среднее
Рис. 20. a –усеченное среднее при размере локального окна 9 9.
9.
Фильтр типа a –усеченное среднее можно представить выражением
(5)
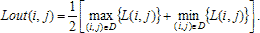
Суть работы фильтра, представленного выражением (5), можно объяснить так. Из локальной области D удаляются 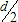 наибольших и
наибольших и 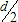 наименьших значений пикселей. Оставшиеся значения усредняются и формируют результат.
наименьших значений пикселей. Оставшиеся значения усредняются и формируют результат.
Из приведенных на рис. 19 и 20 изображений видно, что фильтр типа α–усеченное среднее является эффективным инструментом для удаления импульсных шумов. Конечно, нужно подобрать соответствующий размер локальной апертуры.
В данной работе приведены примеры работы нескольких наиболее известных методов пространственной фильтрации. Также в этой работе мы показали влияние изменения размеров локальной апертуры на результат обработки.
Литература.
- Прэтт У. Цифровая обработка изображений – М.: Мир, 1982. – 790 с.
- Гонсалес Р., Вудс Р., Эддтис С. Цифровая обработка изображений в среде MATLAB. Москва: Техносфера, 2006. – 616 с.
Программная реализация приведенных в материале методов (m-файл).
clear;
L=imread('leo1.bmp');
L=L(:,:,1);
figure, imshow(L);
[N M]=size(L);
L=imnoise(L,'salt & pepper',0.01);
figure, imshow(L);
L=double(L)./255;
q=1.5;n=3; m=n;
n1=fix(n/2);m1=fix(m/2);
a=L(1,1);b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1; for j=1:m1;
L1(i,j)=a; L3(i,j)=b; L6(i,j)=c; L8(i,j)=d;
end;end;
L2=L(1,1:M); L02=L2;
for i=1:n1-1; L2=[L2;L02]; end;
L7=L(N,1:M); L07=L7;
for i=1:n1-1; L7=[L7;L07]; end;
L4=L(1:N,1); L4=L4'; L04=L4;
for i=1:m1-1; L4=[L4;L04]; end;
L4=L4'; L5=L(1:N,M); L5=L5'; L05=L5;
for i=1:m1-1; L5=[L5;L05]; end;
L5=L5'; L1=[L1;L4]; L1=[L1;L6]; L1=L1'; L2=[L2;L]; L2=[L2;L7];
L2=L2'; L3=[L3;L5]; L3=[L3;L8]; L3=L3'; L1=[L1;L2]; L1=[L1;L3];
Lr=L1';
clear L1; clear L2; clear L3; clear L4;
clear L5; clear L6; clear L7; clear L8;
for i=1+n1:N+n1;
disp(i);
for j=1+m1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=Lr(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
D(n1+1+a,m+1)=Lr(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
Lout1(i,j)=sum(sum(D.^(q+1)))/sum(sum(D.^q+eps)); %Контргармоническое среднее
Lout2(i,j)=sum(sum(D))./(m*n); %Арифметическое среднее
Lout3(i,j)=prod(prod(D)).^(1/(m*n)); %Геометрическое среднее
Lout4(i,j)=(m*n)/sum(sum(1./(D+eps))); %Гармоническое среднее
Lout5(i,j)=median(median(D)); %медиана
Lout6(i,j)=max(D(:)); %max
Lout7(i,j)=min(D(:)); %min
Lout8(i,j)=0.5*(max(D(:))+min(D(:))); %срединная точка
d=6;
Dus=sort(D(:));
Dus=Dus(d/2+1:end-d/2);
Lout9(i,j)=mean(Dus); %а–усеченное среднее
end;
end;
Lout1=Lout1(n1+1:N+n1,m1+1:M+m1);
Lout2=Lout2(n1+1:N+n1,m1+1:M+m1);
Lout3=Lout3(n1+1:N+n1,m1+1:M+m1);
Lout4=Lout4(n1+1:N+n1,m1+1:M+m1);
Lout5=Lout5(n1+1:N+n1,m1+1:M+m1);
Lout6=Lout6(n1+1:N+n1,m1+1:M+m1);
Lout7=Lout7(n1+1:N+n1,m1+1:M+m1);
Lout8=Lout8(n1+1:N+n1,m1+1:M+m1);
Lout9=Lout9(n1+1:N+n1,m1+1:M+m1);
figure, imshow(Lout1);title('Контргармоническое среднее');
figure, imshow(Lout2);title('Арифметическое среднее');
figure, imshow(Lout3);title('Геометрическое среднее');
figure, imshow(Lout4);title('Гармоническое среднее');
figure, imshow(Lout5);title('Медиана');
figure, imshow(Lout6);title('Максимум по окрестности');
figure, imshow(Lout7);title('Минимум по окрестности');
figure, imshow(Lout8);title('Срединная точка');
figure, imshow(Lout9);title('a-усеченное среднее');
Деконволюция
В пакете Image Processing Toolbox системы MATLAB существует довольно много функций для решения тех или иных задач обработки изображений, которые оперируют такими понятиями как функция распространения точки, обращение двумерной свертки (например, deconvblind, deconvlucy, deconvreg, deconvwnr [2] и др.). Рассмотрим это более детально с точки зрения теории.
Деконволюция
Решение задачи деконволюции заключается в обращении двумерной свертки. Термин "деконволюция" охватывает наиболее важные и широко используемые методы обработки изображений. Необходимость в такой операции возникает во всех областях науки, связанных с измерениями. По методах деконволюции существует большое число работ [1].
Задача деконволюции может быть решена несколькими способами. Выбор наиболее подходящего для решения этой задачи метода зависит от ряда факторов, в том числе от формы и протяженности функции распространения точки (ФРТ), характера исходного изображения и степени усечения его кадровым окном записывающего устройства.
Какой бы метод не использовался, почти всегда необходимо провести предварительную обработку заданного искаженного изображения для преобразования его в форму, удобную для выполнения процедуры деконволюции. Предварительную обработку целесообразно разделить на пять категорий: сглаживание, разбиение на фрагменты, аподизацию (взвешивание обрабатываемого отрезка сигнала весовой функцией), расширение границ и сверхразрешение. Под сглаживанием изображения здесь понимается уменьшение зашумленности. Разбиение на фрагменты включает разделение изображения с пространственно-зависимой ФРТ на фрагменты, в каждом из которых ФРТ может приближенно рассматриваться как пространственно-инвариантная. Аподизация - это метод, позволяющий уменьшить влияние кадрового окна (записывающего устройства), которое производит усечение изображения. Однако этот метод может быть менее эффективным, нежели метод расширения границ, который мы удачно применяли в ряде случаев. Известны две модификации метода расширения границ - простое расширение и расширение с перекрыванием. Второй метод, как правило, более предпочтителен, поскольку в нем используются преимущества условия согласованности периодических сверток. Это еще один пример того, как повышается эффективность численного метода, когда более полно учитываются особенности исследуемой задачи в плане математической физики. Сверхразрешение рассматривается как процедура предварительной обработки, поскольку в конечном счете она позволяет уменьшить зашумленность.
Существует также мультипликативная деконволюция, которая является наиболее распространенным методом восстановления изображения, представимого в виде согласованной свертки. Искаженное изображение, которое не является таким, следует преобразовать к виду согласованной свертки.
Метод субтрактивной деконволюции оказывается особенно полезным, когда дефекты, имеющиеся в записанном изображении, связаны не с потерей разрешения, а с искажением небольших деталей, например в случае, когда ФРТ имеет такой же узкий основной лепесток, как и разрешаемая деталь, но обладает широким хвостом значительной амплитуды или характеризуется высокими боковыми лепестками. Метод субтрактивной деконволюции можно легко модифицировать таким образом, чтобы включить пространственно-зависимые искажения, хотя вычислительная реализация этих методов становится тогда очень сложной.
Существуют различные подходы к задаче деконволюции. Эти подходы включают нерекурсивный и рекурсивный методы фильтрации в плоскости изображения, прямые матричные методы и методы максимальной энтропии и максимального правдоподобия.
Метод согласованной деконволюции, который возник из исследований комплексных нулей в частотной плоскости, является в основном одномерным методом, к которому можно так же широко обращаться, как и к методу мультипликативной деконволюции.
Одним из наиболее важных практических методов деконволюции является метод слепой деконволюции. Отметим, что все методы обработки спекл-изображений можно рассматривать как частные случаи слепой деконволюции.
Кроме известных традиционных приложений деконволюции существуют и различные ее экзотические применения. Одно из наиболее замечательных таких применений - восстановление методом слепой деконволюции записей голосов знаменитых певцов на старых граммофонных пластинках.
Интеграл свертки представляется выражением
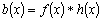 |
(1) |
где h(x) - функция, задающая искажение; f(x) - функция, которую необходимо восстановить.
Согласно теореме о свертке фурье-образ величины (1) равен
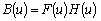 |
(2) |
где F(u) - функция, связанная с функцией f(x) двумерным преобразованием Фурье; H(u) - фурье-образ оптической передаточной функции.
Идеализированная задача конечной деконволюции такова: заданы функции b(x) и h(x) , требуется восстановить функцию f(x) при условии, что все три величины имеют конечную протяженность.
Из соотношения (2) следует, что эту задачу можно решить следующим образом
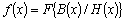 |
(3) |
Операция деления внутри фигурных скобок в выражении (3) называется простой инверсной фильтрацией. Термин "фильтрация" здесь употребляется по аналогии с классической теорией цепей и современной теорией обработки сигналов. Классический фильтр представляет собой устройство, которое изменяет спектр временных частот сигнала. Спектр B(u) есть функция пространственной частоты.
Оптическая передаточная функция H(u) изменяет спектр пространственных частот B(u) в результате применения указанной выше операции деления.
Поскольку обработанные изображения обычно хранятся в памяти ЭВМ в виде квантованных значений, в технике обработки изображений, как правило, используются цифровые, а не классические аналоговые фильтры. Цифровой фильтр определяется дискретным массивом, вообще говоря, комплексных чисел, который изменяет в процессе некоторой операции обработки спектр пространственных частот. Следовательно, обе функции, h(x) в формуле (1) и H(u) в формуле (2), могут рассматриваться как фильтры (и в большей части приложений они реализуются в цифровом виде). Общепринятая классификация цифровых фильтров возникла в теории обработки сигналов как функций времени, и этой классификацией можно пользоваться в теории обработки одномерных изображений, т. е. сигналов как функций (одной) пространственной переменной. Мы перенесем соответствующую терминологию на двумерный случай. Понятие "отсчета" в теории обработки сигналов переходит в понятие "элемента изображения" в теории обработки изображений. Как отсчеты, так и элементы изображений должны квантоваться по амплитуде до их цифровой обработки. Изображение, к которому должна быть применена операция фильтрации, называется заданным изображением, и о нем говорят как о состоящем из заданных элементов изображения. Элементы профильтрованного изображения называются выходными элементами изображения. В случае нерекурсивного цифрового фильтра каждый выходной элемент изображения представляет собой взвешенную сумму заданных элементов изображения. В случае же рекурсивного цифрового фильтра каждый выходной элемент изображения есть взвешенная сумма заданных элементов изображения и рассчитанных ранее выходных элементов изображения. Все практически реализуемые цифровые фильтры, конечно, описываются массивами конечных размеров (в одномерном случае конечный фильтр часто называют коротким). Цифровой фильтр называется прямым, если он применяется в плоскости изображения, и спектральным - если он применяется в частотной плоскости. Каузальный фильтр является односторонним в том смысле, что его отклик всегда отстает от входного воздействия (это несколько искусственно в двумерном случае, но, конечно, имеет очень важное значение для операций одномерной фильтрации, которые лежат в основе обработки сигналов как функций времени). Каузальные фильтры почти всегда реализуются как прямые. Мультипликативный цифровой фильтр представляет собой спектральный фильтр, в котором каждый выходной отсчет получается как произведение заданного элемента входного сигнала на один элемент массива фильтра.
Если бы все существенные стороны практических задач деконволюции сводились к формуле (3), то все содержание настоящей публикации можно было легко вместить в небольшой статье. Однако в задаче деконволюции встречается очень много практических трудностей. Это объясняется тем, что обрабатываемые данные на практике всегда искажены.
Прежде чем ставить практическую задачу деконволюции, исследуем некоторые свойства согласованности сверток.
В одномерном случае соотношение (2) представляется в виде
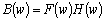 |
(4) |
где вещественная переменная u заменена комплексной переменной w . Если функции f(x) и h(x) имеют конечную протяженность, так что протяженность функции b(x) тоже конечна, то их спектры характеризуются множествами нулей в комплексной w -плоскости.
Если заданное множество Zg представить в виде множества вещественных нулей Zgr и нулей, которые могут быть комплексными Zgc , то можно записать
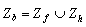 |
(5) |
Это означает, что одномерная задача деконволюции является согласованной только в том случае, если все нули функции H(w) будут также и нулями функции B(w) . Следовательно, величины b(x) и h(x) нельзя задавать независимо; заранее должно быть известно, что они удовлетворяют соотношению (1). То же относится и к двумерным сверткам.
Теперь вернемся к периодически продолженному (с перекрыванием) идеальному искаженному изображению imb(x) и к его спектру IMb(x) . Последний можно записать в виде
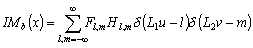 |
(6) |
где 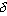 (·) - дельта-функция; Fi,m - коэффициенты Фурье истинного изображения f(x) , являющиеся также отсчетами функции F(u) , которые рассматриваются в теореме отсчетов. Эти отсчеты берутся в точках растра (l/L1 , m/L2 ) в частотной плоскости. Величины Hl,m входящие в выражение (6) - это отсчеты оптической передаточной функции H(u) в тех же самых точках растра:
(·) - дельта-функция; Fi,m - коэффициенты Фурье истинного изображения f(x) , являющиеся также отсчетами функции F(u) , которые рассматриваются в теореме отсчетов. Эти отсчеты берутся в точках растра (l/L1 , m/L2 ) в частотной плоскости. Величины Hl,m входящие в выражение (6) - это отсчеты оптической передаточной функции H(u) в тех же самых точках растра:
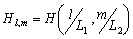 |
(7) |
где l и m - произвольные целые числа.
Теперь мы можем поставить идеализированную задачу периодической деконволюции: заданы функции imb(x) и h(x), требуется найти функцию f(x) [зная, что f(x) и h(x) - функции конечной протяженности, а imb(x) - периодическая функция].
По заданной функции b(x) можно рассчитать функцию B(u) и сразу же найти, что
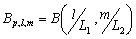 |
(8) |
Аналогичным образом вычисляются отсчеты оптической передаточной функции Hl,m . Из выражения (6) видно, что каждое значение Fl,m дается операцией деления 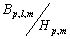 , которая всегда может быть выполнена, если значения Hl,m отличны от нуля. Такой простой подход адекватен в случае функций b(x) и h(x) , выбранных достаточно независимо, поскольку функция Imb(u) в соответствии с выражением (6) фактически существует только в вышеупомянутых точках растра. Но подобный подход неприемлем в идеализированной задаче в случае конечной свертки, так как тогда B(u) - непрерывная функция переменной u.
, которая всегда может быть выполнена, если значения Hl,m отличны от нуля. Такой простой подход адекватен в случае функций b(x) и h(x) , выбранных достаточно независимо, поскольку функция Imb(u) в соответствии с выражением (6) фактически существует только в вышеупомянутых точках растра. Но подобный подход неприемлем в идеализированной задаче в случае конечной свертки, так как тогда B(u) - непрерывная функция переменной u.
Поэтому удивительно, что единственным условием согласованности для периодических сверток оказывается требование, чтобы величины Hl,m могли быть нулевыми только при тех значениях l и m , при которыхBp,l,m=0 . Это условие называется условием согласованности периодических сверток. Подчеркнем, что ни одна величина .Hl,m не может быть точно равна нулю при реальном измерении функции h(x) , или, что эквивалентно, функции H(u) , так что периодические свертки всегда на практике являются согласованными (они, конечно, очень сильно зашумлены, когда большое число величин Hl,m "малы" при значениях l и m , отвечающих существенно отличным от нуля значениям величин Bp,l,m ).
Практическая задача деконволюции ставится следующим образом: заданы функции b(x) и h(x) , требуется найти функцию f(x) , зная, что 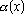 - усеченный вариант функции записываемого изображения r(x).
- усеченный вариант функции записываемого изображения r(x).
Одно из "золотых правил" в задаче реконструкции изображений состоит в том, что следует избегать обработки данных, содержащих какие-либо разрывы непрерывности, из которых наиболее нежелательны обрезания и усечения, поскольку при их наличии почти всегда возникают ложные детали (часто называемые артефактами, особенно в медицинских приложениях). Таким образом, как правило, желательно проводить предварительную обработку изображения 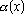 , чтобы по возможности полностью компенсировать все имеющиеся в них разрывы и другие устранимые дефекты.
, чтобы по возможности полностью компенсировать все имеющиеся в них разрывы и другие устранимые дефекты.
Любой вид предварительной обработки может, конечно, вносить свой шум в добавление к искажению изображения f(x) , уже имеющемуся в записываемом изображении r(x) . Но если разрывы не устранены, то соответствующие артефакты, как правило, преобладают над любым дополнительным шумом, вносимым предварительной обработкой. "Выровненную" форму изображения 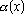 обозначим здесь через a(x) и будем называть предварительно обработанным записанным изображением. Хотя в результате проведения предварительной обработки должны изменяться все три величины, редко имеется какой-либо способ оценить, насколько именно, а потому обычно не имеет смысла говорить о различии между изображениями a(x) и r(x). Далее мы будем рассматривать эти два изображения как идентичные, по крайней мере на том кадре
обозначим здесь через a(x) и будем называть предварительно обработанным записанным изображением. Хотя в результате проведения предварительной обработки должны изменяться все три величины, редко имеется какой-либо способ оценить, насколько именно, а потому обычно не имеет смысла говорить о различии между изображениями a(x) и r(x). Далее мы будем рассматривать эти два изображения как идентичные, по крайней мере на том кадре 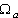 (т. е. в той области плоскости изображения), где умещается предварительно обработанный вариант изображения
(т. е. в той области плоскости изображения), где умещается предварительно обработанный вариант изображения 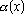 смысла . Поэтому будем считать, что
смысла . Поэтому будем считать, что
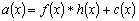 |
(9) |
Такое предположение не сказывается на общности рассуждений, поскольку шум c(x) включает эффекты произвольного аддитивного искажения, связанного с предварительной обработкой.
Теперь мы введем понятие "восстановимого истинного изображения" 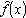 . Это оценка изображения f(x) , которую можно получить, исходя из изображения
. Это оценка изображения f(x) , которую можно получить, исходя из изображения 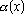 .
.
При любом рациональном подходе к решению практической задачи деконволюции сначала получают предварительно обработанное изображение a(x) из заданного изображения 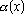 . Затем выбирается подходящая процедура деконволюции для получения
. Затем выбирается подходящая процедура деконволюции для получения 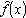 на основе h(x) и a(x) . Некоторые из этих процедур можно рассматривать как процесс получения модифицированной функции распространения точки
на основе h(x) и a(x) . Некоторые из этих процедур можно рассматривать как процесс получения модифицированной функции распространения точки 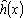 , которая связана с предварительно обработанным записанным изображением и восстановимым истинным изображением соотношением
, которая связана с предварительно обработанным записанным изображением и восстановимым истинным изображением соотношением
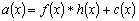 |
(10) |
Коэффициенты Фурье функции 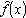 удобно обозначить через
удобно обозначить через 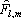 , а для обозначения спектров функций a(x) , c(x) ,
, а для обозначения спектров функций a(x) , c(x) , 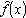 и
и 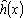 использовать соответствующие заглавные буквы со "шляпкой" или без нее.
использовать соответствующие заглавные буквы со "шляпкой" или без нее.
Если есть опасение, что различия между 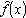 и f(x) сильно увеличатся из-за отсутствия согласованности между функциями a(x) и h(x) , взятыми явно конечными, то можно обратиться к формуле
и f(x) сильно увеличатся из-за отсутствия согласованности между функциями a(x) и h(x) , взятыми явно конечными, то можно обратиться к формуле
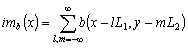
для периодического изображения imb(x) с заменой b на a . Тогда спектр IMb(u) свертки дается выражением (6), но с заменой величин 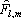 и
и 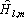 величинами Fl,m и Hl,m соответственно. Напомним, что на периодические свертки не оказывает влияния несогласованность, которая, как уже говорилось, может искажать свертки величин, имеющих конечные протяженности.
величинами Fl,m и Hl,m соответственно. Напомним, что на периодические свертки не оказывает влияния несогласованность, которая, как уже говорилось, может искажать свертки величин, имеющих конечные протяженности.
Литература:
1.Бейтс Р., Мак-Доннелл М. Восстановление и реконструкция изображений: Пер. с англ. - М.: Мир, 1989. - 336 с.
2. Дьяконов В. MATLAB. Обработка сигналов и изображений. Специальный справочник. - СПб.: Питер, 2002. - 608 с.
Предварительная обработка изображений
Успешность восстановления изображений сильно зависит от качества предварительной обработки, в результате которой из записанного изображения 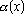 получают изображение a(x) . Мы разделяем предварительную обработку на пять категорий: сглаживание, разбиение на фрагменты, аподизацию, расширение границ и сверхразрешение [1].
получают изображение a(x) . Мы разделяем предварительную обработку на пять категорий: сглаживание, разбиение на фрагменты, аподизацию, расширение границ и сверхразрешение [1].
Обычно для более полного уменьшения эффектов зашумления проводят сглаживание изображения . Хотя эта процедура часто носит главным образом косметический характер, она может иметь и более важное практическое значение. Напомним, что величина c(x) (см. "Деконволюция", формула (9)) учитывает эффекты, связанные с нелинейностями записи, шумом записи изображения, ошибками в передаче битов, отсутствием некоторой информации (т. е. отсутствием отдельных элементов изображений или целых групп их), насыщением, а также с загрязнением и царапинами, которые искажают фотографии. Сглаживание можно рассматривать как двумерный аналог простейшей обработки сигналов, имеющей целью исключить весь шум, спектральные составляющие которого лежат вне полосы временных частот, соответствующей сигналу, передаваемому рассматриваемым каналом связи. Большинство видов помех, перечисленных выше, можно считать помехами с независимыми отсчетами, тогда как характерные детали изображений обычно коррелированны в пределах нескольких соседних элементов изображения. Иначе говоря, спектр пространственных частот шума существенно шире, чем спектр изображения, и в этом случае весьма эффективна пространственная фильтрация изображения 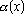 , оставляющая только те спектральные составляющие шума c(x) , которые разрешены в той же степени, что и деталь в истинном изображении.
, оставляющая только те спектральные составляющие шума c(x) , которые разрешены в той же степени, что и деталь в истинном изображении.
Опыт показывает, что точность восстановленного изображения в значительно большей степени определяется уровнем зашумленности, остающимся в изображении после предварительной обработки, нежели фактически используемым методом деконволюции.
Методы деконволюции прямо применимы только в случае пространственно-инвариантной функции распространения точки (ФРТ).
Нарушение условия пространственной инвариантности меняет характер задачи деконволюции, существенно увеличивая вычислительную сложность и стоимость расчетов даже при использовании методов, пригодных в случае пространственно-зависимых ФРТ. Во многих практических ситуациях такое нарушение связано по большей части не с какими-либо факторами принципиального значения, а с геометрическими искажениями, вносимыми в процессе записи (такие искажения часто вызываются, например, линзами в устройствах, формирующих изображение). Поэтому мы будем рассматривать коррекцию геометрических искажений одновременно со сглаживанием. Для компенсации геометрических искажений, приводящей к практически пространственно-инвариантной ФРТ, можно использовать методы коррекции геометрических искажений. Приведем пример. Предположим, что некоторая сцена фотографируется с вращающегося летательного аппарата, в котором камера жестко закреплена. Плоскость, в которой лежит фотопленка камеры, будет плоскостью изображения. Зная геометрические соотношения между рассматриваемой сценой и летательным аппаратом, мы можем рассчитать положение осевой точки (точки пересечения оси вращения с плоскостью изображения). Даже если камера хорошо сфокусирована, записанное изображение искажается пространственно-зависимой ФРТ, которая в каждой точке изображения с вращательным смазом представляется дугой окружности с центром в данной осевой точке. Угловая протяженность этой дуги пропорциональна произведению времени экспозиции на скорость вращения летательного аппарата. Соответствующая процедура коррекции геометрических искажений должна приводить к преобразованию каждой дуги в отрезок прямой линии постоянной длины. Тогда преобразованная ФРТ становится пространственно-инвариантной, соответствующей линейному смазу. После компенсации смаза с помощью какого-либо наиболее подходящего метода деконволюции исходная геометрия восстанавливается в результате соответствующей коррекции.
В случае пространственно-зависимых ФРТ, не допускающих эффективного применения процедуры коррекции геометрических искажений, существуют два подхода. Можно использовать один из прямых методов. Однако компьютерная реализация этих методов настолько сложна, что они имеют практическую ценность только при обработке изображений небольших размеров (скажем, 128х128 элементов), а также в том случае, когда ФРТ изменяется лишь по одной координате. Второй, обычно более предпочтительный, подход - разбиение записанного изображения на ряд смежных фрагментов одинакового размера. Принимается, что искажение каждого фрагмента связано с формой реальной ФРТ в его центре. Все нарушения этого предположения включаются в полную зашумленность фрагмента изображения, размер которого должен быть настолько мал, чтобы не допустить избыточной зашумленности. В то же время, как показывает наш опыт, размер фрагмента изображения должен быть по крайней мере в четыре - восемь раз больше эффективного размера ФРТ. При всем этом предполагается, что реальная ФРТ изменяется на записанном изображении плавно и медленно (это условие часто выполняется на практике). Таким образом, разбиение на фрагменты дает возможность свести задачу восстановления изображения, описываемого пространственно-зависимой ФРТ, к последовательности практических задач деконволюции. Полное восстановленное изображение получается путем составления мозаики из отдельных восстановленных фрагментов.
Обозначим область плоскости изображения, занимаемую заданным (но сглаженным, как описано выше) записанным изображением, через  . Это согласуется с определениями, которые связывают записываемое и фактически записанное изображения r(x) и
. Это согласуется с определениями, которые связывают записываемое и фактически записанное изображения r(x) и 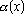 . Однако записываемое изображение r(x) в большей части практических приложений фактически усекается до вида
. Однако записываемое изображение r(x) в большей части практических приложений фактически усекается до вида 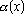 , чем и объясняется, почему эти два изображения, вообще говоря, различны. Напомним, что
, чем и объясняется, почему эти два изображения, вообще говоря, различны. Напомним, что 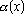 - зашумленный вариант изображения b(x) . Последнее является фактически интересующим нас изображением, поскольку к нему мы хотели бы применить операцию деконволюции. Поскольку изображение b(x) выходит за пределы вышеуказанного кадра, логично предположить, что то же самое имеет место и для изображения
- зашумленный вариант изображения b(x) . Последнее является фактически интересующим нас изображением, поскольку к нему мы хотели бы применить операцию деконволюции. Поскольку изображение b(x) выходит за пределы вышеуказанного кадра, логично предположить, что то же самое имеет место и для изображения 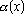 . Заметим, что изображение
. Заметим, что изображение 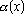 может все же отличаться от изображения r(x) . Поэтому для этого кадра мы введем другой символ Г . Имеет смысл пытаться восстанавливать только те части изображения f(x) , которые оказывают влияние на вид изображения b(x) в пределах кадра Г . Это части изображения f(x) , которые в исходном состоянии находятся в кадре Г , а также части этого изображения, которые вносятся в результате действия ФРГ в пределы кадра Г извне его. Обозначим через
может все же отличаться от изображения r(x) . Поэтому для этого кадра мы введем другой символ Г . Имеет смысл пытаться восстанавливать только те части изображения f(x) , которые оказывают влияние на вид изображения b(x) в пределах кадра Г . Это части изображения f(x) , которые в исходном состоянии находятся в кадре Г , а также части этого изображения, которые вносятся в результате действия ФРГ в пределы кадра Г извне его. Обозначим через  кадр, содержащий сумму этих частей. Кадр
кадр, содержащий сумму этих частей. Кадр  может быть построен путем размещения центра кадра ФРТ
может быть построен путем размещения центра кадра ФРТ 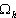 на внешней границе кадра Г и перемещения ее по этой границе (см. "Деконволюция", формула (1)). Тогда кадр и будет представлять объединение всех точек в кадре Г и всех точек, охватываемых кадром
на внешней границе кадра Г и перемещения ее по этой границе (см. "Деконволюция", формула (1)). Тогда кадр и будет представлять объединение всех точек в кадре Г и всех точек, охватываемых кадром 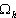 при его прохождении по области Г .
при его прохождении по области Г .
Поскольку части истинного изображения, лежащие вне кадра  , полностью теряются, можно предположить, что изображение f(x) лежит в пределах кадра
, полностью теряются, можно предположить, что изображение f(x) лежит в пределах кадра  . Поэтому далее будем считать, что
. Поэтому далее будем считать, что
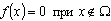 |
(1) |
откуда, естественно, следует равенство
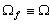 |
(2) |
Так как изображение f(x) существует на кадре  , из-за "размывающего" действия ФРТ h(x) оно должно сказываться в пределах большего кадра. Этот больший кадр содержит все части изображения b(x) , которые теряются при усечении изображения r(x) , а потому мы обозначим его через
, из-за "размывающего" действия ФРТ h(x) оно должно сказываться в пределах большего кадра. Этот больший кадр содержит все части изображения b(x) , которые теряются при усечении изображения r(x) , а потому мы обозначим его через 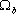 . Поскольку же
. Поскольку же 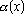 есть зашумленный вариант изображения b(x) , область
есть зашумленный вариант изображения b(x) , область  идентична области
идентична области 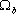 .
.
Хотя мы знаем о существовании изображения 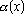 в пределах кадра
в пределах кадра 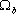 , оно задается только на кадре Г . Обычно целесообразно провести дальнейшую обработку (кроме сглаживания) для более полной компенсации эффектов усечения, а также несогласованности операции свертки. Итак, нужно, чтобы предварительно обработанное записанное изображение (см. "Деконволюция", формула (9)) удовлетворяло условию
, оно задается только на кадре Г . Обычно целесообразно провести дальнейшую обработку (кроме сглаживания) для более полной компенсации эффектов усечения, а также несогласованности операции свертки. Итак, нужно, чтобы предварительно обработанное записанное изображение (см. "Деконволюция", формула (9)) удовлетворяло условию
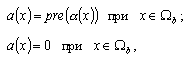 |
(3) |
где через pre{} обозначены операции, описываемые ниже
Усечение изображения 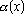 имеет столь важное значение с практической точки зрения, что нужно остановиться на его последствиях. Сначала конкретизируем форму кадра Г . Мы будем рассматривать только прямоугольные и круговые кадры, поскольку они чаще встречаются в приложениях. Таким образом, если L1 и L2 есть x и y -протяженности прямоугольного кадра г или если R - радиус кругового кадра Г , следует, что
имеет столь важное значение с практической точки зрения, что нужно остановиться на его последствиях. Сначала конкретизируем форму кадра Г . Мы будем рассматривать только прямоугольные и круговые кадры, поскольку они чаще встречаются в приложениях. Таким образом, если L1 и L2 есть x и y -протяженности прямоугольного кадра г или если R - радиус кругового кадра Г , следует, что
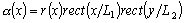 |
(4) |
или
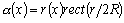 |
(5) |
где за начало координат взят центр кадра Г . Эти два варианта изображения 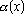 удобно исследовать раздельно. Из определений
удобно исследовать раздельно. Из определений
 |
(6) |
а также выражения (4) и теоремы о свертке следует, что
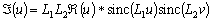 |
(7) |
где sinc(u) - фурье-образ rect(x) [2].
Взяв теперь фурье-образ функции (5) и вспомнив первое из двух определений (6), увидим, что
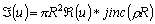 |
(8) |
где 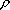 - радиальная координата в частотной плоскости и
- радиальная координата в частотной плоскости и
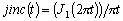 |
(9) |
причем J1 - функция Бесселя первого рода первого порядка.
Отметим, что sinc(t) - осциллирующая функция, имеющая центральный пик (часто называемый основным лепестком ) приблизительно единичной ширины и бесконечную последовательность меньших пиков (иногда называемых боковыми лепестками), каждый из которых имеет эффективную ширину, равную 1/2, и амплитуду, которая уменьшается сравнительно медленно (по закону 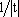 ). Эти боковые лепестки могут привести к неприемлемым артефактам, если изображение
). Эти боковые лепестки могут привести к неприемлемым артефактам, если изображение 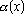 подвергается операции фильтрации без соответствующей предварительной обработки. Хотя это относится в первую очередь к изображению
подвергается операции фильтрации без соответствующей предварительной обработки. Хотя это относится в первую очередь к изображению 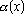 , определенному выражением (4), то же самое справедливо и для изображения, заданного выражением (5). Функция jinc , введенная в формуле (8), аналогична функции sinc . Она фактически эквивалентна двум функциям sinc , входящим в формулу (7). Отметим, что типичная фильтрация может быть описана соотношением
, определенному выражением (4), то же самое справедливо и для изображения, заданного выражением (5). Функция jinc , введенная в формуле (8), аналогична функции sinc . Она фактически эквивалентна двум функциям sinc , входящим в формулу (7). Отметим, что типичная фильтрация может быть описана соотношением
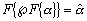 |
(10) |
где 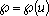 - мультипликативный фильтр, предназначенный для получения из изображения
- мультипликативный фильтр, предназначенный для получения из изображения  изображения
изображения 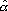 , имеющего некоторые желательные характеристики. Боковые лепестки функции jinc и двух функций sinc искажают внешнее преобразование Фурье в формуле (10), часто приводя к очень неприятным пульсациям большой амплитуды в той области плоскости изображения, где велики значения
, имеющего некоторые желательные характеристики. Боковые лепестки функции jinc и двух функций sinc искажают внешнее преобразование Фурье в формуле (10), часто приводя к очень неприятным пульсациям большой амплитуды в той области плоскости изображения, где велики значения 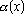 , маскирующие низкоамплитудные детали в фильтрованном изображении.
, маскирующие низкоамплитудные детали в фильтрованном изображении.
Поскольку функция 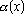 тождественно равна нулю вне кадра Г , обычно не удается достичь (в восстановленном изображении) разрешения, лучшего, чем соответствующее ширине главных лепестков функций sinc в формуле (7) или функции jinc в формуле (8). В то же время часто оказывается возможным уменьшить влияние боковых лепестков функций sinc и jinc путем соответствующей предварительной обработки.
тождественно равна нулю вне кадра Г , обычно не удается достичь (в восстановленном изображении) разрешения, лучшего, чем соответствующее ширине главных лепестков функций sinc в формуле (7) или функции jinc в формуле (8). В то же время часто оказывается возможным уменьшить влияние боковых лепестков функций sinc и jinc путем соответствующей предварительной обработки.
Если мы знаем, что более интересные для нас части изображения f(x) лежат ближе к центру кадра Г , то в тех случаях, когда размер последнего существенно больше размера кадра 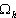 , предварительная обработка может состоять в аподизации. Она заключается в умножении функции
, предварительная обработка может состоять в аподизации. Она заключается в умножении функции 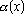 на функцию окна m=m(x) , которая плавно уменьшается до нуля на внешней границе кадра Г и равна нулю везде вне кадра Г . Вследствие этого область
на функцию окна m=m(x) , которая плавно уменьшается до нуля на внешней границе кадра Г и равна нулю везде вне кадра Г . Вследствие этого область 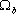 оказывается равной кадру Г . Обращаясь теперь к формуле (3), можно получить, что предварительно обработанное записанное изображение принимает вид
оказывается равной кадру Г . Обращаясь теперь к формуле (3), можно получить, что предварительно обработанное записанное изображение принимает вид
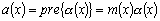 |
(11) |
где 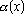 - сглаженное изображение, полученное из фактически записанного изображения.
- сглаженное изображение, полученное из фактически записанного изображения.
Аподизация неизбежно приводит к потере разрешения, но обычно это "окупается" устранением указанных выше артефактов. В стандартных пособиях приводятся многие функции окна, обеспечивающие удовлетворительный компромисс между уменьшением боковых лепестков и потерей разрешения. Поэтому нам представляется что достаточно продемонстрировать некоторые общие свойства функций окна на примере особенно "гибкой" функции окна, которой не уделялось достаточного внимания в соответствующей литературе.
Поскольку здесь рассматриваются только изображения  , описываемые выражениями (4) и (5), по-видимому, не имеет особого смысла изучать функции окна, которые не обладают свойством круговой симметрии или не разделяются на сомножители, зависящие от переменных x и y по отдельности. Поэтому достаточно исследовать одномерные функции окна, например m(x) (через x обозначены переменные x , y или r ). В качестве величины L , удобно взять размер (усеченного) фактически записанного изображения в x-направлении. Приняв обозначение M(u)=M=F(m) и предположив, что m - функция, аналитическая на интервале
, описываемые выражениями (4) и (5), по-видимому, не имеет особого смысла изучать функции окна, которые не обладают свойством круговой симметрии или не разделяются на сомножители, зависящие от переменных x и y по отдельности. Поэтому достаточно исследовать одномерные функции окна, например m(x) (через x обозначены переменные x , y или r ). В качестве величины L , удобно взять размер (усеченного) фактически записанного изображения в x-направлении. Приняв обозначение M(u)=M=F(m) и предположив, что m - функция, аналитическая на интервале 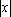 <L/2 (т. е. "непрерывно гладкая", иначе говоря, бесконечно дифференцируемая), мы видим, что интеграл Фурье, определяющий величину M , можно взять по частям и получить следующее выражение:
<L/2 (т. е. "непрерывно гладкая", иначе говоря, бесконечно дифференцируемая), мы видим, что интеграл Фурье, определяющий величину M , можно взять по частям и получить следующее выражение:
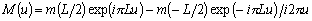 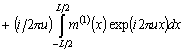 |
(12) |
где введено обозначение
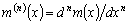 |
(13) |
Если взять интеграл (12), то появляется возможность анализировать боковые лепестки функции M(u) . Чтобы боковые лепестки быстрее уменьшались с возрастанием величины  , необходимо обеспечить выполнение условия
, необходимо обеспечить выполнение условия
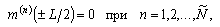 |
(14) |
где 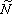 - положительное целое число.
- положительное целое число.
Однако, как уже отмечалось выше, следует учитывать зависимость между уровнем боковых лепестков и потерями разрешения.
Литература.
1. Бейтс Р., Мак-Доннелл М. Восстановление и реконструкция изображений: Пер. с англ.- М.: Мир, 1989. - 336.
2. Bracewell R.N. The Fourier Transform and its Applications. - N.Y.: McGraw-Hill, 1978.
Расширение границ изображений. Сверхразрешение
В функции распространения точки могут учитываться линейный смаз, расфокусировка и другие виды искажений.При сильном искажении отношение размеров кадров 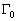 и
и ![]() может быть весьма малым.
может быть весьма малым.
Влияние, оказываемое усечением изображения 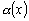 , можно уменьшать более сложным, чем аподизация, методом экстраполяции с области
, можно уменьшать более сложным, чем аподизация, методом экстраполяции с области 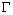 на кадр
на кадр 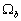 . Очевидно, что нечего и пытаться восстанавливать изображение
. Очевидно, что нечего и пытаться восстанавливать изображение 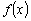 вне области
вне области 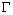 . Единственная цель данного вида предварительной обработки состоит в замене усеченного изображения изображением, которое:
. Единственная цель данного вида предварительной обработки состоит в замене усеченного изображения изображением, которое:
а) свободно от скачкообразных изменений вблизи своей границы;
б) имеет правильный размер, соответствующий восстанавливаемой части истинного изображения (т. е. существует на кадре 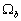 );
);
в) содержит всю записанную информацию.
Такой вид предварительной обработки будем называть расширением границ. Эта процедура описывается соотношением
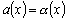 при
при 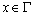 .
.
Существуют два способа расширения границ. Простое расширение границ состоит в том, что функцию 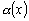 продолжают с области Г на внешнюю границу кадра
продолжают с области Г на внешнюю границу кадра 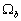 вдоль прямых линий, перпендикулярных этой границе
вдоль прямых линий, перпендикулярных этой границе 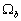 . Такая процедура, конечно, выполняется просто, когда области
. Такая процедура, конечно, выполняется просто, когда области 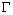 и
и 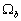 прямоугольные (что соответствует большей части практических приложений).
прямоугольные (что соответствует большей части практических приложений).
Хотя простое расширение границ приводит к менее удовлетворительным результатам в центральной области восстановленного изображения, чем аподизация, оно всегда позволяет извлечь больший объем информации, содержащийся в истинном изображении. Такая процедура эффективна также как метод компенсации усечения изображения ![]() . Однако на нее оказывает отрицательное влияние несогласованность операции деконволюции.
. Однако на нее оказывает отрицательное влияние несогласованность операции деконволюции.
В методе расширения границ с перекрыванием несогласованность свертки устраняется тем, что предварительно обработанное изображение ![]() считается периодическим. Плоскость изображения следует рассматривать как состоящую из смежных кадров
считается периодическим. Плоскость изображения следует рассматривать как состоящую из смежных кадров ![]() , равных кадру
, равных кадру ![]() . Будем называть эти кадры основными ячейками. Внутренняя ячейка, представляющая собой кадр, конгруэнтный области
. Будем называть эти кадры основными ячейками. Внутренняя ячейка, представляющая собой кадр, конгруэнтный области 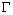 , центрирована с каждой основной ячейкой. Под границей ячейки понимается граница между основной и соответствующей внутренней ячейкой. Под предварительно обработанным записанным изображением по-прежнему будем понимать изображение, задаваемое определением
, центрирована с каждой основной ячейкой. Под границей ячейки понимается граница между основной и соответствующей внутренней ячейкой. Под предварительно обработанным записанным изображением по-прежнему будем понимать изображение, задаваемое определением
![]() при
при ![]() ,
,
![]() при
при ![]() .
.
Таким образом, область 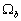 следует рассматривать как бесконечно повторяющуюся в плоскости изображения, так что в каждой основной ячейке будет находиться копия изображения
следует рассматривать как бесконечно повторяющуюся в плоскости изображения, так что в каждой основной ячейке будет находиться копия изображения ![]() . Каждую копию области
. Каждую копию области 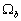 назовем исходной ячейкой. Поскольку область
назовем исходной ячейкой. Поскольку область 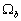 больше области
больше области ![]() , изображения на каждой исходной ячейке переходят и в соседние основные ячейки. Эффект перекрывания имеет место только в пределах границ ячеек. Следовательно, изображение
, изображения на каждой исходной ячейке переходят и в соседние основные ячейки. Эффект перекрывания имеет место только в пределах границ ячеек. Следовательно, изображение ![]() совпадает с изображением
совпадает с изображением ![]() на каждой внутренней ячейке, но отличается тем, что оно соответствующим образом скорректировано в пределах границы каждой ячейки. Конечно, такая коррекция должна обеспечить периодичность изображения
на каждой внутренней ячейке, но отличается тем, что оно соответствующим образом скорректировано в пределах границы каждой ячейки. Конечно, такая коррекция должна обеспечить периодичность изображения ![]() в том смысле, что его функциональное поведение повторяется в окрестностях противоположных точек (которые определяются далее). Значение интенсивности изображения
в том смысле, что его функциональное поведение повторяется в окрестностях противоположных точек (которые определяются далее). Значение интенсивности изображения ![]() в произвольной точке на внешней границе основной ячейки должно быть зеркальным повторением значения интенсивности изображения в противоположной точке, которая определяется следующим образом. Если ось
в произвольной точке на внешней границе основной ячейки должно быть зеркальным повторением значения интенсивности изображения в противоположной точке, которая определяется следующим образом. Если ось ![]() проходит через основную ячейку, то двумя противоположными точками называются точки пересечения оси
проходит через основную ячейку, то двумя противоположными точками называются точки пересечения оси ![]() с внешней границей основной ячейки.
с внешней границей основной ячейки.
Отметим, что изображением ![]() , полученным в результате расширения границ с перекрыванием в пределах каждой основной ячейки, аппроксимируется периодически продолженное идеальное искаженное изображение. Практически успешность процедуры расширения границ сильно зависит от выполнения следующего требования "гладкости". Изображение
, полученным в результате расширения границ с перекрыванием в пределах каждой основной ячейки, аппроксимируется периодически продолженное идеальное искаженное изображение. Практически успешность процедуры расширения границ сильно зависит от выполнения следующего требования "гладкости". Изображение ![]() в пределах границы произвольной ячейки должно быть по крайней мере столь же гладким, как и изображение
в пределах границы произвольной ячейки должно быть по крайней мере столь же гладким, как и изображение ![]() в пределах любой внутренней ячейки. Оценку выполнения этого требования вполне допустимо осуществлять визуально. Данным требованием предотвращается появление в изображении
в пределах любой внутренней ячейки. Оценку выполнения этого требования вполне допустимо осуществлять визуально. Данным требованием предотвращается появление в изображении ![]() ложных составляющих с высокими пространственными частотами, благодаря чему повышается общая устойчивость процесса восстановления изображений. Еще одно преимущество процедуры расширения границ с перекрыванием перед процедурой простого расширения состоит в том, что покрывается менее половины области и допускается меньше произвола. Эта процедура требует минимума экстраполяции для заполнения границы каждой ячейки и поэтому оказывается, вообще говоря, более точной. Если вспомнить основную задачу деконволюции, то методы простого расширения границ и расширения с перекрыванием можно рассматривать как средства сведения практической задачи деконволюции к задачам, соответственно, идеализированной конечной и периодической деконволюции, но с минимизацией вредного влияния искажений, которые неизбежно зашумляют записанные изображения. Очевидно, что процедуру расширения границ с перекрыванием можно реализовать столь же непосредственно, как и простое расширение границ, но практически она часто дает гораздо лучшие результат ы. Тем не менее процедура простого расширения границ тоже нередко применяется, особенно в тех случаях, когда метод с перекрыванием по какой-либо технической причине нельзя использовать.
ложных составляющих с высокими пространственными частотами, благодаря чему повышается общая устойчивость процесса восстановления изображений. Еще одно преимущество процедуры расширения границ с перекрыванием перед процедурой простого расширения состоит в том, что покрывается менее половины области и допускается меньше произвола. Эта процедура требует минимума экстраполяции для заполнения границы каждой ячейки и поэтому оказывается, вообще говоря, более точной. Если вспомнить основную задачу деконволюции, то методы простого расширения границ и расширения с перекрыванием можно рассматривать как средства сведения практической задачи деконволюции к задачам, соответственно, идеализированной конечной и периодической деконволюции, но с минимизацией вредного влияния искажений, которые неизбежно зашумляют записанные изображения. Очевидно, что процедуру расширения границ с перекрыванием можно реализовать столь же непосредственно, как и простое расширение границ, но практически она часто дает гораздо лучшие результат ы. Тем не менее процедура простого расширения границ тоже нередко применяется, особенно в тех случаях, когда метод с перекрыванием по какой-либо технической причине нельзя использовать.
Потери разрешения в процессе записи, связанные с недостатками устройства, формирующего изображение (например, с аберрациями, которые препятствуют достижению дифракционного предела), можно рассматривать как вклад в полный шум, поскольку они приводят к ухудшению восстановленного изображения, которого можно было бы избежать. Поэтому целесообразно предусматривать процедуру сверхразрешения на этапе предварительной обработки, поскольку эта процедура позволяет иногда воспользоваться преимуществом дуальности частотной плоскости и плоскости изображения для восстановления части потери разрешения без операции деконволюции (последнюю, конечно, можно выполнить позднее, чтобы попытаться в еще большей степени уменьшить потерю разрешения). Отметим в связи с этим также и очень важный психологический фактор. Люди неохотно терпят какие-либо ограничения. Поэтому так естественно попытаться превзойти дифракционный предел!
Предположим, что некоторый спектр записывается на интервале длиной ![]() прямой линии с центром в начале частотной плоскости. Из теоремы о проекции следует, что результат преобразования Фурье наблюдаемого спектра представляет собой проекцию с разрешением по пространственной частоте, равным
прямой линии с центром в начале частотной плоскости. Из теоремы о проекции следует, что результат преобразования Фурье наблюдаемого спектра представляет собой проекцию с разрешением по пространственной частоте, равным ![]() . Очевидно, что данная проекция может иметь сверхразрешение, если известно, как расширить спектр за границы интервала длиной
. Очевидно, что данная проекция может иметь сверхразрешение, если известно, как расширить спектр за границы интервала длиной ![]() . Поскольку истинное изображение реконструируется по его проекциям, ясно, что нужно достичь сверхразрешения данных и в двумерном случае, если то возможно в одномерном случае.
. Поскольку истинное изображение реконструируется по его проекциям, ясно, что нужно достичь сверхразрешения данных и в двумерном случае, если то возможно в одномерном случае.
Для этого необходимо рассмотреть одномерное изображение конечной протяженности ![]() и его фурье-образ
и его фурье-образ ![]() .
.
Если ![]() - функция конечной протяженности, то
- функция конечной протяженности, то ![]() - целая функция, а значит, спектр
- целая функция, а значит, спектр ![]() аналитически продолжается на всю частотную плоскость при условии, что функция
аналитически продолжается на всю частотную плоскость при условии, что функция 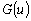 точно известна в конечном диапазоне значений
точно известна в конечном диапазоне значений ![]() . Но именно последнее условие часто приводит к неприятностям. Все виды "шума", которые неизбежно искажают результаты измерений, обычно столь сильно ограничивают диапазон "продолжения" пространственных частот, что указанная выше возможность редко оказывается реализуемой практически. Некоторое улучшение может быть достигнуто, если разложить функцию
. Но именно последнее условие часто приводит к неприятностям. Все виды "шума", которые неизбежно искажают результаты измерений, обычно столь сильно ограничивают диапазон "продолжения" пространственных частот, что указанная выше возможность редко оказывается реализуемой практически. Некоторое улучшение может быть достигнуто, если разложить функцию 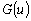 на сферические гармоники и воспользоваться их свойством одновременной ортогональности в конечном и бесконечном диапазонах, но зашумленность снова, как правило, снижает эффективность такой процедуры. Основная причина того, почему изложенный выше подход к сверхразрешению редко оказывается успешным (даже если исходное разрешение сравнительно низкое), состоит в том, что при таком подходе не учитывается условие вещественности и неотрицательности значений изображения. К сожалению, не ясно, как включить эти ограничения в описанную методику аналитического продолжения. Необходимы другие подходы, описанные ниже.
на сферические гармоники и воспользоваться их свойством одновременной ортогональности в конечном и бесконечном диапазонах, но зашумленность снова, как правило, снижает эффективность такой процедуры. Основная причина того, почему изложенный выше подход к сверхразрешению редко оказывается успешным (даже если исходное разрешение сравнительно низкое), состоит в том, что при таком подходе не учитывается условие вещественности и неотрицательности значений изображения. К сожалению, не ясно, как включить эти ограничения в описанную методику аналитического продолжения. Необходимы другие подходы, описанные ниже.
Много говорилось о возможностях в отношении сверхразрешения, предоставляемых методом мак симальной энтропии, который наиболее удобно рассматривать с использованием ДПФ. Мы рассмотрим только одномерный случай. Определим энтропию ![]() следующим образом:
следующим образом:
| (1) |
Неотрицательная вещественная константа ![]() обычно полагается равной нулю или единице. Но, по-видимому, нет особых оснований для такого ограничения, если исходить из термодинамических аналогий. Единственный критерий приемлемости метода обработки изображений - это качество получаемых результатов, а потому можно испробовать и другие значения константы
обычно полагается равной нулю или единице. Но, по-видимому, нет особых оснований для такого ограничения, если исходить из термодинамических аналогий. Единственный критерий приемлемости метода обработки изображений - это качество получаемых результатов, а потому можно испробовать и другие значения константы ![]() . Рассматриваемый метод заключается в продолжении функции
. Рассматриваемый метод заключается в продолжении функции 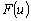 , обеспечивающем максимум энтропии
, обеспечивающем максимум энтропии ![]() . Вся суть этого метода, возможно, в том, что логарифмы в определении (1) исключают получение отрицательных значений для изображения с вещественными значениями. Данный метод частот приводит к впечатляющим результатам, но они очень сильно за висят от некоторых деталей истинного изображения, например спектр
. Вся суть этого метода, возможно, в том, что логарифмы в определении (1) исключают получение отрицательных значений для изображения с вещественными значениями. Данный метод частот приводит к впечатляющим результатам, но они очень сильно за висят от некоторых деталей истинного изображения, например спектр 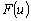 может резко измениться, если к изображению
может резко измениться, если к изображению 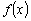 добавить небольшой фон. В настоящее время метод максимальной энтропии изучен недостаточно, чтобы о нем можно было судить вполне объективно. Однако это один из немногих методов, при которых в сверхразрешенном изображении автоматически учитывается требование неотрицательности.
добавить небольшой фон. В настоящее время метод максимальной энтропии изучен недостаточно, чтобы о нем можно было судить вполне объективно. Однако это один из немногих методов, при которых в сверхразрешенном изображении автоматически учитывается требование неотрицательности.
Более совершенный метод сверхразрешения - алгоритм Герхберга. Этот алгоритм является устойчивым в большом числе случаев, хотя, конечно, уровень зашумленности ограничивает достижимую степень сверхразрешения. Кроме того, данный алгоритм является гибким и удобным для эффективной реализации в двумерном случае. Несколько близких алгоритмов вытекают из следующего обобщения алгоритма Герхберга.
Пусть ![]() и
и ![]() - верхняя и нижняя границы величины
- верхняя и нижняя границы величины ![]() ,
, ![]() и
и ![]() - соответствующие границы величины
- соответствующие границы величины ![]()
| (2) |
| (3) |
Предположим, что существует такая функция 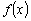 , для которой неравенства (2) и (3) действительно выполняются. Для этого, конечно, нужно лишь, чтобы ограничения были не слишком жесткими. Практика показывает, что при итерационном применении условий (2) и (3) начальная оценка для функции
, для которой неравенства (2) и (3) действительно выполняются. Для этого, конечно, нужно лишь, чтобы ограничения были не слишком жесткими. Практика показывает, что при итерационном применении условий (2) и (3) начальная оценка для функции 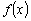 сходится к некоторой функции, скажем
сходится к некоторой функции, скажем ![]() , удовлетворяющей условиям (2) и (3). Кроме того, величина
, удовлетворяющей условиям (2) и (3). Кроме того, величина ![]() уменьшается при сужении указанных ограничений, если это производится постепенно в ходе выполнения итераций. На начальных итерациях важно предусмотреть "запас" при выборе нижних границ для изображения и его спектра. Слишком жесткие границы, при которых функция
уменьшается при сужении указанных ограничений, если это производится постепенно в ходе выполнения итераций. На начальных итерациях важно предусмотреть "запас" при выборе нижних границ для изображения и его спектра. Слишком жесткие границы, при которых функция 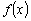 не удовлетворяет условиям (2) и (3), приводят к ложным результатам.
не удовлетворяет условиям (2) и (3), приводят к ложным результатам.
Изложенное выше освещает одну важную сторону преобразования Фурье. Как мы знаем, существует соотношение дуальности между частотной плоскостью и плоскостью изображения,т. е., зная функцию 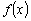 , мы можем найти ее спектр
, мы можем найти ее спектр 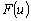 , и наоборот. Формулы (2) и (3) говорят о том, что существует еще и соотношение дуальности для точности, с которой производится восстановление функции
, и наоборот. Формулы (2) и (3) говорят о том, что существует еще и соотношение дуальности для точности, с которой производится восстановление функции 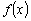 и ее спектра
и ее спектра ![]() . По заданным функциям
. По заданным функциям ![]() и
и ![]() можно рассчитать правильные границы спектра
можно рассчитать правильные границы спектра 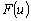 , и наоборот. Еще важнее то, что, зная функции
, и наоборот. Еще важнее то, что, зная функции ![]()
![]() в ограниченной области плоскости изображения и соответствующие спектры
в ограниченной области плоскости изображения и соответствующие спектры ![]() и
и ![]() в ограниченной области частотной плоскости, можно получить согласованную оценку
в ограниченной области частотной плоскости, можно получить согласованную оценку ![]() на плоскости изображения. Кроме того, можно экстраполировать найденные границы в двух данных плоскостях, причем промежутки между верхними и нижними границами, конечно, расширяются с увеличением степени экстраполяции.
на плоскости изображения. Кроме того, можно экстраполировать найденные границы в двух данных плоскостях, причем промежутки между верхними и нижними границами, конечно, расширяются с увеличением степени экстраполяции.
Итак, мы имеем возможность при экстраполяции изображений налагать на изображения не только требование неотрицательности значений изображения, но и его границы. Конкретная априорная информация относительно функции 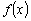 может быть использована непосредственно при расчете функций
может быть использована непосредственно при расчете функций ![]() и
и ![]() . Алгоритмы сверхразрешения оказываются наиболее эффективными в том случае, когда различия между функциями
. Алгоритмы сверхразрешения оказываются наиболее эффективными в том случае, когда различия между функциями ![]() и
и ![]() минимальны.
минимальны.
Поэтому желательно, чтобы имеющаяся априорная информация об изображении в кадре ![]() , относилась к возможно большей части кадра и даже выходила за его пределы. Интересным примером к сказанному могут служить изображения гористых поверхностей планет и их спутников, освещаемых Солнцем под малым углом, полученные с космических кораблей. Такие изображения почти не зависят от атмосферных эффектов и содержат обширные области глубокой тени. Если сделать вполне допустимое априорное предположение о том, что теневые области черные и имеют резкие границы, то мы получим основу для ограничений в алгоритмах сверхразрешения. Записанное изображение соответствующим образом калибруется и сглаживается, а затем интерполируется для увеличения числа отсчетов (например, в 4 раза в каждом направлении). Производится идентификация теневых областей, после чего применяется алгоритм сверхразрешения. В одномерных реализациях этого подхода нам удавалось в 3 раза повысить разрешение полных изображений.
, относилась к возможно большей части кадра и даже выходила за его пределы. Интересным примером к сказанному могут служить изображения гористых поверхностей планет и их спутников, освещаемых Солнцем под малым углом, полученные с космических кораблей. Такие изображения почти не зависят от атмосферных эффектов и содержат обширные области глубокой тени. Если сделать вполне допустимое априорное предположение о том, что теневые области черные и имеют резкие границы, то мы получим основу для ограничений в алгоритмах сверхразрешения. Записанное изображение соответствующим образом калибруется и сглаживается, а затем интерполируется для увеличения числа отсчетов (например, в 4 раза в каждом направлении). Производится идентификация теневых областей, после чего применяется алгоритм сверхразрешения. В одномерных реализациях этого подхода нам удавалось в 3 раза повысить разрешение полных изображений.
Заметим, что разность функций 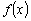 и
и ![]() можно разбить на две части:
можно разбить на две части:
| (4) |
где ![]() и
и ![]() - корректируемая и некорректируемая составляю щие шума, определяемые следующим образом:
- корректируемая и некорректируемая составляю щие шума, определяемые следующим образом: ![]() удовлетворяет ограничениям (это означает, что данная составляющая не меняется при выполнении алгоритма), а <
удовлетворяет ограничениям (это означает, что данная составляющая не меняется при выполнении алгоритма), а < ![]() не удовлетворяет ограничениям (откуда следует, что эта составляющая постепенно уменьшается по амплитуде в ходе итерационного процесса). Термин "шум" мы используем здесь в несколько другом смысле, чем раньше, но это не оказывает какого-либо влияния на ход наших рассуждений. Заметим, что алгоритм сверхразрешения может быть эффективным, только если функции
не удовлетворяет ограничениям (откуда следует, что эта составляющая постепенно уменьшается по амплитуде в ходе итерационного процесса). Термин "шум" мы используем здесь в несколько другом смысле, чем раньше, но это не оказывает какого-либо влияния на ход наших рассуждений. Заметим, что алгоритм сверхразрешения может быть эффективным, только если функции ![]() и
и ![]() не флуктуируют в противофазе друг с другом и если величина
не флуктуируют в противофазе друг с другом и если величина ![]() в общем превышает величину
в общем превышает величину ![]() . На практике эти условия часто выполняются.
. На практике эти условия часто выполняются.
Любая априорная информация, которая может быть включена в алгоритм экстраполяции, полезна. Хорошим примером применения нашей процедуры может служить случай подчеркивания деталей изображения. Само собой разумеющееся предположение о том, что деталь имеет некоторую форму,- очень ценная априорная информация. Она позволяет ввести кадр определенной формы, размеры которого несколько больше размеров детали и за пределами которого функция ![]() равна нулю. Это пример простого, но сильного ограничения, при котором алго ритмы сверхразрешения оказываются очень эффективными.
равна нулю. Это пример простого, но сильного ограничения, при котором алго ритмы сверхразрешения оказываются очень эффективными.
Литература.
1. Бейтс Р., Мак-Доннелл М. Восстановление и реконструкция изображений: Пер. с англ.- М.: Мир, 1989. - 336.
2. Bracewell R.N. The Fourier Transform and its Applications. - N.Y.: McGraw-Hill, 1978.
Реконструкция размытых изображений в MATLAB
Рассмотрим некоторые подходы к решению задачи восстановления изображений с использованием функции протяженности точки. При реализации алгоритмов в среде MATLAB будем использовать соответствующие функции (deblurring functions) пакета Image Processing Toolbox.
Определим некоторые понятия, которыми будем пользоваться в процессе изложения материала.
Деконволюция - процесс, обратный к свертке.
Оператор (функция) искажения - это оператор, который используется для моделирования искаженных изображений. Искажения, вносимые функцией протяженности точки, являются аналогичными тем, которые возникают на практике.
Функция оптического преобразования - в частотной области функция оптического преобразования характеризует отзыв линейной, инвариантной системы на импульс. Функция оптического преобразования является Фурье-преобразованием функции протяженности точки.
Функция протяженности точки - в пространственной области функция протяженности точки характеризует степень, с которой оптическая система размывает (распространяет) точечный свет. Функция протяженности точки является инверсным преобразованием Фурье от функции оптического преобразования.
Рассмотрим коротко основы технологии обработки размытых изображений.
Причины размытости изображений.
Причиной низкого качества (размытости) изображений могут быть различные факторы. Это может быть перемещение камеры в процессе захвата изображений, большое время экспозиции, розфокусировка, атмосферная турбулентность, рассеяние света в конфокальных микроскопах и т. д.
Модель размытых изображений.
Размытые и искаженные изображения приближенно могут быть описаны выражением
![]() ,
,
где ![]() - размытое изображение;
- размытое изображение;
![]() - оператор искажения, определяемый функцией протяженности точки. Свертка этой функции с изображением, является причиной искажений;
- оператор искажения, определяемый функцией протяженности точки. Свертка этой функции с изображением, является причиной искажений;
![]() - исходное изображение;
- исходное изображение;
![]() - аддитивный шум, который вносится во время захвата изображений и искажает их.
- аддитивный шум, который вносится во время захвата изображений и искажает их.
Функция протяженности точки
Исходя из рассмотренной модели, фундаментальная задача восстановления размытых изображений состоит в деконволюции размытого изображения с функцией протяженности точки, которая в точности отображает искажения. Качество обработки размытых изображений определяется, главным образом, знаниями о функции протяженности точки.
Проиллюстрируем это на примере. Для создания функции протяженности точки используем функцию fspecial, которая будет симулировать искажения, обусловленные движением, зададим также длину размытия (LEN=31), и угол степени размытия (THETA=11). После того, как создана функция протяженности точки, используем, например, функцию imfilter для свертки с исходным изображением I, и создания размытого изображения.
I = imread('peppers.png');
I = I(60+[1:256],222+[1:256],:);
figure; imshow(I); title('Original Image');
LEN = 31;
THETA = 11;
PSF = fspecial('motion',LEN,THETA); % создание функции протяженности точки
Blurred = imfilter(I,PSF,'circular','conv');
figure; imshow(Blurred); title('Blurred Image');
 |
| Исходное изображение Размытое изображение |
Использование функций обработки размытых изображений
В пакете Image Processing Toolbox системы MATLAB существует четыре функции обработки размытых изображений:
- deconvwnr - выполняет восстановление размытых изображений с использованием винероской фильтрации;
- deconvreg - выполняет восстановление размытых изображений с использованием регуляризационных фильтров;
- deconvlucy - выполняет восстановление размытых изображений с использованием алгоритма Лаки-Ричардсона (Lucy-Richardson);
- deconvblind - выполняет восстановление размытых изображений с использованием алгоритма слепой деконволюции;
Функции протяженности точки могут принимать различный вид, который будет определять искажения на изображении. Функция deconvwnr используется при обработке изображений с небольшим разрешением. Функция deconvreg выполняет восстановление минимального квадратного разрешения, которое потом будет характеризовать результирующее изображение. Используя эти функции существует возможность понизить уровень шума в процессе обработки изображений, но при этом нужно задавать некоторые его параметры.
В основу функции deconvlucy положен алгоритм Лаки-Ричардсона (Lucy-Richardson). Эта функция является итерационной, использует технологию оптимизации и статистику Пуассона. Используя эту функцию, не нужно указывать информацию о аддитивном шуме искаженных изображений.
Функция deconvblind используется для реализации алгоритма слепой деконволюции, когда неизвестна функция протяженности точки, искажающая изображение. Результатом работы функции deconvblind является восстановленное изображение и функция протяженности точки. При выполнении алгоритма используются итерационные модели, аналогичные функции deconvlucy.
Восстановление размытых изображений методами винеровской фильтрации
Для восстановления изображений функция deconvwnr использует фильтр Винера. Винеровская деконволюция может быть эффективной, когда частотная характеристика изображения и аддитивного шума известны, хотя бы в небольшой степени. При отсутствии шума фильтр Винера превращается в идеальный инверсный фильтр.
Для восстановления размытых изображений используется модель, учитывающая те особенности функции протяженности точки, которые являются причинами искажений. Когда функция протяженности точки известна точно, тогда результат восстановления размытых изображений очень хороший.
1. Считываем изображение в рабочее пространство MATLAB.
I = imread('peppers.png');
I = I(10+[1:256],222+[1:256],:);
figure;imshow(I);title('Original Image');

Исходное изображение
2. Создание функции протяженности точки.
LEN = 31;
THETA = 11;
PSF = fspecial('motion',LEN,THETA);
3. Симуляция размытости на изображении.
Blurred = imfilter(I,PSF,'circular','conv');
figure; imshow(Blurred);title('Blurred Image');
Размытое изображение
4. Восстановление размытого изображения.
wnr1 = deconvwnr(Blurred,PSF);
figure;imshow(wnr1);
title('Restored, True PSF');

Изображение восстановленное методами винеровской фильтрации
Анализ результатов обработки
Результаты работы функции deconvolution можно использовать для определения оптимальных аргументов при реализации функции deconvwnr. Используя эти аргументы можно определить соотношение шум-сигнал и/или автокорреляционную функцию для усовершенствования результатов восстановления.
Структурное распознавание на основе меры схожести символьных строк
Существуют различные подходы к решению задачи распознавания объектов. В этом материале будут рассмотрены некоторые методы структурного распознавания. Суть структурного распознавания состоит в представлении интересующих объектов в виде символьных строк, деревьев, графов и других дескрипторов. Также важным моментом является формирование критериев распознавания на основе выбранного описания объектов.
В отличие от других подходов, особенностью структурного метода распознавания является то, что он работает только с информацией, представленной в символьном виде. Следует отметить, что система Matlab имеет целый ряд специализированных функций для обработки символьных строк. Однако, кроме различных функций обработки, для решения задач распознавания необходимо иметь меру схожести символьных строк, которая бы работала аналогично формулам вычисления расстояний между n-мерными векторами.
Мера схожести символьных строк
Одна из таких мер была предложена Тзе и Янгом в 1981 году. Наиболее простую меру схожести строк можно представить в виде следующего аналитического выражения
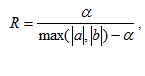
где a, b – строки;
α – число совпадений между строками a и b.
Рассмотренная мера равна бесконечности при полном совпадении строк и равна нулю, когда таких совпадений не существует.
Далее рассмотрим задачу распознавания объектов на основе сопоставления строк.
Пример 1.
Считаем изображения трех различных объектов – круга (рис. 1), квадрата (рис. 2) и треугольника (рис. 3).
L=imread('im1.bmp');
L=L(:,:,1);
L=double(L)./255;
iptsetpref('ImshowBorder','tight');
figure, imshow(L);

Рис. 1. Изображение круга.
L=imread('im2.bmp');
L=L(:,:,1);
L=double(L)./255;
iptsetpref('ImshowBorder','tight');
figure, imshow(L);

Рис. 2. Изображение квадрата.
L=imread('im3.bmp');
L=L(:,:,1);
L=double(L)./255;
iptsetpref('ImshowBorder','tight');
figure, imshow(L);

Рис. 3. Изображение треугольника.
Чтобы продемонстрировать эффективность рассмотренной выше меры схожести для распознавания объектов, сначала границы представленных объектов необходимо приблизить ломаной линией с различными параметрами (различным размером ячейки приближения).
Приближение ломаной линией минимальной длины
Если речь идет о приближении, то сразу возникает вопрос о точности такого приближения. Наиболее точным приближение будет тогда, когда число отрезков ломаной и число точек границы будут совпадать. Однако на практике суть такого приближения состоит в том, чтобы с помощью наименьшего количества отрезков приблизить форму объекта так, чтобы она была узнаваема. Для этого можно использовать функцию minperpoly [1].
Сформируем результаты приближения контуров объектов функцией minperpoly с различной длиной ячейки (2, 5 и 11 пикселей).
Для первого объекта (круга)
cellsize=2;
[x,y]=minperpoly(L,cellsize);
L1=zeros(256);
figure, imshow(L1);
line([y;y(1)],[x;x(1)],'color',[1 1 1]);

Рис. 4. Приближение контура первого объекта (круга) с размером ячеек 2.
cellsize=5;
[x,y]=minperpoly(L,cellsize);
L1=zeros(256);
figure, imshow(L1);
line([y;y(1)],[x;x(1)],'color',[1 1 1]);
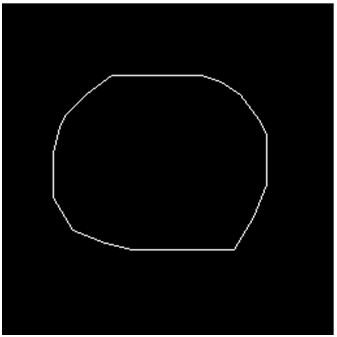
Рис. 5. Приближение контура первого объекта (круга) с размером ячеек 5.
cellsize=11;
[x,y]=minperpoly(L,cellsize);
L1=zeros(256);
figure, imshow(L1);
line([y;y(1)],[x;x(1)],'color',[1 1 1]);

Рис. 6. Приближение контура первого объекта (круга) с размером ячеек 11.
Аналогично приближаем контуры двух других объектов (квадрата и треугольника) с различным размером ячеек.

Рис. 7. Приближение контура второго объекта (квадрата) с размером ячеек 2.

Рис. 8. Приближение контура второго объекта (квадрата) с размером ячеек 5.

Рис. 9. Приближение контура второго объекта (квадрата) с размером ячеек 11.

Рис. 10. Приближение контура третьего объекта (треугольника) с размером ячеек 2.

Рис. 11. Приближение контура третьего объекта (треугольника) с размером ячеек 5.

Рис. 12. Приближение контура третьего объекта (треугольника) с размером ячеек 11.
Таким образом, сформированы три набора изображений различных объектов – круга, квадрата и треугольника. А каждый набор состоит из изображений приближенного контура одного и того же объекта, но с различным размером ячеек.
На основе этих данных можем вычислить меру схожести строк изображений в пределах одного набора, а также между наборами данных.
Для этого будем использовать выражение, которое приведено в начале этого материала и реализовано в виде функции strsimilarity [1]:
L=imread('image1.bmp');
L=L(:,:,1);
L1=imread('image2.bmp');
L1=L1(:,:,1);
R1=strsimilarity(char(L(64,:)),char(L1(64,:)))
R2=strsimilarity(char(L(128,:)),char(L1(128,:)))
R3=strsimilarity(char(L(192,:)),char(L1(192,:)))
Представим полученные данные в виде таблиц.
Таблица 1. Вычисление меры схожести строк для изображения круга
| Изображение приближения контура круга с размером ячеек 5 (рис. 5) | Изображение приближения контура круга с размером ячеек 11 (рис. 6) | Номер строки | |
| Изображение приближения контура круга с размером ячеек 2 (рис. 4) | |||
| 127 | 20,3333 | n=64 | |
| 63 | 16,0667 | n=128 | |
| 2,0843 | 2,0843 | n=192 |
Таблица 2. Вычисление меры схожести строк для изображения квадрата
| Изображение приближения контура квадрата с размером ячеек 5 (рис. 8) | Изображение приближения контура квадрата с размером ячеек 11 (рис. 9) | Номер строки | |
| Изображение приближения контура квадрата с размером ячеек 2 (рис. 7) | |||
| 84,3333 | 18,6923 | n=64 | |
| 127 | 24,6000 | n=128 | |
| 127 | 35,5714 | n=192 |
Таблица 3. Вычисление меры схожести строк для изображения треугольника
| Изображение приближения контура треугольника с размером ячеек 5 (рис. 11) | Изображение приближения контура треугольника с размером ячеек 11 (рис. 12) | Номер строки | |
| Изображение приближения контура треугольника с размером ячеек 2 (рис. 10) | |||
| 127 | 9,6667 | n=64 | |
| 50,2000 | 127 | n=128 | |
| 225 | 17,2857 | n=192 |
Таблица 4. Вычисление меры схожести строк для изображений из различных наборов, которые были приближены с размером ячейки 2
| Изображение приближения контура квадрата с размером ячеек 5 (рис. 7) | Изображение приближения контура треугольника с размером ячеек 11 (рис. 10) | Номер строки | |
| Изображение приближения контура круга с размером ячеек 2 (рис. 4) | |||
| 2,7647 | 2,3684 | n=64 | |
| 13,2222 | 1,9091 | n=128 | |
| 2,0118 | 3,0635 | n=192 |
Таблица 5. Вычисление меры схожести строк для изображений из различных наборов, которые были приближены с размером ячейки 5
| Изображение приближения контура квадрата с размером ячеек 5 (рис. 8) | Изображение приближения контура треугольника с размером ячеек 11 (рис. 10) | Номер строки | |
| Изображение приближения контура круга с размером ячеек 5 (рис. 5) | |||
| 2,8209 | 2,3684 | n=64 | |
| 11,8000 | 2,1605 | n=128 | |
| 0,5422 | 0,7655 | n=192 |
Таблица 6. Вычисление меры схожести строк для изображений из различных наборов, которые были приближены с размером ячейки 11
| Изображение приближения контура квадрата с размером ячеек 5 (рис. 9) | Изображение приближения контура треугольника с размером ячеек 11 (рис. 12) | Номер строки | |
| Изображение приближения контура круга с размером ячеек 11 (рис. 6) | |||
| 2,8209 | 1,9091 | n=64 | |
| 22,2727 | 2,4133 | n=128 | |
| 0,5901 | 0,9394 | n=192 |
Проанализируем полученные данные. Из представленных в таблицах данных видно, что в большинстве случаев значение коэффициента схожести строк изображений в пределах одного набора (таблицы 1-3) значительно выше значений коэффициентов схожести строк изображений из различных наборов (таблицы 4-6). Это свойство лежит в основе рассматриваемого структурного распознавания объектов.
Пример 2.
Рассмотрим еще один пример структурного распознавания на основе сопоставления строк. Однако теперь к координатам точек приближенного контура (x,y) объекта будет добавлен некоторый шум.
x=x+p.*randn(length(x),1);
y=y+p.*randn(length(y),1);
где p = 1,3,7 – параметр, который устанавливает уровень зашумленности.
В результате описанных преобразований получим следующий набор данных.

Рис. 13. Приближение контура круга с добавлением шумовой составляющей при p=1.

Рис. 14. Приближение контура круга с добавлением шумовой составляющей при p=3.

Рис. 15. Приближение контура круга с добавлением шумовой составляющей при p=7.

Рис. 16. Приближение контура квадрата с добавлением шумовой составляющей при p=1.

Рис. 17. Приближение контура квадрата с добавлением шумовой составляющей при p=3.

Рис. 18. Приближение контура квадрата с добавлением шумовой составляющей при p=7.
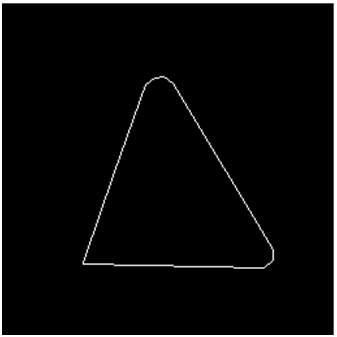
Рис. 19. Приближение контура треугольника с добавлением шумовой составляющей при p=1.

Рис. 20. Приближение контура треугольника с добавлением шумовой составляющей при p=3.
Рис. 21. Приближение контура треугольника с добавлением шумовой составляющей при p=7.
На основе полученных изображений вычисляется значение меры схожести строк соответствующих данных. Результаты проведенных вычислений представлены в таблицах 7-10.
Таблица 7. Вычисление меры схожести строк для изображений круга с различным уровнем наложенного шума.
| Изображение приближения контура круга с размером ячеек 8 и p=3 (рис. 14) | Изображение приближения контура круга с размером ячеек 8 и p=7 (рис. 15) | Номер строки | |
| Изображение приближения контура круга с размером ячеек 8 и p=1 (рис. 13) | |||
| 63 | 27,4444 | n=74 | |
| 255 | 27,4444 | n=128 | |
| 27,4444 | 12,4737 | n=182 |
Таблица 8. Вычисление меры схожести строк для изображений квадрата с различным уровнем наложенного шума.
| Изображение приближения контура квадрата с размером ячеек 8 и p=3 (рис. 17) | Изображение приближения контура квадрата с размером ячеек 8 и p=7 (рис. 18) | Номер строки | |
| Изображение приближения контура квадрата с размером ячеек 8 и p=1 (рис. 16) | |||
| 35,5714 | 31 | n=74 | |
| 41,6667 | 35,5714 | n=128 | |
| 63 | 17,2857 | n=182 |
Таблица 9. Вычисление меры схожести строк для изображений треугольника с различным уровнем наложенного шума.
| Изображение приближения контура треугольника с размером ячеек 8 и p=3 (рис. 20) | Изображение приближения контура треугольника с размером ячеек 8 и p=7 (рис. 21) | Номер строки | |
| Изображение приближения контура треугольника с размером ячеек 8 и p=1 (рис. 19) | |||
| 50,2000 | 10,1304 | n=74 | |
| 41,6667 | 16,0667 | n=128 | |
| 35,5714 | 84,3333 | n=182 |
Таблица 10. Вычисление меры схожести строк для изображений разных объектов с одинаковым уровнем наложенного шума.
| Изображение приближения контура квадрата с размером ячеек 8 и p=7 (рис. 18) | Изображение приближения контура треугольника с размером ячеек 8 и p=7 (рис. 21) | Номер строки | |
| Изображение приближения контура круга с размером ячеек 8 и p=7 (рис. 15) | |||
| 3,3390 | 1,8132 | n=74 | |
| 11,8000 | 1,8764 | n=128 | |
| 6,1111 | 11,1905 | n=182 |
В данном эксперименте нами проведены вычисления значений меры схожести для двух наборов изображений. Первый набор состоял из изображений одного и того же объекта, но с различным уровнем наложенного шума. Второй набор – это изображения разных объектов с одинаковым уровнем наложенного шума. Значения коэффициента схожести для набора изображений одного и того же объекта значительно выше значений коэффициентов схожести, которые вычислены для изображений разных объектов.
Таким образом, для выбора (распознавания) нужного изображения объекта из базы данных поступают следующим образом. Необходимо иметь изображение объекта, который необходимо распознать – так называемый эталон. Далее вычисляют значение меры схожести строк изображения эталона и каждого изображения из базы. Максимальное значение меры схожести будет соответствовать максимально похожему на эталон объекту.
Программы, которые используются в материале.
1) Приближение границ объектов.
clear;
%Считывание исходного изображения
L=imread('im1.bmp');
%Использование одной цветовой составляющей
L=L(:,:,1);
L=double(L)./255;
iptsetpref('ImshowBorder','tight');
%Визуализация исходного изображения
figure, imshow(L);
%Приближение границ объектов ломаной минимальной длины
cellsize=7; %Размер ячейки
[x,y]=minperpoly(L,cellsize);
x=
L1=zeros(256);
figure, imshow(L1);
line([y;y(1)],[x;x(1)],'color',[1 1 1]);
2) Вычисление меры схожести.
clear;
%Считывание исходных данных
L=imread(im1.bmp');
L=L(:,:,1);
L1=imread('im2.bmp');
L1=L1(:,:,1);
%Вычисление меры схожести
R1=strsimilarity(char(L(74,:)),char(L1(74,:)))
R2=strsimilarity(char(L(128,:)),char(L1(128,:)))
R3=strsimilarity(char(L(182,:)),char(L1(182,:)))
- Rafael C. Gonsales, Richard E. Woods, Steven L. Eddins. Digital Image Processing using Matlab. Rafael
Границы изображений: Края и их обнаружение
Рассмотрим задачу выделения и локализации краев (границ). Края — это такие кривые на изображении, вдоль которых происходит резкое изменение яркости или ее производных по пространственным переменным. Наиболее интересны такие изменения яркости, которые отражают важные особенности изображаемой поверхности. К ним относятся места, где ориентация поверхности меняется скачкообразно, либо один объект загораживает другой, либо ложится граница отброшенной тени, либо отсутствует непрерывность в отражательных свойствах поверхности и т.п. В любом случае нужно локализовать места разрывов яркости или ее производных, чтобы узнать нечто о вызвавших их свойствах изображенного объекта. Рассмотрим также применение дифференциальных операторов для выделения тех особенностей изображения, которые помогают локализовать участки, где можно обнаружить фрагмент края.
Вполне естественно, что зашумленность измерений яркости ограничивает возможность выделить информацию о краях. Мы обнаруживаем противоречие между чувствительностью и точностью, и приходим к выводу, что короткие края должны обладать большей контрастностью, чем длинные, чтобы их можно было распознать. Выделение краев можно рассматривать как дополнение к сегментации изображения, поскольку края можно использовать для разбиения изображений на области, соответствующие различным поверхностям.
Интуитивно краем обычно является граница между двумя областями, каждая из которых имеет приблизительно равномерную яркость. Часто края на изображениях возникают как результат наличия силуэтных линий объектов. В этом случае две упомянутые области являются изображениями двух разных поверхностей. Края также возникают из-за отсутствия непрерывности в ориентации поверхности и разрывов в ее отражательных свойствах. Если мы возьмем сечение функции яркости вдоль прямой, расположенной под прямым углом к краю, то, как правило, обнаружим скачок в ее значениях. На практике перепад не будет резким ввиду размывания и ограничений, вносимых зрительным устройством. Кроме того, иногда яркостные перепады вдоль краев лучше моделируются в виде скачков в первых производных яркости, нежели в самой яркости.
Ниже мы воспользуемся простой моделью для получения некоторого представления об операторах, которые могли бы усилить (обострить) края на изображении, увеличивая перепады яркости в их окрестности. Изображения с обостренными краями необходимо подвергнуть дальнейшей обработке для выделения линий и кривых. До сих пор наибольшие усилия концентрировались именно на задаче обострения краев и меньше — на обнаружении и локализации их фрагментов, однако недавно положение дел изменилось. Меньше всего внимания уделялось работе над объединением фрагментов краев в более крупные единицы, т. е. в линии и кривые на изображении.
Дифференциальные операторы
Простейшей моделью края на изображении является прямая, разделяющая две контрастные области (рис. 1). Нам понадобится единичная ступенчатая функция и (z), определяемая в виде
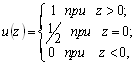
имея в виду, что она является интегралом от одномерного единичного импульса:
![]() .
.
Предположим, что край располагается вдоль прямой ![]() . Тогда яркость изображения можно записать в виде
. Тогда яркость изображения можно записать в виде
![]() .
.
Частные производные описываются уравнениями:
![]() ,
,
![]() .
.
![]()
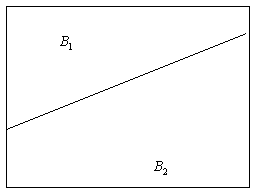
Рис. 1. Идеальный край в виде прямой, разделяющей две области постоянной яркости.
Эти дифференциальные операторы являются направленными, поскольку результат их действия зависит от ориентации края. Вектор (![]() ,
, ![]() ) называется градиентом яркости. Градиент яркости представляет собой вектор, не зависящий от выбора системы координат, в том смысле, что он сохраняет свою величину и ориентацию по отношению к лежащему в основе образу, когда этот образ поворачивается или сдвигается.
) называется градиентом яркости. Градиент яркости представляет собой вектор, не зависящий от выбора системы координат, в том смысле, что он сохраняет свою величину и ориентацию по отношению к лежащему в основе образу, когда этот образ поворачивается или сдвигается.
Дискретные аппроксимации
Рассмотрим группу элементов изображения размером 2x2:
![]()
![]()
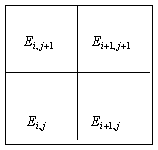
Производные в центральной точке этой группы можно оценить следующим образом:
![]() ,
,
![]() ,
,
где ![]() — расстояние между центрами соседних элементов. Каждая оценка представляет собой среднее двух конечно-разностных приближений.
— расстояние между центрами соседних элементов. Каждая оценка представляет собой среднее двух конечно-разностных приближений.
Конечно-разностная аппроксимация производной всегда относится к определенной точке. Так, обычная конечно-разностная формула дает оценку, которая является несмещенной по отношению к точке, расположенной посередине между точками отсчета оцениваемой функции. Формулы, приведенные выше для оценки частных производных, выбраны именно такими потому, что они не смещены относительно одной и той же точки, а именно относительно общей угловой вершины в центре четырех рассматриваемых элементов изображения (пикселов). Теперь квадрат градиента можно аппроксимировать следующим образом:
![]() .
.
Если выполнить эти простые вычисления для всего изображения, то мы получим большие значения в тех местах, где яркость изменяется быстро. В областях постоянной яркости выход равен нулю. (Если присутствует шум, то выход отличен от нуля, но достаточно мал.) Результаты такой обработки можно занести в новый массив изображения, в котором края уже будут значительно усилены.
Аналогично рассматривают группу элементов размером 3![]() 3.
3.
Выделение и локализация края
Если сигнал, полученный в результате усиления краев, существенно превышает шум, мы можем сделать вывод о том, принадлежит ли определенная точка краю или нет. Такое решение не является абсолютно надежным, так как добавляемый шум в данной точке может оказаться значительным. Все, что мы можем сделать,— это уменьшить вероятность подобного события, выбирая порог таким образом, чтобы число ошибочно отнесенных к краю точек лежало в допустимых пределах.
Если порог слишком высок, слабовыраженные края будут пропущены. Таким образом, существует противоречие между двумя видами ошибок. Увеличивая размер участков, по которым производится усреднение, или (что одно и то же) уменьшая частоту, выше которой подавляются частотные компоненты изображения, мы можем снизить влияние шума и упростить выделение слабовыраженных краев. Однако тут же мы сталкиваемся с противоположной проблемой, вызванной тем, что с увеличением участков в них могут попасть другие края. Тем самым мы видим, что для распознавания коротких краев необходимо, чтобы они были более контрастны.
Изображение с обостренными краями будет иметь большие значения яркости не только в тех пикселах, которые непосредственно расположены на крае, но и в некоторых соседних. Этот эффект особенно ярко проявляется в тех случаях, когда в целях уменьшения шума изображение предварительно сглаживается. Отсюда возникает проблема локализации краев. Если бы не шум, мы могли бы надеяться обнаружить максимальные значения яркости непосредственно на крае. Эти экстремальные значения могли бы затем использоваться для подавления соседних больших значений.
При использовании в качестве оператора квадрата градиента на обработанном изображении каждому краю будет соответствовать гребень с высотой, пропорциональной квадрату перепада яркости. В случае операторов Лапласа или квадратичной вариации возникнут два параллельных гребня по каждую сторону от края. При использовании лапласиана эти гребни будут иметь противоположные знаки и край будет проходить там, где происходит смена знака.
Рано или поздно будет необходимо выяснить физическую причину возникновения края. Что в трехмерной сцене вызвало изменения в функции яркости, обнаруженные детектором края? До настоящего времени на эту проблему обращали мало внимания.
Основную часть последних достижений в задаче выделения краев можно отнести на счет попыток построения оптимальных операторов выделения края и более детального изучения противоречия между выделением и локализацией. Многое, конечно, зависит от выбора критерия оптимальности и базовой модели изображения. Играет роль также ограниченность простейшей модели края как идеальной ступенчатой функции, на которую наложен шум, и упоминались более реалистичные альтернативы.
Одна из проблем, связанных с разработкой методов выделения краев, состоит в том, что предположения, на которых они основаны, часто неприложимы в реальных случаях. Хотя многие поверхности на самом деле обладают постоянной отражательной способностью, неверно, что их изображения будут иметь равномерную яркость. Яркость зависит от многих факторов. И обратно, элементы изображения, соответствующие точкам поверхности различных объектов, могут иметь одинаковые полутоновые уровни. Только в особых случаях изображение можно с пользой рассматривать как совокупность областей постоянной яркости.

Рис. 2. Фотография некоторой карты.
|
а ) |
б ) |
|
в ) |
г ) |
|
д ) |
е ) |
Рис. 3. Участки краев, выделенные детектором края: а) фильтр Собеля; б) фильтр Превита; в) фильтр Робертса; г) фильтр лапласиан–гауссиан; д) линейный фильтр; е) фильтрация методом Канни.
Одна из трудностей при разработке вычислительных схем для выделения краев заключается в недостаточно ясной формулировке самого задания. Как нам узнать, был ли край “пропущен” или где-то появился “ложный” край? Ответ на этот вопрос зависит от того, как мы собираемся использовать результат.
Для иллюстрации некоторых из изложенных выше мыслей здесь приводятся результаты, полученные реализацией различных операторов выделения краев. На рис. 2 показано изображение некоторой карты. Рис. 3 демонстрирует результат работы различных детекторов края с этим изображением.
В пакете обработки изображений (Image Processing Toolbox) системы MATLAB операции выделения края реализуются с помощью функции edge.
Литература
- Criffith A.K., Edge Detection in Simple Scenes Using A Priori Information, IEEE Trans. On Computers, 22, № 5, 551 – 561 (1971).
- Хорн Б.К.П. Зрение роботов: Пер. с англ. – М.; Мир, 1989. – 487 с., ил.
Оптимизация палитры изображений
Одной из наиболее удобных форм представления информации, которая возникает при разного рода исследованиях, является изображение. Все изображения можно условно разделить на четыре типа - бинарные, полутоновые, палитровые и полноцветные. Бинарные и полутоновые представляют собой двумерные массивы чисел, которые являются эквивалентами яркостей. Полноцветные изображения хранятся в виде трехмерных массивов. Для доступа к значениям интенсивностей, составляющих цвета пикселя, необходимо указать координаты (k, l) и номер составляющей: 1 - для R, 2 - для G и 3 - для B. Палитровые изображения хранятся в виде двумерных массивов, в трех столбцах которых размещены значения интенсивностей R, G, B.
Каждый графический файл состоит из двух основных частей - оглавления и непосредственно данных. В первой части содержится информация о структуре графического файла. Рассмотрим палитровые изображения как наиболее распространенные. В большинстве случаев после оглавления в файле палитрового изображения помещена палитра цветов. Для реальных изображений эта палитра имеет большие размеры, что существенно влияет на объем графического файла.
При передаче информации по каналам связи, а также при решении некоторых практических задач важным является минимизация размера файла. Этого можно достичь за счет оптимизации палитры изображения. Искажение визуального качества при этом должно быть минимально.
К решению этой актуальной задачи можно подходить по-разному. Известные подходы, которые базируются на так называемой "безопасной" палитре или выборе наиболее встречающихся цветов, не дают хорошего результата. Это объясняется тем, что при преобразованиях с фиксированной палитрой, не проводится анализ цветности обрабатываемого изображения. Поэтому для изображений, которые содержат лишь оттенки одного цвета, метод с использованием "безопасной" палитры неэффективен. Метод, основанный на использовании наиболее встречающихся цветов, хорошо обрабатывает изображения, которые содержат много оттенков, и неэффективен для обработки изображений с большим количеством основных цветов.
Это привело к необходимости создания в некоторой степени универсального метода преобразования палитры цветных изображений. Анализ известных подходов подтолкнул к использованию кластерного анализа гистограммы изображений. Рассмотрим методы кластерного анализа более детально.
Каждая независимая измеряемая величина называется признаком. Основная парадигма заключается в том, чтобы выбрать п измеряемых величин объекта, подлежащего классификации, и затем рассмотреть результат как точку в n-мерном пространстве признаков. Вектор признаков образуется как совокупность этих величин. Было исследовано много различных алгоритмов для разбиения пространства признаков на части, используемые для классификации. Считается, что неизвестный объект принадлежит классу, соответствующему той части, в которую попал вектор признаков.
Что все это значит для машинного видения? После того как изображение разбито на сегменты, измерения можно производить в каждой области изображения. Затем можно попытаться идентифицировать объект, породивший каждую область, с помощью классификации, основанной на этих измерениях. Примерами простых характеристик являются площадь, периметр, минимальный и максимальный моменты инерции области бинарного изображения.
Для этих методов необходимо получение достаточной информации, обеспечивающей оптимальное разбиение n-мерного пространства характеристик. Если мы знаем истинные распределения вероятностей, границы разбиения можно выбрать так, чтобы минимизировать некоторый критерий допустимых ошибок. Однако, обычно эти распределения оцениваются по конечному числу примеров, взятых из каждого класса, и часто можно работать непосредственно с этой информацией, а не с оценкой плотности вероятности.
Основным предположением здесь является то, что точки, принадлежащие одному и тому же классу, образуют кластер, а точки, принадлежащие различным классам, разделены. Иногда эти предположения не подтверждаются: методы классификации образов не годятся, например, для различения рациональных и иррациональных чисел или черных и белых квадратов на шахматной доске.
Серьезной проблемой в применении машинного видения является то, что изображение представляет собой двумерную проекцию трехмерного реального тела. Трудно решить задачу в полном объеме, пользуясь лишь простыми характеристиками, основанными непосредственно на изображении и не зависящими от пространственного положения объекта, освещения и расстояния до объекта. Методы распознавания образов будут хорошо работать лишь тогда, когда они основываются на характеристиках, которые не зависят от конкретных методов получения изображения, т.е. когда мы можем оценить истинные свойства объекта, например, отражательную способность и форму. Но для этого, естественно, задача распознавания должна быть уже в основном решена.
Классификация по ближайшему соседу
Предположим, что имеются образцы, полученные для каждого класса. Пусть xi,j - вектор признаков для j-го образца i-го класса. Один из возможных путей для классификации неизвестного вектора х заключается в нахождении образца, ближайшего к неизвестному, и определении класса, к которому он относится. Для некоторых k и l это означает, что если |xk,l -x|<|хi,j - x| для всех i и j, то неизвестный х принадлежит классу k.
При использовании этой простой идеи возникают две проблемы. Во-первых, хотя образцы, соответствующие отдельным классам, часто образуют кластеры, эти кластеры могут перекрываться. Неизвестный вектор, попавший в область перекрытия, может рассматриваться как принадлежащий тому классу, представитель которого оказался поблизости. Классификация в таких областях по существу случайна. Возможно, что это лучшее, что можно сделать, однако простая граница всегда предпочтительнее.
Возможно, мы получим лучшие результаты, если просмотрим несколько соседей. Неизвестному вектору можно, например, приписать класс, встречающийся чаще всего среди k ближайших соседей. Это приведет к несколько лучшим результатам в пересекающихся областях, так как обеспечит оценку того, для какого из классов получилась наибольшая плотность вероятности.
Вторая проблема при классификации по ближайшему соседу связана с вычислениями. Если примеров много, то требуется большой объем памяти. Более того, если не использовать какой-либо схемы для разделения пространства, придется вычислять расстояние между неизвестным объектом и всеми образцами. Тем не менее, это хороший метод, который не требует многих предположений о распределении вероятностей для представителей класса.
В некоторых случаях кластеры образуют не перекрывающиеся пятна. Если выпуклые оболочки кластеров не пересекаются, грани выпуклой оболочки можно использовать вместо всех образцов в кластере. В конечном счете, это приводит к значительной экономии, как времени, так и вычислений.
Большим преимуществом классификации по ближайшему соседу является то, что кластеры могут иметь сложную форму; им не обязательно быть симметричными относительно вращения или даже выпуклыми.
Классификация по ближайшей центроиде
Теперь предположим, что образцы каждого класса образуют шарообразный кластер и что кластеры, соответствующие различным классам, примерно одинакового радиуса и не слишком пересекаются друг с другом. В этом случае запоминать все образцы для каждого класса кажется расточительным. Вместо этого можно использовать для представления каждого класса его центр тяжести. Считается, что неизвестный вектор принадлежит тому классу, центр тяжести которого находится к нему ближе всего.
Использование этого метода позволяет значительно уменьшить и память, и вычисления. Более того, классы здесь разделяются гладкими границами. Отметим, что эти компоненты являются гипермногогранниками, ограниченными гиперплоскостями. (Гипермногогранники — это обобщение выпуклого многогранника для числа измерений больше трех. Они образуются пересечением полупространств.) Чтобы показать, что границы являются гиперплоскостями, предположим, что х — точка на границе между частями, содержащими центроиды 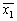 и
и 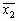 , тогда
, тогда 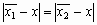 . Возведя в квадрат обе части равенства, получим
. Возведя в квадрат обе части равенства, получим 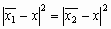 или
или 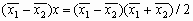 . Это уравнение линейно по х. Оно описывает гиперплоскость с нормалью
. Это уравнение линейно по х. Оно описывает гиперплоскость с нормалью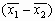 , проходящую через точку
, проходящую через точку 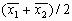 . Таким образом, границей является гиперплоскость, ортогонально секущая пополам отрезок, соединяющую две центроиды.
. Таким образом, границей является гиперплоскость, ортогонально секущая пополам отрезок, соединяющую две центроиды.
Этот простой метод разделения пространства признаков хорошо работает в том случае, когда кластеры симметричны относительно вращения и примерно одинаковых радиусов, или когда они хорошо разделены.

Рис. 1. Диаграмма разброса площадей цитоплазмы и ядра для пяти типов белых кровяных телец. Буква обозначает различные классы, подчеркнутая буква — центроиду. Штриховые линии показывают линейные границы, оптимально разделяющие классы. Несколько образцов классифицировано неверно.
Автоматическое формирование кластера
Иногда кластеры, образуемые точками, выражены настолько явно, что можно попытаться построить автоматический способ определения принадлежности точек одному и тому же кластеру. Как правило, это связано с самообучением. Некоторые из этих методов используют последовательное слияние имеющихся кластеров. Сначала каждая точка данных рассматривается как отдельный эмбриональный кластер. На каждом шаге итерационного процесса выявляются два кластера, содержащие две точки, расположенные друг к другу ближе, чем любые две точки других кластеров. Эти два кластера сливаются. Итерационный процесс заканчивается, когда, либо найдено ожидаемое число кластеров, либо расстояние до следующей точки, добавляемой к кластеру, превышает заданный порог. Для управления этими процессами разработаны многочисленные эвристики.
Противоположная стратегия разъединяет имеющиеся кластеры вдоль линий "разрежения". Первоначально весь набор точек рассматривается как один большой кластер. На каждом этапе определяется кластер, который можно разбить на два. Итерационный процесс заканчивается когда, либо достигнуто желаемое число кластеров, либо дальнейшее разбиение неперспективно по некоторому предварительно определенному критерию. Однако в большинстве интересующих нас случаев мы знаем, какие точки принадлежат одному классу.
Применение методов кластеризации эффективно при разработке методов машинного видения. Классическим примером применения кластеризации являются методы распознавания символом. Также методы кластерного анализа применяются при оптимизации палитры изображений, что, в свою очередь, актуально при решении задач компактного представления данных при их передаче.
- Duda R. O., Hart P.E., Pattern Classification and Scene Analysis, john Wiley & Sons, New York, 1973.
- Хорн Б.К.П. Зрение роботов: Пер. с.англ. - М.: Мир, 1989. - 487 с., ил.
Кодирование и сжатие изображений: задачи кодирования
Визуальная информация, подлежащая обработке на ЭВМ, может вводиться в запоминающее устройство со специального датчика (устройства ввода) или представлять собой результат некоторых вычислений. В том и другом случае такая информация сопоставляется с некоторой картиной, зрительно воспринимаемой человеком. Это сопоставление по сути и является принципиальным отличием визуальной информации от числовой, логической, символьной или какой-либо другой, которая может быть представлена в памяти ЭВМ [4].
Очевидно, что визуальная информация должна с определенной степенью точности отражать состояние яркости или прозрачности каждой точки зрительно воспринимаемой картины. Для простоты в дальнейшем будем рассматривать только плоские картины. Чтобы представить визуальную информацию в цифровой форме, необходимо дискретизировать пространство (плоскость) и проквантовать значение яркости в каждой дискретной точке. Наиболее просто и естественно дискретизация достигается с помощью координатной сетки, образованной линиями, параллельными осям х и у декартовой системы координат. В каждом узле такой решетки делается отсчет яркости или прозрачности носителя зрительно воспринимаемой информации, которая затем квантуется и представляется в памяти ЭВМ. Рисунок 1 иллюстрирует процесс кодирования на примере изображения с четырьмя градациями яркости.
 |
|
| a) | b) |
| Рис. 1. Кодирование визуальной информации: а - исходное изображение; б - его рецепторное представление. | |
Результат представлен на рис. 1, б в виде матрицы, элементами аij которой служат отсчеты в узлах решетки.
Такое представление визуальной информации называется рецепторным [3], естественным [1], поэлементным или матричным [2]. Оно заслуживает внимания хотя бы потому, что наиболее удобно описывает процессы ввода и вывода изображений и позволяет легко установить однозначное соответствие между картиной и ее представлением в памяти ЭВМ. Широкий класс датчиков, используемых для ввода оптической информации в ЭВМ, представляет собой набор светочувствительных элементов (рецепторов), преобразующих световой сигнал в электрический. В процессе ввода рецепторы, расположенные в узлах рецепторной сетки, опрашиваются в определенной последовательности и снимаемые с них сигналы преобразуются в цифровую форму. Таким образом получается последовательность отсчетов в узлах координатной сетки. Например, при использовании телевизионных датчиков, информация, содержащаяся в телевизионном кадре, считывается построчно, т. е. отсчеты во времени образуют следующую последовательность:
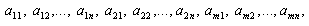
где aij - элемент матрицы отсчетов, расположенный на пересечении i-й строки и j-го столбца; m - число строк матрицы, соответствующее числу строк в кадре; n - число столбцов матрицы, соответствующее числу элементов в строке.
При использовании других датчиков (например, твердотельных) отсчеты могут выдаваться в иной последовательности. Во всех случаях поэлементный способ представления изображений находит применение в качестве промежуточного при считывании визуальной информации. Этот способ удобно использовать и при отображении информации на видеоконтрольных устройствах. В связи с этим задачу кодирования визуальной информации будем рассматривать как задачу преобразования естественной формы представления в форму, удобную для хранения и обработки в ЭВМ.
Учитывая, что любая обработка информации может рассматриваться как ее перекодирование, будем отличать первичные, или абсолютные, кодовые описания от вторичных, или относительных [1]. Не давая строгих определений, укажем лишь на два существенных отличия таких кодовых описаний. Во-первых, первичные способы представления в отличие от вторичных должны быть универсальными, т. е. допускать возможность восстановления соответствующего изображения с точностью, определяемой параметрами рецепторной решетки и числом К уровней квантования, и не учитывать специфику вводимых изображений или дальнейших алгоритмов их обработки. Во-вторых, первичное представление можно достаточно просто получить из естественного так, чтобы перекодирование осуществлялось относительно простыми устройствами в процессе ввода информации в ЭВМ. Примером первичного описания визуальной информации служит ее поэлементное кодирование. Вторичные способы представления информации могут существенно отличаться от первичных (или естественного) и получаться в результате достаточно сложных алгоритмов обработки визуальной информации. Например, можно предложить весьма компактные способы представления принципиальных электрических схем, основанные на перечислении элементов, встречающихся в схеме, с указанием мест расположения на чертеже самих элементов и соединяющих их линий. В качестве примера вторичного описания можно привести описание изображения в некотором пространстве признаков, используемых в дальнейшем для распознавания образов.
Для того чтобы далее формализовать задачу кодирования, удобно более четко выделить структурные единицы визуальной информации. Назовем всю подлежащую записи в ЭВМ визуальную информацию картиной или сценой. Будем предполагать, что она представлена в естественной форме. На размеры картины никаких ограничений не накладывается. В частном случае ее размеры могут превышать размеры рецепторного поля оптического датчика, используемого для ввода информации в ЭВМ. В этом случае картина разбивается на прямоугольные области, называемые растрами или кадрами (рис. 2).
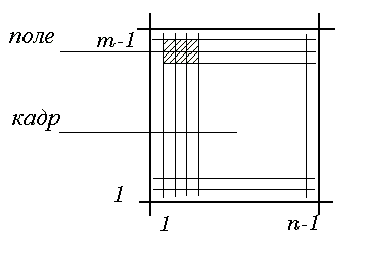 |
| Рис. 2. Структурные единицы машинного представления визуальной информации |
Каждый растр по размерам соответствует рецепторному полю датчика и содержит mxn отсчетов, образующих прямоугольную матрицу, состоящую из m строк и п столбцов. Каждый отсчет характеризуется числом К уровней квантования видеосигнала. Обычно полагают K=2k, где k - целое. Иногда выделяют еще одну структурную единицу информации - поле. Поле - это часть кадра, образованная несколькими соседними отсчетами. Параметры m, n и k выбирают в зависимости от требуемой точности представления информации с учетом возможностей оптического датчика. Например, если в качестве такого датчика используют телекамеру, работающую в стандартном режиме, число строк и столбцов растра обычно изменяется в пределах от 256 до 512, а число различимых уровней серого не превышает 256 (k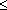 8).
8).
В общем случае для поэлементной записи кадра требуется память, содержащая
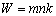 |
(2) |
бит информации. Если оценить W, то можно убедиться в том, что для поэлементного представления кадра требуется значительный объем памяти. Например, пусть m=n=256 и k=6. В этом случае W=6·216. При определении способа размещения информации в памяти ЭВМ необходимо учитывать тот факт, что память ЭВМ имеет словарную структуру, т. е. существует минимальное адресуемое слово фиксированной длины s. В общем случае s не равно и не кратно k. Здесь можно предложить два подхода к решению задачи размещения отсчетов в словах памяти ЭВМ.
В первом из них для представления визуальной информации используют все разряды всех слов выделенного массива. В этом случае достигается наибольшая компактность представления и требуется меньший объем памяти. Его оценка при поэлементном кодировании дается формулой (2). Однако такое размещение неудобно для обработки информации, так как некоторые отсчеты оказываются размещенными в нескольких словах. При другом подходе каждый отсчет целиком представляется некоторым машинным словом. Но при этом в общем случае используются не все разряды машинных слов, что приводит к увеличению требуемого объема памяти. Например, если принять подход, при котором каждый отсчет размещается в отдельном слове, то для представления одного кадра потребуется mn машинных слов.
Естественно сформулировать задачу кодирования как задачу получения такого представления визуальной информации, которое занимает минимальный объем памяти ЭВМ и в то же время удобно для обработки. Практическая значимость минимизации объема памяти становится более очевидной, если учесть, что во многих случаях требуется анализировать картины значительных размеров, содержащие сотни, а может быть тысячи растров. Чтобы получить какие-то численные оценки, рассмотрим реальный пример, в котором размеры обрабатываемой картины составляют 200x300 мм и каждый отсчет представляется словом, содержащим восемь двоичных разрядов. Если при этом шаг рецепторной сетки равен 0,1 мм, то потребуется память порядка 6 Мбайт.
Оценим качество или эффективность кода средним количеством бит, приходящихся на один отсчет:
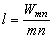 |
(3) |
где Wmn - объем памяти, требуемый для представления одного кадра размером mxn.
Если не учитывать возможные потери, обусловленные словарной организацией памяти, для поэлементного способа кодирования в соответствии с (3) l=k. Предполагая, что требуемый при поэлементном кодировании объем памяти удается сократить, положим lmax=k .Введем в рассмотрение коэффициент сокращения
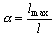 |
(4) |
характеризующий сокращение объема памяти по сравнению с по элементным кодированием.
Основные методы кодирования
Для оценки возможностей и путей построения эффективных кодов, рассмотрим математическую модель визуальной информации. Будем считать, что значение яркости в каждой точке (х, у) представляется случайной функцией F(x,y) , а отсчет а есть случайная величина, выбранная из конечной генеральной совокупности 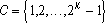 . Можно предложить несколько моделей случайного выбора, отличающихся сложностью описания и степенью соответствия реальным процессам. В простейшей из них положим, что отсчеты независимы и каждый из них принимает i=e значение с вероятностью p(i) , т. е. p(a=ai)=p(ai) , ai
. Можно предложить несколько моделей случайного выбора, отличающихся сложностью описания и степенью соответствия реальным процессам. В простейшей из них положим, что отсчеты независимы и каждый из них принимает i=e значение с вероятностью p(i) , т. е. p(a=ai)=p(ai) , ai 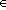 C . В этом случае энтропия hi(a) каждого отсчета а равна
C . В этом случае энтропия hi(a) каждого отсчета а равна
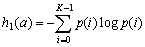 |
(5) |
Если сделать еще одно упрощающее предположение и принять, что все значения отсчетов равновероятны, т. е. p(i)=1/K , получим h1=k бит. В этом частном случае в соответствии с теоремой Шеннона [4] не существует способов кодирования, для которых l<k .
Сжатие информации возможно, если принять во внимание неравномерность распределения значений отсчетов и их взаимную зависимость. Оценку сокращения избыточности за счет учета неравномерности распределения дает формула (5), т.е. максимальный коэффициент сокращения (4) равен k/h1 . Как показали исследования телевизионных изображений, избыточность, вносимая не одинаковой вероятностью значений отсчетов, относительно невелика и позволяет сократить объем памяти не более чем в 1,5 раза.
Более существенного сокращения можно достичь, если учесть реально существующую статистическую зависимость между отсчетами. Наиболее просто учесть такую зависимость, описывая последовательность отсчетов цепью Маркова [4]. С этой целью линейно упорядочим отсчеты в соответствии с каким-либо способом сканирования плоскости, например в виде (1). В первом приближении примем во внимание зависимость только между соседними отсчетами. Опишем такую зависимость с помощью условных вероятностей p(i/j) . Здесь p(i/j) - вероятность того, что отсчет имеет значение i при условии, что предыдущий равен 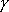 . Тогда условная энтропия h2(a/j) символа цепи Маркова, вычисленная при условии, что предыдущий символ имеет значение j , равна
. Тогда условная энтропия h2(a/j) символа цепи Маркова, вычисленная при условии, что предыдущий символ имеет значение j , равна
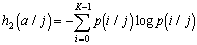
Выражение для безусловной энтропии h2(a) можно получить, усреднив h2(a/j) :
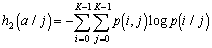 |
(6) |
где p(j,i)=p(j)p(i/j) - вероятность события, заключающегося в том, что два соседних символа имеют значения j , i . Формула (6) допускает естественное обобщение, когда модель учитывает статистическую зависимость каждого отсчета от поля изображения A(r-1) , содержащего r-1 отсчетов:
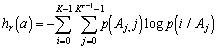 |
(7) |
где p(Aj,i) - вероятность события, заключающегося в том, что после r-1 отсчетов, образующих слово Aj , следует отсчет с яркостью i ; p(i/Ai) - условная вероятность того, что после комбинации Ai следует отсчет с яркостью i . Естественно, что h1 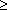 h2
h2 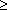 h3 (при r
h3 (при r 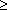 2 ). Причем hr зависит от того, какие r-1 элементов изображения образуют поле A(r-1) . Обычно рассматривают статистическую зависимость между несколькими соседними элементами каждой строки и каждого столбца матрицы отсчетов. Полагая l=hr , можно получить оценку максимально достижимых коэффициентов сокращения для каждой модели визуальной информации.
2 ). Причем hr зависит от того, какие r-1 элементов изображения образуют поле A(r-1) . Обычно рассматривают статистическую зависимость между несколькими соседними элементами каждой строки и каждого столбца матрицы отсчетов. Полагая l=hr , можно получить оценку максимально достижимых коэффициентов сокращения для каждой модели визуальной информации.
Учет статистической зависимости между отсчетами лежит в основе построения первичных способов кодирования визуальной информации. Такие коды интенсивно разрабатывали и исследовали в основном для передачи телевизионных изображений, и соответствующие результаты довольно широко представлены в литературе. Очевидно, что коды, используемые только для передачи и воспроизведения изображений и коды, предназначенные для обработки изображений в ЭВМ, должны удовлетворять различным требованиям. Во-первых, к таким кодам предъявляют разные требования по точности представления изображения. При передаче телевизионных изображений предполагается, что в конце передачи картина будет воспроизведена на экране телевизора и воспринята человеком. Поэтому при создании соответствующих кодов учитывают свойства зрения. Оказывается, что не всегда изображение, субъективно воспринимаемое как хорошее, достаточно точно отображает отдельные детали, необходимые для промышленного зрения. Во-вторых, процессы кодирования и декодирования информации при ее передаче существенно отличаются от процессов хранения и обработки информации в ЭВМ. В результате, коды, допускающие достаточно простую аппаратную реализацию передачи информации, оказываются "неудобными" для представления информации в ЭВМ. Так, коды, используемые в цифровом телевидении, не учитывают особенности словарной структуры памяти ЭВМ, используемые в ЭВМ способы адресации информации и организации массивов и их описаний, возможности многократного считывания отдельных элементов изображения, а также ряд других особенностей программной обработки информации. Несмотря на весомость отличий в требованиях, предъявляемых к кодам, методы кодирования, используемые в цифровом телевидении, при выборе способа представления визуальной информации в ЭВМ заслуживают самого тщательного изучения. Ниже приводится краткий обзор таких методов.
Статистические методы кодирования информации.Статистические коды относятся к неравномерным, т. е. одинаковым по размерам элементам изображения присваиваются кодовые слова неравной длины. Сжатие информации достигается за счет того, что для представления наиболее вероятных значений яркостей выбирают короткие кодовые слова, а для наименее вероятных - длинные.
Относительно просто такой код получается, если принять модель, в которой отсчеты считаются независимыми. Если известно распределение вероятностей p(i) , то для построения эффективных кодов можно воспользоваться методикой Хаффмена или Шеннона - Фано [4]. При этом можно получить хорошее приближение к предельно достижимому коэффициенту сокращения, затрачивая на представление каждого символа в среднем слово длиною h1 бит.
Сложнее строятся коды, в которых учитывается статистическая зависимость между яркостями в соседних точках изображения. В этом случае кодовое слово, сопоставленное определенному значению яркости, изменяется в зависимости от значения яркости в предшествующей точке. Таким образом, способ кодирования каждого i-ro отсчета определяется значением соседнего (i-1)-го отсчета. Построить эффективные коды можно по следующей методике. Перебираются все возможные значения яркости j=0,1,2,...,2k-1 предшествующего элемента и для каждого j строится свой код Хаффмена или Шеннона - Фано, исходя из распределения условных вероятностей p(i/j) . В качестве предшествующего элемента обычно используют соседний отсчет в строке или столбце. Как показали соответствующие исследования телевизионных изображений, на этом пути можно сжать изображение в два-три раза.
Дальнейшее сокращение объема памяти можно получить, если учитывать не один, а одновременно два или три соседних отсчета. Однако при этом существенно усложняется процедура кодирования и декодирования, а выигрыш относительно невелик. Так, учет двух предыдущих элементов (например, соседних по строке и столбцу) позволяет сократить описание, получающееся при учете только одного соседнего элемента, на 20-25%. В связи с этим кодирование триад широкого распространения не получило.
Другой подход к кодированию изображения с учетом предшествующего элемента заключается в представлении разностей соседних отсчетов. Разности кодируются по той же методике Хаффмена и Шеннона - Фано с учетом соответствующей функции распределения вероятностей. Теоретический предел сокращения объема памяти при кодировании разностей как и при кодировании пар отсчетов определяется формулой (6).
Статистические методы кодирования обладают двумя существенными недостатками. Во-первых, статистические свойства зависят от характера представляемого изображения. В связи с этим необходим процесс адаптации, что усложняет использование таких кодов. Во-вторых, статистические коды обладают малой помехоустойчивостью. Искажение одного символа влечет искажение и всех последующих. В связи с этим периодически требуется представлять значение некоторых опорных элементов независимо от значений их соседей.
Кодирование серий.Серией называется последовательность отсчетов, имеющих одинаковое значение. Все изображение можно представить в виде последовательности серий. В полутоновых изображениях серии обычно содержат небольшое число элементов. Поэтому в таких случаях переходят к приближенному описанию, определяя серию как последовательность элементов, значения которых отличаются одно от другого не более чем на  , где (
, где (  - порог, определяющий требуемую точность представления информации).
- порог, определяющий требуемую точность представления информации).
Для представления изображений в виде серий задают либо координаты граничных элементов, либо длины серий. Число символов, требуемое для представления строки в двух рассмотренных способах кодирования, совпадает и равно числу серий. Однако количество разрядов, необходимое для представления длин серий, статистически меньше, чем при задании координат граничных элементов. Таким образом, из двух способов кодирование длинных серий требует меньшего объема памяти, но обладает меньшей помехоустойчивостью, так как ошибка в одном коде искажает всю строку. Под представление длины серии отводят элемент списка. Число разрядов этого элемента выбирают меньшим, чем требуемое для представления максимальной длины, равной числу отсчетов в строке. При этом, если длина серии не представляется одним элементом, серия разбивается на несколько серий максимальной длины. Для того чтобы распознать подобные ситуации, в каждом элементе кодирования выделяется поле под представление признака серии - значения яркости отсчетов, принадлежащих серии. Наиболее удобно кодирование серий используется для представления двухградационных изображений.
Кодирование с предсказанием.Основная идея способа кодирования с предсказанием заключается в том, что каждый отсчет ai можно предсказать на основе анализа нескольких предыдущих отсчетов ai1 , ai2 ,…,air . В результате предсказания получается некоторая оценка 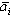 i-го отсчета как функция предыдущих отсчетов
i-го отсчета как функция предыдущих отсчетов
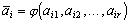 |
(8) |
Для представления изображения используются разности между предсказанными и истинными значениями отсчетов
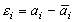 |
(9) |
называемые ошибками предсказания. Если известны значения отсчетов в нескольких базовых точках и матрица ошибок предсказания, то по (8) и (9) можно восстановить изображение. Ошибка предсказания задается одним из ранее рассмотренных способов. При правильно выбранной функции предсказания энтропия ошибок существенно меньше энтропии отсчетов, рассматриваемых без учета взаимосвязи, что и позволяет сократить объем памяти для представления изображения.
Как правило, функция предсказания выбирается из класса линейных:
Причем в качестве предшествующих элементов используют обычно не более трех элементов растра. Соответственно различают одно, двух или трехмерные предсказатели. В одномерном предсказателе значение отсчета предсказывается равным предшествующему в строке, в двухмерном - для предсказания используют значения предшествующего элемента той же строки и соответствующего элемента предыдущей строки, в трехмерном (дополнительно к перечисленным двум) - предшествующий элемент предыдущей строки. Для двух и трехмерных предсказателей коэффициенты выбирают по критерию минимальной среднеквадратичной ошибки предсказания. Предсказание основывается на статистической зависимости каждого отсчета от предшествующих. Максимальный коэффициент сокращения  можно оценить по (4) и (7), положив l=hr(a) .Как показали исследования, кодирование с предсказанием позволяет достичь сжатия информации в 3-3,5 раза.
можно оценить по (4) и (7), положив l=hr(a) .Как показали исследования, кодирование с предсказанием позволяет достичь сжатия информации в 3-3,5 раза.
Прочие методы кодирования.В заключение приведем краткое описание некоторых вариантов кодирования, которые интенсивно развиваются для передачи визуальной информации. Здесь следует прежде всего назвать адаптивные методы кодирования. В них в процессе передачи информации так или иначе исследуются статистические свойства сигналов и в соответствии с результатами корректируется способ кодирования. Поскольку все рассмотренные выше коды опираются на статистические свойства изображений, адаптация возможна для каждого из них. Недостаток адаптивных алгоритмов, затрудняющих их применение для представления визуальной информации в ЭВМ, связан с относительной сложностью декодирования информации. Этот недостаток становится весьма существенным, если в процессе обработки информации значение каждого отсчета необходимо считывать и восстанавливать несколько раз. В связи с этим представляется, что процессы адаптации могут эффективно использоваться в системах промышленного зрения для настройки алгоритмов дискретизации видеосигнала с целью компенсации искажений, обусловленных неравномерностью освещенности и другими аналогичными причинами, но не для представления изображений в памяти ЭВМ.
Широко обсуждаются в литературе алгоритмы кодирования изображений, основанные на преобразованиях Фурье, Адамара, Хаара или Карунена - Лоэва [1-4]. При таком кодировании изображение представляется набором полученных в результате преобразования коэффициентов. Кодирование с преобразованием позволяет достичь существенного сжатия информации и хорошего качества передачи телевизионных сигналов. Однако из-за сложности алгоритмов декодирования оно пока находит применение лишь в специальных системах обработки изображений.
Литература.
- Васильев В.И. Распознающие системы. Справочник. - Киев: Наукова думка, 1983. - 422 с.
- Методы передачи изображений. Сокращение избыточности / У.К. Прэтт, Д.Д. Сакрисон, Х.Г. Мусман и др.; Пер. с англ. / Под ред. У.К. Прэтта. - М., Радио и связь, 1983. - 264 с.
- Томашевский Д.И., Масютин Г.Г., Явич А.А., Преснухин В.В.Графические средства автоматизации проэктирования РЭА. - М.: Сов. радио, 1980. - 224 с.
- Бутаков Е.А. и др. Обработка изображений на ЭВМ/ Е.А.Бутаков, В.И. Островский, И.Л. Фадеев. - М.: Радио и связь, 1987. - 240 с.: ил.
Некоторые области практического применения методов обработки изображений и распознавания образов (геофизические наблюдения, применение в биологии, применение на транспорте)
В данной работе рассматриваются результаты исследований проблем обработки визуальной информации, которые основываются на использовании методов распознавания образов [1-4, 9]. Современное развитие технологий автоматической обработки визуальной информации позволяет применять их в системах технического зрения при выполнении широкого ряда производственных операций, контроля продукции и др.
На этапе исследований методов распознавания объектов на изображении целесообразно использовать систему MATLAB. С помощью функций BWLABEL, IMFEATURE и др. производится поиск и вычисление признаков объектов.
ГЕОФИЗИЧЕСКИЕ НАБЛЮДЕНИЯ
Дистанционное обнаружение
Вряд ли стоит здесь подробно останавливаться на роли и важности наблюдения за поверхностью Земли и других планет — это и различные спутники, и корабли многоразового использования, и орбитальные станции, и многое другое. Каждая из этих систем, наполненных различными приборами и устройствами восприятия, выдает огромные потоки информации. Поскольку число потенциальных потребителей этой информации быстро возрастает, представляется необходимым выполнять автоматическую классификацию наблюдений за минимальное время, согласованное со срочностью запросов. Идеальным было бы обрабатывать каждое изображение по мере его восприятия, т.е. в реальном масштабе времени, и выдавать результаты непосредственно заинтересованным пользователям.
Перечень областей, для которых требуется выполнять орбитальные наблюдения, можно продолжать почти неограниченно. Это обнаружение облачных образований и наблюдение за их изменениями, обнаружение выбросов и загрязнения водных пространств, наблюдение за снежным покровом и ростом сельскохозяйственных культур, оценка ущерба от стихийных бедствий, обнаружение пожаров и засушливых зон, определение изменений береговой линии, обнаружение обильных снегопадов и т.д. К этому можно добавить многочисленные и разнообразные применения в военном деле.
Во многих задачах возникает необходимость автоматической классификации изображений в реальном масштабе времени. Действительно, если, например, получатель информации интересуется ходом роста сельскохозяйственных культур, а изображения полей закрыты густой облачностью, то нет смысла сохранять такие изображения. И наоборот, если для потребителя представляет интерес облачный покров, то такие изображения содержат важные признаки, и они должны быть ему направлены.

Рис. 1. Упрощенная схема процесса телеобнаружения: 1 – Земля; 2 – датчик; 3 – предварительная обработка на борту; 4 – передача телеметрической информации; 5 – прием телеметрической информации; 6 – обработка, классификация, распознавание; 7 – использование.
Упрощенная схема системы дистанционного наблюдения показана на рис. 1. Предварительная обработка данных, выполняемая на борту спутника, необходима для уменьшения влияния атмосферных или иных помех. Такие же операции повторяются на Земле после приема информации с орбиты, наряду с другими операциями (обработки, распределения и др.). В перспективе, по мере развития космической техники, особенно в целях навигации (наземной, морской и воздушной), будут разрабатываться методы обнаружения движущихся объектов, наведения датчиков и отслеживания траекторий, которые могли бы выполняться на борту летательного аппарата.
Одна из наиболее важных задач, примыкающих к этой области, это обнаружение облаков и выработка признаков для автоматического различения их от снегового покрова. Такая операция необходима для устранения ошибок при наведении навигационных приборов.
Применение в сейсмологии
Сейсмические волны можно наблюдать и записывать в любой точке земной поверхности. Для этого предназначены сейсмографы — приборы, обладающие чрезвычайно высокой чувствительностью к механическим колебаниям Земли. Автоматическое дешифрирование этих записей представляет огромный интерес для понимания явлений, происходящих в толще земной коры. В частности, проводились работы по выявлению различий в сейсмограммах, вызванных различными причинами — землетрясениями и ядерными взрывами.
Поскольку сейсмограммы имеют достаточно большую продолжительность, то было предложено [9] отображать их в форме фраз, слов, символов. Такой же метод используется при описании биологических сигналов, в частности, электрокардиограмм и электроэнцефалограмм. Первая и наиболее серьезная трудность на этом пути — представление исходной информации.
Очень важно правильно выбрать параметры первичного разбиения сигнала на отдельные отрезки. Чем они короче, тем более простым оказывается их представление, но в то же время тем длиннее становится время распознавания, так как оно растет пропорционально числу исследуемых отрезков. Кроме того, чем короче отрезки, тем они более чувствительны к шумам. В типовом режиме одна запись длится 120 с., скорость измерений — 10 отсчетов в секунду, и запись делят на 20 отрезков по 60 замеров в каждом.
Типичные примеры записи сейсмограмм показаны на рис. 2. Глаз сразу усматривает сходство между кривыми а и в, а также между б и г, хотя в каждой из этих пар представлены записи, вызванные разными источниками. Это доказывает, что задача классификации не так проста, как кажется на первый взгляд. Кроме того, чем дальше размещен сейсмограф от эпицентра землетрясения или от места взрыва, тем больше визуальное сходство между сигналами.
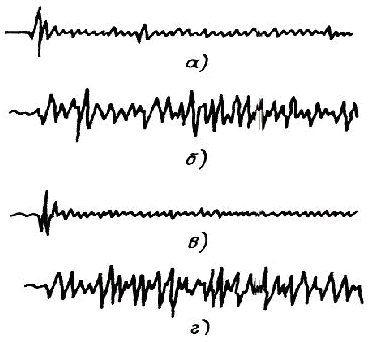
Рис. 2. Примеры сейсмограмм: а, б – землетрясения: в, г – взрывы.
Для решения задачи автоматической классификации в частотной области можно было бы использовать аппарат спектрального анализа. Однако она решается и более простыми средствами, при помощи всего двух признаков, характеризующих каждый отрезок. Это соответственно энергия сигнала за время длительности отрезка и число переходов сигнала через нуль. Множество этих значений и представляет массив исходных данных. Каждый отрезок представляется двухкомпонентным вектором: хг (энергия) и х2 (число переходов через нуль). Можно использовать и другие признаки, но это приводит лишь к усложнению вычислений.
Следующий этап – классификация, устанавливающая связь со словами, входящими в словарь описаний.
Для классификации сейсмических волн была разработана грамматика, реализуемая на детерминированном конечном автомате.
ПРИМЕНЕНИЕ В БИОЛОГИИ
Электрокардиография
Электрокардиография представляет собой один из методов исследования работы сердца, основанный на записи разности электрических потенциалов, возникающей в процессе сердечной деятельности. Диагностические возможности метода исключительно широки. Разность потенциалов снимается с определенных участков поверхности кожи с помощью электродов, изготовленных из соответственно подобранного металла. Поскольку снимаемые сигналы имеют амплитуду порядка милливольт, они поступают на вход усилителя, после которого подаются на регистрацию.
Схематически сердце может быть представлено в виде электрического диполя переменной длины, зависящей от сердечного ритма. Форма электрического сигнала, изменяющегося во времени, и его амплитуда зависят от точки съема. Обычно расположение электродов стандартно. Так, ЭКГ ДП соответствует разности потенциалов между правой рукой и левой ногой. Типичная осциллограмма ЭКГ-сигнала показана на рис. 3.
Буквы PQRST, предложенные Эйнтховеном, позволяют в удобной форме описывать отдельные особенности этой непрерывной кривой. Периодический сигнал ЭКГ имеет сравнительно простую структуру, поэтому уже достаточно давно была предложена процедура его автоматического распознавания на основе грамматического описания [7].
Рис. 3. Типичная электрокардиограмма: 1 – электрическая ось сердца.
Используемая здесь сегментация несколько отлична от той, которая была предложена Эйнтховеном. Описание ЭКГ составляется из четырех символов — р, r, b, t, каждый из которых соответствует определенному участку кривой (см. рис. 3). Символ р соответствует волне Р, r — RS-переходу, b — относительно плоской части, разделяющей экстремумы S и Т (около 0,1 с), t — волне Т. Если за начало отсчета принять волну Р, то в таких обозначениях нормальная ЭКГ может быть описана последовательностями символов: prbtb, prbtbb, prbtbbb и т. д.
Синтаксические описания такого вида могут быть получены с использованием грамматики G:
G=[Vt, Vn, Р, S],
где Vt=[р,r, t, b], Vn=[S, А, В, С, D, E, H], a множество Р правил подстановок таково:
S  pA pA |
A  rB rB |
B  bc bc |
C  D D |
D  b b |
D  bE bE |
E  b b |
E  bH bH |
E  pA pA |
H  b b |
H  bS bS |
H  pA pA |
Такой тип распознающего автомата весьма примитивен: он способен обнаруживать лишь грубые отклонения от нормы. В действительности анализ аномальной ЭКГ представляет собой серьезную задачу, которая выполняется квалифицированным специалистом.
ПРИМЕНЕНИЕ НА ТРАНСПОРТЕ
Распознавание автомобилей
Работы по совершенствованию дорожного движения требуют изучения транспортных потоков. Для того чтобы сведения о частоте движения автомашин были достоверными, необходимо проводить измерения при прохождении автомобилями одного и того же отрезка пути. Одно из возможных решений [9] состоит в том, чтобы характеризовать каждую машину на входе контролируемого участка, а затем распознавать машины на выходе с помощью одних и тех же средств. Обработка данных, полученных таким способом, позволяет получить информацию о плотности и средней скорости движущегося потока.
Известны различные методы распознавания автомашин. Один из них основан на анализе издаваемого ими шума [9], другие — на изучении их теплового портрета [1, 2, 9]. Однако опыт показывает, что для данной задачи эти методы слишком сложны. Хорошие результаты можно получить при помощи значительно более простых средств — подземных датчиков в виде индукционной петли, несложных в изготовлении и обслуживании.
Принцип действия индукционного датчика достаточно прост. На проезжей части, под дорожным покрытием, расположена проволочная петля, связанная с устройством обработки данных. В результате прохождения автомашины импеданс петли изменяется (явление взаимной индукции), вызывая изменение напряжения в схеме, с которой петля соединена. Полученный сигнал после аналого-цифрового преобразования используется для обработки в ЭВМ. Два примера осциллограмм сигналов, вызванных прохождением автомашин, показаны на рис. 4.
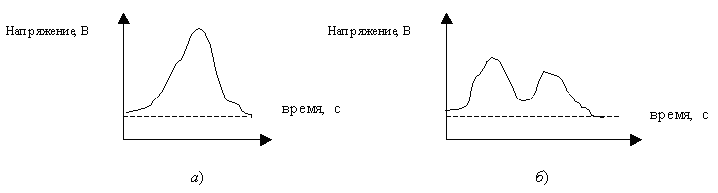
Рис. 4. Осциллограммы сигналов от автомобилей: а – легковая машина; б – грузовая машина с двухосным прицепом.
Формы сигналов от легковой машины и от грузовика сильно отличаются друг от друга. Для удобства дальнейшей обработки сигналы приводят к нормализованному виду путем введения коррекции, зависящей от скорости и траектории движения.
Путем распознавания этих сигналов можно получить данные о средней скорости и количестве машин в единицу времени. Этот метод может быть использован и в других областях, где приходится наблюдать за линейным перемещением как дискретных объектов, так и движущихся непрерывно (листовой прокат, проволока и т.п.).
Распознавание самолетов
Автоматическое распознавание летательных аппаратов (в том числе самолетов) представляет собой исключительно важную задачу для управления воздушным движением. Разумеется, хорошо известны специальные системы активного распознавания с помощью автоответчиков, принцип которых состоит в том, что автоматический приемопередатчик (автоответчик), установленный на борту самолета, излучает определенный код по запросу с Земли. Однако его использование не всегда возможно, поэтому были предложены и другие методы, в частности классификация самолетов по их контурам [5,6-8].
Были разработаны метод грамматического описания контура [9] и грамматика, объем которой должен учесть все разнообразие положений самолета относительно наблюдателя. Однако продолжительность обработки информации этим методом слишком велика и не дает возможности создания прибора, который действовал бы в реальном масштабе времени, по крайней мере, в процессе сближения с самолетом.
Другой метод распознавания основан на использовании инвариантных характеристик контура самолета [9]. В качестве таких инвариант рассматриваются центральные моменты, вычисляемые по формуле:
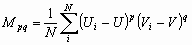
где 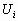 и
и 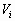 — координаты
— координаты 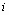 -й точки изображения, a
-й точки изображения, a 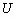 и
и 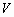 — их средние значения по множеству из
— их средние значения по множеству из 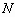 точек. Были исследованы несколько моментов:
точек. Были исследованы несколько моментов:
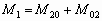
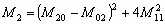
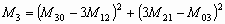 и т. д.
и т. д.
Эти моменты являются составляющими многомерного вектора, описывающего каждый контур. Группирование выполняется по правилу ближайшего соседства. Однако в работе [6] было показано, что при такой классификации несколько различных моделей самолетов попадают в один и тот же класс, а такое совпадение во многих задачах недопустимо.
Третий метод заключается в представлении самолета вектором, составляющими которого являются коэффициенты разложения контура в ряд Фурье. Поскольку контур, как правило, замкнут, то его разлагают в ряд как периодическую функцию. В противном случае разомкнутый контур рассматривают как один период периодической функции [9]. Ряд Фурье записывают в виде:
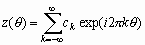 ,
,
где 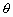 – угол отклонения радиус-вектора z. Комплексные коэффициенты ряда вычисляются:
– угол отклонения радиус-вектора z. Комплексные коэффициенты ряда вычисляются: 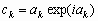 .
.
Достоинство этого метода состоит в том, что при соответствующей нормировке такое описание не зависит от изменения масштаба, угла поворота и сдвига.
Для распознавания необходимо составить библиотеку контуров всех возможных типов самолетов, подлежащих классификации. Разделение на классы выполняется по принципу минимального расстояния от границы раздела классов.
- Фу К., Гонсалес Р., Ли К. Робототехника: Пер.с англ. / Под ред. В.Г.Градецкого. – М.: Мир, 1989. – 624 с.
- J. P. Gambotto et T. S. Huang, "Motion analysis of isolated targets in infrared image sequences", 7th Int. Conf. on Pattern Recognition, Montreal, 1984. P. 534—538.
- J. P. Gambotto, "Correspondance analysis for target tracking in infrared images", 7th Int. Conf. on Pattern Recognition, Montreal, 1984. P. 526—530.
- L. Gerardin, "La bionique", Hachette Paris, 1968.
- Жерарден Л. Бионика. Пер. с франц. М. Н. Ковалевой. Под ред. и с предисл. проф. В. И. Гусельникова. М.: Мир, 1971. 231 с.
- S. С. Guinot, A. Faure, J. P. Lallemand, A. Leblond et D. Murguet, "Etude de systemes mecaniques evolues et rapides dotes d'intelligence artificielle", Contrat DRET 80—624, sept. 1981.
- J. F.Gilmoreet, W. B. Pemberton "Asuivey of aircraft classification algorithms", 7th Int. Conf. on Pattern Recognition, Montreal 1984. P. 559—562.
- R. C. Gonzales et M. G. Thomason, "Syntactic pattern recognition", Edit. Addison Wesley, Londres, 1978. P. 118—120.
- Восприятие и распознавание образов / Пер. С фр. А.В. Серединского; под ред. Г.П. Катыса. - М.: Машиностроение, 1989 г. - 272 с.: ил.
Распознавание рукописных знаков
Задача распознавания рукописных знаков окончательно еще не решена, так как существует много как теоретических, так и практических трудностей, связанных с огромным многообразием возможных написаний отдельных рукописных знаков. Многие работы в этой области так или иначе связаны с общим принципом, который получил название анализа посредством синтеза, предусматривающим, что процедура распознавания строится на основе знаний о процессе синтеза рукописных знаков. На множестве рукописных знаков выделяется несколько элементов, называемых штрихами, из которых можно построить любой символ по определенным правилам соединения штрихов. Генерируемые по этим правилам знаки представляют собой некоторый идеализированный стандарт [1].
В некоторых работах также используется принцип анализа через синтез. В них рассматриваются отдельные рукописные знаки (буквы и цифры) в процессе их написания. Предполагается, что знаки пишутся на сетчатке в виде тонких контурных линий так, как это делается при написании рукописных знаков с помощью светового карандаша на экране дисплея.
Различные реализации рукописных знаков одного класса отличаются друг от друга переносом, масштабом, наклоном, пропорциями и т. д. Для обеспечения инвариантности описания к этим преобразованиям рассматриваются последовательности элементарных направлений, каждое из которых характеризует взаимное расположение двух соседних точек изображения на сетчатке. Всего выбрано восемь возможных элементарных направлений ![]() , а изображение описывается в виде
, а изображение описывается в виде
![]() ,
,
где ![]() ,
, ![]() , --
, -- ![]() -й элемент изображения, являющийся одним из элементарных изображений
-й элемент изображения, являющийся одним из элементарных изображений ![]() ;
; ![]() - длина изображения.
- длина изображения.
Последовательности, состоящие из элементов, направление и порядок следования которых сохраняются постоянными для всех реализаций знаков одного класса, называются штрихами. Искажения изображений знаков одного класса по масштабу и отношению длин отдельных участков вызывают изменение только длины соответствующих штрихов. Изменяя в допустимых пределах длину отдельных штрихов добавлением или выбрасыванием некоторого числа элементов, можно получить множество изображений одного класса. Для соблюдения пропорций знаков при их написании требуется с некоторой точностью вписывать их в рамку определенного размера. Кроме того, для каждого из штрихов изображения данного класса вводятся либо только минимальные, либо минимальные и максимальные размеры. Правило генерации рукописных знаков заключается в добавлении элементов соответствующего направления к штрихам минимальной длины изображения данного класса. В результате применения этого правила генерируются идеализированные рукописные знаки, называемые, как и при использовании принципа допустимых преобразований, эталонами данного класса:
![]() ,
,
где ![]() -
- ![]() -й элемент эталона, определенный на множестве допустимых направлений
-й элемент эталона, определенный на множестве допустимых направлений ![]() .
.
Воздействие шума, вызванного, например, колебанием кончика пера или дискретностью сетчатки, учитывается заданием распределения ![]() , определенного на множестве элементарных направлений.
, определенного на множестве элементарных направлений.
Для построения алгоритма распознавания используется метод максимального правдоподобия. Решающее правило определяется выражением
| (1) |
Здесь максимум ищется по всем классам и всем возможным эталонам длиной ![]() , построенным в соответствии с правилами синтеза. С помощью этого правила ищется эталон длиной
, построенным в соответствии с правилами синтеза. С помощью этого правила ищется эталон длиной ![]() , синтезированный из исходных эталонов минимальной длины, ближайший к изображению
, синтезированный из исходных эталонов минимальной длины, ближайший к изображению ![]() .
.
Для реализации решающего правила (1) вместо величины ![]() можно использовать монотонно убывающую функцию от этой величины. В качестве такой функции предлагается использовать функцию вида
можно использовать монотонно убывающую функцию от этой величины. В качестве такой функции предлагается использовать функцию вида
| (2) |
где ![]() - функция близости элементов входного изображения
- функция близости элементов входного изображения ![]() и эталона
и эталона ![]() , определяемая целым положительным числом, пропорциональным абсолютной величине угла между двумя сравниваемыми элементарными направлениями.
, определяемая целым положительным числом, пропорциональным абсолютной величине угла между двумя сравниваемыми элементарными направлениями.
С учетом выражения (2) решающее правило может быть определено следующим образом:
![]() .
.
Это означает, что среди всех классов ![]() ищется такой класс
ищется такой класс ![]() , эталон длиной
, эталон длиной ![]() которого дает минимальное значение функции отличия (или максимальное значение функции сходства).
которого дает минимальное значение функции отличия (или максимальное значение функции сходства).
Процесс синтеза эталона ![]() из эталона минимальной длины может быть представлен в виде графа, приведенного на рис. 1 и построенного для изображения, состоящего из четырех штрихов. Каждому элементу входного изображения на графе соответствует одна тонкая наклонная линия. Элементам эталона минимальной длины соответствуют горизонтальные линии. Если на
из эталона минимальной длины может быть представлен в виде графа, приведенного на рис. 1 и построенного для изображения, состоящего из четырех штрихов. Каждому элементу входного изображения на графе соответствует одна тонкая наклонная линия. Элементам эталона минимальной длины соответствуют горизонтальные линии. Если на ![]() -м месте в эталоне может стоять
-м месте в эталоне может стоять ![]() -й элемент минимального эталона, то на пересечении
-й элемент минимального эталона, то на пересечении ![]() -й вертикальной и
-й вертикальной и ![]() -й горизонтальной линий должна находиться вершина графа с индексом
-й горизонтальной линий должна находиться вершина графа с индексом ![]() (называемая допустимой). Допустимые вершины графа соединяются стрелками, направленными сверху вниз и слева направо. Вершины
(называемая допустимой). Допустимые вершины графа соединяются стрелками, направленными сверху вниз и слева направо. Вершины ![]() соединяются с вершинами
соединяются с вершинами ![]() или
или ![]() . Любая возможная эталонная последовательность
. Любая возможная эталонная последовательность ![]() , полученная из минимальной эталонной последовательности
, полученная из минимальной эталонной последовательности ![]() , представляется на графе путем, который начинается в точке
, представляется на графе путем, который начинается в точке ![]() ,
, ![]() и оканчивается в точке
и оканчивается в точке ![]() . Присвоив каждой допустимой вершине графа с индексами
. Присвоив каждой допустимой вершине графа с индексами ![]() значение
значение ![]() , задачу о нахождении ближайшего к входному изображению эталона можно свести к задаче о нахождении длины кратчайшего пути на графе. Эта задача решается в соответствии с рекуррентными соотношениями
, задачу о нахождении ближайшего к входному изображению эталона можно свести к задаче о нахождении длины кратчайшего пути на графе. Эта задача решается в соответствии с рекуррентными соотношениями
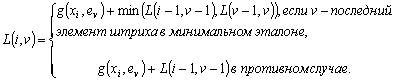
Здесь ![]() - кратчайший путь из начальной вершины в вершину с индексами
- кратчайший путь из начальной вершины в вершину с индексами ![]() . Значение
. Значение ![]() дает длину кратчайшего пути.
дает длину кратчайшего пути.
Эталон ![]() находится простым перебором.
находится простым перебором.
В некоторых работах приводится анализ ограничений на минимальную длину штрихов. Кроме того, предлагается правило синтеза эталонов, согласно которому добавление элементов в штрихи возможно только
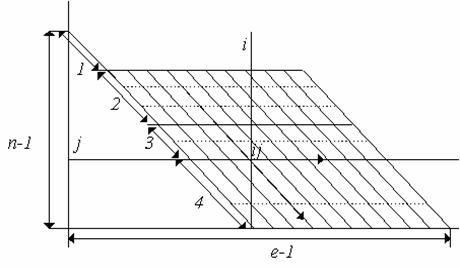
Рис. 1. Процесс синтеза эталона: / - 4 - штрихи.
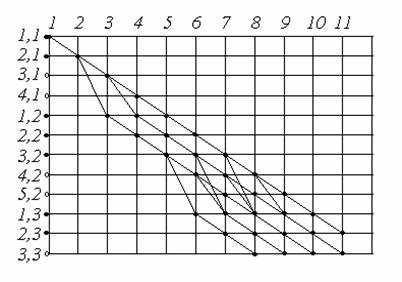
Рис. 2. Граф, состоящий из трех штрихов.
за последним элементом штриха, что уменьшает число возможных путей на графе за счет отбрасывания остальных возможных вариантов добавления элементов.
Экспериментальная проверка описанного алгоритма показала, что некоторые "трудные" знаки, например ![]() и
и ![]() , оказываются трудно различимыми, так как они не различаются ни порядком, ни направлением последовательности штриха. Это вызвало необходимость ввести более жесткие ограничения на допустимые варианты генерируемых эталонов путем установления допустимых изменений штрихов эталона снизу и сверху. Отличие такого алгоритма от описанного выше состоит в том, что изменения длины штрихов минимального эталона ограничены сверху пределом, определяемым для каждого класса. Для этой цели используется схема построения графа, приведенная на рис. 2. Горизонтальные линии графа соответствуют элементам генерируемого эталона. Каждая горизонтальная линия, имеющая двойную индексацию
, оказываются трудно различимыми, так как они не различаются ни порядком, ни направлением последовательности штриха. Это вызвало необходимость ввести более жесткие ограничения на допустимые варианты генерируемых эталонов путем установления допустимых изменений штрихов эталона снизу и сверху. Отличие такого алгоритма от описанного выше состоит в том, что изменения длины штрихов минимального эталона ограничены сверху пределом, определяемым для каждого класса. Для этой цели используется схема построения графа, приведенная на рис. 2. Горизонтальные линии графа соответствуют элементам генерируемого эталона. Каждая горизонтальная линия, имеющая двойную индексацию ![]() (индекс
(индекс ![]() указывает порядковый номер элемента в штрихе, имеющем порядковый номер
указывает порядковый номер элемента в штрихе, имеющем порядковый номер ![]() ), отмечена либо черной точкой, либо кружком. Черной точкой отмечаются элементы, обязательные для эталона, кружком - не обязательные.
), отмечена либо черной точкой, либо кружком. Черной точкой отмечаются элементы, обязательные для эталона, кружком - не обязательные.
Граф представляет собой наибольший из возможных эталонов данного класса. Граф, приведенный на рис. 2, состоит из трех штрихов. Вертикальные линии графа соответствуют элементам входного изображения. Минимальная длина эталона 7, максимальная 12. Входное изображение состоит из 11 элементов. Каждая вершина графа определяется тремя координатами: ![]() , где
, где ![]() - номер элемента входного изображения.
- номер элемента входного изображения.
Каждой вершине графа соответствует некоторая величина ![]() , определяемая как кратчайший путь в эту вершину из начальной точки. Вычисление кратчайшего пути из начальной точки в конечную осуществляется по рекуррентным формулам
, определяемая как кратчайший путь в эту вершину из начальной точки. Вычисление кратчайшего пути из начальной точки в конечную осуществляется по рекуррентным формулам
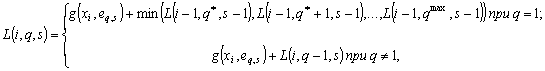
где ![]() - результат сравнения элементов эталона
- результат сравнения элементов эталона ![]() с элементом входного изображения
с элементом входного изображения ![]() ;
;![]() - номер последнего в штрихе обязательного элемента;
- номер последнего в штрихе обязательного элемента;![]() - номер последнего в штрихе необязательного элемента.
- номер последнего в штрихе необязательного элемента.
Алгоритмы были проверены экспериментально моделированием их на вычислительной машине. В качестве входных изображений выбирались "трудные" изображения - наиболее близкие по написанию рукописные символы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Размеры сетчатки, ограничивающие один знак, были равны
. Размеры сетчатки, ограничивающие один знак, были равны ![]() мм. В качестве эталонов минимальной длины были выбраны "хорошо написанные" знаки в прямоугольнике
мм. В качестве эталонов минимальной длины были выбраны "хорошо написанные" знаки в прямоугольнике ![]() мм. В целом алгоритмы показали достаточно высокую работоспособность. Однако оба алгоритма сильно зависят от способа написания символов. Широкое варьирование начальных точек написания приводит к дополнительным ошибкам при распознавании. Поэтому при использовании описанных алгоритмов следует накладывать дополнительные ограничения на способ написания знаков.
мм. В целом алгоритмы показали достаточно высокую работоспособность. Однако оба алгоритма сильно зависят от способа написания символов. Широкое варьирование начальных точек написания приводит к дополнительным ошибкам при распознавании. Поэтому при использовании описанных алгоритмов следует накладывать дополнительные ограничения на способ написания знаков.
Рассмотрим коротко историю создания некоторых первых отечественных и зарубежных читающих автоматов. Заметные успехи в области практического применения систем для распознавания визуальных изображений достигнуты главным образом в создании устройств для распознавания изображений печатных букв и цифр. Существующие автоматы позволяют читать с требуемой надежностью только знаки фиксированных начертаний. Попытки создания автоматов для визуального чтения рукописных букв произвольного начертания пока нельзя считать успешными [2].
Если заглянуть в историю, то среди первых разработок, прошедших испытания, можно выделить читающие автоматы Р711 и РУТА-701 Вильнюсского СКВ вычислительных машин.
Автомат Р711 разработан для чтения машинописного текста с высокой надежностью. Весь текст документа автомат прочитывает за один проход. Документы являются малоформатными и содержат не более четырех строк. Автомат может прочесть все цифры и восемь вспомогательных знаков, напечатанных типографским способом или на специальной пишущей машинке, снабженной специальными шрифтами. Кроме того, автомат может воспринимать и рукописные знаки, вписываемые в заранее напечатанные клетки.
При испытании автомата Р711 вероятности отказа и ошибки для документов, которые соответствовали установленным требованиям, были порядка ![]() . Документы, не соответствующие по качеству, перед началом испытания отбраковывались. При исключении предварительной отбраковки документов вероятности отказов и ошибок заметно повышались. Было изготовлено два образца автомата Р711.
. Документы, не соответствующие по качеству, перед началом испытания отбраковывались. При исключении предварительной отбраковки документов вероятности отказов и ошибок заметно повышались. Было изготовлено два образца автомата Р711.
Автомат РУТА-701 предназначен для ввода в вычислительную машину многострочных документов. Автомат читает десять цифр и четыре служебных символа. Рукописные цифры должны, так же как и в автомате Р711, вписываться в небольшие прямоугольники, заранее напечатанные на документе краской, не воспринимаемой автоматом. Максимальная скорость чтения автомата составляет 220 знаков в секунду. Вероятность ошибки имеет порядок ![]() . Машинописные цифры распознаются методом сравнения с эталоном, рукописные цифры - с помощью специально выбранной системы признаков. В обоих случаях необходима центровка изображения.
. Машинописные цифры распознаются методом сравнения с эталоном, рукописные цифры - с помощью специально выбранной системы признаков. В обоих случаях необходима центровка изображения.
Существовали автоматы, в основу которых положен метод сравнения с эталоном. Критерием сходства в этом автомате служит расстояние по Хеммингу. Сначала производится центрирование изображения, а затем предварительная классификация по наличию и расположению линий знака. После этого уже осуществляется сравнение с эталоном. Автомат предназначен для чтения типографских текстов и рассчитан на несколько таких шрифтов. Эталоны всех знаков каждого шрифта хранятся в памяти и вызываются по мере необходимости в оперативную память. Скорость действия автомата около 100 знаков в секунду, вероятность ошибки - порядка ![]() .
.
Многошрифтовой автомат фирмы "Radio Corporation of America" был сконструирован так, что изображение в нем считывается с помощью электронно-лучевой трубки типа "бегущий луч" и фотоумножителя, а затем воспроизводится на экране двухлучевого кинескопа в виде позитива и негатива. С помощью оптического размножителя полученные на экране изображения проектируются на эталонные маски, которые представляют собой высококонтрастные позитивные и негативные изображения эталона. Позитивное изображение накладывается на эталон-негатив, а негативное изображение - на эталон-позитив. Степень несовпадения распознаваемого знака с данным эталоном характеризуется результирующим световым потоком по каждому каналу. Распознавание производится по наименьшему световому потоку. В каждом канале установлены фотоумножители и интеграторы, которые преобразуют световые потоки в соответствующие электрические сигналы. В автомате предусмотрена специальная система управления, которая выполняет следующие действия: переключение операций (поиск знака, поиск строки, чтение знака) и центровку знака. Кроме того, в автомате используется так называемая принудительная идеализация распознаваемых знаков. Это осуществляется с помощью специальной системы автоматического регулирования яркости и контрастности изображения распознаваемого знака, полученного на экране двухлучевого кинескопа.
Автомат позволяет считывать и вводить в ЦВМ две печатные строки со стандартного бланка размером ![]() мм. Скорость подачи документов составляет 6 документов в секунду, скорость чтения - 500 знаков в секунду. Автомат обладает высокой надежностью распознавания: одна ошибка на 200 000 знаков, т. е. число ошибочных ответов не превышает 0,0005%. Следует, однако, отметить, что приведенные цифры характеризуют испытание 16-канального макета, причем при оценке надежности не указывается качество печати распознаваемых знаков.
мм. Скорость подачи документов составляет 6 документов в секунду, скорость чтения - 500 знаков в секунду. Автомат обладает высокой надежностью распознавания: одна ошибка на 200 000 знаков, т. е. число ошибочных ответов не превышает 0,0005%. Следует, однако, отметить, что приведенные цифры характеризуют испытание 16-канального макета, причем при оценке надежности не указывается качество печати распознаваемых знаков.
Уровень развития современных средств распознавания печатных символов достаточно высокий, что позволяет применять их даже на бытовом уровне при распознавании печатных символов отсканированных документов. Распознавание рукописных знаков остается пока открытой задачей.
Литература.
- Ковалевский В.А. Оптимальный алгоритм распознавания некоторых последовательностей изображений. - Кибернетика, 1967, № 4, с. 75 - 81.
- Васильев В.И. Распознающие системы. Киев: Наукова думка, 1983.
Коррекция неравномерной засветки изображения.
Для иллюстрации улучшения изображения с неравномерной засветкой используем изображение зерен риса. Также проведем их идентификацию и на основе такого анализа вычислим некоторые статистические характеристики зерен на изображении.
Последовательность действий:
Шаг 1: Считывание изображения.
Шаг 2: Использование морфологической операции раскрытия для оценки фона.
Шаг 3: Извлечение фона из исходного изображения.
Шаг 4: Увеличение контрастности изображения.
Шаг 5: Пороговая обработка изображения.
Шаг 6: Присвоение меток объектам изображения.
Шаг 7: Исследование матрицы меток.
Шаг 8: Измерение характеристик объектов на изображении.
Шаг 9: Вычисление статистических свойств объектов изображения.
Шаг 10: Построение гистограммы по полю зерен.
Шаг 1: Считывание изображения
I=imread('rice.png');
imshow(I)

Шаг 2: Использование морфологической операции раскрытия для оценки фона
Отметим, что яркость фона является различной в разных частях изображения. Используем функцию IMOPEN для анализа (оценки) яркости фона.
background=imopen(I, strel('disk', 15));
% Отобразим поверхность фона
figure, surf(double(background(1:8:end, 1:8:end))), zlim([0 255]);
set(gca, 'ydir', 'reverse');
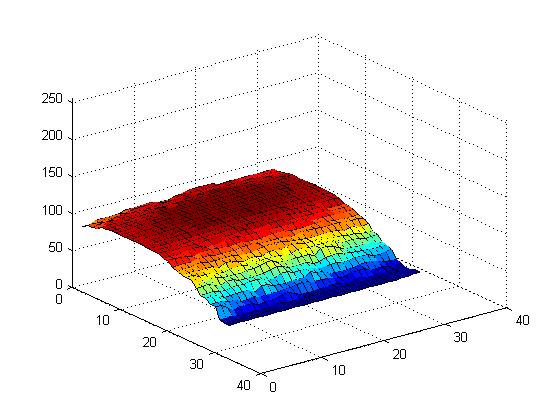
Шаг 3: Извлечение фона из исходного изображения
Таким образом, у нас имеется изображение и его фон в формате uint8. Далее, используя функцию IMSUBTRACT, проведем операцию извлечения фона из изображения.
I2=imsubtract(I, background);
imshow(I2)

Шаг 4: Увеличение контрастности изображения
I3=imadjust(I2);
imshow(I3);

Шаг 5: Пороговая обработка изображения
Создадим бинарное изображение на основе данного.
level=graythresh(I3);
bw=im2bw(I3, level);
imshow(bw)

Шаг 6: Присвоение меток объектам изображения
Функция BWLABEL отмечает все связные компоненты на бинарном изображении. Точность результата зависит от размеров объектов, оценки фона. Проводится анализ отмеченных объектов, поскольку на изображении некоторые зерна риса соприкасаются.
[labeled, numObjects]=bwlabel(bw, 4); % 4-связные numObjects % Число всех отдельных объектов на изображении. numObjects= 101
Шаг 7: Исследование матрицы меток
Каждый отдельный объект является отмеченным некоторым числом. Например, большая часть зерен отмечена числом 50.
rect=[105 125 10 10];
grain=imcrop(labeled, rect)
grain=
0 0 50 50 50 50 50 50 50 50 0
0 0 50 50 50 50 50 50 50 50 0
0 0 50 50 50 50 50 50 50 50 0
0 0 50 50 50 50 50 50 50 50 0
0 0 50 50 50 50 50 50 50 50 0
0 0 50 50 50 50 50 50 50 50 0
0 0 50 50 50 50 50 50 50 50 0
0 0 0 50 50 50 50 50 50 50 0
0 0 0 50 50 50 50 50 50 0 0
0 0 0 50 50 50 50 50 50 0 0
0 0 0 0 50 50 50 0 0 0 0
Одним из путей просмотра матрицы меток является ее отображение в виде псевдоцветного индексного изображения. На этом изображении числа, которые идентифицируют каждый объект в матрице меток, отображаются различными цветами. Используем функцию LABEL2RGB для выбора палитры, цвета фона и цветов объектов в матрице меток.
RGB_label=label2rgb(labeled, @spring, 'c', 'shuffle');
imshow(RGB_label)

Шаг 8: Измерение характеристик объектов на изображении
Функция REGIONPROPS проводит анализ объектов или характеристик окрестности на изображении и возвращает результаты в виде структур массива. При обработке изображения с отмеченными компонентами, для каждого объекта создается свой структурный элемент. Используем функцию regionprops для создания массива структур, содержащего некоторые основные свойства отмеченных объектов изображения.
graindata=regionprops(labeled, 'basic') graindata= graindata(50).Area ans = 203
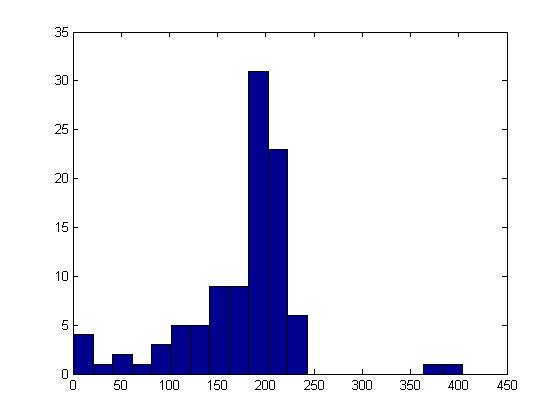
Сегментация цветных изображений на основе кластеризации по методу k-средних.
Рассмотрим задачу, основной целью которой является автоматическая сегментация на основе кластеризации (метод k-средних) цветных изображений, представленных в цветовом пространстве L*a*b*.
Содержание
- Шаг1: Считывание изображения.
- Шаг 2: Преобразование изображения из цветовой системы RGB в цветовую систему L*a*b*.
- Шаг 3: Классификация цветов в пространстве 'a*b*' с использованием кластеризации (метод k-средних).
- Шаг 4: Присвоение меток каждому пикселю изображения на основе метода k-средних.
- Шаг 5: Создание сегментированного изображения на основе цветного.
- Шаг 6: Сегментация ядер на основании отдельного изображения.
Шаг1: Считывание изображения.
Считаем файл hestain.png, который содержит изображение гемотоксина и эозина (H&E). Здесь применен метод окрашивания для детального анализа патологий.
he=imread('hestain.png'); imshow(he), title('H&E изображение'); text(size(he, 2),size(he, 1)+15,... 'Image courtesy of Alan Partin, Johns Hopkins University', ... 'FontSize',7,'HorizontalAlignment','right');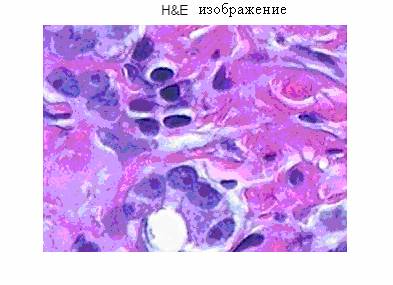
Шаг 2: Преобразование изображения из цветовой системы RGB в цветовую систему L*a*b*.
Какое количество цветов видно на изображении, когда не принимать во внимание возможность комбинации яркостей? На самом деле их три: белый, голубой и розовый. Следует отметить различия этих цветов между собой. Цветовое пространство L*a*b* (оно еще известно как CIELAB или CIE L*a*b*) дает возможность различать эти визуальные различия.
Цветовое пространство L*a*b* получено на основе трехцветных значений CIE XYZ. Пространство L*a*b* включает информацию о значении интенсивности 'L*', значении цветности 'a*', которое показывает какой цвет выбран на красно-зеленой оси и значение цветности 'b*' показывает какой цвет выбран на голубо-желтой оси. Вся информация о цветах содержится в значениях 'a*' и 'b*'. Оценить разницу между двумя цветами можно с использованием евклидового расстояния.
Преобразуем изображение в цветовое пространство L*a*b* с использованием функций makecform и applycform.cform=makecform('srgb2lab'); lab_he=applycform(he, cform);Шаг 3: Классификация цветов в пространстве 'a*b*' с использованием кластеризации (метод k-средних).
Кластеризация приводит до разделения объектов на группы. Кластеризация методом k-средних приводит также к локализации объектов в пространстве. Поиск разделения, т.е. какой объект к какому классу принадлежит, происходит на основе анализа метрического расстояния между объектами.
Далее на основании информации о цветах в пространстве 'a*b*', каждому пикселю объекта присваивается значение 'a*' и 'b*'. Используем кластеризацию методом k-средних для разделения объектов на три кластера. Для этого используем евклидовую метрику.ab=double(lab_he(:, :, 2:3)); nrows=size(ab, 1); ncols=size(ab, 2); ab=reshape(ab, nrows*ncols, 2); nColors=3; [cluster_idx cluster_center]=kmeans(ab, nColors, 'distance', 'sqEuclidean', ... 'Replicates',3);Шаг 4: Присвоение меток каждому пикселю изображения на основе метода k-средних.
Для каждого объекта на исходном изображении метод k-средних возвращает индекс соответствующего кластера. Значение параметра cluster_center, которое получено в результате применения метода k-средних будет использовано при дальнейшей демонстрации метода. Отметим пиксели, которые содержаться в cluster_index.
pixel_labels=reshape(cluster_idx, nrows,ncols); imshow(pixel_labels, []), title('изображение, отмеченное кластерными индексами');
Шаг 5: Создание сегментированного изображения на основе цветного.
Используя параметр pixel_labels, можно разделить объекты на изображении hestain.png по цветах. segmented_images=cell(1, 3); rgb_label=repmat(pixel_labels, [1 1 3]); for k=1 : nColors color=he; color(rgb_label~=k)=0; segmented_images{k}=color; end imshow(segmented_images{1}), title('объекты в кластере 1');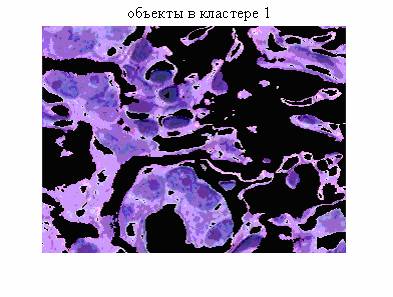
imshow(segmented_images{2}), title('объекты в кластере 2');
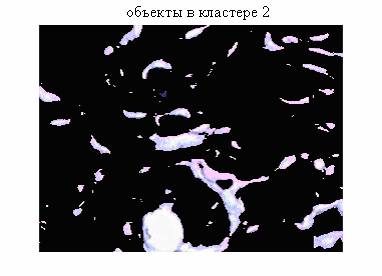
mshow(segmented_images{3}), title('объекты в кластере 3');
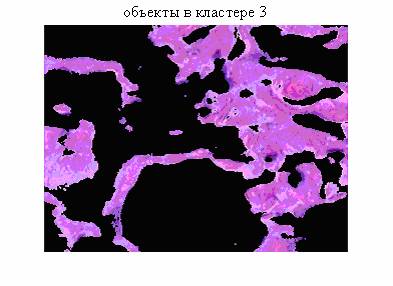
Шаг 6: Сегментация ядер на основании отдельного изображения.
Рассмотрим изображение, которое содержит синие объекты. Отметим, что они являются темно-синими и светло-синими. Используя значение 'L*' в цветовом пространстве L*a*b* можно отделить темно-синие объекты от светло-синих.
Напомним, что параметр 'L*' содержит значения интенсивностей для каждого цвета. Найдем кластеры, которые содержат синие объекты. Получим значения интенсивностей объектов в этом кластере и обработаем их пороговым методом с использованием функции im2bw.
Параметр cluster_center содержит среднее значение 'a*' и 'b*' для каждого кластера. Синий кластер имеет второе наибольшее значение cluster_center.mean_cluster_val=zeros(3, 1); for k=1:nColors mean_cluster_val(k)=mean(cluster_center(k)); end [mean_cluster_val,idx]=sort(mean_cluster_val); blue_cluster_num=idx(2); L=lab_he(:, :, 1); blue_idx=find(pixel_labels==blue_cluster_num); L_blue=L(blue_idx); is_light_blue=im2bw(L_blue,graythresh(L_blue));
Используем маску is_light_blue для того, чтобы пометить те пиксели, которые являются частью синего ядра. Отобразим синие ядра на разделенном изображении.
nuclei_labels=repmat(uint8(0), [nrows ncols]); nuclei_labels(blue_idx(is_light_blue==false))=1; nuclei_labels=repmat(nuclei_labels, [1 1 3]); blue_nuclei=he; blue_nuclei(nuclei_labels~=1)=0; imshow(blue_nuclei), title('синие ядра');
Сегментация цветных изображений на основе цветового пространства L*a*b*
Рассмотрим задачу, основной целью которой является идентификация и анализ различных цветов изображения в пространстве L*a*b*. Изображение получено с помощью пакета Image Acquisition Toolbox.
Содержание
- Шаг 1: Получение изображения.
- Шаг 2: Вычисление выборки цветов в цветовом пространстве L*a*b* для каждой локальной области.
- Шаг 3: Классификация каждого пикселя с использованием принципа ближайшей окрестности.
- Шаг 4: Отображение результатов классификации по ближайшей окрестности.
- Шаг 5: Отображение значений 'a*' и 'b*' отмеченных цветов.
Шаг 1: Получение изображения.
Считываем файл fabric.png, который представляет собой изображение некоторой материи. Для получения файла fabric.png можно использовать следующие функции пакета Image Acquisition Toolbox.
% Использование захватчика изображений, камеры Pulnix TMC-9700 % и получение данных в формате NTSC. % vidobj=videoinput('matrox', 1, 'M_NTSC_RGB'); % Окно предварительного просмотра. % preview(vidobj); % Захват данных. % fabric=getsnapshot(vidobj); % imwrite(fabric, 'fabric.png', 'png'); % Удаление изменений. % delete(vidobj) % clear vidobj; fabric=imread('fabric.png'); figure(1), imshow(fabric), title('Материя');
Шаг 2: Вычисление выборки цветов в цветовом пространстве L*a*b* для каждой локальной области.
Существует возможность просмотра шести основных цветов изображения: фоновый цвет, красный, зеленый, пурпурный (фиолетовый), желтый и красно-фиолетовый (magenta). Отметим, что визуально эти цвета очень легко различаются между собой. Цветовое пространство L*a*b* (еще известное как CIELAB или CIE L*a*b*) позволяет четко отмечать эти визуальные различия.
Цветовое пространство L*a*b* получено на основе трехцветных значений CIE XYZ. Пространство L*a*b* включает информацию о значении интенсивности 'L*', значении цветности 'a*' (показывает какой цвет выбран на красно-зеленой оси) и значении цветности 'b*' (показывает какой цвет выбран на голубо-желтой оси).
Отметим, что при анализе цветов используются окрестности небольших размеров и при их вычислении берется усреднение в пространстве 'a*b*'. Эти цветовые метки можно использовать при классификации каждого пикселя.
Для упрощения демонстрации примера, считаем координаты области, которые хранятся в MAT-file.
load regioncoordinates; nColors=6; sample_regions=false([size(fabric, 1) size(fabric, 2) nColors]); for count=1:nColors sample_regions(:, :, count)=roipoly(fabric, region_coordinates(:, 1, count), ... region_coordinates(:, 2, count)); end imshow(sample_regions(:, :, 2)), title('Пример красной области');
Преобразуем RGB-изображение материи в L*a*b*-изображение с использованием функций makecform и applycform.
cform=makecform('srgb2lab'); lab_fabric=applycform(fabric, cform); Вычислим средние значения 'a*' и 'b*' для каждой области представленной roipoly. Эти значения могут служить маркерами в пространстве 'a*b*'. a=lab_fabric(:, :, 2); b=lab_fabric(:, :, 3); color_markers=repmat(0, [nColors, 2]); for count=1:nColors color_markers(count, 1)=mean2(a(sample_regions(:, : ,count))); color_markers(count, 2)=mean2(b(sample_regions(:, :, count))); end Например, усреднение по красному цвету в цветовом пространстве 'a*b*' производится так disp(sprintf('[%0.3f,%0.3f]', color_markers(2, 1), color_markers(2, 2)));Шаг 3: Классификация каждого пикселя с использованием принципа ближайшей окрестности.
Каждый цветовой маркер представляется некоторыми значениями 'a*' и 'b*'. Поэтому существует возможность классификации каждого пикселя изображения lab_fabric на основе вычисления евклидового расстояния между пикселем и цветовым маркером. Минимальное евклидовое расстояние соответствует минимальному расстоянию между рассматриваемыми пикселями и маркером. Например, если дистанция между двумя пикселями и красным цветовым маркером является минимальной, то пиксели будут отмечены как красные.
Создадим массив, который содержит цветовые метки, т.е. 0=background, 1=red, 2=green, 3=purple, 4=magenta и 5=yellow.
color_labels=0:nColors-1; Создадим матрицы с использованием принципа классификации по близлежащей окрестности. a=double(a); b=double(b); distance=repmat(0, [size(a), nColors]); Выполнение классификации for count=1:nColors distance(:, :, count)=((a-color_markers(count, 1)).^2+... (b-color_markers(count, 2))^2).^0.5; end [value, label]=min(distance, [], 3); label=color_labels(label); clear value distance;Шаг 4: Отображение результатов классификации по ближайшей окрестности.
Матрица меток содержит цветные метки для каждого пикселя на изображении. Матрица меток используется для разделения объектов на исходном изображении по цветах.
rgb_label=repmat(label, [1 1 3]); segmented_images=repmat(uint8(0), [size(fabric), nColors]); for count=1:nColors color=fabric; color(rgb_label~=color_labels(count))=0; segmented_images(:, :, :, count)=color; end imshow(segmented_images(:, :, :, 2)), title('Красные объекты');
imshow(segmented_images(:, :, :, 3)), title('Зеленые объекты');
imshow(segmented_images(:, :, :, 4)), title('Фиолетовые объекты');
imshow(segmented_images(:, :, :, 5)), title('Красно-фиолетовые объекты');
imshow(segmented_images(:, :, :, 6)), title('Желтые объекты');

Шаг 5: Отображение значений 'a*' и 'b*' отмеченных цветов.
Покажем, как производится разделение различных групп цветов на основе классификации по принципу ближайшей окрестности и их отображение в системе 'a*' и 'b*'.
purple=[119/255 73/255 152/255]; plot_labels={'k', 'r', 'g', purple, 'm', 'y'}; figure for count=1:nColors plot(a(label==count-1),b(label==count-1),'.','MarkerEdgeColor', ... plot_labels{count}, 'MarkerFaceColor', plot_labels{count}); hold on; end title('Размещение сегментированных пикселей в пространстве ''a*b*'' '); xlabel('''a*'' values'); ylabel('''b*'' values');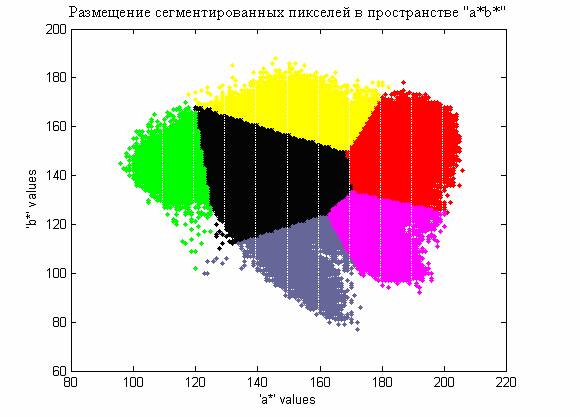
Уменьшение количества градаций цветных изображений
Довольно часто возникает задача уменьшения количества градаций, которые используются при визуализации цветных изображений. Иными словами, задача заключается в модификации палитры. Ранее нами уже были рассмотрены некоторые подходы к решению этой задачи. В этом материале рассмотрим еще несколько методов уменьшения количества цветов, которые используются при визуализации цветных изображений.
Метод 1. Суть этого метода состоит в том, что диапазон каждой цветовой составляющей делится на нужное количество градаций. Однако разделение выполняется таким образом, чтобы на изображении было также равное количество пикселей, которые принимают значения из всех поддиапазонов.
Продемонстрируем программную реализацию данного метода.
Сначала считаем исходное изображение из графического файла в рабочее пространство Matlab.
L=imread('im.bmp'); L=double(L);Далее визуализируем его.
figure, imshow(L./255);

Определим размеры исходного изображения и количество градаций цветовых составляющих для нового изображения.
[N M k]=size(L);
%Количество цветовrgb=2;
Теперь будем обрабатывать каждую цветовую составляющую отдельно.
Рассмотрим преобразование красной цветовой составляющей более подробно.
Сначала необходимо выделить первый цветовой шар изображения.
LR=L(:,:,1);
Далее необходимо построить гистограмму распределения значений первого цветового шара изображения.
HR=hist(LR(:),256);
Теперь необходимо реализовать разделение исходного диапазона на поддиапазоны. Как уже отмечалось выше, главное условие при проведении такого разделения заключается в том, что на исходном изображении должно быть одинаковое количество пикселей, которые принимают значения из каждого поддиапазона. Это позволит максимально сохранить детальность на преобразованном изображении.
for KolColor=1:rgb; Htemp=0; i=1; while i<256; Htemp=Htemp+HR(i); if Htemp>=( KolColor /rgb-1/(2*rgb))*N*M; PorogR(KolColor)=i; i=256; end; i=i+1; end; end;
Аналогичные преобразования реализуются для зеленой и синей цветовой составляющих.
%========Зеленая цветовая составляющая ============LG=L(:,:,2); HG=hist(LG(:),256); for KolColor =1:rgb; Htemp=0; i=1; while i<256; Htemp=Htemp+HG(i); if Htemp>=( KolColor /rgb-1/(2*rgb))*N*M; PorogG(KolColor)=i; i=256; end; i=i+1; end; end;
%===========Синяя цветовая составляющая==========LB=L(:,:,3); HB=hist(LB(:),256); for KolColor =1:rgb; Htemp=0; i=1; while i<256; Htemp=Htemp+HB(i); if Htemp>=( KolColor /rgb-1/(2*rgb))*N*M; PorogB(KolColor)=i; i=256; end; i=i+1; end; end;
После модификации градаций, необходимо соответственно модифицировать и значения пикселей изображения. Причем это необходимо сделать таким образом, чтобы новое модифицированное значение пикселя было расположено максимально близко к предыдущему немодифицированному значению.
for i=1:N; disp(i); for j=1:M; [y NomerR]=min(abs(PorogR-L(i,j,1))); [y NomerG]=min(abs(PorogG-L(i,j,2))); [y NomerB]=min(abs(PorogB-L(i,j,3))); L1(i,j,1)=PorogR(NomerR); L1(i,j,2)=PorogG(NomerG); L1(i,j,3)=PorogB(NomerB); end; end;
Представим результат преобразований.
figure, imshow(L1./255);

Отметим, что этот результат получен при двух градациях каждой цветовой составляющей.
Если диапазоны каждой цветовой составляющей разделить на семь поддиапазонов, то получим следующий результат.

Если же диапазоны цветовых составляющих разделить на 15 поддиапазонов, то получим такой результат.

Из проведенных экспериментов можно сделать вывод, что результат преобразования во многом зависит от количества градаций – чем их больше, тем результат более визуально приемлемый.
Метод 2. В предыдущем методе анализ и последующее преобразование проводилось над всем изображением сразу, т.е. метод был глобальным. В этом методе рассмотрим применение этой же методики только к локальным окрестностям. В большинстве случаев такой подход обеспечивает более детальную обработку изображений.
Сначала считаем исходное изображение и визуализируем его.
L=imread('im.bmp'); L=double(L(:,:,:)); figure, imshow(L./255);
Далее необходимо определить размеры изображения, количество цветовых составляющих исходного изображения и количество градаций цветовых составляющих, которые будут на модифицированном изображении.
[N M k]=size(L);
%Количество цветовrgb=2;
Поскольку этот метод предусматривает обработку с использованием локальных апертур, то для корректной программной реализации необходимо провести расширение границ исходного изображения. Проведем расширение границ для каждой цветовой составляющей отдельно.
%Расширение исходного массива R-цветовой составляющейLR=(L(:,:,1)); m=7;n=m;n1=fix(n/2);m1=fix(m/2); a=LR(1,1);b=LR(1,M);c=LR(N,1);d=LR(N,M); for i=1:n1; for j=1:m1; LR1(i,j)=a; LR3(i,j)=b; LR6(i,j)=c; LR8(i,j)=d; end;end; LR2=LR(1,1:M); LR02=LR2; for i=1:n1-1; LR2=[LR2;LR02]; end; LR7=LR(N,1:M); LR07=LR7; for i=1:n1-1; LR7=[LR7;LR07]; end; LR4=LR(1:N,1); LR4=LR4'; LR04=LR4; for i=1:m1-1; LR4=[LR4;LR04]; end; LR4=LR4'; LR5=LR(1:N,M); LR5=LR5'; LR05=LR5; for i=1:m1-1; LR5=[LR5;LR05]; end; LR5=LR5'; LR1=[LR1;LR4]; LR1=[LR1;LR6]; LR1=LR1'; LR2=[LR2;LR]; LR2=[LR2;LR7]; LR2=LR2'; LR3=[LR3;LR5]; LR3=[LR3;LR8]; LR3=LR3'; LR1=[LR1;LR2]; LR1=[LR1;LR3]; LRR=LR1'; clear LR1; clear LR2; clear LR3; clear LR4; clear LR5; clear LR6; clear LR7; clear LR8; clear LR;
%Расширение исходного массива G-цветовой составляющейLG=(L(:,:,2)); a=LG(1,1);b=LG(1,M);c=LG(N,1);d=LG(N,M); for i=1:n1; for j=1:m1; LG1(i,j)=a; LG3(i,j)=b; LG6(i,j)=c; LG8(i,j)=d; end;end; LG2=LG(1,1:M); LG02=LG2; for i=1:n1-1; LG2=[LG2;LG02]; end; LG7=LG(N,1:M); LG07=LG7; for i=1:n1-1; LG7=[LG7;LG07]; end; LG4=LG(1:N,1); LG4=LG4'; LG04=LG4; for i=1:m1-1; LG4=[LG4;LG04]; end; LG4=LG4'; LG5=LG(1:N,M); LG5=LG5'; LG05=LG5; for i=1:m1-1; LG5=[LG5;LG05]; end; LG5=LG5'; LG1=[LG1;LG4]; LG1=[LG1;LG6]; LG1=LG1'; LG2=[LG2;LG]; LG2=[LG2;LG7]; LG2=LG2'; LG3=[LG3;LG5]; LG3=[LG3;LG8]; LG3=LG3'; LG1=[LG1;LG2]; LG1=[LG1;LG3]; LRG=LG1'; clear LG1; clear LG2; clear LG3; clear LG4; clear LG5; clear LG6; clear LG7; clear LG8; clear LG;
%Расширение исходного массива B-цветовой составляющейLB=(L(:,:,3)); a=LB(1,1);b=LB(1,M);c=LB(N,1);d=LB(N,M); for i=1:n1; for j=1:m1; LB1(i,j)=a; LB3(i,j)=b; LB6(i,j)=c; LB8(i,j)=d; end;end; LB2=LB(1,1:M); LB02=LB2; for i=1:n1-1; LB2=[LB2;LB02]; end; LB7=LB(N,1:M); LB07=LB7; for i=1:n1-1; LB7=[LB7;LB07]; end; LB4=LB(1:N,1); LB4=LB4'; LB04=LB4; for i=1:m1-1; LB4=[LB4;LB04]; end; LB4=LB4'; LB5=LB(1:N,M); LB5=LB5'; LB05=LB5; for i=1:m1-1; LB5=[LB5;LB05]; end; LB5=LB5'; LB1=[LB1;LB4]; LB1=[LB1;LB6]; LB1=LB1'; LB2=[LB2;LB]; LB2=[LB2;LB7]; LB2=LB2'; LB3=[LB3;LB5]; LB3=[LB3;LB8]; LB3=LB3'; LB1=[LB1;LB2]; LB1=[LB1;LB3]; LRB=LB1'; clear LB1; clear LB2; clear LB3; clear LB4; clear LB5; clear LB6; clear LB7; clear LB8; clear LB; Lr(:,:,1)=LRR; Lr(:,:,2)=LRG; Lr(:,:,3)=LRB;
Таким образом, нами сформирован массив исходного изображения Lr с расширенными границами.
Далее все операции будут аналогичны, как и в методе 1. Как уже отмечалось, главная особенность такой обработки будет заключаться в том, что она будет выполняться не сразу над всем изображением, а над его локальными окрестностями.
for i=1+n1:N+n1; disp(i); for j=1+m1:M+m1; if j==1+m1; D=0; % Формирование локальной окрестности for a=-n1:n1; for b=-m1:m1; D(n1+1+a,m1+1+b,1:3)=Lr(i+a,j+b,1:3); end; end; end; if j>1+m1; for a=-n1:n1; D(n1+1+a,m+1,1:3)=Lr(i+a,j+m1,1:3); end; D=D(1:n,2:m+1,1:3); end;
Далее обработка будет выполняться для каждой цветовой составляющей отдельно.
%Для цветовой R-составляющей изображения LRmal=D(:,:,1); HR=0; HR=hist(LRmal(:),256); PorihR=ones(1,rgb); for KilkistKolioriv=1:rgb; Htemp=0; t=1; while t<256; Htemp=Htemp+HR(t); if Htemp>=(KilkistKolioriv/rgb-1/(2*rgb))*n*m; PorihR(KilkistKolioriv)=t; t=256; end; t=t+1; end; end; %Для цветовой G-составляющей изображения LGmal=D(:,:,2); HG=0; HG=hist(LGmal(:),256); PorihG=ones(1,rgb); for KilkistKolioriv=1:rgb; Htemp=0; t=1; while t<256; Htemp=Htemp+HG(t); if Htemp>=(KilkistKolioriv/rgb-1/(2*rgb))*n*m; PorihG(KilkistKolioriv)=t; t=256; end; t=t+1; end; end; %Для цветовой B-составляющей изображения LBmal=D(:,:,3); HB=0; HB=hist(LBmal(:),256); PorihB=ones(1,rgb); for KilkistKolioriv=1:rgb; Htemp=0; t=1; while t<256; Htemp=Htemp+HB(t); if Htemp>=(KilkistKolioriv/rgb-1/(2*rgb))*n*m; PorihB(KilkistKolioriv)=t; t=256; end; t=t+1; end; end;
Теперь значения интенсивностей цветовых составляющих пикселей данной локальной окрестности нужно модифицировать в соответствии с новыми градациями.
[y NomerR]=min(abs(PorihR-Lr(i,j,1))); [y NomerG]=min(abs(PorihG-Lr(i,j,2))); [y NomerB]=min(abs(PorihB-Lr(i,j,3))); L1(i,j,1)=PorihR(NomerR); L1(i,j,2)=PorihG(NomerG); L1(i,j,3)=PorihB(NomerB); end; end;Возвращаем изображение к исходным размерам
L1=L1(n1:n1+N,m1:m1+M,:);
и визуализируем результат
figure, imshow(L1./255);
В данном методе количество градаций и размер локальной апертуры могут быть различными. Поэтому продемонстрируем результаты, которые получены при разных количествах градаций цветовых составляющих и разных размерах локальных апертур.
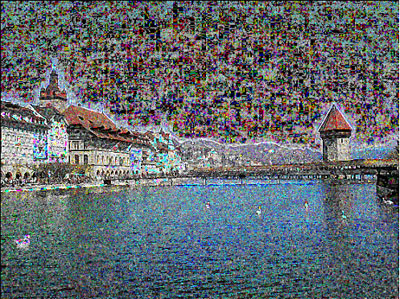
Результат получен при двух градациях цветовых составляющих и размерах локальной апертуры 3x3.
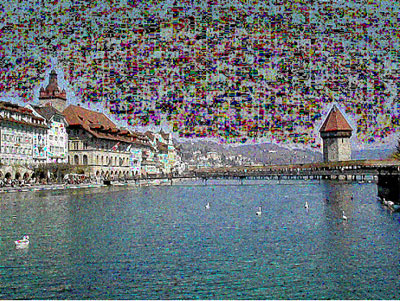
Результат получен при семи градациях цветовых составляющих и размерах локальной апертуры 3x3.

Результат получен при пятнадцати градациях цветовых составляющих и размерах локальной апертуры 3x3.
Из проведенных экспериментов видно, что при увеличении количества градаций цветовых составляющих результат визуально улучшается. Однако в областях изображения с почти одинаковыми значениями интенсивности данный метод дает некорректный результат.
Увеличение размеров локальной апертуры приводит к улучшению работы метода в областях с почти одинаковыми значениями интенсивности. Так при пятнадцати градациях цветовых составляющих и размерах локальной апертуры 7х7 получим результат, который представлен на изображении внизу.

Метод 3. Суть следующего метода состоит в том, что модификации будут подвергаться не отдельные цветовые составляющие, а одновременно будет модифицирован весь вектор значений цветовых составляющих. Для проведения таких преобразований сначала необходимо задать набор новых векторов значений цветовых составляющих. В данной реализации будут использованы векторы значений цветовых составляющих, которые соответствуют красному, зеленому, синему, черному и белому цветам. Критерием замены исходного вектора на новый будет минимальное расстояние между этими векторами в пространстве RGB.
Рассмотрим программную реализацию этого метода боле подробно.
Сначала считываем исходное изображение в рабочее пространство Matlab и визуализируем его.
L=imread('im.bmp'); L=double(L(:,:,:)); figure, imshow(L./255);
Далее определяем размеры матрицы исходного файла и количество цветовых составляющих.
[N M k]=size(L);
После этого вычисляем расстояние в системе RGB между вектором значений пикселя исходного изображения и векторами значений для заданных цветов. Значения исходного вектора значений заменяются значениями того вектора, который в системе RGB расположен наиболее близко к исходному.
for i=1:N; disp(i); for j=1:M; %Красный цвет a(1)=sqrt((L(i,j,1)-255)^2+(L(i,j,2)-0)^2+(L(i,j,3)-0)^2); %Зеленый цвет a(2)=sqrt((L(i,j,1)-0)^2+(L(i,j,2)-255)^2+(L(i,j,3)-0)^2); %Синий цвет a(3)=sqrt((L(i,j,1)-0)^2+(L(i,j,2)-0)^2+(L(i,j,3)-255)^2); %Черный цвет a(4)=sqrt((L(i,j,1)-0)^2+(L(i,j,2)-0)^2+(L(i,j,3)-0)^2); %Белый цвет a(5)=sqrt((L(i,j,1)-255)^2+(L(i,j,2)-255)^2+(L(i,j,3)-255)^2); [y nomer]=min(a); if nomer==1; L(i,j,1)=255;L(i,j,2)=0;L(i,j,3)=0; end; if nomer==2; L(i,j,1)=0;L(i,j,2)=255;L(i,j,3)=0; end; if nomer==3; L(i,j,1)=0;L(i,j,2)=0;L(i,j,3)=255; end; if nomer==4; L(i,j,1)=0;L(i,j,2)=0;L(i,j,3)=0; end; if nomer==5; L(i,j,1)=255;L(i,j,2)=255;L(i,j,3)=255; end; end; end;
Результат представлен на изображении внизу.
figure, imshow(L);
С точки зрения визуального восприятия результат не является наилучшим. Это можно объяснить тем, что набор выбранных цветов (красный, зеленый, синий, черный и белый) не был оптимальным. Поэтому для получения более приемлемого результата необходимо оптимизировать выбор набора цветов.

Метод 4. Этот метод является наиболее простым с точки зрения программной реализации. Его суть состоит в том, что значения интенсивностей пикселей будут округляться к тому или иному числу, значение которого будет зависеть, в том числе, от заданного количества цветов преобразованного изображения.
Сначала считываем изображение и визуализируем его.
L=imread('im.bmp'); L=double(L(:,:,:)); figure, imshow(L./255);
Далее необходимо задать количество градаций для каждой цветовой составляющей, которые будут использоваться при визуализации модифицированного изображения.
%Количество цветов rgb=2;Теперь будем выполнять модификацию значений интенсивностей пикселей в соответствии с изложенным выше подходом.
L=round(L./(256/(rgb-1))).*(256/(rgb-1)); figure, imshow(L./255);
Конечно, качество изображений, которые получены в результате таких преобразований, напрямую зависит от количества использованных градаций. Внизу приведены результаты преобразования при различных количествах градаций цветовых составляющих.

Результат получен при двух градациях цветовых составляющих.
Результат получен при семи градациях цветовых составляющих.

Результат получен при пятнадцати градациях цветовых составляющих.
Анализ рассмотренных нами методов уменьшения цветов на изображении позволяет сделать следующие выводы:
- Уменьшение количества цветов всегда приводит к потере визуального качества изображения.
- Более корректно обрабатывать не отдельные цветовые составляющие, поскольку это приводит к нарушению баланса цветности, а нужно анализировать и преобразовывать вектор цветов в целом.
- Эффективность решения задачи уменьшения количества цветов на изображении во многом зависит от цветовой гаммы исходного изображения.
Обнаружение вращений и масштабных искажений на изображении
Когда известна информация относительно искажений изображения, которые заключаются в вращении и изменении масштаба, тогда для обработки применяют функцию cp2tform. Эта функция служит для восстановления изображений.
Содержание:
- Шаг 1: Считывание изображения.
- Шаг 2: Изменение размеров изображения.
- Шаг 3: Вращение изображения.
- Шаг 4: Выбор контрольных точек.
- Шаг 5: Предварительные преобразования.
- Шаг 6: Определение масштаба и угла.
- Шаг 7: Восстановление изображения. Шаг 1: Считывание изображения. Считаем изображение в рабочее пространство. I=imread('cameraman.tif'); imshow(I)
-

Шаг 2: Изменение размеров изображения. scale=0.6; J=imresize(I, scale); % Изменение масштаба. Шаг 3: Вращение изображения. theta=30; K=imrotate(J, theta); % Изменение угла. figure, imshow(K)

Шаг 4: Выбор контрольных точек. Выберем контрольные точки с помощью Control Point Selection Tool. input_points=[129.87 141.25; 112.63 67.75]; base_points=[135.26 200.15; 170.30 79.30]; cpselect(K,I, input_points, base_points); Запишем контрольные точки, выбирая в меню File опцию Save Points to Workspace. Также перезапишем переменные input_points и base_points. Шаг 5: Предварительные преобразования. Найдем структуру TFORM, которая согласуется с контрольными точками. t=cp2tform(input_points, base_points, 'linear conformal'); После выполнения шагов 6 и 7, снова повторяются шаги 5-7, только взамен опции 'linear conformal' используется 'affine'. Это приводит к улучшению результатов. Шаг 6: Определение масштаба и угла. Структура TFORM содержит матрицу преобразований t.tdata.Tinv. После того как стали известны типы искажений (вращение и масштабирование), проводят операции по восстановлению масштаба и угла. Let sc=s*cos(theta) Let ss=s*sin(theta) Тогда, Tinv=t.tdata.Tinv=[sc -ss 0; ss sc 0; tx ty 1] где параметры tx и ty являются сдвигом по x и y соответственно. ss=t.tdata.Tinv(2, 1); sc=t.tdata.Tinv(1, 1); scale_recovered=sqrt(ss*ss+sc*sc) theta_recovered=atan2(ss, sc)*180/pi scale_recovered= 0.6000 theta_recovered= 29.3699Итак, значение параметра scale_recovered находится в пределах 0.6, а значение параметра theta_recovered около 30.
Шаг 7: Восстановление изображения.
Для получения исходного изображения необходимо произвести обратные преобразования с использованием структуры TFORM. Также нужно знать размер исходного изображения.
Разрешительная способность восстановленного изображения будет немного ниже, чем на исходном. Уменьшение информации, а также внесенные искажения на восстановленном изображении, в сравнении с исходным, являются следствием проведенных преобразований.D=size(I); recovered=imtransform(K, t, 'XData', [1 D(2)], 'YData', [1 D(1)]); % Сравнение восстановленного изображения и исходного. figure, imshow(I) title('исходное изображение') figure, imshow(recovered) title('восстановленное изображение')

Регистрация изображений с помощью нормированной кросс-корреляции
Иногда одни изображения являются подмножествами других. С помощью методов нормированной кросс-корреляции существует возможность определения их расположения и регистрации.
Ключевая концепция Нормированная кросс-корреляция, прозрачность Ключевые функции normxcorr2, max, ind2sub Обзор примеров Приведенные примеры включают следующие шаги:
- Шаг 1: Считывание изображения.
- Шаг 2: Выбор подобласти для каждого изображения.
- Шаг 3: Нормированная кросс-корреляция и поиск координат пиков.
- Шаг 4: Поиск общих относительных различий между изображениями.
- Шаг 5: Анализ подизображения, полученного из основного изображения.
- Шаг 6: Отображение вырезанного изображения на пустом изображении с размерами исходного.
- Шаг 7: Свойство прозрачности исходного изображения. Шаг 1: Считывание изображения. onion=imread('onion.png'); peppers=imread('peppers.png'); imshow(onion) figure, imshow(peppers)
-

Шаг 2: Выбор подобласти для каждого изображения
Важной является процедура выбора похожей подобласти. Изображение sub_onion является тем эталоном, на основании которого производится поиск sub_peppers. Методы выбора этой подобласти делятся на итеративные и неитеративные.% неитеративный rect_onion=[111 33 65 58]; rect_peppers=[163 47 143 151]; sub_onion=imcrop(onion,rect_onion); sub_peppers=imcrop(peppers,rect_peppers); % или % итеративный [sub_onion,rect_onion]=imcrop(onion); [sub_peppers,rect_peppers]=imcrop(peppers); % отображение подизображений figure, imshow(sub_onion) figure, imshow(sub_peppers)

Шаг 3: Нормированная кросс-корреляция и поиск координат пиков
Вычисление нормированной кросс-корреляции и отображение ее поверхности. Пики матрицы кросс-корреляции, которые попали на подизображение (sub_images) свидетельствуют о наивысшей корреляции. Функция normxcorr2 работает только с полутоновыми изображениями, однако попробуем применить ее для обработки подизображений.
c=normxcorr2(sub_onion(:, :, 1), sub_peppers(:, :, 1));
figure, surf(c), shading flat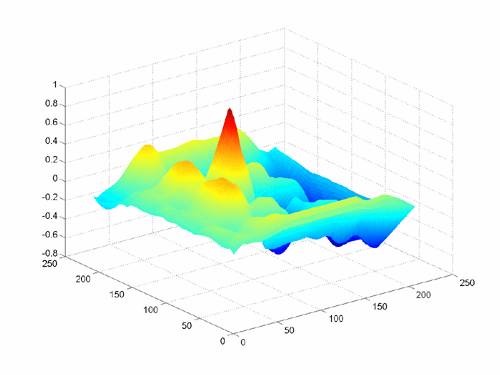
Шаг 4: Поиск общих относительных различий между изображениями
Общие различия между изображениями характеризуются положением пиков в матрице кросс-корреляции, а также размерами и местонахождением подизображений.% поиск на основании корреляции [max_c, imax]=max(abs(c(:))); [ypeak, xpeak]=ind2sub(size(c), imax(1)); corr_offset=[(xpeak-size(sub_onion, 2)) (ypeak-size(sub_onion, 1))]; % относительное месторасположение подизображений rect_offset=[(rect_peppers(1)-rect_onion(1)) (rect_peppers(2)-rect_onion(2))]; % поиск на основании общих относительных различий offset=corr_offset+rect_offset; xoffset=offset(1); yoffset=offset(2); Шаг 5: Анализ подизображения, полученного из основного изображения Подизображение на исходном изображении. xbegin=xoffset+1; xend=xoffset+size(onion, 2); ybegin=yoffset+1; yend=yoffset+size(onion, 1); % Получение рассматриваемого подизображения и сравнение его с исходным extracted_onion=peppers(ybegin:yend, xbegin:xend, :); if isequal(onion, extracted_onion) disp('onion.png получено из peppers.png') end Шаг 6: Отображение подизображения на пустом изображении с размерами исходного Расположим подизображение на исходном изображении на основании анализа различий. recovered_onion=uint8(zeros(size(peppers))); recovered_onion(ybegin:yend, xbegin:xend, :)=onion; figure, imshow(recovered_onion)
Шаг 7: Свойство прозрачности исходного изображения Создание прозрачной (или полупрозрачной) маски для непрозрачного исходного изображения. [m, n, p]=size(peppers); mask=ones(m, n); i=find(recovered_onion(:, :, 1)==0); mask(i)=.2; % экспериментирование с различными значениями прозрачности % наложение полупрозрачного рисунка figure, imshow(peppers(:,:,1)) % отображение только красной составляющей hold on h=imshow(recovered_onion); % отображение recovered_onion set(h, 'AlphaData', mask)
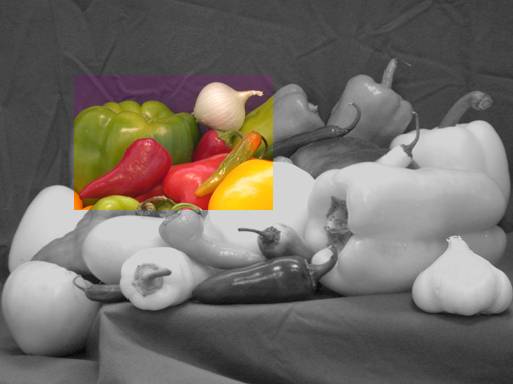
Наложение двух изображений
Приведем пример наложения последовательности нескольких изображений. Результат представляет собой наложение двух изображений, одно из которых представляет собой стационарный маятник, а другое - движущийся маятник.
Содержание:
- Шаг 1: Захват фонового изображения.
- Шаг 2: Обработка регистрируемых данных. Шаг 1: Захват фонового изображения. Произведем захват снимка и принимаем его в качестве фонового. vidobj=videoinput('winvideo', 1, 'RGB24_320X240'); preview(vidobj) pause(1) background=getsnapshot(vidobj); imshow(background);
-

Шаг 2: Обработка регистрируемых данных. Полученные данные используем для обработки и отображения изображений в реальном масштабе времени. Обработка заключается в вычислении линейной комбинации между изображениями. pause(2); set(gcf, 'DoubleBuffer', 'on'); vidobj.FramesPerTrigger=20; start(vidobj) % Вычисление линейной комбинации между текущим и фоновым изображениями. current=getdata(vidobj, 1); transparent=imlincomb(0.5, current, 0.5, background); % Отображение обработанного изображения. imshow(transparent);

% Повторение для всех изображений. while (vidobj.FramesAvailable>0), % Вычисление линейной комбинации между текущим и фоновым изображениями. current=getdata(vidobj, 1); transparent=imlincomb(0.5, current, 0.5, background); % Отображение обработанного изображения. imshow(transparent); end
% Очистка рабочего пространства. delete(vidobj) clear vidobj
Технология повышения контрастности изображений.
Пакет Image Processing Toolbox содержит несколько классических функций улучшения изображений. Эти функции являются очень эффективными при повышении контраста: imadjust, histeq, и adapthisteq. Приведем их сравнительный анализ при использовании для улучшения полутоновых и цветных изображений.
План последовательности действий
- Шаг 1: Считывание изображения.
- Шаг 2: Изменение размеров изображения.
- Шаг 3: Улучшение полутонового изображения.
- Шаг 4: Улучшение цветных изображений.
Шаг 1: Считывание изображений.
Считаем два полутоновых изображения: pout.tif и tire.tif. Также считаем индексное RGB-изображение: shadow.tif.
pout=imread('pout.tif'); tire=imread('tire.tif'); [X map]=imread('shadow.tif'); shadow=ind2rgb(X,map);Шаг 2: Изменение размеров изображения.
Для более удобного сравнения изображений преобразуем их размеры так, чтобы они имели одинаковую ширину. Высота изображений изменится пропорционально в соответствии с исходным изображением.
width=210; images={pout, tire, shadow}; for k=1:3 dim=size(images{k}); images{k}=imresize(images{k}, [width*dim(1)/dim(2) width], 'bicubic'); end pout=images{1}; tire=images{2}; shadow=images{3};Шаг 3: Улучшение полутоновых изображений.
Проведем сравнительный анализ эффективности использования следующих функций к улучшению изображений:
imadjust - увеличение контраста изображений путем изменения диапазона интенсивностей исходного изображения.
histeq - выполнение операции эквализации (выравнивания) гистограммы. В этом подходе увеличение контрастности изображения происходит путем преобразования гистограммы распределения значений интенсивностей элементов исходного изображения. Существуют также другие подходы к видоизменению гистограмм.
adapthisteq - выполнение контрастно-ограниченного адаптивного выравнивания гистограммы. Здесь методика повышения контрастности изображений базируется на анализе и эквализации гистограмм локальных окрестностей изображения.
pout_imadjust=imadjust(pout); pout_histeq=histeq(pout); pout_adapthisteq=adapthisteq(pout); imshow(pout); title('Original'); figure, imshow(pout_imadjust); title('Imadjust');

figure, imshow(pout_histeq); title('Histeq'); figure, imshow(pout_adapthisteq); title('Adapthisteq');

tire_imadjust=imadjust(tire); tire_histeq=histeq(tire); tire_adapthisteq=adapthisteq(tire); figure, imshow(tire); title('Original'); figure, imshow(tire_imadjust); title('Imadjust');

figure, imshow(tire_histeq); title('Histeq'); figure, imshow(tire_adapthisteq); title('Adapthisteq');

Проведем краткий анализ эффективности обработки изображений с помощью функций imadjust, histeq и adapthisteq. В основе этих функций лежат разные методы: в imadjust - преобразование диапазона яркостей элементов изображения, в histeq - эквализация гистограммы и в adapthisteq - адаптивное выравнивание гистограммы. Каждый из этих методов (функций) нацелен на устранение некоторого недостатка, поэтому может быть применен для эффективной обработки такого класса изображений, на которых есть такой тип искажений.
Один из критериев выбора того или иного метода может базироваться на анализе гистограммы распределения значений яркостей элементов изображения.
figure, imhist(pout), title('pout.tif'); figure, imhist(tire), title('tire.tif');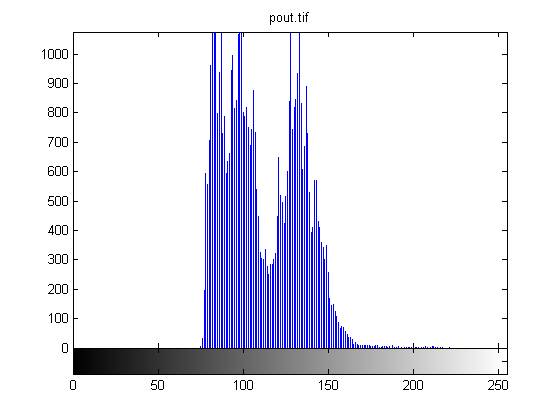
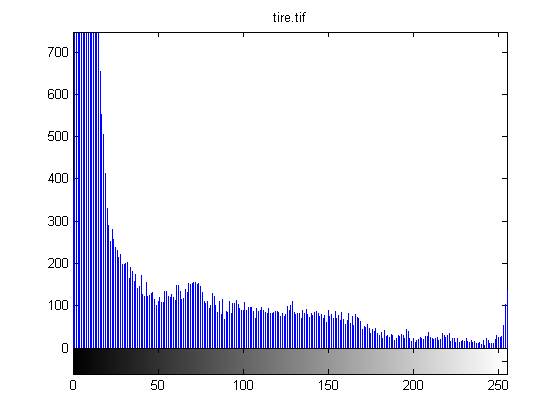
В качестве примера рассмотрим гистограммы изображений pout.tif и tire.tif. Гистограмма изображения pout.tif занимает только центральную часть возможного диапазона яркостей. Таким образом, для растяжения динамического диапазона можно использовать функцию imadjust. Гистограмма изображения tire.tif характеризуется неравномерностью распределения. Для выравнивания гистограммы можно применить функцию histeq.
Шаг 4: Улучшение цветных изображений
Одним из путей улучшения контраста цветных изображений является преобразование цветовых пространств, которое приводит к изменению значений составляющих цвета. Одним из таких преобразований является замена цветового пространства RGB на L*a*b*.
srgb2lab=makecform('srgb2lab'); lab2srgb=makecform('lab2srgb'); shadow_lab=applycform(shadow, srgb2lab); % Значение интенсивности из диапазона от 0 до 100, преобразуется в диапазон % [0 1] (преобразования выполняются в формате double) % и далее применяются некоторые методы повышения контрастности max_luminosity=100; L=shadow_lab(:, :, 1)/max_luminosity; shadow_imadjust=shadow_lab; shadow_imadjust(: ,: , 1)=imadjust(L)*max_luminosity; shadow_imadjust=applycform(shadow_imadjust, lab2srgb); shadow_histeq=shadow_lab; shadow_histeq(: ,: , 1)=histeq(L)*max_luminosity; shadow_histeq=applycform(shadow_histeq, lab2srgb); shadow_adapthisteq=shadow_lab; shadow_adapthisteq(: ,: , 1)=adapthisteq(L)*max_luminosity; shadow_adapthisteq=applycform(shadow_adapthisteq, lab2srgb); figure, imshow(shadow); title('Original'); figure, imshow(shadow_imadjust); title('Imadjust');

Original Imadjust figure, imshow(shadow_histeq); title('Histeq'); figure, imshow(shadow_adapthisteq); title('Adapthisteq');

Histeq Adapthisteq Улучшение мультиспектральных цветных изображений
Часто возникает необходимость в улучшении мультиспектральных данных и формировании на их основе изображения, которое является пригодным для визуального анализа.
Рассмотрим основные подходы к улучшению изображений, полученных на основе мультиспектральных данных. Для этого используем аэрокосмический снимок части Парижа (Франция). Изображение представлено программой Erdas в формате LAN. Оно было зафиксировано в семи диапазонах спектра. Концепция дальнейшей обработки сводится к следующему:
- Считывание мультиспектральных данных из LAN-файла с помощью программы Erdas.
- Построение цветовых составляющих на основе комбинации различных диапазонов спектра.
- Улучшение изображения с использованием растяжения контраста.
- Улучшение изображения с использованием декорреляционного растяжения.
Последовательность действий:
Шаг 1: Построение составляющих мультиспектрального изображения в формате truecolor. Шаг 2: Использование гистограммы для исследования цветовых составляющих изображения. Шаг 3: Использование корреляции для анализа составляющих truecolor. Шаг 4: Улучшение truecolor-составляющих с помощью растяжения контраста. Шаг 5: Ограничение гистограммы при растяжении контраста. Шаг 6: Улучшение цветовых составляющих изображения с помощью метода декорреляционного растяжения. Шаг 7: Ограничение гистограммы при декорреляционном растяжении. Шаг 8: Построение и улучшение CIR-составляющих.
Шаг 1: Построение составляющих мультиспектрального изображения в формате truecolor.
LAN-файл paris.lan содержит 7-диапазонное аэрокосмическое изображение с размерами 512-на-512. Значения пикселей представлены в формате целых 8-битных чисел без знака.
Для считывания 3, 2 и 1 диапазона из LAN-файла в MATLAB используют функцию multibandread. Эти диапазоны взяты из различных частей спектра. Когда их отобразить в красной, зеленой и голубой плоскостях, получим RGB изображение со стандартными truecolor-составляющими. Последний аргумент в функции multibandread описывает какие диапазоны спектра используются.truecolor=multibandread('paris.lan', [512, 512, 7], 'uint8=>uint8', ... 128, 'bil', 'ieee-le', {'Band','Direct',[3 2 1]}); Составляющие truecolor имеют очень небольшой контраст и цвет их несбалансированный. figure imshow(truecolor); text(size(truecolor,2), size(truecolor,1) + 15,... 'Image courtesy of Space Imaging, LLC',... 'FontSize', 7, 'HorizontalAlignment', 'right')
Шаг 2: Использование гистограммы для исследования цветовых составляющих изображения.
Просматривая гистограмму красной составляющей, можно увидеть какие данные сконцентрированы в небольшой части имеющегося динамического диапазона.
figure
imhist(truecolor(:, :, 1))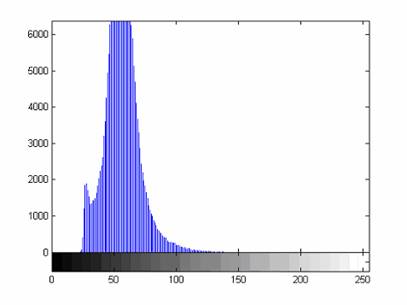
Шаг 3: Использование корреляции для анализа составляющих truecolor.
Между составляющими компонентами изображения существует некоторая связь, т.е. корреляция. Графически эту зависимость можно представить так.r=truecolor(:, :, 1); g=truecolor(:, :, 2); b=truecolor(:, :, 3); figure plot3(r(:), g(:), b(:), '.') grid('on') xlabel('Red') ylabel('Green') zlabel('Blue')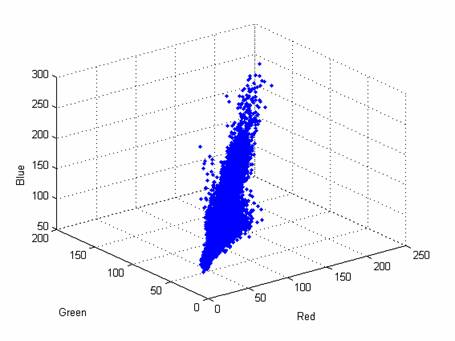
Такое представление составляющих изображения позволяет отобразить их корреляционные зависимости и объясняет псевдомонохроматический вид составляющих.
Шаг 4: Улучшение truecolor-составляющих с помощью растяжения контраста.
При использовании функции imadjust для линейного растяжения контраста, происходит восстановление (улучшение) изображения.
stretched_truecolor=imadjust(truecolor, stretchlim(truecolor)); figure imshow(stretched_truecolor)

Шаг 5: Ограничение гистограммы при растяжении контраста.
Гистограмма красной составляющей после применения растяжения контраста показывает, каким образом распределены данные во всем динамическом диапазоне. Эта гистограмма показана на рисунке ниже.
figure imhist(stretched_truecolor(:, :, 1))
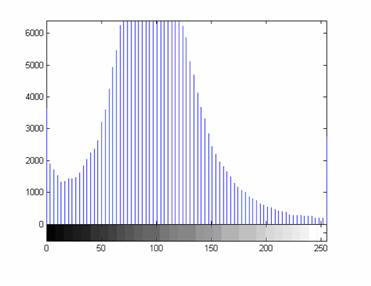
Шаг 6: Улучшение цветовых составляющих изображения с помощью метода декорреляционного растяжения.
Другой путь улучшения truecolor-составляющих состоит в использовании метода декорреляционного растяжения, который улучшает их расположение в метрическом пространстве с точки зрения высокой корреляции спектральных диапазонов. Для выполнения декорреляционного растяжения используется функция decorrstretch (эта функция аналогична линейному растяжению контраста).
decorrstretched_truecolor=decorrstretch(truecolor, 'Tol', 0.01); figure imshow(decorrstretched_truecolor)

Кроме того, поверхность характеризуется хорошо различимыми локальными областями различных цветов. Иными словами, такие области характеризуются большими спектральными различиями. В качестве примера отметим зеленую область в левой части изображений. В реальности эта область является парком в западной части Парижа.
Шаг 7: Ограничение гистограммы при декорреляционном растяжении.
Продемонстрируем эту процедуру на примере. r=decorrstretched_truecolor(:, :, 1); g=decorrstretched_truecolor(:, :, 2); b=decorrstretched_truecolor(:, :, 3); figure plot3(r(:), g(:), b(:), '.') grid('on') xlabel('Red') ylabel('Green') zlabel('Blue')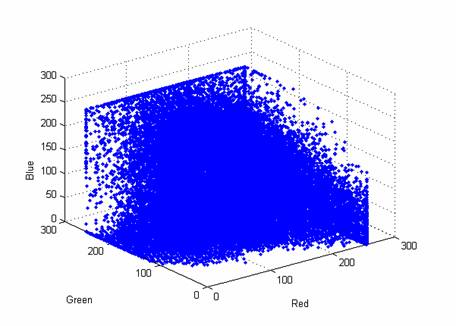
Шаг 8: Построение и улучшение CIR-составляющих.
Аэрокосмические летательные аппараты могут фиксировать изображения как в видимом, так и в невидимом диапазонах спектра. Для визуализации изображений в невидимом спектре используют преобразование в формат RGB. При решении рассматриваемой задачи используют диапазон, который находится вблизи инфракрасного диапазона (near infrared (NIR)). Также возможно его использование вместе с другими диапазонами для исследования, например, задач экологического состояния региона.
Рассмотрим визуализацию изображения, полученного в так называемом CIR-диапазоне (color infrared (CIR)). CIR=multibandread('paris.lan', [512, 512, 7], 'uint8=>uint8', ... 128, 'bil', 'ieee-le', {'Band','Direct',[4 3 2]}); Для усиления некоторых характеристик изображения используют декорреляционное растяжение. stretched_CIR=decorrstretch(CIR, 'Tol', 0.01); figure imshow(stretched_CIR)
Следует отметить, что свойства инфракрасных составляющих изменяются в зависимости от свойств сканируемого объекта. Поэтому такие изображения могут быть использованы для дистанционного исследования земной поверхности.
Регистрация аэрофотографий на ортофотоснимках
Два изображения одной и той же сцены могут сравниваться только в том случае, если они представлены в одинаковых координатных системах. Представим процесс преобразования изображения в одной из координатных систем в другое изображение.
Ключевые понятия Регистрация изображений, контрольные точки, геометрические преобразования, ортофотоснимки Ключевые функции cpselect, cp2tform, imtransform Демонстрация примера включает следующие шаги:
- Шаг 1: Считывание изображения.
- Шаг 2: Выбор контрольных точек.
- Шаг 3: Выбор геометрических преобразований.
- Шаг 4: Преобразование незарегистрированных изображений.
- Шаг 5: Просмотр зарегистрированных изображений.
Шаг 1: Считывание изображения.
Изображение westconcordorthophoto.png представляет собой ортофотоснимок, на котором изображена некоторая часть поверхности земли. Изображение westconcordaerial.png являет собой незарегистрированное аэроизображение и содержит некоторые искажение относительно ортофотоснимка.
unregistered=imread('westconcordaerial.png');
figure, imshow(unregistered)
figure, imshow('westconcordorthophoto.png')

Шаг 2: Выбор контрольных точек.
Первым шагом на пути совмещения представленных выше изображений является выбор контрольных точек с помощью функции cpselect.
load westconcordpoints
cpselect(unregistered(:, :, 1),'westconcordorthophoto.png',...
input_points,base_points)
С помощью специального пакета существует возможность выбора соответствующих контрольных точек. Контрольные точки используются в качестве маркеров для совмещения (привязки) двух изображений. Четырех пар контрольных точек уже достаточно для поиска (привязки). На основании этих точек делается заключение о том, какие геометрические преобразования нужно проделать в дальнейшем.
При идентификации аэрофотоснимка может возникнуть необходимость в добавлении пары контрольных точек.
Для запоминания контрольных точек необходимо в меню File выбрать опцию Save Points to Workspace. После запоминания точек следует перезаписать переменные input_points и base_points.
Шаг 3: Выбор геометрических преобразований.
На предварительных шагах было определено аэрофотоизображение и соответствующее ему топографическое изображение. На исходном аэрофотоизображении возможны геометрические искажения. С помощью функции cp2tform осуществляется поиск параметров проекционных искажений.
t_concord=cp2tform(input_points, base_points, 'projective');
Шаг 4: Преобразование незарегистрированных изображений.
Совмещая изображения с помощью выбранных контрольных точек существует возможность выявления геометрических искажений. А применение функции imtransform приводит к устранению этих искажений. Следует отметить, что выбор значений 'XData' и 'YData' обеспечивает еще более точное совмещение (калибровку) с ортофотоснимком.
Info=imfinfo('westconcordorthophoto.png');
registered=imtransform(unregistered, t_concord, ...
'XData', [1 info.Width], 'YData', [1 info.Height]);
Шаг 5: Просмотр зарегистрированных изображений.
figure, imshow(registered)
Визуальный анализ полученных результатов свидетельствует о их приемлемости. В другом случае, для получения еще более эффективного результата, следует начать обработку с шага 2 и выбрать большее число контрольных точек.
Пространственные преобразования изображений
Большинство свойств пространственных преобразований наиболее наглядно демонстрируются на примере изображения шахматной доски.
Ключевые понятия Пространственные преобразования, координатная система, линейные конформные отображения, аффинные преобразования, проекции, полиномы, кусочно-линейный, бочкообразные искажения Ключевые функции checkerboard, maketform, imtransform, makeresampler, tformarray Приведем демонстрационные примеры, которые будут включать:
- Изображение 1: Создание шахматной доски.
- Изображение 2: Применение линейных конформных преобразований.
- Изображение 3: Применение аффинных преобразований.
- Изображение 4: Применение проекционных преобразований.
- Изображение 5: Применение полиномиальных преобразований.
- Изображение 6: Применение кусочно-линейных преобразований.
- Изображение 7: Применение синусоидальных преобразований.
- Изображение 8: Применение бочкообразных преобразований.
- Изображение 9: Применение инверсных бочкообразных преобразований.
Изображение 1: Создание шахматной доски.
Шахматная доска представляет собой изображение прямоугольника с шестнадцатью ячейками. С помощью такого изображения исследование геометрических преобразований будет наиболее наглядным.
Геометрические преобразования заключаются в преобразовании из одной системы координат в другую. В этом примере изображение представляет собой сетку в виде шахматной доски, представленную в некоторой исходной координатной системе. Каждое преобразование проводится в различных координатных системах. При вычислении геометрических преобразований исходное изображение находится в координатах (x, y), а преобразованное изображение - в координатах (u, v).
В дальнейшем изображение шахматной доски I будет использовано в качестве исходного при демонстрации различных примеров.
I=checkerboard(10, 2);
figure
subplot(331)
imshow(I)
title('original')
Изображение 2: Применение линейных конформных преобразований.
Линейные конформные преобразования могут включать поворот, масштабирование и сдвиг. Очертания и углы остаются постоянными. Параллельные линии остаются параллельными, прямые линии остаются прямыми.Для линейных конформных преобразований: [u v]=[ x y 1] T. Параметр T представляет собой матрицу с размерностью 3x2, которая зависит от четырех параметров. % Четыре параметра. scale=1.2; % коэффициент масштабирования angle=40*pi/180; % угол поворота tx=0; % сдвиг по x ty=0; % сдвиг по y sc=scale*cos(angle); ss=scale*sin(angle); T=[ sc -ss; ss sc; tx ty]; Далее линейные конформные преобразования используются как подмножество аффинных преобразований. После этого создается структура TFORM: t_lc=maketform('affine', T); I_linearconformal=imtransform(I, t_lc, 'FillValues', .3); subplot(332) imshow(I_linearconformal); title('linear conformal')
Что касается сдвига, то когда изменения в одном из направлений tx или ty отличны от нуля, то это не влияет на результирующее изображение. Чтобы увидеть координаты, которые соответствуют нашим преобразованиям, включая сдвиг, нужно провести следующие вычисления:
[I_linearconformal, xdata, ydata]=imtransform(I, t_lc, 'FillValues', .3);
figure, imshow(xdata, ydata, I_linearconformal), axis on
Отметим, что параметры xdata и ydata соответствуют сдвигу. Для описания той части изображения, которую нужно рассмотреть (проанализировать), в функции imtransform используются параметры 'XData' и 'YData'.
Изображение 3: Применение аффинных преобразований.
При аффинных преобразованиях размерности x и y можно масштабировать или вырезать при сдвиге. Параллельные линии остаются параллельными, прямые линии остаются прямыми. Линейные конформные преобразования являются подмножеством аффинных преобразований.
Выражение для аффинных преобразований аналогично выражению для линейных конформных преобразований: [u v]=[ x y 1] T. Параметр T представляет собой матрицу 3x2 с шестью различными элементами.
T=[1 0.1;
1 1;
0 0];
t_aff=maketform('affine', T);
I_affine=imtransform(I, t_aff, 'FillValues', .3);
subplot(333)
imshow(I_affine)
title('affine')
Изображение 4: Применение проекционных преобразований.
При проекционных преобразованиях четырехугольник остается четырехугольником. Прямые линии остаются прямыми линиями. Аффинные преобразования являются подмножеством проекционных преобразований.
Для проекционных преобразований: [up vp wp]=[x y w] T, гдеu = up / wp
v = vp / wp.Параметр T представляет собой матрицу с размерностью 3x3 с девятью различными элементами.
T = [A D G
B E H
C F I]Что касается матричных преобразований, то эквивалентными являются два выражения:
u = (Ax + By + C) / (Gx + Hy + 1)
v = (Dx + Ey + F) / (Gx + Hy + 1)T=[1 0 0.008; 1 1 0.01; 0 0 1]; t_proj=maketform('projective', T); I_projective=imtransform(I, t_proj, 'FillValues', .3); subplot(334) imshow(I_projective) title('projective')
Изображение 5: Применение полиномиальных преобразований.
При полиномиальных преобразованиях полиномиальная функция от x и y определяет способ отображения.
Для полиномиальных преобразований второго порядка:[u v] = [1 x y x*y x^2 y^2] T Оба параметра u и v являются полиномами второго порядка относительно x и y. Каждый полином второго порядка характеризуется, в свою очередь, шестью параметрами. При определении всех коэффициентов размерность T составляет 6x2.
xybase=reshape(randn(12, 1), 6, 2); t_poly=cp2tform(xybase, xybase, 'polynomial', 2); % Двенадцать элементов T. T= [0 0; 1 0; 0 1; 0.001 0; 0.02 0; 0.01 0]; t_poly.tdata=T; I_polynomial=imtransform(I, t_poly, 'FillValues', .3); subplot(335) imshow(I_polynomial) title('polynomial')
Изображение 6: Применение кусочно-линейных преобразований.
При кусочно-линейных преобразованиях, линейные преобразования применяются отдельно к различным частям изображения. В этом примере правая часть изображения является растянутой, а левая часть не изменена.imid=round(size(I, 2)/2); I_left=I(:, 1:imid); stretch=1.5; % Коэффициент растяжения size_right=[size(I, 1) round(stretch*imid)]; I_right=I(:, imid+1:end); I_right_stretched=imresize(I_right, size_right); I_piecewiselinear=[I_left I_right_stretched]; subplot(336) imshow(I_piecewiselinear) title('piecewise linear')
Последние три примера показывают методы восстановления изображений с нерегулярными искажениями.
Изображение 7: Применение синусоидальных преобразований. [nrows, ncols]=size(I); [xi, yi]=meshgrid(1:ncols, 1:nrows); a1=5; % амплитуда синусоиды. a2=3; u=xi+a1*sin(pi*xi/imid); v=yi-a2*sin(pi*yi/imid); tmap_B=cat(3, u, v); resamp=makeresampler('linear', 'fill'); I_sinusoid=tformarray(I, [], resamp, [2 1], [1 2], [], tmap_B, .3); subplot(337) imshow(I_sinusoid) title('sinusoid')
Изображение 8: Применение бочкообразных преобразований.
Бочкообразные искажения приводят к возникновению заметных радиальных искажений относительно центра. Чем дальше от центра, тем искажения стают все более заметными, в результате стороны стают выпуклыми.% Радиальные бочкообразные искажения xt=xi(:)-imid; yt=yi(:)-imid; [theta, r]=cart2pol(xt, yt); a=.001; % Амплитуда кубического выражения. s=r+a*r.^3; [ut, vt]=pol2cart(theta, s); u=reshape(ut, size(xi))+imid; v=reshape(vt, size(yi))+imid; tmap_B=cat(3, u, v); I_barrel=tformarray(I, [], resamp, [2 1], [1 2], [], tmap_B, .3); subplot(338) imshow(I_barrel) title('barrel')
Изображение 9: Применение инверсных бочкообразных преобразований.
Особенностью восстановления изображений с так называемыми инверсными бочкообразными искажениями является применение отрицательных амплитуд. Чем дальше от центра изображения, тем больше проявляются такие искажения. В результате стороны получаются вогнутыми.% Радиальные инверсные бочкообразные искажения xt=xi(:)-imid; yt=yi(:)-imid; [theta,r]=cart2pol(xt, yt); a=-0005; % Амплитуда при кубических преобразованиях. s=r+a*r.^3; [ut, vt]=pol2cart(theta, s); u=reshape(ut, size(xi))+imid; v=reshape(vt, size(yi))+imid; tmap_B=cat(3, u, v); I_pin=tformarray(I, [], resamp, [2 1], [1 2], [], tmap_B, .3); subplot(339) imshow(I_pin) title('pin cushion')
Исследование конформных преобразований
Пространственные функции трансформации изображений очень широко применяются при исследованиях конформных преобразований. Конформные преобразования, в свою очередь, применяются для обработки изображений с целью достижения некоторых эффектов.
Ключевые понятия:
Преобразование изображений, конформное отображение, вектор преобразований, контроль отображения
Ключевые функции:
maketform, imtransform, tformfwd
Обзор демонстраций.
Демонстрационные примеры включают следующие шаги:
- Шаг 1: Деформация изображений с помощью конформных преобразований.
- Шаг 2: Исследование отображения изображений с помощью линий сетки, окружностей и т.п.
- Шаг 3: Достижение специальных эффектов на результирующем изображении с помощь использования метода частичных масок.
- Шаг 4: Повторение эффекта на разных изображениях.
Шаг 1: Деформация изображений с помощью конформных преобразований.
В этом демонстрационном примере деформации изображений в качестве инверсных преобразований используются преобразования типа (z+1/z)/2.
Двумерные пространственные преобразования f являются конформными, если (x, y)=f(u, v) есть заданными с помощью аналитической функции F и x+i*y=F(u+i*v).
Подобные преобразования называются конформными отображениями. Конформные отображения имеют много свойств и применений; одно из важных свойств преобразований изображений состоит в сохранении локальных образов.
Аналитическая функция G, где G(z)=(z+1/z)/2, определяет конформные отображения, которые характеризуются достаточно сильными нелинейными преобразованиями. На основе этих преобразований линии, в зависимости от своего месторасположения, преобразуются в части окружностей (или в части окружностей цилиндров в случае трехмерных преобразований) или в прямые линии. (См. pp. 340-341 in Strang, Gilbert, Introduction to Applied Mathematics, Wellesley-Cambridge Press, Wellesley, MA, 1986.)
В этом демонстрационном примере покажем применение функции G для определения инверсных преобразований с целью искажения прямоугольного изображения. Результат четко демонстрирует суть преобразований, а также понимание особенностей конформных отображений.
Инверсные преобразования g можно определить как (u, v)=g(x, y) или представить в виде w=G(z), где w =u+i*v и z=x+i*y.
Считываем исходное изображение, которое разбито на 300x500 подизображений и отобразим их.
A=imread('peppers.png'); A=A(31:330, 1:500, :); figure, imshow(A); title('Original Image');
Используем функцию maketform для создания структуры TFORM с возможностью применения в качестве INVERSE_FCN аргумента следующих функций:
Инверсная функция: ipex004.m
function U=ipex004( X, t )
Z=complex(X(:, 1), X(:, 2));
R=abs(Z);
W=(Z+1./Z)/2;
U(:, 2)=imag(W);
U(:, 1)=real(W);conformal=maketform('custom', 2, 2, [], @ipex004, []); Определим границы отображения исходного и преобразованного изображений. Отметим, что параметры uData и vData сохраняют свою пропорциональность согласно исходному изображению (5/3). uData=[ -1.25 1.25]; % Граница для REAL(w) vData=[ 0.75 -0.75]; % Граница для IMAG(w) xData=[ -2.4 2.4 ]; % Граница для REAL(z) yData=[ 2.0 -2.0 ]; % Граница для IMAG(z) В функцию imtransform необходимо включать параметр SIZE c соотношением сторон, пропорциональных xData и yData (6/5), а также опцию просмотра результата. B=imtransform( A, conformal, 'cubic', ... 'UData', uData,'VData', vData,... 'XData', xData,'YData', yData,... 'Size', [300 360], 'FillValues', 255); figure, imshow(B); title('Transformed Image');
Сравним исходное и преобразованное изображение. Отметим, что в результате преобразований границы объектов изображений определенным образом искажаются. Также следует отметить такую особенность, что некоторые объекты исходного изображения на трансформированном изображении могут появляться дважды. Еще одной особенностью преобразований такого типа является то, что в центре преобразованного изображения образуется отверстие, состоящие из четырех полуокружностей.
Фактически большинство точек исходных данных отображается после проведенных преобразований двумя точками - одна на внутренней части и одна на внешней. Внутренняя часть является значительно меньше соответствующей ей внешней части.
Шаг 2: Исследование отображения изображений с помощью линий сетки, окружностей и т.п.
Когда преобразования задаются с помощью функции maketform, тогда для трансформации правильных геометрических объектов можно применить функцию tformfwd (особенно, для прямоугольной сетки и равномерного массива окружностей). В этом примере рассматриваются однозначные преобразования, поскольку одной исходной точке соответствуют две преобразованные. Таким образом, обработку исходных данных можно производить двумя различными функциями.
Когда принять, что w=(z+1/z)/2 или представить это в другом виде (z^2+2*w*z+1=0), тогда z=w+/sqrt(w^2-1).
Получение положительного и отрицательного квадратного корня приводит к необходимости разделения процесса преобразований. Покажем применение и управление функцией maketform в первом варианте:
Функция: Forward1.m
function X=Forward1( U, t )
W=complex(U(:, 1),U(:, 2));
Z=W+sqrt(W.^2-1);
X(:, 2)=imag(Z);
X(:, 1)=real(Z);Возможен другой способ построения преобразований:
Функция: Forward2.m
function X=Forward1( U, t )
W=complex(U(:, 1),U(:, 2));
Z=W-sqrt(W.^2-1);
X(:, 2)=imag(Z);
X(:, 1)=real(Z);Функция ipex005 создает типичные объекты TFORM с возможностью ее ручного управления
t1=maketform('custom', 2, 2, @Forward1, [], []);
t2=maketform('custom', 2, 2, @Forward2, [], []);
и использования вместе с tformfwd для преобразования объектов типа сетка из линий и массив окружностей.
Четыре изображения внизу демонстрируют работу функции ipex005. В первом случае это изображение типа сетка из линий и во втором случае - это массив окружностей:
Программный источник функции ipex005 размещается в matlabroot/toolbox/images/imdemos/ipex005.m.
ipex005(A,uData,vData,B,xData,yData)
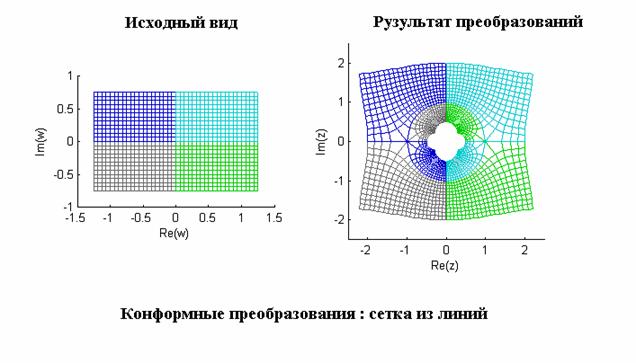
До начала преобразований сетка из линий представляет собой квадранты, окрашенные в соответствующий цвет. Полезность такого окрашивания квадрантов особенно ценна после проведения соответствующих преобразований. С их помощью на результирующем изображении четко видно проведенные пространственные изменения. Отметим, что каждый квадрант условно подвергается двухэтапным преобразованиям - во внутренней стороне окружности и внешней стороне окружности. Разные части квадранта подвергаются различной степени искажений.
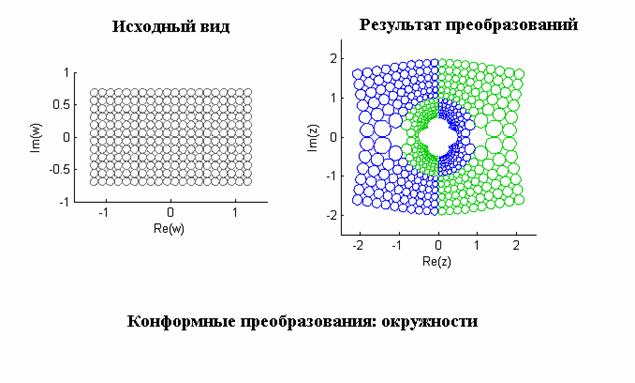
Равномерная сетка, состоящая из окружностей одинакового размера, преобразуется в окружности, которые упакованы в соответствии тангенциальной зависимостью. При таком виде преобразований положительные значения преобразований отображаются зеленым цветом, а отрицательные - синим и определяются как
 . Также отметим, что при преобразованиях нелинейно изменяется диаметр окружности.
. Также отметим, что при преобразованиях нелинейно изменяется диаметр окружности.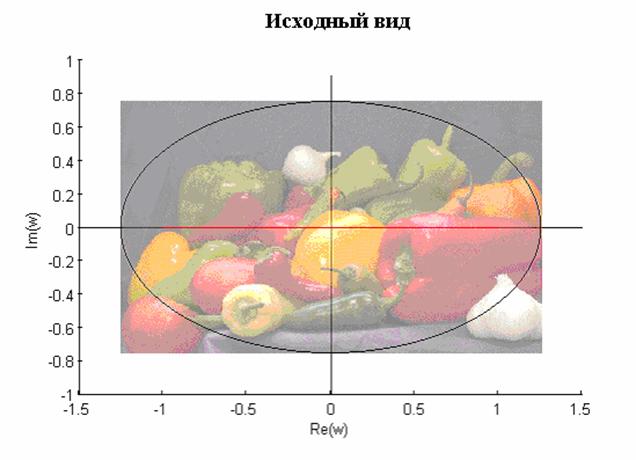
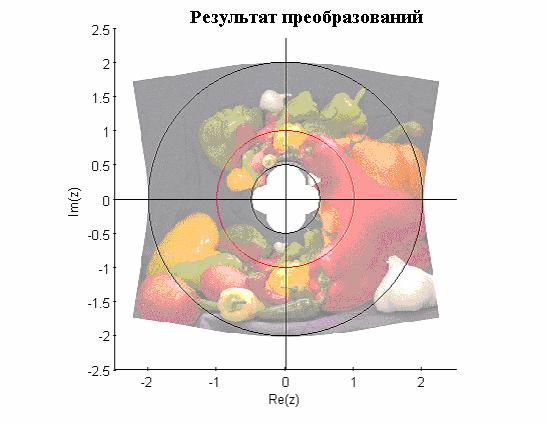
Графика MATLAB позволяет удобно отображать сдвиг и масштабирование локальных объектов преобразованного изображения. Использование полупрозрачного режима отображения позволяет наглядно понять суть проводимых преобразований. Наибольшим искажениям подвергаются объекты, размещенные в центральной части изображения. Более детально это представлено на двух верхних рисунках.
Шаг 3: Достижение специальных эффектов на результирующем изображении с помощь использования метода частичных масок.
При инверсной функции преобразования структура TFORM возвращает вектор значений для получения результирующего изображения. При этом также используются функции imtransform и tformarray. Эти действия, в основном, детально описаны в начале (см. Шаг 1). Нужно только с помощью функции maketform('custom'...) преобразовать структуру TFORM с целью ручного управления INVERSE_FCN:
Инверсная функции: ipex006.m
function U=ipex006( X, t )
Z=complex(X(:, 1), X(:, 2));
W=(Z+1./Z)/2;
q=0.5<=abs(Z)&abs(Z)<=2;
W(~q)=complex(NaN, NaN);
U(:, 2)=imag(W);
U(:, 1)=real(W);Программный источник функции размещается в matlabroot/toolbox/images/imdemos/ipex006.m. В принципе, функция ipex006 аналогична функции ipex004, описанной в Шаге 1, за исключением двух дополнительных линеек:
q=0.5<=abs(Z)&abs(Z)<=2;
W(~q)=complex(NaN, NaN);Эти данные являются основными при инверсных преобразованиях. В более общем виде эти преобразования можно представить так:
ring=maketform('custom', 2, 2, [], @ipex006, []); Bring=imtransform( A, ring, 'cubic',... 'UData', uData, 'VData', vData,... 'XData', [-2 2], 'YData', yData,... 'Size', [400 400], 'FillValues', 255 ); figure, imshow(Bring); title('Transformed Image With Masking');
Полученный результат, по сюжету, аналогичный исходному, за исключением нескольких объектов на внешней части окружности.
Шаг 4: Повторение эффекта на разных изображениях
Проведем так называемые преобразования по окружности, которые описаны в Шаге 3, с другими изображениями, увидим результирующий эффект и возможное практическое применение.
Для этого сначала считаем исходное изображение и отобразим его.
C=imread('greens.jpg'); figure, imshow(C); title('Winter Greens Image');
Далее проводятся так называемые преобразования по окружности. D=imtransform( C, ring, 'cubic',... 'UData', uData, 'VData', vData,... 'XData', [-2 2], 'YData', [-2 2],... 'Size', [400 400], 'FillValues', 255 ); figure, imshow(D); title('Transformed and Masked Winter Greens Image');
Создание обивочных материалов с использованием изображений
При рассмотрении этого демонстрационного примера, создается структура TFORM, которая описывает способы обработки изображений при решении задач создания обивочных материалов. Исследуем наиболее эффектные преобразования на примере сетки из прямых и окружностей. При этом будем также использовать такие функции как imtransform и tformarray.
Ключевые слова
Вырезание изображения, аффинные преобразования, преобразования векторов
Ключевые функции
maketform, makeresampler, imtransform, tformfwd
Демонстрационный пример включает следующие шаги:
- Шаг 1: Первичное преобразование изображений.
- Шаг 2: Исследование преобразований.
- Шаг 3: Сравнительный анализ различных методов.
- Шаг 4: Реализация методов с параметрами 'circular' и 'symmetric'.
Шаг 1: Первичное преобразование изображений.
В двумерном случае, при создании обивочных материалов на основе изображений, преобразования заключаются в трансформации исходной пары координат [u v] в пару результирующих координат [x y]. Это можно представить в таком виде
x=u+a*v
y=v(1) где
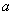 является константой.
является константой.В отдельных случаях применяют аффинные преобразования, которые можно записать так как
[ x y 1 ]=[ u v 1 ]*[ 1 0 0 a 1 0 0 0 1](2) Значения x и y определяются из выражения 1.
Приняв, что
 , создадим структуру аффинных преобразований с использованием функции maketform.
, создадим структуру аффинных преобразований с использованием функции maketform.a=0.45; T=maketform('affine', [1 0 0; a 1 0; 0 0 1] ); Теперь необходимо выбрать, считать и просмотреть изображение, которое будет использоваться при преобразованиях. A=imread('football.jpg'); h1=figure; imshow(A); title('Исходное изображение');
Выберем фон, на котором будет размещено это изображение, например, оранжевый.
orange=[255 127 0]';
Считаем и используем параметр T для преобразования данных в A. Эти преобразования можно представить следующим образом:
B=imtransform(A, T, 'cubic', 'FillValues', orange);
При проведении подобного рода преобразований используют кубическую интерполяцию вдоль строк и столбцов. В данном случае, взамен этой интерполяции, будет использоваться интерполяция по ближайшей окрестности. При этом для формирования результата применяется функция imtransform.
R=makeresampler({'cubic', 'nearest'}, 'fill');
B=imtransform(A, T, R, 'FillValues', orange);
h2=figure; imshow(B);
Шаг 2: Исследование преобразований.
Проведение преобразований сетки из линий и массива окружностей с использованием функции tformfwd является одним из путей осмысленного понимания трансформаций данного вида.
Скрипт ipex001 формирует сетку из линий, наложенную на исходное изображение и отображает на нем. Этот программный продукт содержится в /toolbox/images/imdemos/ipex001.m.
ipex001

Скрипт ipex002 реализует ту же процедуру, только с использованием окружностей. Этот программный продукт содержится в /toolbox/images/imdemos/ipex002.m.
ipex002

Шаг 3: Сравнительный анализ различных методов.
При реализации технологии вырезания изображений, функция imtransform заполняет оранжевыми треугольниками места, где нет данных. Известно пять модификаций рассматриваемого метода. При этом используется пять различных параметров ('fill', 'replicate', 'bound', 'circular' и 'symmetric'). Проведем сравнительный анализ первых трех параметров.
Первая опция 'fill' вместе с опциями 'XData' и 'YData' используется в функции imtransform для принудительной установки фона вокруг изображения.
Bf=imtransform(A, T, makeresampler({'cubic', 'nearest'},... 'fill'), 'XData', [-49 500], 'YData', ... [-49 400], 'FillValues', orange); figure, imshow(Bf); title('Pad Method=''fill''');
При использовании второй опции 'replicate' нет необходимости в заполнении пространства вокруг исходного изображения.
Br=imtransform(A, T, makeresampler({'cubic', 'nearest'}, ... 'replicate'), 'XData', [-49 500], 'YData', ... [-49 400]); figure, imshow(Br); title('Pad Method=''replicate''');
Теперь рассмотрим применение третьей опции 'bound'.
Bb=imtransform(A, T, makeresampler({'cubic', 'nearest'}, ... 'bound'), 'XData', [-49 500], 'YData', ... [-49 400], 'FillValues', orange); figure, imshow(Bb); title('Pad Method=''bound''');
Результаты обработки исходного изображения с помощью исследуемого метода при установке опций 'fill' и 'bound' являются очень похожими. Разница состоит в том, что при использовании опции 'bound' при обработке используется кубическая интерполяция и результирующее изображение получается немного размытым. Рассмотрим этот момент более детально и проанализируем результаты обработки с использованием двух опций ('fill' и 'bound') на элементном уровне.
Cf=imtransform(A, T, makeresampler({'cubic', 'nearest'}, ... 'fill'), 'XData', [423 439], 'YData', ... [245 260], 'FillValues', orange); Cb=imtransform(A, T, makeresampler({'cubic', 'nearest'}, ... 'bound'), 'XData', [423 439], 'YData', ... [245 260], 'FillValues', orange); Cf=imresize(Cf, 12, 'nearest'); Cb=imresize(Cb, 12, 'nearest'); figure; subplot(1, 2, 1); imshow(Cf); title('Pad Method=''fill'''); subplot(1, 2, 2); imshow(Cb); title('Pad Method=''bound''');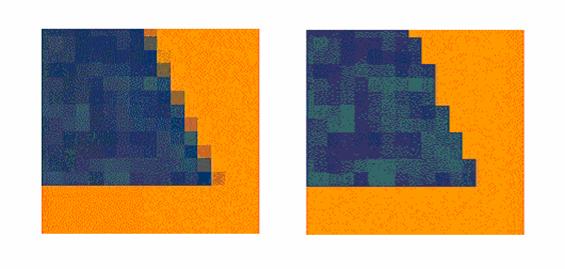
Шаг 4: Реализация методов с параметрами 'circular' и 'symmetric'.
Оставшиеся две опции определяют два подхода. Один из них использует опцию 'circular' и состоит в повторяемости исходного изображения вдоль каждой размерности, второй - использует опцию 'symmetric' и состоит в повторяемости зеркальных отражений исходного изображения. Продемонстрируем это на конкретных примерах.
Thalf=maketform('affine', [1 0; a 1; 0 0]/2); Bc=imtransform(A, Thalf,makeresampler({'cubic', 'nearest'}, ... 'circular'), 'XData', [-49 500], 'YData', ... [-49 400], 'FillValues', orange); figure, imshow(Bc); title('Pad Method=''circular''');
Bs=imtransform(A, Thalf, makeresampler({'cubic', 'nearest'}, ... 'symmetric'), 'XData', [-49 500], 'YData', ... [-49 400], 'FillValues', orange); figure, imshow(Bs); title('Pad Method=''symmetric''');
Извлечение данных из трехмерных магниторезонансных изображений
Функции imtransform и tformarray могут быть использованы при интерполяции и других преобразованиях трехмерных магниторезонансных изображений, особенно при получении числовых характеристик.
Ключевые термины Аффинные, традиционные и комплексные преобразования, трехмерные и двухмерные преобразования, исходный массив преобразований, дискретизация выбранных размерностей Ключевые функции maketform, makeresampler, imtransform, tformarray Просмотр демонстрационного примера.
Демонстрация включает следующие шаги:- Шаг 1: Считывание и просмотр магниторезонансных изображений (горизонтальные срезы).
- Шаг 2: Получение сагиттальных данных на основе горизонтальных срезов с использованием функции imtransform.
- Шаг 3: Получение сагиттальных данных на основе горизонтальных срезов с использованием функции tformarray.
- Шаг 4: Получение сагиттальных данных и отображение их в виде последовательности.
- Шаг 5: Получение корональных данных и отображение их в виде последовательности.
Шаг 1: Считывание и просмотр магниторезонансных изображений (горизонтальные срезы).
В этом примере используются магниторезонансные данные, которые представлены в MATLAB и используются при описании функций montage и immovie. Считывание магниторезонансных изображений добавляет две переменные в рабочее пространство: D (128x128x1x27, в формате uint8) и полутоновую палитру map (89x3, в формате double).
Переменная D включает 27 горизонтальных срезов магниторезонансных данных сканирования человеческого черепа с размерностью 128x128. Значения элементов D находятся в диапазоне от 0 до 88. Таким образом, палитра обеспечивает генерацию изображения в диапазоне, пригодном для визуального анализа. Размерность данных в D должна быть согласована с функцией immovie. Первых две размерности являются пространственными. Третья размерность представляет собой размерность цвета. Числа третьей размерности указывают на индексы в палитре, например, size(D, 3) и используются для описания RGB-составляющих цвета. Четвертая размерность является временной и только в очень редких случаях используется в качестве пространственной координаты. Приведенные выше пространственные размерности в D используются в функциях imtransform или tformarray для преобразования слайдов горизонтальных срезов в сагиттальные данные. Пространственные размерности D размещены в такой последовательности:- Размерность 1: От передней до задней части головы (ростральная (rostral) и каудальная (caudal) части)
- Размерность 2: С левой части головы на правую
- Размерность 4: От верхней части головы к нижней (inferior и superior).
Данные, которые представляют собой набор из 27 горизонтальных срезов, подвергаются последующей обработке. Для предотвращения непредсказуемых ситуаций при обработке данных, в примере используется функция iptgetpref.
truesizewarning=iptgetpref('TruesizeWarning'); iptsetpref('TruesizeWarning', 'off'); load mri; figure; immovie(D, map); montage(D, map); title('Horizontal Slices');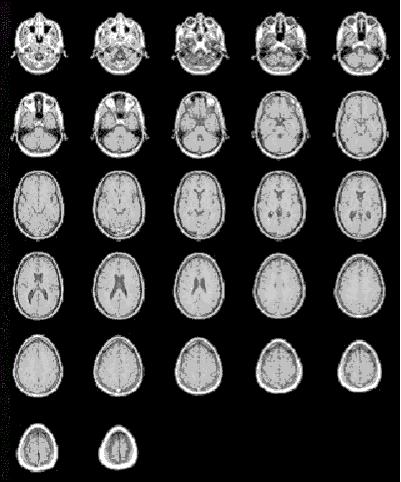
Шаг 2: Получение сагиттальных данных на основе горизонтальных срезов с использованием функции imtransform.
Существует возможность создания среднесагиттальных срезов, полученных на основе магниторезонансных данных, взятых из D и преобразованных с учетом анализа разных интервалов среза и пространственной ориентации.
Согласно сказанному выше, получение среднесагиттальных срезов проводят следующим образом.
M1=D(:, 64, :, :); size(M1)
Также существует возможность просмотра M1 как изображения с размерностью 128x1x1x27. С использованием функции reshape данные M1 можно преобразовать в изображение с размерностью 128x27, с дальнейшим просмотром с помощью imshow.
M2=reshape(M1, [128 27]); size(M2)
figure, imshow(M2, map);
title('Sagittal - Raw Data');
Размерности в M2 следующие:
- Размерность 1: От передней до задней части головы (ростральная (rostral) и каудальная (caudal) части)
- Размерность 2: От верхней части головы к нижней (inferior и superior).
Качество визуального просмотра можно улучшить, изменив пространственное расположение (ориентацию) изображения и изменив масштаб вдоль одной из осей с коэффициентом 2.5. Для улучшения визуального просмотра также используются аффинные преобразования.
T0=maketform('affine', [0 -2.5; 1 0; 0 0]);
Параметр, который применяется при реализации функции maketform и представляет собой блок 2x2
[ 0 -2.5
1 0 ]
характеризует описанные выше преобразования поворота и масштабирования. После преобразований получим:- Размерность 1: От верхней части головы к нижней (inferior и superior).
- Размерность 2: От передней до задней части головы (ростральная (rostral) и каудальная (caudal) части)
Выражение
imtransform(M2, T0, 'cubic')
применяется для преобразования данных из T в M2 и обеспечения приемлемой разрешительной способности при интерполяции вдоль направления сверху вниз. Однако, при такого рода преобразованиях отпадает необходимость в проведении кубической интерполяции в направлении от передней части головы к задней. Поэтому окрестности в этом направлении определяются с большей степенью эффективности.
R2=makeresampler({'cubic', 'nearest'}, 'fill');
M3=imtransform(M2, T0, R2);
figure, imshow(M3, map);
title('Sagittal - IMTRANSFORM')
Шаг 3: Получение сагиттальных данных на основе горизонтальных срезов с использованием функции tformarray.
В этом пункте мы получим результаты аналогичные результатам, полученным в пункте 2. Только теперь для преобразования трехмерных данных в двухмерные, а также для других операций будем использовать функцию tformarray. В шаге 2 начальные данные представляют собой трехмерный массив, а результат обработки представлен в виде двумерного массива. При преобразованиях используется функция imtransform, которая создает массив М3, а также промежуточные двумерные массивы M1 и M2.
При использовании аргумента типа TDIMS_A в функции tformarray существует возможность проведения определенных преобразований для исходного массива. В результате этих преобразований получится изображение с такими размерностями:- Размерность 1: Сверху вниз (исходная размерность)
- Размерность 2: От передней до задней части головы (ростральная (rostral) и каудальная (caudal) части, исходная размерность)
Таким образом, получим примерный сагиттальный вид с исходной размерностью 2 при параметре tdims_a=[4 1 2]. Параметр tform можно получить, проводя двухмерные аффинные преобразования, которые заключаются в масштабировании размерности 1 с коэффициентом 2.5 и прибавлении к массиву значения 68.5. Вторая часть преобразований, которые заключаются в получении 64-го сагиттального плана, описывается функцией INVERSE_FCN:
Инверсная функция: ipex003.m function U=ipex003( X, t ) U=[X repmat(t.tdata, [size(X, 1) 1])]; Определение коэффициентов T2 и Tc.
T1=maketform('affine', [-2.5 0; 0 1; 68.5 0]);
T2=maketform('custom', 3, 2, [], @ipex003, 64);
Tc=maketform('composite', T1, T2);
Проведем некоторые преобразования для определения третьей размерности.
R3=makeresampler({'cubic', 'nearest', 'nearest'}, 'fill');
Функция tformarray преобразовывает третью пространственную размерность и массив D трансформируется в двумерные данные. Таким образом, исходное изображение с размерами 66x128 с 27 видов растягивается до 66 в вертикальном направлении.
M4=tformarray(D, Tc, R3, [4 1 2], [1 2], [66 128], [], 0);
Полученный результат идентичен результату, полученному при обработке функцией imtransform.
figure, imshow(M4, map);
title('Sagittal - TFORMARRAY');
Шаг 4: Получение сагиттальных данных и отображение их в виде последовательности.
Создадим четырехмерный массив (трехмерные данные и размерность цветности), который используется для генерации движений слева направо с использованием более 30 снимков. Массив преобразований имеет такую структуру:- Размерность 1: Сверху вниз.
- Размерность 2: От передней до задней части головы (ростральная (rostral) и каудальная (caudal) части)
- Размерность 4: Слева направо.
В качестве первого шага проведем следующие преобразования - трансформируем исходный массив с использованием параметра TDIMS_A=[4 1 2]. Преобразования будут заключаться в перестановке и масштабировании элементов массива в вертикальной размерности.
T3=maketform('affine', [-2.5 0 0; 0 1 0; 0 0 0.5; 68.5 0 -14]);
Теперь в массиве преобразований tformarray параметр TSIZE_B=[66 128 35] включает 35 четырехразмерных слайдов.
S=tformarray(D, T3, R3, [4 1 2], [1 2 4], [66 128 35], [], 0);
Для просмотра движения сагиттальных слайдов они соответствующим образом монтируются.
figure;
immovie(S, map);
S2=padarray(S, [6 0 0 0], 0, 'both');
montage(S2, map);
title('Sagittal Slices');
Шаг 5: Получение корональных данных и отображение их в виде последовательности.
Создание корональных слайдов почти аналогично созданию сагиттальных. Для этого изменим параметр TDIMS_A из [4 1 2] на [4 2 1]. Создадим серию из 45 слайдов и смонтируем из них движения. Размерности результирующего массива:- Размерность 1: Сверху вниз.
- Размерность 2: Слева направо.
- Размерность 4: От задней до передней части головы (ростральная (rostral) и каудальная (caudal) части)
T4=maketform('affine', [-2.5 0 0; 0 1 0; 0 0 -0.5; 68.5 0 61]); В функции tformarray параметр TSIZE_B=[66 128 48] описывает размерности изображений. C=tformarray(D, T4, R3, [4 2 1], [1 2 4], [66 128 45], [], 0); Для просмотра движения кадры соответствующим образом монтируются. figure; immovie(C, map); C2=padarray(C, [6 0 0 0], 0, 'both'); montage(C2, map); title('Coronal Slices');
Отметим, что большинство операций преобразования описанных выше массивов возможно корректировать в ручном режиме.
iptsetpref('TruesizeWarning', truesizewarning);Поиск длины маятника в движении
Проведем захват серии изображений с помощью пакета Image Acquisition Toolbox и затем проанализируем их с помощью Image Processing Toolbox. Рассмотрим это на примере задачи по вычислению длины маятника в движении.
Содержание- Шаг 1: Захват изображений.
- Шаг 2: Выбор области колебания маятника.
- Шаг 3: Сегментация маятника в каждом фрейме.
- Шаг 4: Поиск центра сегментированного маятника в каждом фрейме.
- Шаг 5: Вычисление радиуса колебания маятника.
Шаг 1: Захват изображений. Считываем кадры изображений маятника в движении. Кадры изображений, после их захвата с помощью Image Acquisition Toolbox, хранятся в виде MAT-файла pendulum.mat. % Доступ к захваченным изображениям (видеообъектам). % vidobj=videoinput('winvideo', 1, 'RGB24_352x288'); % Формирование объекта на основе пяти фреймов. % set(vidobj, 'FrameGrabInterval', 5); % Формирование большего числа фреймов. % nFrames=50; % set(vidobj, 'FramesPerTrigger', nFrames); % Доступ к видеоустройству. % src=getselectedsource(vidobj); % Настройка исходного устройства на формирование 30 кадров в секунду. % set(src, 'FrameRate', '30'); % Открытие окна просмотра. % preview(vidobj); % Начало захвата изображений. % start(vidobj); % Определение окончания захвата данных. % wait(vidobj, 10); % Извлечение фреймов из памяти. % frames=getdata(vidobj); % Удаление рабочих переменных. % delete(vidobj) % clear vidobj % Считывание MAT-файла. load pendulum; immovie(frames);
Шаг 2: Выбор области колебания маятника. Мы можем наблюдать колебания маятника в верхней половине каждого кадра в серии изображений. Создадим новую серию кадров, которая содержит только область с колеблющимся маятником. При создании новой серии изображений используем функцию imcrop. nFrames=size(frames, 4); first_frame=frames(:, :, :, 1); first_region=imcrop(first_frame, rect); frame_regions=repmat(uint8(0), [size(first_region) nFrames]); for count=1:nFrames frame_regions(:, :, :, count)=imcrop(frames(:, :, :, count), rect); end immovie(frame_regions);

Шаг 3: Сегментация маятника в каждом фрейме.
Отметим, что маятник представлен в виде потемнения на фоне. Операцию сегментирования можно провести, преобразив фрейм в полутоновое изображение и далее использовать функцию im2bw с некоторым порогом. Далее нужно удалить фон с помощью функций imopen и imclearborder.% Получение массива, содержащего сегментированное изображение маятника. seg_pend=false([size(first_region, 1) size(first_region, 2) nFrames]); centroids=zeros(nFrames, 2); se_disk=strel('disk', 3); for count=1:nFrames fr=frame_regions(:, :, :, count); imshow(fr) pause(0.2) gfr=rgb2gray(fr); gfr=imcomplement(gfr); imshow(gfr) pause(0.2) bw=im2bw(gfr, .7); % пороговая обработка bw=imopen(bw, se_disk); bw=imclearborder(bw); seg_pend(:, :, count)=bw; imshow(bw) pause(0.2) end
Шаг 4: Поиск центра сегментированного маятника в каждом фрейме.
Мы можем наблюдать как изменяется форма и расположение маятника в различных фреймах. Теперь необходимо решить непростую задачу поиска центра маятника. Информацию, найденную при решении этой задачи, используем для определения длины маятника. Для вычисления центра маятника будем использовать функции bwlabel и regionprops.for count=1:nFrames lab=bwlabel(seg_pend(:, :, count)); property=regionprops(lab, 'Centroid'); pend_centers(count, :)=property.Centroid; end Отображение центра маятника с помощью функции plot. x=pend_centers(:, 1); y=pend_centers(:, 2); figure plot(x, y, 'm.'), axis ij, axis equal, hold on; xlabel('x'); ylabel('y'); title('центр маятника');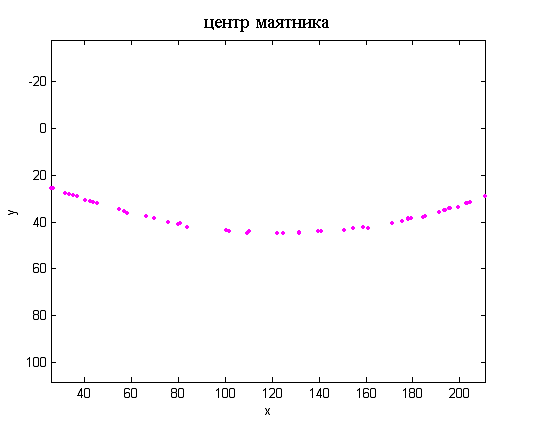
Шаг 5: Вычисление радиуса колебания маятника.
Запишем основное выражение окружности: (x-xc)^2+(y-yc)^2=radius^2, где (xc, yc) является центром, параметры a, b, c в уравнении x^2+y^2+a*x+b*y+c=0 представлены в виде a=-2*xc, b=-2*yc и c=xc^2+yc^2-radius^2.
Параметры a, b и c можно найти с помощью метода наименьших квадратов. Тогда выражение можно представить как a*x+b*y+c=-(x^2+y^2) или в виде [a; b; c]*[x y 1]=-x^2-y^2. Представим это выражение в виде операции обратного деления.Радиус окружности является длиной маятника в пикселях. abc=[x y ones(length(x), 1)]\[-(x.^2+y.^2)]; a=abc(1); b=abc(2); c=abc(3); xc=-a/2; yc=-b/2; circle_radius=sqrt((xc^2+yc^2)-c); pendulum_length=round(circle_radius) pendulum_length= 253 Отобразим окружность и ее центр, совмещая с центром маятника. circle_theta=pi/3:0.01:pi*2/3; x_fit=circle_radius*cos(circle_theta)+xc; y_fit=circle_radius*sin(circle_theta)+yc; plot(x_fit, y_fit, 'b-'); plot(xc, yc, 'bx', 'LineWidth', 2); plot([xc x(1)], [yc y(1)], 'b-'); text(xc-110,yc+100,sprintf('длина маятника=%d пикселя', pendulum_length));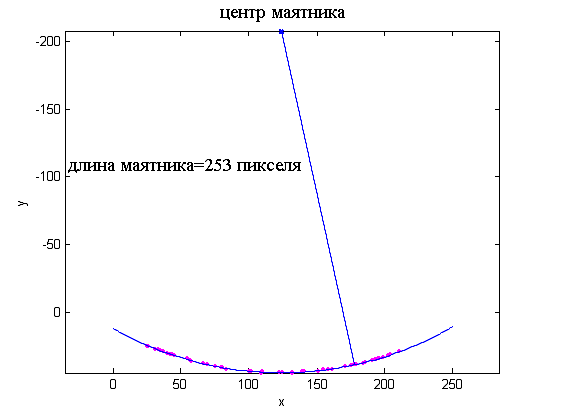
Гранулометрия
Обработка изображений применяется во многих сферах деятельности человека. Развитие информационных технологий способствует повышению качественного уровня анализа данных. Также прогресс компьютерной техники влияет на быстродействие и достоверность такой обработки. Приведем несколько наглядных примеров из тех областей, где применяется обработка изображений и, в частности, гранулометрия.
В первую очередь, это медицина. Гранулометрия в медицине применяется для подсчета количества определенных объектов на изображениях срезов биологических тканей. Например, позволяет автоматически выделять различные объекты изображения и оценивать их процентный состав в зависимости от площади; также применяется при анализе крови (построении и анализе эритроцитарной гистограммы, подсчете тромбоцитов и т.д.). Это может быть также анализ снимков микроскопа (подсчет бактерий, анализ хромосом и т.д.). Похожая область - это анализ фармацевтических препаратов при их изготовлении.
Вторая задача, где применяется гранулометрия - это анализ состава материалов в промышленности. Это может быть количественный анализ зерен в зернистых структурах (сталях, сплавах и т.п.) и получение их распределения по размерам и форме; оценка параметров включений и дефектов (размеры, форма, распределение). Причем все эти измерения, в большинстве случаев производятся автоматически, т.е. частицы сначала выделяются, измеряются и классифицируются. Ниже приведены примеры двух изображений, которые могут использоваться при гранулометрических исследованиях.
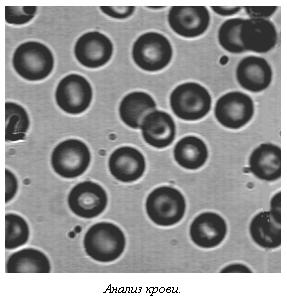
Под термином гранулометрия подразумевается измерение и классификация объектов изображения по одному из имеющихся параметров, например, размеру. Рассмотрим более детально решение этой задачи на конкретном примере. Результатом обработки является гистограмма, показывающая процентное содержание объектов каждого класса.
Содержание- Считывание изображения.
- Улучшение контрастности изображения.
- Определение яркости поверхности на улучшенном изображении.
- Вычисление первой производной распределения.
- Формирование объектов (снежинок) с учетом вычисленного радиуса.
Считывание изображения.
Считываем файл 'snowflakes.png', который представляет собой изображение хлопьев снега.
I=imread('snowflakes.png');
figure, imshow(I)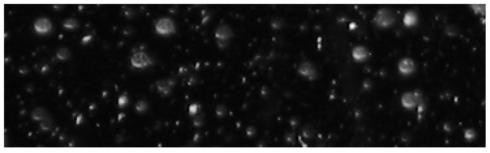
Улучшение контрастности изображения.
Эффективность решения любой задачи по обработке изображений, в большой мере, зависит от качества исходных данных. В данном случае, когда необходимо идентифицировать объекты и анализировать их размер, то высокое качество исходного изображения является одним из необходимых условий. Для решения задачи повышения контрастности изображения в системе Matlab можно использовать функцию ADAPTHISTEQ. Эта функция реализует контрастно-ограниченную адаптивную эквализацию (выравнивание) гистограммы. Для коррекции яркостей изображения используется функция IMADJUST, которая позволяет управлять диапазоном яркостей изображения.
claheI=adapthisteq(I, 'Divisions', [10 10]);
claheI=imadjust(claheI);
imshow(claheI);
Определение яркости поверхности на улучшенном изображении.
При решении задач гранулометрии результат измерения интенсивностей элементов исследуемого изображения представляется в виде функции. Эта функция привязана к размерам исходного изображения. Каждому объекту изображения присваиваются определенные параметры, основной из которых - размер. На основании этих параметров производится построение гистограммы распределения объектов по определенных признаках. Вторым параметром, на основании которого осуществляется распределение, является интенсивность (яркость) объектов изображения.
for counter=0:22
remain=imopen(claheI, strel('disk', counter));
intensity_area(counter+1)=sum(remain(:));
end
figure,plot(intensity_area, 'm - *'), grid on;
title('Функция зависимости суммы пикселей раскрытого изображения от их радиуса');
xlabel('радиус раскрытия (в пикселях)');
ylabel('значение суммы пикселей раскрытых объектов (интенсивность)');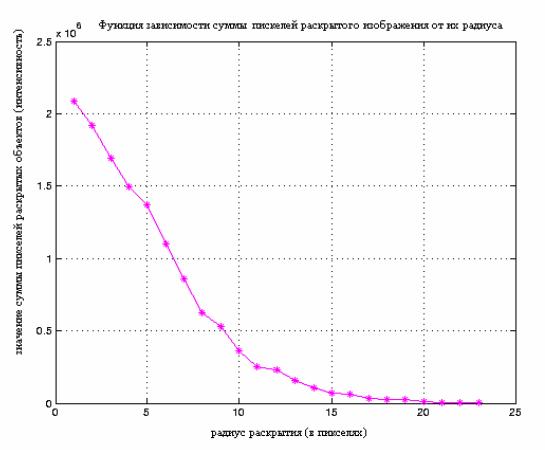
Вычисление первой производной распределения.
Распределение объектов изображения, полученное в результате гранулометрической обработки, характеризуется также рядом параметров. Одним из них является первая производная, которая вычисляется при помощи функции DIFF.
intensity_area_prime=diff(intensity_area);
plot(intensity_area_prime, 'm-*'), grid on;
title('Granulometry (Size Distribution) of Snowflakes');
set(gca, 'xtick', [0 2 4 6 8 10 12 14 16 18 20 22]);
xlabel('радиус снежинок (в пикселях)');
ylabel('зависимость суммы пикселей снежинок от радиуса');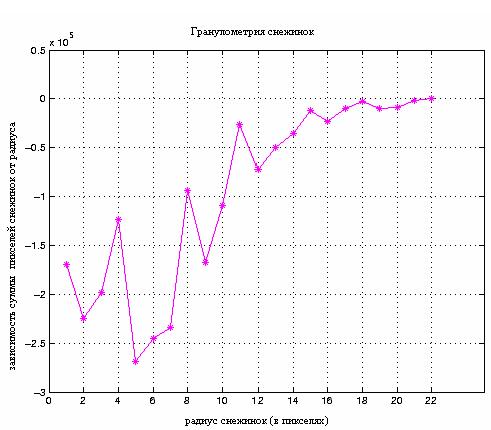
Формирование объектов (снежинок) с учетом вычисленного радиуса
Отметим минимум, который встречается на полученном графе. Этот минимум характеризует наиболее мелкие объекты (снежинки) на изображении. Более отрицательная минимальная точка свидетельствует о повышении кумулятивной интенсивности снежинок в зависимости от их радиуса.
open5=imopen(claheI, strel('disk', 5));
open6=imopen(claheI, strel('disk', 6));
rad5=imsubtract(open5, open6);
imshow(rad5, []);
Идентификация округлых предметов
Рассмотрим задачу, основной целью которой будет идентификация округлых объектов с помощью функции bwboundaries.
Содержание
- Шаг 1: Считывание изображения.
- Шаг 2: Пороговая обработка изображения.
- Шаг 3: Устранение шума.
- Шаг 4: Поиск границ объектов изображения.
- Шаг 5: Определение округлости объектов.
Шаг 1: Считывание изображения. Считаем данные из pills_etc.png. RGB=imread('pillsetc.png'); imshow(RGB);
Шаг 2: Пороговая обработка изображения. Преобразуем исследуемое изображение в бинарное и таким образом подготовим его для применения функции bwboundaries, которая реализует выделение границ объектов. I=rgb2gray(RGB); threshold=graythresh(I); bw=im2bw(I, threshold); imshow(bw)
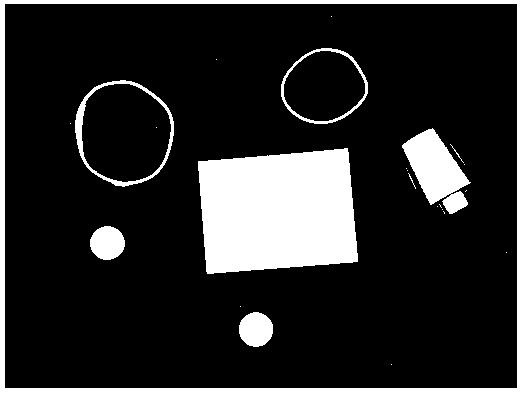
Шаг 3: Устранение шума. С использованием морфологических функций устраним объекты, которые не являются объектами нашего интереса, т.е. шум. % удаление всех объектов, содержащих меньше чем 30 пикселей bw=bwareaopen(bw,30); % заполнение пустот se=strel('disk', 2); bw=imclose(bw, se); bw=imfill(bw,'holes'); imshow(bw)
Шаг 4: Поиск границ объектов изображения. При решении этого вопроса будем рассматривать только внешние границы. Опция 'noholes' приводит к ускорению обработки с помощью функции bwboundaries и повышает достоверность выделения границ объектов изображения. [B, L]=bwboundaries(bw, 'noholes'); % отображение матрицы меток и извлечение границ imshow(label2rgb(L, @jet, [.5 .5 .5])) hold on for k=1:length(B) boundary=B{k}; plot(boundary(:, 2), boundary(:, 1), 'w', 'LineWidth', 2) end
Шаг 5: Определение округлости объектов.
Измерим площадь каждого объекта и его периметр. Эти данные будут использованы при вычислении характеристики округлостей объектов:
metric=4*pi*area/perimeter^2.
Параметр metric является достоверным только в случае идеальной окружности и является меньшим при других формах исследуемого объекта. Кроме того, при решении задач подобного рода, можно контролировать установку порога бинаризации, что приведет к улучшению качества обработки. При обработке исследуемых изображений использовался порог, равный 0.94.
Используем функцию regionprops для получения измерений площади для всех объектов. Отметим, что матрица меток, возвращаемая функцией bwboundaries, может повторно использоваться в функции regionprops.stats=regionprops(L, 'Area', 'Centroid'); threshold=0.94; % окружность границ for k=1:length(B) % получение координат границ (X, Y), соответствующих метке 'k' boundary=B{k}; % вычисление измерений на основе периметра объектов delta_sq=diff(boundary).^2; perimeter=sum(sqrt(sum(delta_sq, 2))); % получение вычисленной площади, соответствующей метке 'k' area=stats(k).Area; % вычисление характеристики округлости metric metric=4*pi*area/perimeter^2; % отображение результатов metric_string=sprintf('%2.2f', metric); % маркирование объектов if metric>threshold centroid=stats(k).Centroid; plot(centroid(1), centroid(2), 'ko'); end text(boundary(1, 2)-35, boundary(1, 1)+13, metric_string,'Color', 'y',... 'FontSize', 14, 'FontWeight', 'bold'); end title(['Metrics closer to 1 indicate that ',... 'the object is approximately round']);
Измерение углов пересечения
Часто в машинном зрении применяются автоматические измерения различных геометрических параметров с применением технологии захвата и обработки изображений. Измерение угла и определение точки пересечения двух элементов некоторой конструкции выполняется с использованием функции bwtraceboundary, которая реализует также автоматическое отслеживание границ.
Содержание
- Шаг 1: Считывание изображения.
- Шаг 2: Определение области интереса.
- Шаг 3: Пороговая обработка изображения.
- Шаг 4: Поиск начальных точек каждой границы.
- Шаг 5: Отслеживание границ.
- Шаг 6: Подгонка линий границ.
- Шаг 7: Определение угла пересечения.
- Шаг 8: Поиск точки пересечения.
- Шаг 9: Отображение результатов.
Шаг 1: Считывание изображения. Считаем изображение из графического файла gantrycrane.jpg и определим область интереса при решении этой задачи. Это изображение портала подъемного крана. RGB=imread('gantrycrane.png'); imshow(RGB); text(size(RGB, 2), size(RGB, 1)+15, 'Image courtesy of Jeff Mather', ... 'FontSize', 7, 'HorizontalAlignment', 'right'); line([300 328], [85 103], 'color', [1 1 0]); line([268 255], [85 140], 'color', [1 1 0]); text(150, 72, 'Измерение углов', 'Color', 'y', ... 'FontWeight', 'bold');
Шаг 2: Определение области интереса. Вырежем изображение, содержащее только те элементы конструкции крана, угол между которыми мы хотим определить. Далее необходимо определить контур двух металлических конструкций.
% Координаты области интереса можно задать вручную, % далее отображаем нужную область с помощью imview start_row=34; start_col=208; cropRGB=RGB(start_row:163, start_col:400, :); imshow(cropRGB) offsetX=start_col-1; offsetY=start_row-1;

Шаг 3: Пороговая обработка изображения. Преобразуем исследуемое изображение в бинарное. Далее эти бинарные данные будут использованы для получения координат границ с помощью функции bwtraceboundary.
I=rgb2gray(cropRGB); threshold=graythresh(I); BW=im2bw(I, threshold); BW=~BW; % дополнение изображения (объект интереса должен быть белым) imshow(BW)

Шаг 4: Поиск начальных точек каждой границы. Функция bwtraceboundary требует описания определенных точек контура. Эти точки являются стартовыми при отслеживании границ объектов. Функция bwtraceboundary также требует описание исследуемого изображения, представленное в специальной форме. dim=size(BW); % горизонтальное направление col1=4; row1=min(find(BW(:, col1))); % угловое направление row2=12; col2=min(find(BW(row2, :))); Шаг 5: Отслеживание границ.
Функция bwtraceboundary позволяет реализовать также процедуру определения координат граничных точек. Для увеличения достоверности вычисленных углов и точек при расчетах нужно использовать максимальное число исследуемых граничных точек. Это число определяется экспериментально. При проведении процедуры определения координат границ также необходимо указывать направление отслеживания.
boundary1=bwtraceboundary(BW, [row1, col1], 'N', 8, 70); % установим направление отслеживания - против часовой стрелки, сверху вниз boundary2=bwtraceboundary(BW, [row2, col2], 'E', 8, 90,'counter'); imshow(RGB); hold on; % отображение результатов на исходном изображении plot(offsetX+boundary1(:, 2), offsetY+boundary1(:, 1), 'g', 'LineWidth', 2); plot(offsetX+boundary2(:, 2), offsetY+boundary2(:, 1), 'g', 'LineWidth', 2);

Шаг 6: Подгонка линий границ.
Из набора пар координат (X,Y), полученных на прежнем шаге, нужно отбросить заведомо ложные, которые не принадлежат искомой линии. Для проведения этой процедуры каждой точке контура необходимо на основании некоторого критерия присвоить соответствующий весовой коэффициент.
Уравнение линии y=[x 1]*[a; b]. Параметры 'a' и 'b' определяются на основании критерия минимальной квадратической ошибки с использованием функции polyfit.ab1=polyfit(boundary1(:, 2), boundary1(:, 1), 1); ab2=polyfit(boundary2(:, 2), boundary2(:, 1), 1); Шаг 7: Определение угла пересечения. Используем функцию dot для поиска угла. vect1=[1 ab1(1)]; % создание вектора на основании линейных выражений vect2=[1 ab2(1)]; dp=dot(vect1, vect2); % вычисление длины вектора length1=sqrt(sum(vect1.^2)); length2=sqrt(sum(vect2.^2)); % вычисление угла angle=180-acos(dp/(length1*length2))*180/pi angle= 129.5860 Шаг 8: Поиск точки пересечения. Решение системы двух выражений в порядке получения координат (X,Y) точек пересечения. intersection=[1 ,-ab1(1); 1, -ab2(1)] \ [ab1(2); ab2(2)]; % получение результата на исходном, % т.е. не вырезанном изображении. intersection=intersection+[offsetY; offsetX] intersection= 143.0453 295.7910 Шаг 9: Отображение результатов. inter_x=intersection(2); inter_y=intersection(1); % отображение точек пересечения plot(inter_x, inter_y, 'yx', 'LineWidth', 2); text(inter_x-60, inter_y-30, [sprintf('%1.3f', angle), '{\circ}'],... 'Color', 'y', 'FontSize', 14, 'FontWeight', 'bold'); interString=sprintf('(%2.1f, %2.1f)', inter_x, inter_y); text(inter_x-10, inter_y+20, interString,... 'Color', 'y', 'FontSize', 14, 'FontWeight', 'bold');
Измерение радиуса части мотка ленты
Рассмотрим задачу определения радиуса круглого объекта. В качестве примера возьмем катушку ленты. Решение задачи будет усложняться тем, что на изображении представлено только часть исследуемого объекта. При решении этой задачи будем использовать функцию bwtraceboundary.
Содержание
- Шаг 1: Считывание изображения.
- Шаг 2: Пороговая обработка изображения.
- Шаг 3: Определение положения начальной точки границы объекта.
- Шаг 4: Отслеживание границ.
- Шаг 5: Подгонка окружности на выделенные границы.
Шаг 1: Считывание изображения.
Считаем изображение из файла tape.png. RGB=imread('tape.png'); imshow(RGB); text(15,15,'Измерение радиуса',... 'FontWeight','bold','Color','y');
Шаг 2: Пороговая обработка изображения.
Преобразуем изображение в бинарное для последующего получения координат границ с помощью функции bwtraceboundary.
I=rgb2gray(RGB);
threshold=graythresh(I);
BW=im2bw(I, threshold);
imshow(BW)
Шаг 3: Определение положения начальной точки границы объекта.
Для реализации функции bwtraceboundary нужно указать начальную точку определения границы. Эта точка используется для начала отслеживания границы.
dim=size(BW);
col=round(dim(2)/2)-90;
row=min(find(BW(:, col)));
Шаг 4: Отслеживание границ.
Результатом работы функции bwtraceboundary является поиск (X, Y) - координат точек границ исследуемого объекта. Для более точного определения радиуса исследуемого объекта нужно использовать максимальное число точек, которые принадлежат границе.
connectivity=8;
num_points=180;
contour=bwtraceboundary(BW, [row, col], 'N', connectivity, num_points);
imshow(RGB);
hold on;
plot(contour(:, 2), contour(:, 1), 'g', 'LineWidth', 2);
Шаг 5: Подгонка окружности на выделенные границы. Отобразим основное уравнение окружности: (x-xc)^2+(y-yc)^2=radius^2, где (xc, yc) - центр окружности. Это же уравнение можно представить в другом виде через параметры a, b, c x^2+y^2+a*x+b*y+c=0, где a=-2*xc, b=-2*yc, c=xc^2+yc^2-radius^2 Параметры a, b, c нужны для вычисления радиуса. x=contour(:, 2); y=contour(:, 1); % при вычислении радиуса будет % использоваться метод наименьших квадратов abc=[x y ones(length(x), 1)]\[-(x.^2+y.^2)]; a=abc(1); b=abc(2); c=abc(3); % вычислим положение центра и радиус xc=-a/2; yc=-b/2; radius=sqrt((xc^2+yc^2)-c) % отобразим вычисленный центр plot(xc, yc, 'yx', 'LineWidth', 2); % отобразим полную окружность theta=0:0.01:2*pi; % используем параметрическое представление % окружности для получения координат точек Xfit=radius*cos(theta)+xc; Yfit=radius*sin(theta)+yc; plot(Xfit, Yfit); message=sprintf('Вычисленный радиус равен %2.3f пикселей', radius); text(15, 15, message, 'Color', 'y', 'FontWeight', 'bold'); radius= 80.7567
В работе приведен пример решения задачи определения радиуса окружности мотка ленты. Следует отметить, что представленная задача находит свое применение в реальных системах управления различными автоматизированными технологическими процессами. Такое внедрение компьютерных технологий приводит к повышению эффективности производства. Приведенные выше подходы также нашли свое применение в различных системах дистанционного контроля. Однако точность измерений во многом зависит от качества используемой аппаратуры.
Обнаружение объектов с помощью сегментации изображений
Если контраст объект-фон является достаточным, тогда обнаружить такой объект не представляет труда. Применим средства выделения границ и морфологические функции для обнаружения некоторого медицинского объекта.
Ключевые слова: Обнаружение границ, структурный элемент, эрозия, морфологические операторы, сегментация Ключевые функции: edge, strel, imdilate, imerode, imfill, imclearborder Демонстрационный пример
Демонстрационный пример включает следующие шаги:- Шаг 1: Считывание изображения.
- Шаг 2: Детектирование всего объекта.
- Шаг 3: Заполнение промежутков.
- Шаг 4: Морфологическое расширение изображений.
- Шаг 5: Заполнение внутренних промежутков.
- Шаг 6: Операции со связными объектами на границе.
- Шаг 7: Сглаживание объекта.
Шаг 1: Считывание изображения.
Считаем некоторое медицинское изображение из файла 'cell.tif'.
I=imread('cell.tif');
figure, imshow(I), title('original image');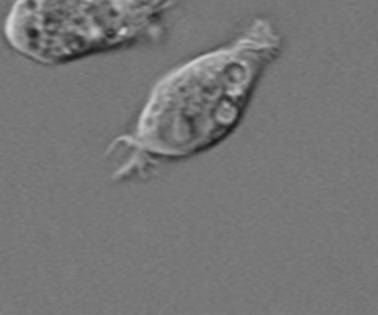
Шаг 2: Детектирование всего объекта.
На изображении представлено два объекта и только один из них видно полностью. Наша задача заключается в выделении этого объекта. Другими словами этот объект необходимо сегментировать. Качество сегментации в большой мере зависит от того насколько сильно объект отличается от фона. Поэтому усиление контрастности изображения приводит к увеличению качества детектирования.
Одним их путей детектирования является применение оператора Собеля с использованием некоторого порогового значения. В данном случае пороговое значение определим с помощью функции graythresh. Создадим некоторую градиентную маску и применим ее в функции выделения края.
BWs=edge(I, 'sobel', (graythresh(I)*.1));
figure, imshow(BWs), title('binary gradient mask');
Шаг 3: Заполнение промежутков.
Бинарная градиентная маска отображает линии с высоким контрастом на изображении. Сравнивая исходное и обработанное изображения, можно сделать вывод, что эти линии вполне точно описывают контуры объекта интереса.
se90=strel('line', 3, 90);
se0=strel('line', 3, 0);
Шаг 4: Морфологическое расширение изображений.
Бинарная градиентная маска при выполнении морфологической операции расширения использует последовательно вертикальные и горизонтальные структурные элементы. Для выполнения операции морфологического расширения используется функция imdilate.
BWsdil=imdilate(BWs, [se90 se0]);
figure, imshow(BWsdil), title('dilated gradient mask');
Шаг 5: Заполнение внутренних промежутков.
Применение морфологической операции расширения для обработки контуров с помощью градиентной маски дает вполне приемлемый результат, который заключается в заполнении отверстий в середине исследуемого объекта. Для реализации данного шага используется функция imfill.
BWdfill=imfill(BWsdil, 'holes');
figure, imshow(BWdfill);
title('binary image with filled holes');
Шаг 6: Операции со связными объектами на границе.
На предыдущем этапе была проведена операция сегментации. Однако эта операция затронула не только исследуемый объект. Каждый объект, который имеет связные границы на изображении, может быть удален с помощью функции imclearborder. Связность в функции imclearborder устанавливается на уровне 4 по диагонали.
BWnobord=imclearborder(BWdfill, 4);
figure, imshow(BWnobord), title('cleared border image');
Шаг 7: Сглаживание объекта.
И наконец, чтобы проведенная обработка выглядела более натурально, необходимо провести сглаживание с помощью морфологической операции эрозии с использованием специального структурного элемента. Создадим этот элемент с использованием функции strel.
seD=strel('diamond', 1);
BWfinal=imerode(BWnobord, seD);
BWfinal=imerode(BWfinal, seD);
figure, imshow(BWfinal), title('segmented image');
Существуют также альтернативные методы отображения сегментированных объектов. Приведем пример с использованием функции bwperim.
BWoutline=bwperim(BWfinal);
Segout=I;
Segout(BWoutline)=255;
figure, imshow(Segout), title('outlined original image');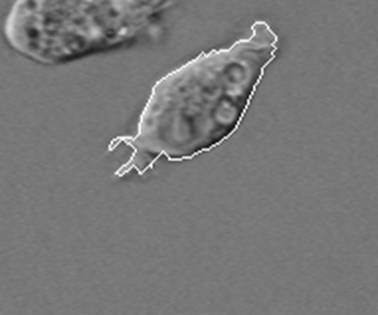
Реконструкция изображений по их проекционным данным
В этом примере рассмотрим применение функций radon, iradon, fanbeam и ifanbeam для получения проекций изображений и обратную реконструкцию данных на основе их проекций. В функциях radon и iradon для получения проекций используется параллельно-лучевая геометрия, а в функциях fanbeam и ifanbeam - веерно-лучевая геометрия. Для того, чтобы сравнить параллельно-лучевую и веерно-лучевую геометрии, создадим некоторые синтезированные проекции для каждой геометрии и затем применим их для восстановления исходного изображения.
Практической задачей, где применяется реконструкция изображений, является рентгеновская томография, где проекции формируются на основании измерения ослабления радиации при прохождении через разные физические среды. В результате на изображении отображаются данные о структуре среза исследуемого объекта. Проекционные данные формируются и хранятся в специальной медицинской аппаратуре. На основании этих данных существует возможность реконструкции изображения исследуемых органов. В среде Matlab моделирование восстановления вида объекта по его томографическим проекциям можно реализовать с помощью функций iradon и ifanbeam.
Функция iradon применяется для реконструкции изображений из параллельно-лучевых проекций. В параллельно-лучевой геометрии каждая проекция формируется в результате линейной комбинации изображений, представляющих некоторый исследуемый орган под разными углами. Функция ifanbeam применяется для реконструкции данных на основании их веерно-лучевых проекций, которые получены из одного источника излучения, но зафиксированы несколькими датчиками.
Рассмотрим применение пакета Image Processing Toolbox для моделирования описанных выше процедур при использовании обеих геометрий.
Содержание
- Создание фантома головы.
- Параллельные лучи - вычисление синтезированных проекций.
- Параллельные лучи - реконструкция фантома головы на основании проекционных данных.
- Веерные лучи - вычисление синтезированных проекций.
- Веерные лучи - реконструкция фантома головы на основании проекционных данных.
Создание фантома головы.
Тестовое изображение фантома головы Шеппа-Логана может быть сгенерировано с помощью функции phantom. Изображение фантома иллюстрирует много особенностей, которые в действительности свойственны реальным томографическим изображениям головы человека. Размещенные в центре фантома объекты в виде эллипса моделируют реальные внутренние особенности строения головы человека.
P=phantom(256); imshow(P)
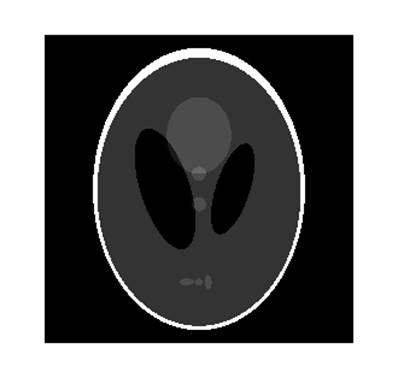
Параллельные лучи - вычисление синтезированных проекций.
Рассмотрим вычисление синтезированных проекций на основе параллельно-лучевой геометрии с разным числом углов. Для обработки этих данных используется функция radon, а результат представляется в виде матрицы, в которой каждый столбец представляет собой преобразование Радона для одного значения угла.
theta1=0:10:170; [R1, xp]=radon(P, theta1); num_angles_R1=size(R1, 2) num_angles_R1= 18 theta2=0:5:175; [R2, xp]=radon(P, theta2); num_angles_R2=size(R2, 2) num_angles_R2= 36 theta3=0:2:178; [R3, xp]=radon(P, theta3); num_angles_R3=size(R3, 2) num_angles_R3= 90 Отметим, что для каждого угла проекция вычисляется на основании N точек вдоль оси xp, где N является константой, которая зависит от расстояния до всех точек изображения, спроектированных под разными углами. N_R1=size(R1, 1) N_R2=size(R2, 1) N_R3=size(R3, 1) N_R1= 367 N_R2= 367 N_R3= 367 Таким образом, когда мы используем меньший фантом головы, при вычислении проекций требуется меньшее число точек вдоль оси xp. P_128=phantom(128); [R_128, xp_128]=radon(P_128, theta1); N_128=size(R_128, 1) N_128= 185 Отобразим проекционные данные R3. Некоторые свойства изображения исходного фантома видны на изображении R3. Первый столбец R3 соответствует проекциям нулевого угла, которые интегрированы в вертикальном направлении. Последний столбец соответствует проекциям под 90 градусов, которые просуммированы в горизонтальном направлении. figure, imagesc(theta3, xp, R3) colormap(hot) colorbar xlabel('Параллельный поворот угла - \theta'); ylabel(' Параллельное расположение датчиков x\ '); На изображении представлена зависимость местонахождения сенсоров от поворота угла.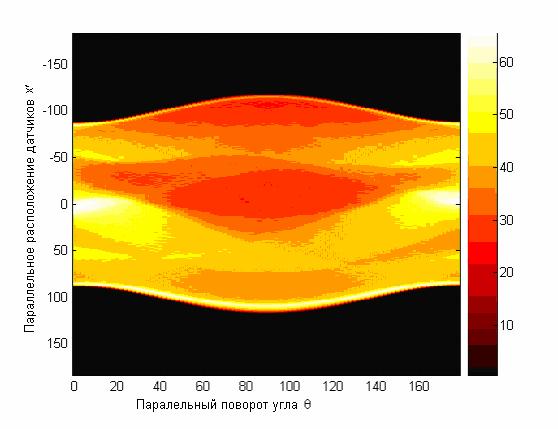
Параллельные лучи - реконструкция фантома головы на основании проекционных данных.
Для каждого параллельного поворота-приращения при реконструкции используется соответствующая синтезированная проекция. При практической реализации реконструкции всегда известна геометрия источников и сенсоров.
Следующие три примера реконструкции (I1, I2 и I3) демонстрируют эффект изменения числа углов, по которым сделаны проекции. Для I1 и I2 некоторые особенности, которые четко заметны на исходном фантоме, видны не очень качественно. Что касается, элипсообразных предметов, то они достаточно хорошо заметны на каждом изображении. Результирующее изображение I3 наиболее точно соответствует исходному изображению.
Как уже отмечалось выше, на изображениях I1 и I2 есть некоторые артефакты, которые искажают действительную информацию. Для устранения этих артефактов используют большее число углов.
% Построение результирующей размерности % при реконструкции с использованием % размеров исходного изображения P. output_size=max(size(P)); dtheta1=theta1(2)-theta1(1); I1=iradon(R1, dtheta1, output_size); figure, imshow(I1)
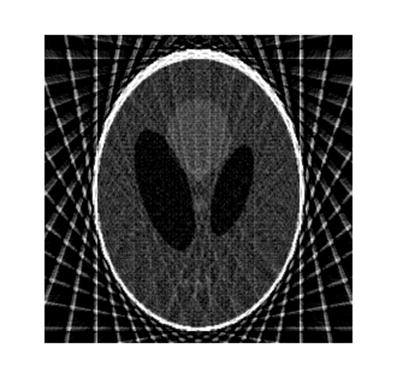
dtheta2=theta2(2)-theta2(1); I2=iradon(R2, dtheta2, output_size); figure, imshow(I2)
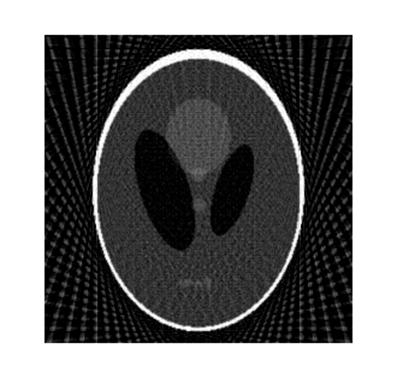
dtheta3=theta3(2)-theta3(1); I3=iradon(R3, dtheta3, output_size); figure, imshow(I3)
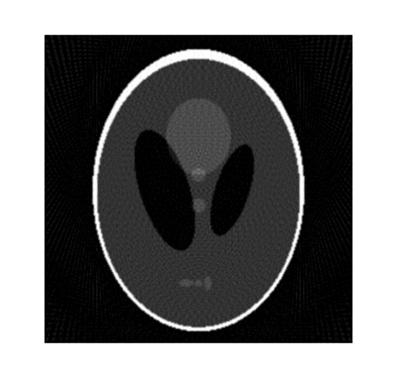
Веерные лучи - вычисление синтезированных проекций.
Рассмотрим вычисление синтезированных проекций с использованием веерно-лучевой геометрии и переменной 'FanSensorSpacing'.
D=250; dsensor1=2; F1=fanbeam(P, D, 'FanSensorSpacing', dsensor1); dsensor2=1; F2=fanbeam(P, D, 'FanSensorSpacing', dsensor2); dsensor3=0.25; [F3, sensor_pos3, fan_rot_angles3]=fanbeam(P, D, ... 'FanSensorSpacing', dsensor3); Отобразим проекционные данные F3. Отметим, что веерный угловой поворот в диапазоне от 0 до 360 градусов может быть преобразован в модель с использованием 180 градусов, поскольку некоторые свойства будут идентичны с обеих сторон. Некоторые свойства на изображении при веерно-лучевых проекциях могут быть связаны с некоторыми свойствами на изображениях параллельно-лучевых проекций и наоборот. figure, imagesc(fan_rot_angles3, sensor_pos3, F3) colormap(hot) colorbar xlabel('Веерный поворот угла (в градусах) ') ylabel('Веерное расположение датчиков (в градусах)')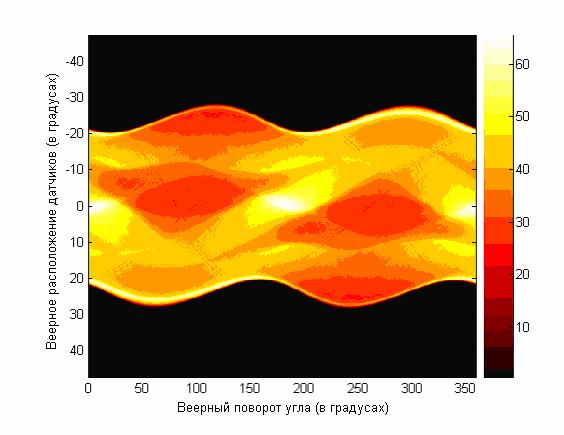
Веерные лучи - реконструкция фантома головы на основании проекционных данных.
Каждому веерному расположению сенсоров в пространстве соответствует своя синтезированная проекция. При практической реализации реконструкции всегда известна геометрия источников и сенсоров изображения P.
Изменение значения 'FanSensorSpacing' приводит к изменению числа сенсоров, которые используются при изменении угла. При каждой веерно-лучевой реконструкции используется поворот на все значения угла. Использование данных при различных поворотах угла влияет на качество результата обработки.
Отметим, что 'FanSensorSpacing' является только одним параметром из нескольких, которые можно контролировать при использовании функций fanbeam и ifanbeam. Также существует возможность конвертации между параллельными и веерно-параллельными данными. Для этого используют функций fan2para и para2fan.
Ifan1=ifanbeam(F1, D, 'FanSensorSpacing', dsensor1, 'OutputSize', output_size); figure, imshow(Ifan1)
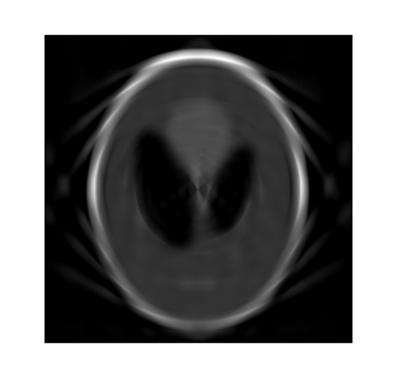
Ifan2=ifanbeam(F2, D, 'FanSensorSpacing', dsensor2, 'OutputSize', output_size); figure, imshow(Ifan2)
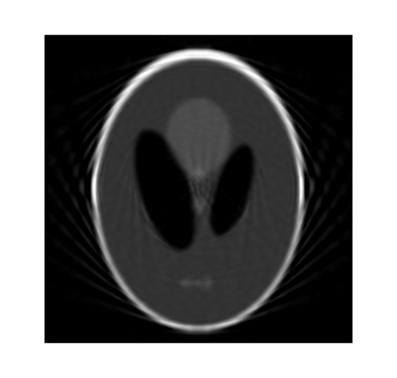
Ifan3=ifanbeam(F3, D, 'FanSensorSpacing', dsensor3, 'OutputSize', output_size); figure, imshow(Ifan3)
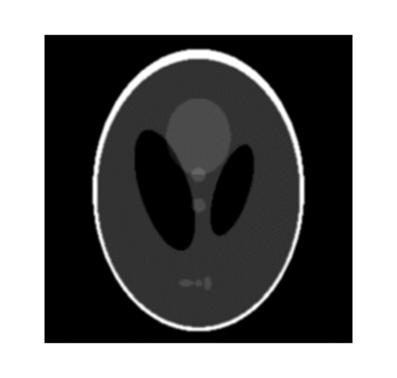
Сегментация методом управляемого водораздела
Довольно часто при анализе изображений возникает задача разделения пикселей изображений на группы по некоторым признакам. Такой процесс разбиения на группы называется сегментацией. Наиболее известными являются два вида сегментации - сегментация по яркости для бинарных изображений и сегментация по цветовым координатам для цветных изображений. Методы сегментации можно рассматривать как формализацию понятия выделяемости объекта из фона или понятий связанных с градиентом яркости. Алгоритмы сегментации характеризуются некоторыми параметрами надежности и достоверности обработки. Они зависят от того, насколько полно учитываются дополнительные характеристики распределения яркости в областях объектов или фона, количество перепадов яркости, форма объектов и др.
Существует много изображений, которые содержат исследуемый объект достаточно однородной яркости на фоне другой яркости. В качестве примера можно привести рукописный текст, ряд медицинских изображений и т.д. Если яркости точек объекта резко отличаются от яркостей точек фона, то решение задачи установления порога является несложной задачей. На практике это не так просто, поскольку исследуемое изображение подвергается воздействию шума и на нем допускается некоторый разброс значений яркости. Известно несколько аналитических подходов к пороговому ограничению по яркости. Один из методов состоит в установлении порога на таком уровне, при котором общая сумма элементов с подпороговой яркостью согласована с априорными вероятностями этих значений яркости.
Аналогичные подходы можно применить для обработки цветных и спектрозональных изображений. Существует также такой вид сегментации как контурная сегментация. Довольно часто анализ изображений включает такие операции, как получение внешнего контура изображений объектов и запись координат точек этого контура. Известно три основных подхода к представлению границ объекта: аппроксимация кривых, прослеживание контуров и связывание точек перепадов. Для полноты анализа следует отметит, что есть также текстурная сегментация и сегментация формы.
Наиболее простым видом сегментации является пороговая сегментация. Она нашла очень широкое применение в робототехнике. Это объясняется тем, что в этой сфере изображения исследуемых объектов, в своем большинстве, имеют достаточно однородную структуру и резко выделяются их фона. Но кроме этого, для достоверной обработки нужно знать, что изображение состоит из одного объекта и фона, яркости которых находятся в строго известных диапазонах и не пересекаются между собой.
Развитие технологий обработки изображений привело к возникновению новых подходов к решению задач сегментации изображений и применении их при решении многих практических задач.
В данной работе рассмотрим относительно новый подход к решению задачи сегментации изображений - метод водораздела. Коротко объясним название этого метода и в чем его суть.
Предлагается рассматривать изображение как некоторую карту местности, где значения яркостей представляют собой значения высот относительно некоторого уровня. Если эту местность заполнять водой, тогда образуются бассейны. При дальнейшем заполнении водой, эти бассейны объединяются. Места объединения этих бассейнов отмечаются как линии водораздела.
Разделение соприкасающихся предметов на изображении является одной из важных задач обработки изображений. Часто для решения этой задачи используется так называемый метод маркерного водораздела. При преобразованиях с помощью этого метода нужно определить "водосборные бассейны" и "линии водораздела" на изображении путем обработки локальных областей в зависимости от их яркостных характеристик.
Метод маркерного водораздела является одним из наиболее эффективных методов сегментации изображений. При реализации этого метода выполняются следующие основные процедуры:
-
Вычисляется функция сегментации. Она касается изображений, где объекты размещены в темных областях и являются трудно различимыми.
-
Вычисление маркеров переднего плана изображений. Они вычисляются на основании анализа связности пикселей каждого объекта.
-
Вычисление фоновых маркеров. Они представляют собой пиксели, которые не являются частями объектов.
-
Модификация функции сегментации на основании значений расположения маркеров фона и маркеров переднего плана.
-
Вычисления на основании модифицированной функции сегментации.
В данном примере среди функций пакета Image Processing Toolbox наиболее часто используются функции fspecial, imfilter, watershed, label2rgb, imopen, imclose, imreconstruct, imcomplement, imregionalmax, bwareaopen, graythresh и imimposemin.
Содержание
- Шаг 1: Считывание цветного изображения и преобразование его в полутоновое.
- Шаг 2: Использование значения градиента в качестве функции сегментации.
- Шаг 3: Маркировка объектов переднего плана.
- Шаг 4: Вычисление маркеров фона.
- Шаг 5: Вычисление по методу маркерного водораздела на основании модифицированной функции сегментации.
- Шаг 6: Визуализация результата обработки.
Шаг 1: Считывание цветного изображения и преобразование его в полутоновое.
Считаем данные из файла pears.png rgb=imread('pears.png'); и представим их в виде полутонового изображения. I=rgb2gray(rgb); imshow(I) text(732,501,'…',... 'FontSize',7,'HorizontalAlignment','right')
Шаг 2: Использование значения градиента в качестве функции сегментации.
Для вычисления значения градиента используется оператор Собеля, функция imfilter и другие вычисления. Градиент имеет большие значения на границах объектов и небольшие (в большинстве случаев) вне границ объектов.
hy=fspecial('sobel'); hx=hy'; Iy=imfilter(double(I), hy, 'replicate'); Ix=imfilter(double(I), hx, 'replicate'); gradmag=sqrt(Ix.^2+Iy.^2); figure, imshow(gradmag,[]), title('значение градиента')
Таким образом, вычислив значения градиента, можно приступить к сегментации изображений с помощью рассматриваемого метода маркерного водораздела.
L=watershed(gradmag); Lrgb=label2rgb(L); figure, imshow(Lrgb), title('Lrgb')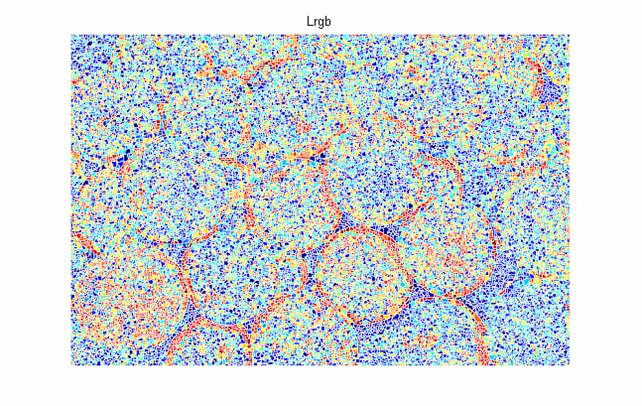
Однако, без проведения еще дополнительных вычислений, такая сегментация будет поверхностной.
Шаг 3: Маркировка объектов переднего плана.
Для маркировки объектов переднего плана могут использоваться различные процедуры. В этом примере будут использованы морфологические технологии, которые называются "раскрытие через восстановление" и "закрытие через восстановление". Эти операции позволяют анализировать внутреннюю область объектов изображения с помощью функции imregionalmax.
Как было сказано выше, при проведении маркировки объектов переднего плана используются также морфологические операции. Рассмотрим некоторые из них и сравним. Сначала реализуем операцию раскрытия с использованием функции imopen.
se=strel('disk', 20); Io=imopen(I, se); figure, imshow(Io), title('Io')
Далее вычислим раскрытие с использованием функций imerode и imreconstruct.
Ie=imerode(I, se); Iobr=imreconstruct(Ie, I); figure, imshow(Iobr), title('Iobr')
Последующие морфологические операции раскрытия и закрытия приведут к перемещению темных пятен и формированию маркеров. Проанализируем операции морфологического закрытия. Для этого сначала используем функцию imclose:
Ioc=imclose(Io, se); figure, imshow(Ioc), title('Ioc')
Далее используем функцию imdilate, которая применяется вместе с функцией imreconstruct. Отметим, что для реализации операции imreconstruct необходимо провести операцию дополнения изображений.
Iobrd=imdilate(Iobr, se); Iobrcbr=imreconstruct(imcomplement(Iobrd), imcomplement(Iobr)); Iobrcbr=imcomplement(Iobrcbr); figure, imshow(Iobrcbr), title('Iobrcbr')
Сравнительный визуальный анализ Iobrcbr и Ioc показывает, что представленная реконструкция на основе морфологических операций открытия и закрытия является более эффективной в сравнении с стандартными операциями открытия и закрытия. Вычислим локальные максимумы Iobrcbr и получим маркеры переднего плана.
fgm=imregionalmax(Iobrcbr); figure, imshow(fgm), title('fgm')
Наложим маркеры переднего плана на исходное изображение.
I2=I; I2(fgm)=255; figure, imshow(I2), title('fgm, наложенное на исходное изображение')
Отметим, что при этом некоторые скрытые или закрытые объекты изображения не являются маркированными. Это свойство влияет на формирование результата и многие такие объекты изображения не будут обработаны с точки зрения сегментации. Таким образом, маркеры переднего плана отображают границы только большинства объектов. Представленные таким образом границы подвергаются дальнейшей обработке. В частности, это могут быть морфологические операции.
se2=strel(ones(5, 5)); fgm2=imclose(fgm, se2); fgm3=imerode(fgm2, se2);
В результате проведения такой операции пропадают отдельные изолированные пиксели изображения. Также можно использовать функцию bwareaopen, которая позволяет удалять заданное число пикселей.
fgm4=bwareaopen(fgm3, 20); I3=I; I3(fgm4)=255; figure, imshow(I3) title('fgm4, наложенное на исходное изображение')
Шаг 4: Вычисление маркеров фона.
Теперь проведем операцию маркирования фона. На изображении Iobrcbr темные пиксели относятся к фону. Таким образом, можно применить операцию пороговой обработки изображения.
bw=im2bw(Iobrcbr, graythresh(Iobrcbr)); figure, imshow(bw), title('bw')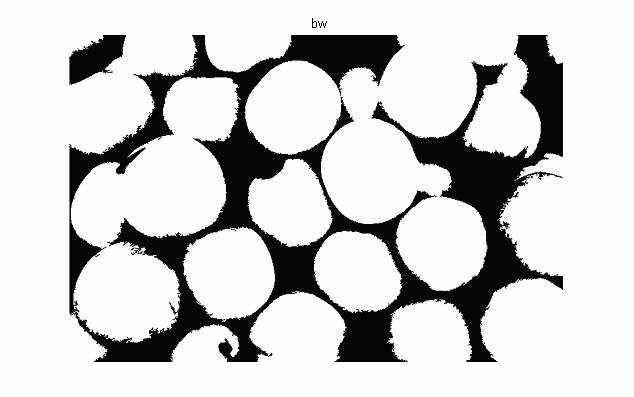
Пиксели фона являются темными, однако нельзя просто провести морфологические операции над маркерами фона и получить границы объектов, которые мы сегментируем. Мы хотим "утоньшить" фон таким образом, чтобы получить достоверный скелет изображения или, так называемый, передний план полутонового изображения. Это вычисляется с применением подхода по водоразделу и на основе измерения расстояний (до линий водораздела).
D=bwdist(bw); DL=watershed(D); bgm=DL==0; figure, imshow(bgm), title('bgm')
Шаг 5: Вычисление по методу маркерного водораздела на основании модифицированной функции сегментации.
Функция imimposemin может применяться для точного определения локальных минимумов изображения. На основании этого функция imimposemin также может корректировать значения градиентов на изображении и таким образом уточнять расположение маркеров переднего плана и фона.
gradmag2=imimposemin(gradmag, bgm | fgm4);
И наконец, выполняется операция сегментации на основе водораздела.
L=watershed(gradmag2);
Шаг 6: Визуализация результата обработки.
Отобразим на исходном изображении наложенные маркеры переднего плана, маркеры фона и границы сегментированных объектов.
I4=I; I4(imdilate(L==0, ones(3, 3))|bgm|fgm4)=255; figure, imshow(I4) title('Маркеры и границы объектов, наложенные на исходное изображение')
В результате такого отображения можно визуально анализировать месторасположение маркеров переднего плана и фона.
Представляет интерес также отображение результатов обработки с помощью цветного изображения. Матрица, которая генерируется функциями watershed и bwlabel, может быть конвертирована в truecolor-изображение посредством функции label2rgb.
Lrgb=label2rgb(L, 'jet', 'w', 'shuffle'); figure, imshow(Lrgb) title('Lrgb')
Также можно использовать полупрозрачный режим для наложения псевдоцветовой матрицы меток поверх исходного изображения.
figure, imshow(I), hold on himage=imshow(Lrgb); set(himage, 'AlphaData', 0.3); title('Lrgb, наложенное на исходное изображение в полупрозрачном режиме')
Восстановление изображений методом слепой деконволюции
Наиболее целесообразно использовать метод слепой деконволюции тогда, когда исследователь не располагает информацией об имеющихся искажениях (размытие и шум). Алгоритм восстанавливает одновременно изображение и функцию протяженности точки (PSF). Дополнительные характеристики оптической системы (например, камеры) могут быть использованы в качестве исходных параметров, что приведет к улучшению восстановления изображений. Вид функции протяженности точки PSF задается пользователем перед выполнением операции восстановления.
Ключевые термины: Слепая деконволюция; восстановление изображений; функция протяженности точки PSF Ключевые функции: deconvblind, edge, imdilate, imfilter Содержание демонстрационного примера
Демонстрационный пример включает следующие шаги:- Шаг 1: Считывание изображения.
- Шаг 2: Симуляция размытостей.
- Шаг 3: Восстановление размытого изображения с использованием функции протяженности точки с различными параметрами.
- Шаг 4: Повышение качества восстановления.
- Шаг 5: Использование дополнительных ограничений для функции протяженности точки при восстановлении изображений.
Шаг 1: Считывание изображения. На данном этапе приведем пример считывания яркостного полутонового изображения. I=imread('cameraman.tif'); figure;imshow(I); title('Исходное изображение');
Шаг 2: Симуляция размытостей.
Проведем симулирование реалистических размытых изображений (например, в результате движения камеры или недостаточной фокусировки объектива). В этом примере симуляция размытостей на изображении достигается в результате свертки гауссовского фильтра с исходным изображением. Для этого можно использовать также функцию imfilter. Гауссовский фильтр представляется функцией протяженности точки PSF.
PSF=fspecial('gaussian', 7, 10);
Blurred=imfilter(I, PSF ,'symmetric', 'conv');
figure; imshow(Blurred);title('Размытое изображение');
Шаг 3: Восстановление размытого изображения с использованием функции протяженности точки с различными параметрами.
Для иллюстрации того, насколько важно иметь информацию о параметрах истинной функции протяженности точки, приведем три варианта восстановления.
В первом варианте восстановления (J1 и P1) используется малоразмерный массив UNDERPSF. Иными словами, предполагается, что функция протяженности точки является именно такой. Размер массива UNDERPSF является на 4 пикселя меньше по каждой размерности относительно размеров истинной функции протяженности точки.
UNDERPSF=ones(size(PSF)-4);
[J1 P1]=deconvblind(Blurred, UNDERPSF);
figure; imshow(J1); title('Восстановление с малоразмерной PSF');
Во втором варианте восстановления (J2 и P2) используется массив единиц OVERPSF, размерность которого по обоим направлениям на 4 пикселя больше истинной размерности функции протяженности точки PSF.
OVERPSF=padarray(UNDERPSF, [4 4], 'replicate', 'both');
[J2 P2]=deconvblind(Blurred, OVERPSF);
figure;imshow(J2); title('Восстановление с большими размерами PSF');
В третьем варианте восстановления (J3 и P3) используется массив единиц INITPSF, размерность которого аналогична размерности истинной PSF.
INITPSF=padarray(UNDERPSF, [2 2], 'replicate', 'both');
[J3 P3]=deconvblind(Blurred, INITPSF);
figure; imshow(J3); title('Восстановление с INITPSF');
Анализ восстановления PSF.
Во всех трех вариантах восстановления использовалась функция протяженности точки PSF. Следующие изображения демонстрируют анализ восстановления истинных параметров функции протяженности точки PSF на основе рассуждений с использованием догадок.
Истинная PSF в виде гауссовского фильтра имеет максимальное значение в центре (белый цвет) и убывает по мере отдаления от него.
figure;
subplot(221);imshow(PSF, [], 'notruesize');
title('Истинная PSF');
Функция протяженности точки P1, полученная при первом восстановлении, явно не соответствует истинному размеру. Это приводит к сильному искажению сигнала, особенно на краях. В результате, на обработанном изображении не будет достигнуто нужного уровня улучшения.
subplot(222); imshow(P1, [] ,'notruesize');
title('Восстановленная малоразмерная PSF');
Функция протяженности точки P2, полученная при втором восстановлении, приводит к очень большим размытостям на краях объектов изображения. Это говорит о том, что восстановление нужно проводить с функцией протяженности точки PSF, размеры которой будут меньше. Тогда, соответственно, искажения на результирующем изображении будут меньше и не так заметны.
subplot(223);imshow(P2, [] ,'notruesize');
title('Восстановление с большими размерами PSF');
И, наконец, функция протяженности точки P3, полученная при третьем восстановлении, представляет собой нечто среднее между P1 и P2. Массив P3 наиболее похож на истинную функцию протяженности точки PSF. И соответственно, результирующее изображение является наилучшим по качеству.
subplot(224); imshow(P3, [], 'notruesize');
title('Восстановленная истинная PSF');
Шаг 4: Повышение качества восстановления.
Искажения в восстановленном изображении J3 наиболее заметны в областях с высоким контрастом и вдоль границ объектов изображения. Рассмотрим методы понижения этих искажений с использованием так называемых взвешенных функций. В процессе восстановления изображения и функции протяженности точки PSF алгоритм присваивает каждому пикселю некоторый вес в соответствии с массивом WEIGHT. В нашем примере обработка начинается с обнаружения "высококонтрастных" пикселей с использованием функции края edge. Методом проб и ошибок определяется нужный порог. В нашем случае он равен 0.3.
WEIGHT=edge(I, 'sobel', .3);
Для расширения области используется функция imdilate и дискообразные структурные элементы. se=strel('disk', 2);
WEIGHT=1-double(imdilate(WEIGHT, se));
Далее применяются морфологические операции закрытия пикселей на краях и присвоение им значения 0.
WEIGHT([1:3 end-[0:2]], :)=0;
WEIGHT(:, [1:3 end-[0:2]])=0;
figure; imshow(WEIGHT);title('Массив весов');
Теперь при проведении операции восстановления изображения будет применяться функция deconvblind вместе с массивом весов WEIGHT, что приведет к увеличению числа итераций (до 30). Таким образом подавляются почти все искажения, которые были на восстановленном изображении.
[J P]=deconvblind(Blurred, INITPSF, 30, [], WEIGHT);
figure; imshow(J); title('Восстановленное изображение');
Шаг 5: Использование дополнительных ограничений для функции протяженности точки при восстановлении изображений.
В этом примере рассмотрим использование некоторых дополнительных ограничений при формировании функции протяженности точки PSF. Зададим некоторую функцию FUN, которая возвращает модифицированный массив PSF и который, в свою очередь, применяется в функции deconvblind. В этом примере функция FUN модифицирует массив PSF, проводя коррекцию ее размеров. Отметим, что эта операция не приводит к изменению значений в центре функции протяженности точки PSF.
str='padarray(PSF(P1+1:end-P1, P2+1:end-P2), [P1 P2])';
FUN=inline(str, 'PSF', 'P1', 'P2');
Далее, как было сказано ранее, FUN используется в функции deconvblind.
В этом примере исходные размеры PSF, OVERPSF, являются на 4 пикселя больше от истинного значения. P1=2 и P2=2 являются исходными параметрами в FUN при поиске истинного значения функции протяженности точки PSF.
[JF PF]=deconvblind(Blurred, OVERPSF, 30, [], WEIGHT, FUN, 2, 2);
figure; imshow(JF);title('Восстановленное изображение');
При данных параметрах получим результат, который очень похож на результат, полученный на Шаге 4.
Когда в качестве исходной взять функцию протяженности точки PSF с очень большими размерами, тогда получим результат аналогичный Шагу 3.Реконструкция изображений с использованием регуляризационного фильтра
Регуляризационная деконволюция эффективно используется при решении задач восстановления изображений (например, размытых) при условиях ограниченной информации о природе искажений. Такое применение является наиболее эффективным с точки зрения наименьшей среднеквадратической ошибки.
Содержание.
- Шаг 1: Считывание изображения.
- Шаг 2: Симуляция размытостей и шума.
- Шаг 3: Восстановление размытых и зашумленных изображений.
- Шаг 4: Ослабление шумовой составляющей.
- Шаг 5: Использование коэффициента Лагранжа.
- Шаг 6: Использование дифференциальной обработки.
-
Шаг 1: Считывание изображения.
Считаем RGB-изображение и вырежем из него часть размером 256
 256
256 3. Далее к этому изображению будет применяться функция deconvreg.
3. Далее к этому изображению будет применяться функция deconvreg.I=imread('tissue.png');I=I(125+[1:256], 1:256,:);
figure; imshow(I); title('Исходное изображение');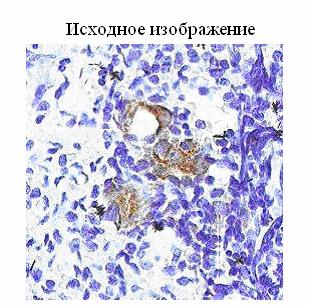
Шаг 2: Симуляция размытостей и шума.
Проведем симулирование реальных изображений, которые содержат размытости (например, результат движения камеры или недостаточной фокусировки) и шумовую составляющую. Размытости на изображении формируются при свертке исходного изображения с фильтром Гаусса (можно использовать функцию imfilter). При этом также используется функция протяженности точки PSF.
PSF=fspecial('gaussian', 11, 5);Blurred=imfilter(I, PSF, 'conv');
figure; imshow(Blurred);
title('Размытое изображение');
Зашумленное изображение будем формировать, добавляя к размытому изображению гауссовский шум (при этом можно использовать функцию imnoise).
V=.02;
BlurredNoisy=imnoise(Blurred,'gaussian',0,V);
figure;imshow(BlurredNoisy);
title('Размытое и зашумленное изображение');
Шаг 3: Восстановление размытых и зашумленных изображений.
При восстановлении изображений для анализа шумовой составляющей используется еще один параметр NP. Продемонстрируем чувствительность этого метода к этому параметру при трех реализациях.
При первой реализации reg1 используем точное значение параметра NP. Отметим, что результатом работы метода является два параметра. Первый, reg1, представляет непосредственно восстановленное изображение. Второй параметр, LAGRA, представляет собой скаляр, точнее множитель Лагранжа.
NP=V*prod(size(I)); % коэффициент шума.
[reg1 LAGRA]=deconvreg(BlurredNoisy, PSF, NP);
figure, imshow(reg1),title('Восстановление с NP');
При второй реализации метода, reg2, используется значение NP, которое отличается от прежнего в сторону увеличения, что будет влиять на разрешение.
reg2=deconvreg(BlurredNoisy, PSF, NP*1.3);
figure; imshow(reg2);
title('Восстановление с большим NP');
При третьей реализации reg3 используется значение NP, которое меньше того, которое использовалось при первой реализации.
reg3=deconvreg(BlurredNoisy, PSF, NP/1.3);
figure; imshow(reg3);
title('Восстановление с небольшим значением NP');
Шаг 4: Ослабление шумовой составляющей.
В этом примере рассмотрим применение функции edgetaper для уменьшения шумовой составляющей. Эта функция будет реализована перед функцией deconvolution. Полученный результат лучше прежних реализаций.
Edged=edgetaper(BlurredNoisy, PSF);
reg4=deconvreg(Edged, PSF, NP/1.3);
figure;imshow(reg4);
title('Применение функции edgetaper');
Шаг 5: Использование коэффициента Лагранжа.
При проведении операции восстановления размытого и зашумленного изображения предполагается использование некоторого множителя Лагранжа. В этом случае параметром NP, определяющим уровень зашумленности, можно проигнорировать.
Для иллюстрации чувствительности алгоритма к значению LAGRA, проведем три реализации этого подхода. При первой реализации (reg5) используем значение LAGRA, полученное при первой реализации в Шаге 3.
reg5=deconvreg(Edged, PSF, [], LAGRA);
figure; imshow(reg5);
title('Восстановление с LAGRA');
При второй реализации (reg6) используем значение 100*LAGRA. Это должно привести к размытости изображения.
reg6=deconvreg(Edged, PSF, [], LAGRA*100);
figure; imshow(reg6);
title('Восстановление с большим значением LAGRA');
При третьей реализации используем значение LAGRA/100, что приведет к более слабой размытости изображения.
reg7=deconvreg(Edged, PSF, [], LAGRA/100);
figure; imshow(reg7);
title('Восстановление с небольшим параметром LAGRA');
Шаг 6: Использование дифференциальной обработки.
Рассмотрим пример восстановления размытого и зашумленного изображения с применением параметра дифференциальной обработки (REGOP). Для этого используем одномерный лапласиан.
REGOP=[1 -2 1];
reg8=deconvreg(BlurredNoisy, PSF, [], LAGRA, REGOP);
figure; imshow(reg8);
title('Дифференциальная обработка');Восстановление изображений с использованием метода Лаки-Ричардсона
Рассмотрим алгоритм Лаки-Ричардсона, который предназначен для восстановления размытых изображений. Наиболее эффективно этот алгоритм применять для обработки искаженных данных, для которых известна функция протяженности точки (point-spread function PSF) или так называемый оператор размытия, а также имеется некоторая информация о происхождении и характере шума. Размытое и зашумленное изображение восстанавливается итерационным способом.
Ключевые термины:
Деконволюция, восстановление изображения, функция протяженности точки, алгоритм Лаки-Ричардсона
Ключевые функции
deconvlucy, edgetaper, imfilter, imnoise
Основные шаги демонстрационного примера:
- Шаг 1: Считывание изображения.
- Шаг 2: Симуляция размытостей и шума.
- Шаг 3: Восстановление размытого и зашумленного изображения.
- Шаг 4: Интерактивный анализ восстановления.
- Шаг 5: Обработка шумовой составляющей.
- Шаг 6: Создание модели изображения.
- Шаг 7: Симуляция размытостей.
- Шаг 8: Моделирование взвешенного массива (массив WEIGHT).
- Шаг 9: Моделирование функции протяженности точки PSF.
Шаг 1: Считывание изображения.
Для рассмотрения дальнейших примеров считаем некоторое RGB-изображение и вырежем из него часть с размерами 256
 256
256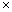 3.
3.I=imread('board.tif');I=I(50+[1:256], 2+[1:256], :);
figure; imshow(I); title('Исходное изображение');
Шаг 2: Симуляция размытостей и шума.
Симулируем реалистическое изображение, содержащее размытости (например, в результате движения или плохой фокусировки камеры) и шум (например, случайные выбросы). Размытость можно симулировать с помощью свертки гауссовского фильтра с изображением (можно использовать функцию imfilter). Гауссовский фильтр представляется функцией протяженности точки (PSF).
PSF=fspecial('gaussian', 5, 5);Blurred=imfilter(I, PSF, 'symmetric', 'conv');
figure; imshow(Blurred); title('Размытое изображение');
Для симуляции зашумленного изображения к размытому изображению добавляем гауссовский шум с отклонением V. Для этого можно использовать функцию (imnoise). Далее значение отклонения V будет использовано в качестве параметра затухания.
V=.002;
BlurredNoisy=imnoise(Blurred, 'gaussian', 0, V);
figure; imshow(BlurredNoisy); title('Размытое и зашумленное изображение');
Шаг 3: Восстановление размытого и зашумленного изображения.
Проведем восстановление размытого и зашумленного изображения с использованием функции протяженности точки (PSF) и 5 итераций (по умолчанию 10). Результирующий массив имеет тот же формат представления данных, что и исходный.
luc1=deconvlucy(BlurredNoisy, PSF, 5);
figure; imshow(luc1); title('Восстановленное изображение, NUMIT=5');
Шаг 4: Интерактивный анализ восстановления.
Результирующее изображение меняется с каждой итерацией. Для исследования процесса восстановления изображений можно реализовать функцию deconvolution в пошаговом режиме, т.е. анализировать результат на каждой итерации.
luc1_cell=deconvlucy({BlurredNoisy}, PSF, 5);В этом случае luc1_cell представляет собой некоторый массив. Результирующий массив содержит четыре числовых массива, первый из которых представляет размытое изображение, второй - то же изображение в формате double, третий - результат предпоследней операции и четвертый - некоторые параметры обработки.
Таким образом, в последующей итерации используются результаты предварительной с применением функции deconvlucy. По умолчанию реализуется 10 итераций (NUMIT=10). Рассмотрим пример с использованием 15 итераций.
luc2_cell=deconvlucy(luc1_cell, PSF);
luc2=im2uint8(luc2_cell{2});figure; imshow(luc2); title('Восстановленное изображение, NUMIT=15');
Шаг 5: Обработка шумовой составляющей.
Следующее изображение luc2 получено в результате 15 итерации. Несмотря на то, что качество изображения значительно лучше, чем после 5 итерации, на изображении проявляются различного рода дефекты обработки. Эти дефекты не соответствуют реальной структуре изображения и объясняются наличием шумовой составляющей.
Для контроля над шумовой составляющей используем опцию, которая описывается параметром DAMPAR. Параметр DAMPAR представляется в том же формате, что и исходное изображение. Рассмотрим пример применения параметра DAMPAR, который используется для обработки шума со стандартным отклонением равным 3. Отметим, что изображение является также размытым.
DAMPAR=im2uint8(3*sqrt(V));
luc3=deconvlucy(BlurredNoisy, PSF, 15, DAMPAR);
figure; imshow(luc3);
title('Восстановление изображения с параметром DAMPAR, NUMIT=15');
В следующей части демонстрационного примера рассмотрим параметры WEIGHT и SUBSMPL, которые применяются в функции deconvlucy. Для этого симулируем некоторое простое изображение.
Шаг 6: Моделирование простого изображения.
Создадим бинарное изображение.
I=zeros(32); I(5, 5)=1; I(10, 3)=1; I(27, 26)=1; I(29, 25)=1;
figure; subplot(231); imshow(1-I, []);
set(gca, 'Visible', 'on', 'XTickLabel', [], 'YTickLabel', [], ...
'XTick', [7 24], 'XGrid', 'on', 'YTick', [5 28], 'YGrid', 'on')
title('Данные');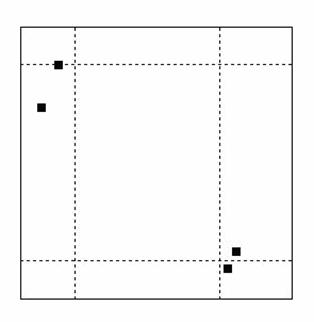
Шаг 7: Симуляция размытостей.
Рассмотрим пример размытого изображения, которое получено из исходного путем применения фильтра Гаусса, функции протяженности точки PSF и свертки их с исходным изображением.
PSF=fspecial('gaussian', 15, 3);Blurred=imfilter(I, PSF, 'conv', 'sym');
Обработаем это изображение следующим образом. Создадим некоторую весовую функцию в виде массива WEIGHT и разобьем изображение на части. В центральной части будет размещено размытое изображение, неискаженные же пиксели будут размещены на краях изображения за пунктирной линией.
WT=zeros(32); WT(6:27, 8:23)=1;
CutImage=Blurred.*WT;
Для уменьшения влияния краев изображения, применяется функция edgetaper вместе с функцией протяженности точки PSF.
CutEdged=edgetaper(CutImage, PSF);
subplot(232); imshow(1-CutEdged, [], 'notruesize');
set(gca, 'Visible', 'on', 'XTickLabel', [], 'YTickLabel', [], ...
'XTick', [7 24], 'XGrid', 'on', 'YTick', [5 28], 'YGrid', 'on');
title('Наблюдение');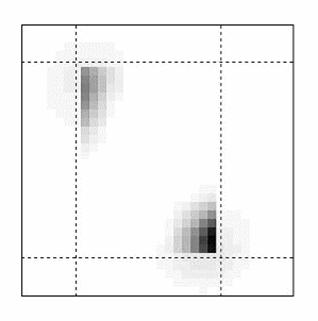
Шаг 8: Моделирование взвешенного массива (массив WEIGHT).
Алгоритм присвоения каждому пикселю некоторого значения согласно массиву WEIGHT приводит к восстановлению изображения. В нашем примере будут использоваться только значения центральных пикселей (в них параметр WEIGHT принимает значение 1), значения "плохих" пикселей будут исключены из оптимизации. При реализации данного алгоритма следует отметить точность расположения результирующих точек.
luc4=deconvlucy(CutEdged, PSF, 300, 0, WT);
subplot(233); imshow(1-luc4, [], 'notruesize');
set(gca, 'Visible', 'on', 'XTickLabel', [], 'YTickLabel', [] ,...
'XTick', [7 24] ,' XGrid', 'on', 'YTick', [5 28], 'YGrid', 'on');
title('Восстановление');
Шаг 9: Моделирование функции протяженности точки PSF.
Функция deconvlucy применяется для восстановления рассматриваемого размытого изображения с использованием функции протяженности точки PSF. Рассмотрим зависимость качества восстановления изображений от удачного выбора функции протяженности точки.
Binned=squeeze(sum(reshape(Blurred, [2 16 2 16])));
BinnedImage=squeeze(sum(Binned, 2));
Binned=squeeze(sum(reshape(PSF(1:14, 1:14), [2 7 2 7])));
BinnedPSF=squeeze(sum(Binned, 2));
subplot(234); imshow(1-BinnedImage, [], 'notruesize');
set(gca, 'Visible', 'on', 'XTick', [], 'YTick', []);

Проведем восстановление изображения BinnedImage с использованием смоделированной функции протяженности точки BinnedPSF. Отметим, что на изображении luc5 размещено только три объекта.
luc5=deconvlucy(BinnedImage, BinnedPSF, 100);
subplot(235); imshow(1-luc5, [], 'notruesize');
set(gca, 'Visible', 'on', 'XTick', [], 'YTick', []);

Рассмотрим еще один пример восстановления изображений с применением более точной функции протяженности точки. Восстановленное изображение (luc6) характеризируется более точным расположением объектов. Изменяя параметры, попробуем разделить объект в нижнем правом углу, что должно привести к улучшению восстановления.
luc6=deconvlucy(BinnedImage, PSF, 100, [], [], [], 2);
subplot(236); imshow(1-luc6, [], 'notruesize');
set(gca, 'Visible', 'on', 'XTick', [], 'YTick', []);

Некоторые подходы к улучшению визуального качества изображений с затемненными участками
Как уже не раз отмечалось, изображение является одной из наиболее удобных форм представления информации. Однако, довольно часто, эти данные не обладают нужным уровнем визуального качества. Это затрудняет проведение их анализа и принятие на его основе достоверных решений. Поэтому актуальной является задача повышения визуального качества такого рода изображений. В этой работе рассмотрим вопросы повышения качества изображений с затемненными участками. Эту задачу можно обобщить на улучшение визуального качества тех изображений, в которых интенсивности пикселей информационных областей сосредоточены в узком динамическом диапазоне.
Подходы, которые применяются для решения этой задачи, могут быть самыми разнообразными. Стандартной методики, определяющей какой метод и когда применять, не существует. В большинстве случаев выбор того или другого метода делают на основе анализа гистограммы исследуемого изображения. Также следует отметить, что рассмотренные методы разрабатывались для обработки полутоновых изображений и применять их для обработки цветных изображений следует очень осторожно, поскольку это может привести к нарушению соотношений между составляющими цвета.
Шаг 1. Считывание исходного изображения.
Считаем исходное изображение (рис.1) в рабочее пространство Matlab и выведем его на экран монитора.
L=imread('krepost.bmp');
figure, imshow(L);
Также определим основные параметры (размерности) этого изображения.
[N M s]=size(L);

Рис. 1. Исходное изображение.
Шаг 2. Построение гистограммы исходного изображения.
Выбор того или другого метода обработки базируется на анализе его гистограммы. Построим гистограмму исходного изображения. Поскольку данное изображение является многомерным, то следует строить гистограмму по каждой цветовой составляющей.
imhist(L(:,:,1)); %красная составляющая.
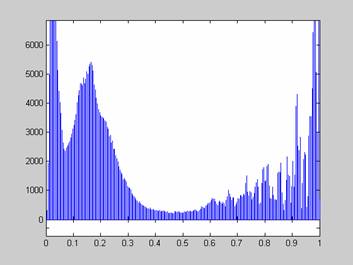
Рис. 2. Гистограмма исходного изображения (красная составляющая).
imhist(L(:,:,2)); %зеленая составляющая.
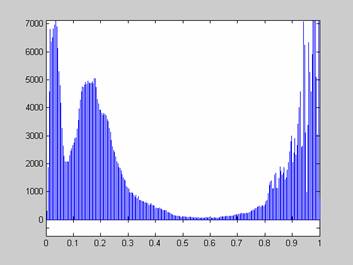
Рис. 3. Гистограмма исходного изображения (зеленая составляющая).
imhist(L(:,:,3)); %синяя составляющая.
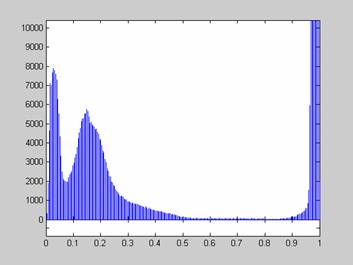
Рис. 4. Гистограмма исходного изображения (синяя составляющая).
Анализ гистограммы подтверждает тот факт, что основную часть изображения составляют темные и светлые области. Количество элементов изображения со средними значениями интенсивности существенно меньше. Известно, что наиболее приемлемым, с точки зрения визуального восприятия, являются изображения, гистограмма которых является равномерной. Из этого следует, что нужно провести такие преобразования, которые привели бы к растяжению диапазона интенсивностей темных и светлых областей. Теперь, исходя из своего опыта и знаний, исследователь подбирает нужный метод. Рассмотрим несколько подходов к решению данной задачи, а также проанализируем их преимущества и недостатки.
Шаг 3. Арифметические операции с изображениями.
Наиболее простой метод, который приведет к увеличению детализации темных областей, заключается в реализации арифметических операций с исследуемым изображением.
Lvyh=L+64/255; % гистограмма сдвинута на 64 градации вправо.

Рис. 5. Обработка с использованием арифметических операций.
Такие операции приводят к тому, что гистограмма исследуемого изображения сдвигается на некоторое значение в среднюю часть диапазона, которая является наиболее приемлемой с точки зрения визуального восприятия.
Исходное изображение и гистограммы его цветовых составляющих

Исходное изображение
Красная составляющая
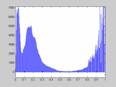
Зеленая составляющая
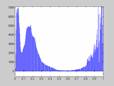
Синяя составляющая
Результирующее изображение и гистограммы его цветовых составляющих

Результат применения
арифметических операций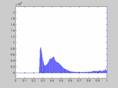
Красная составляющая

Зеленая составляющая

Синяя составляющая
Рис. 6. Сравнение гистограмм цветовых составляющих исходного и результирующего изображений.
Как видно с рис. 6 применением арифметических операций можно достигать определенного уровня качества визуального восприятия. Однако данный метод имеет очень сильный недостаток, который заключается в том, что, улучшая одну область (в данном случае темную), интенсивности пикселей светлых областей сдвигаются к максимуму, что приводит к утере информации. Поэтому применять этот метод следует с учетом информативности тех или иных областей.
Шаг 4. Растяжение динамического диапазона интенсивностей пикселей изображения.
Если интенсивности пикселей потенциально информационных областей сосредоточены в узком динамическом диапазоне, тогда можно использовать еще один подход. Он заключается в растяжении динамического диапазона интенсивностей пикселей изображения. Проводятся эти преобразования согласно выражению
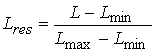
(1) где
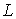 ,
, 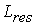 - массив значений соответственно исходного и результирующего изображений;
- массив значений соответственно исходного и результирующего изображений;
Напомним, что преобразования по формуле (1) эффективны в том случае, если интенсивности пикселей потенциально информационных областей сосредоточены в узком динамическом диапазоне. Если применить эти преобразования к исходному выражению (рис. 1), то желаемого эффекта не достигнем, поскольку гистограммы его цветовых компонент занимают весь возможный диапазон.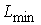 ,
, 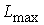 - соответственно минимальное и максимальное значения исходного изображения.
- соответственно минимальное и максимальное значения исходного изображения.
Улучшения визуального качества исходного изображения можно достигнуть, если модифицировать выражение (1), т.е. сделать растяжение динамического диапазона интенсивностей пикселей изображения нелинейным
 , , |
(2) |
где α - коэффициент нелинейности.
Реализуем такое преобразование исходного изображения (рис.1) при α=0.5.
for k=1:3;
Lmin=min(min(L(:, :, k)));Lmax=max(max(L(:, :, k)));
for i=1:N; for j=1:M;
Lvyh(i, j, k)=(((L(i, j, k)-Lmin)/(Lmax-Lmin)))^.5; % реализация преобразований за выражением (2)
if Lvyh(i, j, k)>1; % защита от выхода за диапазон [0, 1]
Lvyh(i, j, k)=1;
end;
if Lvyh(i, j, k)<0;
Lvyh(i, j, k)=0;
end;
end; end;
end;
figure, imshow(Lvyh);

Рис. 7. Результат нелинейного растяжения динамического диапазона интенсивностей пикселей изображения.
Из приведенной части программы видно, что нелинейные преобразования проводятся для каждой цветовой составляющей. В цикле программы реализована также защита от выхода значений интенсивностей пикселей за пределы диапазона [0, 1].
В этой работе были рассмотрены наиболее простые методы повышения визуального качества изображений с затемненными участками. Эти методы служат основой для построения более сложных и эффективных методов обработки данных.
Реализация некоторых методов видоизменения гистограмм в системе Matlab
Как уже не раз отмечалось, одной из важнейших характеристик изображения является гистограмма распределения яркостей его элементов. Ранее мы уже кратко рассматривали теоретические основы видоизменения гистограмм, поэтому в этой работе больше внимания уделим практическим аспектам реализации некоторых методов преобразования гистограмм в системе Matlab. При этом отметим, что видоизменение гистограмм является одним из методов улучшения визуального качества изображений.
Содержание:
Шаг 1: Считывание исходного изображения.
Шаг 2: Равномерное преобразование гистограммы.
Шаг 3: Экспоненциальное преобразование гистограммы.
Шаг 4: Преобразование гистограммы по закону Рэлея.
Шаг 5: Преобразование гистограммы по закону степени ![]() .
.
Шаг 6: Гиперболическое преобразование гистограммы.
Шаг 1: Считывание исходного изображения.
Считаем из файла исходное изображение в рабочее пространство Matlab и выведем его на экран монитора.
L=imread('lena.bmp');
figure, imshow(L);
Так как исследуемое исходное изображение полутоновое, то будем рассматривать только одну составляющую многомерного массива ![]() .
.

Рис. 1. Исходное изображение.
Поскольку в работе рассматриваются гистограммные методы преобразования, то построим также гистограмму ![]() исходного изображения.
исходного изображения.
H=imhist(L);
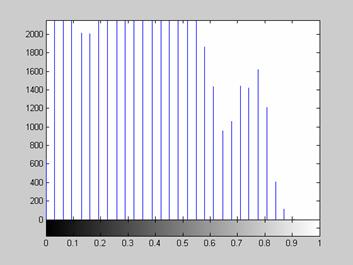
Рис.2. Гистограмма исходного изображения.
Шаг 2: Равномерное преобразование гистограммы.
Равномерное преобразование гистограммы осуществляется по формуле
| (1) |
где ![]() ,
, ![]() - минимальное и максимальное значения элементов массива интенсивностей
- минимальное и максимальное значения элементов массива интенсивностей ![]() исходного изображения;
исходного изображения;
![]() - функция распределения вероятностей исходного изображения, которая аппроксимируется гистограммой распределения
- функция распределения вероятностей исходного изображения, которая аппроксимируется гистограммой распределения 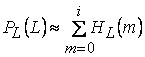 . Другими словами, речь идет о кумулятивной гистограмме изображения.
. Другими словами, речь идет о кумулятивной гистограмме изображения.
В среде Matlab это можно реализовать следующим образом. Вычисляем кумулятивную гистограмму исходного изображения
CH=cumsum(H)./(N*M);
![]() - вектор значений гистограммы исходного изображения, а
- вектор значений гистограммы исходного изображения, а ![]() ,
, ![]() - размеры данного изображения, которые определяются с помощью функции size
- размеры данного изображения, которые определяются с помощью функции size
[N M]=size(L);
Далее, согласно формуле (1), определяем значения интенсивностей пикселей результирующего изображения.
L1(i,j)=CH(ceil(255*L(i,j)+eps));
figure, imshow(L1);
Значение eps используется вместе с функцией ceil для того, чтобы избежать присвоения индексам кумулятивной гистограммы ![]() нулевых значений. Результат применения метода равномерного преобразования гистограммы представлен на рис. 3.
нулевых значений. Результат применения метода равномерного преобразования гистограммы представлен на рис. 3.

Рис. 3. Исходное изображение, обработанное методом равномерного преобразования гистограммы.
Гистограмма, преобразованного согласно формуле (1) изображения, представлена на рис. 4. Она действительно занимает почти весь динамический диапазон и является равномерной.
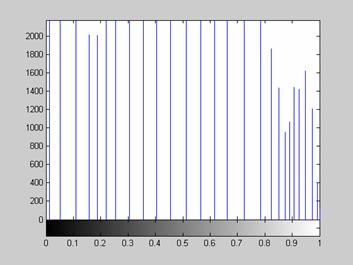
Рис. 4. Гистограмма изображения, представленного на рис. 3.
О равномерной передаче уровней интенсивностей элементов изображения свидетельствует также и его кумулятивная гистограмма (рис. 5).
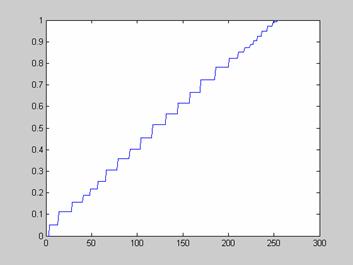
Рис.5. Кумулятивная гистограмма изображения, представленного на рис. 3.
Далее рассмотрим методы видоизменения гистограмм, которые аналогичны к рассмотренному подходу и будут отличаться только выражениями преобразования.
Шаг 3: Экспоненциальное преобразование гистограммы.
Экспоненциальное преобразование гистограммы осуществляется по формуле
| (2) |
где ![]() - некоторая константа, характеризующая крутизну экспоненциального преобразования.
- некоторая константа, характеризующая крутизну экспоненциального преобразования.
В Matlab преобразования по формуле (2) можно реализовать следующим образом.
L2(i,j)=-(1/alfa1)*log10(1-CH(ceil(255*L(i,j)+eps)));
figure, imshow(L2);

Рис. 6. Исходное изображение после обработки методом экспоненциального преобразования гистограммы.
Гистограмма изображения, обработанного методом экспоненциального преобразования, представлена на рис. 7.
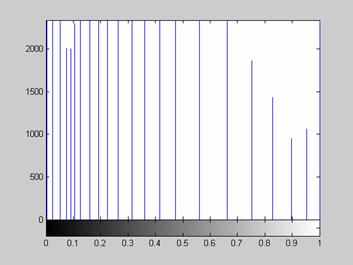
Рис. 7. Гистограмма изображения, обработанного методом экспоненциального преобразования.
Наиболее четко экспоненциальный характер преобразований проявляется на кумулятивной гистограмме обработанного изображения, которая представлена на рис. 8.
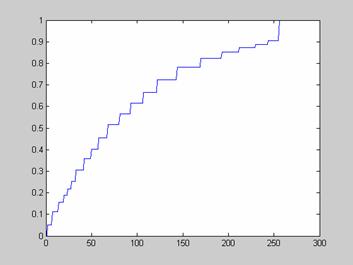
Рис. 8. Кумулятивная гистограмма изображения, обработанного методом экспоненциального преобразования.
Шаг 4: Преобразование гистограммы по закону Рэлея.
Преобразование гистограммы по закону Рэлея осуществляется согласно выражению
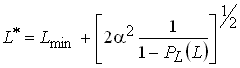 , , |
(3) |
где ![]() - некоторая константа, характеризующая гистограмму распределения интенсивностей элементов результирующего изображения.
- некоторая константа, характеризующая гистограмму распределения интенсивностей элементов результирующего изображения.
Приведем реализацию данных преобразований в среде Matlab.
L3(i,j)=sqrt(2*alfa2^2*log10(1/(1-CH(ceil(255*L(i,j)+eps)))));
figure, imshow(L3);

Рис. 9. Исходное изображение, обработанное методом преобразования гистограммы по закону Рэлея.
Гистограмма изображения, обработанного методом преобразования по закону Рэлея, представлена на рис. 10.
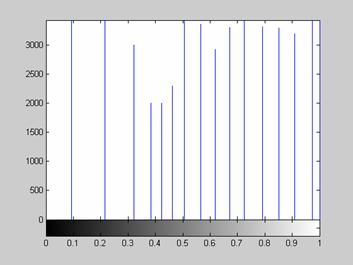
Рис. 10. Гистограмма изображения, обработанного методом преобразования по закону Рэлея.
Кумулятивная гистограмма изображения, обработанного методом преобразования по закону Рэлея, представлена на рис. 11.
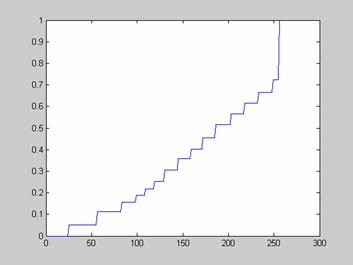
Рис. 11. Кумулятивная гистограмма изображения, обработанного методом преобразования по закону Рэлея.
Шаг 5: Преобразование гистограммы по закону степени ![]() .
.
Преобразование гистограммы изображения по закону степени ![]() реализуется согласно выражению
реализуется согласно выражению
| (4) |
В среде Matlab этот метод можно реализовать следующим образом.
L4(i,j)=(CH(ceil(255*L(i,j)+eps)))^(2/3);
figure, imshow(L4);

Рис. 12. Исходное изображение, обработанное методом преобразования гистограммы по закону степени ![]() .
.
Гистограмма распределения интенсивностей элементов обработанного изображения представлена на рис. 13.
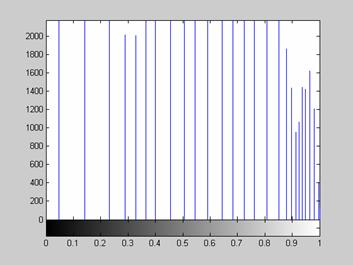
Рис. 13. Гистограмма изображения, обработанного методом преобразования гистограммы по закону степени ![]() .
.
Кумулятивная гистограмма обработанного изображения, которая наиболее четко демонстрирует характер передачи уровней серого, представлена на рис. 14.
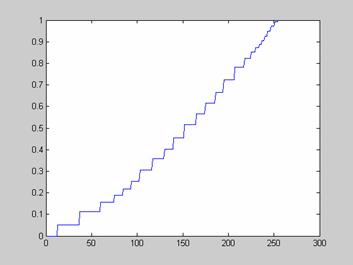
Рис. 14. Кумулятивная гистограмма изображения, обработанного методом преобразования по закону степени ![]() .
.
Шаг 6: Гиперболическое преобразование гистограммы.
Гиперболическое преобразование гистограммы реализуется согласно формуле
| (5) |
где ![]() - некоторая константа, относительно которой осуществляется гиперболическое преобразование гистограммы. Фактически параметр
- некоторая константа, относительно которой осуществляется гиперболическое преобразование гистограммы. Фактически параметр ![]() равен минимальному значению интенсивности элементов изображения.
равен минимальному значению интенсивности элементов изображения.
В среде Matlab этот метод может быть реализован следующим образом
L5(i,j)=.01^(CH(ceil(255*L(i,j)+eps))); % в данном случае А=0,01
figure, imshow(L5);

Рис. 15. Исходное изображение, обработанное методом гиперболического преобразования.
Гистограмма распределения интенсивностей элементов обработанного таким образом изображения представлена на рис. 16.
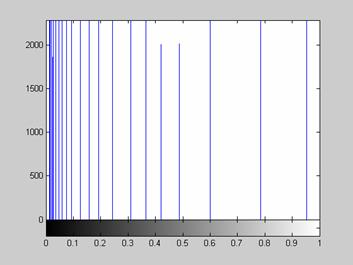
Рис. 16. Гистограмма изображения, обработанного методом гиперболического преобразования.
Кумулятивная гистограмма, форма которой соответствует характеру проводимых преобразований, представлена на рис. 17.
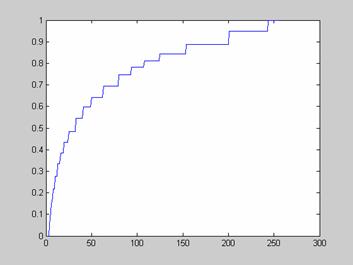
Рис. 17. Кумулятивная гистограмма изображения, обработанного методом гиперболического преобразования.
В данной работе были рассмотрены некоторые методы видоизменения гистограмм. Результатом применения каждого метода является то, что гистограмма распределения яркостей элементов обработанного изображения принимает определенную форму. Такого рода преобразования могут применяться для устранения искажений при передаче уровней квантирования, которым были подвергнуты изображения на этапе формирования, передачи или обработки данных.
Отметим также, что рассмотренные методы могут быть реализованы не только глобально, но и в скользящем режиме. Это приведет к усложнению вычислений, поскольку нужно будет анализировать гистограмму на каждом локальном участке. Однако, с другой стороны, такие преобразования, в отличие от глобальной реализации, позволяют увеличивать детальность локальных участков.
Подавление шумов на изображениях
Довольно часто при формировании визуальных данных результирующие изображения получаются зашумленными. Это объясняется несовершенством аппаратуры, влиянием внешних факторов и т.п. В конечном результате это приводит к ухудшению качества визуального восприятия и снижению достоверности решений, которые будут приниматься на основе анализа таких изображений. Поэтому актуальной является задача устранения или снижения уровня шумов на изображениях. Решению задачи фильтрации шумов посвящено очень много работ, существуют различные методы и алгоритмы. В этой работе рассмотрим только некоторые подходы и возможности их реализации в системе Matlab.
Содержание:
Шаг 1: Считывание исходного изображения.
Шаг 2: Формирование зашумленных изображений.
Шаг 3: Использование медианного фильтра для устранения импульсного шума.
Шаг 4: Подавление шумовой составляющей с использованием операции сглаживания.
Шаг 5: Пороговый метод подавления шумов.
Шаг 6: Низкочастотная фильтрация с использованием шумоподавляющих масок.
Шаг 1: Считывание исходного изображения.
Считаем изображение из файла в рабочее пространство Matlab и отобразим его на экране монитора.
L=imread('kinder.bmp');
figure, imshow(L);

Рис.1 Исходное изображение.
Шаг 2: Формирование зашумленных изображений.
В системе Matlab (Image Processing Toolbox) существует возможность формирования и наложения на изображение трех типов шумов. Для этого используется встроенная функция imnoise, которая предназначена, в основном, для создания тестовых изображений, используемых при выборе и исследовании методов фильтрации шума. Рассмотрим несколько примеров наложения шума на изображения.
1) Добавление к изображению импульсного шума (по умолчанию плотность шума равна доле искаженных пикселей):
L2=imnoise(L,'salt&pepper', 0.05);
figure, imshow(L2);

Рис.2. Зашумленное изображение (импульсный шум).
2) Добавление к изображению гауссовского белого шума (по умолчанию математическое ожидание равно 0, а дисперсия - 0,01):
L1=imnoise(L,'gaussian');
figure, imshow(L1);

Рис.3. Зашумленное изображение (гауссовский шум).
3) Добавление к изображению мультипликативного шума (по умолчанию математическое ожидание равно 0, а дисперсия 0,04):
L3=imnoise(L,'speckle',0.04);
figure, imshow(L3);

Рис.4. Зашумленное изображение (мультипликативный шум).
Шаг 3: Использование медианного фильтра для устранения импульсного шума.
Одним из эффективных путей устранения импульсных шумов на изображении является применение медианного фильтра. Наиболее эффективным вариантом является реализация в виде скользящей апертуры.
for i=1+n1:N+n1;
disp(i)
for j=1+m1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=Lr(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
D(n1+1+a,m+1)=Lr(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
Lvyh(i,j)=median(D(:));
end;
end;
Lvyh=Lvyh(n1+1:N+n1, m1+1:M+m1);
figure, imshow(Lvyh);
Для наглядного сравнения приведем три изображения вместе: исходное, зашумленное и восстановленное.
|
Исходное изображение |
Зашумленное изображение (импульсный шум) |
Восстановленное изображение |
Рис. 5. Восстановление изображения, искаженного импульсным шумом, с применением метода медианной фильтрации.
Восстановленное изображение лишь незначительно отличается от исходного изображения и значительно лучше, с точки зрения визуального восприятия, зашумленного изображения.
Шаг 4: Подавление шумовой составляющей с использованием операции сглаживания.
Существует класс изображений, для которых подавление шумовой составляющей возможно реализовать с помощью операции сглаживания (метод низкочастотной пространственной фильтрации). Этот подход может применяться к обработке изображений, содержащих области большой площади с одинаковым уровнем яркости. Отметим, что уровень шумовой составляющей должен быть относительно небольшим.
F=ones(n,m); % n и m размерность скользящей апертуры
Lser=filter2(F,Lroshyrena,'same')/(n*m);
|
Исходное изображение |
Зашумленное изображение |
Восстановленное изображение |
Рис. 6. Восстановление изображения, искаженного импульсным шумом с применением операции сглаживания.
Недостаток этого метода, в отличие от метода медианной фильтрации, состоит в том, что он приводит к размыванию границ объектов изображения.
Шаг 5: Пороговый метод подавления шумов.
Элементы изображения, которые были искажены шумом, заметно отличаются от соседних элементов. Это свойство легло в основу многих методов подавления шума, наиболее простой из которых, так называемый пороговый метод. При использовании этого метода последовательно проверяют яркости всех элементов изображения. Если яркость данного элемента превышает среднюю яркость локальной окрестности, тогда яркость данного элемента заменяется на среднюю яркость окрестности.
for i=1+n1:N+n1;
disp(i)
for j=1+m1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=Lr(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
D(n1+1+a,m+1)=Lr(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
LS=mean(mean(D));
if abs(Lr(i,j)-LS)>10/255; % Установка порога
Lvyh(i,j)=LS;
else
Lvyh(i,j)=Lr(i,j);
end;
end;
end;
Lvyh=Lvyh(n1+1:N+n1,m1+1:M+m1,:);
figure, imshow(Lvyh);
|
Исходное изображение |
Зашумленное изображение |
Восстановленное изображение |
Рис. 7. Восстановление изображения, искаженного импульсным шумом, с применением порогового метода подавления шумов.
Шаг 6: Низкочастотная фильтрация с использованием шумоподавляющих масок.
В Шаге 4 было рассмотрено применение операции сглаживания для устранения шума. Рассмотрим примеры низкочастотной фильтрации с использованием других шумоподавляющих масок. Это могут быть следующие маски:
Маска 1: 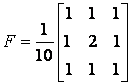 Маска 2:
Маска 2: 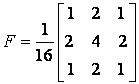 .
.
Маски для подавления шума представлены в виде нормированного массива для получения единичного коэффициента передачи, чтобы при подавлении шума не было искажений средней яркости. На рисунках представлено результат обработки зашумленного изображения маской 1 и маской 2.
F=(1/10)*[1 1 1; 1 2 1; 1 1 1];
Lvyh=filter2(F,L,'same')/(3*3);
figure, imshow(Lvyh);

Рис. 8. Результат восстановления зашумленного импульсным шумом изображения с применением маски 1.
F=(1/16)*[1 2 1; 2 4 2; 1 2 1];
Lvyh=filter2(F,L,'same')/(3*3);
figure, imshow(Lvyh);

Рис. 9. Результат восстановления зашумленного импульсным шумом изображения с применением маски 2.
Это были примеры подавления импульсных шумов. Рассмотрим аналогичные примеры подавления гауссовского и мультипликативного шумов.
|
Зашумленное гауссовским шумом изображение |
Восстановленное изображение с применением маски 1 |
Восстановленное изображение с применением маски 2 |
Рис. 10. Результат восстановления зашумленного гауссовским шумом изображения с применением маски 1 и маски 2.
|
Зашумленное мультипликативным шумом изображение |
Восстановленное изображение с применением маски 1 |
Восстановленное изображение с применением маски 2 |
Рис. 11. Результат восстановления зашумленного мультипликативным шумом изображения с применением маски 1 и маски 2.
Отметим, что универсальных методов нет и к обработке каждого изображения следует подходить индивидуально. Если речь идет о медианной и низкочастотной фильтрации, то качество обработки во многом зависит от удачного выбора размеров локальной апертуры.
Рассмотренные методы после некоторой модификации можно применять для обработки цветных изображений. Приведем пример подавления импульсного шума на цветном изображении.
Возьмем некоторое исходное изображение (рис. 12):
L=imread('lily.bmp');
figure, imshow(L);

Рис. 12. Исходное цветное изображение.
Наложим на него импульсный шум с некоторыми характеристиками:
L=imnoise(L,'salt&pepper',0.05);
figure, imshow(L);

Рис. 13. Зашумленное изображение.
Далее для каждой цветовой составляющей применим операцию медианной фильтрации.
for k=1:s; % обработка отдельно по каждой составляющей
L=Lin(:,:,k);
for i=1+n1:N+n1; disp(i) for j=1+m1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1; for b=-m1:m1;
D(n1+1+a,m1+1+b)=L(i+a,j+b);
end; end;
end;
if j>1+m1;
for a=-n1:n1; D(n1+1+a,m+1)=L(i+a,j+m1); end;
D=D(1:n,2:m+1);
end;
Lres(i,j)=median(D(:));
end; end;
end;

Рис. 14. Восстановленное изображение с применением метода медианной фильтрации.
Представленные выше методы являются довольно эффективными алгоритмами восстановления изображений, которые были искажены импульсным, гауссовским или мультипликативным шумом. Эти методы служат основой для построения других более сложных методов решения задач по устранению шумовой составляющей на изображениях.
Текстурная сегментация с использованием текстурных фильтров
Текстурная сегментация используется для идентификации областей на основе их текстуры. Рассмотрим задачу сегментации двух видов ткани на изображении с использованием текстурных фильтров.
Содержание:
- Шаг 1: Считывание изображения.
- Шаг 2: Выделение текстуры изображения.
- Шаг 3: Создание грубой маски для выделения нижней текстуры.
- Шаг 4: Использование грубой маски для сегментации верхней текстуры.
- Шаг 5: Отображение результатов сегментации.
- Использование других текстурных фильтров для сегментации.
Шаг 1: Считывание изображения.
Считаем изображение из файла bag.png.
I = imread('bag.png');
figure, imshow(I);

![]()
Шаг 2: Выделение текстуры изображения.
Используем функцию entropyfilt для выделения текстуры изображения. Функция entropyfilt возвращает массив, где каждый пиксель содержит значение энтропии в окрестности соответствующего пикселя. Размер окрестности составляет ![]() элементов. Энтропия является статистической характеристикой случайного процесса.
элементов. Энтропия является статистической характеристикой случайного процесса.
Eim = mat2gray(E); imshow(Eim);
![]()

Шаг 3: Создание грубой маски для выделения нижней текстуры.
Пороговое масштабирование изображения Eim приводит к сегментации текстуры. Выбранное значение порога равно 0.8, поскольку это позволяет выделить границы текстуры.
BW1 = im2bw(Eim, .8); imshow(BW1); figure, imshow(I);
![]()
![]()


Сегментированные объекты представлены на бинарном изображении BW1. При сравнении изображений BW1 и I отметим, что верхняя текстура сегментирована слишком чрезмерно (много белых объектов), а нижняя текстура сегментирована почти нераздельно. Для выделения нижней текстуры можно использовать также функцию bwareaopen.
BWao = bwareaopen(BW1,2000); imshow(BWao);
![]()

Для сглаживания границ можно использовать функцию imclose, а также морфологические операции открытия и закрытия объектов на изображении BWao. При обработке используются те же окрестности, что и в функции entropyfilt.
nhood = true(9); closeBWao = imclose(BWao,nhood); imshow(closeBWao)
![]()

Использование функции imfill для заполнения объектов в closeBWao.
roughMask = imfill(closeBWao,'holes');
Шаг 4: Использование грубой маски для сегментации верхней текстуры.
Сравним бинарное roughMask и исходное I изображения. Отметим, что маска для нижней текстуры не является наилучшей. Поэтому будем использовать roughMask для сегментации верхней текстуры.
imshow(roughMask); figure, imshow(I);
![]()
![]()


Получим такое изображение верхней текстуры с использованием roughMask.
I2 = I; I2(roughMask) = 0; imshow(I2);
![]()

Использование функции entropyfilt для вычисления текстуры изображения.
E2 = entropyfilt(I2); E2im = mat2gray(E2); imshow(E2im);
![]()

Порог E2im с использованием graythresh.
BW2 = im2bw(E2im,graythresh(E2im)); imshow(BW2) figure, imshow(I);
![]()
![]()


При сравнении изображений BW2 и I отметим наличие только двух сегментированных объектов на BW2. Используем функцию bwareaopen для получения маски для верхней текстуры.
mask2 = bwareaopen(BW2,1000); imshow(mask2);
![]()

Шаг 5: Отображение результатов сегментации.
Используем mask2 для получения верхней и нижней текстуры изображения I.
texture1 = I; texture1(~mask2) = 0; texture2 = I; texture2(mask2) = 0; imshow(texture1); figure, imshow(texture2);
![]()
![]()

Очертание границ между текстурами.
boundary = bwperim(mask2); segmentResults = I; segmentResults(boundary) = 255; imshow(segmentResults);
![]()

Использование других текстурных фильтров для сегментации.
Взамен функции entropyfilt можно использовать функции stdfilt и rangefilt вместе с другими морфологическими функциями для получения аналогичных результатов сегментации.
S = stdfilt(I,nhood); imshow(mat2gray(S));
![]()

R = rangefilt(I,ones(5)); imshow(R);
![]()

Поиск растительности на мультиспектральных изображениях
Растительность, которая покрывает земную поверхность, может быть зафиксирована с помощью дистанционного зондирования Земли. В основу положен анализ свойств составляющих мультиспектральных изображений.
В примере продемонстрированы различия между красной и ультракрасной составляющими LANDSAT-изображения. Эти различия могут использоваться для идентификации областей, содержащих растительность. Для этого используем изображение части Парижа (Франция), содержащее семь спектральных шаров и представленное в формате Erdas LAN.
Содержание:
- Шаг 1: Импортирование мультиспектральных шаров из файла изображения.
- Шаг 2: Улучшение мультиспектральных составляющих с помощью декорреляционного растяжения.
- Шаг 3: Формирование инфракрасного изображения.
- Шаг 4: Вычисление признаков растительности на основе проведения арифметических операций с MATLAB-массивом.
- Шаг 5: Локализация растительности - пороговая обработка изображений.
- Шаг 6: Анализ спектральных и пространственных составляющих.
Шаг 1: Импортирование мультиспектральных шаров из файла изображения.
LAN-файл paris.lan содержит 7-слойное Landsat-изображение с размерностью 512![]() 512. 128-битный заголовок представляет собой последовательность значений пикселей, которые являются метками начала информации в порядке возрастания числа слоев. Они хранятся в виде 8-битных чисел без знака.
512. 128-битный заголовок представляет собой последовательность значений пикселей, которые являются метками начала информации в порядке возрастания числа слоев. Они хранятся в виде 8-битных чисел без знака.
Первый шаг заключается в считывании 4, 3 и 2 слоев из LAN-файла с использованием функции MATLAB multibandread. Слои 4, 3 и 2 рассматриваемого изображения получены в инфракрасной области, а также видимой красной и видимой зеленой частях электромагнитного спектра. Когда их представить в виде красной, зеленой и синей составляющей соответственно, то такое RGB-изображение представляет стандартные составляющие инфракрасного изображения. Последний исходный аргумент в функции multibandread описывает соответственно красную и другие составляющие, которые были рассмотрены выше.
CIR = multibandread('paris.lan', [512, 512, 7], 'uint8=>uint8',...
128, 'bil', 'ieee-le', {'Band','Direct',[4 3 2]});
Считываемые данные хранятся в виде массива с размерностью 512![]() 512
512![]() 3, представленного в формате uint8. По сути, это является RGB-изображением, представленным псевдоцветами. При визуализации такого изображения его красная составляющая соответствует ультракрасному слою, зеленая - красному и синяя - зеленому слою. На изображении CIR река Сена представлена в виде потемнения, а зеленая растительность представлена красным (парки и тени деревьев). Повсюду на изображении низкий контраст, а цвета не насыщены.
3, представленного в формате uint8. По сути, это является RGB-изображением, представленным псевдоцветами. При визуализации такого изображения его красная составляющая соответствует ультракрасному слою, зеленая - красному и синяя - зеленому слою. На изображении CIR река Сена представлена в виде потемнения, а зеленая растительность представлена красным (парки и тени деревьев). Повсюду на изображении низкий контраст, а цвета не насыщены.
figure
imshow(CIR)
title('CIR Composite (Un-enhanced)')
text(size(CIR,2), size(CIR,1) + 15,...
'Image courtesy of Space Imaging, LLC',...
'FontSize', 7, 'HorizontalAlignment', 'right')
![]()

Шаг 2: Улучшение мультиспектральных составляющих с помощью декорреляционного растяжения.
Для повышения эффективности проведения визуального анализа, полезно провести предварительную обработку по улучшению таких изображений. Для этого можно использовать метод декорреляционного растяжения. При этом применяется функция decorrstretch, которая проводит улучшение цветов для всех каналов и может также проводить некоторые контрастные преобразования.
decorrCIR = decorrstretch(CIR, 'Tol', 0.01);
figure
imshow(decorrCIR)
title('CIR Composite with Decorrelation Stretch')

Наиболее удобно и очевидно свойства поверхности отображать и изучать с помощью цветных изображений. Для этого можно использовать спектральное представление, поскольку такие изображения имеют большой контраст и хорошо поддаются анализу.
Кроме того, из этих изображений можно получить информацию о различных характеристиках растительности. Особенно отчетливо это проявляется в ультракрасной области. Поэтому ультракрасные изображения отображаются красным каналом в нашем представлении и несут информацию о растительности. В качестве примера отметим, что ярко красным цветом представлен парк (маслины г. Булонь), который находится в западной части Парижа около изгиба Сены.
Анализируя такие изображения можно четко идентифицировать не только растительность, но и здания, воду и т.п.
Шаг 3: Формирование инфракрасного изображения.
Интересные результаты дает сравнение изображений ультракрасной (отображается красной составляющей) и красной (отображается зеленой составляющей) части спектра. Это удобно для получения некоторых индивидуальных свойств объектов. Это также удобно для преобразования формата uint8 в формат single.
NIR = im2single(CIR(:,:,1)); red = im2single(CIR(:,:,2));
Просматривая две цветовые составляющие изображения вместе в виде полутоновых изображений, можно увидеть существующие различия.
figure
imshow(red)
title('Visible Red Band')
figure
imshow(NIR)
title('Near Infrared Band')
![]()
![]()

Приведем пример с использованием команды plot. Используя эту команду можно попиксельно отобразить разброс точек или, другими словами, график рассеяния (в данном случае синей составляющей), где X-координата определяет значение пикселя в синей составляющей изображения, а Y-координата, соответствующее значение в ультракрасной составляющей.
figure
plot(red, NIR, '+b')
set(gca, 'XLim', [0 1], 'XTick', 0:0.2:1,...
'YLim', [0 1], 'YTick', 0:0.2:1);
axis square
xlabel('red level')
ylabel('NIR level')
title('NIR vs. Red Scatter Plot')
![]()
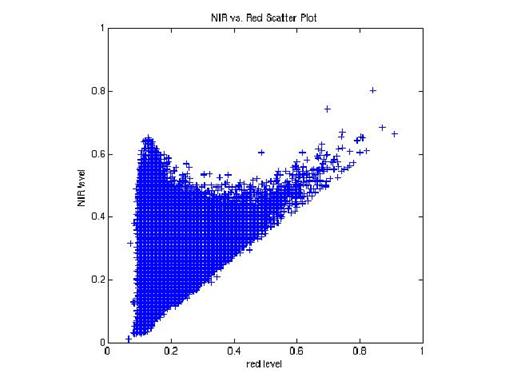
На основе представление графика рассеяния изображения Парижа можно анализировать городскую растительность, в частности, деревья и уровень озеленения. Когда пиксели занимают место около диагонали, то это говорит об уровне подобия ультракрасной и красной составляющих изображения. На основе этих данных можно говорить также о других характеристиках поверхности Земли.
Шаг 4: Вычисление признаков растительности на основе проведения арифметических операций с MATLAB-массивом.
На основе исследования графика рассеяния элементов ультракрасной и красной составляющих изображения можно говорить о локализации пикселей, содержащих густые массивы растительности. Однако при этом следует учитывать зашумленность, особенно в темных областях изображений с небольшими значениями яркости пикселей. Отметим также разницу между ультракрасной и красной составляющими изображения за счет различной интенсивности хлорофилла. Для дальнейших исследований целесообразно использовать так называемый индекс нормированной разности растительности. Он определяется как отношение попиксельной разницы между ультракрасной и красной составляющими изображения к их сумме:
ndvi = (NIR - red) ./ (NIR + red);
Отметим, что система MATLAB позволяет проводить описанную выше операцию с помощью одной командной строки.
Переменная ndvi представляется в виде двумерного массива в формате single с теоретическим диапазоном [-1 1]. Этот теоретический диапазон нужно описать при визуализации данных в виде полутонового изображения.
figure
imshow(ndvi,'DisplayRange',[-1 1])
title('Normalized Difference Vegetation Index')
![]()

Река Сена отображается на ndvi-изображении в виде потемнения. Большие светлые области у левого и правого края изображения отображают парки.
Шаг 5: Локализация растительности - пороговая обработка изображений.
Для идентификации объектов на изображении по возможным значениям представляющих их пикселей используется пороговая обработка ndvi-изображения.
threshold = 0.4; q = (ndvi > threshold);
В процентном соотношении это можно представить так
100 * numel(NIR(q(:))) / numel(NIR)
ans =
5.2204
или 5 процентов.
Парк, а также другие небольшие по площади области растительности отображаются белым цветом, если представить данные в виде логического или бинарного изображения.
figure
imshow(q)
title('NDVI with Threshold Applied')
![]()

Шаг 6: Анализ спектральных и пространственных составляющих.
При помощи спектрального и пространственного представления, а также соответствующей пороговой обработки можно локализировать объекты интереса и представить их в более контрастном виде. Для этого используется не только пороговая обработка соответствующих составляющих изображения, но и анализ графика рассеяния.
% Создание изображения с характеристическим отношением 12. h = figure;
p = get(h,'Position');
set(h,'Position',[p(1,1:3),p(3)/2])
subplot(1,2,1)
% Создание графика рассеяния.
plot(red, NIR, '+b')
hold on
plot(red(q(:)), NIR(q(:)), 'g+')
set(gca, 'XLim', [0 1], 'YLim', [0 1])
axis square
xlabel('red level')
ylabel('NIR level')
title('NIR vs. Red Scatter Plot')
% Отображение NDVI-изображения.
subplot(1,2,2)
imshow(q)
set(h,'Colormap',[0 0 1; 0 1 0])
title('NDVI with Threshold Applied')
![]()
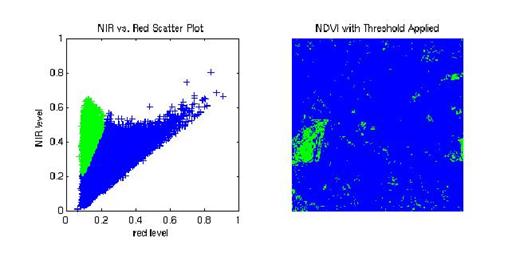
Распознавание объектов на основе вычисления их признаков
Каждый объект можно охарактеризовать набором некоторых признаков. Количество признаков зависит от сложности самого объекта. Точность подбора признаков будет влиять на эффективность распознавания объекта, который описывается этим набором.
Рассмотрим пример распознавания простых объектов на основе набора признаков. При реализации метода в качестве основных будем использовать две функции bwlabel и imfeature, которые встроены в приложение Image Processing Toolbox.
Сначала считаем исходное тестовое изображение в рабочее пространство Matlab
L=imread('test_image.bmp');
и визуализируем его
figure, imshow(L);

Сделаем некоторые замечания относительно исходного изображения. В нашем случае исходные данные представлены бинарным изображением. Это несколько упрощает нашу задачу, поскольку основной акцент в этом примере сделан на распознавание объектов. Однако при решении задач распознавания на основе реальных изображений, в большинстве случаев, важной является задача преобразования исходного изображения в бинарное. Качество решения этой задачи во многом определяет эффективность дальнейшего распознавания.
Функции bwlabel и imfeature в качестве исходных данных используют полутоновые двумерные изображения. Поскольку изображение test_image.bmp было сформировано как бинарное, но сохранено в формате bmp, то из трехмерной матрицы изображения L, которая содержит три идентичных цветовых шара, необходимо выделить один из шаров, например, первый.
L=L(:,:,1);
Такого же результата можно достичь, используя функцию rgb2gray. Таким образом, матрица L представляет бинарное двумерное изображение.
Для дальнейших расчетов определим размеры этого изображения
[N,M]=size(L);
Далее необходимо локализировать, т.е. определить расположение объектов на изображении. Для этого будем использовать функцию bwlabel, которая ищет на бинарном изображении связные области пикселей объектов и создает матрицу, каждый элемент которой равен номеру объекта, которому принадлежит соответствующий пиксель исходного изображения. Параметр num дополнительно возвращает количество объектов, найденных на исходном бинарном изображении.
[L num]=bwlabel(L,8);
Кроме того, в функции bwlabel указывается еще один параметр – значение связности.
Далее приступаем к вычислению признаков объектов, которые отмечены в матрице номеров объектов L. Рассмотрим этот вопрос более подробно. Значения признаков возвращаются в массиве структур feats. Как было отмечено ранее, при распознавании объектов могут использоваться любые наборы признаков.
В рамках этого примера применим наиболее наглядный статистический подход к классификации объектов на основе морфометрических признаков. К основным морфометрическим признакам относятся коэффициенты формы:
- ‘solidity’ – коэффициент выпуклости: равен отношению площади к выпуклой площади объекта. Представляется числом в диапазоне (0,1].
- ‘extent’ – коэффициент заполнения: равен отношению площади объекта к площади ограничивающего прямоугольника. Представляется числом в диапазоне (0,1].
- ‘eccentricity’ – эксцентриситет эллипса с главными моментами инерции, равными главным моментам инерции объекта. Представляется числом в диапазоне (0,1].
Поскольку в данном примере используется тестовое изображение объектов простой формы, то из перечисленных признаков в программной реализации будем использовать только коэффициент заполнения ‘extent’. Как было сказана ранее, параметр ‘extent’ определяется отношением площади объекта к площади ограничивающего прямоугольника. Для круга этот параметр будет равен 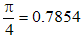 , а для квадрата – 1. Но эти данные приведены для случая, когда круг и квадрат имеют идеальную форму. Если форма круга или квадрата искажена, то значения параметра ‘extent’ также могут отличаться от приведенных выше значений. Поэтому коэффициенты формы могут вычисляться с некоторой погрешностью. Таким образом, вводя некоторую погрешность в коэффициент формы, допускаются некоторые ее искажения. Причем значение погрешности пропорционально степени искажения. Однако слишком большое значение погрешности может привести к неправильному распознаванию объектов.
, а для квадрата – 1. Но эти данные приведены для случая, когда круг и квадрат имеют идеальную форму. Если форма круга или квадрата искажена, то значения параметра ‘extent’ также могут отличаться от приведенных выше значений. Поэтому коэффициенты формы могут вычисляться с некоторой погрешностью. Таким образом, вводя некоторую погрешность в коэффициент формы, допускаются некоторые ее искажения. Причем значение погрешности пропорционально степени искажения. Однако слишком большое значение погрешности может привести к неправильному распознаванию объектов.
Дополнительно также будем определять центр масс объекта с помощью опции ‘centroid’.
feats=imfeature(L,'Centroid','Extent',8);
Перепишем значения признаков из массива структур feats в отдельные массивы:
Extent=zeros(num);
CentX=zeros(num);
CentY=zeros(num);
for i=1:1:num;
Extent(i)=feats(i).Extent;
CentX(i)=feats(i).Centroid(1);
CentY(i)=feats(i).Centroid(2);
end;
Также в рамках этого примера реализуем следующее. Для наглядности, каждый распознанный объект будет подписан. Для реализации этого возможны различные подходы. Один самых простых – это помещать около распознанного объекта изображение с его названием. Для этого прежде нужно сформировать изображения с названиями объектов и считать их в рабочее пространство Matlab. Поскольку на тестовом изображении присутствуют только круги и квадраты, то сформирует и считаем соответствующие изображения.
Krug=imread('krug.bmp');
Kvadrat=imread('kvadrat.bmp');
d=0.15; % погрешность коэффициента формы
for i=1:num;
L(round(CentY(i)):round(CentY(i))+1,round(CentX(i)):round(CentX(i))+1)=0;
if (abs(Extent(i)-0.7822)<d)==1;
L(round(CentY(i)):round(CentY(i))+24,round(CentX(i)):round(CentX(i))+44)=Krug;
end;
if ( abs(Extent(i)-1)<d)==1;
L(round(CentY(i)):round(CentY(i))+24,round(CentX(i)):round(CentX(i))+44)=Kvadrat;
end;
end;
Представим результат распознавания
figure, imshow(L);
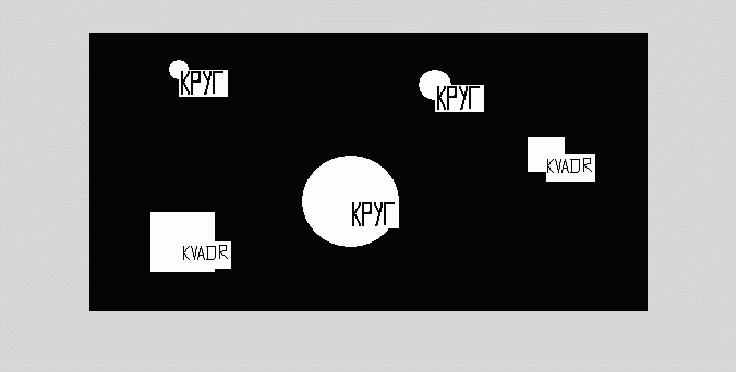
Существуют также другие подходы к распознаванию объектов на основе набора признаков. Они различны по своей вычислительной сложности, эффективности и т.п. Однако, в дальнейших материалах рассмотрим те подходы, которые могут быть реализованы с помощью функций, встроенных в систему Matlab.
Распознавание объектов на основе вычисления коэффициента корреляции
Рассмотрим пример распознавания объектов на изображении с использованием корреляционного подхода. В большинстве случаев, при решении такого рода задач необходимо кроме исходного изображения иметь также изображение объекта, который будет распознаваться. Выберем в качестве исходного следующее изображение:
L=imread('abc.bmp');
и визуализируем его
figure, imshow(L);

Также нам необходимо иметь эталонные изображения объектов (букв), которые необходимо распознать.
L1=imread('a.bmp');
figure, imshow(L1);

L2=imread('b.bmp');
figure, imshow(L2);

L3=imread('c.bmp');
figure, imshow(L3);

Следующий шаг заключается в вычислении коэффициента корреляции между матрицами исходного изображения и соответствующего эталона. Для этого используется функция corr2. При этом следует помнить, что функция corr2 вычисляет коэффициент корреляции между матрицами одинакового размера. Поэтому из большей матрицы исходного изображения будем вырезать части, которые равны матрице эталонного изображения (см. рис.). Далее будем вычислять коэффициент корреляции между каждой частью исходного изображения и каждым эталоном.
Итак, коэффициент корреляции между первым эталоном (буква А) и исходным изображением вычисляется следующим образом.
for p=1:3; L_t=L(:,SH*(p-1)+1:SH*p); k(p)=corr2(L1,L_t); end;
Значения коэффициентов корреляции для первого эталона (буква А) и трех частей исходного изображения представлены на графике
figure, plot(k);
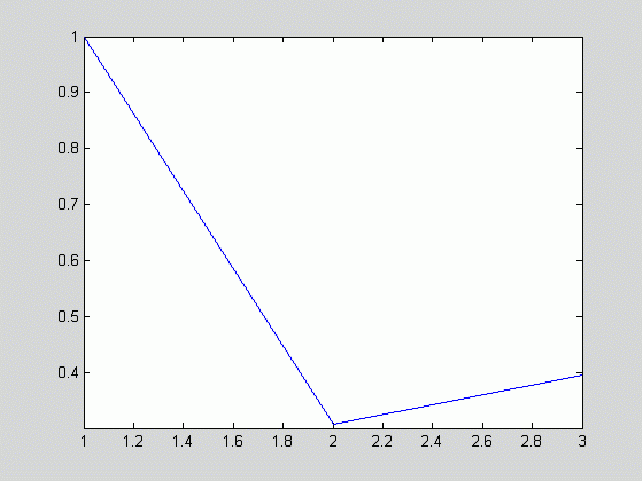
Расположение максимума коэффициента корреляции свидетельствует о том, что эта часть исходного изображения максимально похожа на эталон. Определим, расположение максимального значения коэффициента корреляции.
R=find(k==max(k))
R =
1
Из рисунка видно, максимальное значение корреляции достигается между матрицей первого эталона (буква А) и первой частью исходного изображения, где и размещена буква А.
Аналогичным образом вычисляются коэффициенты корреляции между другими эталонами (вторым и третьим) и исходным изображением.
Графики значений коэффициентов корреляции для второго и третьего эталона приведены на рисунке.
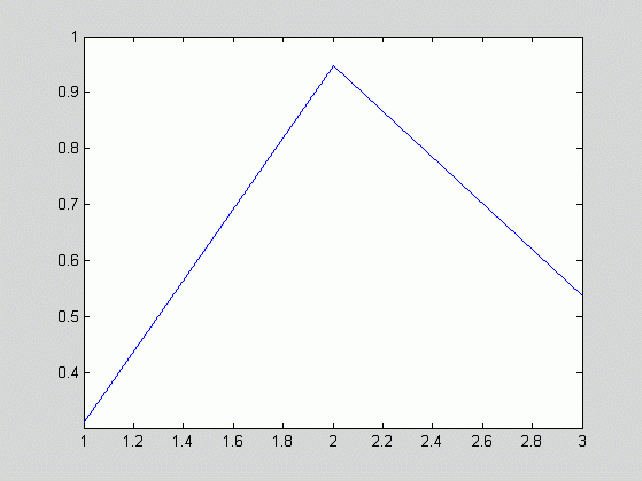
График значений коэффициентов корреляции для второго эталона и трех частей исходного изображения.
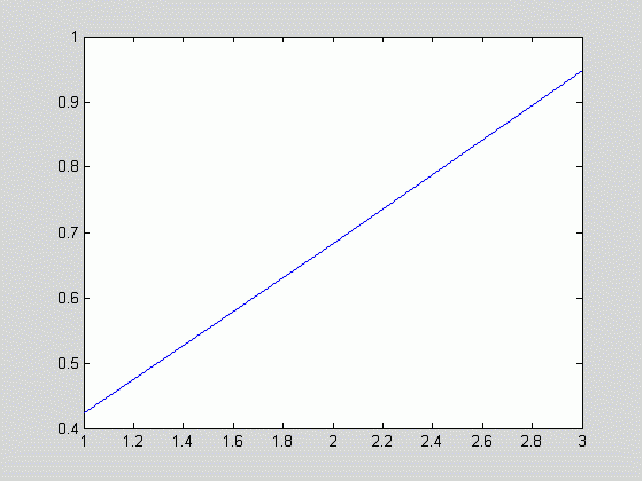
График значений коэффициентов корреляции для третьего эталона и трех частей исходного изображения.
Из двух приведенных выше рисунков видно, что максимального значения коэффициенты корреляции достигают во второй и третьей части изображения. Это соответствует наибольшей схожести, т.е. распознаванию второго эталона и второй части исходного изображения, а также третьего эталона и третьей части исходного изображения.
Таким образом, нами был рассмотрен подход к распознаванию объектов на основе вычисления коэффициента корреляции между матрицами их изображений. Этот подход получил довольно широкое распространение. Однако при распознавании реальных объектов корреляционный метод характеризуется большой вычислительной сложностью. Связано это с масштабированием и поворотами распознаваемого изображения.
Анализ признаков объектов
Ранее уже отмечалось, что каждый объект изображения можно охарактеризовать набором признаков, которые могут служить основой для их анализа и распознавания. В приложении Image Processing Toolbox для вычисления признаков объектов используется функция imfeature.
В данном материале рассмотрим все типы признаков объектов, которые вычисляются с помощью функции imfeature. Условно их можно разбить на пять групп:
- признаки типов изображений объекта;
- признаки размеров объекта;
- признаки определения площади объекта;
- признаки формы объекта;
- другие признаки.
Сначала считаем некоторое исходное изображение, которое будем использовать в наших примерах и визуализируем его.
L=imread('test_image.bmp');
figure, imshow(L);

Исходное изображение
Далее проиллюстрируем разницу между различными типами изображений. Чтобы приступить к выполнению этого задания сначала необходимо выполнить поиск объектов на изображении и вычисление их признаков:
[L num]=bwlabel(L,8);
Сформируем изображение самого объекта
feats=imfeature(L,'Image',8); Image=feats(1).Image; figure, imshow(Image);

Изображение самого объекта
Сформируем изображение с “залитыми” дырами
feats=imfeature(L,'FilledImage',8); FilledImage=feats(1).FilledImage; figure, imshow(FilledImage);
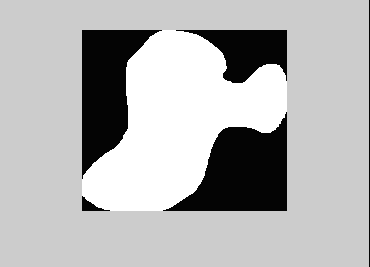
Изображение с “залитыми” дырами
Сформируем изображение “залитого” пикселями объекта выпуклого многоугольника, в который вписан объект:
feats=imfeature(L,'ConvexImage',8); ConvexImage=feats(1).ConvexImage; figure, imshow(ConvexImage);

Изображение “залитого” пикселями объекта выпуклого многоугольника, в который вписан объект
Довольно часто возникает необходимость описания габаритных размеров объекта различными способами. Для этого используются следующие опции – “BoundingBox”, ”ConvexHull”, ”Extrema”,”PixelList”. Рассмотрим использование этих опций на примере нашего исходного изображения.
- Получение координат прямоугольника, ограничивающего объект.
feats=imfeature(L,'BoundingBox',8); feats = BoundingBox: [31.5000 37.5000 205 181]
Результат представлен в виде массива [x y width height] , где (x,y) – координаты левого верхнего угла прямоугольника, width – ширина, height – высота прямоугольника.Используя код
line([BoundingBox (1) BoundingBox (1)+ BoundingBox (3) BoundingBox (1)+ BoundingBox (3) BoundingBox (1) BoundingBox (1)],[ BoundingBox (2) BoundingBox (2) BoundingBox (2)+ BoundingBox (4) BoundingBox (2)+ BoundingBox (4) BoundingBox (2)]);
прямоугольник, который ограничивает объект, для наглядности можно визуализировать.

Прямоугольник, ограничивающий объект - Получение координат выпуклого многоугольника, в который вписан объект. Для этого используется опция “ConvexHull”.
feats=imfeature(L,'ConvexHull',8); ConvexHull=feats.ConvexHull;
Результат представляется в виде матрицы, каждая строка которой содержит (x,y) координаты вершин описанного выше многоугольника.
Для наглядности визуализируем этот многоугольник на основании полученных координат.
line(ConvexHull(:,1),ConvexHull(:,2))

Выпуклый многоугольник, в который вписан объект - Опция “Extrema” позволяет получить экстремальные координаты объекта. Результат представлен матрицей, которая содержит все экстремальные координаты объекта.
feats=imfeature(L,'Extrema',8);
Для наглядности отметим эти точки на изображении.
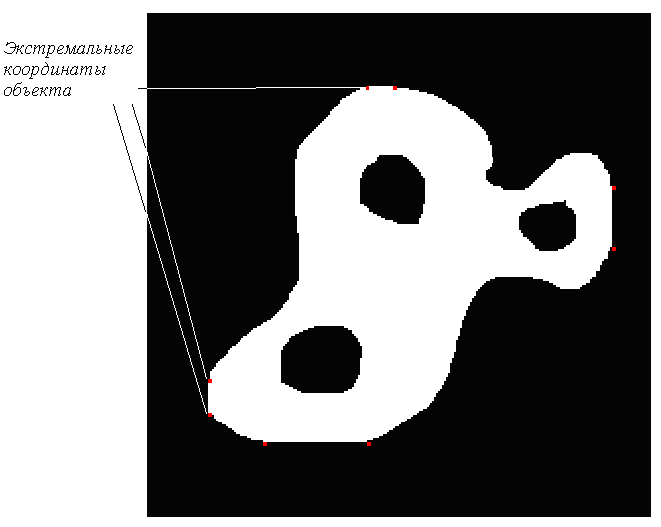
- Для получения списка всех пикселей объекта используется опция “PixelList”.
feats=imfeature(L,'PixelList',8); PixelList=feats.PixelList;
Для того, чтобы убедиться в том, что выбранные пиксели действительно принадлежат объекту, представим их всех серым цветом. Для этого используем следующий код
[q w]=size(PixelList); for i=1:q; L(PixelList(i,2),PixelList(i,1))=0.5; end; figure, imshow(L);
Отметим, что у всех перечисленных выше признаков, координаты приведены в пространственной системе координат. Далее рассмотрим набор опций, которые применяются при оценивании формы или при классификации объектов. Одним из основных признаков в этом случае является площадь. Рассмотрим несколько способов вычисления площади.
- Использование опции “Area” приводит к вычислению площади, числовое значение которой равно количеству пикселей объекта
feats=imfeature(L,'Area',8); Area=feats.Area Area = 17959
- Для вычисления полной площади, числовое значение которой соответствует общему количеству пикселей объекта и пикселей дыр в объекте, что равно также площади изображения FilledImage, используется опция “FilledArea”.
feats=imfeature(L,'FilledArea',8); FilledArea=feats.FilledArea FilledArea = 20670
- Существует возможность вычисления выпуклой площади. Под выпуклой площадью имеется ввиду площадь выпуклого многоугольника, в который вписан объект.
feats=imfeature(L,'ConvexArea',8); ConvexArea=feats.ConvexArea ConvexArea = 25278Эта площадь соответствует площади изображения ConvexImage.
Среди основных морфометрических признаков следует выделить также:
- Центр масс объекта, который определяется с помощью опции “Centroid”. Результат представляется двухэлементным массивом, который содержит координаты центра масс в пространственной системе координат.
feats=imfeature(L,'Centroid',8); Centroid=feats.Centroid Centroid = 128.4878 128.8137
- Эквивалентный диаметр, который определяется с помощью опции “EquivDiameter”.
feats=imfeature(L,'EquivDiameter',8); EquivDiameter=feats.EquivDiameter EquivDiameter = 151.2154
- Длина максимальной оси инерции объекта определяется с помощью опции “MajorAxisLength”.
feats=imfeature(L,'MajorAxisLength',8); MajorAxisLength=feats.MajorAxisLength MajorAxisLength = 223.9145
- Минимальной оси инерции объекта определяется с помощью опции “MinorAxisLength”.
feats=imfeature(L,'MinorAxisLength',8); MinorAxisLength=feats.MinorAxisLength MinorAxisLength = 145.7130
- Для определения ориентации объекта, которая определяется углом (в градусах) между максимальной осью инерции и осью Х, используется опция “Orientation”.
feats=imfeature(L,'Orientation',8); Orientation=feats.Orientation Orientation = 46.1221
- Для вычисления числа Эйлера, которое определяется разницей между числом объектов и числом дыр в них, используется опция “EulerNumber”.
feats=imfeature(L,'EulerNumber',8); EulerNumber=feats.EulerNumber EulerNumber = –2
Далее рассмотрим еще набор коэффициентов, которые необходимы для математического описания формы объекта. Определять числовые значения этих коэффициентов будем для изображений двух объектов – круга и квадрата. Это даст возможность увидеть разницу значений коэффициентов для объектов с различной формой.
Сначала необходимо считать изображения круга и квадрата.
L1=imread('krug.bmp');
figure, imshow(L1);

L2=imread('kv.bmp');
figure, imshow(L2);

Код для вычисления соответствующих коэффициентов формы выглядит следующим образом –
- для вычисления коэффициента выпуклости, который равен отношению площади к выпуклой площади объекта
feats=imfeature(L,'Solidity ',8); Solidity=feats.Solidity
- для вычисления коэффициента заполнения, который равен отношению площади объекта к площади ограничивающего прямоугольника
feats=imfeature(L,'Extent ',8); Extent=feats.Extent
- для вычисления эксцентриситета эллипса с главными моментами инерции, равными главным моментам инерции объекта
feats=imfeature(L,'Eccentricity',8); Eccentricity=feats.Eccentricity
Результаты вычисления различных коэффициентов формы для двух изображений представлены в таблице.
| Коэффициенты формы | Изображение круга | Изображение квадрата |
| ‘Solidity’ | 0.9806 | 1 |
| ‘Extent’ | 0.7800 | 1 |
| ‘Eccentricity’ | 0.0042 | 0.03323 |
Проанализируем представленные выше результаты более детально.
Коэффициент выпуклости (‘Solidity’), который как было сказано выше, равен отношению площади к выпуклой площади объекта. Если объект представлены кругом или квадратом, то значение этого коэффициента принимает значение, которое равно единице. При вычислениях эти значения могут несколько отличаться от единицы, что объясняется ошибками дискретизации при представлении объектов.
Второй параметр (‘Extent’) – коэффициент заполнения – определяется отношением площади объекта к площади ограничивающего прямоугольника. Естественно, что для квадрата этот коэффициент будет равен единице. Для круга этот коэффициент определяется отношением площади круга 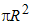 к площади ограничивающего прямоугольника (2R)2, что равно
к площади ограничивающего прямоугольника (2R)2, что равно
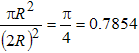 .
.
Как уже отмечалось ранее, при вычислениях коэффициента заполнения для реальных или симулированных объектов (в данном случае круга), его значения могут отличаться от расчетных. Это объясняется ошибками дискретизации, искажениями формы и т.п.
Третий коэффициент формы – эксцентриситет (‘Eccentricity’) – характеризует степень сплюснутости объекта. Определяется он выражением
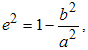
где a – большая полуось орбиты, b – малая полуось орбиты.
Для окружности эксцентриситет равен нулю, для параболы он равен единице.
В таблице результаты несколько отличаются от теоретических, что можно объяснить ошибками дискретного представления объектов.
Пример.
Рассмотрим пример анализа некоторых объектов на медицинском изображении. Для этого считаем и визуализируем исходное изображение.
clear;
L=imread('medimage.jpg');
figure, imshow(L);
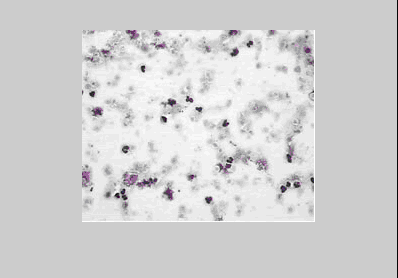
Поскольку функции, которые будут использованы в дальнейшем, работают с полутоновыми и бинарными изображениями, то преобразуем исходное изображение в полутоновое.
L=L(:,:,1); L=double(L)./255; figure, imshow(L);
Это можно сделать также и другим способом – для преобразования полноцветных изображений в полутоновые в системе Matlab существует функция rgb2gray.
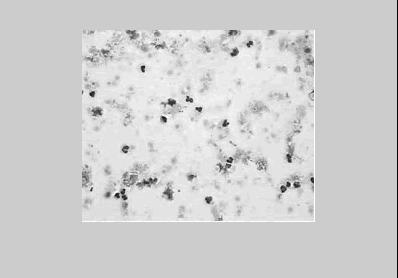
Выделим объекты интереса, которые отображены на полутоновом изображении темным цветом. Для этого будем использовать функцию бинаризации по заданным цветам roicolor. Порог бинаризации лучше выбирать на основе гистограммы полутонового изображения.
imhist(L)
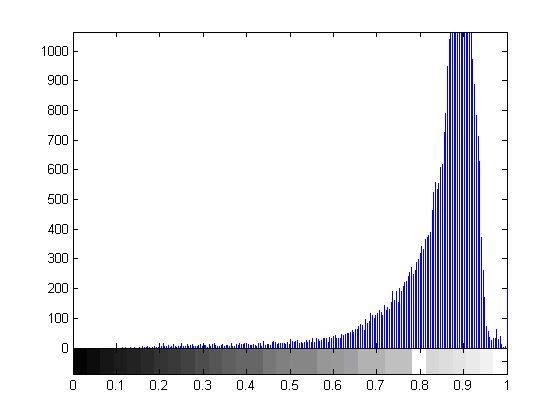
Из гистограммы полутонового изображения видно, что областей с низким уровнем яркости на изображении сравнительно немного и они соответствуют нашим объектам интереса. Поэтому пороговое значение можно выбрать на уровне 0,5 .
BW=roicolor(L,0,.5); figure, imshow(BW);
Результат бинаризации представлен на изображении внизу.

Из полученного изображения видно, что кроме объектов интереса на нем представлены также другие включения. Их необходимо удалить. Ранее уже рассматривались некоторые подходы к решению подобных задач, например, фильтрация. Теперь же решим эту задачу иначе. Сначала вычислим площади всех объектов на изображении.
[BW1 num]=bwlabel(BW,8); feats=imfeature(BW1,'Area',8); Areas=zeros(num); for i=1:num; Areas(i)=feats(i).Area; end;
При дальнейшем анализе будем учитывать только эти объекты, площадь которых больше некоторого порогового уровня.
idx=find(Areas>10); BW=ismember(BW1,idx); figure, imshow(BW);
На результирующем изображении представлены объекты, площадь которых выше указанного порогового уровня, в данном случае, 10 пикселей.

Проанализируем также распределение объектов интереса по площади. Для этого необходимо сначала также выполнить поиск объектов.
[BW1 num]=bwlabel(BW,8);
Далее необходимо вычислить площади объектов
feats=imfeature(BW1,'Area',8);
и построить гистограмму распределения числовых значений площадей объектов.
figure,hist([feats.Area]);
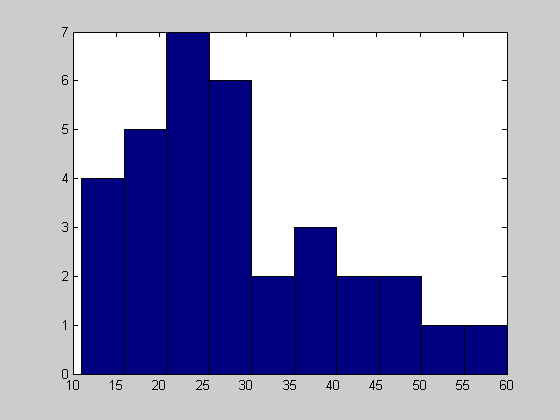
В данном материале рассмотрены возможности системы Matlab по вычислению признаков объектов, которые служат основой для решения задач анализа и распознавания.
Некоторые аспекты задачи распознавания номерных знаков автомобилей
Рассмотрим некоторые вопросы, которые могут возникнуть при решении задачи распознавания номерных знаков автомобилей. Для этого сформируем исходное изображение и считаем его в рабочее пространство MATLAB.
I=imread('inputimage.bmp');
figure,imshow(I);
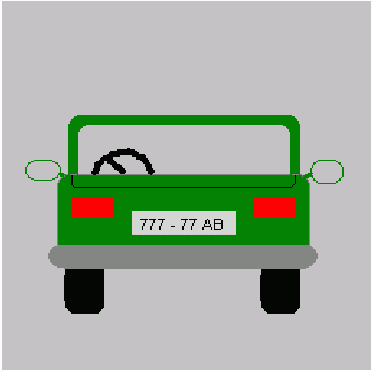
Для упрощения дальнейших расчетов и программной реализации преобразуем полноцветное исходное изображений в полутоновое. Существует много методов перехода от полноцветного изображения к полутоновому. В системе MATLAB есть функция rgb2gray, которая реализует это преобразование.
I=rgb2gray(I); figure, imshow(I);
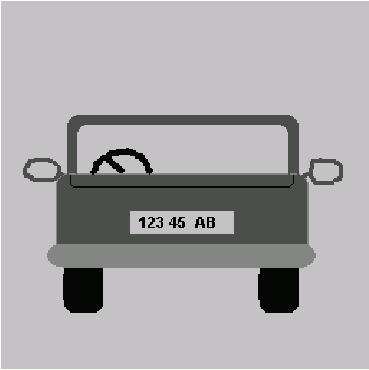
Одним из недостатков функции rgb2gray является то, что она не всегда корректно выполняет преобразование полноцветного изображения в полутоновое. Например, на полутоновом изображении, в отличие от полноцветного, отсутствуют фары красного цвета. В данном случае это не является принципиальным, поскольку для нас важно как обрабатывается изображение номера, но все же для корректности будем использовать другой подход.
I=I(:,:,1); I=rgb2gray(I);
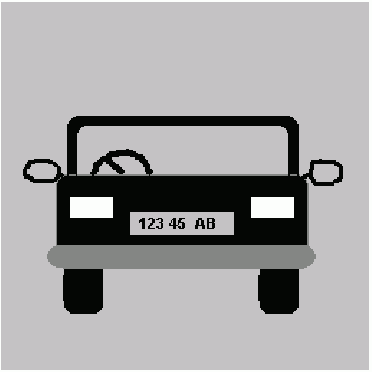
Это изображение обработано более корректно, поскольку не было утеряно никаких деталей на изображении.
Теперь, как и при решении большинства других задач, необходимо провести предварительную обработку исходных изображений. Этот этап особенно важен при решении задач распознавания. От качества решения этапа предварительной обработки во многом будет зависеть эффективность решения задачи распознавания в целом.
К наиболее распространенным дефектам, которые могут присутствовать на исходных изображениях, относятся шум и низкий уровень контрастности. Продемонстрируем некоторые способы подавления шума и повышения контрастности исходных изображений с помощью встроенных функций MATLAB. Для этого сформируем сначала исходное изображение с наличием шума. В качестве примера рассмотрим импульсный шум.
I=imnoise(I,'salt & pepper', 0.005); figure, imshow(I);

Для устранения импульсных выбросов используем медианную фильтрацию, которую выполним с помощью функции median.
for i=1:N;
for j=1:M-2;
I(i,j)=median(median(I(i,j:j+2)));
end;
end;
figure, imshow(I);
Результат обработки представлен на изображении внизу.
Рассмотрим пример повышения контрастности исходного изображения. Для демонстрации этого примера сформируем размытое изображение.
Используем функцию imfilter для повышения контрастности размытого изображения.
h = fspecial('unsharp')
h =
-0.1667 -0.6667 -0.1667
-0.6667 4.3333 -0.6667
-0.1667 -0.6667 -0.1667
I = imfilter(I,h);
figure, imshow(I);
После проведения предварительной обработки приступаем к определению расположения номерных знаков изображения. Для этого сначала необходимо определить общее количество объектов на изображении.
[L num]=bwlabel(L,8);
Таким образом, определены все объекты, которые размещены на изображении. После этого приступаем к вычислению признаков этих объектов.
feats=imfeature(L,'Centroid','Extent',8);
Extent=zeros(num);
CentX=zeros(num);
CentY=zeros(num);
for i=1:1:num;
Extent(i)=feats(i).Extent;
CentX(i)=feats(i).Centroid(1);
CentY(i)=feats(i).Centroid(2);
end;
Приведем результаты вычислений некоторых признаков для всех объектов изображения. В качестве примера был выбран коэффициент заполнения, который равен отношению площади объекта к площади ограничивающего прямоугольника.
Extent =
0.7328 0 0 0 0 0 0 0 0 0 0 0 0
0.8268 0 0 0 0 0 0 0 0 0 0 0 0
1.0000 0 0 0 0 0 0 0 0 0 0 0 0
1.0000 0 0 0 0 0 0 0 0 0 0 0 0
0.8752 0 0 0 0 0 0 0 0 0 0 0 0
0.5959 0 0 0 0 0 0 0 0 0 0 0 0
0.8325 0 0 0 0 0 0 0 0 0 0 0 0
1.0000 0 0 0 0 0 0 0 0 0 0 0 0
1.0000 0 0 0 0 0 0 0 0 0 0 0 0
1.0000 0 0 0 0 0 0 0 0 0 0 0 0
1.0000 0 0 0 0 0 0 0 0 0 0 0 0
1.0000 0 0 0 0 0 0 0 0 0 0 0 0
0.9028 0 0 0 0 0 0 0 0 0 0 0 0
Для объекта, который представляет изображение номерного знака, параметр “Extent” будет равен заранее известному числу. Поскольку соотношение сторон номерных постоянно, то этот параметр также будет постоянным. Вероятность присутствия на изображении объекта, который описывался бы тем же значением параметра “Extent”, небольшая. Но для повышения достоверности локализации можно использовать еще и другие параметры.
Таким образом, зная числовое значение параметра “Extent”, можно определить номер объекта интереса. Путь это значение будет равно 0,8325. Этому значению соответствуют координаты (7, 1). Зная эти координаты, из CentX и CentY можно определить координаты расположения номерных знаков на изображении.
CentX = 129.1411 0 0 0 0 0 0 0 0 0 0 0 0 29.4241 0 0 0 0 0 0 0 0 0 0 0 0 50.0000 0 0 0 0 0 0 0 0 0 0 0 0 63.5000 0 0 0 0 0 0 0 0 0 0 0 0 132.8050 0 0 0 0 0 0 0 0 0 0 0 0 85.6120 0 0 0 0 0 0 0 0 0 0 0 0 126.6611 0 0 0 0 0 0 0 0 0 0 0 0 139.0000 0 0 0 0 0 0 0 0 0 0 0 0 146.5000 0 0 0 0 0 0 0 0 0 0 0 0 146.5000 0 0 0 0 0 0 0 0 0 0 0 0 189.5000 0 0 0 0 0 0 0 0 0 0 0 0 204.0000 0 0 0 0 0 0 0 0 0 0 0 0 226.4205 0 0 0 0 0 0 0 0 0 0 0 0 CentY = 127.0666 0 0 0 0 0 0 0 0 0 0 0 0 118.2042 0 0 0 0 0 0 0 0 0 0 0 0 121.0000 0 0 0 0 0 0 0 0 0 0 0 0 143.5000 0 0 0 0 0 0 0 0 0 0 0 0 102.7486 0 0 0 0 0 0 0 0 0 0 0 0 115.7129 0 0 0 0 0 0 0 0 0 0 0 0 154.4911 0 0 0 0 0 0 0 0 0 0 0 0 154.0000 0 0 0 0 0 0 0 0 0 0 0 0 152.5000 0 0 0 0 0 0 0 0 0 0 0 0 156.0000 0 0 0 0 0 0 0 0 0 0 0 0 143.5000 0 0 0 0 0 0 0 0 0 0 0 0 121.0000 0 0 0 0 0 0 0 0 0 0 0 0 119.3692 0 0 0 0 0 0 0 0 0 0 0 0
Таким образом, координаты размещения центра масс интересующего нас объекта, т.е. номерных знаков, равны
CentX(7,1) ans = 126.6611 CentY(7,1) ans = 154.4911
Выделим изображение номерного знака на изображении.
Для этого необходимо заранее знать значение Extent, которое свойственно изображению номерного знака. Как было сказано выше, это значение будет постоянно, поскольку форма номерного знака не изменяется и равно 0.8325.
[x y]=find(Extent==0.8325);
Таким образом, можно определить координаты центра масс объекта, т.е. номерного знака, изображению которого свойственно значение Extent = 0,8325 . После этого локализируем изображение номерного знака.
xi=round(CentX(x,y)); yj=round(CentY(x,y));
Известно, что после использования выражения [L num]=bwlabel(L,8), каждый объект на изображении L будет отображаться одинаковым значением яркости L(yj,xi). Однако локализация изображения номерного знака по яркости только одного элемента L(yj,xi) не всегда дает хороший результат. Дело в том, что на изображении номерного знака присутствуют также другие объекты, например, цифры и буквы, которые будут обозначены другим, отличным от L(yj,xi), значением яркости. Поэтому для повышения достоверности локализации изображения номерного знака вместо одного значения L(yj,xi), целесообразно использовать также и несколько окрестных элементов [L(yj,xi), L(yj+6,xi), L(yj-6,xi)].
for i=1:N;
disp(i);
for j=1:M;
if L(i,j)==median([L(yj,xi),L(yj+6,xi),L(yj-6,xi)]);
L(i,j)=ORIG(i,j);
else
L(i,j)=0;
end;
end;
end;
figure, imshow(L);

После локализации номерных знаков на изображении, можно приступить к их распознаванию.
Существуют различные подходы к решению задачи распознавания объектов. Некоторые из них рассмотрены в материалах "Распознавание объектов на основе вычисления их признаков", "Распознавание объектов на основе вычисления коэффициента корреляции".
Анализ серии изображений с распределенной обработкой данных
Существуют задачи, при решении которых необходимо обрабатывать серию изображений. При этом изображения хранятся в различных графических файлах. Такие ситуации, например, могут возникать, когда через некоторые промежутки времени формируются изображения, которые фиксируют состояние некоторого динамического процесса.
При рассмотрении данного примера обработки серии изображений будет использоваться приложение Distributed Computing Toolbox. Рассмотрим основные этапы решения этой задачи:
- Формирование названий файлов, которые подлежат обработке.
- Определение алгоритмов, которые будут использоваться при обработке серии изображений.
- Доступ к Job Manager.
- Определение исполняющих функций.
- Формирование переменной Job для Job Manager.
- Формирование задач для Job.
- Формирование результата.
- Отображение результата.
Формирование названий файлов, которые подлежат обработке
Опишем путь к папке, которая содержит изображения, и далее используем эту информацию при создании списка названий файлов. В нашем примере графические файлы представляют собой 10 биомедицинских изображений клеток ткани. Эти файлы представляют собой только первые 10 из 100 захваченных изображений.
fileFolder = fullfile(matlabroot,'toolbox','images','imdemos');
dirOutput = dir(fullfile(fileFolder,'AT3_1m4_*.tif'));
fileNames = {dirOutput.name}'
fileNames =
'AT3_1m4_01.tif'
'AT3_1m4_02.tif'
'AT3_1m4_03.tif'
'AT3_1m4_04.tif'
'AT3_1m4_05.tif'
'AT3_1m4_06.tif'
'AT3_1m4_07.tif'
'AT3_1m4_08.tif'
'AT3_1m4_09.tif'
'AT3_1m4_10.tif'
Визуализируем одно из этих изображений.
I = imread(fileNames{1});
imshow(I);
text(size(I,2),size(I,1)+15, ...
'Image files courtesy of Alan Partin', ...
'FontSize',7,'HorizontalAlignment','right');
text(size(I,2),size(I,1)+25, ....
'Johns Hopkins University', ...
'FontSize',7,'HorizontalAlignment','right');
Определение алгоритмов, которые будут использоваться при обработке серии изображений
Сформируем функцию обработки изображений, которая будет локализировать отдельные клетки на биомедицинских изображениях. Эта функция размещена в директории fileFolder. Протестируем ее на одном из изображений.
segmentedCells = ipexbatchDetectCells(I); figure, imshow(segmentedCells);
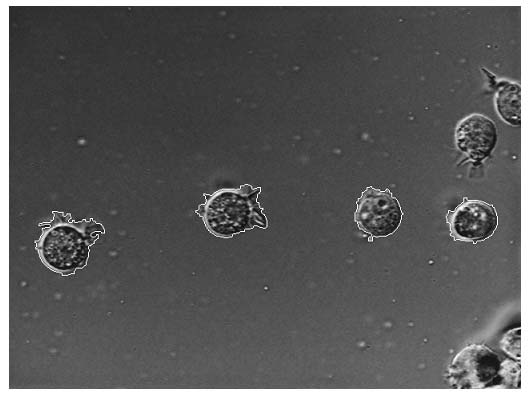
Для просмотра ipexbatchDetectCells используем:
detectCellsPath = fullfile(matlabroot,'toolbox','images','imdemos', ...
'ipexbatchDetectCells.m');
type(detectCellsPath);
function segmentedCells = ipexbatchDetectCells(I)
%ipexbatchDetectCells Algorithm to detect cells in image.
% segmentedCells = ipexbatchDetectCells(I) detects cells in the cell
% image I and returns the result in segmentedCells.
%
% Supports batch processing demo, ipexbatch.m,
% ("Batch Processing of Image Files Using Distributed Computing").
% Copyright 2005 The MathWorks, Inc.
% $Revision: 1.1.6.3 $ $Date: 2006/06/15 20:09:42 $
% Use |edge| and the Sobel operator to calculate the threshold
% value. Tune the threshold value and use |edge| again to obtain a
% binary mask that contains the segmented cell.
[junk threshold] = edge(I, 'sobel');
fudgeFactor = .5;
BW = edge(I,'sobel', threshold * fudgeFactor);
se90 = strel('line', 3, 90);
se0 = strel('line', 3, 0);
BWdilate = imdilate(BW, [se90 se0]);
BWnobord = imclearborder(BWdilate, 4);
BWopen = bwareaopen(BWnobord,200);
BWclose = bwmorph(BWopen,'close');
BWfill = imfill(BWclose, 'holes');
BWoutline = bwperim(BWfill);
segmentedCells = I;
segmentedCells(BWoutline) = 255;
Доступ к Job Manager
Job Manager является составляющей приложения Distributed Computing, которая координирует выполнение работ по распределению конкретных задач.
if ~exist('jobManagerName','var')
jobManagerName = 'default_jobmanager';
end
jobManager = findResource('jobmanager','Name', jobManagerName);
if numel(jobManager) > 1
msg1 = sprintf('Found more than one job manager. Picking the first one');
msg2 = sprintf('\nlocated on host %s. ', get(jobManager(1),'Hostname'));
msg3 = 'Make sure that its workers can access the ';
msg4 = sprintf('directory:\n%s.',fileFolder);
warning('%s%s%s%s', msg1, msg2, msg3, msg4);
jobManager = jobManager(1);
end
Определение исполняющих функций
Функция анализа изображений ipexbatchDetectCells предназначена для доступа к данным изображения в качестве исходных данных и возвращения модифицированного изображения в качестве результата. Однако отметим, что приложение Distributed Computing Toolbox оперирует не с данными изображения, а с названиями файлов изображений:
data = ipexbatchProcessFile(fileNames{1});
Для просмотра ipexbatchProcessFile, используем:
processFilePath = fullfile(matlabroot,'toolbox','images','imdemos', ...
'ipexbatchProcessFile.m');
type(processFilePath);
function data = ipexbatchProcessFile(imageFile)
%ipexbatchProcessFile Algorithm used to process image file.
% DATA = ipexbatchProcessFile(FILENAME) processes image file FILENAME and
% returns the result in DATA.
%
% Supports batch processing demo, ipexbatch.m,
% ("Batch Processing of Image Files Using Distributed Computing").
% Copyright 2005 The MathWorks, Inc.
% $Revision: 1.1.6.3 $ $Date: 2006/06/15 20:09:42 $
imageFilePath = fullfile(matlabroot,'toolbox','images','imdemos',imageFile);
I = imread(imageFilePath);
data.Filename = imageFilePath;
data.Original = I;
data.Final = ipexbatchDetectCells(I);
Формирование переменной Job для Job Manager
После формирования job manager (функция управления заданиями) необходимо приступить к формированию переменной job для jobManager.
job = createJob(jobManager, 'FileDependencies', ...
{processFilePath,detectCellsPath});
get(job)
Name: 'job_70'
ID: 70
UserName: 'isimon'
Tag: ''
State: 'pending'
RestartWorker: 0
Timeout: Inf
MaximumNumberOfWorkers: 2.1475e+009
MinimumNumberOfWorkers: 1
CreateTime: 'Tue Jun 07 18:05:24 EDT 2005'
SubmitTime: ''
StartTime: ''
FinishTime: ''
Tasks: [0x1 double]
FileDependencies: {2x1 cell}
JobData: []
Parent: [1x1 distcomp.jobmanager]
UserData: []
QueuedFcn: []
RunningFcn: []
FinishedFcn: []
Формирование задач для Job
numFcnOutputArgs = 1;
for k = 1:length(fileNames)
task(k) = createTask(job, @ipexbatchProcessFile, numFcnOutputArgs, ...
{fileNames{k}});
end
firstTaskState = get(task(1),'State')
firstTaskState =
pending
submit(job)
firstTaskState = get(task(1),'State')
firstTaskState =
pending
Формирование результата
После определения всех процедур до окончания обработки пользователь может:
- продолжать работать в системе MATLAB и периодически контролировать процесс обработки;
- получить результат обработки после окончания вычислений. Выберем вторую опцию –waitForState.
waitForState(job) firstTaskState = get(task(1),'State') firstTaskState = finished
В нашем примере анализируется только 10 изображений, поэтому результаты обработки всех 10 задач считываются в рабочее пространство MATLAB с использованием getAllOutputArguments. results = getAllOutputArguments(job);
Отображение результата
figure
for k = 1:length(results)
imshow(results{k}.Original);
pause(1);
imshow(results{k}.Final);
pause(1);
end
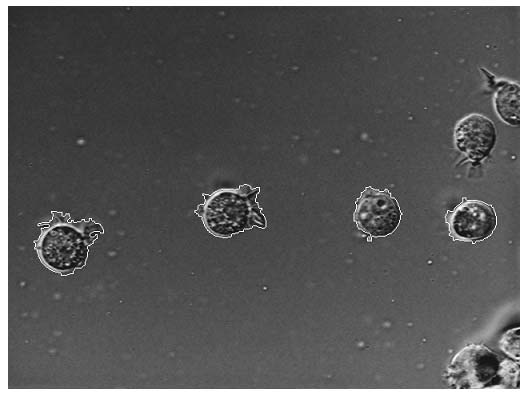
Основное преимущество распределенных вычислений проявляется при обработке серии файлов изображений. Состоит это преимущество в поиске компромисса между скоростью вычислений и загруженностью памяти вычислительной машины.
При решении такого рода задач, т.е. при наличии последовательно захваченных кадров изображений, интересно будет представить эту серию в виде видеопоследовательности. Для этого допустим, что исходные данные представлены серией изображений I1,I2,...I10.
Считаем их из соответствующих файлов в рабочее пространство MATLAB.
I1=imread('I1.bmp');
I2=imread('I2.bmp');
I3=imread('I3.bmp');
I4=imread('I4.bmp');
I5=imread('I5.bmp');
I6=imread('I6.bmp');
I7=imread('I7.bmp');
I8=imread('I8.bmp');
I9=imread('I9.bmp');
I10=imread('I10.bmp');
Далее выполним преобразование полноцветных изображений в палитровые. У всех кадров формируемой видеопоследовательности должна быть одинаковая палитра, поэтому первое изображение преобразовываем с подбором оптимальной палитры map и применяем эту палитру к остальным изображениям.
[I1, map]=rgb2ind(I1,200); [I2]=rgb2ind(I2,map); [I3]=rgb2ind(I3,map); [I4]=rgb2ind(I4,map); [I5]=rgb2ind(I5,map); [I6]=rgb2ind(I6,map); [I7]=rgb2ind(I7,map); [I8]=rgb2ind(I8,map); [I9]=rgb2ind(I9,map); [I10]=rgb2ind(I10,map);
Формируем многокадровое палитровое изображение.
II=cat(4,I1,I2,I3,I4,I5,I6,I7,I8,I9,I10);
Формируем матрицу видеопоследовательности.
II_mov=immovie(II,map);
Выводим 5 раз видеопоследовательность на экран с частотой 10 кадров в секунду.
movie(II_mov,5,10);
В системе MATLAB существуют также другие подходы к визуализации серии изображений. Для этого можно, например, использовать функцию вывода на экран всех кадров многокадрового изображения montage
montage(II);

Сглаживание цветных изображений
В предыдущих материалах говорилось, что большинство методов обработки цветных изображений можно условно разделить на две группы. Согласно первому подходу обработке подлежат отдельные значения пикселей одной или всех цветовых составляющих. Во втором подходе составляющие цвета обрабатываются как единое целое. В некоторых случаях эти методы дают одинаковый результат.
Рассмотрим метод сглаживания цветных изображений.
Линейные пространственные фильтры для сглаживания изображений строятся функцией fspecial с использованием трех опций – ‘average’, ’disc’ и ‘gaussian’. После генерации фильтра, выполняется непосредственная процедура фильтрации с помощью функции imfilter.
Процесс сглаживания некоторого цветного rgb-изображения I состоит из трех основных шагов:
- Считаем исходное изображение и визуализируем его:
I=imread(‘westconcordaerial.bmp’); figure, imshow(I);

Выделим отдельные цветовые компоненты изображения:
IR=I(:,:,1); figure, imshow(IR);

IG=I(:,:,2); figure, imshow(IG);

IB=I(:,:,1); figure, imshow(IB);

- С помощью функции fspecial сформируем некоторый сглаживающий фильтр f.
f=fspecial(‘average’,15);
Далее проведем сглаживание каждой цветовой компоненты отдельно с помощью функции
imfilter с опцией ‘replicate’. IR_filtered=imfilter(IR,f,‘replicate’); figure, imshow(IR_filtered);

IG_filtered=imfilter(IG,f,‘replicate’); figure, imshow(IG_filtered);

IB_filtered=imfilter(IB,f,‘replicate’); figure, imshow(IB_filtered);

- Теперь из сглаженных цветовых компонент необходимо реконструировать обработанное rgb-изображение.
I_filtered=cat(3, IR_filtered, IG_filtered, IB_filtered); figure, imshow(I_filtered);

Однако описанную операцию сглаживания rgb-изображения можно проделать и без разложения на цветовые составляющие.
I_filtered=imfilter(I,f); figure, imshow(I_filtered);

Рассмотрим пример сглаживания этого же исходного изображений в цветовой системе HSV
- Преобразуем исходное изображение в цветовую систему HSV.
I=rgb2hsv(I);
- Разделим исходное изображение I, которое представлено в цветовой системе HSV, на отдельные цветовые составляющие.
H=I(:,:,1);S=I(:,:,2);V=I(:,:,3);
- Будем использовать то же фильтр, чтобы увидеть разницу между сглаживанием в пространстве RGB и сглаживанием только компоненты интенсивности V, которая получена при конвертации изображения в цветовое пространство HSV.
f=fspecial('average',15); V_filtered=imfilter(V,f,'replicate'); I=cat(3, H,S,V_filtered); I=hsv2rgb(I); figure, imshow(I);

Из приведенных выше изображений видно, что результаты фильтрации изображений, которые представлены в цветовых системах RGB и HSV, существенно различаются. Причина, возможно, в том, что компоненты цветового фона и насыщенности не изменялись, а компоненты интенсивности были существенно сглажены. Для того, чтобы убедиться в этом, реализуем сглаживание по всех цветовых компонентам.
V_filtered=imfilter(V,f,'replicate'); H_filtered=imfilter(H,f,'replicate'); S_filtered=imfilter(S,f,'replicate'); I=cat(3, H_filtered,S_filtered,V_filtered); I=hsv2rgb(I); figure, imshow(I);
Представим результат преобразования.
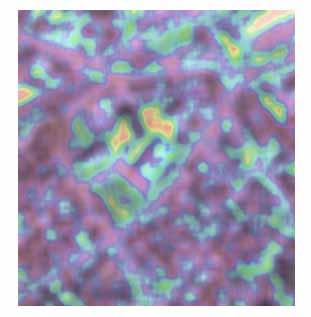
Как видно из представленного изображения, сглаживание всех цветовых компонент изображения, которое представлено в пространстве HSV, не является корректным.
На основе проведенных экспериментов можно сделать вывод, что результаты сглаживания изображения, которое представлено в цветовых системах RGB и HSV, существенно отличаются. Степень этого различия зависит от размера сглаживающей маски.
Построение гистограмм
Гистограмма распределения интенсивностей пикселей является одной из наиболее важных характеристик изображения. Именно гистограмма, в некоторых случаях, может служить основой для выбора того или иного метода обработки изображения.
Поэтому в данной работе рассмотрим методы построения гистограмм с использованием функций Matlab. Для этого сначала считаем и визуализируем исходное изображение.
I=imread('pout.tif');
figure, imshow(I);
title('Исходное изображение')

Исходное изображение
Один из наиболее простых и распространенных способов построения гистограммы H изображения состоит в использовании функции imhist. Синтаксис использования функции imhist следующий:
H=imhist(InputImage,b), где InputImage – исходное изображение; b – количество отсчетов.
Параметр b является необязательным. По умолчанию параметр b равен 256. Рассмотрим два примера построения гистограммы без указания и с указанием числа отсчетов.
%=======Построение гистограммы с помощью функции imhist без указания
%=======количества отсчетов
figure,imhist(I);
title('Гистограмма исходного изображения (использование функции imhist без указания числа отсчетов)')
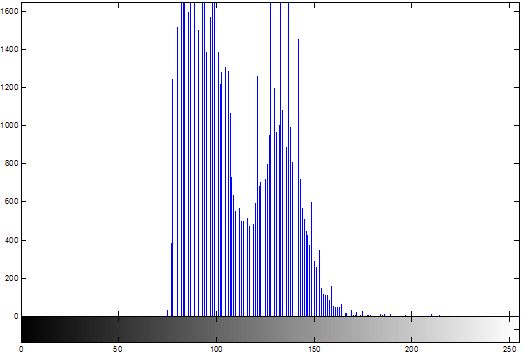
Гистограмма исходного изображения (использование функции imhist с указанием числа отсчетов)
%=======Построение гистограммы с помощью функции imhist с указанием числа
%=======отсчетов t
t=64;
figure,imhist(I,t);
title('Гистограмма исходного изображения (использование функции imhist с указанием числа отсчетов)')
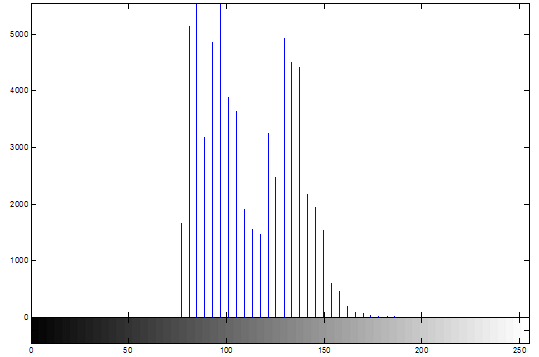
Гистограмма исходного изображения (использование функции imhist с указанием числа отсчетов
Конечно, функция imhist наиболее часто используется, но в системе Matlab существуют также другие средства, с помощью которых можно построить гистограмму изображения.
С помощью функции bar можно построить так называемую столбчатую диаграмму. Синтаксис использования этой функции следующий:
bar(horz,I,width),
где I – исходное изображение; horz – вектор приращений по горизонтальной шкале; width – параметр, управляющий толщиной столбиков гистограммы.
%Построение столбчатой гистограммы
h=imhist(I);
h1=h(1:5:256);
horz=1:5:256;
figure, bar(horz,h1);
title('Столбчатая гистограмма')
axis([0 255 0 2000]);
set(gca,'xtick',0:50:255)
set(gca,'ytick',0:200:2000)
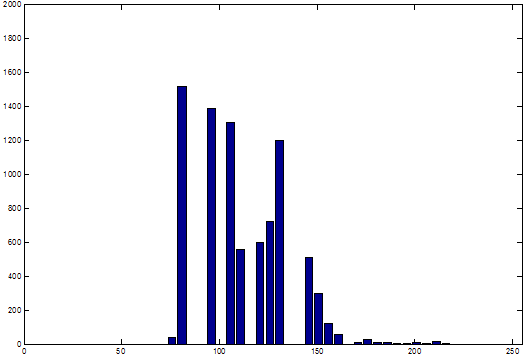
Столбчатая гистограмма
Так называемая стеблевая гистограмма строится аналогично столбчатой гистограмме.
%=========Стеблевая гистограмма================================
h=imhist(I);
h1=h(1:5:256);
horz=1:5:256;
figure, stem(horz,h1,'fill');
title('Стеблевая гистограмма')
axis([0 255 0 2000]);
set(gca,'xtick',0:50:255)
set(gca,'ytick',0:200:2000)
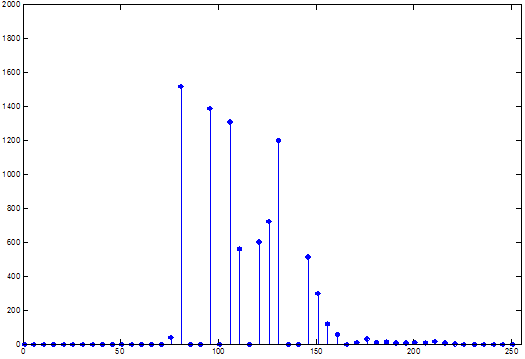
Стеблевая гистограмма
Также гистограмму изображения можно построить с помощью функции plot. Эта функция строит график по точкам, соединяя их отрезками прямых линий.
%========Использование функции plot===========================
h=imhist(I);
figure, plot(h);
title('Использование функции plot для построения гистограммы')
axis([0 255 0 2000]);
set(gca,'xtick',0:50:255)
set(gca,'ytick',0:200:2000)
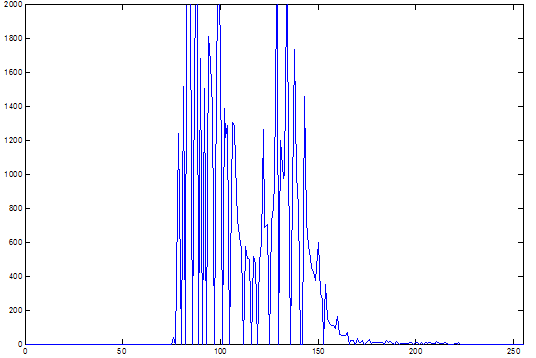
Использование функции plot для построения гистограммы
В приведенных нами примерах масштабирование осей координат на графиках производилось вручную. Однако это можно делать и автоматически с использованием следующих функций
ylim('auto')
xlim('auto')
%================ПРОГРАММА ПОСТРОЕНИЯ ГИСТОГРАММЫ ИЗОБРАЖЕНИЙ================
==================С ИСПОЛЬЗОВАНИЕМ РАЗЛИЧНЫХ ФУНКЦИЙ===========================
clear;
I=imread('pout.tif');
%=======Визуализация исходного изображения================
figure, imshow(I);
title('Исходное изображение')
%=======Построение гистограммы с помощью функции imhist без указания
%количества отсчетов
figure,imhist(I);
title('Гистограмма исходного изображения (использование функции imhist без указания числа отсчетов)')
%=======Построение гистограммы с помощью функции imhist с указанием числа отсчетов t
t=64;
figure,imhist(I,t);
title('Гистограмма исходного изображения (использование функции imhist с указанием числа отсчетов)')
%=======Столбчатая гистограмма==================
h=imhist(I);
h1=h(1:5:256);
horz=1:5:256;
figure, bar(horz,h1);
title('Столбчатая гистограмма')
axis([0 255 0 2000]);
set(gca,'xtick',0:50:255)
set(gca,'ytick',0:200:2000)
%=========Стеблевая гистограмма================================
h=imhist(I);
h1=h(1:5:256);
horz=1:5:256;
figure, stem(horz,h1,'fill');
title('Стеблевая гистограмма')
axis([0 255 0 2000]);
set(gca,'xtick',0:50:255)
set(gca,'ytick',0:200:2000)
%========Использование функции plot===========================
h=imhist(I);
figure, plot(h);
title('Использование функции plot для построения гистограммы')
axis([0 255 0 2000]);
set(gca,'xtick',0:50:255)
set(gca,'ytick',0:200:2000)
Видоизменение гистограмм
Как уже отмечалось выше, гистограмма является одной из наиболее информативных характеристик изображения. Одной из наиболее известных операций, которые проводятся с гистограммой изображения, является эквализация. Ее суть состоит в выравнивании гистограммы, т.е. проведении таких преобразований, чтобы на изображении в равных количествах присутствовали пиксели с различными значениями из заданного динамического диапазона интенсивностей.
Однако, такие преобразования не всегда эффективны. Результат таких преобразований зависит от гистограммы исходного изображения. Довольно часто изображения владеют высоким качеством визуального восприятия, но при этом их гистограмма не является равномерной. Поэтому в данной работе рассмотрим задачу преобразования формы гистограммы изображения к заданному виду.
Сначала сформируем несколько гистограмм с различной формой.
%Равномерный закон распределения гистограммы
H1=256.*ones(1,256);
figure,plot(H1);
title('Равномерная гистограмма');
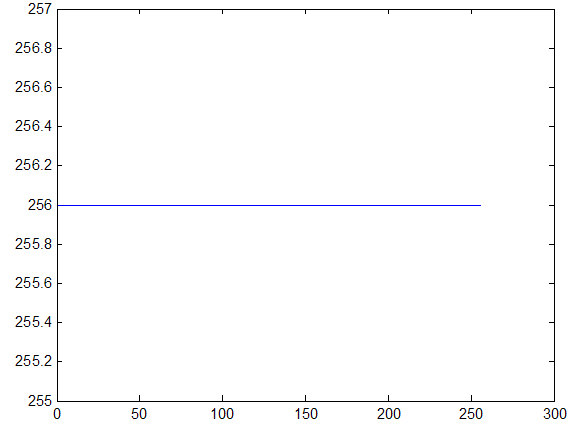
Равномерная гистограмма
%Треугольный закон распределения гистограммы
H2=[512:-2:2];
figure,plot(H2);
title('Треугольная гистограмма');
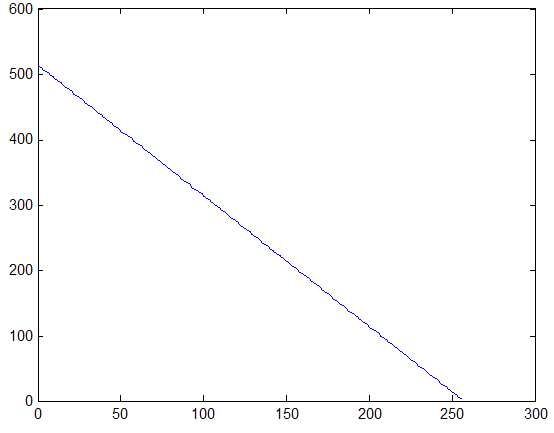
Треугольная гистограмма
%Пилообразный закон распределения гистограммы
H31=[4:4:508];
H32=[512:-4:0];
H3=[H31,H32];
H3=H3(:);
H3=H3';
figure,plot(H3);
title('Пилообразная гистограмма');
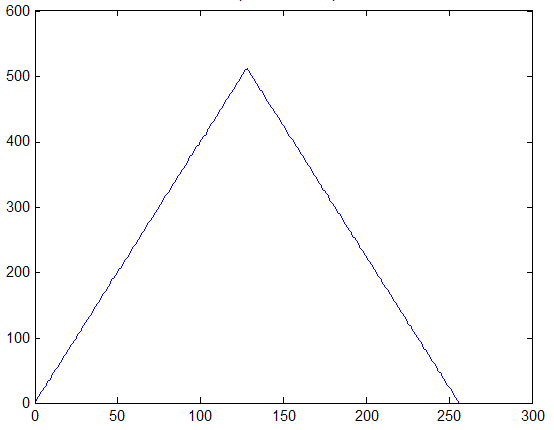
Пилообразная гистограмма
%Экспоненциальный закон распределения гистограммы
H4=260.75*(-log(1:255)+5.5413);
figure,plot(H4);
title('Экспоненциальная гистограмма');
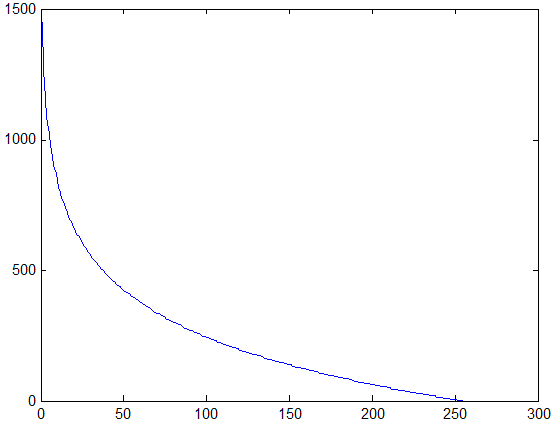
Экспоненциальная гистограмма
%Синусно-экспоненциальный закон распределения гистограммы
x=[0:255];
H5=7000.*exp(-x/85).*abs(cos(pi/2-pi*(x+15)/45));
figure,plot(H5);
title('Синусно-экспоненциальная гистограмма');
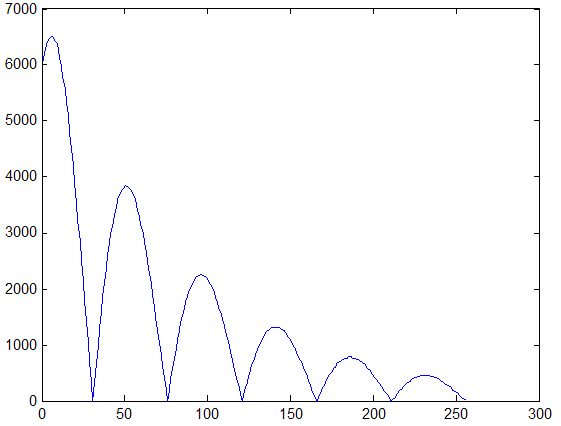
Синусно-экспоненциальная гистограмма
%Нормальный закон распределения гистограммы
x=[0:255];
H6=65536.*(1/((127.5/3)*sqrt(2*pi))).*exp(-((x-127.5).^2)/(2*((127.5/3)^2)));
H6=round(H6);
figure,plot(H6);
title('Нормальный закон распределения гистограммы');
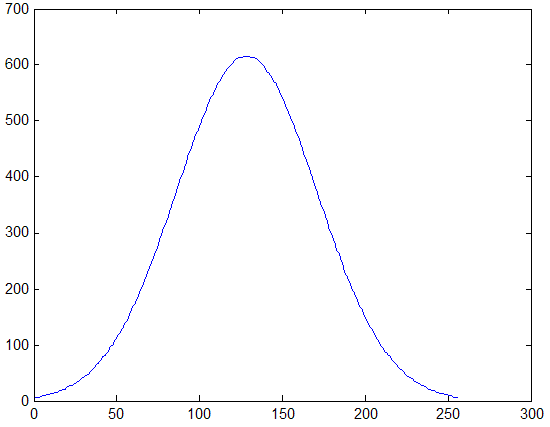
Нормальный закон распределения гистограммы
Теперь считаем некоторое исходное изображение и визуализируем его.
L=imread('liftingbody.png');
figure, subplot(221);
imshow(L);
title('Исходное изображение');

Исходное изображение
Следующие эксперименты будут заключаться в преобразовании изображения к такому виду, чтобы его гистограмма приняла желаемую форму. Для этого будем использовать следующий код:
Lvyh=histeq(L,H2);
где L – матрица интенсивностей исходного изображения; Lvyh – матрица интенсивностей результирующего изображения; H2 – желаемая гистограмма.
- Равномерная гистограмма.
 Исходное изображение |
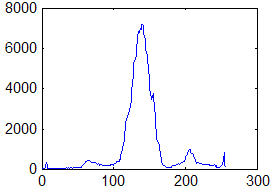 Гисторамма исходного изображения |
 Результирующие изображение |
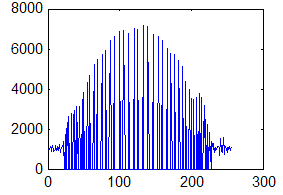 Гисторамма преобразованного изображения |
- Треугольная гистограмма.
 Исходное изображение |
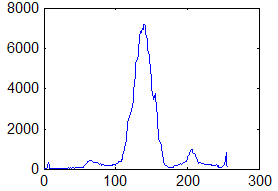 Гисторамма исходного изображения |
 Результирующие изображение |
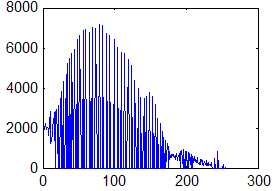 Гисторамма преобразованного изображения |
- Пилообразная гистограмма.
 Исходное изображение |
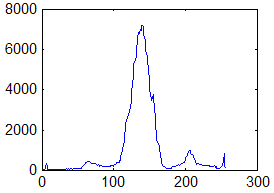 Гисторамма исходного изображения |
 Результирующие изображение |
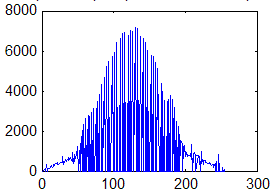 Гисторамма преобразованного изображения |
- Экспоненциальная гистограмма.
 Исходное изображение |
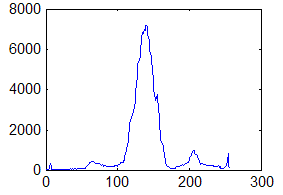 Гисторамма исходного изображения |
 Результирующие изображение |
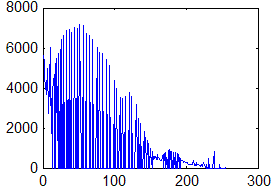 Гисторамма преобразованного изображения |
- Синусно-экспоненциальная гистограмма.
 Исходное изображение |
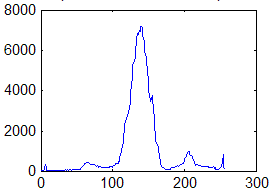 Гисторамма исходного изображения |
 Результирующие изображение |
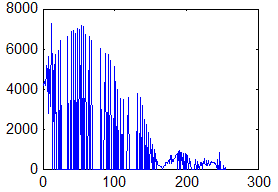 Гисторамма преобразованного изображения |
- Нормальный закон распределения гистограммы.
 Исходное изображение |
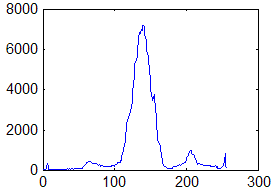 Гисторамма исходного изображения |
 Результирующие изображение |
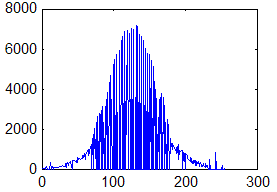 Гисторамма преобразованного изображения |
Нами проведены преобразования, в результате которых гистограмма распределения значений интенсивностей пикселей изображения приобрела желаемую форму (равномерную, треугольную, пилообразную, экспоненциальную, синусно-экспоненциальную, нормальную). Однако, полученные результирующие изображения не всегда характеризовались высоким качеством визуального восприятия. Это нетрудно объяснить, особенно в случае треугольной, экспоненциальной и синусно-экспоненциальной гистограмм, где основная часть изображения сосредоточена в темной области. В общем случае, каждое изображение при обработке методами гистограммных преобразований требует индивидуального подхода.
%===============================================================
%======ПРОГРАММА, КОТОРАЯ ФОРМИРУЕТ ГИСТОГРАММУ============
%===============================================================
zak=input('Закон распределения гистограммы')
if zak==0;
%Равномерный закон распределения гистограммы
H1=256.*ones(1,256);
end;
if zak==1;
%Треугольный закон распределения гистограммы
H2=[512:-2:2];
end;
if zak==2;
%Пилообразный закон распределения гистограммы
H31=[4:4:508];
H32=[512:-4:0];
H3=[H31,H32];
H3=H3(:);
H3=H3';
end;
if zak==3;
%Экспоненциальный закон распределения гистограммы
H4=260.75*(-log(1:255)+5.5413);
end;
if zak==4;
%Синусно-экспоненциальный закон распределения гистограммы
x=[0:255];
%H5=826.4752.*exp(-x/145).*abs(cos(pi/2-pi*(x+15)/45));
H5=7000.*exp(-x/85).*abs(cos(pi/2-pi*(x+15)/45));
end;
if zak==5;
%Нормальный закон распределения гистограммы
x=[0:255];
H6=65536.*(1/((127.5/3)*sqrt(2*pi))).*exp(-((x-127.5).^2)/(2*((127.5/3)^2)));
H6=round(H6);
end;
if zak==0;
H=H1;
disp('Равномерная гистограмма');
figure,plot(H);
title('Равномерная гистограмма');
end;
if zak==1;
H=H2;
disp('Треугольная гистограмма');
figure,plot(H);
title('Треугольная гистограмма');
end;
if zak==2;
H=H3;
disp('Пилообразная гистограмма');
figure,plot(H);
title('Пилообразная гистограмма');
end;
if zak==3;
H=H4;
disp('Экспоненциальная гистограмма');
figure,plot(H);
title('Экспоненциальная гистограмма');
end;
if zak==4;
H=H5;
disp('Синусно-экспоненциальная гистограмма');
figure,plot(H);
title('Синусно-экспоненциальная гистограмма');
end;
if zak==5;
H=H6;
disp('Нормальный закон распределения гистограммы');
figure,plot(H);
title('Нормальный закон распределения гистограммы');
end;
ylim('auto')
ylim('auto')
%========================================================
%==========ПРОГРАММА ВИДОИЗМЕНЕНИЯ ГИСТОГРАММЫ====
%========================================================
clear;
L=imread('liftingbody.png');
L=double(L)./255;
hist_zak; %Эталонная гистограмма
H2=H;
Lvyh=histeq(L,H2);
figure, subplot(221);
imshow(L);
title('Исходное изображение');
subplot(223);
imshow(Lvyh);
title('Результирующее изображение');
subplot(222);
h=imhist(L);
plot(h);
title('Гистограмма исходного изображения');
ylim('auto')
ylim('auto')
subplot(224);
h=imhist(Lvyh);
plot(h);
title('Гистограмма преобразованного изображения');
ylim('auto')
ylim('auto')
Визуализация объектов
Довольно часто существует необходимость визуализировать не только внешнюю, но и внутреннюю часть объекта. Для этого при визуализации объектов используют свойство прозрачности. Рассмотрим пример визуализации некоторой трехмерной фигуры.
[x y z v]=flow; p=patch(isosurface(x,y,z,v,-3)); isonormals(x,y,z,v,p); set(p,'facecolor','red','edgecolor','none'); daspect([1 1 1]); view(3); axis tight; grid on; camlight;lighting gouraud;
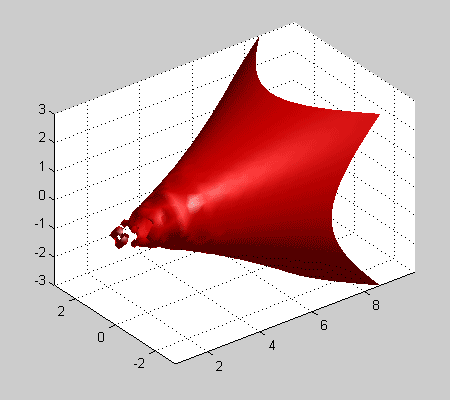
Из рисунка видно, что представленная фигура абсолютно не прозрачна. Степень прозрачности можно задавать с помощью функции alpha.
При alpha=0.8 изображение будет такое
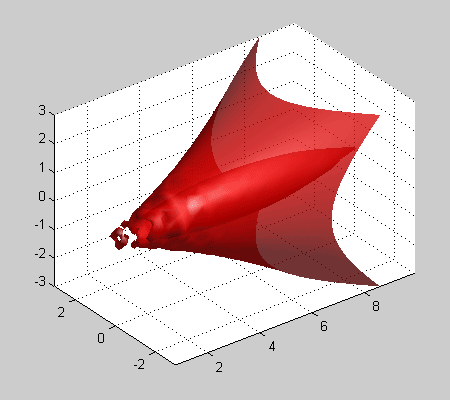
При alpha=0.5 изображение будет такое
При alpha=0.2 изображение будет такое
Из представленных изображений видно, что при уменьшении параметра alpha от 1 до 0, уровень прозрачности изменяется от полного отсутствия до абсолютной прозрачности.
Построение закрашенных многоугольников
Для построения закрашенных многоугольников может применяться объект patch.
t=0:pi/3:2*pi; a=t(1:length(t)-1); patch(sin(a),cos(a),1:length(a),'Facecolor','interp'); colormap cool; axis equal;
В общем случае, объект patch может использоваться для построения произвольного многоугольника:
patch(x,y,z,colordata),
где x,y и z – массивы координат вершин многоугольника; colordata – информация о цвете.
Приведем еще один пример построения закрашенного многоугольника.
x=[-1 -1 1 1];y=[-1 1 1 -1]; % вершины многоугольника z=[1:4]; patch(x,y,z,'Facecolor','interp'); colormap cool; axis equal;
Визуализация срезов черепной коробки человека
Система Matlab располагает средствами визуализации срезов черепной коробки человека с использованием изображений, полученных методом магнитного резонанса.
Рассмотрим два способа визуализации.
Первый способ.
load mri; D=squeeze(D); [N M k]=size(D); for i=1:k; figure,image(D(:,:,i)); axis image; colormap(map); end;
Второй способ.
phandles=contourslice(D,[],[],[1,12,19,27],8); view(3); axis tight;daspect([1,1,.4]); set(phandles,'LineWidth',2);
Построение реалистического изображения черепной коробки
В системе Matlab существует возможность визуализации не только срезов, но и реалистического изображения черепной коробки.
load mri; D=squeeze(D); Ds=smooth3(D); hiso=patch(isosurface(Ds,5),'FaceColor',[1,.75,.65],'Edgecolor','none'); hcap=patch(isocaps(D,5),'FaceColor','interp','Edgecolor','none'); colormap(map);view(45,30);axis tight; daspect([1,2,.4]) lightangle(45,30); set(gcf,'Renderer','zbuffer'); lighting phong; isonormals (Ds,hiso); set(hcap, 'AmbientStrength',.6) set(hiso,'SpecularColorReflectance',0,'SpecularExponent',50);
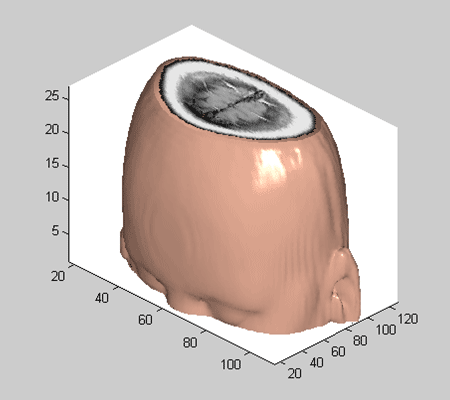
Визуализация фрагмента объекта
Также в системе Matlab существует возможность визуализации части трехмерного объекта. Продемонстрируем это на примере визуализации черепной коробки.
load mri; D=squeeze(D); [x,y,z,D]=subvolume(D,[60,80,nan,80,nan,nan]); p1=patch(isosurface(x,y,z,D,5),'FaceColor','red','Edgecolor','none'); isonormals(x,y,z,D,p1); p2=patch(isocaps(x,y,z,D,5),'FaceColor','interp','Edgecolor','none'); view(3); axis tight; daspect([1,1,.4]);colormap(gray(100)) camlight right;camlight left;lighting gouraud

Изменяя параметры строки
[x,y,z,D]=subvolume(D,[30,80,nan,80,nan,nan]);
можно визуализировать произвольную часть черепной коробки.
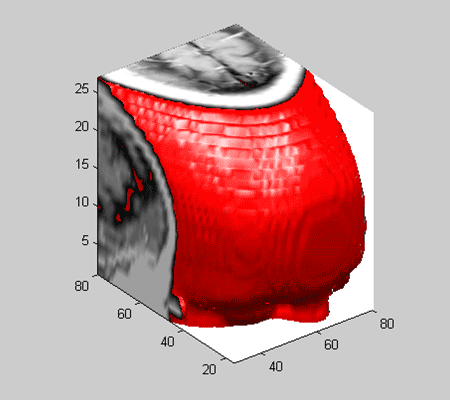
Пространственная визуализация струи
Покажем пример пространственной визуализации струи жидких или газообразных веществ.
[x,y,z,v]=flow;
xmin=min(x(:));ymin=min(y(:));zmin=min(z(:));
xmax=max(x(:));ymax=max(y(:));zmax=max(z(:));
hslice=surf(linspace(xmin,xmax,100),linspace(ymin,ymax,100),zeros(100));
rotate(hslice,[-1,0,0],-45);
xd=get(hslice,'XData');yd=get(hslice,'YData');zd=get(hslice,'ZData');
delete(hslice);
h=slice(x,y,z,v,xd,yd,zd);
set(h,'FaceColor','interp','DiffuseStrength',.8)
hold on;
hx=slice(x,y,z,v,xmax,[],[]);
set(hx,'FaceColor','interp','EdgeColor','none')
hy=slice(x,y,z,v,[],ymax,[]);
set(hy,'FaceColor','interp','EdgeColor','none')
hz=slice(x,y,z,v,[],[],zmin);
set(hz,'FaceColor','interp','EdgeColor','none')
daspect([1,1,1]);axis tight;box on
view(-38.5,16);camzoom(1.4);camproj perspective
lightangle(-45,45);colormap(jet(24));
set(gcf,'Renderer','zbuffer');colormap(flipud(jet(24)));
caxis([-5,2.4832]);colorbar('horiz');
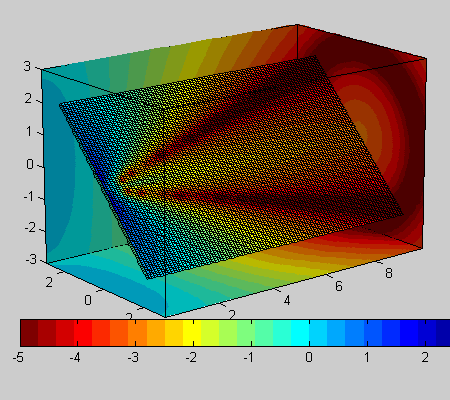
Визуализация электрических разрядов
Приведем пример визуализации развития электрического разряда.
load wind; xmin=min(x(:)); xmax=max(x(:));ymax=max(y(:));zmin=min(z(:)); wind_speed=sqrt(u.^2+v.^2+w.^2); hsurfaces=slice(x,y,z,wind_speed,[xmin,100,xmax],ymax,zmin); set(hsurfaces,'FaceColor','interp','EdgeColor','none'); hcont=contourslice(x,y,z,wind_speed,[xmin,100,xmax],ymax,zmin); [sx,sy,sz]=meshgrid(80,20:10:50,0:5:15); hlines=streamline(x,y,z,u,v,w,sx,sy,sz); set(hlines,'LineWidth',2,'Color','r'); view(3); daspect([2,2,1]); axis tight
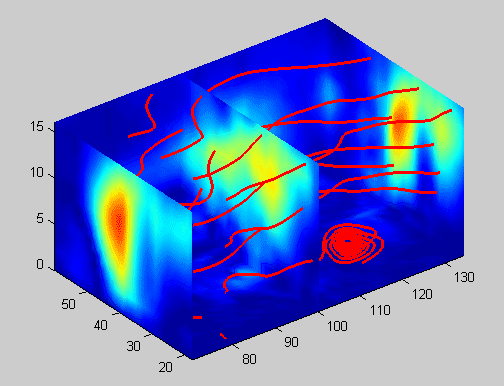
Визуализация вихрей
Рассмотрим два примера визуализации вихрей.
Пример 1.
load wind;[sx,sy,sz]=meshgrid(100,20:2:50,5);
verts=stream3(x,y,z,u,v,w,sx,sy,sz);
sl=streamline(verts);
view(-10.5,18);daspect([2 2 0.125]); axis tight; box on;
iverts =interpstreamspeed(x,y,z,u,v,w,verts,0.05);
set(gca,'drawmode','fast'); streamparticles(iverts,15,'Animate',10,'ParticleAlignment','on',...
'MarkerEdgeColor','none','MarkerFaceColor','red','Marker','o');
Пример 2.
load wind;[sx,sy,sz]=meshgrid(80,20:1:55,5); verts=stream3(x,y,z,u,v,w,sx,sy,sz); sl=streamline(verts); iverts=interpst reamspeed(x,y,z,u,v,w,verts,.025); axis tight; view(30,30); daspect([1 1 .125]); camproj perspective; camva(8); set(gca,'DrawMode','fast'); box on; streamparticles(iverts,35,'animate',10,'ParticleAlignment','on');
Визуализация струй с помощью конусов
Продемонстрируем один из примеров исследования движения газовых или жидкостных струй.
load wind; wind_speed=sqrt(u.^2+v.^2+w.^2); hiso=patch(isosurface(x,y,z,wind_speed,40)); isonormals(x,y,z,wind_speed,hiso); set(hiso,'FaceColor','red','EdgeColor','none'); hcap=patch(isocaps(x,y,z,wind_speed,40),'FaceColor','interp','EdgeColor','none'); colormap hsv; daspect([1 1 1]); [f verts]=reducepatch(isosurface(x,y,z,wind_speed,30),0.07); h1=coneplot(x,y,z,u,v,w,verts(:,1),verts(:,2),verts(:,3),3); set(h1,'FaceColor','blue','EdgeColor','none'); xrange=linspace(min(x(:)),max(x(:)),10); yrange=linspace(min(y(:)),max(y(:)),10); zrange=3:4:15; [cx,cy,cz]=meshgrid(xrange,yrange,zrange); h2=coneplot(x,y,z,u,v,w,cx,cy,cz,2); set(h2,'FaceColor','green','EdgeColor','none'); axis tight; box on;camproj perspective; camzoom(1.25);view(65,45); camlight(-45,45);set(gcf,'Renderer','zbuffer'); lighting phong;set(hcap,'AmbientStrength',.6);
- Дьяконов В.П. MATLAB 6.5 SP1/7/7 SP1+Simulink 5/6. Работа с изображениями и видеопотоками. – М.: СОЛОН–Пресс. 2005. –400 стр.
Применение методов улучшения изображений при разработке системы видеонаблюдения
В настоящее время существует много различных систем видеонаблюдения. Различия, которые существуют между этими системами, можно объяснить разными условиями наблюдения, степенью надежности, уровнем автоматизации и т.д. Другими словами, задача видеонаблюдения является проблемно-ориентированной, поэтому архитектура и методы, которые реализованы в системе, зависят от особенностей поставленной задачи наблюдения.
В рамках этого материала остановимся на подходах, которые применяются для обработки визуальных данных, которые получены при построении автоматизированной системы видеонаблюдения.
Методы улучшения цифровых изображений, сформированных системой видеоналюдения
Основными методами, которые применяются в системах видеонаблюдения, являются так называемые методы предварительной обработки или методы улучшения. Это можно объяснить тем, что изображения, которые регистрируются системой, не всегда характеризуются высоким качеством визуального восприятия. Дело в том, что системы видеонаблюдения работают в различных погодных условиях, а также не только в светлое, но в темное время суток.
Рассмотрим более детально несколько различных методов, которые применяются в системах видеонаблюдения.
Усиление контрастности
Низкий контраст является одним из наиболее распространенных дефектов фотографических и телевизионных изображений. Причины могут быть самые различные – плохое качество аппаратуры, внешние условия и т.п. Что касается систем видеонаблюдения, то, в этом случае, недостаточно высокое качество регистрируемых изображений объясняется условиями съемки (погодные условия, темное время суток).
Приведем программную реализацию метода повышения локальных контрастов.
Сначала считаем исходное изображение.
L=imread('1.bmp');
figure,imshow(L);title('Исходное изображение');
Исходное изображение
Поскольку исходное изображение имеет три цветовых составляющих, то при реализации метода будем обрабатывать каждую цветовую составляющую отдельно.
Обработка R-цветовой составляющей исходного изображения
L_R=L(:,:,1);
figure,imshow(L_R); title('R-цветовая составляющая исходного изображения');
L_R=im2double(L_R);
R-цветовая составляющая исходного изображения
h=fspecial('unsharp');
L_R_contr=conv2(L_R,h);
L_R_contr=im2uint8(L_R_contr);
figure,imshow(L_R_contr); title('R-цветовая составляющая исходного изображения после контрастирования');
R-цветовая составляющая исходного изображения после контрастирования
Обработка G-цветовой составляющей исходного изображения
L_G=L(:,:,2);
figure,imshow(L_G); title('G-цветовая составляющая исходного изображения');
L_G=im2double(L_G);
G-цветовая составляющая исходного изображения
L_G_contr=conv2(L_G,h);
L_G_contr=im2uint8(L_G_contr);
figure,imshow(L_G_contr); title('G-цветовая составляющая исходного изображения после контрастирования');
G-цветовая составляющая исходного изображения после контрастирования
Обработка B-цветовой составляющей исходного изображения
L_B=L(:,:,3);
figure,imshow(L_B); title('B-цветовая составляющая исходного изображения');
L_B=im2double(L_B);
B-цветовая составляющая исходного изображения
L_B_contr=conv2(L_B,h);
L_B_contr=im2uint8(L_B_contr);
figure,imshow(L_B_contr); title('B-цветовая составляющая исходного изображения после контрастирования');
B-цветовая составляющая исходного изображения после контрастирования
Восстановим результирующее цветное изображение из трех цветовых составляющих.
L(:,:,1)=L_R_contr;
L(:,:,2)=L_G_contr;
L(:,:,3)=L_B_contr;
figure,imshow(L);title('Исходное изображение после контрастирования');
Исходное изображение после контрастирования
Для того, чтобы продемонстрировать эффективность метода, мы использовали слишком большой коэффициент усиления контрастности. При практическом использовании метода он должен быть меньше.
Коррекция динамического диапазона
Рассмотрим еще один метод улучшения изображений – метод коррекции динамического диапазона интенсивностей элементов изображения. Известно, что при недостаточном освещении формируются изображения с ограниченным динамическим диапазоном. Поэтому использование метода коррекции динамического диапазона в системах видеонаблюдения очень актуально, поскольку система должна работать как в светлое, так и в темное время суток.
Считаем исходное изображение
L=imread('3.bmp');
figure,imshow(L);title('Исходное изображение');
k=.25;
Исходное изображение
L_R=L(:,:,1);
figure,imshow(L_R); title('R-цветовая составляющая исходного изображения');
R-цветовая составляющая исходного изображения
L_R=im2double(L_R);
Lmin=min(min(L_R));
Lmax=max(max(L_R));
L_R_stretch=((L_R-Lmin)./(Lmax-Lmin)).^k;
L_R_stretch1=medfilt2(L_R_stretch);
L_R_stretch1=im2uint8(L_R_stretch1);
figure,imshow(L_R_stretch); title('R-цветовая составляющая после коррекции динамического диапазона');
R-цветовая составляющая после коррекции динамического диапазона
На изображении, которое получено после коррекции динамического диапазона, видно присутствие импульсной шумовой составляющей. Ее желательно устранить с помощью медианной фильтрации. Аналогично поступим со всеми цветовыми составляющими изображения.
figure,imshow(L_R_stretch1);
title('R-составляющая после коррекции динамического диапазона (медианная фильтрация)');
R-составляющая после коррекции динамического диапазона (медианная фильтрация)
L_G=L(:,:,2);
figure,imshow(L_G); title('G-цветовая составляющая исходного изображения');
G-цветовая составляющая исходного изображения
L_G=im2double(L_G);
Lmin=min(min(L_G));
Lmax=max(max(L_G));
L_G_stretch=((L_G-Lmin)./(Lmax-Lmin)).^k;
L_G_stretch1=medfilt2(L_G_stretch);
L_G_stretch1=im2uint8(L_G_stretch1);
figure,imshow(L_G_stretch); title('G-цветовая составляющая после коррекции динамического диапазона');
G-цветовая составляющая после коррекции динамического диапазона
figure,imshow(L_G_stretch1);
title('G-составляющая после коррекции динамического диапазона (медианная фильтрация)');
G-составляющая после коррекции динамического диапазона (медианная фильтрация)
L_B=L(:,:,3);
figure,imshow(L_B); title('B-цветовая составляющая исходного изображения');
B-цветовая составляющая исходного изображения
L_B=im2double(L_B);
Lmin=min(min(L_B));
Lmax=max(max(L_B));
L_B_stretch=((L_B-Lmin)./(Lmax-Lmin)).^k;
L_B_stretch1=medfilt2(L_B_stretch);
L_B_stretch1=im2uint8(L_B_stretch1);
figure,imshow(L_B_stretch); title('B-цветовая составляющая после коррекции динамического диапазона');
B-цветовая составляющая после коррекции динамического диапазона
figure,imshow(L_B_stretch1);
title('B-составляющая после коррекции динамического диапазона (медианная фильтрация)');
B-составляющая после коррекции динамического диапазона (медианная фильтрация)
L(:,:,1)=L_R_stretch;
L(:,:,2)=L_G_stretch;
L(:,:,3)=L_B_stretch;
L1(:,:,1)=L_R_stretch1;
L1(:,:,2)=L_G_stretch1;
L1(:,:,3)=L_B_stretch1;
figure,imshow(L);title('Исходное изображение после коррекции динамического диапазона');
Исходное изображение после коррекции динамического диапазона
figure,imshow(L1);
title('Исходное изображение после коррекции динамического диапазона (медианная фильтрация)');
Исходное изображение после коррекции динамического диапазона (медианная фильтрация)
Разностный метод
Довольно часто изображения с искусственно подчеркнутыми границами визуально воспринимаются лучше, чем фотометрически совершенная продукция.
Приведем один из вариантов метода подчеркивания границ.
L=imread('1.bmp');
figure,imshow(L);title('Исходное изображение');
k=1.4;
Исходное изображение
L_R=L(:,:,1);
figure,imshow(L_R); title('R-цветовая составляющая исходного изображения');
R-цветовая составляющая исходного изображения
L_R=im2double(L_R);
Lser=mean(mean(L_R));
L_R_sharp=Lser+k*(L_R-Lser);
L_R_sharp=im2uint8(L_R_sharp);
figure,imshow(L_R_sharp); title('R-цветовая составляющая после подчеркивания границ');
R-цветовая составляющая после подчеркивания границ
L_G=L(:,:,2);
figure,imshow(L_G); title('G-цветовая составляющая исходного изображения');
G-цветовая составляющая исходного изображения
L_G=im2double(L_G);
Lser=mean(mean(L_G));
L_G_sharp=Lser+k*(L_G-Lser);
L_G_sharp=im2uint8(L_G_sharp);
figure,imshow(L_G_sharp); title('G-цветовая составляющая после подчеркивания границ');
G-цветовая составляющая после подчеркивания границ
L_B=L(:,:,3);
figure,imshow(L_B); title('B-цветовая составляющая исходного изображения');
B-цветовая составляющая исходного изображения
L_B=im2double(L_B);
Lser=mean(mean(L_B));
L_B_sharp=Lser+k*(L_B-Lser);
L_B_sharp=im2uint8(L_B_sharp);
figure,imshow(L_B_sharp); title('B-цветовая составляющая после подчеркивания границ');
B-цветовая составляющая после подчеркивания границ
L(:,:,1)=L_R_sharp;
L(:,:,2)=L_G_sharp;
L(:,:,3)=L_B_sharp;
figure,imshow(L);title('Исходное изображение после подчеркивания границ');
Исходное изображение после подчеркивания границ
Выравнивание гистограммы
Изображения, которые формируются в системе видеонаблюдения, довольно часто бывают или слишком темными, или слишком светлыми. Это можно объяснить тем, что изображения могут формироваться в различное время суток и при различных погодных условиях. Для улучшения визуального качества таких изображений может применяться метод выравнивания гистограммы. Приведем один из вариантов его реализации.
L=imread('3.bmp');
figure,imshow(L);title('Исходное изображение');
Исходное изображение
L_R=L(:,:,1);
figure,imshow(L_R); title('R-цветовая составляющая исходного изображения');
R-цветовая составляющая исходного изображения
L_R=im2double(L_R);
L_R_sharp=histeq(L_R);
L_R_sharp1=medfilt2(L_R_sharp,[7 7]);
L_R_sharp=im2uint8(L_R_sharp1);
figure,imshow(L_R_sharp); title('R-цветовая составляющая после выравнивания гистограммы');
R-цветовая составляющая после выравнивания гистограммы
L_G=L(:,:,2);
figure,imshow(L_G); title('G-цветовая составляющая исходного изображения');
G-цветовая составляющая исходного изображения
L_G=im2double(L_G);
L_G_sharp=histeq(L_G);
L_G_sharp1=medfilt2(L_G_sharp,[7 7]);
L_G_sharp=im2uint8(L_G_sharp1);
figure,imshow(L_G_sharp); title('G-цветовая составляющая после выравнивания гистограммы');
G-цветовая составляющая после выравнивания гистограммы
L_B=L(:,:,3);
figure,imshow(L_B); title('B-цветовая составляющая исходного изображения');
B-цветовая составляющая исходного изображения
L_B=im2double(L_B);
L_B_sharp=histeq(L_B);
L_B_sharp1=medfilt2(L_B_sharp,[7 7]);
L_B_sharp=im2uint8(L_B_sharp1);
figure,imshow(L_B_sharp); title('B-цветовая составляющая после выравнивания гистограммы');
B-цветовая составляющая после выравнивания гистограммы
L(:,:,1)=L_R_sharp;
L(:,:,2)=L_G_sharp;
L(:,:,3)=L_B_sharp;
figure,imshow(L);title('Исходное изображение после выравнивания гистограммы');
Исходное изображение после выравнивания гистограммы
Таким образом, в рамках данного материала нами рассмотрен набор методов улучшения изображений, которые могут применяться при построении автоматизированной системы видеонаблюдения. В основном, методы улучшения были направлены на коррекцию динамического диапазона изображений, а также устранение шумов. Как уже отмечалось, эти недостатки изображения можно объяснить недостаточным освещением в темное время суток и погодными условиями.
Улучшение изображений с яркостными искажениями
Одним из наиболее распространенных недостатков при формировании изображений являются яркостные искажения. Поэтому в рамках данного материала рассмотрим некоторые подходы к решению задачи коррекции яркостных искажений изображений с целью повышения их визуального качества. Поскольку преимущественно речь идет о коррекции затемненных или осветленных изображений, то целесообразно перейти из цветового пространства RGB в цветовое пространство YUV. Эта цветовая модель широко применяется в телевещании и обработке видеоданных. Отличительной особенностью цветового пространства YUV является то, что в нем используется явное разделение информации о яркости и цвете.
Цвет представляется как 3 компоненты - яркость (Y) и две цветоразностных (U и V).
Конверсия в RGB и обратно осуществляется по следующим формулам:
R = Y + (1.4075 * (V — 128)); G = Y — (0.3455 * (U — 128) — (0.7169 * (V — 128)); B = Y + (1.7790 * (U — 128);
Y = R * 0.299 + G * 0.587 + B * 0.114; U = R * ?0.169 + G * ?0.332 + B * 0.500 + 128; V = R * 0.500 + G * ?0.419 + B * ?0.0813 + 128.
Рассмотрим реализацию нашей задачи в среде Matlab. Сначала считаем изображение в рабочее пространство.
clear;
L_rgb=imread('canoe.bmp');
Далее определим размеры исходного изображения, представим в формате double и визуализируем.
[N M s]=size(L_rgb);
L_rgb=double(L_rgb)./255;
figure, imshow(L_rgb);
title('Исходное изображение в цветовом пространстве RGB');

Конвертируем изображение из цветового пространства RGB в YCBCR(YUV). Для этого будем использовать встроенную функцию
rgb2ycbcr
.
L_ycbcr=rgb2ycbcr(L_rgb);
figure, imshow(L_ycbcr);
title('Исходное изображение в цветовом пространстве YCBCR');

Проанализируем вид и интенсивность цветовых составляющих изображения.
figure,imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR');

figure,imshow(L_ycbcr(:,:,2));
title('Cb составляющая изображения в цветовом пространстве YCBCR');

figure,imshow(L_ycbcr(:,:,3));
title('Cr составляющая изображения в цветовом пространстве YCBCR');

Как мы уже говорили ранее, в данном материале остановимся на коррекции только составляющей Y, которая содержит информацию о яркости изображения. Существуют различные подходы к преобразованию Y-составляющей. Один из них состоит в преобразовании динамического диапазона Y-составляющей.
%Преобразование составляющей Y, которая содержит информацию о яркости изображения
% Метод 1
L_ycbcr(:,:,1)=((L_ycbcr(:,:,1)-min(min(L_ycbcr(:,:,1))))./
(max(max(L_ycbcr(:,:,1)))-min(min(L_ycbcr(:,:,1))))).^.5;
figure,subplot(221),imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR до модификации');
subplot(222),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей до модификации');
subplot(223),imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR после модификации');
subplot(224),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей после модификации');
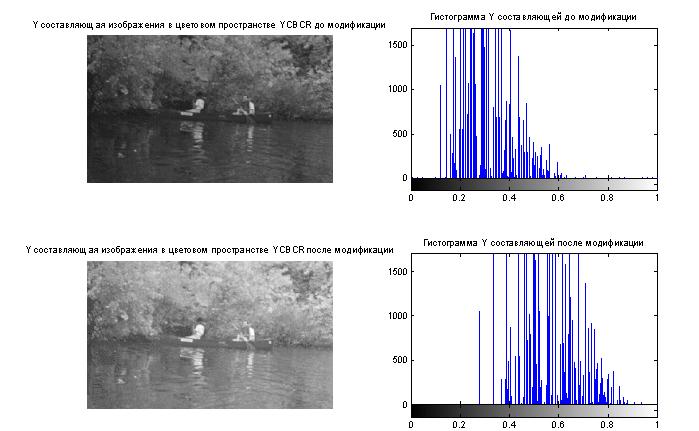 Результат коррекции динамического диапазона Y составляющей представлен на изображении внизу.
Результат коррекции динамического диапазона Y составляющей представлен на изображении внизу.

Рассмотрим еще один подход к коррекции Y-составляющей, который заключается в выравнивании ее гистограммы. Отметим, что дополнительно уровень яркости можно регулировать также с помощью параметра k.
figure,subplot(221),imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR до модификации');
subplot(222),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей до модификации');
k=1.25;
F=histeq(L_ycbcr(:,:,1));
L_ycbcr(:,:,1)=k.*F;
subplot(223),imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR после модификации');
subplot(224),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей после модификации');
Представим результат модификации Y-составляющей при k=1.
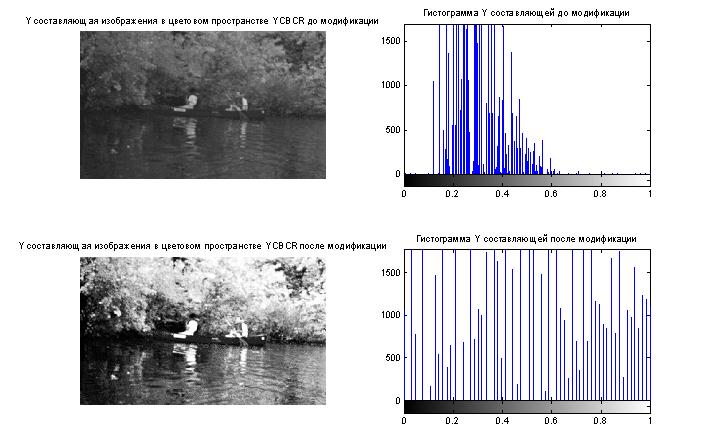

Представим результат модификации Y-составляющей при k=0,75.
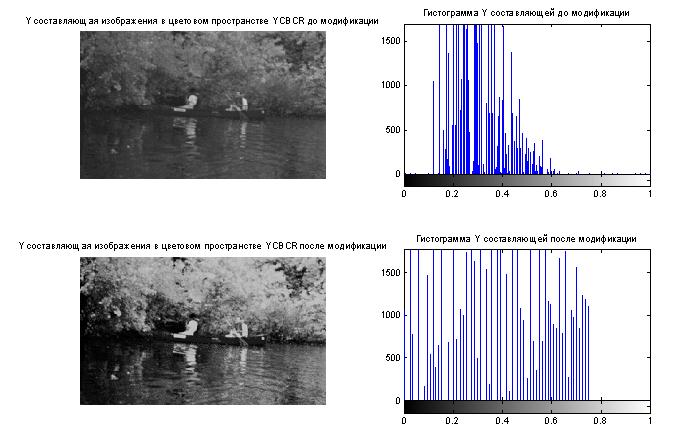

Представим результат модификации Y-составляющей при k=1,25.
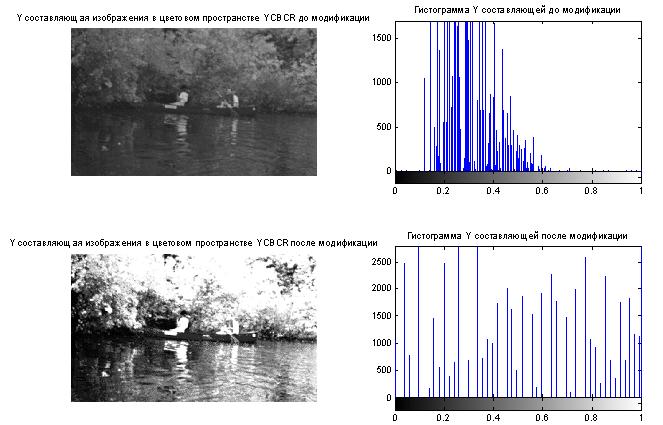

Рассмотрим третий подход к модификации Y-составляющей. Для этого будет использован метод нечеткого маскирования. При этом отметим, что степень усиления также можно регулировать с помощью параметра k.
k=.85;
L_ycbcr(:,:,1)=L_ycbcr(:,:,1)+k.*(L_ycbcr(:,:,1)-mean(mean(L_ycbcr(:,:,1))));
figure,subplot(221),imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR до модификации');
subplot(222),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей до модификации');
subplot(223),imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR после модификации');
subplot(224),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей после модификации');
Представим результат модификации Y-составляющей при k=-0,25.
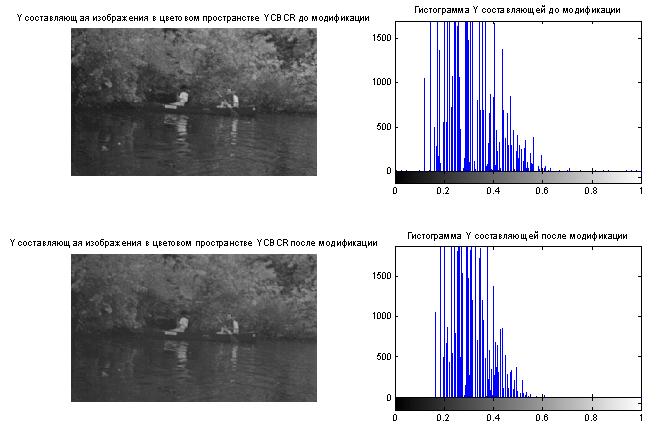

Представим результат модификации Y-составляющей при k=0,25.
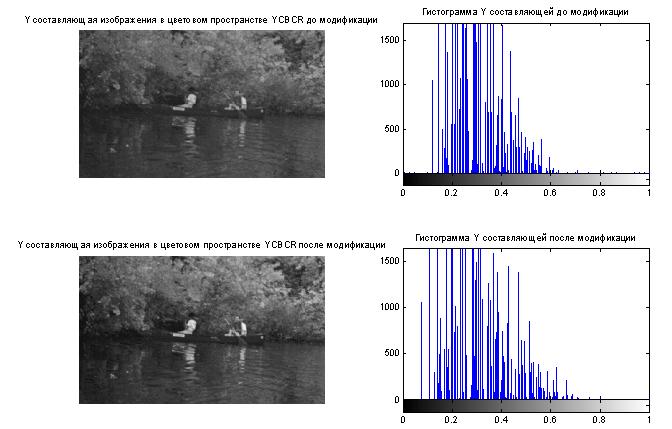

Представим результат модификации Y-составляющей при k=0,85.
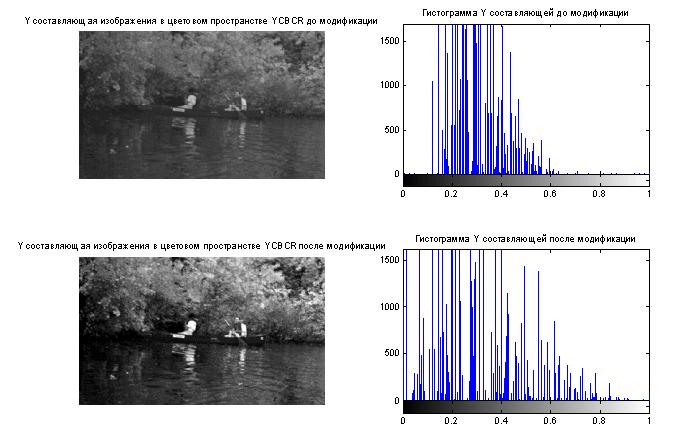

Рассмотрим еще один подход к модификации Y-составляющей с помощью встроенной функции imfilter.
H = fspecial('unsharp');
L_ycbcr(:,:,1) = imfilter(L_ycbcr(:,:,1),H,'replicate');
figure,subplot(221),imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR до модификации');
subplot(222),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей до модификации');
subplot(223);
imshow(L_ycbcr(:,:,1)); title('Y составляющая изображения в цветовом пространстве YCBCR после модификации');
subplot(224),imhist(L_ycbcr(:,:,1));title('Гистограмма Y составляющей после модификации');
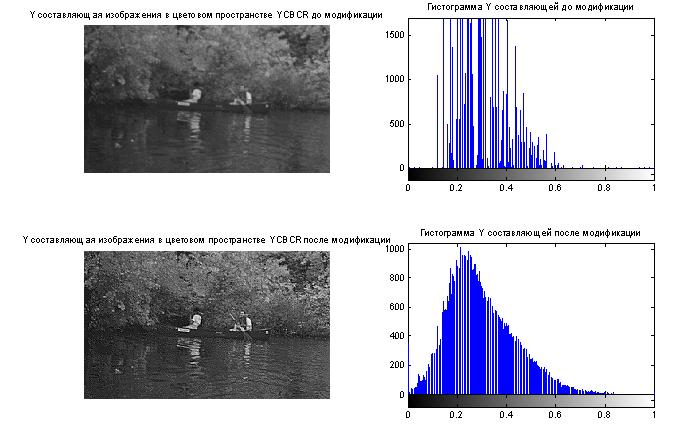

Следующий подход к модификации Y составляющей является наиболее простым, но, в отдельных случаях, довольно эффективным методом. Его суть состоит в увеличении всех значений яркостной составляющей.
for i=1:N;
disp(i);
for j=1:M;
if L_ycbcr(i,j,1)<.2;
L_ycbcr(:,:,1)=L_ycbcr(:,:,1)+.25;
end;
end;
end;
subplot(223);
imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR после модификации');
subplot(224),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей после модификации');
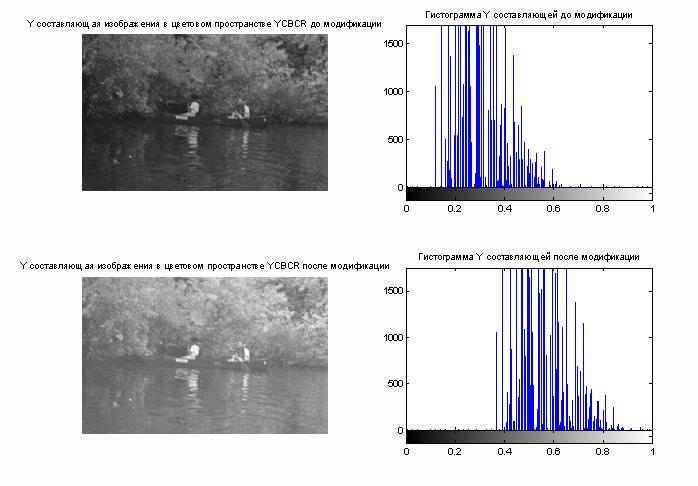

Программа, реализующая приведенные выше методы:
%===== УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ С ЯРКОСТНЫМИ ИСКАЖЕНИЯМИ =====
clear;
L_rgb=imread('canoe.bmp');
[N M s]=size(L_rgb);
L_rgb=double(L_rgb)./255;
figure, imshow(L_rgb);
title('Исходное изображение в цветовом пространстве RGB');
% Конвертирование из цветового пространства RGB в YCBCR
L_ycbcr=rgb2ycbcr(L_rgb);
figure, imshow(L_ycbcr);
title('Исходное изображение в цветовом пространстве YCBCR');
figure,imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR');
figure,imshow(L_ycbcr(:,:,2));
title('Cb составляющая изображения в цветовом пространстве YCBCR');
figure,imshow(L_ycbcr(:,:,3));
title('Cr составляющая изображения в цветовом пространстве YCBCR');
figure,subplot(621),imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR до модификации');
subplot(622),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей до модификации');
%Преобразование составляющей Y, которая содержит информацию о яркости изображения
% Метод 1
L_ycbcr1(:,:,1)=((L_ycbcr(:,:,1)-min(min(L_ycbcr(:,:,1))))./
(max(max(L_ycbcr(:,:,1)))-min(min(L_ycbcr(:,:,1))))).^.5;
subplot(623),imshow(L_ycbcr1(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR после модификации (Метод 1)');
subplot(624),imhist(L_ycbcr1(:,:,1));
title('Гистограмма Y составляющей после модификации (Метод 1)');
% Метод 2
k=1.25;
F=histeq(L_ycbcr(:,:,1));
L_ycbcr2(:,:,1)=k.*F;
subplot(625),imshow(L_ycbcr2(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR после модификации (Метод 2)');
subplot(626),imhist(L_ycbcr2(:,:,1));
title('Гистограмма Y составляющей после модификации (Метод 2)');
% Метод 3
k=.85;
L_ycbcr3(:,:,1)=L_ycbcr(:,:,1)+k.*(L_ycbcr(:,:,1)-mean(mean(L_ycbcr(:,:,1))));
subplot(627),imshow(L_ycbcr3(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR после модификации (Метод 3)');
subplot(628),imhist(L_ycbcr3(:,:,1));
title('Гистограмма Y составляющей после модификации (Метод 3)');
% Метод 4
H = fspecial('unsharp');
L_ycbcr(:,:,1) = imfilter(L_ycbcr(:,:,1),H,'replicate');
subplot(629);
imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR после модификации (Метод 4)');
subplot(6,2,10),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей после модификации (Метод 4)');
% Метод 5
for i=1:N;
disp(i);
for j=1:M;
if L_ycbcr(i,j,1)<.2;
L_ycbcr(:,:,1)=L_ycbcr(:,:,1)+.15;
end;
end;
end;
subplot(6,2,11);
imshow(L_ycbcr(:,:,1));
title('Y составляющая изображения в цветовом пространстве YCBCR после модификации (Метод 5)');
subplot(6,2,12),imhist(L_ycbcr(:,:,1));
title('Гистограмма Y составляющей после модификации (Метод 5)');
L_ycbcr=255.*L_ycbcr;
% Конвертирование из цветового пространства YCBCR в RGB
L_rgb=ycbcr2rgb(L_ycbcr./255);
% Визуализация результатат преобразования
figure, imshow(L_rgb);
title('Результат модификации изображений с яркостными искажениями');
Некоторые алгоритмы повышения визуального качества изображений
Известно, что изображение с подчеркнутыми границами объектов воспринимается, с визуальной точки зрения, как более качественное. Рассмотрим один из подходов к повышению визуального качества изображений с использованием метода Канни.
Считаем исходное изображение.
clear;
I = imread('hestain.bmp');
Рассматривать метод будем на примере полутонового изображения. Поскольку исходное изображение представлено в формате rgb, то для получения полутонового изображения возьмем только один цветовой шар.
I=I(:,:,1);
Отметим, что преобразование полноцветного изображения в полутоновое можно выполнить также с использованием встроенной функции rgb2gray.
I=double(I)./255;
figure, imshow(I);title('Исходное изображение');
Исходное изображение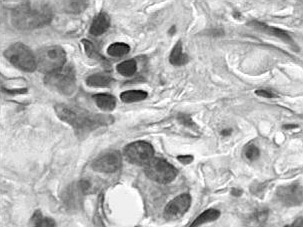
Далее локализируем границы, которые необходимо усилить. Для этого будем использовать метод Канни.
BW = edge(I,'canny');
figure, imshow(BW);
title('Выделение границ на исходном изображении методом Канни');
Выделение границ на исходном изображении методом Канни
После того, как были определены границы объектов изображения, проводится их подчеркивание путем изменения интенсивности пикселей. Значения интенсивности пикселя может уменьшаться или увеличиваться, в зависимости от значений интенсивности пикселей окрестности.
if BW(i,j)==1;
box_mean=mean(I(i-r:i+r,j-r:j+r));
if I(i,j)<box_mean;
a=.3;
else
a=-.3;
end;
Iout(i,j)=I(i,j)*(1+a);
else
Iout(i,j)=I(i,j);
end;
Изображение с подчеркнутыми краями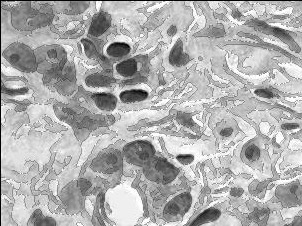
Также отметим, что усиление границ объектов изображения не является постоянным, а зависит от конкретного изображения. Для регулировки усиления используется параметр a.
Программа, реализующая описанный выше метод.
%Повышение визуального качества изображений путем
подчеркивания границ
clear;
I = imread('hestain.bmp');
I=I(:,:,1);
I=double(I)./255;
figure, imshow(I);
title('Исходное изображение');
%Выделение границ методом Канни
BW = edge(I,'canny');
figure, imshow(BW);
title('Выделение границ на исходном изображении методом Канни');
[N M]=size(I);
%Подчеркивание границ
r=1;
for i=2:N-1;
disp(i);
for j=2:M-1;
if BW(i,j)==1;
box_mean=mean(I(i-r:i+r,j-r:j+r));
if I(i,j)<box_mean;
a=.3;
else
a=-.3;
end;
Iout(i,j)=I(i,j)*(1+a);
else
Iout(i,j)=I(i,j);
end;
end;
end;
figure, imshow(Iout);
title('Изображение с подчеркнутыми краями');
Улучшение визуального качества изображений с использованием среднеквадратического отклонения значений интенсивности пикселей локальных окрестностей.
Большое количество методов улучшения изображений при реализации используют анализ свойств локальных окрестностей. Это позволяет сделать метод адаптивным, что, в свою очередь положительно влияет на результат улучшения изображения. В данной работе в качестве характеристики локальных окрестностей будем использовать среднеквадратическое отклонение значений интенсивности пикселей локальных окрестностей.
Приведем пример реализации метода. Для начала считаем исходное изображение.
I = imread('hestain.bmp');
Как и в предыдущем примере при реализации метода будем использовать только одну цветовую составляющую rgb-изображения.
I=I(:,:,1);
I=double(I)./255;
figure, imshow(I);title('Исходное изображение');
Исходное изображение
Следующий шаг заключается в определении значений среднеквадратического отклонения интенсивностей окрестности. Этот параметр является важной характеристикой локальной окрестности. Он будет использоваться при преобразовании значений интенсивностей пикселей.
for i=1+r:N-r;
disp(i);
for j=1+r:M-r;
box=I(i-r:i+r,j-r:j+r);
S(i,j)=std(box(:));
end;
end;
Среднеквадратическое отклонение значений интенсивностей пикселей изображения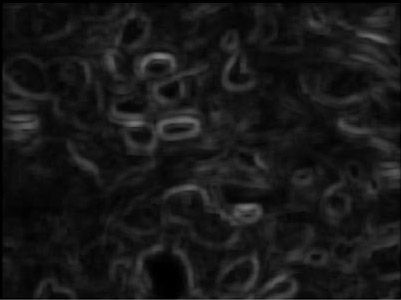
Как было сказано выше, при формировании результата учитываются значения среднеквадратического отклонения интенсивностей пикселей локальной окрестности.
if I(i,j)>mean(box); I(i,j)=I(i,j)+k*S(i,j); else I(i,j)=I(i,j)-k*S(i,j); end;
Изображение с подчеркнутыми границами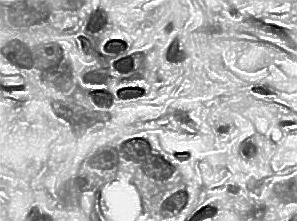
Программа, реализующая описанный выше метод.
%Подчеркивание границ объектов изображения
clear;
I = imread('hestain.bmp');
I=I(:,:,1);
I=double(I)./255;
figure, imshow(I);title('Исходное изображение');
[N M]=size(I);
%Подчеркивание границ
k=.65;
r=3;
for i=1+r:N-r;
disp(i);
for j=1+r:M-r;
box=I(i-r:i+r,j-r:j+r);
S(i,j)=std(box(:));
if I(i,j)>mean(box);
I(i,j)=I(i,j)+k*S(i,j);
else
I(i,j)=I(i,j)-k*S(i,j);
end;
end;
end;
I=I(1+r:N-r,1+r:M-r);
I(I<0)=0;
I(I>1)=1;
figure, imshow(S);
title('Среднеквадратическое отклонение значений
интенсивностей пикселей изображения');
figure, imshow(I);
title('Изображение с подчеркнутыми границами');
Улучшение цветных изображений с использованием среднеквадратических отклонений интенсивностей локальных окрестностей
В основу рассматриваемого подхода к улучшению цветных изображений положен метод растяжения динамического диапазона. Однако чрезмерное усиление значений интенсивностей не всегда приводит к желательным результатам, особенно, если речь идет о цветных изображениях. Поэтому в этом методе будет реализовано регулируемое усиление значений интенсивностей пикселей. Следует также отметить, что важным параметром при улучшении изображений является размер локальной окрестности. Он существенно влияет на детальность результирующего изображения.
Приведем пример программной реализации метода.
Сначала исходное изображение считывается в рабочее пространство Matlab.
I = imread('forest.bmp');
I=double(I)./255;
figure, imshow(I);title('Исходное изображение');
Исходное изображение
Далее для каждой из цветовых составляющих определяются параметры локальных окрестностей – минимум, максимум и среднеквадратическое отклонение интенсивностей пикселей. Все эти параметры определены для локальной окрестности с размерами r.
min_box_r=min(min(I(i-r:i+r,j-r:j+r,1)));
min_box_g=min(min(I(i-r:i+r,j-r:j+r,2)));
min_box_b=min(min(I(i-r:i+r,j-r:j+r,3)));
max_box_r=max(max(I(i-r:i+r,j-r:j+r,1)));
max_box_g=max(max(I(i-r:i+r,j-r:j+r,2)));
max_box_b=max(max(I(i-r:i+r,j-r:j+r,3)));
sigm_r=std2(I(i-r:i+r,j-r:j+r,1));
sigm_g=std2(I(i-r:i+r,j-r:j+r,2));
sigm_b=std2(I(i-r:i+r,j-r:j+r,3));
Также задается соответствующий коэффициент усиления
Kr=15*sigm_r;Kg=15*sigm_g;Kb=15*sigm_b;
и определяются значения интенсивностей цветовых составляющих результирующего изображения.
Iout(i,j,1)=I(i,j,1)*(1-Kr)+(I(i,j,1)-min_box_r)/(max_box_r-min_box_r+eps)*Kr; Iout(i,j,2)=I(i,j,2)*(1-Kg)+(I(i,j,2)-min_box_g)/(max_box_g-min_box_g+eps)*Kg; Iout(i,j,3)=I(i,j,3)*(1-Kb)+(I(i,j,3)-min_box_b)/(max_box_b-min_box_b+eps)*Kb;
Приведем результаты, которые получены при различных значениях размеров локальных окрестностей и различных значениях коэффициента усиления.
1) Размер локальной окрестности 3 x 3, коэффициент усиления Kr = Kg = Kb = 3.

2) Размер локальной окрестности 3 x 3, коэффициент усиления Kr = Kg = Kb = 7.

3) Размер локальной окрестности 3 x 3, коэффициент усиления Kr = Kg = Kb = 15.

4) Размер локальной окрестности 7 x 7, коэффициент усиления Kr = Kg = Kb = 3.

5) Размер локальной окрестности 7 x 7, коэффициент усиления Kr = Kg = Kb = 7.

6) Размер локальной окрестности 7 x 7, коэффициент усиления Kr = Kg = Kb = 15.

7) Размер локальной окрестности 15 x 15, коэффициент усиления Kr = Kg = Kb = 3.

8) Размер локальной окрестности 15 x 15, коэффициент усиления Kr = Kg = Kb = 7.

9) Размер локальной окрестности 15 x 15, коэффициент усиления Kr = Kg = Kb = 15.

Из представленных результатов видно, что описанный выше метод является эффективным средством улучшения цветных изображений. Используя различные размеры локальных окрестностей и значения коэффициентов K, можно регулировать уровень детальности изображения и интенсивности пикселей.
Программа, реализующая описанный выше метод.
%Улучшение качества цветных изображений
clear;
I = imread('forest.bmp');
I=double(I)./255;
figure, imshow(I);title('Исходное изображение');
[N M k]=size(I);
%Підкреслення границь
r=fix(15/2);
for i=1+r:N-r;
disp(i);
for j=1+r:M-r;
min_box_r=min(min(I(i-r:i+r,j-r:j+r,1)));
min_box_g=min(min(I(i-r:i+r,j-r:j+r,2)));
min_box_b=min(min(I(i-r:i+r,j-r:j+r,3)));
max_box_r=max(max(I(i-r:i+r,j-r:j+r,1)));
max_box_g=max(max(I(i-r:i+r,j-r:j+r,2)));
max_box_b=max(max(I(i-r:i+r,j-r:j+r,3)));
sigm_r=std2(I(i-r:i+r,j-r:j+r,1));
sigm_g=std2(I(i-r:i+r,j-r:j+r,2));
sigm_b=std2(I(i-r:i+r,j-r:j+r,3));
Kr=15*sigm_r;Kg=15*sigm_g;Kb=15*sigm_b;
Iout(i,j,1)=I(i,j,1)*(1-Kr)+(I(i,j,1)-min_box_r)/(max_box_r-min_box_r+eps)*Kr;
Iout(i,j,2)=I(i,j,2)*(1-Kg)+(I(i,j,2)-min_box_g)/(max_box_g-min_box_g+eps)*Kg;
Iout(i,j,3)=I(i,j,3)*(1-Kb)+(I(i,j,3)-min_box_b)/(max_box_b-min_box_b+eps)*Kb;
end;
end;
Iout=Iout(1+r:N-r,1+r:M-r,:);
figure, imshow(Iout);
%imwrite(Iout,'15_15.jpg');
Пороговая обработка цветных изображений
Существует очень много подходов к решению задачи пороговой обработки цветных изображений. В данном материале эту задачу будем решать через анализ интенсивности, насыщенности, цветового фона и нормированных цветовых составляющих.
Для этого сначала считаем и визуализируем некоторое цветное изображение.
L=imread('fabric.png');
L=double(L)./255;
figure, imshow(L);
title('Исходное изображение');
Исходное изображение
Теперь сформируем и визуализируем значения интенсивности исходного изображения и построим их гистограмму.
I=L(:,:,1)+L(:,:,2)+L(:,:,3);
figure, subplot(211);imshow(I);title('Интенсивность');
subplot(212); imhist(I);
imwrite(I,'I.bmp');
Интенсивность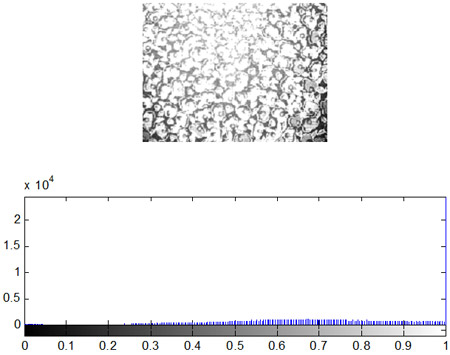
Сформируем нормированное значение r составляющей изображения и визуализируем ее. Также построим гистограмму полученных данных.
r=L(:,:,1)./(I+eps);
figure, subplot(211);imshow(r);title('Составляющая r');
subplot(212); imhist(r);
imwrite(r,'r.bmp');
Составляющая r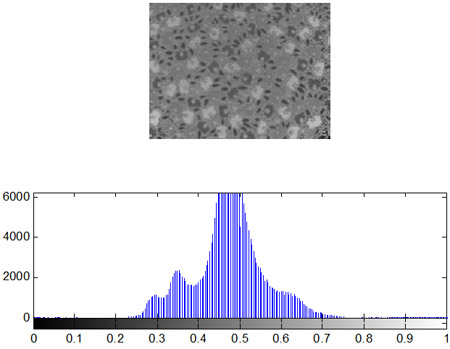
Аналогично сформируем и визуализируем g цветовую составляющую исходного изображения и построим ее гистограмму.
g=L(:,:,2)./(I+eps);
figure, subplot(211);imshow(g);title('Составляющая g');
subplot(212); imhist(g);
imwrite(g,'g.bmp');
Составляющая g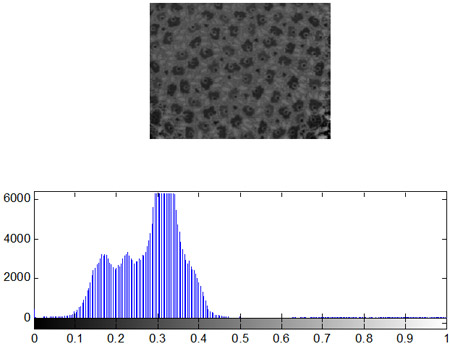
Далее сформируем и визуализируем b цветовую составляющую исходного изображения и построим ее гистограмму.
b=L(:,:,3)./(I+eps);
figure, subplot(211);imshow(b);title('Составляющая b');
subplot(212); imhist(b);
imwrite(b,'g.bmp');
Составляющая b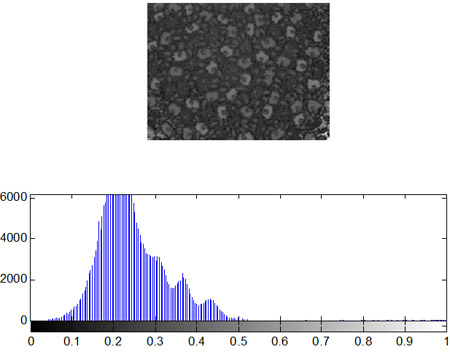
Также необходимо сформировать значения насыщенности S изображения.
[N M]=size(r);
for i=1:N;
disp(i);
for j=1:M;
MINIMUM=min([r(i,j) g(i,j) b(i,j)]);
S(i,j)=1-3*MINIMUM;
end;
end;
S(S<0)=0;
Визуализируем эти данные и построим их гистограмму.
figure, subplot(211);imshow(S);title('Насыщенность S');
subplot(212); imhist(S);
imwrite(S,'S.bmp');
Насыщенность S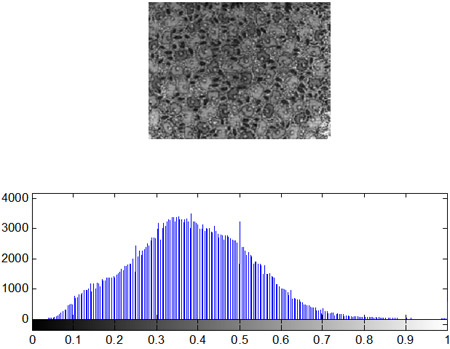
Сформируем также значения насыщенности F изображения, визуализируем их и построим гистограмму.
F=acos((2*r-g-b)./(sqrt(6).*sqrt( (r-1/3).^2+(g-1/3).^2+(b-1/3).^2)));
figure, subplot(211);imshow(F);title('Цветовой фон F');
subplot(212); imhist(F);
imwrite(F,'F.bmp');
Цветовой фон F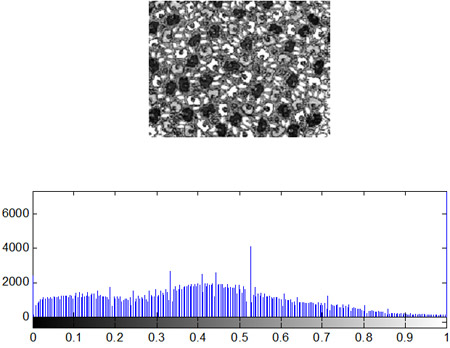
Таким образом, нами сформированы наборы данных (r-, g-, b-цветовые составляющие, насыщенность S, интенсивность I и фон F), которые будут использованы при проведении пороговых операций над исходным изображением.
Далее на основе анализа гистограммы полученных данных выберем пороговое значение и проведем бинаризацию изображения:
1) Для изображения значений интенсивности исходного изображения. Пороговое значение равно среднеарифметическому значению уровней интенсивности.
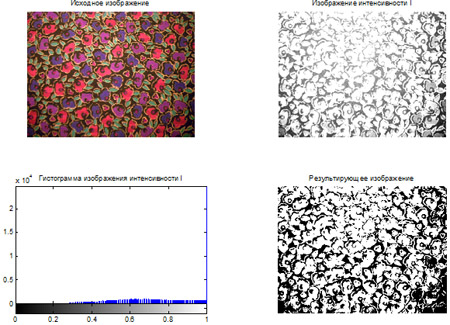
2) Для r цветовой составляющей изображения. Гистограмма r цветовой составляющей изображения имеет несколько ярко выраженных мод, которые и будут определять пороговые значения для обработки этого изображения. Это позволит выделить несколько типов объектов.
а) Пороговое значение определяется диапазоном [0, 0.31).
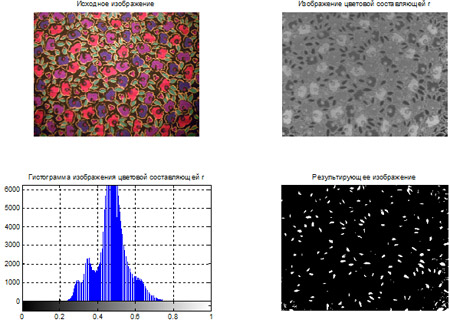
б) Пороговое значение определяется диапазоном [0.31, 0.39).
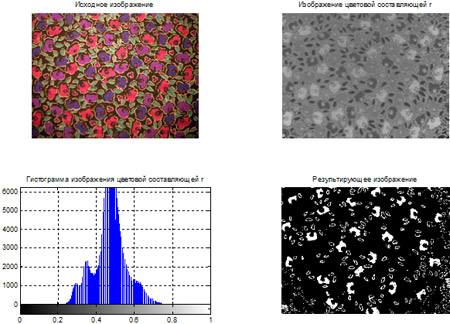
3) Для g цветовой составляющей изображения. Также как и в предыдущем случае, гистограмма распределения этой цветовой составляющей имеет несколько ярко выраженных мод, которые будут основой для выбора порогового значения.
а) Пороговое значение определяется диапазоном [0, 0.2).
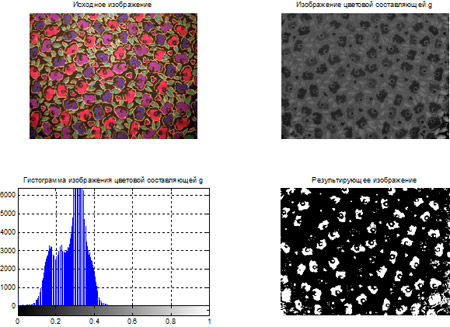
б) Пороговое значение определяется диапазоном [0.2, 0.25).
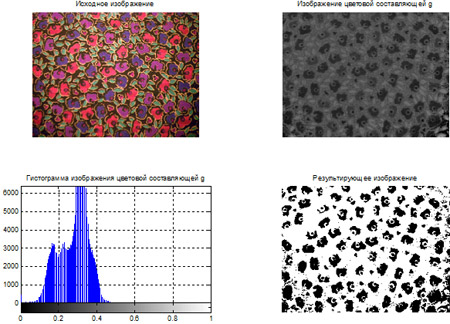
4) Для b цветовой составляющей изображения. Гистограмма этой цветовой составляющей также имеет несколько мод, анализ которых будет служить основой для выбора пороговых значений.
а) Пороговое значение определяется диапазоном [0, 0.35).
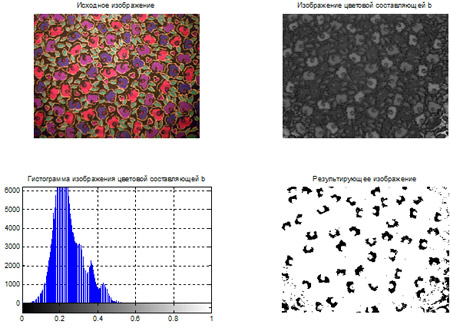
б) Пороговое значение определяется диапазоном [0.35, 0,4).
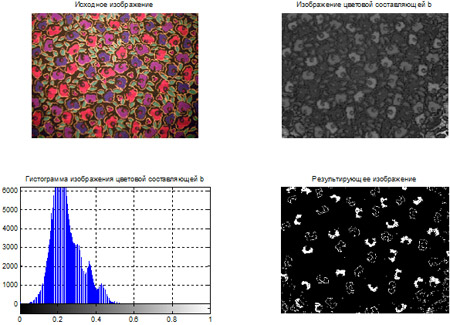
в) Пороговое значение определяется диапазоном [0.4, 0,5).
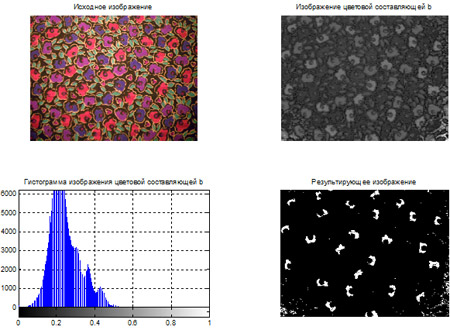
5) Для значений насыщенности S изображения. В этом случае пороговое значение можно выбирать как по гистограмме, так и экспериментальным путем. Пусть пороговое значение будет определяться диапазоном [0, 0.25).
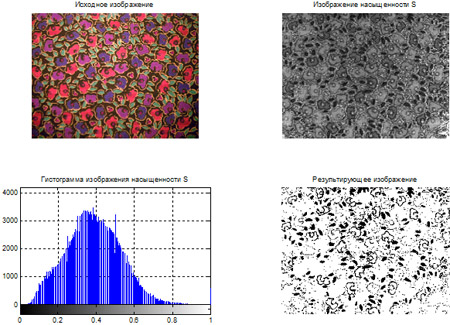
6) Для значений цветового фона F изображения. В этом случае гистограмма имеет две моды, на основе которых будут определены пороговые значения.
а) Пороговое значение определяется диапазоном [0, 0.25).
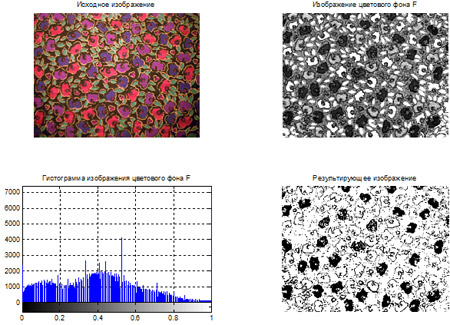
б) Пороговое значение определяется диапазоном [0.6, 1).
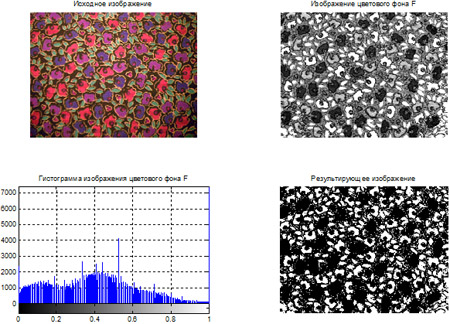
Бывают случаи, когда для выделения объектов на изображении необходимо использовать все или несколько параметров (значения цветовых составляющих, интенсивность, насыщенность и значения фона). Приведем пример программы, когда для выделения объектов (например, зеленого листья) использовались все параметры.
clear;
L=imread('fabric.png');
L=double(L)./255;
figure,imshow(L);title('Исходное изображение');
R=imread('r.bmp');
R=R(:,:,1);
R=double(R)./255;
G=imread('g.bmp');
G=G(:,:,1);
G=double(G)./255;
B=imread('b.bmp');
B=B(:,:,1);
B=double(B)./255;
F=imread('F.bmp');
F=F(:,:,1);
F=double(F)./255;
I=imread('I.bmp');
I=I(:,:,1);
I=double(I)./255;
S=imread('S.bmp');
S=S(:,:,1);
S=double(S)./255;
[N M]=size(R);
%Lser=mean(mean(R));
for i=1:N;
disp(i);
for j=1:M;
if ((R(i,j)-0)<.4)&((G(i,j)-0)>.35)&((B(i,j)-0)<.4)&
((F(i,j)-0)>.1)&((S(i,j)-0)>.1)&((I(i,j)-0)>.1);
L(i,j,1)=0;L(i,j,2)=1;L(i,j,3)=0;
end;
end;
end;
figure,imshow(L);title('Результирующее изображение');
Результирующее изображение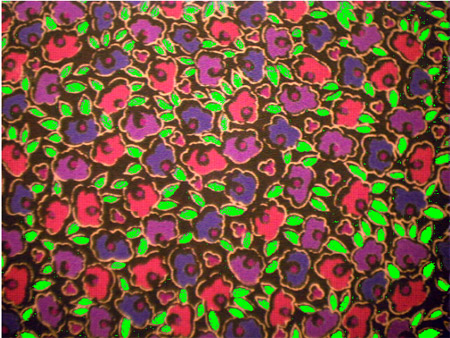
Тексты программ, которые использовались при подготовке материала.
1) Программа, которая реализует формирование исходных данных для проведения пороговых операций.
clear;
%L=imread('peppers.png');
%L=imread('tissue.png');
%L=imread('greens.jpg');
L=imread('fabric.png');
L=double(L)./255;
figure, imshow(L);title('Исходное изображение');
I=L(:,:,1)+L(:,:,2)+L(:,:,3);
figure, subplot(211);imshow(I);title('Интенсивность');
subplot(212); imhist(I);
imwrite(I,'I.bmp');
r=L(:,:,1)./(I+eps);
figure, subplot(211);imshow(r);title('Составляющая r');
subplot(212); imhist(r);
imwrite(r,'r.bmp');
g=L(:,:,2)./(I+eps);
figure, subplot(211);imshow(g);title('Составляющая g');
subplot(212); imhist(g);
imwrite(g,'g.bmp');
b=L(:,:,3)./(I+eps);
figure, subplot(211);imshow(b);title('Составляющая b');
subplot(212); imhist(b);
imwrite(b,'b.bmp');
[N M]=size(r);
for i=1:N;
disp(i);
for j=1:M;
MINIMUM=min([r(i,j) g(i,j) b(i,j)]);
S(i,j)=1-3*MINIMUM;
end;
end;
S(S<0)=0;
figure, subplot(211);imshow(S);title('Насыщенность S');
subplot(212); imhist(S);
imwrite(S,'S.bmp');
F=acos((2*r-g-b)./(sqrt(6).*sqrt( (r-1/3).^2+(g-1/3).^2+(b-1/3).^2)));
figure, subplot(211);imshow(F);title('Цветовой фон F');
subplot(212); imhist(F);
imwrite(F,'F.bmp');
2) Программа, которая реализует пороговую обработку на основе значений цветовых составляющих, интенсивности, насыщенности и значений фона.
clear;
L=imread('fabric.png');
figure, subplot(221);imshow(L);title('Исходное изображение');
L=imread('F.bmp');
L=L(:,:,1);
L=double(L)./255;
subplot(222);imshow(L);title('Изображение цветового фона F');
subplot(223);imhist(L);grid;title('Гистограмма изображения цветового фона F');
[N M]=size(L);
Lser=mean(mean(L));
for i=1:N;
disp(i);
for j=1:M;
if L(i,j)>0.6;
L(i,j)=1;
else L(i,j)=0;
end;
end;
end;
subplot(224);imshow(L);title('Результирующее изображение');
Формирование ночного изображения на основе дневного и наоборот
Формирование ночного изображения на основе дневного
Новые возможности цифровой обработки изображений предоставляют пользователю широкие возможности для разнообразных преобразований. В данной работе будет рассмотрено одно из таких преобразований, а именно — виртуальное преобразование условий формирования изображений.
Ночные изображения, в отличие от дневных, характеризуются более низким суммарным контрастом, более низкой яркостью и размытыми границами объектов. Таким образом, можно предположить, что для получения ночного изображения необходимо понизить контраст, яркость и размыть границы на дневном изображении. Еще одной особенностью ночных изображений является более весомое присутствие оттенков синей цветовой составляющей.
Приведем пример программной реализации описанного выше метода формирования ночного изображения на основе дневного. Для этого сначала считаем в рабочее пространство Matlab некоторое исходное изображение в формате rgb, которое сделано в дневное время суток.
%Считывание исходного изображения
L_rgb=imread('krepost.bmp');
[N M s]=size(L_rgb);
L_rgb=double(L_rgb)./255;
figure, imshow(L_rgb);
title('Исходное изображение в цветовом пространстве RGB');

Как уже было сказано выше, ночные изображения характеризуются более весомым присутствием синей составляющей. Для проведения последующих операций преобразуем изображение из цветового пространства rgb в цветовое пространство xyz.
%Преобразование изображения из цветового пространства rgb в цветовое
%пространство xyz
trans=[0.5149 0.3244 0.1607; 0.2654 0.6704 0.0642; 0.0248 0.1248 0.8504];
for i=1:N;
disp(i);
for j=1:M;
L_xyz(i,j,:)=[L_rgb(i,j,1) L_rgb(i,j,2) L_rgb(i,j,3)]*trans;
end;
end;
figure, imshow(L_xyz);title('Исходное изображение в цветовом пространстве XYZ');

Следующий шаг заключается в формировании двух размытых затемненных изображений. Для этого будем использовать свертку исходного изображения с фильтром Гаусса. Стандартное отклонение в функции fspecial выбирается таким образом, чтобы подавить мелкие детали, которые невидимы ночью.
%Формирование первого размытого изображения
h = fspecial('gaussian',[11 11],0.1);
L_xyz_blur_1 = imfilter(L_xyz,h,'replicate');
figure, imshow(L_xyz_blur_1);
title('Первое размытое исходное изображение в цветовом пространстве XYZ');

%Формирование второго размытого изображения
h = fspecial('gaussian',[11 11],0.1)./6;
L_xyz_blur_2 = imfilter(L_xyz,h,'replicate');
figure, imshow(L_xyz_blur_2);
title('Второе размытое исходное изображение в цветовом пространстве XYZ');

Далее приступаем к формированию ночного изображения на основе дневного. При этом существует два варианта решения этой задачи.
%Вариант 1
a=0.2;
L_nigth_1=L_xyz_blur_2+a.*(L_xyz_blur_1-L_xyz_blur_2);
figure, imshow(L_nigth_1);
title('Ночное изображение (вариант 1)');

%Вариант 2
a=2;
L_nigth_2=L_xyz_blur_2+(L_xyz_blur_1-L_xyz_blur_2).*(1/a);
figure, imshow(L_nigth_2);
title('Ночное изображение (вариант 2)');

В этой части материала нами приведен пример формирования ночного изображения на основе дневного. Для обеспечения реалистичности ночных изображений используются два основных параметра – значение стандартного среднеквадратического отклонения в функции fspecial и коэффициент усиления a.
Программа, которая реализует приведенный выше метод:
%===== Формирование ночного изображения на основе дневного =====
clear;
%Считывание исходного изображения
L_rgb=imread('krepost.bmp');
[N M s]=size(L_rgb);
L_rgb=double(L_rgb)./255;
figure, imshow(L_rgb);
title('Исходное изображение в цветовом пространстве RGB');
%Преобразование изображения из цветового пространства rgb в цветовое
%пространство xyz
trans=[0.5149 0.3244 0.1607; 0.2654 0.6704 0.0642; 0.0248 0.1248 0.8504];
for i=1:N;
disp(i);
for j=1:M;
L_xyz(i,j,:)=[L_rgb(i,j,1) L_rgb(i,j,2) L_rgb(i,j,3)]*trans;
end;
end;
figure, imshow(L_xyz);
title('Исходное изображение в цветовом пространстве XYZ');
%Формирование первого размытого изображения
h = fspecial('gaussian',[11 11],0.1);
L_xyz_blur_1 = imfilter(L_xyz,h,'replicate');
figure, imshow(L_xyz_blur_1);
title('Первое размытое исходное изображение в цветовом пространстве XYZ');
%Формирование второго размытого изображения
h = fspecial('gaussian',[11 11],0.1)./6;
L_xyz_blur_2 = imfilter(L_xyz,h,'replicate');
figure, imshow(L_xyz_blur_2);
title('Второе размытое исходное изображение в цветовом пространстве XYZ');
a=0.2;
L_nigth_1=L_xyz_blur_2+a.*(L_xyz_blur_1-L_xyz_blur_2);
figure, imshow(L_nigth_1);
title('Ночное изображение (вариант 1)');
a=2;
L_nigth_2=L_xyz_blur_2+(L_xyz_blur_1-L_xyz_blur_2).*(1/a);
figure, imshow(L_nigth_2);
title('Ночное изображение (вариант 2)');
Формирование дневного изображения на основе ночного
В рамках данного материала интересно будет рассмотреть обратную задачу — формирование дневного изображения на основе ночного. Прежде чем приступить к решению данной задачи, еще раз определим основные отличия между изображениями, которые сформированы в дневное и ночное время суток. Прежде всего, они отличаются значениями интенсивностей пикселей, поэтому при имитации дневного изображения на основе ночного необходимо проводить коррекцию динамического диапазона яркостей. Второй особенностью, которая отличает изображения сделанные в дневное время суток от ночных изображений, является более четкая видимость мелких деталей. Для повышения детализации изображений необходимо будет проводить операцию контрастирования или подчеркивания границ.
Итак, приведем пример формирования дневного изображения на основе ночного.
Сначала считаем в рабочее пространство Matlab в качестве исходного ночное изображение, которое было сформировано в первой части материала.
%Считывание исходного изображения
L_rgb=imread('L_nigth_1.bmp');
[N M s]=size(L_rgb);
L_rgb=double(L_rgb)./255;
figure,imshow(L_rgb);
title('Исходное изображение в цветовом пространстве RGB');
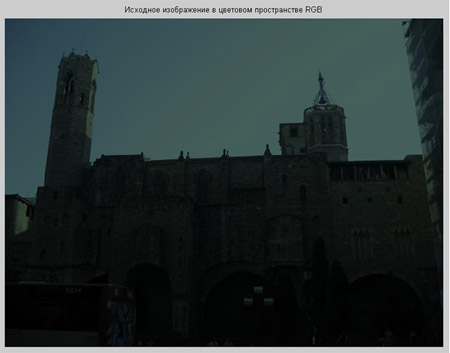
Построим гистограммы значений интенсивностей цветовых составляющих пикселей исходного изображения и проанализируем их.
figure, subplot(321),imshow(L_rgb(:,:,1));
title('Цветовая составляющая r');
subplot(323),imshow(L_rgb(:,:,2));
title('Цветовая составляющая g');
subplot(325),imshow(L_rgb(:,:,3));
title('Цветовая составляющая b');
subplot(322),imhist(L_rgb(:,:,1));
title('Гистограмма составляющей r');
subplot(324),imhist(L_rgb(:,:,2));
title('Гистограмма составляющей g');
subplot(326),imhist(L_rgb(:,:,3));
title('Гистограмма составляющей b');
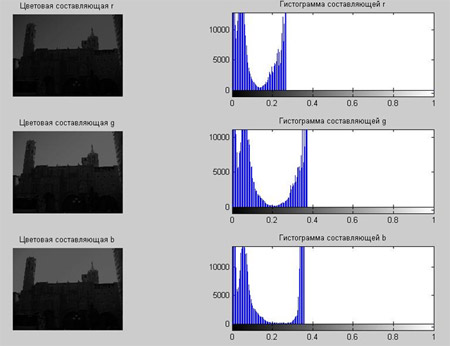
Из приведенных гистограмм видно, что значения интенсивностей цветовых составляющих находятся в довольно ограниченном диапазоне, что отрицательно влияет на зрительное восприятие таких изображений. Проведем операцию растяжения динамического диапазона значений интенсивностей цветовых составляющих.
%Коррекция динамического яркостного диапазона L_r_new=(L_rgb(:,:,1)-min(min(L_rgb(:,:,1))))./(max(max(L_rgb(:,:,1)))-min(min(L_rgb(:,:,1)))); L_g_new=(L_rgb(:,:,2)-min(min(L_rgb(:,:,2))))./(max(max(L_rgb(:,:,2)))-min(min(L_rgb(:,:,2)))); L_b_new=(L_rgb(:,:,3)-min(min(L_rgb(:,:,3))))./(max(max(L_rgb(:,:,3)))-min(min(L_rgb(:,:,3))));
Визуализируем сначала каждую из скорректированных цветовых составляющих отдельно.
figure, subplot(321),imshow(L_r_new);
title('Скорректированная составляющая r');
subplot(323),imshow(L_g_new);
title('Скорректированная составляющая g');
subplot(325),imshow(L_b_new);
title('Скорректированная составляющая b');
subplot(322),imhist(L_r_new);
title('Гистограмма составляющей r');
subplot(324),imhist(L_g_new);
title('Гистограмма составляющей g');
subplot(326),imhist(L_b_new);
title('Гистограмма составляющей b');
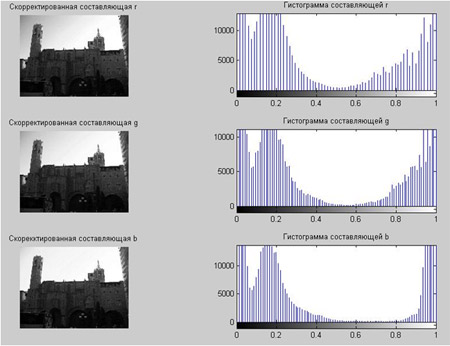
Из представленных изображений видно, что каждая из скорректированных цветовых составляющих занимает весь динамический диапазон. Теперь представим эти составляющие в виде цветного изображения.
L_new(:,:,1)=L_r_new; L_new(:,:,2)=L_g_new; L_new(:,:,3)=L_b_new;
figure, imshow(L_new);
title('Исходное изображение с скорректированным динамическим диапазоном интенсивностей');
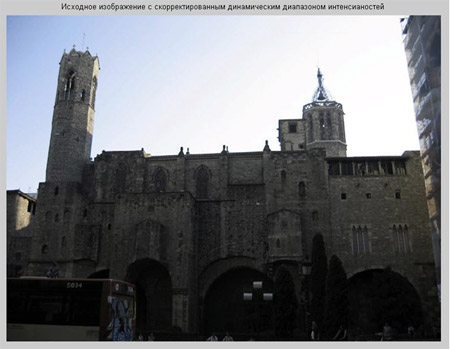
Существенным недостатком полученного изображения является то, что оно характеризуется низким контрастом. Этим объясняется плохая видимость мелких деталей и низкое визуальное качество в целом.
Для устранения этого недостатка необходимо провести операцию повышения контрастности изображений. В данном примере эта операция проводится отдельно для каждой цветовой составляющей. Такое действие дает хороший результат, но более корректно такие операции проводить, рассматривая не отдельные цветовые составляющие, а цвет пикселя в целом. Это позволит обойти проблему разбалансировки цветов.
%Повышение резкости изображения
h = fspecial('unsharp',0.2);
L_r_new_unsharp = imfilter(L_r_new,h,'replicate');
L_g_new_unsharp = imfilter(L_g_new,h,'replicate');
L_b_new_unsharp = imfilter(L_b_new,h,'replicate');
Сформируем результирующее изображение.
L_new_unsharp(:,:,1)=L_r_new_unsharp;
L_new_unsharp(:,:,2)=L_g_new_unsharp;
L_new_unsharp(:,:,3)=L_b_new_unsharp;
figure, imshow(L_new_unsharp);
title('Исходное изображение с скорректированными динамическим диапазоном и контрастностью');

Интересно будет сравнить исходное дневное изображение из первой части материала и сформированное программным способом.
|
|
|
| Исходное дневное изображение | Сформированное изображение |
Проводя анализ исходного и сформированного программным путем изображений, можно сказать, что по качеству визуального восприятия результирующее изображение не уступает исходному, что свидетельствует об эффективности предложенного метода.
Дополнительно отметим, что качество результирующего изображения можно повысить, улучшив зрительное восприятие затемненных областей. Корректировка будет проводиться для каждой цветовой составляющей отдельно.
%Коррекция динамического яркостного диапазона
L_r_new = imadjust(L_rgb(:,:,1),[0; .3],[],.7);
L_g_new = imadjust(L_rgb(:,:,2),[0; .3],[],.7);
L_b_new = imadjust(L_rgb(:,:,3),[0; .3],[],.7);
figure, subplot(321),imshow(L_r_new);
title('Скорректированная составляющая r');
subplot(323),imshow(L_g_new);
title('Скорректированная составляющая g');
subplot(325),imshow(L_b_new);
title('Скорректированная составляющая b');
subplot(322),imhist(L_r_new);
title('Гистограмма составляющей r');
subplot(324),imhist(L_g_new);
title('Гистограмма составляющей g');
subplot(326),imhist(L_b_new);
title('Гистограмма составляющей b');
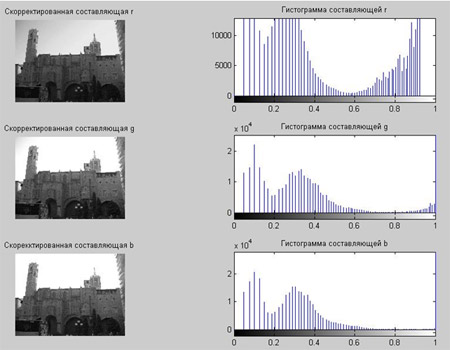
В некоторых случаях целесообразно провести дополнительное контрастирование изображения. И результат представляется в следующем виде.
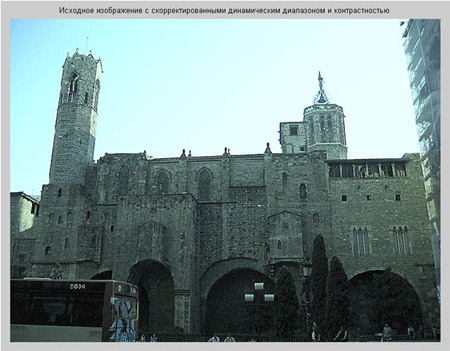
Программа, которая реализует метод имитации дневных изображений на основе ночных:
%===== Формирование дневных изображений на основе ночных =====
clear;
%Считывание исходного изображения
L_rgb=imread('n1.bmp');
[N M s]=size(L_rgb);
L_rgb=double(L_rgb)./255;
figure,imshow(L_rgb);
title('Исходное изображение в цветовом пространстве RGB');
figure, subplot(321),imshow(L_rgb(:,:,1));
title('Цветовая составляющая r');
subplot(323),imshow(L_rgb(:,:,2));
title('Цветовая составляющая g');
subplot(325),imshow(L_rgb(:,:,3));
title('Цветовая составляющая b');
subplot(322),imhist(L_rgb(:,:,1));
title('Гистограмма составляющей r');
subplot(324),imhist(L_rgb(:,:,2));
title('Гистограмма составляющей g');
subplot(326),imhist(L_rgb(:,:,3));
title('Гистограмма составляющей b');
%Коррекция динамического яркостного диапазона
L_r_new=(L_rgb(:,:,1)-min(min(L_rgb(:,:,1))))./(max(max(L_rgb(:,:,1)))-min(min(L_rgb(:,:,1))));
L_g_new=(L_rgb(:,:,2)-min(min(L_rgb(:,:,2))))./(max(max(L_rgb(:,:,2)))-min(min(L_rgb(:,:,2))));
L_b_new=(L_rgb(:,:,3)-min(min(L_rgb(:,:,3))))./(max(max(L_rgb(:,:,3)))-min(min(L_rgb(:,:,3))));
figure, subplot(321),imshow(L_r_new);
title('Скорректированная составляющая r');
subplot(323),imshow(L_g_new);
title('Скорректированная составляющая g');
subplot(325),imshow(L_b_new);
title('Скорректированная составляющая b');
subplot(322),imhist(L_r_new);
title('Гистограмма составляющей r');
subplot(324),imhist(L_g_new);
title('Гистограмма составляющей g');
subplot(326),imhist(L_b_new);
title('Гистограмма составляющей b');
L_new(:,:,1)=L_r_new; L_new(:,:,2)=L_g_new; L_new(:,:,3)=L_b_new;
figure, imshow(L_new);
title('Исходное изображение с скорректированным
динамическим диапазоном интенсивностей');
%Повышение резкости изображения
h = fspecial('unsharp',0.2);
L_r_new_unsharp = imfilter(L_r_new,h,'replicate');
L_g_new_unsharp = imfilter(L_g_new,h,'replicate');
L_b_new_unsharp = imfilter(L_b_new,h,'replicate');
L_new_unsharp(:,:,1)=L_r_new_unsharp;
L_new_unsharp(:,:,2)=L_g_new_unsharp;
L_new_unsharp(:,:,3)=L_b_new_unsharp;
figure, imshow(L_new_unsharp);
title('Исходное изображение с скорректированными
динамическим диапазоном и контрастностью');
- W.B.Thompson, P.Shirley A Spatial Post-Processing Algorithm for Images of Night Scenes, 2002
- Е.Макарова, А. Конушин. Формирование ночного изображения на основе дневного
Обнаружение лиц на основе цвета
Существует большое количество задач, одной из составляющих которых является вопрос автоматического распознавания лиц на изображениях. Подходов к решению этого вопроса существует много, однако в рамках данного материала рассмотрим метод автоматического обнаружения лиц на изображениях на основе анализа цвета.
Считаем некоторое исходное изображение в рабочее пространство Matlab.
clear;
%Считывание исходного изображения
L=imread('im.jpg');
[N M s]=size(L);
L=double(L)./255;
figure, imshow(L);
title('Исходное изображение');

Далее необходимо на изображении лица выбрать пиксели с характерным цветом, определить среднее значение их интенсивности и среднеквадратическое отклонение.
[x,y,z]=impixel; r=median(z(:,1)); std_r=std(z(:,1)); g=median(z(:,2)); std_g=std(z(:,2)); b=median(z(:,3)); std_b=std(z(:,3));
На основе знаний о значениях интенсивностей пикселей лица и их возможных вариациях проводится сегментация изображения.
%Сегментация на основе анализа цвета.
for i=1:N;
disp(i);
for j=1:M;
if (abs(L(i,j,1)-r)<std_r)&(abs(L(i,j,2)-g)<std_g)&(abs(L(i,j,3)-b)«std_b);
L1(i,j)=1;
else
L1(i,j)=0;
end;
end;
end;
figure, imshow(L1);title('Исходное изображение после сегментации');

Целью сегментации было выделение лица на изображении. Однако, вполне естественно, что на изображении присутствовали и другие объекты, значения интенсивностей пикселей которых совпали с интенсивностью пикселей лица. В результате на сегментированном изображении кроме лица выделились и другие объекты. Теперь на сегментированном изображении предстоит найти изображение нужного объекта, т.е. лица. Критерии поиска могут быть разными. Это может быть площадь, форма и др. В данном примере в качестве критерия для поиска лица выберем площадь. Исходя из выбранного ранее способа сегментации, можно предположить, что лицо занимает наибольшую площадь. Поэтому выбор критерия для поиска лица на основе площади позволит удалить другие объекты, которые меньше за площадью.
%Удаление объектов, площадь которых меньше некоторой заданной величины (для удаления шума)
[mitka num]=bwlabel(L1,8);
feats=imfeature(mitka,'Area',8);
Areas=zeros(num);
for i=1:num;
Areas(i)=feats(i).Area;
end;
idx=find(Areas>750);
L1=ismember(mitka,idx);
figure,imshow(L1);title('После удаления шума (небольших объектов)');

Удалим также и другие объекты на сегментированном изображении лица.
L1=1-L1;
[mitka num]=bwlabel(L1,8);
feats=imfeature(mitka,'Area',8);
Areas=zeros(num);
for i=1:num;
Areas(i)=feats(i).Area;
end;
idx=find(Areas>750);
L1=ismember(mitka,idx);
L1=1-L1;
figure,imshow(L1);
title('После удаления шума (небольших объектов)');

Здесь следует отметить, что выбранного нами критерия может быть недостаточно для достоверного определения объекта поиска, т.е. изображения лица. Такое может произойти в том случае, если на изображении присутствуют другие объекты с похожим цветом, лицо может быть в тени, быть под наклоном и т.п. Поэтому необходимо использовать также другие критерии для поиска изображения лица. Такие критерии могут базироваться на априорной информации о форме лица.
Таким образом, для повышения достоверности распознавания критерий поиска лица на изображении должен быть комплексным.
Далее проводим выделение выбранного лица, например, прямоугольником.
MIN_i=N;MIN_j=M;MAX_i=0;MAX_j=0;
for i=1:N;
disp(i);
for j=1:M;
if L1(i,j)==1;
if i<MIN_i;
MIN_i=i;
end;
if j<MIN_j;
MIN_j=j;
end;
if i>MAX_i;
MAX_i=i;
end;
if j>MAX_j;
MAX_j=j;
end;
end;
end;
end;
figure, imshow(L);
line([MIN_j MAX_j],[MIN_i MIN_i]);hold on;
line([MAX_j MAX_j],[MIN_i MAX_i]);
line([MAX_j MIN_j],[MAX_i MAX_i]);
line([MIN_j MIN_j],[MIN_i MAX_i]);hold off;

Программа, реализующая приведенный выше метод:
%==========ОБНАРУЖЕНИЕ ЛИЦ НА ОСНОВЕ ЦВЕТА=======
clear;
%Считывание исходного изображения
L=imread('im.jpg');
[N M s]=size(L);
L=double(L)./255;
figure, imshow(L);title('Исходное изображение');
%Выбор пикселей лица с характерным цветом
[x,y,z]=impixel;
r=median(z(:,1)); std_r=std(z(:,1));
g=median(z(:,2)); std_g=std(z(:,2));
b=median(z(:,3)); std_b=std(z(:,3));
%Сегментация на основе анализа цвета
for i=1:N;
disp(i);
for j=1:M;
if (abs(L(i,j,1)-r)<std_r)&(abs(L(i,j,2)-g)<std_g)&(abs(L(i,j,3)-b)<std_b);
L1(i,j)=1;
else
L1(i,j)=0;
end;
end;
end;
figure, imshow(L1);title('Исходное изображение после сегментации');
%Удаление объектов, площадь которых меньше некоторой
заданной величины (для удаления шума)
[mitka num]=bwlabel(L1,8);
feats=imfeature(mitka,'Area',8);
Areas=zeros(num);
for i=1:num;
Areas(i)=feats(i).Area;
end;
idx=find(Areas>750);
L1=ismember(mitka,idx);
figure,imshow(L1);title('После удаления шума (небольших объектов)');
L1=1-L1;
[mitka num]=bwlabel(L1,8);
feats=imfeature(mitka,'Area',8);
Areas=zeros(num);
for i=1:num;
Areas(i)=feats(i).Area;
end;
idx=find(Areas>750);
L1=ismember(mitka,idx);
L1=1-L1;
figure,imshow(L1);title('После удаления шума (небольших объектов)');
%STATS = regionprops(L1,'Eccentricity');
MIN_i=N;MIN_j=M;MAX_i=0;MAX_j=0;
for i=1:N;
disp(i);
for j=1:M;
if L1(i,j)==1;
if i<MIN_i;
MIN_i=i;
end;
if j<MIN_j;
MIN_j=j;
end;
if i>MAX_i;
MAX_i=i;
end;
if j>MAX_j;
MAX_j=j;
end;
end;
end;
end;
figure, imshow(L);
line([MIN_j MAX_j],[MIN_i MIN_i]);hold on;
line([MAX_j MAX_j],[MIN_i MAX_i]);
line([MAX_j MIN_j],[MAX_i MAX_i]);
line([MIN_j MIN_j],[MIN_i MAX_i]);hold off;
Если же на изображении присутствует несколько лиц одновременно, то рассмотренный выше метод необходимо модифицировать. Рассмотрим это более детально. Первые несколько шагов (считывание исходного изображения, выбор характерных пикселей, сегментация и фильтрация) аналогичны, как и в предыдущем методе, поэтому мы приведем только результаты выполнения этих операций.

Исходное изображение
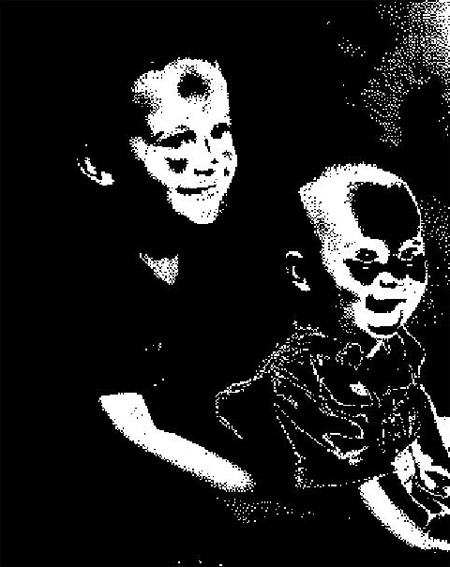
Исходное изображение после сегментации

Изображение после фильтрации объектов, которые представлены пикселями со значениями равными 1.

Изображение после фильтрации объектов, которые представлены пикселями со значениями равными 0.
Далее необходимо проанализировать объекты на изображении. Сначала с помощью функции bwlabel определим общее количество объектов на изображении и отметим их.
Lmitky = bwlabel(L1,4); figure,imshow(Lmitky);

Изображение меток
На основе анализа условий съемки и площадей отмеченных объектов определяем расположение лиц на изображении.
H=hist(Lmitky(:),max(max(Lmitky))); Nomer=find(H>4000);
Конечно, для повышения достоверности определения лиц на изображении, нужно использовать также и другие критерии, которые могут базироваться на основе анализа формы изображения лица.
figure, imshow(L);
for r=2:length(Nomer);
MIN_i=N;MIN_j=M;MAX_i=0;MAX_j=0;
for i=1:N;
for j=1:M;
if Lmitky(i,j)==Nomer(r);
if i<MIN_i;
MIN_i=i;
end;
if j<MIN_j;
MIN_j=j;
end;
if i>MAX_i;
MAX_i=i;
end;
if j>MAX_j;
MAX_j=j;
end;
end;
end;
end;
line([MIN_j MAX_j],[MIN_i MIN_i]);hold on;
line([MAX_j MAX_j],[MIN_i MAX_i]);
line([MAX_j MIN_j],[MAX_i MAX_i]);
line([MIN_j MIN_j],[MIN_i MAX_i]);hold off;
end;
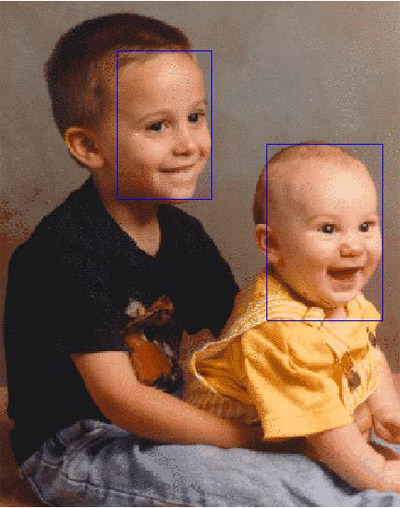
Результат
Приведем еще один пример, подтверждающий то, что при распознавании лиц на изображения, нужно использовать более надежные критерии распознавания, нежели просто площадь. Доказательством тому служит изображение, которое приведено внизу. Распознавание изображения лица по яркости и площади привело к тому, что кроме лиц, выделились также и руки. Как уже было отмечено выше, для недопущения таких ошибок необходимо использовать также другие критерии, например, анализировать форму.

Модифицированная программа для обнаружения нескольких лиц на изображении:
%==========ОБНАРУЖЕНИЕ ЛИЦ НА ОСНОВЕ ЦВЕТА=======
clear;
%Считывание исходного изображения
L=imread('kids.bmp');
%L=imread('im.jpg');
[N M s]=size(L);
L=double(L)./255;
figure, imshow(L);title('Исходное изображение');
%Выбор пикселей лица с характерным цветом
[x,y,z]=impixel;
r=median(z(:,1)); std_r=std(z(:,1));
g=median(z(:,2)); std_g=std(z(:,2));
b=median(z(:,3)); std_b=std(z(:,3));
%Сегментация на основе анализа цвета
for i=1:N;
disp(i);
for j=1:M;
if (abs(L(i,j,1)-r)<std_r)&(abs(L(i,j,2)-g)<std_g)&(abs(L(i,j,3)-b)<std_b);
L1(i,j)=1;
else
L1(i,j)=0;
end;
end;
end;
figure, imshow(L1);title('Исходное изображение после сегментации');
imwrite(L1,'Исходное изображение после сегментации.jpg');
%Удаление объектов, площадь которых меньше
некоторой заданной величины (для удаления шума)
[mitka num]=bwlabel(L1,8);
feats=imfeature(mitka,'Area',8);
Areas=zeros(num);
for i=1:num;
Areas(i)=feats(i).Area;
end;
idx=find(Areas>5750);
L1=ismember(mitka,idx);
figure,imshow(L1);title('После удаления шума (небольших объектов)');
L1=1-L1;
[mitka num]=bwlabel(L1,8);
feats=imfeature(mitka,'Area',8);
Areas=zeros(num);
for i=1:num;
Areas(i)=feats(i).Area;
end;
idx=find(Areas>5750);
L1=ismember(mitka,idx);
L1=1-L1;
figure,imshow(L1);title('После удаления шума (небольших объектов)');
%STATS = regionprops(L1,'Eccentricity');
Lmitky = bwlabel(L1,4);
figure,imshow(Lmitky);
imwrite(Lmitky,'Изображение меток.jpg');
figure, imshow(L);
H=hist(Lmitky(:),max(max(Lmitky)));
Nomer=find(H>4000);
for r=2:length(Nomer);
MIN_i=N;MIN_j=M;MAX_i=0;MAX_j=0;
for i=1:N;
for j=1:M;
if Lmitky(i,j)==Nomer(r);
if i<MIN_i;
MIN_i=i;
end;
if j<MIN_j;
MIN_j=j;
end;
if i>MAX_i;
MAX_i=i;
end;
if j>MAX_j;
MAX_j=j;
end;
end;
end;
end;
line([MIN_j MAX_j],[MIN_i MIN_i]);hold on;
line([MAX_j MAX_j],[MIN_i MAX_i]);
line([MAX_j MIN_j],[MAX_i MAX_i]);
line([MIN_j MIN_j],[MIN_i MAX_i]);hold off;
end;
- Антон Обухов, Сергей Гришин. Метод обнаружения лиц на статических изображениях и видео на основе цвета
Метод управления яркостью изображения
Довольно часто возникает необходимость получения изображений с заданным значением средней интенсивности пикселей. Среднеарифметическое значение интенсивностей пикселей изображения равно
![]()
Если же мы зададим значение Aν равным K, то значения интенсивностей пикселей должны также каким-то образом измениться
![]()
Если в качестве функции преобразования выбрать ![]() , то получим
, то получим
![]()
Из последнего выражения видно, что, подобрав необходимое значение α, можно добиться того, что среднеарифметическое значение интенсивностей пикселей изображения L будет принимать установленное значение K.
Практически этот метод можно реализовать так. Сначала нужно построить зависимость K = f(α). Далее, зная, какое значение α соответствует установленному уровню K, провести преобразование исходного изображения.
Приведем пример программной реализации метода.
Сначала считаем некоторое исходное изображение.
I = imread('kids.bmp');
Для примера нам необходимо полутоновое изображение, поэтому если исходное изображение цветное, то необходимо выделить одну цветовую составляющую.
I=double(I(:,:,1));
figure, imshow(I./255);title('Исходное изображение');
Исходное изображение
Далее, согласно приведенному выше описанию, строим зависимость K = f(α).
a=[0:.01:3];
for i=1:length(a);
K(i)=sum(sum(((I-Imin)./(Imax-Imin)).^a(i)))/(N*M);
if abs(K(i)-R)<.01;
st=a(i);
end;
end;
figure,plot(a,K);
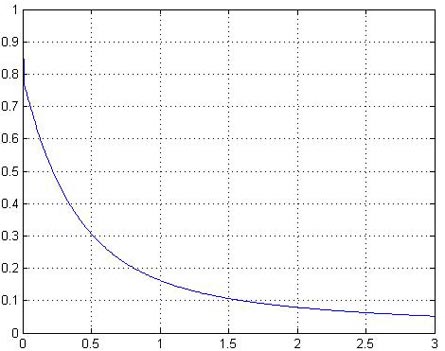
По графику можно определить какое значение должен принимать параметр α, чтобы среднеарифметическое значение интенсивностей изображения было равно K. После этого выполняются преобразования изображения с выбранным значением α.
Iout=((I-Imin)./(Imax-Imin)).^st;
Пример 1.
Приведем примеры реализации метода, результатом которых является формирование изображений с заданными уровнями среднеарифметических значений интенсивностей.
1) Среднеарифметическое значение интенсивностей пикселей изображения K = 0,3.

2) Среднеарифметическое значение интенсивностей пикселей изображения K = 0,4.

3) Среднеарифметическое значение интенсивностей пикселей изображения K = 0,5.

Пример 2.
Приведем такие же результаты для другого изображения.
1) График зависимости K = f(α).
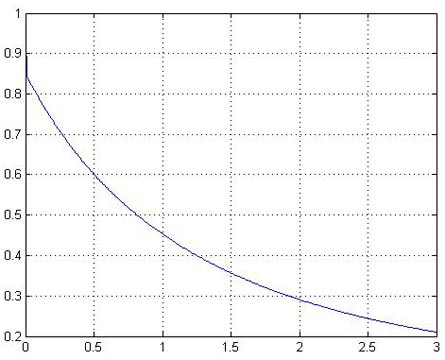
1) Среднеарифметическое значение интенсивностей пикселей изображения K = 0,3.

2) Среднеарифметическое значение интенсивностей пикселей изображения K = 0,5.

3) Среднеарифметическое значение интенсивностей пикселей изображения K = 0,7.

Описанный метод позволяет эффективно управлять среднеарифметическим значением интенсивности пикселей изображения.
Программа, реализующая метод управления яркостью изображения.
%Управление яркостью изображений
clear;
I = imread('kids.bmp');
I=double(I(:,:,1));
figure, imshow(I./255);title('Исходное изображение');
[N M]=size(I);
R=.7;%необходимый уровень яркости изображения.
Imin=min(min(I));
Imax=max(max(I));
a=[0:.01:3];
for i=1:length(a);
K(i)=sum(sum(((I-Imin)./(Imax-Imin)).^a(i)))/(N*M);
if abs(K(i)-R)<.01;
st=a(i);
end;
end;
figure,plot(a,K);
grid;
Iout=((I-Imin)./(Imax-Imin)).^st;
figure, imshow(Iout);
AV=mean(mean(Iout));
disp(AV);
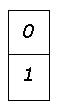
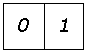
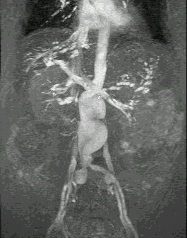
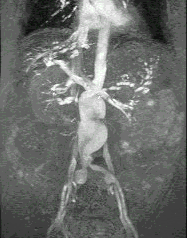
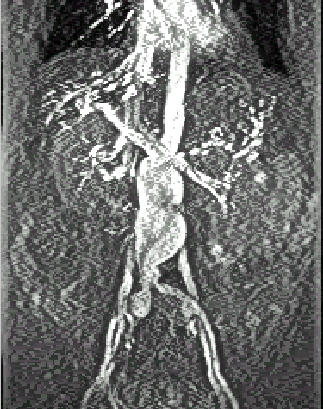
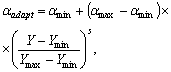 где
где 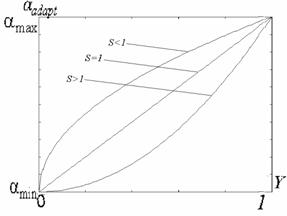
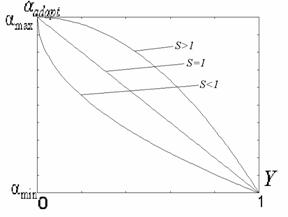
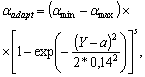
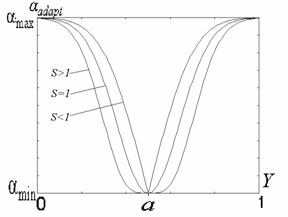
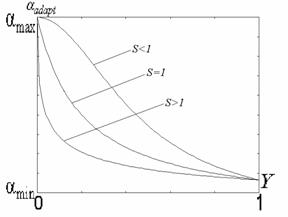










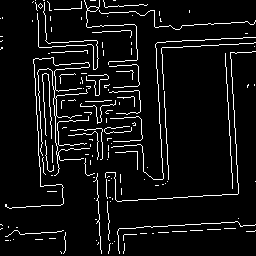


















Комментарии
Спасибо за курс
интересно, спасибо