Учебное пособие по Curve Fitting Toolbox
Информация в данной статье относится к релизам программы MATLAB ранее 2016 года, и поэтому может содержать устаревшую информацию в связи с изменением функционала инструментов. С более актуальной информацией вы можете ознакомиться в разделе документация MATLAB на русском языке.
Автор - Ануфриев Игорь Евгеньевич - канд. физ.-мат. наук, доцент кафедры "Прикладная математика" Санкт-Петербургского государственного политехнического университета. Автор нескольких учебных пособий по MatLab.
Curve Fitting Toolbox - это набор пользовательских графических интерфейсов (GUIs) и M-функций созданных в вычислительной среде MATLAB®.
- Первичную обработку данных, таких как разбиение на области и сглаживание.
- Параметрическую и непараметрическую аппроксимацию: для параметрической аппроксимации можно использовать встроенную библиотеку функций или создать собственную. В библиотеку включены полиномы, экспоненты, дробно-рациональные функции, гауссовы суммы и другие. Для непараметрической аппраксимации используются сглаживающие сплайны и различные интерполяции.
- Стандартный линейный метод наименьших квадратов, нелинейный метод наименьших квадратов, взвешенный метод наименьших квадратов, метод наименьших квадратов с ограничениями и устойчивые методы аппроксимации.
- Возможность оценки качества проведенной аппроксимации.
- Возможности анализа, такие как экстраполяция, дифференцирование и интегрирование.
Основы работы в Curve Fitting Toolbox
1.1. Обзор возможностей Curve Fitting Toolbox
1.2. Функции и приложение cftool с графическим интерфейсом
1.3. Основные этапы работы в приложении cftool
1.3.2. Окно приложения cftool. Импорт данных в приложение cftool
1.3.4. Управление графиками данных, приближений и видом графиков
1.3.5. Стандартные параметрические и непараметрические модели
1.3.6. Создание собственной параметрической модели
1.3.7. Опции, управляющие процессом подбора параметров
1.3.8. Критерии пригодности приближения
1.3.9. Предварительная обработка данных
1.3.10. Сглаживание и фильтрация данных
1.3.11. Экспорт результатов в рабочую среду
1.3.12. Операции с построенным приближением
2.1.1. Приближение без создания объекта с параметрической моделью
2.1.2. Приближение с созданием объекта для параметрической модели
2.1.3. Приближение с созданием объекта для пользовательской линейной параметрической модели
2.1.4. Приближение с созданием объекта для пользовательской нелинейной параметрической модели
2.2. Параметрические и непараметрические модели
2.2.1. Параметрические модели библиотеки Curve Fitting Toolbox
2.2.2. Непараметрические модели библиотеки Curve Fitting Toolbox
2.4. Логическое индексирование
2.5. Управление вычислительным алгоритмом
2.5.1. Способы задания опций вычислительного алгоритма
2.5.2. Зависимость набора опций от модели и способа приближения
2.5.2.1. Опция для задания весов
2.5.2.2. Опция для исключения части данных
2.5.2.3. Опция для масштабирования и центрирования данных
2.5.2.4. Опции для интерполяционных сплайнов
2.5.2.5. Опции для сглаживающего сплайна
2.5.2.6. Опции для линейных параметрических моделей
2.5.2.7. Опции для нелинейных параметрических моделей
2.5.3. Пример подбора параметров нелинейной модели
1.1. Основы работы в Curve Fitting Toolbox
Curve Fitting Toolbox позволяет:
- Работать с данными, заданными при помощи векторов в рабочей среде MATLAB, и, при необходимости, снабжать данные весами, так же задавая вектор их значений.
- Графически отображать исследуемые данные.
- Осуществлять предварительную обработку данных, исключая часть данных по некоторому правилу, по точкам в таблице, или при помощи мыши на графике, или наоборот оставляя часть данных для последующей обработки.
- Сглаживать и фильтровать данные различными способами.
- Приближать данные при помощи параметрических моделей, в которых искомые параметры могут входить как линейно, так и нелинейно. Модели выбираются из библиотеки моделей, или задаются пользователем. Целевая функция ошибки и методы, применяемые для ее минимизации, так же могут быть различными. Допускается задание ограничений на искомые значения параметров. Кроме параметрических моделей, возможна интерполяция данных сплайнами и приближение сглаживающими сплайнами.
- Отображать построенные приближения графически, форматировать графики и сохранять результаты в отдельных графических окнах.
- Вычислять различные критерии пригодности полученного приближения.
- Производить ряд операций с полученными приближениями (вычислять в заданных точках, дифференцировать интегрировать, проводить экстраполяцию), графически отображать результат.
1.2. Функции и приложение cftool с графическим интерфейсом
В состав Curve Fitting Toolbox входит приложение cftool с графическим интерфейсом пользователя, которое позволяет производить все вышеперечисленные действия, и функции, предназначенные для определения параметрической модели, подбора параметров, анализа пригодности приближения, операций с ним и графического отображения результата. Приложение cftool дает возможность пользователю:
- импортировать данные и веса, заданные в векторах рабочей среды MATLAB,
- экспортировать полученное приближение и анализ результатов в рабочую среду MATLAB;
- сохранять сессию в файле для продолжения работы;
- генерировать m-файл с файл-функцией, которая может быть использована для приближения других данных выбранным в cftool способом и для графического отображения результата без использования приложения cftool.
В одной сессии cftool допускается работа одновременно:
- с несколькими наборами данных;
- с различными приближениями для каждого набора;
- с подмножествами данных, полученных после исключения из основного подмножества по различным правилам.
Для работы с приложением cftool практически не требуется знание MATLAB, поскольку все основные операции выполняются при помощи графического интерфейса пользователя. Функции, входящие в состав Curve Fitting Toolbox, могут быть использованы, например, при разработке собственных приложений, в которых требуется реализовать решение задачи о приближении данных параметрической моделью.
Все функции Curve Fitting Toolbox могут быть условно разделены на несколько категорий.
Задание параметрических моделей и различных опций, подбор параметров и вычисление критериев пригодности приближения
fittype - выбор одной из стандартных параметрических и непараметрических моделей или создание произвольной параметрической модели.
fitoptions - задание различных опций, касающихся правил исключения, весов, допустимых границ значений искомых параметров, начального приближения к параметрам, опций вычислительных алгоритмов, применяемых для минимизации целевой функции (ошибки приближения).
fit - основная функция, выполняющая подбор параметров, в которой задаются исходные данные, параметрическая модель, опции (см. выше fitoptions); она возвращает: полученную параметрическую модель с найденными значениями параметров, и различные критерии пригодности полученного приближения.
cfit - создание параметрической модели с заданными значениями параметров (без их определения при помощи функции fit).
Информация о моделях и объектах, создаваемых функциями Curve Fitting Toolbox
cflibhelp - получение информации о стандартных параметрических моделях, входящих в Curve Fitting Toolbox.
disp - получение информации об объектах, создаваемых функциями Curve Fitting Toolbox.
Задание и получение значений свойств объектов, создаваемых функциями Curve Fitting Toolbox
get - получение свойств объектов.
set - задание свойств объектов.
Получение статистической информации о данных и предварительная обработка данных
excludedata - поиск данных, которые должны быть исключены из исходного набора в соответствии с выбранным правилом.
smooth - сглаживание данных с использованием различных способов.
datastats - нахождение минимального и максимального значений, среднего, стандартного отклонения.
Работа с полученным приближением
confint - вычисление доверительных интервалов для вычисленных параметров модели.
predint - нахождение интервалов предсказаний наблюдаемых значений с заданной вероятностью.
differentiate - дифференцирование построенной параметрической модели.
integrate - интегрирование построенной параметрической модели.
feval - вычисление значений параметрических моделей.
plot - построение графиков данных, параметрических моделей, ошибок.
Мы сначала рассмотрим основные этапы работы в приложении cftool, а затем обратимся к использованию функций, входящих в состав Curve Fitting Toolbox.
1.3. Основные этапы работы в приложении cftool
1.3.1. Импорт данных в MATLAB
В приложении cftool возможно приближать данные, записанные в глобальные массивы (вектора) рабочей среды MATLAB. Если данные хранятся в файле, то сначала требуется считать их в вектора, являющимися переменными рабочей среды MATLAB. Вполне возможно, что пользователь Curve Fitting Toolbox не владеет способами и функциями MATLAB для считывания данных, хранящихся в файлах, поэтому мы сначала обсудим, как считать данные из текстового или двоичного файла, или книги Excel и записать их в глобальные переменные. Если данные уже записаны в вектора, то этот раздел можно пропустить и перейти сразу к разделу Окно приложения cftool. Импорт данных в приложение cftool, в котором разбирается назначение окна приложения, перечисляются основные этапы работы и говорится о импорте тех данных в приложение cftool, которые уже находятся в рабочей среде MATLAB.
Для считывания данных из файла в MATLAB существует несколько способов, которые можно разделить на две группы: с использованием функций MATLAB, или приложений с графическим интерфейсом. Предположим, что данные записаны в текстовом файле в два столбика и в качестве разделителя десятичных разрядов используется точка, т.е. файл с данными data.txt имеет следующий формат:
1.25 0.8973
1.44 1.2398
1.54 2.0019Для записи столбцов файла в вектора MATLAB можно воспользоваться Мастером импорта (Import Wizard), для чего следует в меню File основного окна MATLAB выбрать пункт Import Data и в появившемся диалоговом окне открытия файла указать нужный файл. После нажатия в этом окне на кнопку Open появляется окно Мастера импорта (это второй шаг Мастера импорта), в котором можно указать:
-
разделитель чисел в строке (пробел, табуляция, точка с запятой, запятая или произвольный символ-разделитель);
-
сколько первых текстовых строк требуется пропустить при считывании данных из файла, если они есть;
-
посмотреть на содержимое текстового файла и массивов, которые будут созданы в MATLAB.
-
перейти на первый шаг Мастера импорта (кнопка Back), на котором можно выбрать другой файл с данными или получить доступ к системному буферу обмена.
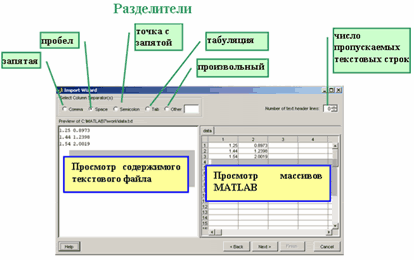
После нажатия кнопки Next появляется окно последнего шага мастера
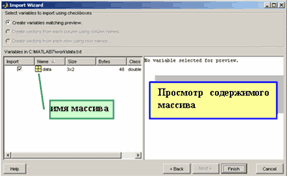
На последнем шаге можно
-
посмотреть содержимое массива с данными, для чего нужно выделить его имя щелчком мыши;
-
переименовать массив, для чего нужно сделать повторный щелчок мышью по его имени и ввести в появившееся поле новое имя.
После нажатия на кнопку Finish в рабочей среде окажется двумерный массив (с двумя столбцами) с выбранным именем. В нашем примере массив будет называться data (или так, как было задано на последнем шаге мастера).
Для последующей работы в приложении cftool следует создать два вектора x и y, содержащие, соответственно, первый и второй столбец массива data. Для этого следует ввести в командной строке MATLAB две команды, в которых производится индексация: для обращения ко всем элементам первого и второго столбцов массива data использовано двоеточие (индексация двоеточием), а номер выделяемого в вектор столбца задается числом:
>> x=data(:,1);
>> y=data(:,2);Массивы данных x и y созданы в рабочей среде MATLAB (см., например, содержимое окна Workspace).
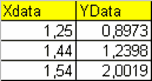
Если первая строка текстового файла с данными содержит заголовки столбцов, т.е. текстовый файл имеет следующий вид
XData YData
1.25 0.8973
1.44 1.2398
1.54 2.0019
то на последнем шаге мастера установка переключателя Create vectors from each column using column names позволит сразу создать в рабочей среде два вектора XData и YData, содержащих, соответственно, первый и второй столбец данных.
Если данные находятся в книге Excel, содержащей один лист, то Мастер импорта также способен создать массив, в который будут записаны эти данные. Если между столбцами данных на листе Excel есть пустые столбцы, то в MATLAB получится массив, содержащий NaN (не числа - Not a Number) в ячейках этих столбцов. Т.е., например, данные Excel, содержащиеся в книге data.xls,

преобразуются в массив data среды MATLAB (имя, как и в предыдущем примере, можно изменить на последнем шаге мастера)
1.25 0.8973
1.44 1.2398
1.54 2.0019а данные Excel

преобразуются в массив data
1.25 NaN NaN 0.8973
1.44 NaN NaN 1.2398
1.54 NaN NaN 2.0019содержащий четыре столбца. Запись содержимого столбцов в вектора из командной строки MATLAB производится аналогично предыдущему примеру, только следует указать не второй столбец, а четвертый.
>> x=data(:,1);
>> y=data(:,4);Для удаления столбцов из массива можно присвоить столбцам пустой массив, задаваемый в MATLAB при помощи квадратных скобок, причем можно указать диапазон столбцов (в нашем примере со второго по третий):
>> A(:,2:3)=[ ]
A =
1.2500 0.8973
1.4400 1.2398
1.5400 2.0019Так же, как и в случае простых текстовых файлов, если столбцы с данными на листе книги Excel снабжены заголовками
то в Мастере импорта появляется возможность создать вектора данных, имена которых совпадают с именами заголовков столбцов, т.е. массивы XData и YData. Для запуска Мастера импорта из командной строки в MATLAB есть функция uiimport. Обращение к ней без входных аргументов
>> uiimportприводит к появлению диалогового окна с первым шагом Мастера импорта, в котором кнопка Browse предназначена для открытия файла. Далее все шаги выполняются аналогично вышеизложенному. Входным аргументом функции uiimport может быть и имя файла, заключенное в апострофы (надо указывать либо полное имя, либо только имя с расширением, но тогда файл будет искаться в текущем каталоге MATLAB и каталогах, установленных в путях поиска MATLAB):
>> uiimport('data.txt')После такого обращения к функции uiimport появляется диалоговое окно со вторым шагом Мастера импорта, работа с которым описана выше.
Для чтения числовых данных из текстовых файлов, имеющих табличную структуру, подходит функция load. Символы-разделители (пробел, точка, точка с запятой, табуляция) интерпретируются как разделители элементов строки. Например, если текстовый файл data.txt содержит
1.25; 0.8973
1.44; 1.2398
1.54; 2.0019то результатом выполнения команды
>> A=load('data.txt')будет двумерный массив
A =
1.2500 0.8973
1.4400 1.2398
1.5400 2.0019Запись содержимого его столбцов в вектора x и y мы уже рассматривали выше, она производится при помощи простых команд
>> x=data(:,1);
>> y=data(:,2);Функция load считает, что файл является текстовым, если его расширение отлично от mat. Если файл имеет расширение mat, то он считается двоичным. Про считывание данных из двоичного файла говорится чуть ниже.
Для считывания данных из Excel в MATLAB есть специальная функция xlsread, которая допускает несколько способов вызова. Рассмотрим основные из них.
Указание имени книги Excel в апострофах в качестве входного аргумента функции xlsread приводит к считыванию данных с первого листа книги. Если первый лист не содержит данных, то функция xlsread вернет пустой массив. При считывании данных с листа книги Excel игнорируются верхние строки и правые столбцы, содержащие текст. Числовые данные, полученные в ячейках листа в результате вычисления по формулам, считываются функцией xlsread как обычные числовые константы, введенные в ячейки.
Если, например, книга ExpData.xls содержит три листа, которые называются Experiment1, Experiment2, Experiment3 и первый лист такой, как на рисунке
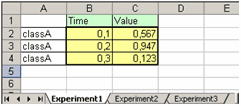
то команда
>> A=xlsread('ExpData.xls')приведет к появлению в рабочей среде следующего массива
A =
0.1000 0.5670
0.2000 0.9470
0.3000 0.1230(выделение значений из столбцов в вектора для импорта в приложение cftool было рассмотрено выше).
Если диапазон значений на первом листе содержит текст и пустые ячейки, то вместо них в возвращаемом функцией xlsread массиве будет находиться NaN (не числа - Not a Number). Например, если содержимое первого листа книги такое
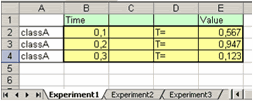
то результатом работы функции xlsread будет массив с четырьмя столбцами и тремя строками
>> A=xlsread('ExpData.xls')
A =
0.1000 NaN NaN 0.5670
0.2000 NaN NaN 0.9470
0.3000 NaN NaN 0.1230Для считывания данных из книги Excel не только с первого, а с произвольного листа, достаточно указать номер листа или его имя (в апострофах) в качестве второго входного аргумента. Если в книге ExpData.xls на втором листе с именем Experiment2 находятся такие данные
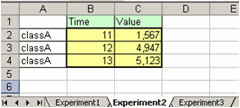
то следующие команды приводят к одинаковым результатам
>> A=xlsread('ExpData.xls',2)
A =
11.0000 1.5670 12.5670
12.0000 4.9470 16.9470
13.0000 5.1230 18.1230
>> A=xlsread('ExpData.xls','Experiment2')
A =
11.0000 1.5670 12.5670
12.0000 4.9470 16.9470
13.0000 5.1230 18.1230Функция xlsread позволяет указать диапазон данных, которые требуется считать. Если диапазон данных указан в качестве ее второго входного аргумента, то происходит считывание данных из этого диапазона на первом листе книги Ecxel, а если во втором входном аргументе xlsread указать имя листа, а диапазон данных - в третьем, то будет производиться считывание данных из заданного диапазона этого листа. В предыдущем примере данные на листе Experiment2 расположены в диапазоне B2:C4, поэтому для их считывания следует применить:
>> A=xlsread('ExpData.xls','Experiment2','B2:C4')
A =
11.0000 1.5670
12.0000 4.9470
13.0000 5.1230Функция xlsread предоставляет удобную возможность интерактивного выделения диапазона считываемых данных. Если в качестве ее второго входного аргумента указать -1, то в Excel откроется книга, имя которой задано в первом входном аргументе функции xlsread, и появится диалоговое окно. Осталось выбрать лист, на листе выделить диапазон данных и нажать на кнопку OK в этом окне. Данные из выбранного диапазона вернутся в выходном аргументе функции xlsread.
Если требуется считать данные со всех листов книги Excel в рабочую среду MATLAB, то удобно занести их в структуру, поля которой будут совпадать с названиями листов книги, а их содержимое будет массивами числовых данных, расположенных на соответствующих листах книги. Перед считыванием данных из книги Excel следует узнать количество и названия листов. Эту информацию возвращает функция xlsinfo. Ее входным аргументом является имя книги, а в выходных возвращается строка с информацией "Microsoft Excel Spreadsheet" и массив ячеек, содержащий имена листов.
>> [type, sheets] = xlsfinfo('ExpData.xls')
type =
Microsoft Excel Spreadsheet
sheets =
'Experiment1' 'Experiment2' 'Experiment3'
В цикле по количеству листов необходимо добавлять поля в структуру, выбирая название поля из соответствующей ячейки, и считывая содержимое листа при помощи функции xlsread, работа с которой разобрана выше. Функция для решения этой задачи приведена ниже. Ее входным аргументом является имя книги Excel, а в выходном она возвращает структуру, содержащую все числовые данные книги.
function S=readxls(fname);
% Считывание данных из книги в структуру с полями,
% являющимися названиями листов
[type, sheets] = xlsfinfo(fname); % получаем количество листов и их названия
S=[]; % сначала структура - пустой массив
% в цикле проходим по листам
for k=1:length(sheets)
sheetname=sheets{k}; % получаем название текущего листа
data=xlsread(fname, sheetname); % считываем с него данные в числовой массив
S=setfield(S,sheetname,data); % делаем числовой массив содержимым поля структуры
endДля приведенной выше книги ExpData.xls с листами Experiment1, Experiment2 и Experiment3 наша функция readxls будет работать следующим образом
>> S=readxls('ExpData.xls')
S =
Experiment1: [3x4 double]
Experiment2: [3x2 double]
Experiment3: []Поле Experiment1 содержит данные из листа Experiment1 книги ExpData.xls. Для доступа к содержимому поля следует указать его имя после имени структуры и разделить их точкой.
>> A=S.Experiment1
A =
0.1000 NaN NaN 0.5670
0.2000 NaN NaN 0.9470
0.3000 NaN NaN 0.1230Рассмотрим еще импорт данных, заданных в двоичном файле. Файлы с данными в двоичном формате имеют расширение mat. Такие примеры, в которых данные читаются из файла в двоичном формате, приводятся в справочной системе, в том числе и по Curve Fitting Toolbox), например, в подкаталоге toolbox\matlab\demos\ содержится файл census.mat, в котором записаны два вектора cdate и pop. Для считывания данных из двоичного файла используется команда load, после нее ставится пробел и задается имя файла (двоичный файл с данными должен быть в текущем каталоге или в каталоге, имя которого записано в пути поиска MATLAB). Имя файла можно указывать без расширения.
>> load censusПосле этого в рабочей среде создаются два массива cdate и pop, содержащих записанные в файле данные. Т.е. в двоичном файле хранятся как имена переменных, так и их содержимое.
Для считывания значений только некоторых переменных из двоичного файла в рабочую среду MATLAB достаточно указать имена соответствующих переменных после имени файла. Например, если в рабочую среде требовалось создать только переменную cdate, содержащую данные из двоичного файла census.mat, то достаточно было выполнить следующую команду
>> load census cdateКоманда load, как и многие команды MATLAB, допускает функциональную форму вызова, но тогда все имена как файла, так и переменных следует задавать в апострофах, т.е. вместо
>> load censusможно писать
>> load('census')Аналогично, команда
>> load census cdateэквивалентна следующей функциональной форме
>> load('census', 'cdate')Функциональная форма записи команды load имеет свои преимущества. Во-первых, имя файла и названия содержащихся в нем переменных могут храниться в строковых переменных, а во-вторых, указание выходного аргумента load приведет к тому, что он станет структурой, имена полей в которой совпадают с именами переменных, содержащихся в двоичном файле, и каждое поле будет содержать соответствующие значения:
>> S=load('census')
S =
cdate: [21x1 double]
pop: [21x1 double]
Еще один способ открытия двоичных файлов заключается в использовании Мастера импорта, работа с которым разбиралась выше. При выборе двоичного файла Мастер импорта открывается для последнего шага, на котором можно посмотреть переменные, записанные в двоичный файл, их размеры и указать имена тех переменных, которые следует загрузить в рабочую среду MATLAB.
Для открытия двоичных файлов можно также выбрать в меню File рабочей среды MATLAB пункт Open, при этом появляется стандартное диалоговое окно открытия файла, в котором выбирается нужный файл. При таком способе открытия двоичного файла все записанные в него переменные автоматически загружаются в рабочую среду.
Далее мы рассмотрим импорт данных в приложение cftool, предназначенное для решения задачи о подборе параметров.
1.3.2. Окно приложения cftool. Импорт данных в приложение cftool
1.3.2. Окно приложения cftool. Импорт данных в приложение cftool
В предыдущем разделе мы разобрали различные способы импорта данных в рабочую среду MATLAB, поскольку при работе с приложением cftool требуется, чтобы приближаемые параметрической моделью данные были записаны в вектора рабочей среды. Будем считать, что импорт данных в приложение cftool уже проделан. Для примера мы сгенерируем данные (просто функция синус, к которой добавлены небольшие погрешности, распределенные по нормальному закону)
>> XData=0:0.25:5;
>> YData=7*sin(XData)+0.1*randn(size(XData));Теперь запустим приложении cftool, для чего достаточно набрать в командной строке MATLAB его имя
>> cftoolПоявляется окно приложения (ниже приведена только часть окна cftool с указанием назначения основных его компонент).
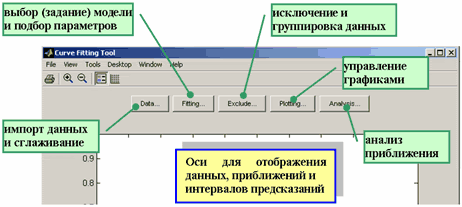
Основные этапы решения задачи о подборе параметров параметрической модели, приближающей данные, в приложении cftool таковы:
-
Импорт данных (кнопка Data);
-
Построение, при необходимости, правил исключения некоторых значений, или исключение вручную в таблице, или группировка данных для приближения их частей различными моделями (кнопка Exclude)
-
Выбор стандартной параметрической или непараметрической модели, входящей в Curve Fitting Toolbox, или создание собственной модели, подбор параметров с предварительным указанием их границ и начальных приближений, целевой функции и методов решения, а также просмотр полученных значений и информации о пригодности полученного приближения (кнопка Fitting).
-
Анализ данных, включающий вычисление полученного приближения в заданных точках (включая экстраполяцию), его интегрирование и дифференцирование (кнопка Analysis).
Кроме того, возможно:
-
Оставить только те графики данных и моделей, которые нужны в данный момент (кнопка Plotting).
-
Форматировать графики данных и построенных параметрических моделей (контекстное меню линий графиков, инструменты окна cftool, меню Tool).
-
Отобразить графически интервалы предсказаний наблюдаемых значений с заданной вероятностью (меню View, пункты Prediction Bounds, Confidence Level).
-
Отобразить графически остатки (меню View, пункт Residuals).
-
Экспортировать приближения и результаты их анализа в рабочую среду MATLAB (эта возможность есть в окнах, в которых строится приближение и проводится анализ).
-
Проводить сглаживание и фильтрацию данных (кнопка Data). Однако, необходимо иметь ввиду, что сглаживание уничтожает стандартное предположение регрессионного анализа о том, что распределение ошибки в исходных данных подчиняется нормальному закону. Если построена достаточно хорошая модель, то остатки (разность значений данных и приближения) также должны подчиняться нормальному закону. Поэтому сглаживание следует использовать как инструмент для получения первоначального предположения о возможной параметрической модели в случае зашумленных данных, а строить модель следует для несглаженных исходных данных.
-
Сгенерировать файл-функцию, которую можно использовать впоследствии автономно от приложения cftool для получения построенного в приложении cftool приближения (меню File, пункт Generate M-file).
-
Сохранить сессию и при следующих запусках приложения cftool восстановить ее (меню File, пункты Save Session, Load Session), а так же удалить все данные, и полученные результаты (меню File, пункт Clear Session).
-
Вывести результаты в отдельное графическое окно (меню File, пункт Print to Figure).
-
Напечатать результаты (меню File, пункт Print).
Приложение cftool позволяет работать с несколькими наборами данных, строить для них различные правила исключения и различные параметрические модели. Поэтому наборы данных, правила исключения и параметрические модели следует снабжать именами. Импортируем наши сгенерированные данные, которые мы ввели выше в вектора XData и YData рабочей среды, в приложение cftool и дадим имя SinWithErr нашему набору данных. Для этого следует нажать кнопку Data. Появляется одноименное окно Data, назначение его элементов управления приведено на рисунке ниже.
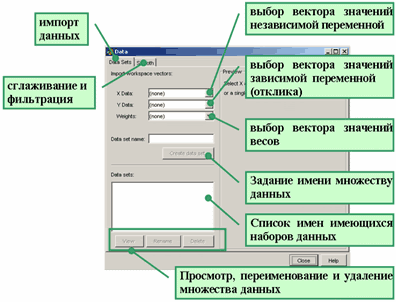
В раскрывающихся списках X Data и Y Data следует выбрать имена глобальных переменных рабочей среды MATLAB, т.е. XData и YData, соответственно. После этого на правой панели окна Data строится примерный график выбранных данных.
Раскрывающийся список Weights предназначен для выбора вектора, содержащего веса. Если это не требуется, то веса можно не указывать, по умолчанию они все равны единице.
После выбора векторов с данными следует задать имя множеству данных. Для этого следует ввести его имя SinWithErr в строку ввода Data set name и нажать кнопку Create data set (она становится доступной после выбора векторов, содержащих данные).
С созданным множеством данных можно проделать следующие операции (предварительно следует выделить его имя в списке Data sets):
-
Отобразить таблицу данных вместе с графиком в отдельном окне, для чего следует нажать кнопку View
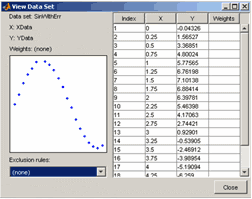
В раскрывающемся списке Exclusion rules окна View Data Set можно выбирать правила исключения, пока он пуст, поскольку никаких правил мы не задавали. -
Переименовать выделенный набор данных, нажав на кнопку Rename, после чего появится диалоговое окно, в которое нужно будет ввести новое имя (пока этого делать не нужно, мы продолжим работу с ним).
-
Удалить выделенный набор данных, нажав на кнопку Delete (этого, очевидно, тоже делать сейчас не нужно).
Множество данных создано, его график отобразился на осях основного окна приложения cftool. В окне Data можно также осуществлять сглаживание данных (вкладка Smooth), выбирая различные способы сглаживания. Этой операции посвящен раздел Сглаживание и фильтрация данных.
Далее мы разберем, как осуществить подбор параметров подходящей параметрической модели, входящей в набор стандартных параметрических моделей Curve Fitting Toolbox.
1.3.3. Приближение стандартными параметрическими и непараметрическими моделями. Работа с несколькими приближениями и несколькими наборами данных.
В предыдущем разделе был описан импорт данных в приложение cftool и создание множества данных с именем SinWithErr. Данные отображены графически маркерами в на осях в основном окне приложения cftool. После того, как создано множество данных, можно переходить к приближению данных одной из стандартных параметрических моделей, если не требуется создание правил исключения или применение процедуры сглаживания для получения представления о возможной параметрической модели в случае сильно зашумленных данных. В этом разделе мы обсудим только технику работы с несколькими стандартными приближениями и несколькими наборами данных, а описание всех стандартных параметрических и непараметрических моделей, создание собственных линейных и нелинейных параметрических моделей, управление вычислительным процессом и критерии пригодности приближения будут описаны в следующих разделах.
Для перехода к диалоговому окну, предназначенному для выбора модели и подбора параметров, следует нажать кнопку Fitting в основном окне приложения cftool. Появляется диалоговое окно Fitting, в котором следует нажать кнопку New fit, после чего все элементы управления данного окна становятся доступными и оно приобретает вид, приведенный ниже на рисунке.
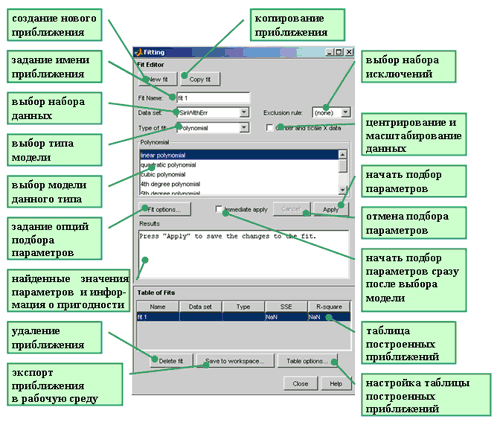
Сначала лучше всего задать имя приближения, связанное с ним по смыслу, вместо предлагаемого по умолчанию имени fit1. Сперва мы будем пользоваться параметрическими моделями, в которой функции, использующиеся для приближения, являются синусом или суммой синусов, поэтому в строке ввода Fit Nameдиалогового окна Fitting введем имя SinModel. После этого в раскрывающемся списке Type of fit выберем Sum of Sin Functions (все стандартные параметрические модели Curve Fitting Toolbox рассмотрены в разделе Стандартные параметрические и непараметрические модели). Cписок, расположенный ниже, сменил название, теперь он называется Sum of Sin Functions и содержит восемь функций, каждая из которых является линейной комбинацией синусов, причем параметры входят как линейно (a1, a2, ..., a8), так и нелинейно (b1, b2, ..., b8 и c1, c2, ..., c8):
a1sin(b1x + c1),
a1sin(b1x + c1) + a2sin(b2x + c2),
a1sin(b1x + c1) + a2sin(b2x + c2) + ... + a8sin(b8x + c8),Выберем в списке первую модель a1sin(b1x + c1) и нажмем кнопку Apply (если установлен флаг Immediate Apply, то подбор параметров начинается сразу же после выбора вида функции без нажатия на кнопку Apply). После вычисления коэффициентов приближения в окно Results выводится следующая информация
1. Информация о модели
General model Sin1:
f(x) = a1*sin(b1*x+c1)2. Найденные значения коэффициентов вместе с доверительными интервалами, соответствующими уровню вероятности 95%
Coefficients (with 95% confidence bounds):
a1 = 7.019 (6.966, 7.072)
b1 = 1 (0.995, 1.006)
c1 = 6.275 (6.261, 6.289)3. Вычисленные критерии пригодности приближения
Goodness of fit:
SSE: 0.1224
R-square: 0.9998
Adjusted R-square: 0.9997
RMSE: 0.08245На оси основного окна приложения cftool вывелся график приближения при найденном значении параметров, а в таблицу Table of Fits выводится имя приближения SinModel, имя набора данных SinWithErr, тип параметрической модели Sum of Sin Function и найденные значения критериев пригодности приближения.
Про различные критерии пригодности приближения, вычисляемые в Curve Fitting Toolbox, говорится в разделе Критерии пригодности приближения. Сейчас мы рассмотрим, как задавать различные начальные значения параметров и организовать работу с несколькими приближениями.
Найденные значения параметров модели a1sin(b1x + c1) таковы
a1 = 7.019, b1 = 1, c1 = 6.275
То, что найденное значение c1 не равно нулю (примерно), не испортило приближения (хотя исходные данные были 7sinx + шум), поскольку c1 = 6.275 ~ 2П, т.е. периоду функции синус. Создадим теперь новое приближение и перед началом процесса подбора параметров установим начальное приближение 0 для параметра c1. Для создания нового приближения следует нажать кнопку New Fit в диалоговом окне Fitting и ввести имя SinModel0 нового приближения в строку ввода Fit Name. После этого необходимо снова выбрать в раскрывающемся списке Type of fit строку Sum of Sin Functions и задать вид функции a1sin(b1x + c1) в расположенном ниже списке Sum of Sin Functions.
Теперь перед началом подбора параметров установим нулевое начальное приближение для параметра . Для этого следует нажать кнопку Fit Options и в появившемся диалоговом окне Fit Options в столбце StartPoint таблицы внизу окна установить для c1 начальное приближение, равное нулю, для чего надо щелкнуть по соответствующей ячейке и ввести 0. Все остальные параметры оставим такими, как они заданы по умолчанию. После чего окно Fit Options можно закрыть (назначение остальных элементов управления, количество которых зависит от выбранной модели, объясняется в разделе Опции, управляющие процессом подбора параметров). 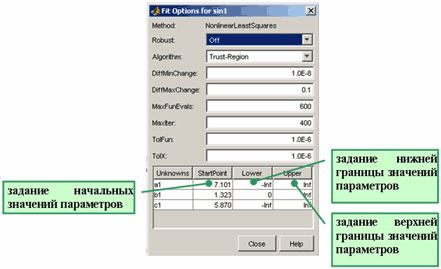
Установив нулевое начальное приближение для параметра c1, снова проделаем подбор параметров, нажав кнопку Apply в диалоговом окне Fitting. По завершении процедуры подбора параметров в окно Results опять выводятся найденные значения коэффициентов модели (теперь значение параметра c1близко к нулевому) вместе с доверительными интервалами, а так же информация о модели и вычисленные критерии пригодности полученного приближения. Оси основного окна приложения cftool теперь содержат графики исходных данных и двух приближений (графики приближений совпадают). При выборе в таблице Table of Fits окна Fitting одного из приближений в области Results автоматически отображается вся информация о нем. Для настройки вида таблицы служит кнопка Table Options (см. раздел Критерии пригодности приближения).
Для удаления приближения достаточно выбрать его в таблице Table of Fits и нажать кнопку Delete. Удалим, например приближение SinModel. Одновременно удаляется его график с осей основного окна приложения cftool.
Построим еще приближение наших данных полиномом третьей степени. Для этого снова нажмем кнопку New Fit и введем в строку ввода Fit Name имя Poly3. Убедимся, что в раскрывающемся списке Type of fitвыбрано полиномиальное приближение (Polynomial) и в списке Polynomial выберем cubic polynomial, после чего нажмем кнопку Apply. Снова в окно Results выводится информация о модели, в данном случае модель линейная (Linear model), поскольку искомые параметры линейно входят в параметрическую полиномиальную модель (полиномиальная регрессия)
Linear model Poly3:
f(x) = p1*x^3 + p2*x^2 + p3*x + p4
выводятся так же найденные значения коэффициентов полинома вместе с доверительными интервалами для уровня вероятности 95%
Coefficients (with 95% confidence bounds):
p1 = 0.6341 (0.5438, 0.7243)
p2 = -6.02 (-6.707, -5.333)
p3 = 13.02 (11.56, 14.48)
p4 = -1.134 (-1.955, -0.3128)
и значения критериев пригодности приближения
Goodness of fit:
SSE: 4.733
R-square: 0.991
Adjusted R-square: 0.9894
RMSE: 0.5276
В таблице Table of Fits добавилась информация о полиномиальном приближении: его имя Poly3, имя набора данных SinWithErr, тип параметрической модели Polynomial и найденные значения критериев пригодности приближения. На осях основного окна приложения cftool теперь отображаются: график исходных данных маркерами, приближение синусом и полиномом: 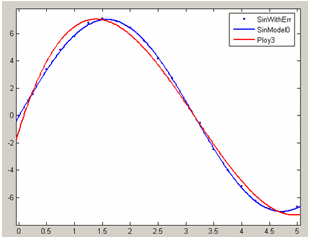
Продолжим работу с приложением cftool для нового набора данных, для чего определим вектора, содержащие данные, в рабочей среде MATLAB (зашумленные данные, подчиняющиеся линейной зависимости):
>> XData1=-3:0.02:3;
>> YData1=0.5*XData1+0.8+0.3*randn(size(XData1));Импортируем данные в приложение cftool выбирая переменные XData1 и YData1 рабочей среды MATLAB в окне Data, как было описано в разделе Окно приложения cftool. Импорт данных в приложение cftool. Дадим имя LinWithErr набору данных и перейдем к окну Fitting. Для создания нового приближения нажмем кнопку New fit, затем введем имя приближения LinModel и выберем в раскрывающемся списке Data setнаше множество данных LinWithErr. Осталось задать полиномиальную модель в раскрывающемся списке Type of fit, выбрать полином первой степени (linear polynomial) в списке Polynomial и нажать кнопку Apply.
Тип модели, найденные значения коэффициентов, критерии пригодности приближения выводятся в окно Results, в таблице Table of fits появилось новое приближение LinModel для нового набора данных LinWithErr с соответствующей информацией. Как и раньше, обновились оси основного окна приложения cftool, теперь они содержат два набора данных и три приближения, что очевидно, не очень наглядно: 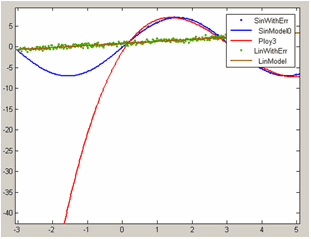
Пределы по оси x выбираются автоматически так, чтобы на графике были представлены оба набора данных, при этом графики приближений оказываются построенными на больших интервалах, чем нужно. В следующем разделе разбирается управление графиками приближений и данных.
1.3.4. Управление графиками данных, приближений и видом графиков
При работе с несколькими приближениями, и особенно, с несколькими наборами данных и приближениями для них очень часто требуется оставить на основных осях приложения cftool только нужные графики. Для управления графиками следует нажать кнопку Plotting в основном окне приложения cftool, что приводит к появлению диалогового окна Plotting
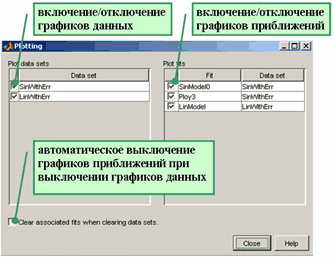
В этом окне в левой области Plot data sets расположены флаги для скрытия графиков данных (рядом с флагами написаны названия множеств данных), а в правой области Plot fits расположены флаги для скрытия графиков приближений (так же рядом с флагами написаны названия приближений). Удобно установить флаг Clear associated fits when clearing data sets, который предназначен для автоматического скрытия графиков приближений при скрытии соответствующих наборов данных.
При скрытии графиков данных или приближений сами множества данных или приближения не удаляются в приложении cftool, при необходимости их можно восстановить на осях основного окна приложения cftool, установив соответствующие флаги в окне Plotting. Если нужно удалить набор данных, то следует нажать кнопку Data в основном окне приложения, далее в списке Data sets диалогового окна Data выбрать имя ненужного набора и нажать кнопку Delete. Вместе с набором данных удалятся и связанные с ним приближения, о чем выводится предупреждение в окне Deleting data sets. Для удаления приближения следует перейти в диалоговое окно Fitting, нажав кнопку Fitting в основном окне приложения, выбрать имя ненужного приближения в таблице Table of fits и нажать кнопку Delete fit.
Мы не будем удалять наборы данных и приближения, а вместо этого выведем графики набора данных SinWithErr и приближений для него SinModel0 и Poly3 в одно графическое окно, а графики набора данных LinWithErr и приближения LinModel в другое графическое окно MATLAB. Для этого оставим сначала на осях основного окна приложения cftool только график SinWithErr и приближений для него SinModel0 и Poly3, сбросив остальные флаги в диалоговом окне Plotting. На осях основного окна приложения cftool остались только графики множества данных SinWithErr и приближений для него SinModel0 и Poly3. После этого выберем в меню File основного окна приложения cftool пункт Print to Figure. Появляется отдельное графическое окно с графиками множества данных SinWithErr и приближений для него SinModel0 и Poly3. Аналогично, в диалоговом окне Plotting оставим включенными флаги только для набора данных LinWithErr и приближения LinModel и выведем их в другое графическое окно MATLAB:
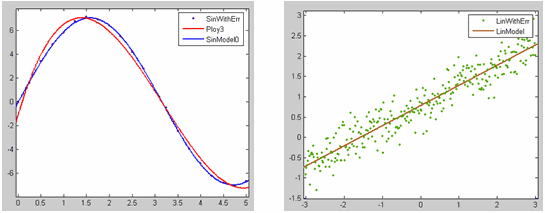
Теперь для форматирования графиков можно пользоваться стандартными средствами графического окна MATLAB.
Приложение cftool также позволяет форматировать графики, построенные в основном окне. Для этого можно использовать:
-
Контекстное меню линии графика приближения для задания цвета линии, типа линии и ее толщины, а также для скрытия линии или удаления соответствующего приближения.
-
Контекстное меню графика данных для задания маркера, цвета линии, ее типа и толщины, а также для скрытия линии.
-
Перемещение легенды при помощи мыши, а также ее контекстное меню для задания ее свойств.
-
Кнопку Legend on/off на панели инструментов основного окна приложения cftool для скрытия и отображения легенды.
-
Кнопку Grid on/off на панели инструментов основного окна приложения cftool для скрытия и отображения сетки.
-
Инструменты Zoom in и Zoom out на панели инструментов основного окна приложения cftool для увеличения или уменьшения графиков.
-
Добавлять к осям счетчики, для интерактивного изменения пределов осей (меню Tools основного окна приложения cftool, пункт Axis Limit Controls).
-
Очищать оси (меню View основного окна приложения cftool, пункт Clear Plot).
-
Добавлять график остатков (меню View основного окна приложения cftool, пункт Residuals, подпункты Scatter Plot - маркерами, Line Plot - непрерывной линией с маркерами).
-
Убирать график остатков (меню View основного окна приложения cftool, пункт Residuals, подпункт None).
-
Строить доверительные интервалы для линии регрессии, соответствующие различным уровням вероятности (для задания вероятности в меню меню View основного окна приложения cftool следует выбрать пункт Confidence Level, а для построения или удаления доверительных интервалов - пункт Prediction Bounds).
На следующем рисунке приведен вид основного окна приложения cftool с графиком остатков и доверительными интервалами линии линейной регрессии, построенной выше для множества данных LinWithErr. Визуальная оценка графика распределения остатков позволяет говорить о хорошем соответствии модели реальному поведению данных.
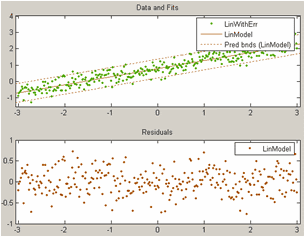
1.3.5. Стандартные параметрические и непараметрические модели
Curve Fitting Toolbox содержит ряд стандартных параметрических и непараметрических моделей, которые выбираются в диалоговом окне Fitting. Для перехода в это окно следует нажать кнопку Fitting в основном окне приложения cftool.
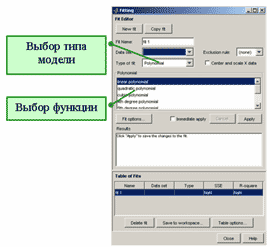
Диалоговое окно Fitting
Всего имеется 10 стандартных типов для параметрического и непараметрического приближения (параметры обозначаются a,b,c,d,a1,b1,p1...).
Параметрические модели
1. Экспоненциальные модели (Exponential)
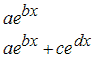
2. Отрезки ряда Фурье (Fourier)
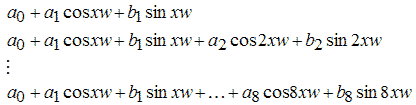
3. Сумма синусов (Sum of Sin Functions)
4. Гауссовы модели (Gaussian)
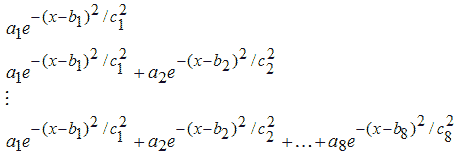
5. Модель Вейбула (Weibull)
![]()
6. Степенные модели (Power)
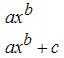
7. Полиномиальные модели (Polynomials)
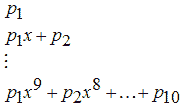
8. Дробно-рациональные модели (Rational)
Эти модели представляются дробью, в числителе и знаменателе которой стоят полиномы до пятой степени включительно. Коэффициент при старшей степени в знаменателе равен единице для однозначного определения дробно-рационального выражения.
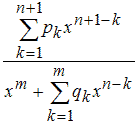
Искомыми являются коэффициенты полиномов, стоящих в числителе и знаменателе дроби.
При выборе модели этого типа в раскрывающемся списке Type of fit появляются два списка для выбора степени числителя и знаменателя
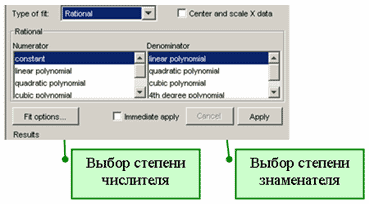
Выбор дробно-рациональной модели в диалоговом окне Fitting
Непараметрические модели
1. Интерполяционные сплайны (Interpolant)
linear - кусочно-линейное приближение (точки данных соединяются отрезками прямых).
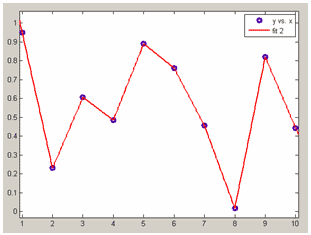
Кусочно- линейное приближение
nearest neibour - кусочно-постоянная интерполяция по ближайшему соседу.
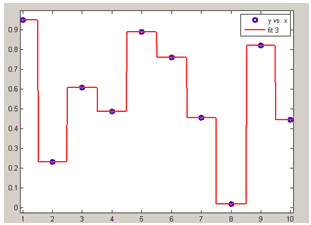
Интерполяция по ближайшему соседу
cubic spline - интерполяция данных кубическим сплайном. Получается тот же самый сплайн, который строит функция spline, входящая в набор функций MATLAB (см. Интерполяция кубическими сплайнами.)
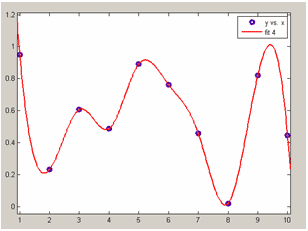
Интерполяция кубическим сплайном
shape-preserving - интерполяция эрмитовым сплайном, т.е. сплайном, сохраняющим форму данных (см. Интерполяция сплайнами, сохраняющими форму (кубическими полиномами Эрмита).)
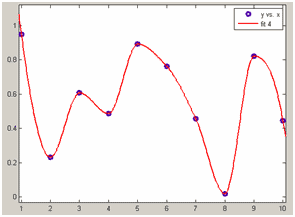
Интерполяция эрмитовым сплайном
(значения сплайна не превосходят значения данных)
2. Сглаживающий сплайн (Smoothing Spline)
Хотя сглаживающий сплайн и относят к непараметрическим моделям, тем не менее он содержит задаваемый пользователем параметр. Сглаживающий сплайн определяется как сплайн, который минимизирует следующий функционал, зависящий так же и от некоторого параметра p.
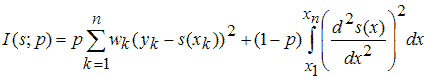
где
(xk,yk)k=1,2,...,n - приближаемые данные;
wk - веса данных (если они не были заданы, то принимаются равными единице);
p - сглаживающий параметр, изменяющийся от 0 до 1, который определяет кривизну получающегося сплайна. Если задавать значения сглаживающего параметра близкие к нулю, то сглаживающий сплайн будет похож на прямую, приближающую данные в смысле наименьших квадратов, поскольку основным в минимизируемом функционале станет второе слагаемое
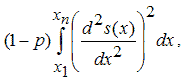
которое как раз и отвечает за гладкость, его минимизация соответствует построению сплайна с наименьшим значением второй производной (ноль, для полинома первого порядка). Напротив, если значение сглаживающего параметра близко к единице, то основным в минимизируемом функционале станет первое слагаемое
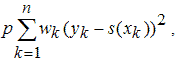
которое отвечает за прохождение сплайна через заданные точки. При p=1 сглаживающий сплайн превращается в обыкновенный кубический сплайн.
На практике при применении сглаживающего сплайна часто значение сглаживающего параметра выбирают примерно равным
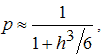
где h - среднее расстояние между точками , в которых определены приближаемые данные.
Значения сглаживающего параметра задаются в диалоговом окне Fitting (соответствующие переключатели, кнопки и область ввода появляются после выбора Smoothing Spline в раскрывающемся списке Type of fit)
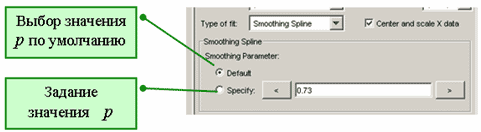
Задание параметра для сглаживающего сплайна
На рисунке ниже приведены сглаживающие сплайны для нескольких различных значений сглаживающего параметра p=1 (то же, что и кубический сплайн), p=0.9 (сглаживающий сплайн), p=0 (линейная функция, приближающая данные в смысле наименьших квадратов).
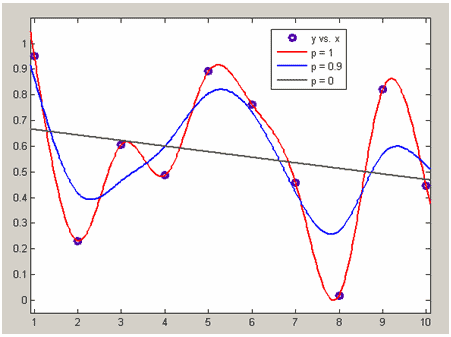
Приближение данных сглаживающим сплайном
для различных значений сглаживающего параметра.
1.3.6. Создание собственной параметрической модели
Кроме предопределенных моделей, описанных в предыдущем пункте Стандартные параметрические и непараметрические модели, пользователь приложения cftool имеет возможность создавать собственные модели, в которые искомые параметры входят как линейно, так и нелинейно. Для создания собственной модели следует в диалоговом окне Fitting в раскрывающемся списке Type of fit выбрать пункт Custom Equations и нажать на кнопку New equation.
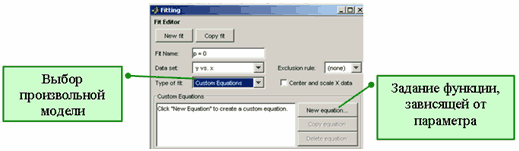
Создание собственной параметрической модели
После этого появляется диалоговое окно Create Custom Equation, содержащее две вкладки:
Linear Equation - для задания параметрической модели, линейно зависящей от искомых параметров
General Equation - для задания произвольной параметрической модели, в которую параметры могут входить нелинейно.
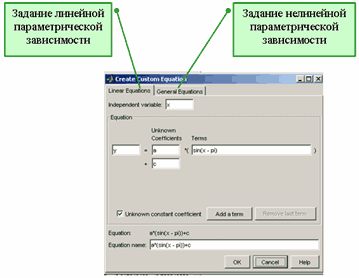
Диалоговое окно Create Custom Equation для
создания собственных линейных и нелинейных параметрических моделей
Для задания линейной параметрической модели следует выбрать независимую переменную в строке ввода Independent variable (можно оставить переменную x, предлагаемую по умолчанию) и последовательно добавлять функции при искомых коэффициентах. Для добавления каждой следующей функции требуется нажать кнопку Add a term.
Пусть, например, требуется создать параметрическую модель
![]()
Для этого изменяем a на a1 в первой строке ввода столбца Unknown Coefficients и набираем в расположенной рядом строке ввода (столбца Terms) вместо sin(x-pi) выражение x*exp(-x). Далее нажимаем кнопку Add a term, изменяем b на a2 и набираем в расположенной рядом строке ввода exp(-x). Последний коэффициент, аддитивно входящий в нашу модель, добавляется автоматически, так как установлен флаг Unknown constant coefficient. Осталось исправить c на a3. В результате области ввода диалогового окна Create Custom Equation должны выглядеть так, как показано ниже на рисунке
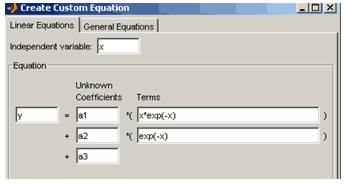
Создание линейной параметрической модели ![]()
Формулы набираются в соответствии с правилами MATLAB с использованием знаков +, -, *, /, ^ (возведение в степень) для арифметических операций, круглых скобок для изменения их приоритета и встроенных математических функций, список которых можно получить, задав в командном окне MATLAB команду
>> help elfunВ следующей таблице приведены наиболее часто используемые функции
|
Тригонометрические функции (аргумент задаётся в радианах) |
|
|
sin, cos, tan, cot |
Синус, косинус, тангенс и котангенс |
|
sec, csc |
Секанс, косеканс |
|
Обратные тригонометрические функции (результат вычисляется в радианах) |
|
|
asin, acos, atan, acot |
Арксинус, арккосинус, арктангенс и арккотангенс |
|
asec, acsc |
Арксеканс, арккосеканс |
|
Гиперболические функции |
|
|
sinh, cosh, tanh, coth |
Гиперболические синус, косинус, тангенс и котангенс |
|
sech, csch |
Гиперболические секанс и косеканс |
|
asinh, acosh, atanh, acoth |
Гиперболические арксинус, арккосинус, арктангенс и арккотангенс |
|
Экспоненциальная функция, логарифмы, степенные функции |
|
|
Exp |
Экспоненциальная функция |
|
log, log2, log10 |
Натуральный логарифм, логарифмы по основанию 2 и 10 |
|
Sqrt |
Квадратный корень |
|
Модуль, знак |
|
|
abs, sign |
Модуль и знак числа |
В строке ввода Equation name внизу диалогового окна Create Custom Equation отображается формула, задающая параметрическую модель. Вместо этой формулы можно ввести произвольное имя для параметрической модели, которое будет ее идентифицировать в дальнейшем при подборе параметров.
Для создания модели осталось нажать кнопку OK, после чего данная модель (формула или имя модели) появляется в списке Custom Equation диалогового окна Fitting. Модели в этом списке можно удалять (кнопка Delete рядом со списком), а также модифицировать и добавлять измененную модель в список (кнопка Copy).
После создания собственной модели можно выбирать встроенные модели для приближения данных, но при выборе в диалоговом окне Fitting в раскрывающемся списке Type of fit пункта Custom Equations появляются все созданные ранее пользовательские параметрические модели.
Схожим образом создается и нелинейная параметрическая модель. Предположим, что требуется определить следующую модель
![]()
Для этого необходимо в диалоговом окне Fitting в раскрывающемся списке Type of fit выбрать пункт Custom Equations, нажать на кнопку New equation и в появившемся диалоговом окне Create Custom Equation перейти на вкладку General Equation.
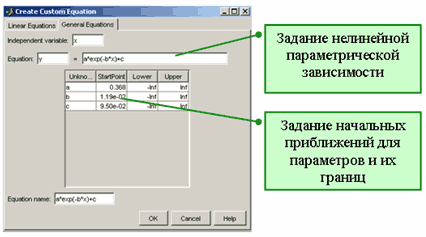
Создание нелинейной параметрической модели ![]()
В строке ввода Independent variable вводится независимая переменная (можно оставить переменную x, предлагаемую по умолчанию), а в строке ввода ниже формула, задающая параметрическую модель. В нашем случае это будет
(a*x^2+b*x+c)*exp(-(a*x^2+b*x+c))Кроме выражения для параметрической модели следует задать в таблице под строкой ввода также границы интервалов, в которых могут находиться искомые параметры (для задания бесконечного интервала достаточно оставить Inf или -Inf для правой, или левой границы, соответственно), и начальные приближения для них. В линейной параметрической модели это не требуется, поскольку приближение по методу наименьших квадратов линейной моделью приводит к решению системы линейных алгебраических уравнений относительно искомых коэффициентов. При приближении данных нелинейными параметрическими моделями решается задача минимизации нелинейной функции и соответствующий алгоритм должен получить начальные значения параметров и границы их возможных значений. Начальные значения могут сильно повлиять на получающееся приближение. Начальные значения параметров и границы допустимых интервалов для них потом можно изменить, воспользовавшись кнопкой Fit options в диалоговом окне Fitting.
В строке ввода Equation name внизу диалогового окна Create Custom Equation отображается формула, задающая параметрическую нелинейную модель. Вместо формулы можно ввести произвольное имя для определяемой параметрической модели, которое будет ее идентифицировать при дальнейшей работе.
Для создания модели осталось нажать кнопку OK внизу диалогового окна Create Custom Equation. Только что созданная модель (формула или имя модели) появляется в списке Custom Equation диалогового окна Fitting. Модели в этом списке можно удалять (кнопка Delete рядом со списком), а также модифицировать и добавлять измененную модель в список (кнопка Copy).
Так же как и в случае линейной параметрической модели, после создания собственной непараметрической модели можно выбирать встроенные или другие пользовательские модели для приближения данных, но при выборе в диалоговом окне Fitting в раскрывающемся списке Type of fit пункта Custom Equations появляются все созданные ранее пользовательские параметрические модели.
Приведем пример того, что начальное приближение к искомым параметрам играет большую роль при подборе параметров в нелинейной модели. В командном окне введем следующие данные в глобальные переменные x и y рабочей среды:
>> x=0:0.1:3;
>> y=exp(-2*x.^2).*sin(4*x.^2)+exp(-x.^2).*sin(x)+0.01*rand(size(x));
Далее импортируем их в приложение cftool так, как описано в разделе Окно приложения cftool. Импорт данных в приложение cftool и дадим имя DATA нашему набору данных. В окне Fitting создадим новое приближение с именем FIT1 (см. раздел Приближение стандартными параметрическими и моделями. Работа с несколькими приближениями и несколькими наборами данных.) и определим следующую нелинейную параметрическую модель
![]()
так, как мы делали это выше в данном разделе, введя выражение
exp(-a*x^2)*sin(b*x^2)+ exp(-с*x^2)*sin(в*x)
в окне Create Custom Equation (на вкладке General Equation). Установим в качестве начальных приближений для параметров следующие значения
a=5
b=5
c=5
d=5Получается хорошее приближение (см. рис. ниже). Теперь создадим еще одно приближение с именем FIT2 с той же самой параметрической моделью и установим другие начальные приближения для параметров
a=-1
b=1
c=1
d=1Для этого следует нажать на кнопку Fit options в диалоговом окне Fitting и в появившемся диалоговом окне в таблице ввести эти значения. После чего сделаем подбор параметров с новыми начальными приближениями, нажав кнопку Apply. Результаты для одной и той же параметрической модели с различными начальными значениями параметров совершенно отличаются друг от друга, второе приближение просто неверно.
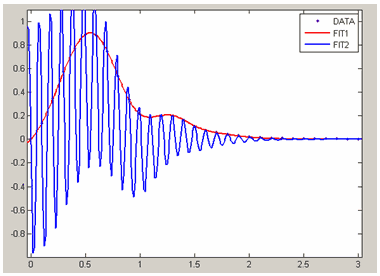
Приближение нелинейной параметрической моделью
с различными начальными приближениями для параметров.
В следующем разделе мы рассмотрим другие опции, которые служат для управления процессом подбора параметров.
1.3.7. Опции, управляющие процессом подбора параметров
Для задания опций вычислительных алгоритмов, использующихся для подбора параметров служит кнопка Fit options диалогового окна Fitting. После нажатия на эту кнопку появляется диалоговое окно, в заголовке которого написано Fit options for и далее указано имя параметрической модели.
В зависимости от типа выбранной параметрической модели состав этого окна может быть различным.
Для сплайновой интерполяции и сглаживающего сплайна это окно не содержит никаких элементов управления, поскольку дополнительных опций соответствующие алгоритмы не требуют. Для линейных моделей можно задавать выбор целевой функции (об этом написано чуть ниже) и границы для искомых коэффициентов.
Для других типов параметрических моделей диалоговое окно Fit options for выглядит следующим образом
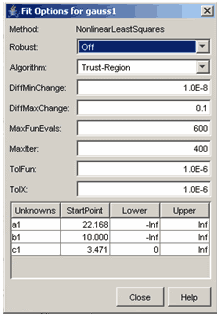
Диалоговое окно Fit options for
для задания опций вычислительных алгоритмов
Вверху окна в области Method выводится информация о том, используется ли линейный (LinearLeastSquares) или нелинейный метод наименьших квадратов (NonlinearLeastSquares), что зависит от того, линейно или нелинейно входят параметры в выбранную параметрическую модель.
Раскрывающийся список Robust содержит четыре возможные опции On, Off, LAR и Bisquare и служит для выбора метода приближения, устойчивого к выбросам в данных. Искомые значения параметров a1,a2,...,akопределяются как решение задачи минимизации суммы квадратов невязок, т.е. суммы квадратов расстояний от точек данных (xj,yj)j=1,2,...,n, до приближающей их кривой y(xj;a1,a2,...,ak):
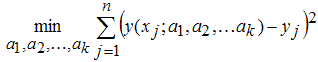
Если данные (xj,yj)j=1,2,...,n снабжены весами (wj)j=1,2,...,n, то решается следующая задача минимизации (если веса не заданы, то по умолчанию они считаются равными единице):
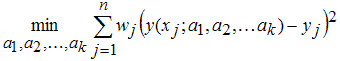
Если имеется выброс в данных, причем соответствующий вес не задан достаточно маленьким, то он может существенно ухудшить приближение, например на следующем графике приведены данные с одним выбросом, приближаемые полиномом первой степени (линейная регрессия). Данные без выброса сгенерированы следующим образом
>> x=1:10;
>> y=2*x+3+randn(size(x));а выброс в девятой точке равен нулю
>> y(9)=0;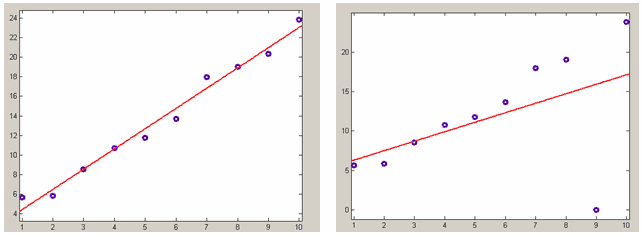
Линейная регрессия данных без выброса (слева) и с выбросом (справа). Коэффициенты линейной функции находятся из условия минимума суммы квадратов невязок, все веса равны единице.
Выброс оказывает такое сильное влияние, поскольку невязка в минимизируемом выражении возводится в квадрат.
Одним из способов уменьшения влияния выбросов на качество получаемого приближения состоит в минимизации суммы не квадратов невязок, а их модулей. Для этого служит опция LAR (least absolute residuals). После выбора LAR в раскрывающемся списке Robust диалогового окна Fit options for и снова провести линейную регрессию, то мы увидим, что выброс в данных намного меньше влияет на получающееся приближение линейной функцией (см. рисунок ниже). С другими типами параметрических моделей дело будет обстоять аналогичным образом.
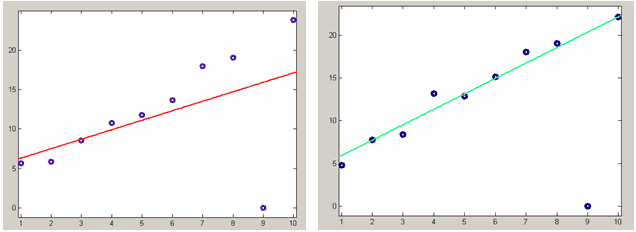
Линейная регрессия данных с выбросом справа. Коэффициенты линейной функции находятся из условия минимума суммы квадратов невязок (слева), или из условия минимума суммы модулей невязок (справа). Все веса равны единице.
Другой способ снижения влияния выбросов на приближение параметрической моделью некоторых данных состоит в назначении весов данным. Чем больший вес имеет та или иная точка, тем большее влияние она оказывает на получающееся приближение. В нашем примере можно было назначить маленький вес выбросу и использовать метод наименьших квадратов (опция Off в раскрывающемся списке Robust диалогового окна Fit options for) для поиска коэффициентов линейной параметрической модели.
Зададим веса всем данным равные единице, кроме выброса, а для выброса установим вес 0.1:
>> w=ones(size(x));
>> w(9)=0.1;Снова приблизим данные линейной параметрической моделью, только теперь следует импортировать их заново в приложение cftool, нажав кнопку Data в основном окне приложения и выбрав массивы x, y и w в раскрывающихся списках XData, Y Data и Weights, соответственно. Перед началом подбора параметров выберем метод наименьших квадратов, для чего следует нажать кнопку Fit options в диалоговом окне Fitting и установить опцию Off в раскрывающемся списке Robust диалогового окна Fit options for. Получающееся приближение приведено на рисунке ниже, заметно, что выброс практически не оказывает влияния на приближение.
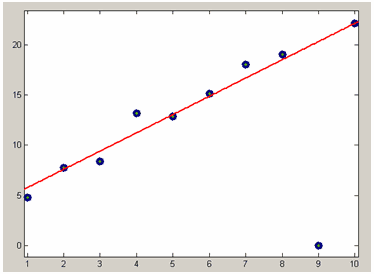
Приближение данных с выбросом линейной моделью по методу наименьших квадратов с весами. Выброс имеет маленький вес по сравнению с весами для остальных данных.
В этом примере можно было назначить точке, в которой есть заметный выброс, нулевой вес, или же воспользоваться предварительной обработкой данных для исключения выбросов (см. раздел Предварительная обработка данных). Однако, в практических задачах не всегда удается так просто определить выбросы или точки данных, которые должны оказывать меньшее влияние на получающееся приближение и назначить им соответствующие веса. Вместо этого можно воспользоваться адаптивным алгоритмом, который последовательно:
-
делает приближение, подбирая параметры по методу наименьших квадратов;
-
вычисляются приведенные невязки (см. более подробно в справочной системе по Curve Fitting Toolbox раздел Fitting Data: Parametric Fitting: The Least Squares Fitting Method);
-
в зависимости от удаленности точек от приближающей их кривой данным назначаются веса по следующему правилу (чем дальше точка, тем меньше ее вес):
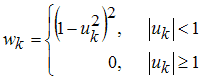
-
если веса достаточно сильно изменились, то переходим к п. 1), а если процесс сошелся, то останавливаем алгоритм, нужное приближение построено.
Поскольку в приведенном выше адаптивном алгоритме присутствует четвертая степень невязки, то он называется Bisquare weights (биквадратные веса). Для выбора такого способа приближения параметрической моделью следует установить опцию Bisquare в раскрывающемся списке Robust диалогового окна Fit options for. Разумеется, если пользователь задал данные и некоторые начальные веса, то они изменятся. Результирующий вес для каждой точки будет являться произведением исходного веса на тот, который вычисляет алгоритм Bisquare weights.
На рисунке ниже приведен результат приближения данных с выбросом линейной параметрической моделью при помощи алгоритма Bisquare weights с автоматическим подбором весов для уменьшения влияния выбросов в данных на получаемое приближение.
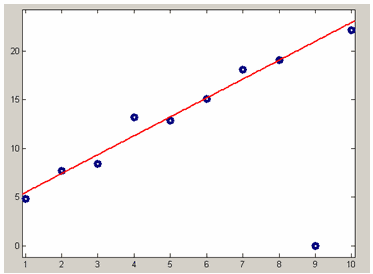
Приближение данных с выбросом линейной моделью при помощи алгоритма isquare weights.
Другие опции в диалоговом окне Fit options for связаны с алгоритмами минимизации целевой функции (в общем случае взвешенной суммы квадратов или модулей невязки).
Раскрывающийся список Algorithm содержит три опции:
-
Trust-Region (метод доверительных областей) - используемый по умолчанию алгоритм минимизации целевой функции. Если на искомые коэффициенты параметрической модели наложены ограничения, то использование этого алгоритма обязательно.
-
Levenberg-Marquardt (метод Левенберга- Марквардта) - можно использовать в задачах без ограничений на коэффициенты.
-
Gauss-Newton - классический метод Ньютона.
Все эти алгоритмы реализованы в функциях Optimization Toolbox, которые и используются при минимизации целевой функции при подборе параметров в параметрических моделях, приближающих данные, в Curve Fitting Toolbox.
Следующие опции в диалоговом окне Fit options for служат для настройки этих алгоритмов.
MaxFunEvals - максимальное количество вычислений минимизируемой функции (для предотвращения зацикливания), по умолчанию минимизируемая функция вычисляется не более 600 раз, после чего алгоритм минимизации останавливается.
MaxIter - максимальное число итераций алгоритма минимизации (для предотвращения зацикливания), по умолчанию делается не более 400 итераций, после чего алгоритм минимизации останавливается.
TolFun - точность по функции (для завершения итерационного алгоритма), по умолчанию 10e-6, при достижении этой точности алгоритм минимизации останавливается.
TolX - точность по искомым параметрам (для завершения итерационного алгоритма), по умолчанию 10e-6, при достижении этой точности алгоритм минимизации останавливается.
DiffMinChange - минимальный шаг по каждой из искомых переменных (параметров модели) для вычисления приближенного вычисления частных производных (используемых в алгоритмах минимизации) при помощи конечных разностей, по умолчанию 10e-8.
DiffMaxChange - минимальный шаг по каждой из искомых переменных (параметров модели) для вычисления приближенного вычисления частных производных (используемых в алгоритмах минимизации) при помощи конечных разностей, по умолчанию 0.1.
В диалоговом окне Fit options for также можно задавать границы для разыскиваемых параметров параметрической модели и начальные приближения. Для стандартных и пользовательских параметрических моделей предлагаются по умолчанию (там где это нужно, в зависимости от типа параметрической модели) следующие границы параметров и начальные приближения.
|
Тип модели |
Начальное приближение |
Ограничения на параметры |
|
Линейная модель, определенная пользователем |
Не требуется |
Нет |
|
Нелинейная модель, определенная пользователем |
Случайное для каждого параметра из интервала [0,1] |
Нет |
|
Экспоненциальные
|
Вычисляется по начальным данным по эвристическому алгоритму |
Нет |
|
Отрезки ряда Фурье
|
Вычисляется по начальным данным по эвристическому алгоритму |
Нет |
|
Гауссова
|
Вычисляется по начальным данным по эвристическому алгоритму |
|
|
Полиномиальная
|
Не требуется |
Нет |
|
Степенные
|
Вычисляется по начальным данным по эвристическому алгоритму |
Нет |
|
Дробно-рациональная
|
Случайное для каждого параметра из интервала [0,1] |
Нет |
|
Сумма синусов
|
Вычисляется по начальным данным по эвристическому алгоритму |
bk > 0 |
|
Вейбула
|
Случайное для каждого параметра из интервала [0,1] |
a > 0,b > 0 |
1.3.8. Критерии пригодности приближения
После приближения данных стандартной параметрической моделью или моделью, заданной пользователем, оценка качества приближения может быть проведена как графически, так и с использованием различных критериев пригодности приближения: SSE (сумма квадратов ошибок), R-square (критерий R-квадрат), Adjusted R-square (уточненный R-квадрат), RSME (корень из среднего для квадрата ошибки). Кроме того, можно вычислить доверительные интервалы для найденных значений параметров модели, соответствующие различным уровням вероятности, и доверительные полосы для приближения и данных, так же соответствующие различным уровням вероятности.
Визуальная оценка качества приближения
Во-первых, построив графики данных и параметрической модели уже можно сделать предварительный вывод о том, насколько хорошо выбранная модель (с найденными значениями параметров) соответствует данным. Например, при приближении следующих данных
x = 0:0.05:5;
y = x.*sin(3*x)+sqrt(4*x)+0.2*rand(size(x));полиномом пятой степени, функцией aebx или a1sin(b1x + c1) + a2sin(b2x + c2) мы вряд ли получим хорошие приближения, что очевидно из соответствующих графиков, приведенных ниже
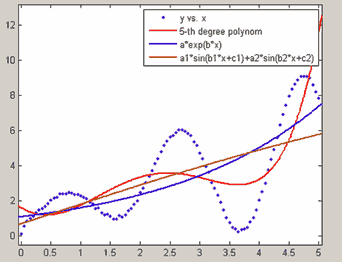
Приближение данных неверной моделью
Во-вторых, визуально о качестве приближения можно судить по распределению ошибок, т.е. разности данных в заданных точках и значений параметрической модели в этих же точках. Если ошибки достаточно равномерно распределены около нуля и в их поведении нет выраженной тенденции, то тем лучше приближение.
Например, если данные
x = 0:0.05:5;
y = 4*x.^2+3*x+3+randn(size(x));приблизить полиномом второй степени ax² + bx + c и моделью ax² + c, в которой пропущено линейное слагаемое, то получим следующие результаты. Ошибки при приближении моделью ax² + bx + c более равномерно распределены около нуля, чем при приближении моделью ax² + c (в приложении cftool использовалась пользовательская модель Custom equation для создания модели ax² + c, см. раздел Создание собственной параметрической модели, для вывода графика ошибок следует в меню View основного окна приложения cftool выбрать пункт Residuals и далее подпункт Scatter Plot или Line Plot). Приведенные ниже графики показывают распределение ошибок для квадратичной моделей с линейным слагаемым и без него.
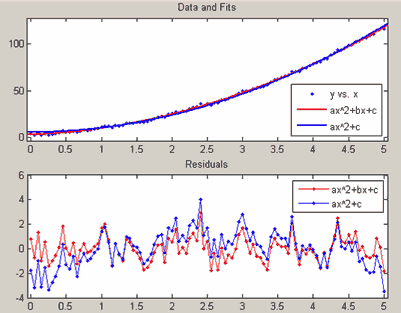
Распределение ошибок для моделей ax² + bx + c и ax² + c.
Для оценки пригодности приближения применяют так же ряд числовых критериев, вычисляемых автоматически в приложении cftol.
Критерии пригодности приближения
Критерий SSE (Sum of squares due to error) - сумма квадратов ошибок.
Критерий SSE вычисляется по формуле:
![]()
где wk - веса (если они не заданы при импорте данных, то считаются равными единице), yk - данные в xk, а ![]() k - значения параметрической модели в xk. Близость SSE к нулю говорит о хорошем качестве приближения данных параметрической моделью.
k - значения параметрической модели в xk. Близость SSE к нулю говорит о хорошем качестве приближения данных параметрической моделью.
Критерий R-квадрат (R-square) - квадрат смешанной корреляции.
Критерий R-квадрат определяется как отношение суммы квадратов относительно регрессии SSR к полной сумме квадратов (SST), т.е.
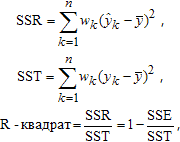
где ![]() - среднее.
- среднее.
Критерий R-квадрат может принимать значения только от нуля до единицы и, как правило, чем ближе он к единице, тем лучше параметрическая модель приближает исходные данные.
Однако, при увеличении числа параметров модели значение критерия R-квадрат может увеличится, хотя вместе с тем, качество приближения не улучшится. В связи с этим часто применяют другой критерий - уточненный R-квадрат, в который входит число коэффициентов параметрической модели.
Уточненный R-квадрат (Adjusted R-square)
Если число данных равно n, а число параметров модели равно m, то критерий уточненный R-квадрат определяется так:
![]()
Его значение не может превышать единицы, а близкие к единице значения уточненного R-квадрат свидетельствуют о хорошем приближении исходных данных параметрической моделью.
Корень из среднего для квадрата ошибки RSME (Root mean Squared Error)
![]()
Близкие к нулю значения RSME означают хорошее приближение исходных данных параметрической моделью.
Значения вышеперечисленных критериев приближения данных параметрической моделью выводятся в окно Results и в таблицу Таble of fits окна Fitting после вычисления параметров модели. Причем имеется возможность управлять количеством выводимых критериев качества приближения и информацией о построенной параметрической модели. Для этого в диалоговом окне Fitting следует нажать на кнопку Table Options… и выбрать нужную информацию (установив соответствующие флаги) в появившемся диалоговом окне Table Options:
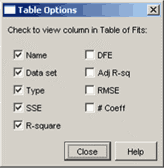
В диалоговом окне Table Options часть флагов (SSE, R-square, Adj R-sq, RMSE) служит для вывода значений критериев приближения данных параметрической моделью, причем имена флагов совпадают с названиями описанных выше критериев приближения, а смысл остальных флагов таков:
-
Name - выводить имя приближения (задание имени приближения описано в разд. Приближение стандартными параметрическими и моделями. Работа с несколькими приближениями и несколькими наборами данных.)
-
Data set - имя множества данных (задание имени множеству данных описано в разделе Окно приложения cftool. Импорт данных в приложение cftool).
-
Type - тип приближения (одна из стандартных параметрических моделей, описанных в разд. Стандартные параметрические и непараметрические модели, или Custom equation, если применялась пользовательская модель, см. разд. Создание собственной параметрической модели).
-
DFE - число степеней свобод, т.е. разность между числом данных и параметров модели.
-
# Coeff - число коэффициентов в параметрической модели.
Доверительные интервалы и полосы
При подборе параметров в приложении cftool вычисляются доверительные интервалы для найденных значений параметров модели, соответствующие некоторому заданному уровню вероятности (по умолчанию он равен 95%). Границы доверительных интервалов для параметров выводятся в область вывода Results диалогового окна Fitting. Например, при приближении данных
x=0:0.01:5;
y=x.^2+2*x+3+0.5*randn(size(x));полиномом второй степени
f(x) = p1*x^2 + p2*x + p3Значения коэффициентов и доверительных интервалов будут такими
p1 = 0.9918 (0.9678, 1.016)
p2 = 2.021 (1.897, 2.145)
p3 = 3.079 (2.944, 3.213)Т.е., с вероятностью 95% первый коэффициент p1 полинома находится в интервале (0.9678, 1.016), второй p2 - в интервале (1.897, 2.145), а третий коэффициент p3 - в интервале (2.944, 3.213).
Для изменения уровня вероятности следует в меню View основного окна приложения выбрать пункт Confidence Level и в подменю установить нужный уровень вероятности, а затем еще раз произвести подбор параметров. Например, для уровня вероятности 90% в предыдущем примере получаются более узкие доверительные интервалы:
p1 = 0.9918 (0.9717, 1.012)
p2 = 2.021 (1.917, 2.125)
p3 = 3.079 (2.966, 3.191)Доверительные интервалы для параметров модели вычисляются по следующей формуле
![]()
где b - найденные значения параметров, t - обратная функция для функции распределения Стьюдента, S - вектор из диагональных элементов матрицы sXTX, где X - матрица плана, s - среднеквадратичная ошибка.
Границы доверительных полос, соответствующих различным уровням вероятности, могут быть построены как для данных, так и для приближения.
Для построения доверительной полосы для данных следует установить нужный уровень вероятности, выбрав в меню View основного окна приложения пункт Confidence Level и задав в подменю нужный уровень вероятности, а затем выбрать в меню View пункт Prediction Bounds. Например, при приближении данных
x=0:0.05:5;
y=3*x.^2+2*x+3+randn(size(x));полиномом второй степени доверительная полоса для данных, соответствующая вероятности 99% приведена ниже
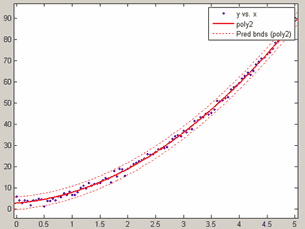
Доверительная полоса для уровня вероятности 95%
Доверительные полосы могут быть также построены в окне Analysis (см. разд. Операции с построенным приближением), для отображения которого на экране следует нажать одноименную кнопку в основном окне приложения cftool. В нем следует:
-
указать абсциссы точек, в которых будет производиться анализ в строке ввода Analyze at Xi=;
-
установить флаг Evaluate fit at Xi;
-
ввести уровень вероятности в строку ввода Level;
-
выбрать переключатель For function или For new observation (в зависимости от того, для чего надо построить доверительную полосу, соответственно, для приближения или для данных);
-
установить флаг Plot results;
-
нажать кнопку Apply.
Результат выводится в отдельном графическом окне.
1.3.9. Предварительная обработка данных
Перед приближением данных некоторой моделью может понадобиться их предварительная обработка, заключающаяся в отбрасывании части данных по некоторым соображениям. Обычно, исключаются выбросы из данных.
Предположим, что есть данные
x=0:0.05:5;
y=2*x.^3-6*x.^2-4*x+3+randn(size(x));
y(10)=15;
y(20)=19;
y(50)=49;и они импортированы в приложение cftool (см. разд. Окно приложения cftool. Импорт данных в приложение cftool). В этих данных, как следует из приведенного ниже графика, очевидно 10-ая, 20-ая и 50-ая точка содержат выбросы, которые следует исключить перед процессом подбора параметров:
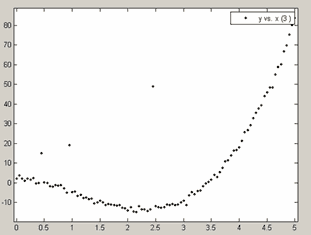
Данные с выбросами
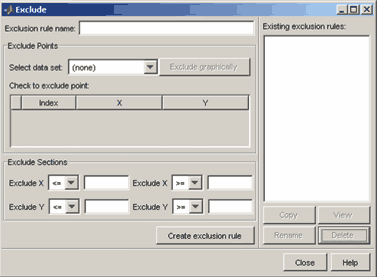
Для того чтобы отбросить часть исходных данных (выбросов), необходимо сформировать правило исключения. Правило исключения задается в диалоговом окне Exclude, которое появляется на экране после нажатия на одноименную кнопку в основном окне приложения cftool:
Окно Exclude для задания правил исключения
Сначала в раскрывающемся списке Select data set следует выбрать имя множества данных, после чего можно начинать процесс исключения части данных одним из нескольких способов.
1-ый способ - в таблице Check to exclude point следует поставить флаги напротив тех данных, которые не должны участвовать в процессе подбора параметров (если данных много, то этот способ может потребовать достаточно много времени).
2-ой способ - графическое исключение, для выбора которого следует нажать кнопку Exclude graphically и в появившемся окне Select Points for Exclusion Rule выделить отбрасываемые точки, или наоборот те, которые оставляются для процесса подбора параметров Что именно выделяется, зависит от того, какой из переключателей установлен. Если установлен переключатель Excludes Them, то будет делаться исключение данных, а если Includes Them - то отбор множества точек, по которым далее будет производиться подбор параметров параметрической модели. Точки выделяются щелчком мыши по ним, можно также выделить сразу несколько точек, обведя их при помощи мыши. Кнопки Exclude All и Include All служат, соответственно, для исключения или отбора всех данных.
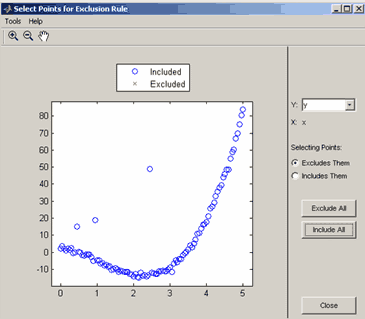
Окно для графического исключения данных
3-ий способ - задание двусторонних неравенств для исключения данных как по значениями x так и по значениями y. Двусторонние неравенства по каждой координате задаются при помощи соответствующих списков и строк ввода, расположенных на панели Exclude Sections диалогового окна Exclude.
После того, как часть данных исключена, следует дать название правилу исключения в строке ввода Exclusion rule name и нажать кнопку Create Exclusion Rule. При подборе параметров имя исключения указывается в списке Exclusion Rule диалогового окна Fitting приложения cftool.
Заметим, что для одного и того же набора данных может быть создано несколько правил исключения (точно так же, как и применено несколько параметрических моделей различных типов, каждая из которых учитывает свое правило исключения). Каждое правило исключения можно удалить, переименовать, скопировать или посмотреть на графике. Для этого служат, соответственно, кнопки Delete, Rename, Copy, View в диалоговом окне Exclude приложения cftool.
1.3.10. Сглаживание и фильтрация данных
Если данные сильно зашумлены, то имеет смысл произвести их сглаживание. Однако следует иметь ввиду, что сглаживание данных приводит к тому, что стандартное предположение относительно нормального распределения ошибки не будет выполняться. Поэтому сглаживание обычно применяется для получения информации о возможном выборе типа параметрической модели, а сам процесс подбора параметров параметрической модели проводят для исходных (несглаженных) данных.
Сглаживание производится по нескольким расположенным подряд данным, причем их число обычно подбирается экспериментально.
В Curve Fitting Toolbox реализовано три способа сглаживания:
-
скользящее среднее (Moving average filtering);
-
взвешенная локальная регрессия;
-
фильтр Савицкого-Голея.
Все эти способы сглаживания производятся в диалоговом окне Data на вкладке Smooth. Окно Data открывается нажатием на кнопку Data в основном окне приложения cftool.
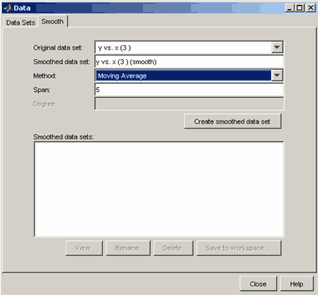
Вкладка Smooth окна Data для сглаживания данных
В раскрывающемся списке Original data set выбирается множество данных (которое надо создать при импорте данных из рабочей среды MATLAB, см. разд. Окно приложения cftool. Импорт данных в приложение cftool).
В строке ввода Smoothed data set вводится имя, которое будет присвоено сглаженным данным.
В раскрывающемся списке Method выбирается один из способов сглаживания.
В строке Span задается число соседних точек, по которым производится сглаживание (для взвешенной локальной регрессии можно задавать меньшее единицы число, оно воспринимается как процент от общего числа точек, используемых для сглаживания).
Для фильтра Савицкого-Голея требуется задание степени полинома для локальной регрессии, степень задается в строке ввода Degree.
Сглаженные данные можно визуализировать (кнопка View), переименовать (кнопка Rename), удалить (кнопка Delete) и сохранить в глобальной переменной рабочей среды MATLAB (см. разд. Экспорт сглаженных данных).
Метод скользящего среднего
В методе скользящего среднего исходные данные yi сглаживаются по следующему правилу
![]()
где 2N + 1 - число точек, выбираемых для сглаживания, т.е. слева и справа от текущей точки выбирается по Nточек (ясно, число точек, участвующих в сглаживании, должно быть нечетным). Данные, расположенные в точках, близких к границам отрезка, не сглаживаются, т.к. не хватает точек справа или слева от текущей, в которой в данный момент производится сглаживание. Ниже на рисунках приведены исходные зашумленные данные
x=0:0.002:5;
y=x.*sin(3*x)+2*randn(size(x));сглаженные с N = 33 точками и сглаженные с N = 191 точкой. Красная линия соответствует незашумленным данным
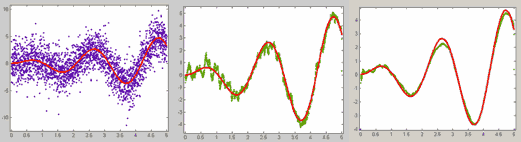
Левый график - зашумленные данные (синим) и незашумленные (красным)
Средний график - сглаженные с N = 33 (зеленым) и незашумленные (красным)
Правый график - сглаженные с N = 191 (зеленым) и незашумленные (красным)
Взвешенная локальная регрессия (lowess и loess)
При сглаживании при помощи взвешенной локальной регрессии для каждого сглаживаемого значения данных , заданного в точке , выбирается набор из фиксированного числа рядом расположенных точек, каждой из которых назначается вес по следующей формуле
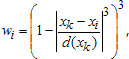
где d(xk) - расстояние от xk до наиболее удаленной точки из набора. Т.е. наибольший вес (равный единице) будет у yk, а наименьший (равный нулю) у данных, расположенных на границах набора. Распределение весов для некоторой точки внутри интервала, где заданы данные, и на краях, показано на следующем графике:
Значения весов для взвешенной локальной регрессии (красными маркерами обозначены точки ), в которых заданы данные
После выбора весов сглаженное значение находится при помощи локальной взвешенной регрессии с определенными выше весами , причем в зависимости от выбора пользователя в раскрывающемся списке Method на вкладке Smooth окна Data делается различная регрессия
-
для Lowess - линейная регрессия;
-
для Loess - квадратичная регрессия.
Кроме опций Lowess и Loess в раскрывающемся списке Method на вкладке Smoothing в окне Data есть еще Robust Lowess и Robust Loess. Эти способы менее чувствительны по отношению к выбросам, поскольку выбор весов осуществляется за несколько итераций, на каждой из которых более удаленным от регрессионной кривой (найденной на предыдущей итерации) точкам назначаются меньшие веса, а если точка сильно удалена, то она вовсе исключается при выполнении локальной линейной или квадратичной регрессии на следующей итерации.
На приведенных ниже графиках представлен результат сглаживания данных с использованием 10% от всех точек и 20% от всех точек.
x=0:0.002:5;
y=x.*sin(3*x)+2*randn(size(x));Красная линия соответствует незашумленным данным
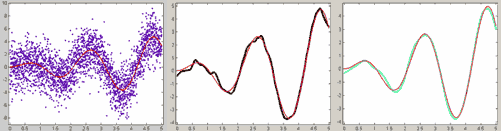
Левый график - зашумленные данные (синим) и незашумленные (красным)
Средний график - сглаженные с 10% от всех точек (черным) и незашумленные (красным)
Правый график - сглаженные с 20% от всех точек(зеленым) и незашумленные (красным)
Фильтр Савицкого-Голея
В фильтре Савицкого-Голея степень полинома, применяемого для локальной регрессии, может быть выше, чем в предыдущем способе сглаживания, при этом выполняется невзвешенная локальная регрессия. Число соседних данных (задаваемое в строке ввода Span) для сглаживания в точке должно быть нечетное, а степень полинома (задаваемая в строке ввода Degree) меньше, чем число соседних данных.
Этот способ фильтрации хорошо подходит для зашумленных сигналов, в которых при сглаживании требуется сохранить высокие частоты. При повышении степени полинома, применяемого в локальной регрессии, лучше воспроизводятся узкие и высокие пики.
1.3.11. Экспорт результатов в рабочую среду
Приложение cftool позволяет экспортировать полученные результаты в рабочую среду MATLAB, причем можно экспортировать сглаженные данные, саму параметрическую модель и критерии ее пригодности, информацию о ходе алгоритма поиска значений параметров и результаты некоторых операций с полученной параметрической моделью.
Экспорт сглаженных данных
После сглаживания (см. разд. Сглаживание и фильтрация данных) сглаженные данные могут быть экспортированы в рабочую среду MATLAB. Это делается при помощи кнопки Save to workspace вкладки Smooth диалогового окна Data. В появляющемся окне следует указать имя структуры (глобальной переменной рабочей среды), в которой будут записаны сглаженные данные, например smdata. Тогда поля x и y структуры smdata будут содержать:
-
smdata.x - точки, в которых заданы исходные данные;
-
smdata.y - сглаженные данные.
Экспорт параметрической модели
После подбора параметров в параметрической модели результаты могут быть экспортированы в рабочую среду MATLAB. Экспорт производится при помощи кнопки Save to workspace диалогового окна Fitting. Предлагается сохранить:
-
саму параметрическую модель (флаг Save fit to MATLAB object named);
-
значения критериев пригодности приближения (флаг Save goodness of fit to MATLAB struct named);
-
информацию, возвращаемую оптимизационным алгоритмом (флаг Save fit output to MATLAB struct named).
Параметрическая модель является объектом (см. Функции Curve Fitting Toolbox). Информация о ней содержит:
-
тип модели и ее вид;
-
найденные значения параметров вместе с доверительными интервалами;
Для работы с параметрической моделью, которая экспортировалась в объекте, можно применять функции Curve Fitting Toolbox (см. разд. Функции Curve Fitting Toolbox). Например, для получения коэффициентов модели используется функция coeffvalues. Предположим, что данные
x=0:0.1:10;
y=sin(x)+0.1*randn(size(x));
были приближены в приложении cftool полиномом пятой степени и построенная параметрическая модель была экспортирована в рабочую среду как объект с именем fittedmodel. Тогда для записи коэффициентов полинома в вектор достаточно выполнить следующую команду:
>> p=coeffvalues(fittedmodel)
p =
0.0009 -0.0330 0.4100 -1.9995 3.2931 -0.5476
Значения критериев пригодности приближения (см. разд. Критерии пригодности приближения) возвращаются в структуре с полями:
-
sse - сумма квадратов ошибок (sum of squares due to error);
-
rsquare - критерий R-квадрат, квадрат смешанной корреляции (coefficient of determination);
-
dfe - число степеней свобод, т.е. разность между числом данных и параметров модели (degrees of freedom);
-
adjrsquare - уточненный критерий R-квадрат (degree-of-freedom adjusted coefficient of determination);
-
rmse - корень из среднего для квадрата ошибки (Root mean Squared Error).
Возвращаемая оптимизационным алгоритмом информация сохраняется в структуре с полями:
-
numobs - число данных;
-
numparam - число параметров в параметрической модели;
-
residuals - вектор невязок;
-
Jacobian - матрица Якоби, используемая при минимизации суммы квадратов невязок;
-
exitflag - флаг, содержащий информацию о причине остановки вычислительного алгоритма подбора параметров модели:
-
если exitflag больше нуля, то решение задачи минимизации суммы квадратов невязок успешно найдено;
-
если exitflag равен нулю, то было достигнуто максимально допустимое число вызовов минимизируемой функции;
-
если exitflag меньше нуля, то была обнаружена расходимость итерационного процесса;
-
-
iterations - число итераций, сделанных при минимизации.
-
funcCount - число вызовов минимизируемой функции
-
algorithm - использовавшийся алгоритм минимизации или QR-разложение для линейной параметрической модели.
Экспорт результатов анализа приближения
Результаты анализа построенного в приложении cftool приближения данных параметрической моделью (доверительные полосы для приближения и данных, значения модели в заданных точках, значения ее первой и второй производных и значение интеграла с переменным верхним пределом) могут быть экспортированы в рабочую среду при помощи кнопки Save to workspace диалогового окна Analysis (см. разд. Операции с построенным приближением).
Результаты сохраняются в структуре с полями:
-
xi - абсциссы точек, в которых производился анализ приближения данных параметрической моделью;
-
boundtype - тип доверительной полосы (для данных или для приближения параметрической моделью)
-
lower - ординаты нижней границы доверительной полосы для данных или для приближения в точках xi;
-
upper - ординаты верхней границы доверительной полосы для данных или для приближения в точках xi;
-
conflevel - уровень вероятности, которому соответствует доверительная полоса для данных или для приближения;
-
yfit - значения параметрической модели в заданных точках xi;
-
d2ydx2 - значения второй производной от параметрической модели в заданных точках xi;
-
dydx - значения первой производной от параметрической модели в заданных точках xi;
-
integral - значение интеграла с переменным верхним пределом от параметрической модели в заданных точках xi;
-
integralstart - нижний предел интегрирования.
1.3.12. Операции с построенным приближением
После построения приближения исходных данных параметрической моделью можно найти:
-
значения построенного приближения в заданных точках;
-
значения первой производной от построенного приближения в заданных точках;
-
значения второй производной от построенного приближения в заданных точках;
-
значения интеграла от построенного приближения в заданных точках;
-
доверительные полосы для данных и построенного приближения, соответствующие различным уровням вероятности
Для анализа приближения следует нажать кнопку Analysis в основном окне приложения cftool. После этого появляется одноименное окно.
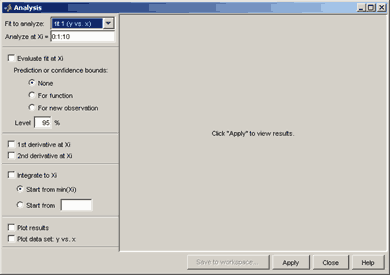
Диалоговое окно Analysis для анализа приближения
В списке Fit to analyze выбирается имя приближения, а в строке ввода Analyze at Xi задается вектор значений независимой переменной, для которых следует вычислить задаваемые далее величины.
После установки флага Evaluate fit at Xi и нажатия на кнопку Apply в диалоговое окно Analysis выводится таблица значений приближения. Если также выбрать один из переключателей For function или For new observation, то в таблице появляются столбцы с ординатами верхней и нижней границы доверительной полосы (соответственно, для приближения или для данных), отвечающей уровню вероятности, установленному в строке ввода Level (95% по умолчанию).
Для добавления в таблицу столбцов со значениями первой и второй производных от приближения достаточно установить соответствующий флаг: 1st derivative at Xi или 2nd derivative at Xi, соответственно. Для вычисления интеграла с переменным верхним пределом (его значениями являются точки, указанные в строке ввода Analyze at Xi) следует установить флаг Integrate to Xi. Если нижний предел интегрирования не совпадает с минимальной абсциссой точек, в которых заданы исходные данные, то его можно указать в строке ввода Start from.
Полученные результаты можно экспортировать в рабочую среду для дальнейшего использования в других приложениях или для работы с ними из командной строки (см. разд. Экспорт результатов анализа приближения), или представить графически, для чего следует установить флаги Plot results (и Plot data set, если нужно вывести также и исходные данные). Все результаты (доверительные полосы, производные и интеграл) отображаются на осях отдельного графического окна.
2. Функции Curve Fitting Toolbox
Приложение с графическим интерфейсом пользователя cftool предоставляет удобную оболочку для работы с функциями Curve Fitting ToolBox, при которой не требуется знания синтаксиса этих функций (см. описание работы в приложении cftool в разделе Основные этапы работы в приложении cftool). Однако, часто бывает нужно написать собственное приложение для приближения данных и его анализа. В этом случае потребуется привлечение функций Curve Fitting ToolBox (если только мы не хотим программировать процесс подбора параметров самостоятельно).
При использовании функций, входящих в состав Curve Fitting ToolBox, доступны все те же самые параметрические и непараметрические модели, что и в приложении cftool, кроме того, можно создавать собственные параметрические линейные и нелинейные модели. Возможна предварительная обработка данных, приближение данных с весами и обработка результатов, включающая вычисление доверительных интервалов для различных уровней вероятности и различные критерии пригодности приближения, интегрирование и дифференцирование полученного приближения и вычисление его в заданных точках. Функции Curve Fitting ToolBox позволяют также управлять процессом построения приближения, в том числе выбирать различные варианты целевой функции, включая способ приближения с адаптивным выбором весов для исключения выбросов.
В Curve Fitting ToolBox функций немного, они разбиты на несколько категорий.
Предварительная обработка данных
- функция excludedata позволяет производить исключение данных из исходного набора по некоторому правилу.
- функция smooth предназначена для сглаживания данных различными способами, включая фильтр Савицкого-Голея.
Получение статистической информации о данных
datastats - нахождение минимального и максимального значений, среднего, медианы, стандартного отклонения.
Построение параметрического приближения
- основная функция fit производит подбор параметров, в ней задаются исходные данные, сама параметрическая модель, настройки алгоритма; она возвращает: построенную параметрическую модель с найденными значениями параметров, и различные критерии пригодности полученного приближения.
- функция fittype позволяет выбрать одну из стандартных моделей или создать произвольную линейную или нелинейную параметрическую модель;
- функция fitoptions предназначена для выбора минимизируемой целевой функции и задания различных опций, управляющих вычислительным процессом подбора параметров линейных и нелинейных параметрических моделей.
- функция cfit служит для создания стандартной или пользовательской параметрических моделей с заданными значениями ее параметров.
Обработка результатов приближения и их визуализация
- функция confint вычисляет доверительные интервалы для найденных параметров модели.
- функция predint находит интервалы предсказаний наблюдаемых значений с заданной вероятностью.
- функция differentiate позволяет продифференцировать построенную параметрическую модель.
- функция integrate находит интеграл от построенной параметрической модели для заданных значений верхнего предела интеграла.
- функция feval вычисляет значения параметрической модели при заданных значениях аргумента.
- функция plot (это не функция MATLAB, она переопределена в Curve Fitting ToolBox) служит для простого построения графиков данных, параметрических моделей, графиков ошибок.
Информация о моделях и объектах, создаваемых функциями Curve Fitting Toolbox
- cflibhelp - получение информации о стандартных параметрических моделях, входящих в Curve Fitting Toolbox.
- disp - вывод в командное окно информации об объектах, создаваемых функциями Curve Fitting Toolbox.
Задание и получение значений свойств объектов, создаваемых функциями Curve Fitting Toolbox
- get - получение свойств объектов.
- set - задание свойств объектов.
2.1. Простые примеры
2.1.1. Приближение без создания объекта с параметрической моделью
Простые примеры
Приближение без создания объекта с параметрической моделью
Предположим, что при помощи функций Curve Fitting Toolbox требуется приблизить некоторые данные полиномом третьей степени по методу наименьших квадратов. Сгенерируем эти данные и запишем их в вектор-столбцы (при созднии x используется ' для транспонирования и получения вектор-столбца из вектор-строки ). Массив данных содержит значения полинома третьей степени с ошибками, распределенными по нормальному закону со средним 0 и среднеквадратическим отклонением 1:
>> x=(0:0.05:3)';
>> y=5*x.^3-10*x.^2-3*x+randn(size(x));
Для приближения эти данных полиномом третьей степени и получения приближения достаточно вызвать функцию Curve Fitting Toolbox, которая называется fit. В самом простом случае ее входными аргументами являются:
-
вектор-столбцы с данными;
-
имя одной из моделей, в нашем случае для приближения полиномом третьей степени имя будет 'poly3' (стандартные параметрические и непараметрические модели описаны в разделах Параметрические модели библиотеки Curve Fitting Toolbox и Непараметрические модели библиотеки Curve Fitting Toolbox).
>> fresult = fit(x,y,'poly3')
Функция fit возвращает полученное приближение (в Curve Fitting Toolbox приближения и модели являются объектами).
fresult =
Linear model Poly3:
fresult(x) = p1*x^3 + p2*x^2 + p3*x + p4
Coefficients (with 95% confidence bounds):
p1 = 5.322 (4.916, 5.729)
p2 = -11.52 (-13.38, -9.667)
p3 = -1.064 (-3.447, 1.32)
p4 = -0.6663 (-1.485, 0.1524)
В данном случае в командное окно MATLAB вывелся вид полиномиальной модели и полученные значения коэффициентов вместе с границами доверительных интервалов, соответствующих уровню вероятности 95%.
Для визуализации данных и построения графика полученного полинома третьей степени служит функция plot, переопределенная в Curve Fitting Toolbox. Если в качестве ее входного аргумента указать полученное приближение fresult, то построится его график. А если вызвать plot с тремя входными аргументами, указав еще и вектора с данными, то на графике отобразятся исходные данные:
>> plot(fresult, x, y)
.gif)
График исходных данных и приближающего их полинома третьей степени
Переопределенная в Curve Fitting Toolbox функция plot удобна еще и тем, что имеет ряд дополнительных входных аргументов, при помощи которых можно построить, в частности: графики ошибок и доверительные полосы. Например следующее обращение к функции plot приводит к появлению в графическом окне еще и графика ошибок для построенного приближения:
>> plot(fresult,x,y,'residuals')
.gif)
Графики данных, приближения и его ошибки
Если полученные значения коэффициентов параметрической модели требуется использовать в дальнейших расчетах, то их следует записать в некоторый массив, например coeff. Для этого нужно вызвать функцию coeffvalues , указав в качестве ее входного аргумента объект fresult:
>> coef=coeffvalues(fresult)
coef =
4.9333 -9.3702 -4.2915 0.5525
Для вычисления значений параметрической модели в заданных точках, в принципе, можно пользоваться этими коэффициентами и функцией polyval, входящей в MATLAB. Однако, в составе Curve Fitting Toolbox имеется функция feval (это переопределенная функция feval, входящая в базовый набор функций MATLAB). Ей надо указать построенную параметрическую модель fresult и вектор с координатами точек, в которых требуется вычислить ее значения. Найдем, например, значения модели в точках от первого до последнего элемента вектора x с шагом 0.001:
>> xx=x(1):0.001:x(end);
>> ff = feval(fresult,xx);
Теперь полученные значения можно использовать, скажем для построения графика приближения:
>> plot(xx,ff)
При таком варианте обращения к plot вызывается обычная функция plot, входящая в базовый набор функций MATLAB, а не переопределенная в Curve Fitting Toolbox.
Приближение с созданием объекта для параметрической модели
В приведенном выше примере мы сразу же вызвали функцию fit, входящую в Curve Fitting Toolbox, указав в ее входных аргументах исходные данные и имя параметрической модели, и получили приближение. Другой способ состоит в предварительном создании параметрической модели при помощи функции fittype и последующем нахождении ее параметров с использованием функции fit.
Приведем пример приближения данных:
>> x=(0:0.05:3)';
>> y=3.45*exp(-2.77*x)+0.05*randn(size(x));
при помощи экспоненциальной модели:
aebxСначала создадим саму модель, а соответствующий ей объект назовем ftype. В Curve Fitting Toolbox экспоненциальная модель входит в библиотеку стандартных моделей и называется 'exp1' (стандартные параметрические и непараметрические модели описаны в разделах Параметрические модели библиотеки Curve Fitting Toolbox и Непараметрические модели библиотеки Curve Fitting Toolbox):
>> ftype = fittype('exp1')
В командное окно выводится вид этой модели:
ftype =
General model Exp1:
ftype(a,b,x) = a*exp(b*x)
Теперь применим функцию fit для получения приближения (объекта fresult), т.е. параметрической модели с найденными значениями параметров. Само приближение запишем в fresult:
>> fresult = fit(x,y,ftype)
В командное окно выводится информация об объекте fresult с полученным приближением: вид модели и найденные значения коэффициентов вместе с границами доверительных интервалов:
fresult =
General model Exp1:
fresult(x) = a*exp(b*x)
Coefficients (with 95% confidence bounds):
a = 3.471 (3.401, 3.542)
b = -2.754 (-2.838, -2.669)
Для визуализации данных и построения графика полученного приближения снова применим переопределенную в Curve Fitting Toolbox функцию plot:
plot(fresult,x,y)
получаем
.gif)
Приближение данных моделью aebx
2.1.2. Приближение с созданием объекта для параметрической модели
В приведенном выше примере мы сразу же вызвали функцию fit, входящую в Curve Fitting Toolbox, указав в ее входных аргументах исходные данные и имя параметрической модели, и получили приближение. Другой способ состоит в предварительном создании параметрической модели при помощи функции fittype и последующем нахождении ее параметров с использованием функции fit.
Приведем пример приближения данных:
>> x=(0:0.05:3)';
>> y=3.45*exp(-2.77*x)+0.05*randn(size(x));
при помощи экспоненциальной модели:
aebxСначала создадим саму модель, а соответствующий ей объект назовем ftype. В Curve Fitting Toolbox экспоненциальная модель входит в библиотеку стандартных моделей и называется 'exp1' (стандартные параметрические и непараметрические модели описаны в разделах Параметрические модели библиотеки Curve Fitting Toolbox и Непараметрические модели библиотеки Curve Fitting Toolbox):
>> ftype = fittype('exp1')
В командное окно выводится вид этой модели:
ftype =
General model Exp1:
ftype(a,b,x) = a*exp(b*x)
Теперь применим функцию fit для получения приближения (объекта fresult), т.е. параметрической модели с найденными значениями параметров. Само приближение запишем в fresult:
>> fresult = fit(x,y,ftype)
В командное окно выводится информация об объекте fresult с полученным приближением: вид модели и найденные значения коэффициентов вместе с границами доверительных интервалов:
fresult =
General model Exp1:
fresult(x) = a*exp(b*x)
Coefficients (with 95% confidence bounds):
a = 3.471 (3.401, 3.542)
b = -2.754 (-2.838, -2.669)
Для визуализации данных и построения графика полученного приближения снова применим переопределенную в Curve Fitting Toolbox функцию plot:
plot(fresult,x,y)
получаем
.gif)
Приближение данных моделью aebx
2.1.3. Приближение с созданием объекта для пользовательской линейной параметрической модели
Приближение с созданием объекта для пользовательской линейной параметрической модели.
Функцию fittype можно применять и для создания собственной параметрической модели, в которую параметры входят как линейно, так и нелинейно. Рассмотрим сначала приближение данных при помощи линейной параметрической модели.
Сгенерируем исходные данные
>> x=(0:0.05:3)';
>> y=1.55*x+5*exp(-x)-2+0.05*randn(size(x));
Мы будем приближать их линейной параметрической моделью с тремя параметрами следующего вида:
p1x + p2e-x + p3При создании объекта с линейной параметрической моделью при помощи функции fittype в качестве ее входного аргумента указывается массив ячеек (для создания массива ячеек используются фигурные скобки), каждая ячейка которого содержит строку со слагаемым, входящим в модель (без искомого коэффициента), т.е. {'x','exp(-x)','1'}. Если обратиться к функции fittype таким образом:
>> ftype = fittype({'x','exp(-x)','1'})
то получим линейную параметрическую модель, в которой коэффициентам автоматически даны имена a, b, c:
ftype =
Linear model:
ftype(a,b,c,x) = a*x + b*(exp(-x)) + c
Если же мы хотим, чтобы коэффициенты назывались именно p1, p2 и p3, то следует указать их имена при создании параметрической модели при помощи функции fittype. Для этого функция fittype вызывается с дополнительной парой аргументов: 'coefficients' и массивом ячеек, каждая ячейка которого содержит строку с именем соответствующего параметра модели {'p1','p2','p3'}:
>> ftype = fittype({'x','exp(-x)','1'},'coefficients',{'p1','p2','p3'})
ftype =
Linear model:
ftype(p1,p2,p3,x) = p1*x + p2*(exp(-x)) + p3
Далее применяем функцию fit для подбора параметров
>> fresult = fit(x,y,ftype)
В командное окно выводится информация об объекте fresult с полученным приближением: вид модели и найденные значения параметров p1, p2 и p3 вместе с границами доверительных интервалов, соответствующих уровню вероятности в 95%:
fresult =
Linear model:
fresult(x) = p1*x + p2*(exp(-x)) + p3
Coefficients (with 95% confidence bounds):
p1 = 1.543 (1.508, 1.578)
p2 = 4.939 (4.821, 5.057)
p3 = -1.963 (-2.053, -1.873)
Для визуализации исходных данных и найденной параметрической модели достаточно вызвать функцию plot:
>> plot(fresult,x,y)
.gif)
Приближение данных линейной моделью p1x + p2e-x + p3
2.1.4. Приближение с созданием объекта для пользовательской нелинейной параметрической модели
Приближение с созданием объекта для пользовательской нелинейной параметрической модели.
Пусть данные сгенерированны следующим образом:
>> x=(0:0.05:3)';
>> y=5.23*log(x+0.15)+0.5*randn(size(x));
Приблизим их нелинейной параметрической моделью, в которую входит два параметра и следующего вида:
aln(x + b)Для этого создадим нелинейную параметрическую модель при помощи функции fittype, указав в ее входном аргументе строку 'a*log(x+b)' с выражением, задающим параметрическую модель:
>> ftype = fittype('a*log(x+b)')
Сама модель и сообщение о том, что она нелинейна, выводятся в командное окно:
ftype =
General model:
ftype(a,b,x) = a*log(x+b)Теперь попытаемся приблизить исходные данные параметрической моделью при помощи функции fit:
>> fresult = fit(x,y,ftype)
При этом выводится сообщение об ошибке, т.к. в процессе поиска параметров под знаком логарифма оказалось неположительное число.
??? Complex value computed by model function, fitting cannot continue.
Try using or tightening upper and lower bounds on coefficients.
Для того, чтобы избежать таких ошибок, следует задавать границы допустимых интервалов изменения параметров. В нашем случае достаточно задать нижнюю границу только для второго параметра , скажем 1e-5. Для этого следует при помощи функции fitoptions сформировать управляющую структуру, которую затем необходимо указать во входных аргументах функции fit, выполняющей подбор параметров модели (более подробно об управлении вычислительными алгоритмами при подборе параметров написано в разд. Управление вычислительным алгоритмом). В функции fitoptions входные аргументы задаются парами:
НазваниеОпции, Значение, НазваниеОпции, Значение, …
Функция fitoptions возвращает управляющую структуру.
В данном случае потребуется задание значения двух опций (будем называть опциями параметры вычислительных алгоритмов, чтобы отличать их от искомых параметров параметрической модели):
-
Method - метод использующийся при нахождении приближения, в нашем случае это нелинейные наименьшие квадраты, т.е. значением опции Method должна быть строка 'NonlinearLeastSquares';
-
Lower - вектор с нижними границами для значений параметров [-Inf 1e-5], где -Inf значит, что первый параметр может быть сколь угодно малым.
>> opts = fitoptions('Method','NonlinearLeastSquares','Lower',[-Inf 1e-5])
В командное окно выводится структура options
opts =
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
Robust: 'Off'
StartPoint: [1x0 double]
Lower: [-Inf 1.0000e-005]
Upper: [1x0 double]
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-008
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-006
TolX: 1.0000e-006в которой поля Method и Lower имеют заданные значения. Смысл остальных полей объяснен в разделе Управление вычислительным алгоритмом.
Теперь укажем созданную управляющую структуру opts в четвертом входном аргументе функции fit
>> fresult = fit(x,y,ftype, opts)
В командное окно выводится информация об объекте fresult с полученным приближением: вид нелинейной параметрической модели и найденные значения параметров a и b вместе с границами доверительных интервалов, соответствующих уровню вероятности в 95%:
fresult =
General model:
fresult(x) = a*log(x+b)
Coefficients (with 95% confidence bounds):
a = 5.309 (5.141, 5.478)
b = 0.1453 (0.1295, 0.1611)
Для визуализации результата осталось применить функцию plot:
>> plot(fresult,x,y)
.gif)
Приближение данных пользовательской параметрической моделью aln(x + b)
2.2. Параметрические и непараметрические модели
Параметрические и непараметрические модели
Для создания объекта с параметрической или непараметрической моделью применяется функция fittype, во входных аргументах которой указывается имя модели из библиотеки моделей, или линейная или нелинейная пользовательская параметрическая модель. Примеры приведены в разделах:
- Приближение без создания объекта с параметрической моделью
- Приближение с созданием объекта для параметрической модели
- Приближение с созданием объекта для пользовательской линейной параметрической модели.
- Приближение с созданием объекта для пользовательской нелинейной параметрической модели.
Кроме того, для модели можно задавать границы изменения параметров, начальные приближения, опции, управляющие вычислительным алгоритмом. В модели могут быть также постоянные параметры, значения которых указываются при подборе параметров во входных аргументах функции fit.
Далее мы приведем входящие в библиотеку Curve Fitting Toolbox параметрические и непараметрические модели и рассмотрим задание основных опций. Для вывода списка всех моделей библиотеки Curve Fitting Toolbox в командное окно есть удобная функция cflibhelp. Она выводит все параметрические и непараметрические модели, а в самом начале выводятся названия типов моделей. Для просмотра моделей одного типа достаточно указать имя типа как параметр cflibhelp, например
>> cflibhelp gaussianили
>> cflibhelp interpolant2.2.1. Параметрические модели библиотеки Curve Fitting Toolbox
Для создания объекта с параметрической моделью следует во входном аргументе функции fittype указать имя модели:
>> ftype = fittype('ИмяПараметрическойМодели')Далее в таблицах приведены имена параметрических моделей из библиотеки Curve Fitting Toolbox, сгруппированных по типам.
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
2.2.2. Непараметрические модели библиотеки Curve Fitting Toolbox
Для создания объекта с непараметрической моделью следует во входном аргументе функции fittype указать имя модели:
>> ftype = fittype('ИмяНепараметрическойМодели')
Далее в таблицах приведены имена параметрических моделей из библиотеки Curve Fitting Toolbox, сгруппированных по типам.
.gif)
Более подробно про интерполяцию сплайнами в приложении cftool, входящем в Curve Fitting Toolbox, написано в разд. Стандартные параметрические и непараметрические модели.
.gif)
Примеры приближения сглаживающими сплайнами приложении cftool, входящем в Curve Fitting Toolbox, приведены в разд. Стандартные параметрические и непараметрические модели.
Приведем пример приближения данных
>> x=(0:0.05:3)';
>> y=1.55*x+5*exp(-x)-2+0.05*randn(size(x));
сглаживающим сплайном без использования приложения cftool. Сначала создается объект с непараметрической моделью:
>> ftype = fittype('smoothingspline')
ftype =
Smoothing spline:
ftype(p,x) = piecewise polynomial computed from p
Далее необходимо при помощи функции fitoptions сформировать управляющую структуру opts, в которой будет выбран метод приближения (в данном случае 'Smooth', соответствующий сглаживанию сплайнами) и значение параметра сглаживающего сплайна, которое мы возьмем равным 0.9:
>> opts = fitoptions('Method','Smooth','SmoothingParam',0.9);
Осталось вызвать функцию fit для построения сплайна и plot для визуализации данных и построения графика получившегося сглаживающего сплайна:
>> fresult = fit(x,y,ftype,opts)
>> plot(fresult,x,y)
.gif)
Приближение данных сглаживающим сплайном
2.3. Исключение части данных
Перед поиском параметров линейной или нелинейной параметрической модели может понадобиться исключение части данных. Например, визуальный анализ данных может указать на наличие явных выбросов, или же просто требуется исключить данные, лежащие вне некоторого диапазона.
В Curve Fitting Toolbox для предварительной обработки данных имеется функция excludedata. Ее входными аргументами являются массивы данных xdata и ydata и один из способов исключения данных. Функция excludedata возвращает логический массив (состоящий из единиц и нулей), в котором нули соответствуют исключаемым данным, т.е. тем данным которые не будут участвовать в формировании целевой функции ошибки в процессе подбора параметров:
outliers = excludedata(xdata,ydata,'НазваниеСпособа', МассивОграничений)
Логический массив outliers затем указывается в качестве входного аргумента функции fit, выполняющей подбор параметров модели.
Данные могут быть исключены одним из четырех способов, приведенных в следующей таблице вместе с соответствующими им массивами ограничений.
|
Способы исключения данных |
|
|
'НазваниеСпособа' |
МассивОграничений |
|
box |
вектор [xmin, xmax, ymin, ymax] из четырех элементов, задающий границы независимой и зависимой переменных, вне которых данные не будут принимать участие в процессе подбора параметров |
|
domain |
вектор [xmin, xmax] из двух элементов, задающий границы независимой переменной, вне которых данные не будут принимать участие в процессе подбора параметров |
|
range |
вектор [ymin, ymax] из двух элементов, задающий границы зависимой переменной, вне которых данные не будут принимать участие в процессе подбора параметров |
|
indices |
вектор индексов тех данных, которые не будут принимать участие в процессе подбора параметров |
Приведем пример, в котором данные имеют несколько явных выбросов:
>> xdata=(0:0.01:2)';
>> ydata=0.6*sin(2.44*xdata)+0.8*exp(-xdata)+ 0.05*randn(size(xdata));
>> ydata(10)=2.3;
>> ydata(50)=2.4;
>> ydata(100)=2.2;
>> ydata(150)=-0.8;.gif)
Данные с выбросами
В этом примере имеет смысл применить способ range для исключения данных, лежащих выше 1.5 и ниже -0.5:
>> outliers = excludedata(xdata,ydata,'range', [-0.5 1.5]);
Теперь зададим собственную нелинейную параметрическую модель с тремя параметрами a, b и c:
(см. разд. Приближение с созданием объекта для пользовательской нелинейной параметрической модели.)
>> ftype=fittype('a*sin(b*x)+c*exp(-x)');
Зададим начальные значения параметров, которые будут являться стартовой точной в алгоритме нелинейной минимизации целевой функции ошибки (она нелинейна, т.к. нелинейна сама модель):
>> spoint=[0.5 2 1];
Найдем теперь параметры модели при помощи функции fit, указав в ее входных аргументах исходные данные, саму модель, начальные значения параметров и исключенные данные
>> fresult=fit(xdata,ydata,ftype,'startpoint',spoint,'exclude',outliers)
Информация об объекте с найденным приближением выводится в командное окно. Она содержит вид модели и полученные значения параметров вместе с границами доверительных интервалов, отвечающими уровню вероятности в 95%:
fresult =
General model:
fresult(x) = a*sin(b*x)+c*exp(-x)
Coefficients (with 95% confidence bounds):
a = 0.5829 (0.5708, 0.5951)
b = 2.454 (2.436, 2.472)
c = 0.8172 (0.7993, 0.8351)
Для визуализации результата удобно применить функцию plot (переопределенную в Curve Fitting Toolbox), во входных аргументах которой указывается не только построенное приближение и исходные данные, но и логический массив, содержащий информацию об исключенных данных:
>> plot(fresult,xdata,ydata,outliers)
На графике исключенным данным и тем, которые принимали участи в процессе подбора параметров, соответствуют разные маркеры.
.gif)
Данные, исключенные данные и приближение
Для исключения данных по более сложным критериям, требуется применять логическое индексирование (это базовое средство MATLAB). Кратко логическое индексирование объяснено в следующем разделе.
2.4. Логическое индексирование
Обычное индексирование в MATLAB заключается в обращении к элементам вектора по индексу или по массиву индексов. Например, если есть вектор
>> y=[1.1 2.2 3.3 4.4 5.5 6.6 7.7 8.8 9.9];то для обращения к его пятому элементу следует писать
>> a=y(5)
a =
5.5000Если в вектор b требуется занести его элементы с четвертого по седьмой, то применятся индексирование при помощи сечения:
>> b=y(5:7)
b =
5.5000 6.6000 7.7000Для доступа к элементам вектора y с четными индексами следует произвести индексацию при помощи вектора индексов:
>> ind=2:2:length(y)
ind =
2 4 6 8
>> d=y(ind)
d =
2.2000 4.4000 6.6000 8.8000Все эти способы относятся к обычной индексации.
Логическая индексация заключается в задании некоторого условия выбора элементов из массива.
Например, если требуется сформировать логический вектор той же длины, что и вектор y, в котором логическая единица соответствует элементам вектора y меньшим пяти, а логический ноль соответствует элементам вектора y большим или равным пяти, то следует записать логическое выражение для массива y с использованием операции сравнения (знака меньше <):
>> index = y<5
index =
1 1 1 1 0 0 0 0 0Если требуется определить элементы, превосходящие, например, в полтора раза среднее значение всех элементов y, то достаточно применить логическое индексирование и функцию mean:
>> index=y>1.5*mean(y)
index =
0 0 0 0 0 0 0 1 1Как обычно для операций сравнения применяются знаки == (два знака = для логического "равно"), >, >=, <, <= и ~= ("не равно").
Для задания более сложных условий требуется применять логические операции, которые приведены в следующей таблице в порядке убывания приоритета (для изменения порядка выполнения логических операции используются круглые скобки). Логические операции имеют также и функциональную форму записи, т.е., например, следующие логические выражения
A&B и and(A,B)
приведут к одинаковому результату.
| Логические операции | ||
| Операция | Обозначение | Функциональная запись |
| отрицание | ~A | not(A) |
| логическое И | A&B | and(A,B) |
| логическое ИЛИ | A | B | or(A,B) |
Здесь A и B - логические массивы, полученные, например, в результате применения операций сравнения к массивам, как в предыдущем примере. К соответствующим элементам массивов A и B поэлементно применяются обычные логические операции и результатом является логический массив.
Если мы хотим для приведенного выше массива y сформировать логический массив, в котором логические единицы отвечают элементам массива y, лежащим от трех до шести, то для этого подойдет следующее логическое выражение:
>> A = y>=3
A =
0 0 1 1 1 1 1 1 1
>> B = y<=6
B =
1 1 1 1 1 0 0 0 0
>> index = A&B
index =
0 0 1 1 1 0 0 0 0Можно, разумеется, было обойтись и без вспомогательных массивов A и B и записать одно выражение:
>> index = (y>=3) & (y<=6)
index =
0 0 1 1 1 0 0 0 0Операции сравнения имеют больший приоритет, чем логические операции, поэтому можно было обойтись и без скобок, т.е. записать
>> index = y>=3 & y<=6однако, выражение со скобками более наглядно.
Приведем еще один пример, в котором задан массив x (значения независимой переменная) и y (y(i) - значения зависимой переменной в x(i)) и требуется сформировать логический массив, в котором логические единицы соответствуют тем элементам массива y, которые лежат в полосе, ограниченной двумя линиями
y = 0.7x + 0.2 и y = 0.7x - 0.2
>> x=0:0.2:3;
>> y=2*sin(x);
>> index = (y<=0.7*x+0.2) & (y>=0.7*x-0.2)
index =
1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0В заключение этого раздела скажем, что полученные логические массивы могут применяться для индексации, т.е. указание логического массива index, сформированного в предыдущем примере, в качестве индекса вектора y приведет к получению вектора из тех элементов y, которые удовлетворяют заданному условию
>> y1=y(index)
y1 =
0 1.61702.5. Управление вычислительным алгоритмом
Перед началом процесса приближения возможно произвести ряд предварительных действий.
Во-первых можно указать:
-
различные веса для данных (см. раздел Опция для задания весов) и использовать таким образом взвешенный метод наименьших квадратов для подбора параметров;
-
часть исключаемых данных при подборе параметров (см. раздел Опция для исключения части данных);
-
нужно или нет масштабировать и центрировать исходные данные перед процессом подбора параметров модели для обеспечения более устойчивых результатов (см. раздел Опция для масштабирования и центрирования данных).
Во-вторых, при наличии ограничений сверху и снизу на искомые параметры линейной или нелинейной параметрической модели их также следует задать (см. раздел Опции для линейных параметрических моделей).
В-третьих, при наличии в данных выбросов имеет смысл воспользоваться адаптивным алгоритмом приближения, который на каждом шаге назначает веса данным так, чтобы уменьшить влияние выбросов на линейную или нелинейную параметрическую модель (см. раздел Опции для линейных параметрических моделей).
В-четвертых, поскольку подбор параметров нелинейных параметрических моделей приводит к задаче минимизации нелинейной функции, то пользователь может выбрать один из трех алгоритмов минимизации и указать его настройки, в том числе точность и критерии останова (см. раздел Опции для нелинейных параметрических моделей).
Далее приведены способы задания опций, управляющих вычислительным алгоритмом подбора параметров, и приведены необходимые примеры.
2.5.1. Способы задания опций вычислительного алгоритма
Для задания опций вычислительного алгоритма, реализующего подбор параметров модели, должен быть создан объект при помощи функции fitoptions, входящей в Curve Fitting Toolbox:
opts = fitoptions('method', 'НазваниеМетода', 'ИмяОпции1', значение1, ...)Далее этот объект opts с опциями указывается:
либо при подборе параметров параметрической модели в списке входных аргументов функции fit:
fresult = fit(xdata, ydata, 'libname', opts)либо при создании параметрической модели в списке входных аргументов функции fittype:
ftype = fittype('expr', 'options', opts)Второй способ задания опций вычислительного алгоритма, реализующего подбор параметров, состоит в указании их прямо перед процессом нахождения неизвестных параметров модели во входных аргументах функции fit:
fresult = fit(xdata, ydata, 'libname', 'ИмяОпции1', значение1, ...)При необходимости использования большого количества моделей для приближения различных наборов данных предпочтительно выделить три этапа при проведении процесса приближения:
-
создание объектов с параметрическими или непараметрическими моделями при помощи функции fittype (см. разд. Параметрические и непараметрические модели и примеры в нем);
-
создание объектов с опциями вычислительного алгоритма так, как описано в этом разделе;
-
подбор модели и параметров модели при помощи функции fit с указанием ей одного из объектов с моделью и одного из объектов с опциями вычислительного алгоритма так, как сделано в примерах этого раздела.
2.5.2. Зависимость набора опций от модели и способа приближения
Количество и вид опций вычислительного алгоритма определяется типом выбранной для приближения линейной или нелинейной параметрической или непараметрической модели и способом приближения. При приближении данных линейной параметрической моделью можно выбрать только:
-
обычный метод наименьших квадратов, или адаптивный алгоритм назначения весов с целью уменьшения влияния выбросов в данных на приближение;
-
нижние и верхние границы для искомых коэффициентов параметрической модели (включая и бесконечные границы).
Для нелинейных параметрических моделей этот набор расширяется. В нелинейном случе допускается выбор:
-
различных алгоритмов минимизации нелинейной целевой функции ошибки;
-
задание настроек этих алгоритмов, включая точность нахождения параметров и критерии останова итерационного процесса минимизации нелинейной целевой функции.
Вне зависимости от линейности или нелинейности выбранной модели при задании опций всегда имеется возможность указать:
-
веса;
-
часть исключаемых данных при подборе параметров;
-
нужно или нет масштабировать и центрировать исходные данные перед процессом подбора параметров.
2.5.2.1. Опция для задания весов
На практике часто встречаются задачи о приближении данных, в которых требуется построить модель, которая по возможности более точно приближает часть данных, а оставшиеся данные менее точно. Это достигается приписыванием весов данным, причем чем больше вес у части данных, тем более точно получается приближение для них. Во взвешенном методе наименьших квадратов минимизируется взвешенная сумма квадратов отклонений, выражающаяся по следующей формулой:
![]()
в которой (xk,yk)k=1,2,...,n являются исходными данными, а (wk)k=1,2,...,n есть заданные веса.
Предположим, что требуется выполнить полиномиальную регрессию следующих данных (в данные с 5-го по последний внесена ошибка):
>> xdata=(-1:0.2:1)';
>> ydata=0.2*xdata.^4+4.6*xdata.^3-xdata-2;
>> n=length(xdata);
>> ydata(5:n)=ydata(5:n)+2*(rand(n-4,1)-0.5);
приблизив их полиномом четвертой степени. Рассмотрим два способа приближения этих данных:
-
с одинаковыми весами (как это делается по умолчанию в функции fit, когда веса не заданы);
-
зададим веса равные 1 для данных с 1-го по 4-ое и веса равные 0.01 для оставшихся данных.
Для задания весов воспользуемся функцией fitoptions. Соответствующая опция называется Weights, ее значением должен быть вектор wts, содержащий веса. Размер этого вектора должен совпадать по размеру с векторами исходных данных:
>> wts=0.01*ones(size(xdata));
>> wts(1:4)=1;
>> opts=fitoptions('Weights',wts)
Примечание
Здесь для создания вектора с весами wts была использована функция ones. Она создает матрицу заданного размера, состоящую из единиц, т.е., например ones(5,1) или ones([5 1]) создает вектор-столбец из пяти единиц. Поскольку функция size возвращает размеры массива в векторе, то ее можно указывать во входном аргументе функции ones, что позволяет строить массивы из единиц, по размеру совпадающие с заданными.
Далее при помощи функции fittype создадим объект ftype, содержащий параметрическую модель - полином четвертой степени. Имя этой стандартной параметрической модели poly4 (стандартные параметрические и непараметрические модели, входящие в библиотеку моделей Curve Fitting Toolbox описаны в разд. Параметрические и непараметрические модели):
>> ftype = fittype('poly4')
Для приближения используем функцию fit, которую вызовем два раза:
-
без сформированного объекта opts с управляющими опциями, результат запишем в fresult;
-
с сформированным объектом opts с управляющими опциями, результат запишем в wfresult.
>> fresult = fit(xdata,ydata,ftype)
>> wfresult = fit(xdata,ydata,ftype,opts)
Далее для сравнения отобразим в одном графическом окне на разных осях, создаваемых при помощи функции subplot, графики двух моделей вместе с исходными данными. Графики построим при помощи переопределенной в Curve Fitting Toolbox функции plot.
Примечание.
Функция subplot создает в графическом окне заданное число осей (по горизонтали и вертикали). Например, при вызове subplot(3,4,5) предполагается, что графическое окно будет разбито на три пары осей по вертикали и четыре по горизонтали, а 5 значит, что будут созданы пятая по счету пара осей (нумерация осей в окне слева направо сверху вниз). Если эти оси уже есть, то они делаются текущими так, что весь следующий графический вывод будет происходить на них.
figure
subplot(1,2,1)
plot(fresult,xdata,ydata)
subplot(1,2,2)
plot(wfresult,xdata,ydata)
Ниже приведены результаты полученные результаты
.gif)
Приближение без весов (слева) и с весами (справа)
2.5.2.2. Опция для исключения части данных
При построении параметрических или непараметрических моделей для приближения данных может возникнуть необходимость исключить часть данных из процесса подбора параметров, например если в данных имеются выбросы. Для задания исключаемой части данных служит опция Exclude, ее значением должен быть логический массив (состоящий из единиц и нулей), в котором нули соответствуют исключаемым данным, т.е. тем данным которые не будут участвовать в формировании целевой функции ошибки в процессе подбора параметров (см. разделы Исключение части данных и Логическое индексирование).
Приведем пример формирования объекта opts для указания исключаемого множества данных и подбора параметров. Рассмотрим данные с очевидными выбросами
>> xdata=(0:0.05:2)';
>> ydata=1.2*exp(-2*xdata)+0.05*randn(size(xdata));
>> ydata(10)=1.8;
>> ydata(15)=1.6;
>> ydata(20)=1.5;
>> ydata(25)=2.2;
>> ydata(30)=-0.9;
>> ydata(40)=-0.8;
>> plot(xdata,ydata,'.').gif)
Данные с выбросами
Создадим логический массив для исключаемого множества, записав нули для тех данных, значения которых лежат вне диапазона [-0.5 1.4]:
>> outliers = excludedata(xdata,ydata,'range', [-0.5 1.4]);
Для приближения данных применим стандартную экспоненциальную параметрическую модель
aebxЕе имя exp1 (стандартные параметрические и непараметрические модели, входящие в библиотеку моделей Curve Fitting Toolbox описаны в разд. Параметрические и непараметрические модели):
>> ftype=fittype('exp1');
Далее при помощи функции fitoptions создадим объект, содержащий информацию об исключаемых из процесса подбора параметров данных:
>> opts=fitoptions('Exclude',outliers)
Приблизим данные экспоненциальной моделью, используя функцию fit, без исключения и получающееся приближение запишем в fresult:
>> fresult = fit(xdata,ydata,ftype)
fresult =
General model Exp1:
fresult(x) = a*exp(b*x)
Coefficients (with 95% confidence bounds):
a = 1.206 (0.6891, 1.722)
b = -1.329 (-2.203, -0.4558)Теперь приблизим данные экспоненциальной моделью с указанием opts с информацией об исключаемой части данных и получающееся приближение запишем в exfresult:
>> exfresult = fit(xdata,ydata,ftype,opts)
exfresult =
General model Exp1:
exfresult(x) = a*exp(b*x)
Coefficients (with 95% confidence bounds):
a = 1.222 (1.164, 1.28)
b = -2.072 (-2.229, -1.914)Заметим, что в случае приближения с исключенными выбросами значения параметров найдены вернее. Отобразим в одном графическом окне на разных осях, создаваемых при помощи функции subplot, графики двух моделей вместе с исходными данными. Графики построим при помощи переопределенной в Curve Fitting Toolbox функции plot, которая позволяет отметить исключаемые данные, если указать соответствующий им логический массив в качестве ее четвертого входного аргумента:
figure
subplot(1,2,1)
plot(fresult,xdata,ydata)
subplot(1,2,2)
plot(exfresult,xdata,ydata,outliers)В результате получаем
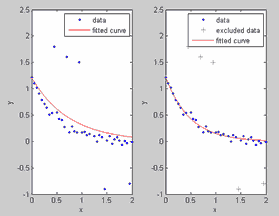
Приближение без исключения выбросов (слева) и с исключением (справа)
2.5.2.3. Опция для масштабирования и центрирования данных
При приближении данных по методу наименьших квадратов получающаяся система линейных уравнений может быть плохо обусловлена, что повлечет ошибки при ее решении, а следовательно, и нахождении параметров модели.
Масштабирование данных (xk,yk)k=1,2,...,n заключается замене xk на ![]() , вычисляемые для k=1,2,...,n по формуле
, вычисляемые для k=1,2,...,n по формуле
![]()
где μ - среднее значение
![]()
а σ соответственно - среднеквадратичное отклонение
![]()
Для автоматического масштабирования данных требуется при формировании функцией fitoptions объекта opts с опциями вычислительного алгоритма указать для опции Normalize значение 'on' (по умолчанию опция Normalize принимает значение 'off', т.е. масштабирование и центрирование не применяется).
Приведем пример. Предположим, что требуется найти приближение следующего набора данных:
>> xdata = [1951; 1952; 1953; 1954; 1955; 1956; 1957];
>> ydata = [1.2; 3.4; 2.9; 4.4; 4.5; 5.1; 4.2];
полиномом четвертой степени. Имя такой полиномиальной модели poly4 (стандартные параметрические и непараметрические модели, входящие в библиотеку моделей Curve Fitting Toolbox описаны в разд. Параметрические и непараметрические модели). Создадим соответствующий ей объект ftype при помощи функции fittype:
>> ftype=fittype('poly4');
Приблизим сначала данные при помощи функции fit без предварительного центрирования и масштабирования (как делается по умолчанию), найденное приближение запишем в объект fresult:
>> fresult=fit(xdata,ydata,ftype);
При этом в командное окно выводится сообщение о том, что соответствующая система линейных уравнений плохообусловлена:
Warning: Equation is badly conditioned. Remove repeated data points
or try centering and scaling.
Выведем найденные значения параметров модели (т.е. коэффициенты полинома четвертой степени) при помощи функции coeffvalues, входящей в Curve Fitting Toolbox. Ее входным аргументом является объект fresult с найденным приближением:
>> format short e
>> c=coeffvalues(fresult)
c =
-3.5997e-002 2.8134e+002 -8.2459e+005 1.0741e+009 -5.2470e+011Посмотрим теперь, как изменятся параметры модели, если в исходные данные внести небольшую ошибку. Добавим к y(1) число 0.01 и измененный вектор значений запишем в переменную ydataerr
>> ydataerr = [1.21; 3.4; 2.9; 4.4; 4.5; 5.1; 4.2];
Снова выполним приближение данных xdata, ydataerr при помощи полинома четвертой степени без предварительного центрирования и масштабирования и выведем получающиеся значения параметров:
>> fresult=fit(xdata,ydataerr,ftype)
>> cerr=coeffvalues(fresult)
cerr =
-3.5883e-002 2.8045e+002 -8.2198e+005 1.0707e+009 -5.2304e+011
Видим, что ошибка в исходных данных в 0.01 привела к ошибке порядка 1e9 в коэффициентах полинома.
Теперь проделаем то же самое с предварительным центрированием и масштабированием данных, сформировав при помощи функции fittype объект opts со включенной опцией центрирования и масштабирования:
>> opts=fitoptions('Normalize','on');
>> nmfresult = fit(xdata,ydata,ftype,opts);
>> c=coeffvalues(nmfresult)
>> nmfresult = fit(xdata,ydataerr,ftype,opts);
>> cerr=coeffvalues(nmfresult)
c =
-7.8367e-001 -8.4010e-002 8.9621e-001 1.2061e+000 3.9108e+000
cerr =
-7.8120e-001 -8.6810e-002 8.9391e-001 1.2080e+000 3.9110e+000Итак, предварительное центрирование и масштабирование данных позволило получить ошибку в параметрах того же порядка, что и ошибка в исходных данных.
2.5.2.4. Опции для интерполяционных сплайнов
Если в Curve Fitting Toolbox производится интерполяция:
-
кусочно-постоянными функциями по ближайшему соседу (опции method установлено значение NearestInterpolant);
-
кусочно-линейными функциями (опции method установлено значение LinearInterpolant);
-
кубическими сплайнами (опции method установлено значение CubicSplineInterpolant);
-
сплайнами, сохраняющими форму данных, т.е. кусочными полиномами Эрмита (опции method установлено значение PchipInterpolant);
то никаких дополнительных опций задавать нельзя и к функции fitoptions обращаются, соответственно, одним из четырех следующих способов:
opts=fitoptions('method', 'NearestInterpolant')
opts=fitoptions('method', 'LinearInterpolant')
opts=fitoptions('method', 'CubicSplineInterpolant')
opts=fitoptions('method', 'PchipInterpolant')
Такой вариант задания опций функцией fitoptions практически не используется, поскольку перечисленные способы интерполяции могут быть указаны сразу при создании объекта с моделью, например, для интерполяции кубическими полиномами Эрмита табличной функции:
>> xdata=(0:0.3:3)';
>> ydata=sin(xdata).^2.*exp(-xdata);
достаточно выполнить следующие команды:
>> ftype=fittype('pchipinterp');
>> fresult=fit(xdata,ydata,ftype)
>> plot(fresult,xdata,ydata)
.gif)
Интерполяция кубическими полиномами Эрмита
2.5.2.5. Опции для сглаживающего сплайна
Если требуется приблизить данные сглаживающим сплайном, то опции method должно быть установлено значение SmoothingSpline. Тогда появляется возможность задать значение параметра, входящего в сглаживающий сплайн. Для этого надо установить опции SmoothingParam необходимое значение от 0 до 1.
Например, приблизим данные
>> xdata=(0:0.05:3)';
>> ydata=xdata.*exp(-xdata)+0.01*randn(size(xdata));
сглаживающим сплайном со значением его параметра 0.9. Для этого сформируем объект opts, задав соответствующие опции во входных аргументах функции fitoptions:
>> opts = fitoptions('Method','SmoothingSpline','SmoothingParam',0.9)
Затем сформируем объект ftype с моделью при помощи функции fittype, указав название модели в ее входном аргументе (стандартные параметрические и непараметрические модели Curve Fitting Toolbox описаны в разделе Параметрические и непараметрические модели)
>> ftype = fittype('smoothingspline')
Вызовем функцию fit для получения приближения fresult и применим переопределенную в Curve Fitting Toolbox функцию plot для визуализации исходных данных и вывода графика полученного сглаживающего сплайна
>> fresult = fit(xdata,ydata,ftype,opts)
>> plot(fresult,xdata,ydata)
.gif)
Приближение данных сглаживающим сплайном
2.5.2.6. Опции для линейных параметрических моделей
Примечание.
Описанные в этом разделе опции задаются также и для нелинейных параметрических моделей.
В случае, когда параметрическая модель содержит только линейно входящие параметры, набор возможных опций, управляющих вычислительным алгоритмом, состоит из выбора устойчивого по отношению к выбросам в данных алгоритма нахождения параметров модели и указания верхних и нижних границ для искомых параметров линейной параметрической модели:
-
Robust - использование устойчивого процесса поиска параметров модели по отношению к выбросам в данных, возможные значения этой опции: 'on' (использовать устойчивый метод), 'off' (по умолчанию устойчивый метод не используется).
-
Lower - Вектор из значений нижних границ для искомых параметров линейной модели. Число элементов в нем должно совпадать с числом параметров модели, если некоторые параметры могут быть сколь угодно малы, то на соответствующей позиции в векторе ставится -Inf (в MATLAB так обозначается минус бесконечность). Если ограничения снизу на параметры модели отсутствуют, то значением является пустой массив, т.е [] (по умолчанию).
-
Upper - Вектор из значений верхних границ для искомых параметров линейной модели. Число элементов в нем должно совпадать с числом параметров модели, если некоторые параметры могут быть сколь угодно велики, то на соответствующей позиции в векторе ставится Inf (в MATLAB так обозначается плюс бесконечность). Если ограничения сверху на параметры модели отсутствуют, то значением является пустой массив, т.е [] (по умолчанию).
В векторах, являющихся значениями опций Lower и Upper, ограничения должны задаваться так, чтобы они соответствовали упорядоченным по алфавиту коэффициентам параметрической модели, т.е., если линейная пользовательская параметрическая модель имеет вид:
![]()
то, например вектор [0.1 2 -3 4.8], являющийся значением свойства Lower, соответствует следующим ограничениям снизу на параметры модели:
![]()
Наличие выбросов в данных может сильно ухудшить качество приближения параметрической моделью, поскольку при поиске параметров исходя из условия минимизации суммы квадратов ошибок
![]()
где (xk,yk)k=1,2,...,n - исходные данные, расстояние от искомой кривой до выброса окажет сильное влияние на значения параметров модели.
Одной из возможностей автоматического снижения влияния выбросов является назначение маленького веса соответствующим данным, или полное исключение выбросов из процесса подбора параметров (см. разделы Опция для задания весов и Опция для исключения части данных). Однако, такая ручная предварительная обработка не всегда может привести к желаемому результату, поскольку не всегда можно точно идентифицировать выброс, или подобрать нужный вес для снижения его влияния на приближение. Поэтому в Curve Fitting Toolbox предусмотрен адаптивный алгоритм построения приближения, в ходе которого данным автоматически присваиваются веса в зависимости от их удаления от полученной на данном шаге линии графика параметрической модели. Для задействования адаптивного алгоритма с целью снижения влияния выбросов в данных на приближение следует установить опции Robust значение 'on'.
В адаптивном алгоритме для снижения влияния выбросов на каждом шаге строится приближение по методу наименьших квадратов и вычисляются приведенные невязки ui (см. более подробно в справочной системе по Curve Fitting Toolbox раздел Fitting Data: Parametric Fitting: The Least Squares Fitting Method) и в зависимости от удаленности точек от приближающей их кривой данным назначаются веса по следующему правилу (чем дальше точка, тем меньше ее вес):
.gif)
Далее процесс приближения повторяется, пока не выполнится некоторое условие сходимости.
Поскольку в описанном выше алгоритме при вычислении весов используется четвертая степень, то он называется bisquare weights (биквадратные веса).
Приведем пример, в котором задание опции Robust значения 'on' улучшает качество приближения. Рассмотрим следующие исходные данные, полученные из закона
y = 3.8x + 2.1внесением распределенной по нормальному закону ошибки
>> xdata=(0:0.5:11)';
>> ydata=3.8*xdata+2.1+2*randn(size(xdata));
в которых есть два выброса (см. график ниже)
>> ydata(2)=35;
>> ydata(20)=5;
.gif)
Данные с выбросами
При помощи функции fittype построим линейную параметрическую модель - полином первой степени - для проведения линейной регрессии (создание пользовательских линейных моделей в Curve Fitting Toolbox описано в разделе Приближение с созданием объекта для пользовательской линейной параметрической модели).
>> ftype=fittype({'x','1'})
ftype =
Linear model:
ftype(a,b,x) = a*x + b
Приблизим сначала данные при помощи обычного метода наименьших квадратов, не указывая никаких опций (тогда обычный метод наименьших квадратов применяется по умолчанию):
>> fres=fit(xdata,ydata,ftype)
Получаем следующие значения параметров модели
res =
Linear model:
fres(x) = a*x + b
Coefficients (with 95% confidence bounds):
a = 2.638 (1.421, 3.854)
b = 8.297 (0.4845, 16.11)
Теперь создадим объект с нужными настройками вычислительного алгоритма:
-
опция Method должна принимать значение 'LinearLeastSquares';
-
опция Robust должна принимать значение 'on'.
>> opts=fitoptions('Method', 'LinearLeastSquares','Robust','on');Приблизим данные с выбросами при помощи адаптивного алгоритма для снижения влияния выбросов на получающееся приближение:
>> frobres=fit(xdata,ydata,ftype,opts)
frobres =
Linear model:
frobres(x) = a*x + b
Coefficients (with 95% confidence bounds):
a = 3.739 (3.199, 4.28)
b = 2.262 (-1.21, 5.734)
Полученные при помощи адаптивного алгоритма результаты соответствуют исходным данным, в отличие от тех, что были получены обычным методом наименьших квадратов, в котором по умолчанию всем данным приписаны равные единице веса. Визуальное сравнение двух приближений также позволяет в этом убедиться. Построим в одном графическом окне на разных осях (создаваемых при помощи функции subplot) приближения вместе с исходными данными
>> figure
>> subplot(1,2,1)
>> plot(fres,xdata,ydata)
>> subplot(1,2,2)
>> plot(frobres,xdata,ydata)
В результате получаем
.gif)
Приближение данных без адаптивного выбора весов (слева) и с адаптивным выбором весов (справа)
2.5.2.7. Опции для нелинейных параметрических моделей
Если параметрическая модель содержит нелинейно входящие параметры, то их поиск приводит к необходимости решения нелинейной задачи оптимизации, возможно с ограничениями на искомые параметры. Поэтому набор опций, управляющих вычислительным алгоритмом поиска параметров, в нелинейном случае больше, чем в случае линейных параметрических моделей.
Так же, как и в случае линейных параметрических моделей можно использовать (см. раздел Опции для линейных параметрических моделей):
-
опцию Robust для выбора адаптивного алгоритма нахождения параметров, устойчивого к выбросам в исходных данных
-
опции Lower и Upper для задания нижних и верхних границ параметров модели.
Задание этих опций в случае линейных и нелинейных параметрических моделей производится аналогично.
Для начала процесса поиска параметров в нелинейном случае (т.е. для начала алгоритма нелинейной оптимизации функции ошибки) требуется начальная точка. Для ее задания служит опция StartPoint. Ее значением должен быть вектор, длина которого совпадает с числом подлежащих определению параметров. Причем, в векторе, задающем начальные значения параметров, они должны задаваться так, чтобы соответствовать упорядоченным по алфавиту коэффициентам параметрической модели, т.е. например, если нелинейная пользовательская параметрическая модель имеет вид:
![]()
то, например вектор [0.1 2 -3 4.8], являющийся значением свойства StartPoint, соответствует следующим начальным значениям параметров модели:
![]()
Для линейной модели, определенной пользователем, начальное приближение не требуется и ограничения на параметры по умолчанию не задаются.
Для нелинейной модели, определенной пользователем, начальное приближение каждого параметра по умолчанию выбирается из отрезка [0, 1], а ограничения на параметры по умолчанию не задаются.
В следующей таблице приведены стандартные модели Curve Fitting Toolbox и выбираемые по умолчанию начальные значения параметров и ограничения.
|
Начальные значения параметров и ограничения для стандартных параметрических моделей |
|||
|
Названия моделей |
Вид моделей |
Начальное приближение |
Ограничения на параметры |
|
Экспоненциальные модели: exp1, exp2 |
|
Вычисляется по начальным данным по эвристическому алгоритму |
Нет |
|
Отрезки ряда Фурье: fourier1, fourier2, ..., fourier8 |
|
Вычисляется по начальным данным по эвристическому алгоритму |
Нет |
|
Гауссовы модели: gauss1, gauss2, ..., gauss8 |
|
Вычисляется по начальным данным по эвристическому алгоритму |
ck > 0 |
|
Полиномиальные модели: poly1, poly2, ..., poly9 |
|
Не требуется |
Нет |
|
Степенные модели: power1, power2 |
|
Вычисляется по начальным данным по эвристическому алгоритму |
Нет |
|
Дробно-рациональные модели: rat01, rat02, …, rat55 (первая цифра - степень числителя, вторая - степень знаменателя) Сумма синусов: sin1, sin2, … , sin8 |
|
Случайное для каждого параметра из интервала [0,1] |
Нет |
|
Сумма синусов: sin1, sin2, … , sin8 |
|
Вычисляется по начальным данным по эвристическому алгоритму |
bk > 0 |
|
Модель Вейбула: weibull |
|
Случайное для каждого параметра из интервала [0,1] |
a > 0 b > 0 |
Для минимизации целевой функции (среднеквадратичной ошибки приближения) возможно выбрать один из трех алгоритмов и указать соответствующее значение в качестве значения свойства Algorithm:
-
Trust-Region (метод доверительных областей) - используемый по умолчанию алгоритм минимизации целевой функции. Если на искомые коэффициенты параметрической модели наложены ограничения, то использование этого алгоритма обязательно.
-
Levenberg-Marquardt (метод Левенберга- Марквардта) - можно использовать в задачах без ограничений на коэффициенты.
-
Gauss-Newton - классический метод Ньютона.
Данные алгоритмы минимизации реализованы в функциях Optimization Toolbox, которые и используются при минимизации целевой функции при подборе параметров в параметрических моделях, приближающих данные, в Curve Fitting Toolbox.
Для настроек алгоритмов минимизации служат следующие опции:
-
TolFun - точность по функции (для завершения итерационного алгоритма нелинейной минимизации), по умолчанию 10e-6, при достижении этой точности алгоритм минимизации останавливается.
-
TolX - точность по искомым параметрам (для завершения итерационного алгоритма нелинейной минимизации), по умолчанию 10e-6, при достижении этой точности алгоритм минимизации останавливается.
-
DiffMinChange - минимальный шаг по каждой из искомых переменных (параметров модели) для вычисления приближенного вычисления частных производных (используемых в алгоритмах нелинейной минимизации) при помощи конечных разностей, по умолчанию 10e-8.
-
DiffMaxChange - максимальный шаг по каждой из искомых переменных (параметров модели) для вычисления приближенного вычисления частных производных (используемых в алгоритмах нелинейной минимизации) при помощи конечных разностей, по умолчанию 0.1.
-
MaxFunEvals - максимальное количество вычислений минимизируемой функции (для предотвращения зацикливания), по умолчанию минимизируемая функция вычисляется не более 600 раз, после чего алгоритм минимизации останавливается.
-
MaxIter - максимальное число итераций алгоритма минимизации (для предотвращения зацикливания), по умолчанию делается не более 400 итераций, после чего алгоритм минимизации останавливается.
2.5.3. Пример подбора параметров нелинейной модели
Возьмем в качестве исходных данные, полученные возмущением данных, которым соответствует нелинейная модель
y = 3ln(x - 0.9) - 7x
>> xdata=(1:0.02:3)';
>> ydata=3*log(xdata-0.9) - 7*xdata + 0.1*randn(size(xdata));
>> plot(xdata,ydata,'.')
.gif)
Исходные данные для приближения нелинейной моделью
При помощи функции fittype построим для них нелинейную модель
>> ftype=fittype('a*log(x-b)+c*x')
Если теперь попытаться сразу применить функцию fit для подбора параметров в нашей модели
>> fres=fit(xdata,ydata,ftype)
то получим сообщение об ошибке
??? Complex value computed by model function, fitting cannot continue.
Try using or tightening upper and lower bounds on coefficients.
поскольку в процессе подбора под логарифмом оказалось неположительное значение.
Выход состоит в указании верхней границы для второго параметра , скажем 0.9 (см. раздел Опции для линейных параметрических моделей). Для этого создадим вектор с верхними границами параметров, положив для и верхние границы равные бесконечности (Inf)
>> up=[Inf 0.9 Inf]
и укажем этот вектор при задании настроек функцией fitoptions:
>> opts=fitoptions('Method', 'NonlinearLeastSquares', 'Upper', up);
Теперь подбор параметров выполняется успешно:
>> fres=fit(xdata,ydata,ftype,opts)
В командное окно выводятся значения коэффициентов вместе с границами доверительных интервалов, отвечающих вероятности 95%
General model:
fres(x) = a*log(x-b)+c*x
Coefficients (with 95% confidence bounds):
a = 2.92 (2.824, 3.016)
b = 0.9064 (0.8946, 0.9183)
c = -6.982 (-7.007, -6.956)
Для визуализации данных и построенного приближения осталось применить переопределенную в Curve Fitting Toolbox функцию plot
>> figure
>> plot(fres,xdata,ydata).gif)
Приближение данных нелинейной параметрической моделью
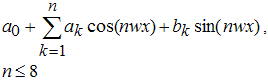
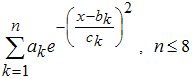
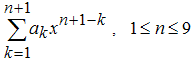
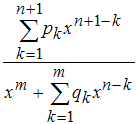
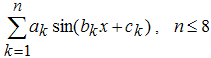
.gif)
.gif)
.gif)
.gif)
Комментарии
Полезный материал!
Можно ли поиметь его в виде книжки, брошюры?
Цельным файлом?